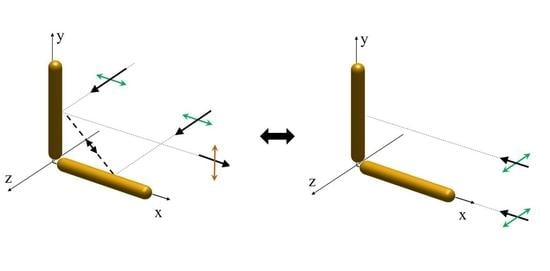
Asymmetric Scattering and Reciprocity in a Plasmonic Dimer
Abstract
1. Introduction
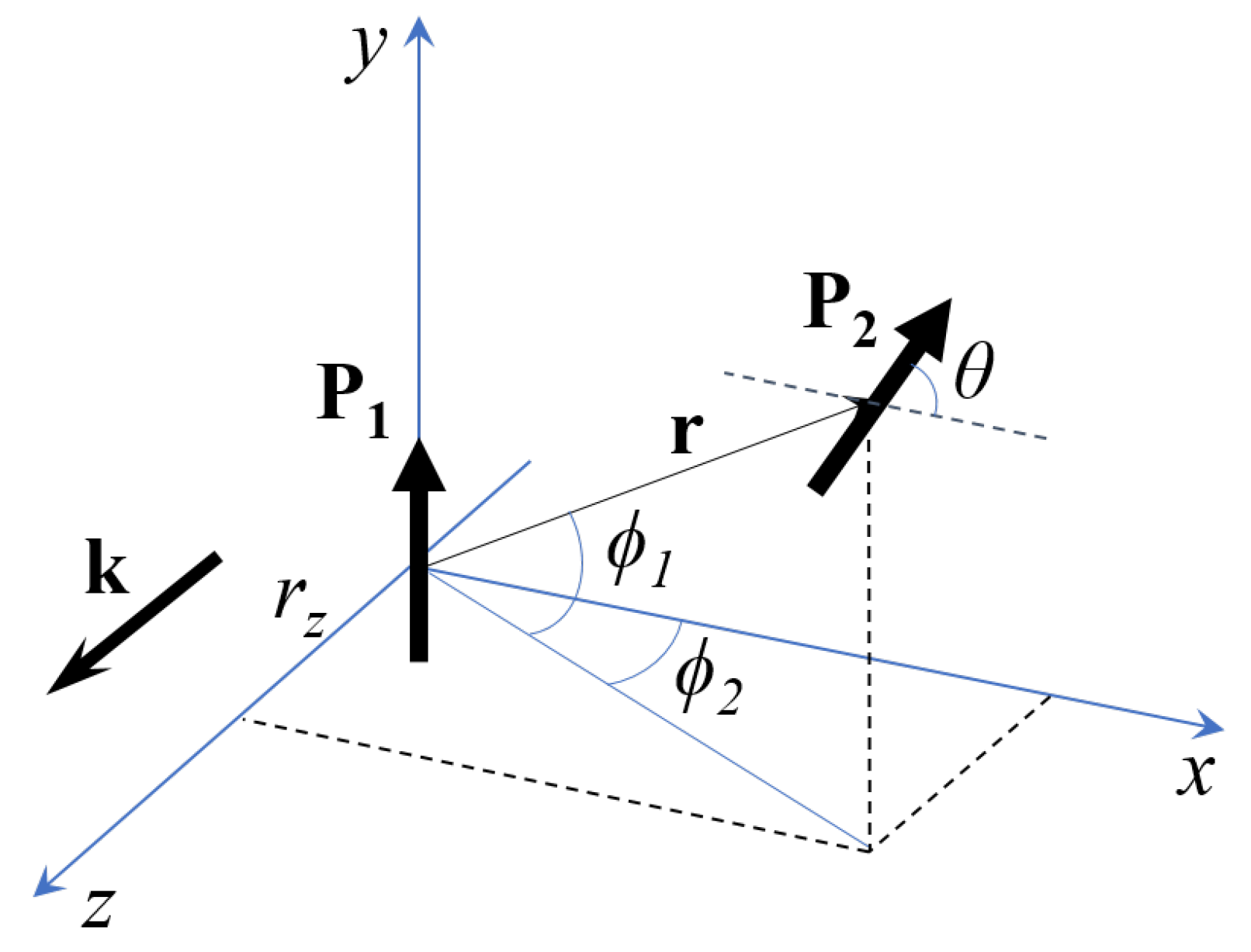
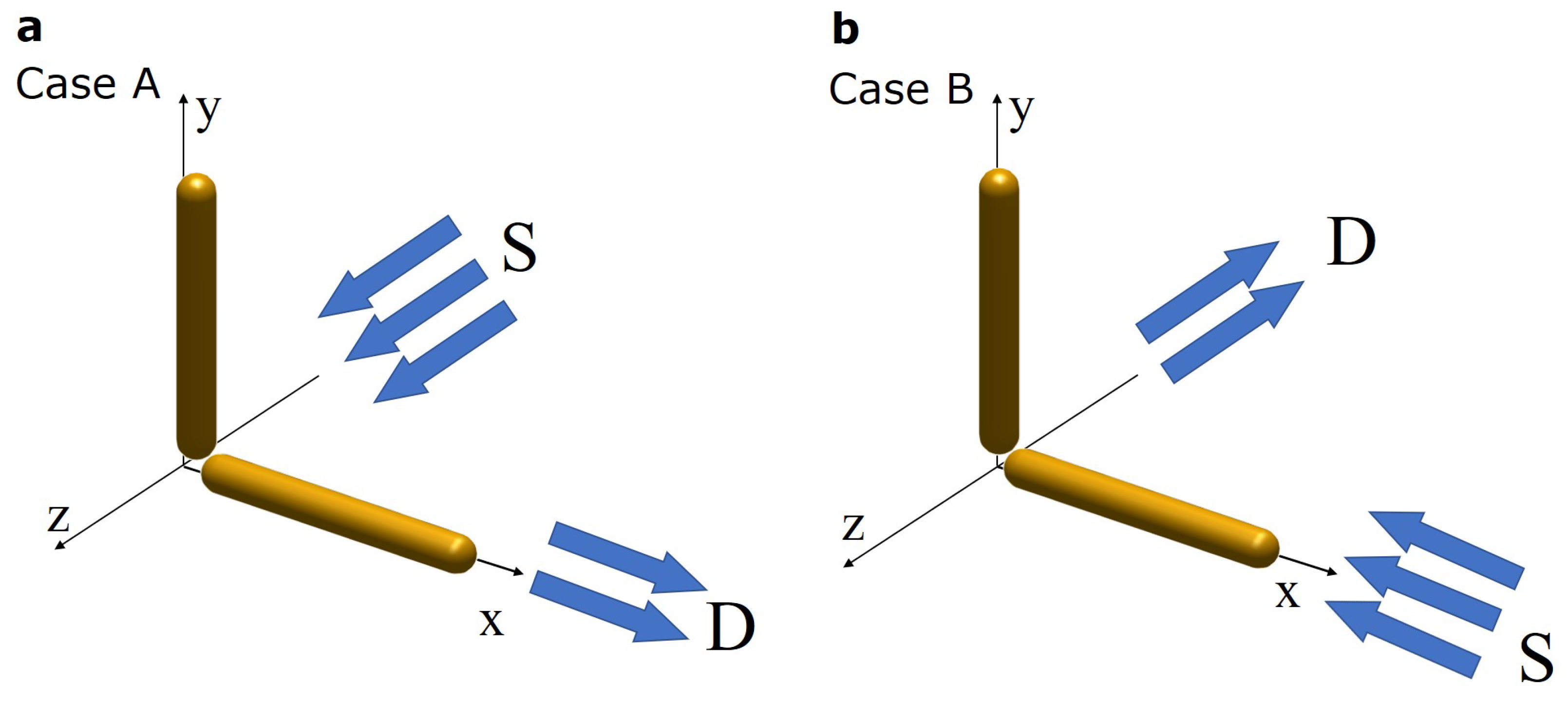
2. Scattering in the Plasmonic Dimer
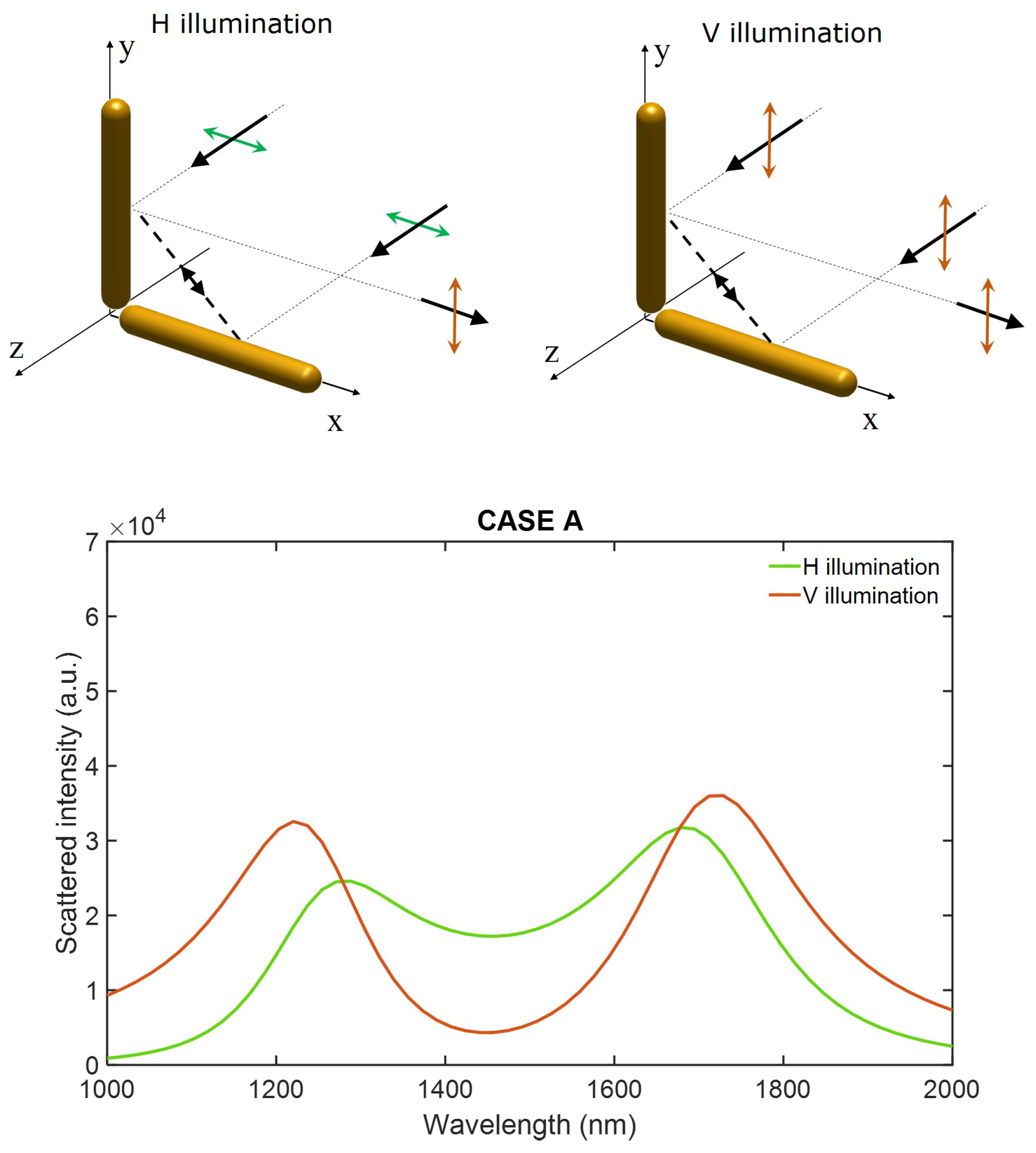
2.1. Simulations
2.2. Calculations
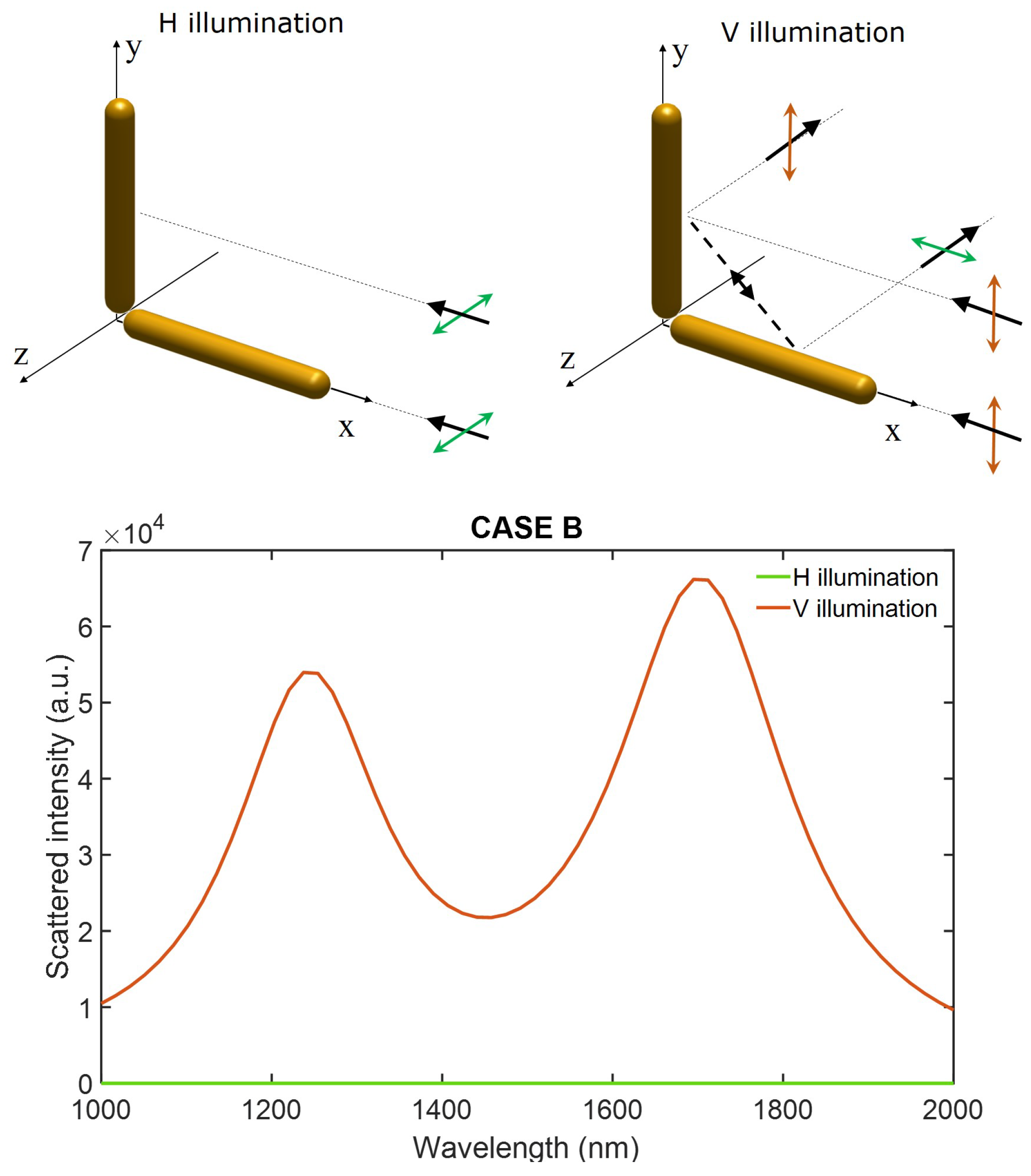
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Potton, R.J. Reciprocity in optics. Rep. Prog. Phys. 2004, 67, 717. [Google Scholar] [CrossRef]
- Mansuripur, M. Reciprocity in classical linear optics. Opt. Photonics News 1998, 9, 53–58. [Google Scholar] [CrossRef]
- Perrin, F. Polarization of Light Scattered by Isotropic Opalescent Media. J. Chem. Phys. 1942, 10, 415–427. [Google Scholar] [CrossRef]
- Hulst, H. Light Scattering by Small Particles; Structure of Matter Series; Wiley: New York, NY, USA, 1957. [Google Scholar]
- Barron, L.D. Molecular Light Scattering and Optical Activity; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Goodarzi, M.; Pakizeh, T. Directional optical absorption and scattering in conical plasmonic nanostructures. Opt. Lett. 2019, 44, 2212–2215. [Google Scholar] [CrossRef] [PubMed]
- Arteaga, O.; Maoz, B.M.; Nichols, S.; Markovich, G.; Kahr, B. Complete polarimetry on the asymmetric transmission through subwavelength hole arrays. Opt. Express 2014, 22, 13719–13732. [Google Scholar] [CrossRef] [PubMed]
- Najafabadi, A.F.; Pakizeh, T. Analytical chiroptics of 2D and 3D nanoantennas. ACS Photonics 2017, 4, 1447–1452. [Google Scholar] [CrossRef]
- Wu, J.; Lu, X.; Zhu, Q.; Zhao, J.; Shen, Q.; Zhan, L.; Ni, W. Angle-resolved plasmonic properties of single gold nanorod dimers. Nano-Micro Lett. 2014, 6, 372–380. [Google Scholar] [CrossRef] [PubMed]
- Black, L.J.; Wang, Y.; De Groot, C.; Arbouet, A.; Muskens, O.L. Optimal polarization conversion in coupled dimer plasmonic nanoantennas for metasurfaces. ACS Nano 2014, 8, 6390–6399. [Google Scholar] [CrossRef] [PubMed]
- Wiecha, P.R.; Black, L.J.; Wang, Y.; Paillard, V.; Girard, C.; Muskens, O.L.; Arbouet, A. Polarization conversion in plasmonic nanoantennas for metasurfaces using structural asymmetry and mode hybridization. Sci. Rep. 2017, 7, 40906. [Google Scholar] [CrossRef] [PubMed]
- Panaro, S.; Ciracì, C. Nonlocal Plasmonic Response and Fano Resonances at Visible Frequencies in Sub-Nanometer Gap Coupling Regime. ACS Photonics 2016, 3, 2467–2474. [Google Scholar] [CrossRef]
- Kuntman, M.A.; Kuntman, E.; Sancho-Parramon, J.; Arteaga, O. Light scattering by coupled oriented dipoles: Decomposition of the scattering matrix. Phys. Rev. B 2018, 98. [Google Scholar] [CrossRef]
- Bidault, S.; Mivelle, M.; Bonod, N. Dielectric nanoantennas to manipulate solid-state light emission. J. Appl. Phys. 2019, 126, 094104. [Google Scholar] [CrossRef]
- Hohenester, U.; Trügler, A. MNPBEM—A Matlab toolbox for the simulation of plasmonic nanoparticles. Comput. Phys. Commun. 2011. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Etchegoin, P.G.; Le Ru, E.; Meyer, M. An analytic model for the optical properties of gold. J. Chem. Phys. 2006, 125, 164705. [Google Scholar] [CrossRef]
- Albella, P.; Poyli, M.A.; Schmidt, M.K.; Maier, S.A.; Moreno, F.; Sáenz, J.J.; Aizpurua, J. Low-loss electric and magnetic field-enhanced spectroscopy with subwavelength silicon dimers. J. Phys. Chem. C 2013, 117, 13573–13584. [Google Scholar] [CrossRef]
- Kuntman, E. Mathematical Work on the Foundation of Jones-Mueller Formalism and Its Application to Nano Optics. Ph.D. Thesis, Universitat de Barcelona, Barcelona, Spain, 2019. [Google Scholar]
- Kuntman, E.; Kuntman, M.A.; Sancho-Parramon, J.; Arteaga, O. Formalism of optical coherence and polarization based on material media states. Phys. Rev. A 2017, 95, 063819. [Google Scholar] [CrossRef]
- Li, J.; Liu, C.; Wu, T.; Liu, Y.; Wang, Y.; Yu, Z.; Ye, H.; Yu, L. Efficient polarization beam splitter based on all-dielectric metasurface in visible region. Nanoscale Res. Lett. 2019, 14, 34. [Google Scholar] [CrossRef] [PubMed]
- Jalas, D.; Petrov, A.; Eich, M.; Freude, W.; Fan, S.; Yu, Z.; Baets, R.; Popović, M.; Melloni, A.; Joannopoulos, J.D.; et al. What is—And what is not—An optical isolator. Nat. Photonics 2013, 7, 579–582. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuntman, M.A.; Kuntman, E.; Arteaga, O. Asymmetric Scattering and Reciprocity in a Plasmonic Dimer. Symmetry 2020, 12, 1790. https://doi.org/10.3390/sym12111790
Kuntman MA, Kuntman E, Arteaga O. Asymmetric Scattering and Reciprocity in a Plasmonic Dimer. Symmetry. 2020; 12(11):1790. https://doi.org/10.3390/sym12111790
Chicago/Turabian StyleKuntman, Mehmet Ali, Ertan Kuntman, and Oriol Arteaga. 2020. "Asymmetric Scattering and Reciprocity in a Plasmonic Dimer" Symmetry 12, no. 11: 1790. https://doi.org/10.3390/sym12111790
APA StyleKuntman, M. A., Kuntman, E., & Arteaga, O. (2020). Asymmetric Scattering and Reciprocity in a Plasmonic Dimer. Symmetry, 12(11), 1790. https://doi.org/10.3390/sym12111790