Analytical Solution of Nonlinear Fractional Volterra Population Growth Model Using the Modified Residual Power Series Method

Abstract

In this paper, we introduce an analytical approximate solution of nonlinear fractional Volterra population growth model based on the Caputo fractional derivative and the Riemann fractional integral of the symmetry order. The residual power series method and Adomain decomposition method are implemented to find an approximate solution of this problem. The convergence analysis of the proposed technique has been proved. A numerical example is given to illustrate the method.

1. Introduction

In recent years, fractional calculus appears frequently in the context of mathematical modeling in various branches of science and engineering such as robotics [1], control theory [2], signal processing [3], economics [4], viscoelasticity [5]. For more details and applications about fractional calculus, we refer the reader to [6,7,8,9]. In most cases, the exact solutions for fractional nonlinear problems, if exist, are not easy to find [10,11,12,13]. In order to describe the behavior of the unknowns of those systems, many researchers usually perform some numerical or approximate analytical methods instead. In this regard, some recent techniques are proposed for solving fractional functional equations. Among them are sorts of integral transform methods which are well combined with the homotopy analysis methods [14,15,16,17,18,19]. The Adomian decomposition method (ADM) [20] and the variational iteration method [21,22] are also mentioned in many contexts. The residual power series method (RPSM) is one of those techniques which quite suits nonlinear fractional differential equations [23,24,25,26,27,28,29,30]. Generalized from the classical power series method, the solution is written on the form of fractional power series. However, the formula of all coefficients can be derived by enormous algebraic manipulations. The main merit of the RPSM is that the series solution, in particular a truncated series solution can be easily obtained.

The study of population growth model is one of the specific fields of science which is gaining attention due to the limitation of resources on our planet. The Volterra model for population growth [31] in a closed system is represented by the nonlinear Volterra integro-differential equation

$$\begin{array}{ccc}\hfill \kappa \frac{du}{dt}& =& u-u^2-u{\int }_0^{t}u\left(\tau \right)d\tau ,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill u\left(0\right)& =& a_0,a_0>0,\hfill \end{array}$$

(2)

where $u\equiv u\left(t\right)$ is the scaled population of identical individuals at a time t and $a_0$ is an initial population. The nondimensional parameter $\kappa =\frac{c}{ab}$ is introduced to explain overall increasing or decreasing rate of the population, where $a>0,b>0$ and $c>0$ denote the birth rate coefficient, the crowding coefficient and the toxicity coefficient, respectively [32].

In this study, we consider the following nonlinear fractional Volterra population growth model of the form:

$$\kappa D_t^{\alpha }u\left(t\right)=u\left(t\right)-u^2\left(t\right)-u\left(t\right)I^{\alpha }u\left(t\right),\alpha \in (0,1],$$

(3)

subject to

$$u\left(0\right)=a_0,a_0>0.$$

(4)

The derivative in the fractional Volterra population growth model (3) is in the Caputo sense and $I^{\alpha }$ is the Riemann–Liouville fractional integral operator of order $\alpha$. In order to keep the symmetry aspect, we set the order of the derivative and the integral to be equal. Due to the nonlinear term in Equation (3), solving this problem by RPSM is most likely cumbersome. In various method mentioned above the well-known Adomian polynomials take their part to handle this difficulty. Actually, the Adomian polynomials was introduced by George Adomian in 1988 [33] as a sequence of series of Maclaurin type embedded in the ADM for nonlinear problems. The ADM has become a powerful technique for analytic approximate solutions to initial value problems. Furthermore, according to [34,35,36] the Adomian polynomials and the ADM itself can be combined well with other methods.

Motivated by the existing methods, the main objective of this paper is to study the nonlinear fractional Volterra population growth model using the residual power series method and the Adomian decomposition method. This method is called modified residual power series method (MRPSM). The remaining sections of this paper are organized as follows. In Section 2, we present some preliminaries of fractional calculus and the fractional power series. Applications of the MRPSM to the nonlinear fractional Volterra population growth model are presented in Section 3. In Section 4, the convergence analysis is investigated. In Section 5, the graphical result is also reported for different values of fractional parameter. Finally, in Section 6 some conclusions are drawn.

2. Preliminaries

In this section, we give some preliminaries of fractional calculus and fractional power series [37,38], which are further used in this paper.

Definition 1.

Let $u\left(t\right)\in C^n(0,\infty )$. The Caputo fractional derivative of order $\alpha >0$ is defined as

$D_t^{\alpha }u\left(t\right)=\left\{\begin{array}{cc}{\displaystyle {\displaystyle \frac{1}{\mathrm{\Gamma }(n-\alpha )}}{\int }_0^t{(t-\tau )}^{n-\alpha -1}{u}^{\left(n\right)}\left(\tau \right)d\tau ,}\hfill & n-1<\alpha <n,\hfill \\ u^{\left(n\right)}\left(t\right),\hfill & \alpha =n\in \mathbb{N},\hfill \end{array}\right.$where n is the smallest integer greater than or equal to α and $\mathrm{\Gamma }(·)$ is the well-known Gamma function.

Theorem 1.

The Caputo fractional derivative of the power function is as follows

$D_t^{\alpha }{t}^p=\left\{\begin{array}{cc}{\displaystyle \frac{\mathrm{\Gamma }(p+1)}{\mathrm{\Gamma }(p-\alpha +1)}}{t}^{p-\alpha },\hfill & n-1<\alpha <n,p>n-1,p\in \mathbb{R},\hfill \\ 0,\hfill & n-1<\alpha <n,p\le n-1,p\in \mathbb{N}.\hfill \end{array}\right.$

Definition 2.

The Riemann–Liouville fractional integral operator $I^{\alpha }$ of order $\alpha >0$ is normally defined by

$$I^{\alpha }u\left(t\right)=\left\{\begin{array}{c}{\displaystyle {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\alpha \right)}}{\int }_0^t\frac{u\left(\tau \right)}{{(t-\tau )}^{1-\alpha }}d\tau ,\alpha >0,}\hfill \\ u\left(t\right), \alpha =0.\hfill \end{array}\right.$$

where $u\left(t\right)$ is a function defined on $(0,t]$.

Theorem 2.

The Riemann–Liouville fractional integral operator of power function is given by

$$\begin{array}{c}\hfill I^{\alpha }{t}^p={\displaystyle \frac{\mathrm{\Gamma }(p+1)}{\mathrm{\Gamma }(p+\alpha +1)}}{t}^{p+\alpha }.\end{array}$$

The following definition and theorem related to the RPSM [38].

Definition 3.

The fractional power series (FPS) about $t=t_0$ is given by

$$\sum _{m=0}^{\infty }{c}_m{(t-t_0)}^{m\alpha }=c_0+c_1{(t-t_0)}^{\alpha }+c_2{(t-t_0)}^{2\alpha }+\cdots ,$$

where $0\le n-1<\alpha$ and $t\ge t_0$.

Theorem 3.

Suppose that f has a fractional power series represent at $t=t_0$ of the form

$$f\left(t\right)=\sum _{m=0}^{\infty }{c}_m{(t-t_0)}^{m\alpha },$$

where $0\le n-1<\alpha ,t_0\le t<t_0+R$ and R is the radius of convergence.

If $D^{m\alpha }f\left(t\right)$, $m=0,1,2,\dots$ are continuous on $(t_0,t_0+R)$, then $c_m=\frac{D^{m\alpha }f\left(t_0\right)}{\mathrm{\Gamma }(1+m\alpha )}$.

3. Modified Residual Power Series Method (MRPSM) for Nonlinear Fractional Volterra Population Growth Model

Consider the fractional nonlinear Volterra population growth model

$$\kappa D_t^{\alpha }u\left(t\right)=u\left(t\right)-u^2\left(t\right)-u\left(t\right)I^{\alpha }u\left(t\right),\alpha \in (0,1],$$

(5)

subject to

$$u\left(0\right)=a_0,a_0>0,$$

(6)

where $\kappa >0$ is a prescribed non-dimensional parameter and $u\left(t\right)$ is the scaled population of identical individuals at time t. The derivative in the fractional Volterra population growth model (5) is in the Caputo sense and $I^{\alpha }$ is the Riemann–Liouville fractional integral operator of order $\alpha .$

According to the RPSM, let $u\left(t\right)$ be the solution of fractional Volterra population growth model of the form:

$$u\left(t\right)=\sum _{n=0}^{\infty }\frac{a_n{t}^{n\alpha }}{\mathrm{\Gamma }(1+n\alpha )}.$$

(7)

Using the initial condition (6), we approximate $u\left(t\right)$ in Equation (7) by

$$u_k\left(t\right)=a_0+\sum _{n=1}^k\frac{a_n{t}^{n\alpha }}{\mathrm{\Gamma }(1+n\alpha )},k=1,2,3,\dots .$$

(8)

To find the residual power series (RPS) coefficient $a_n$, we solve the equation

$$D_t^{(n-1)\alpha }Re{s}_n\left(0\right)=0,n=1,2,3,\dots ,$$

(9)

where $Re{s}_k\left(t\right)$ is the kth residual function and is defined by

$$Re{s}_k\left(t\right)=\kappa D_t^{\alpha }{u}_k\left(t\right)-u_k\left(t\right)+u_k^2\left(t\right)+u_k\left(t\right)I^{\alpha }{u}_k\left(t\right).$$

(10)

Since the fractional Volterra population growth model (5) has a nonlinear term $F\left(u\right)=u^2\left(t\right)$, the Adomian polynomials play their role in dealing with it.

Let

$$u_k\left(t\right)=\sum _{i=0}^k{v}_i,$$

(11)

where $v_0=a_0$ and

$$v_i={\displaystyle \frac{a_i{t}^{i\alpha }}{\mathrm{\Gamma }(1+i\alpha )}},i=1,2,3,\dots ,k.$$

(12)

Let

$$F\left(u_k\left(t\right)\right)=\sum _{n=0}^k{A}_n,$$

(13)

be a nonlinear operator where $A_n$ are called Adomian polynomials and can be determined from the formula

$$A_n=\frac{1}{n!}{\left[\frac{d^n}{d{\lambda }^n}[F\left(\sum _{i=0}^n{\lambda }^i{v}_i\right)]\right]}_{\lambda =0}.$$

(14)

From Equation (11), we can rewritten the nonlinear polynomials $u_k^2\left(t\right)$ as

$$F\left(u_k\left(t\right)\right)={(v_0+v_1+v_2+v_3+\cdots +v_k)}^2=\sum _{n=0}^k{A}_n.$$

Using the Algorithm presented in [39], the Adomian polynomials for $F\left(u_k\left(t\right)\right)=u_k^2\left(t\right)$ are given by

$$\begin{array}{ccc}\hfill A_0& =& v_0^2\hfill \\ \hfill A_1& =& 2v_0{v}_1\hfill \\ \hfill A_2& =& 2v_0{v}_2+v_1^2\hfill \\ \hfill A_3& =& 2v_0{v}_3+2v_1{v}_2\hfill \\ \hfill A_4& =& v_2^2+2v_1{v}_3+2v_0{v}_4\hfill \\ \hfill A_5& =& 2v_2{v}_3+2v_0{v}_5+2v_1{v}_4\hfill \\ \hfill A_6& =& 2v_0{v}_6+2v_1{v}_5+2v_2{v}_4+v_3^2\hfill \\ \hfill A_7& =& 2v_0{v}_7+2v_2{v}_5+2v_3{v}_4+2v_1{v}_6\hfill \\ \hfill A_8& =& 2v_2{v}_6+2v_3{v}_5+v_4^2+2v_0{v}_8+2v_1{v}_7.\hfill \end{array}$$

Other polynomials can be calculated by Equation (14).

To find $a_1$, we substitute the first RPS approximate solution

$$u_1\left(t\right)=a_0+a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}$$

into Equation (10) as follows

$$\begin{array}{c}\hfill \begin{array}{ccc}Re{s}_1\left(t\right)& \hfill =& \kappa D_t^{\alpha }{u}_1\left(t\right)-u_1\left(t\right)+u_1^2\left(t\right)+u_1\left(t\right)I^{\alpha }\left(u_1\left(t\right)\right)\hfill \\ & \hfill =& \kappa D_t^{\alpha }\left(a_0+a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}\right)-\left(a_0+a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}\right)\hfill \\ & & +{\left(a_0+a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}\right)}^2+\left(a_0+a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}\right)I^{\alpha }(a_0+a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )})\hfill \\ & \hfill =& \kappa a_1-\left(a_0+a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}\right)+{\left(a_0+a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}\right)}^2\hfill \\ & & +\left(a_0+a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}\right)\left(a_0\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}+a_1\frac{t^{2\alpha }}{\mathrm{\Gamma }(1+2\alpha )}\right).\hfill \end{array}\end{array}$$

Then, we solve $Re{s}_1\left(0\right)=0$ to get

$$a_1=\frac{1}{\kappa }\left[a_0-a_0^2\right].$$

(15)

To find $a_2$, the second RPS approximate solution is in form

$$u_2\left(t\right)=a_0+a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}+a_2\frac{t^{2\alpha }}{\mathrm{\Gamma }(1+2\alpha )}.$$

(16)

Using Adomian polynomials for $F\left(u_2\left(t\right)\right)=u_2^2\left(t\right)$ and $v_0=a_0$, we have

$$\begin{array}{c}\hfill \begin{array}{ccc}{u}_2^2\left(t\right)\hfill & =\hfill & a_0^2+2a_0{a}_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}+2a_0{a}_2\frac{t^{2\alpha }}{\mathrm{\Gamma }(1+2\alpha )}+{\left(a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}\right)}^2\hfill \\ & & +2a_1{a}_2\frac{t^{3\alpha }}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+2\alpha )}+{\left(a_2\frac{t^{2\alpha }}{\mathrm{\Gamma }(1+2\alpha )}\right)}^2.\hfill \end{array}\end{array}$$

(17)

On substituting Equations (16) and (17) in Equation (10), we have

$$\begin{array}{c}\hfill \begin{array}{ccc}Re{s}_2\left(t\right)& \hfill =& \kappa D_t^{\alpha }{u}_2\left(t\right)-u_2\left(t\right)+u_2^2\left(t\right)+u_2\left(t\right)I^{\alpha }\left(u_2\left(t\right)\right)\hfill \\ & \hfill =& \kappa \left(a_1+a_2\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}\right)-\left(a_0+a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}+a_2\frac{t^{2\alpha }}{\mathrm{\Gamma }(1+2\alpha )}\right)\hfill \\ & & +\left[a_0^2+2a_0{a}_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}+2a_0{a}_2\frac{t^{2\alpha }}{\mathrm{\Gamma }(1+2\alpha )}+{\left(a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}\right)}^2\right.\hfill \\ & & \left.+2a_1{a}_2\frac{t^{3\alpha }}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+2\alpha )}+{\left(a_2\frac{t^{2\alpha }}{\mathrm{\Gamma }(1+2\alpha )}\right)}^2\right]\hfill \\ & & +\left[\left(\frac{a_0^2}{\mathrm{\Gamma }(1+\alpha )}\right)t^{\alpha }+\left(\frac{a_0{a}_1}{{\mathrm{\Gamma }}^2(1+\alpha )}+\frac{a_0{a}_1}{\mathrm{\Gamma }(1+2\alpha )}\right)t^{2\alpha }\right.\hfill \\ & & +\left(\frac{a_0{a}_2}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+2\alpha )}+\frac{a_1^2}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+2\alpha )}+\frac{a_0{a}_2}{\mathrm{\Gamma }(1+3\alpha )}\right)t^{3\alpha }\hfill \\ & & +\left.\left(\frac{a_1{a}_2}{{\mathrm{\Gamma }}^2(1+2\alpha )}+\frac{a_1{a}_2}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+3\alpha )}\right)t^{4\alpha }+\left(\frac{a_2^2}{\mathrm{\Gamma }(1+2\alpha )\mathrm{\Gamma }(1+3\alpha )}\right)t^{5\alpha }\right].\hfill \end{array}\end{array}$$

(18)

On applying the derivative $D_t^{\alpha }$ on Equation (18), we obtain

$$\begin{array}{c}\hfill \begin{array}{ccc}{D}_t^{\alpha }Re{s}_2\left(t\right)& \hfill =& \kappa a_2-\left(a_1+a_2\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}\right)\hfill \\ & & +\left[2a_0{a}_1+2a_0{a}_2\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}+a_1^2\frac{\mathrm{\Gamma }(1+2\alpha )t^{\alpha }}{{\mathrm{\Gamma }}^3(1+\alpha )}\right.\hfill \\ & & \left.+2a_1{a}_2\frac{\mathrm{\Gamma }(1+3\alpha )t^{2\alpha }}{\mathrm{\Gamma }(1+\alpha ){\mathrm{\Gamma }}^2(1+2\alpha )}+a_2^2\frac{\mathrm{\Gamma }(1+4\alpha )t^{3\alpha }}{{\mathrm{\Gamma }}^2(1+2\alpha )\mathrm{\Gamma }(1+3\alpha )}\right]\hfill \\ & & +\left[a_0^2+\left(\frac{a_0{a}_1}{{\mathrm{\Gamma }}^2(1+\alpha )}+\frac{a_0{a}_1}{\mathrm{\Gamma }(1+2\alpha )}\right)\frac{\mathrm{\Gamma }(1+2\alpha )t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}\right.\hfill \\ & & +\left(\frac{a_0{a}_2}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+2\alpha )}+\frac{a_1^2}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+2\alpha )}+\frac{a_0{a}_2}{\mathrm{\Gamma }(1+3\alpha )}\right)\frac{\mathrm{\Gamma }(1+3\alpha )t^{2\alpha }}{\mathrm{\Gamma }(1+2\alpha )}\hfill \\ & & +\left.\left(\frac{a_1{a}_2}{{\mathrm{\Gamma }}^2(1+2\alpha )}+\frac{a_1{a}_2}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+3\alpha )}\right)\frac{\mathrm{\Gamma }(1+4\alpha )t^{3\alpha }}{\mathrm{\Gamma }(1+3\alpha )}+\left(\frac{a_2^2}{\mathrm{\Gamma }(1+2\alpha )\mathrm{\Gamma }(1+3\alpha )}\right)\frac{\mathrm{\Gamma }(1+5\alpha )t^{4\alpha }}{\mathrm{\Gamma }(1+4\alpha )}\right].\hfill \end{array}\end{array}$$

Then, we solve $D_t^{\alpha }Re{s}_2\left(0\right)=0$ to get

$$a_2=\frac{1}{\kappa }\left[a_1-2a_0{a}_1-a_0^2\right].$$

(19)

To find $a_3$, the third RPS approximate solution is in form

$$u_3\left(t\right)=a_0+a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}+a_2\frac{t^{2\alpha }}{\mathrm{\Gamma }(1+2\alpha )}+a_3\frac{t^{3\alpha }}{\mathrm{\Gamma }(1+3\alpha )}.$$

(20)

Using Adomian polynomials and $F\left(u_3\left(t\right)\right)=u_3^2\left(t\right)$, we have

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill u_3^2& \hfill =& a_0^2+2a_0{a}_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}+2a_0{a}_2\frac{t^{2\alpha }}{\mathrm{\Gamma }(1+2\alpha )}+{\left(a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}\right)}^2\hfill \\ & & +2a_0{a}_3\frac{t^{3\alpha }}{\mathrm{\Gamma }(1+3\alpha )}+2a_1{a}_2\frac{t^{3\alpha }}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+2\alpha )}+{\left(a_2\frac{t^{2\alpha }}{\mathrm{\Gamma }(1+2\alpha )}\right)}^2\hfill \\ & & +2a_1{a}_3\frac{t^{4\alpha }}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+3\alpha )}+2a_2{a}_3\frac{t^{5\alpha }}{\mathrm{\Gamma }(1+2\alpha )\mathrm{\Gamma }(1+3\alpha )}+{\left(a_3\frac{t^{3\alpha }}{\mathrm{\Gamma }(1+3\alpha )}\right)}^2.\hfill \end{array}\end{array}$$

(21)

On substituting Equations (20) and (21) in Equation (10), we obtain

$$\begin{array}{c}\hfill \begin{array}{ccc}Re{s}_3\left(t\right)& \hfill =& \kappa D_t^{\alpha }{u}_3\left(t\right)-u_3\left(t\right)+u_3^2\left(t\right)+u_3\left(t\right)I^{\alpha }\left(u_3\left(t\right)\right)\hfill \\ & \hfill =& \kappa \left(a_1+a_2\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}+a_3\frac{t^{2\alpha }}{\mathrm{\Gamma }(1+2\alpha )}\right)\hfill \\ & & -\left(a_0+a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}+a_2\frac{t^{2\alpha }}{\mathrm{\Gamma }(1+2\alpha )}+a_3\frac{t^{3\alpha }}{\mathrm{\Gamma }(1+3\alpha )}\right)\hfill \\ & & +\left[a_0^2+2a_0{a}_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}+2a_0{a}_2\frac{t^{2\alpha }}{\mathrm{\Gamma }(1+2\alpha )}+{\left(a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}\right)}^2\right.\hfill \\ & & +2a_0{a}_3\frac{t^{3\alpha }}{\mathrm{\Gamma }(1+3\alpha )}+2a_1{a}_2\frac{t^{3\alpha }}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+2\alpha )}+{\left(a_2\frac{t^{2\alpha }}{\mathrm{\Gamma }(1+2\alpha )}\right)}^2\hfill \\ & & \left.+2a_1{a}_3\frac{t^{4\alpha }}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+3\alpha )}+2a_2{a}_3\frac{t^{5\alpha }}{\mathrm{\Gamma }(1+2\alpha )\mathrm{\Gamma }(1+3\alpha )}+{\left(a_3\frac{t^{3\alpha }}{\mathrm{\Gamma }(1+3\alpha )}\right)}^2\right]\hfill \\ & & +\left[\left(\frac{a_0^2}{\mathrm{\Gamma }(1+\alpha )}\right)t^{\alpha }+\left(\frac{a_0{a}_1}{{\mathrm{\Gamma }}^2(1+\alpha )}+\frac{a_0{a}_1}{\mathrm{\Gamma }(1+2\alpha )}\right)t^{2\alpha }\right.\hfill \\ & & +\left(\frac{a_0{a}_2}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+2\alpha )}+\frac{a_1^2}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+2\alpha )}+\frac{a_0{a}_2}{\mathrm{\Gamma }(1+3\alpha )}\right)t^{3\alpha }\hfill \\ & & +\left(\frac{a_0{a}_3}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+3\alpha )}+\frac{a_1{a}_2}{{\mathrm{\Gamma }}^2(1+2\alpha )}+\frac{a_1{a}_2}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+3\alpha )}+\frac{a_0{a}_3}{\mathrm{\Gamma }(1+4\alpha )}\right)t^{4\alpha }\hfill \\ & & +\left(\frac{a_1{a}_3}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+4\alpha )}+\frac{a_2^2}{\mathrm{\Gamma }(1+2\alpha )\mathrm{\Gamma }(1+3\alpha )}+\frac{a_1{a}_3}{\mathrm{\Gamma }(1+2\alpha )\mathrm{\Gamma }(1+3\alpha )}\right)t^{5\alpha }\hfill \\ & & +\left.\left(\frac{a_2{a}_3}{\mathrm{\Gamma }(1+2\alpha )\mathrm{\Gamma }(1+4\alpha )}+\frac{a_2{a}_3}{{\mathrm{\Gamma }}^2(1+3\alpha )}\right)t^{6\alpha }+\left(\frac{a_3^2}{\mathrm{\Gamma }(1+3\alpha )\mathrm{\Gamma }(1+4\alpha )}\right)t^{7\alpha }\right].\hfill \end{array}\end{array}$$

(22)

Then, we solve $D_t^{2\alpha }Re{s}_3\left(0\right)=0$ to get

$$a_3={\displaystyle \frac{1}{\kappa }}\left[u_2-\left(2a_0{a}_2+a_1^2\frac{\mathrm{\Gamma }(1+2\alpha )}{{\mathrm{\Gamma }}^2(1+\alpha )}\right)-\left(\frac{a_0{a}_1\mathrm{\Gamma }(1+2\alpha )}{{\mathrm{\Gamma }}^2(1+\alpha )}+a_0{a}_1\right)\right].$$

(23)

The same procedure is performed to obtain $u_4\left(t\right)$ as

$$u_4\left(t\right)=a_0+a_1\frac{t^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}+a_2\frac{t^{2\alpha }}{\mathrm{\Gamma }(1+2\alpha )}+a_3\frac{t^{3\alpha }}{\mathrm{\Gamma }(1+3\alpha )}+a_4\frac{t^{4\alpha }}{\mathrm{\Gamma }(1+4\alpha )},$$

(24)

where the coefficient $a_4$ can be calculated by

$$\begin{array}{c}\hfill \begin{array}{ccc}{a}_4& \hfill =& {\displaystyle \frac{1}{\kappa }}\left[a_3-\left(2a_0{a}_3+2a_1{a}_2\frac{\mathrm{\Gamma }(1+3\alpha )}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+2\alpha )}\right)\right.\hfill \\ & & -\left.\left(a_0{a}_2+\frac{a_1^2\mathrm{\Gamma }(1+3\alpha )}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+2\alpha )}+\frac{a_0{a}_2\mathrm{\Gamma }(1+3\alpha )}{\mathrm{\Gamma }(1+\alpha )\mathrm{\Gamma }(1+2\alpha )}\right)\right].\hfill \end{array}\end{array}$$

(25)

In general, for a positive integer k, the coefficient $a_k$ for the approximate solution $u_k\left(t\right)$ in Equation (8) is supposed to be

$$\begin{array}{c}\hfill \begin{array}{ccc}{a}_k& \hfill =& {\displaystyle \frac{1}{\kappa }}\left[a_{k-1}-\left({\displaystyle \sum _{i=0}^{k-1}{\displaystyle \frac{a_i{a}_{k-1-i}\mathrm{\Gamma }(1+(k-1)\alpha )}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k-1-i\left)\alpha \right)}}}\right)\right.\hfill \\ & & -\left.\left({\displaystyle \sum _{i=0}^{k-2}{\displaystyle \frac{a_i{a}_{k-2-i}\mathrm{\Gamma }(1+(k-1)\alpha )}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k-1-i\left)\alpha \right)}}}\right)\right].\hfill \end{array}\end{array}$$

(26)

We give the proof in the following theorem.

Theorem 4.

The nonlinear fractional Volterra population growth model (5) subject to the initial condition (6) has the approximate solution in the form

$$u_k\left(t\right)=a_0+\sum _{n=1}^k\frac{a_n{t}^{n\alpha }}{\mathrm{\Gamma }(1+n\alpha )},$$

where

$$\begin{array}{c}\hfill \begin{array}{ccc}{a}_k& \hfill =& {\displaystyle \frac{1}{\kappa }}\left[a_{k-1}-\left({\displaystyle \sum _{i=0}^{k-1}{\displaystyle \frac{a_i{a}_{k-1-i}\mathrm{\Gamma }(1+(k-1)\alpha )}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k-1-i\left)\alpha \right)}}}\right)\right.\hfill \\ & & -\left.\left({\displaystyle \sum _{i=0}^{k-2}{\displaystyle \frac{a_i{a}_{k-2-i}\mathrm{\Gamma }(1+(k-1)\alpha )}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k-1-i\left)\alpha \right)}}}\right)\right],\hfill \end{array}\end{array}$$

for $k=1,2,3,\dots .$

Proof. 

Let

$${\displaystyle u_k\left(t\right)=a_0+\sum _{n=1}^k\frac{a_n{t}^{n\alpha }}{\mathrm{\Gamma }(1+n\alpha )}}$$

be the approximate solution of Equation (5) subject to the initial condition (6). Then the kth residual function is expressed as

$$\begin{array}{c}\hfill \begin{array}{ccc}Re{s}_k\left(t\right)& \hfill =& \kappa D_t^{\alpha }{u}_k\left(t\right)-u_k\left(t\right)+u_k^2\left(t\right)+u_k\left(t\right)I^{\alpha }\left(u_k\left(t\right)\right)\hfill \\ & \hfill =& \kappa D_t^{\alpha }\left({\displaystyle \sum _{n=0}^k\frac{a_n{t}^{n\alpha }}{\mathrm{\Gamma }(1+n\alpha )}}\right)-\left({\displaystyle \sum _{n=0}^k\frac{a_n{t}^{n\alpha }}{\mathrm{\Gamma }(1+n\alpha )}}\right)\hfill \\ & & \left[{\displaystyle \sum _{n=0}^k\left({\displaystyle \sum _{i=0}^k\frac{a_i{a}_{n-i}}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(n-i\left)\alpha \right)}}\right)t^{n\alpha }}\right.\hfill \\ & & +\left.{\displaystyle \sum _{n=1}^k\left({\displaystyle \sum _{i=n}^k\frac{a_i{a}_{k+n-i}}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k+n-i\left)\alpha \right)}}\right)t^{(k+n)\alpha }}\right]\hfill \\ & & +\left({\displaystyle \sum _{n=0}^k\frac{a_n{t}^{n\alpha }}{\mathrm{\Gamma }(1+n\alpha )}}\right)I^{\alpha }\left({\displaystyle \sum _{n=0}^k\frac{a_n{t}^{n\alpha }}{\mathrm{\Gamma }(1+n\alpha )}}\right).\hfill \end{array}\end{array}$$

So,

$$\begin{array}{ccc}Re{s}_k\left(t\right)& \hfill =& {\displaystyle \kappa \sum _{n=1}^k\frac{a_n{t}^{(n-1)\alpha }}{\mathrm{\Gamma }(1+(n-1)\alpha )}-\left({\displaystyle \sum _{n=0}^k\frac{a_n{t}^{n\alpha }}{\mathrm{\Gamma }(1+n\alpha )}}\right)}\hfill \\ & & \left[{\displaystyle \sum _{n=0}^k\left({\displaystyle \sum _{i=0}^k\frac{a_i{a}_{n-i}}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(n-i\left)\alpha \right)}}\right)t^{n\alpha }}\right.\hfill \\ & & +\left.{\displaystyle \sum _{n=1}^k\left({\displaystyle \sum _{i=n}^k\frac{a_i{a}_{k+n-i}}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k+n-i\left)\alpha \right)}}\right)t^{(k+n)\alpha }}\right]\hfill \\ & & +\left[{\displaystyle \sum _{n=0}^k\left({\displaystyle \sum _{i=0}^k\frac{a_i{a}_{n-i}}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(n+1-i\left)\alpha \right)}}\right)t^{(n+1)\alpha }}\right.\hfill \\ & & +\left.{\displaystyle \sum _{n=1}^k\left({\displaystyle \sum _{i=n}^k\frac{a_i{a}_{k+n-i}}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k+n+1-i\left)\alpha \right)}}\right)t^{(k+n+1)\alpha }}\right].\hfill \end{array}$$

(27)

Now, operating $D_t^{(k-1)\alpha }$ on both sides of Equation (27) yields

$$\begin{array}{ccc}{D}_t^{(k-1)\alpha }Re{s}_k\left(t\right)& \hfill =& \kappa a_k-\left(a_{k-1}+{\displaystyle \frac{a_k{t}^{\alpha }}{\mathrm{\Gamma }(1+\alpha )}}\right)\hfill \\ & & +\left[{\displaystyle \sum _{i=0}^{k-1}{\displaystyle \frac{a_i{a}_{k-1-i}\mathrm{\Gamma }(1+(k-1)\alpha )}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k-1-i\left)\alpha \right)}}}\right.\hfill \\ & & {\displaystyle +\sum _{i=0}^k{\displaystyle \frac{a_i{a}_{k-i}\mathrm{\Gamma }(1+k\alpha )}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k-i\left)\alpha \right)\mathrm{\Gamma }(1+\alpha )}}{t}^{\alpha }}\hfill \\ & & +\left.{\displaystyle \sum _{n=1}^k\left({\displaystyle \sum _{i=n}^k\frac{a_i{a}_{k+n-i}\mathrm{\Gamma }(1+(k+n\left)\alpha \right)}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k+n-i\left)\alpha \right)\mathrm{\Gamma }(1+(n+1\left)\alpha \right)}}\right)t^{(n+1)\alpha }}\right]\hfill \\ & & +\left[{\displaystyle \sum _{i=0}^{k-2}{\displaystyle \frac{a_i{a}_{k-2-i}\mathrm{\Gamma }(1+(k-1)\alpha )}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k-1-i\left)\alpha \right)}}}\right.\hfill \\ & & {\displaystyle +\sum _{i=0}^{k-1}{\displaystyle \frac{a_i{a}_{k-1-i}\mathrm{\Gamma }(1+k\alpha )}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k-i\left)\alpha \right)\mathrm{\Gamma }(1+\alpha )}}{t}^{\alpha }}\hfill \\ & & +{\displaystyle \sum _{i=0}^k{\displaystyle \frac{a_i{a}_{k-i}\mathrm{\Gamma }(1+(k+1)\alpha )}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k+1-i\left)\alpha \right)\mathrm{\Gamma }(1+2\alpha )}}{t}^{2\alpha }}\hfill \\ & & +\left.{\displaystyle \sum _{n=1}^k\left({\displaystyle \sum _{i=n}^k\frac{a_i{a}_{k+n-i}\mathrm{\Gamma }(1+(k+n+1\left)\alpha \right)}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k+n+1-i\left)\alpha \right)\mathrm{\Gamma }(1+(n+2)\alpha )}}\right)t^{(n+2)\alpha }}\right].\hfill \end{array}$$

Then, we solve $D_t^{(k-1)\alpha }Re{s}_k\left(0\right)=0$ to obtain

$$\begin{array}{c}\hfill \begin{array}{ccc}{a}_k& \hfill =& {\displaystyle \frac{1}{\kappa }}\left[a_{k-1}-\left({\displaystyle \sum _{i=0}^{k-1}{\displaystyle \frac{a_i{a}_{k-1-i}\mathrm{\Gamma }(1+(k-1)\alpha )}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k-1-i\left)\alpha \right)}}}\right)\right.\hfill \\ & & -\left.\left({\displaystyle \sum _{i=0}^{k-2}{\displaystyle \frac{a_i{a}_{k-2-i}\mathrm{\Gamma }(1+(k-1)\alpha )}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k-1-i\left)\alpha \right)}}}\right)\right].\hfill \end{array}\end{array}$$

□

4. Convergence Analysis

Now, we prove the convergence of the MRPSM. We start by Lemma 1 which is a connection between the classical power series (CPS) and the fractional power series.

Lemma 1.

The classical power series ${\sum }_{n=0}^{\infty }{u}_n{t}^n$, $-\infty <t<\infty$, has a radius of convergence R if and only if the fractional power series ${\sum }_{n=0}^{\infty }{a}_n{t}^{n\alpha }$, $t\ge 0$, has a radius of convergence $R^{\frac{1}{\alpha }}$.

Proof. 

See [38]. □

The next theorem indicates that the series solution of nonlinear fractional Volterra population growth model converges in a neighborhood of $t=0$.

Theorem 5.

The fractional power series solution of the nonlinear fractional Volterra population growth model (5) subject to the initial condition (6)

$${\displaystyle u\left(t\right)=\sum _{n=0}^{\infty }\frac{a_n{t}^{n\alpha }}{\mathrm{\Gamma }(1+n\alpha )},}$$

where $a_n$ are the coefficients in Equation (26), has a positive radius of convergence.

Proof. 

From Equation (26), we can see that

$$\begin{array}{ccc}{\displaystyle \frac{\left|a_k\right|}{\mathrm{\Gamma }(1+k\alpha )}}& \hfill \le & \left|{\displaystyle \frac{1}{\kappa }}\right|{\displaystyle \frac{\left|a_{k-1}\right|}{\mathrm{\Gamma }(1+k\alpha )}}+\left|{\displaystyle \frac{1}{\kappa }}\right|{\displaystyle \frac{\left|{\displaystyle \sum _{i=0}^{k-1}{\displaystyle \frac{a_i{a}_{k-1-i}\mathrm{\Gamma }(1+(k-1)\alpha )}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k-1-i\left)\alpha \right)}}}\right|}{\mathrm{\Gamma }(1+k\alpha )}}\hfill \\ & & +\left|{\displaystyle \frac{1}{\kappa }}\right|{\displaystyle \frac{\left|{\displaystyle \sum _{i=0}^{k-2}{\displaystyle \frac{a_i{a}_{k-2-i}\mathrm{\Gamma }(1+(k-1)\alpha )}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k-1-i\left)\alpha \right)}}}\right|}{\mathrm{\Gamma }(1+k\alpha )}}\hfill \\ & \le & \left|{\displaystyle \frac{1}{\kappa }}\right|{\displaystyle \frac{\left|a_{k-1}\right|}{\mathrm{\Gamma }(1+k\alpha )}}\hfill \\ & & {\displaystyle +\left|{\displaystyle \frac{1}{\kappa }}\right|\underset{0\le i\le k-1}{max}\left\{{\displaystyle \frac{\mathrm{\Gamma }(1+(k-1\left)\alpha \right)}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k-1-i\left)\alpha \right)\mathrm{\Gamma }(1+k\alpha )}}\right\}\sum _{i=0}^{k-1}\left|a_i\right|\left|a_{k-1-i}\right|}\hfill \\ & & {\displaystyle +\left|{\displaystyle \frac{1}{\kappa }}\right|\underset{0\le i\le k-2}{max}\left\{{\displaystyle \frac{\mathrm{\Gamma }(1+(k-1\left)\alpha \right)}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k-1-i\left)\alpha \right)\mathrm{\Gamma }(1+k\alpha )}}\right\}\sum _{i=0}^{k-2}\left|a_i\right|\left|a_{k-2-i}\right|}\hfill \\ & =\hfill & A\left|a_{k-1}\right|+B{\displaystyle \sum _{i=0}^{k-1}}\left|a_i\right|\left|a_{k-1-i}\right|+C{\displaystyle \sum _{i=0}^{k-2}}\left|a_i\right|\left|a_{k-2-i}\right|,\hfill \end{array}$$

where $A=\left|{\displaystyle \frac{1}{\kappa }}\right|\mathrm{\Gamma }(1+k\alpha ),B={\displaystyle \underset{0\le i\le k-1}{max}}\left\{{\displaystyle \frac{\mathrm{\Gamma }(1+(k-1\left)\alpha \right)}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k-1-i\left)\alpha \right)\mathrm{\Gamma }(1+k\alpha )}}\right\}\left|{\displaystyle \frac{1}{\kappa }}\right|$

$C={\displaystyle \underset{0\le i\le k-2}{max}}\left\{{\displaystyle \frac{\mathrm{\Gamma }(1+(k-1\left)\alpha \right)}{\mathrm{\Gamma }(1+i\alpha )\mathrm{\Gamma }(1+(k-1-i\left)\alpha \right)\mathrm{\Gamma }(1+k\alpha )}}\right\}\left|{\displaystyle \frac{1}{\kappa }}\right|.$

Let

$$f\left(t\right)=\sum _{k=0}^{\infty }{b}_k{t}^k$$

(28)

where $b_0=\left|a_0\right|,b_1=\frac{\left|a_1\right|}{\mathrm{\Gamma }(1+\alpha )}$ and

$${\displaystyle b_k=A{b}_{k-1}+B\sum _{i=0}^{k-1}{b}_i{b}_{k-1-i}+C\sum _{i=0}^{k-2}{b}_i{b}_{k-2-i},k=2,3,4,\dots }$$

(29)

be the classical power series. Thus,

$$\begin{array}{c}\hfill \begin{array}{ccc}\omega =f\left(t\right)& \hfill =& {\displaystyle b_0+b_{1}t+\sum _{k=2}^{\infty }{b}_k{t}^k}\hfill \\ & \hfill =& {\displaystyle b_0+b_{1}t+A\sum _{k=2}^{\infty }{b}_{k-1}{t}^k+B\sum _{k=2}^{\infty }\left(\sum _{i=0}^{k-1}{b}_i{b}_{k-1-i}\right)t^k+C\sum _{k=2}^{\infty }\left({\displaystyle \sum _{i=0}^{k-2}{b}_i{b}_{k-2-i}}\right)t^k}\hfill \\ & \hfill =& {\displaystyle b_0+b_{1}t+At\sum _{k=1}^{\infty }{b}_k{t}^k+Bt\sum _{k=1}^{\infty }\left(\sum _{i=0}^k{b}_i{b}_{k-i}\right)t^k+C{t}^2\sum _{k=0}^{\infty }\left({\displaystyle \sum _{i=0}^k{b}_i{b}_{k-i}}\right)t^k.}\hfill \end{array}\end{array}$$

Let

$$G(t,\omega )=\omega -b_0-b_{1}t-At(\omega -b_0)-Bt({\omega }^2-b_0^2)-C{t}^2{\omega }^2.$$

(30)

Then

$$G_{\omega }(t,\omega )=1-tA-2Bt\omega -2C{t}^2\omega .$$

Regarding at point $(0,b_0)$, the function $G(t,\omega )$ is 0 and the partial derivative of the function $G(t,\omega )$ with respect to $\omega$ is 1. We can see that $G(t,\omega )$ is an analytic function, so $G(t,\omega )$ has continuous derivatives. By implicit function theorem [40], there is a neighborhood of $(0,b_0)$ so that whenever t is sufficiently close to 0 there is a unique $\omega$ so that $G(t,\omega )=0$. Then, $f\left(t\right)$ is an analytic function in the neighborhood of the point $(0,b_0)$ of the $(t,\omega )$-plane with a positive radius of convergence. From Lemma 1, the series in Equation (7) converges. The proof is complete. □

5. Numerical Example

In this section, a numerical example of the MRPSM for nonlinear fractional Volterra population growth model is presented.

Consider the following nonlinear fractional Volterra population growth model

$$\kappa D_t^{\alpha }u\left(t\right)=u\left(t\right)-u^2\left(t\right)-u\left(t\right)I^{\alpha }u\left(t\right),\alpha \in (0,1],$$

(31)

subject to

$$u\left(0\right)=0.4.$$

(32)

The graphical results of the solution for Equation (31) and initial condition (32) is illustrated through Figure 1, Figure 2 and Figure 3 for different $\alpha$ and $\kappa$ values. Figure 1 represents the behavior of an approximate solution $\kappa =0.7$ with various values of $\alpha$. Figure 2 and Figure 3 show the behavior of an approximate solution for $\alpha =0.75$ and 1 with various values of $\kappa$. We observe that increasing the parameter $\kappa$ resulted in decreasing of the approximate solution.

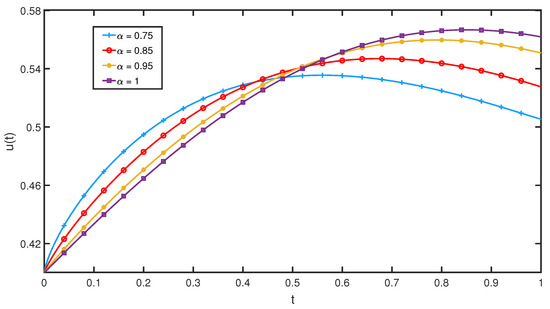
Figure 1. Approximate solution of Equation (31) for various of $\alpha$ and $\kappa =0.7$.

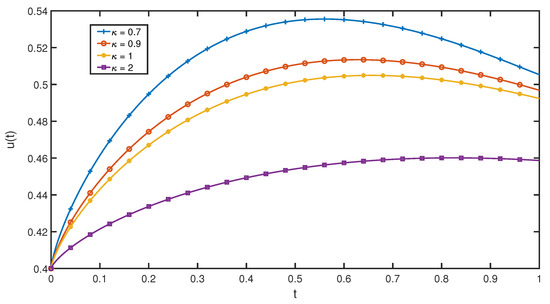
Figure 2. Approximate solution of Equation (31) for various of $\kappa$ and $\alpha =0.75$.

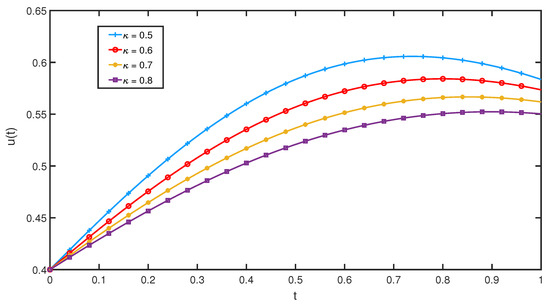
Figure 3. Approximate solution of Equation (31) for various of $\kappa$ and $\alpha =1$.

For $\alpha =1$, Equation (31) becomes the classical Volterra population growth model. Table 1 represents the relation between $\kappa$, $u_{max}$ and $t_{critical}$. The maximum value is presented as $u_{max}$ and the position of $u_{max}$ is presented as $t_{critical}$. The exact value of $u_{max}$ was evaluated by using

$$u_{max}=1+\kappa ln\left({\displaystyle \frac{\kappa }{1+\kappa -u\left(0\right)}}\right)$$

obtained by [32].

Table 1. The approximation of $u_{max}$ and exact value of $u_{max}$ for various of $\kappa$ at $\alpha =1$.

$\mathit{\kappa }$	${\mathit{t}}_{\mathit{c}\mathit{r}\mathit{i}\mathit{t}\mathit{i}\mathit{c}\mathit{a}\mathit{l}}$	Approximate ${\mathit{u}}_{\mathit{m}\mathit{a}\mathit{x}}$	Exact ${\mathit{u}}_{\mathit{m}\mathit{a}\mathit{x}}$	Absolute Errors
0.5	0.738	0.6057712361	0.6057713198	$8.37213\times {10}^{-8}$
0.6	0.800	0.5841115047	0.5841116917	$1.86934\times {10}^{-7}$
0.7	0.852	0.5666724313	0.5666725541	$1.22786\times {10}^{-7}$
0.8	0.896	0.5523073685	0.5523073697	$1.14278\times {10}^{-9}$

In Table 1, we observe that the approximate value of $u_{max}$ decreases as $\kappa$ increases. It is noted that the approximate value of $u_{max}$ is close to the exact value of $u_{max}$ for all values of $\kappa$. In fact, the results reported in Table 1 illustrates the validity and good accuracy of the method.

In order to show the convergence of the MRPSM, the absolute errors of $u_{max}$ for different $\kappa$ values and $\alpha =1$ are shown in Table 2. The absolute error tends to decrease when the number of truncated terms (k) increases. This shows that the method works reasonably for the classical problem. The results for other values of $\alpha$ are shown in Table 3. The approximate solution of $u_{max}$ at each $\alpha$ and $\kappa$ changes slightly when the number of truncated terms increases. We can say that only 20-term approximation is acceptable to explain the behavior of the population with less computational effort. Table 4 demonstrates how the step size h affects the approximation for $\alpha =1$. Compare to the exact values of $u_{max}$ in Table 1, it is natural that the smaller step size is, the better approximation performs. For $h=0.002$, the computation time is less than 0.08 second which we hardly have to wait.

Table 2. Absolute error of $u_{max}$ for various of $\kappa$ and $\alpha =1$.

$\mathit{\kappa }$	$\mathit{k}=20$	$\mathit{k}=25$	$\mathit{k}=30$
0.5	$3.33491\times {10}^{-6}$	$4.48341\times {10}^{-7}$	$8.37213\times {10}^{-8}$
0.6	$1.12750\times {10}^{-6}$	$2.47310\times {10}^{-7}$	$1.86934\times {10}^{-7}$
0.7	$4.28738\times {10}^{-7}$	$1.34831\times {10}^{-7}$	$1.22786\times {10}^{-7}$
0.8	$1.10182\times {10}^{-7}$	$3.89890\times {10}^{-9}$	$1.14278\times {10}^{-9}$

Table 3. The approximation of $u_{max}$ for different $\alpha$ and $\kappa$ values.

$\mathit{\alpha }$	$\mathit{\kappa }$	$\mathit{k}=20$	$\mathit{k}=25$	$\mathit{k}=30$
0.75	0.6	0.5502368550	0.5502415323	0.5502426850
0.85	0.7	0.5469171943	0.5469180381	0.5469181062
0.95	0.8	0.5458638855	0.5458640377	0.5458640426

Table 4. The approximation of $u_{max}$ and computation time for $\alpha =1$ and $k=20$.

h	$\mathit{\kappa }=0.5$		$\mathit{\kappa }=0.7$
	Approximate ${\mathit{u}}_{\mathit{m}\mathit{a}\mathit{x}}$	Computation Time (s)	Approximate ${\mathit{u}}_{\mathit{m}\mathit{a}\mathit{x}}$	Computation Time (s)
0.002	0.605771236096562	0.078953	0.566672431329788	0.075677
0.02	0.605769084446570	0.072933	0.566655106763389	0.070760
0.1	0.605246758144338	0.070844	0.566135276851748	0.067380

6. Conclusions

In this paper, we proposed a computational method called the modified residual power series method (MRPSM) for solving nonlinear fractional Volterra population growth model. A closed form of the fractional power series solution is obtained which is the advantage of this method. The convergence analysis was also investigated. We gave a numerical example supporting that this method is efficiently applicable for the nonlinear fractional Volterra population growth model with high accuracy. Finally, it can easily be applied to other fractional nonlinear initial value problems to obtain numerical or analytical solutions.