The Short-Term Forecasting of Asymmetry Photovoltaic Power Based on the Feature Extraction of PV Power and SVM Algorithm
Abstract
1. Introduction
- (1)
- The effective decomposition of the original PV power output.
- (2)
- The reasonable identification of specified IMFs.
- (3)
- The parameter optimization of the SVM.
- (4)
- The reconstruction of the forecasting result.
2. Related Work
2.1. CEEMDAN Algorithm
- (1)
- Obtain the noisy signal ; , where is the added white noise with unit variance, is the corresponding coefficient, and is the original signal;
- (2)
- Extract the first IMF () from each noisy signal with EMD;
- (3)
- Obtain the first IMF () by taking the average of each ;
- (4)
- Obtain the first residue: ;
- (5)
- Decompose with the EMD algorithm, and extract the first IMF to obtain the second IMF (), where means the coefficient of the added white noise, and the operator indicates the -th IMF with EMD;
- (6)
- Compute the -th residue mode (), and extract the first IMF to generate the -th IMF with Equation (3);
- (7)
- Repeat the above steps until the residue contains fewer than two extrema;
2.2. SVM Algorithm
2.3. PSO Algorithm
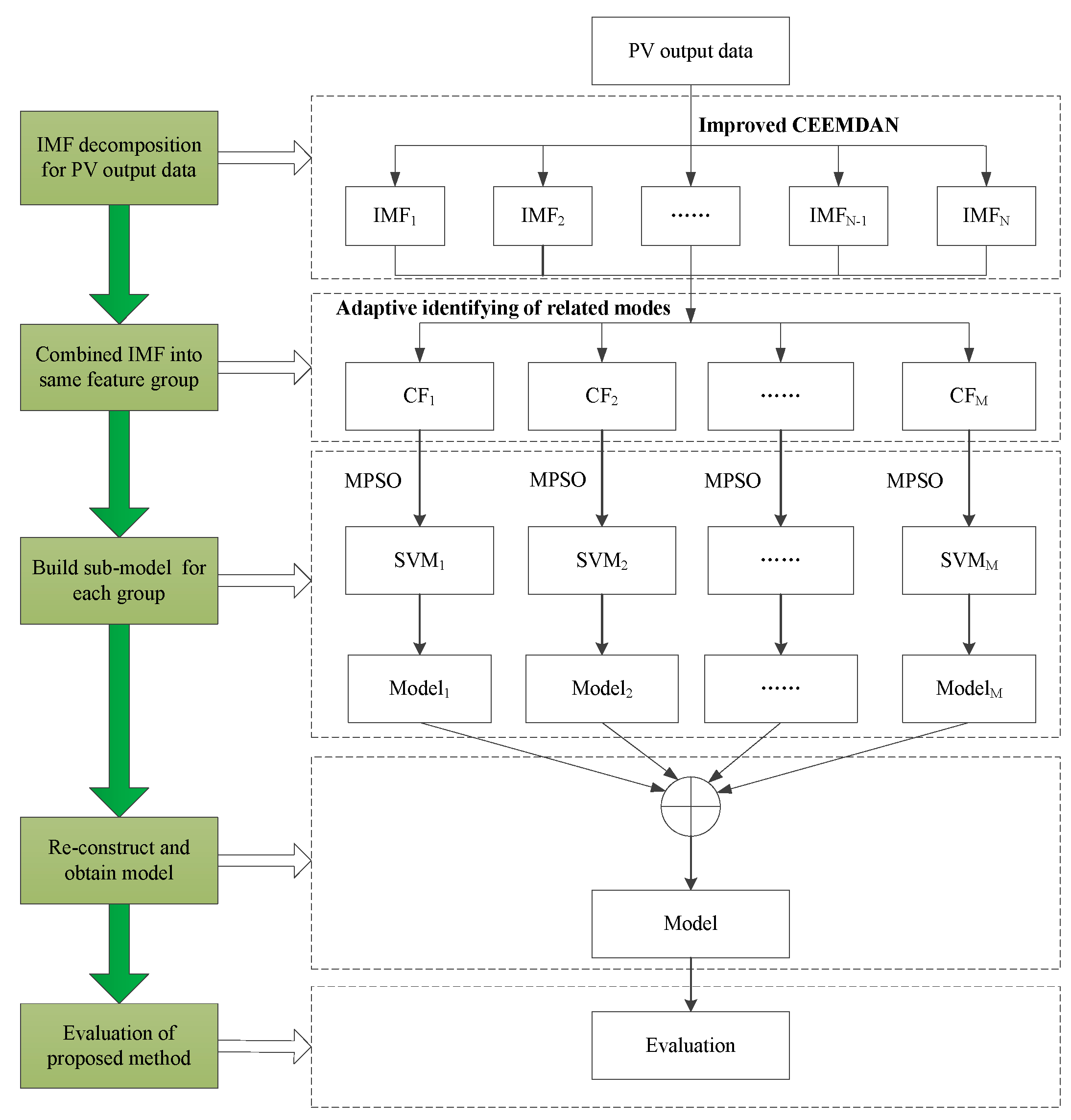
3. Proposed Work
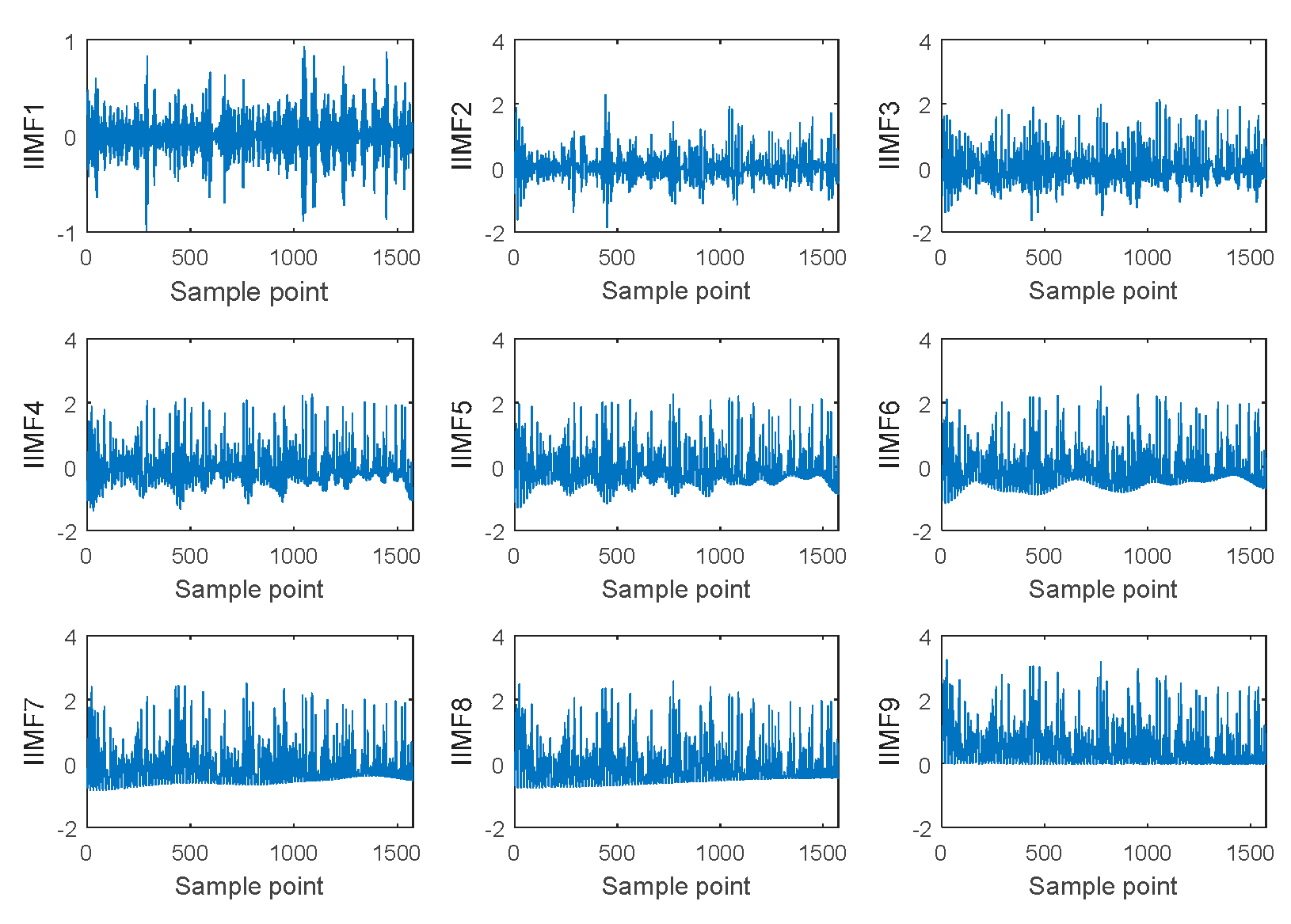
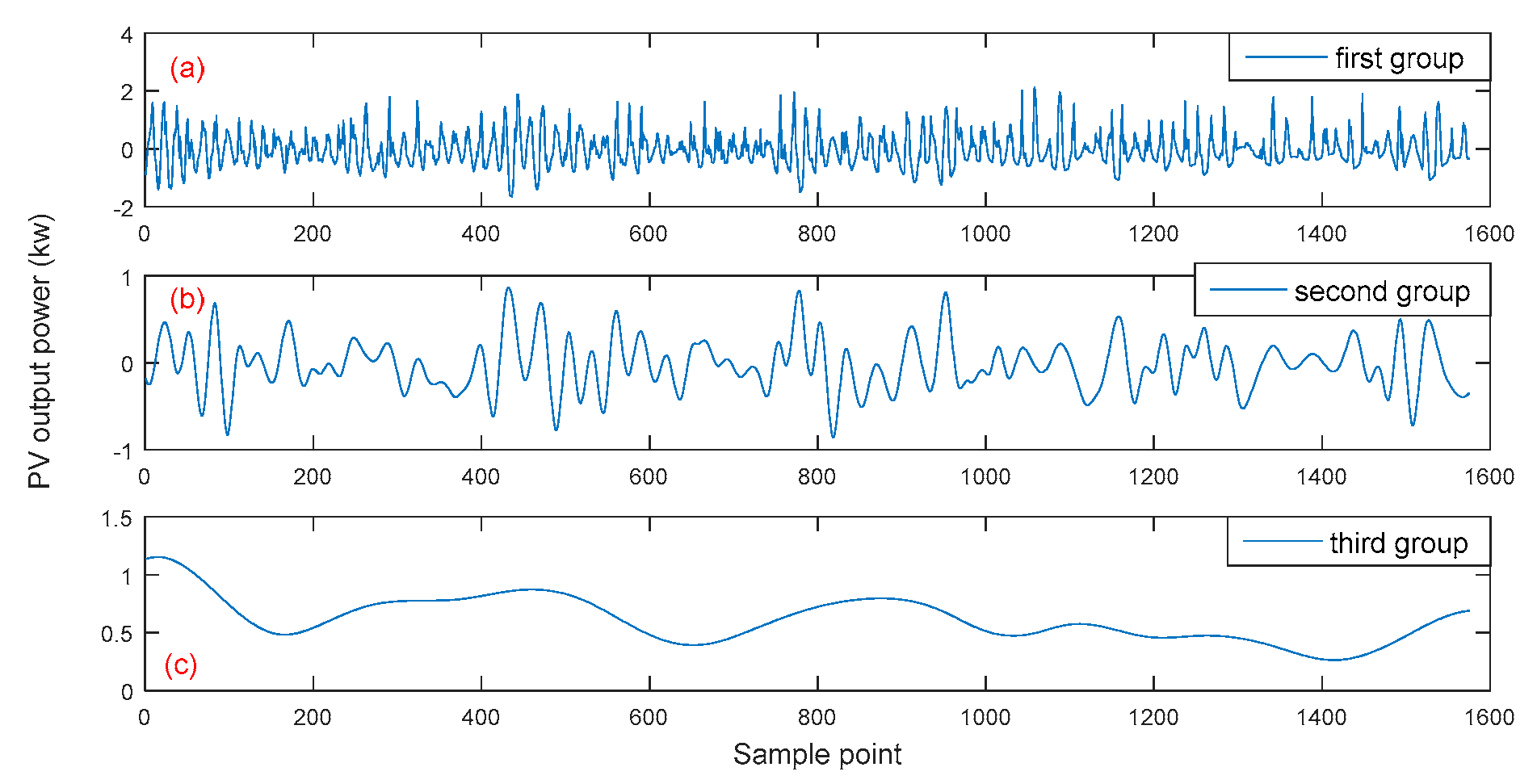
3.1. Effective Decomposition for PV Power
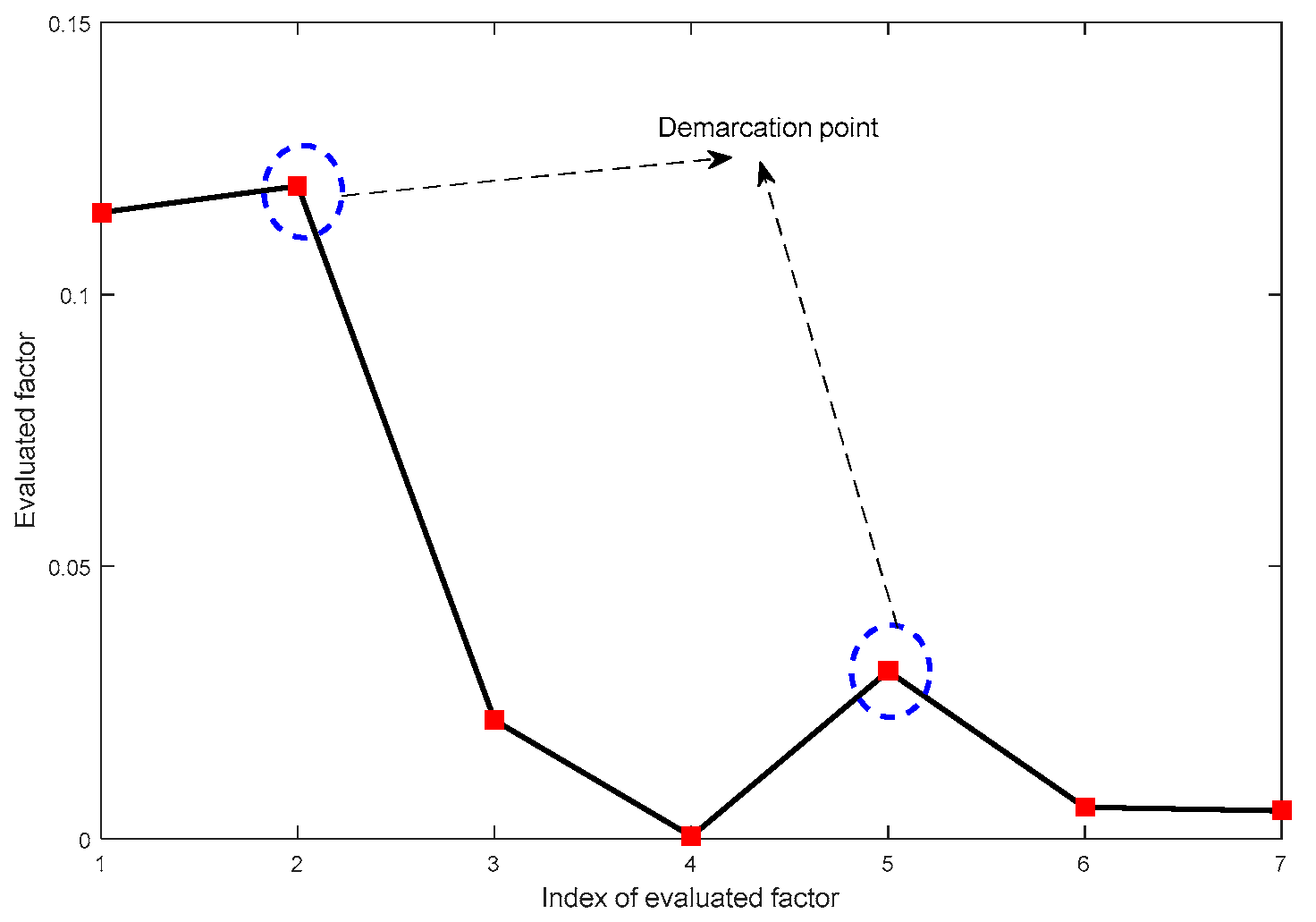
3.2. Selection of Related Modes
3.3. Establishment of the Forecasting Sub-Model for PV Power Output
- (1)
- Determine the training sample for each and the corresponding input variables:where refers to the input vector of the training set, refers to the set of output variable vectors (), is the input variable vector of the -th sample, and is the corresponding output value.
- (2)
- Determine the parameter range of the SVM.
- (3)
- Optimize the parameters of the SVM with the modified PSO (MPSO).
- (4)
- Train the SVM with the training sample and calculate the fitness value of each particle. The fitness value is compared with the global best position . If the fitness value is superior to , the fitness value is considered as . Here, the mean square error (MSE) is used to perform the fitness function:where means the length of the training sample, is the real value of the -th sample, and is the corresponding forecasting power output. If the fitness of each particle is smaller than that of all the particles, the global best position is placed with the local best position .
- (5)
- Update the position and velocity with Equations (8) and (9).
- (6)
- Look for the optimal solution until the end condition is satisfied; otherwise, go back to Step 3.
3.4. Final Forecasting Model
3.5. Evaluation of Forecasting Result
- (1)
- Determination coefficient ().
- (2)
- Mean absolute error (MRE).
- (3)
- Root-mean-square error (RMSE).
- (1)
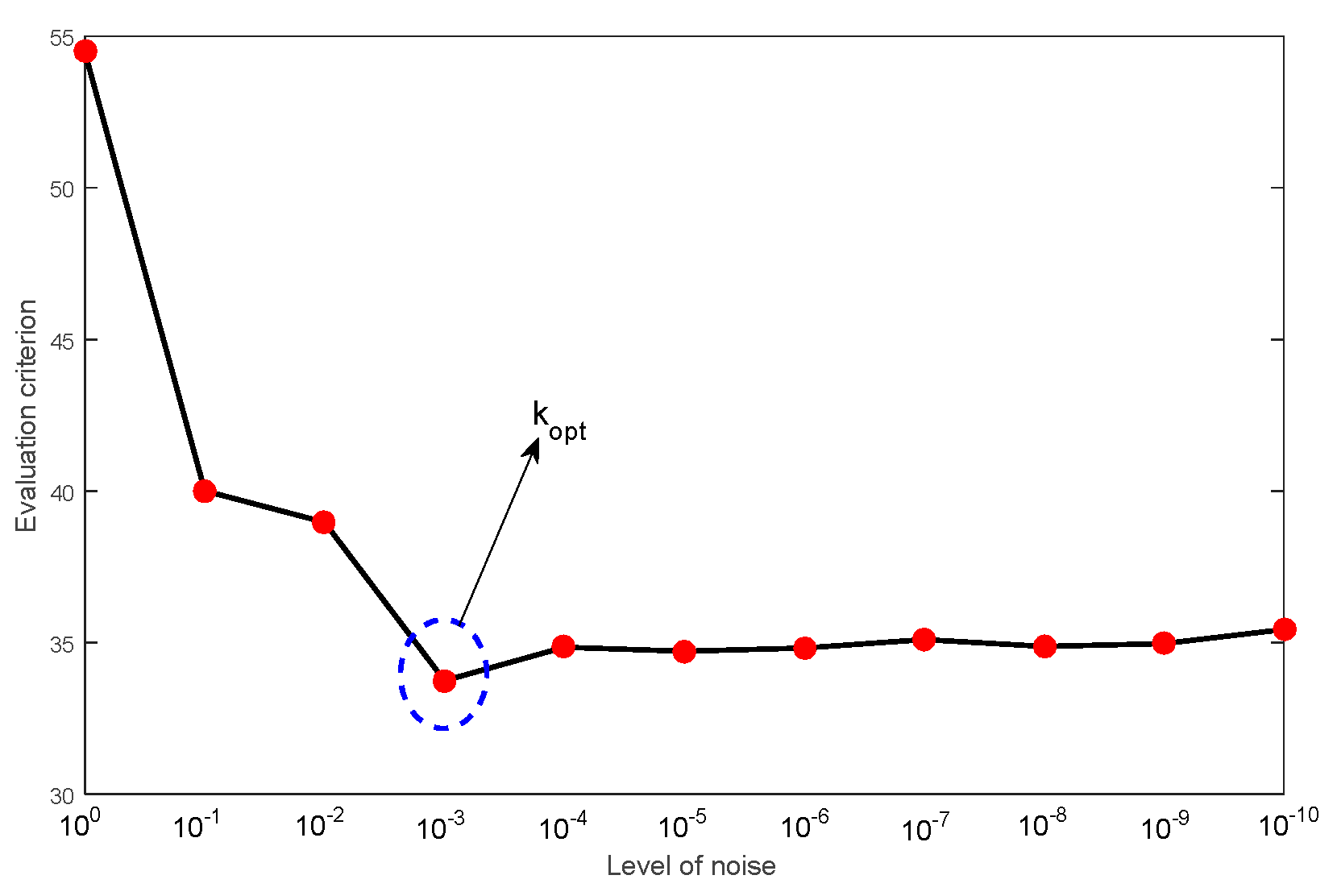
- Decompose the PV power output into the IMFs with physical meaning with the improved CEEMDAN (ICEEMDAN). Here, the two critical parameters (the ensemble size and amplitude of the added white noise) are determined by introducing the noise level.
- (2)
- Classify IMFs into the individual feature groups including the most relevant fluctuation components by introducing the comprehensive factor adaptively. It may avoid the drawbacks of threshold determination depending on the empirical method and is an adaptive way.
- (3)
- Optimize the parameters in the SVM for individual feature groups with the modified PSO (MPSO), and obtain the corresponding sub-forecasting model. The MPSO can enhance the global search ability to make the particle traverse all the space and also local search performance to increase the speed of convergence.
- (4)
- Reconstruct the sub-forecasting model to obtain the final forecasting model.
- (5)
- Evaluate the effectiveness of the proposed method (ICEEMDAN-IF-MPSO-SVM), which comes from Step 1 to Step 4.
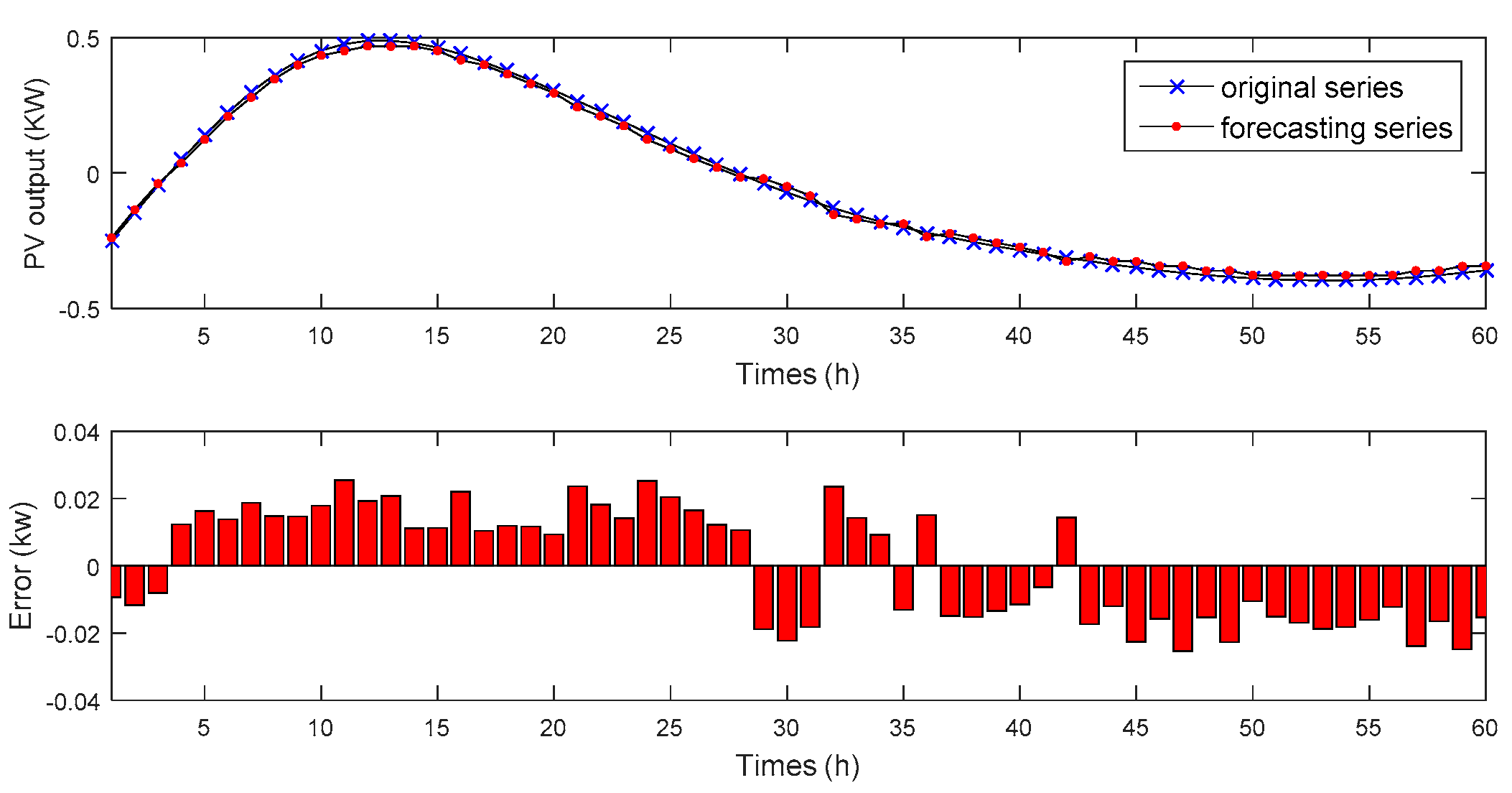
4. Results and Discussion
5. Conclusions
- (1)
- The ICEEMDAN method is introduced to decompose the PV power output into IMFs with physical meaning. The two critical parameters, which include the ensemble size (EN) and amplitude of the added white noise (NA), can be determined by setting the ensemble size as two trails and introducing the noise level. This method can avoid the interference of a spurious mode for the forecasting of PV power output.
- (2)
- The adaptive identified method of the relative mode is proposed to classify the IMFs into the corresponding feature groups. The method can separate the complex fluctuating components in PV power output into single components to enhance the forecasting accuracy.
- (3)
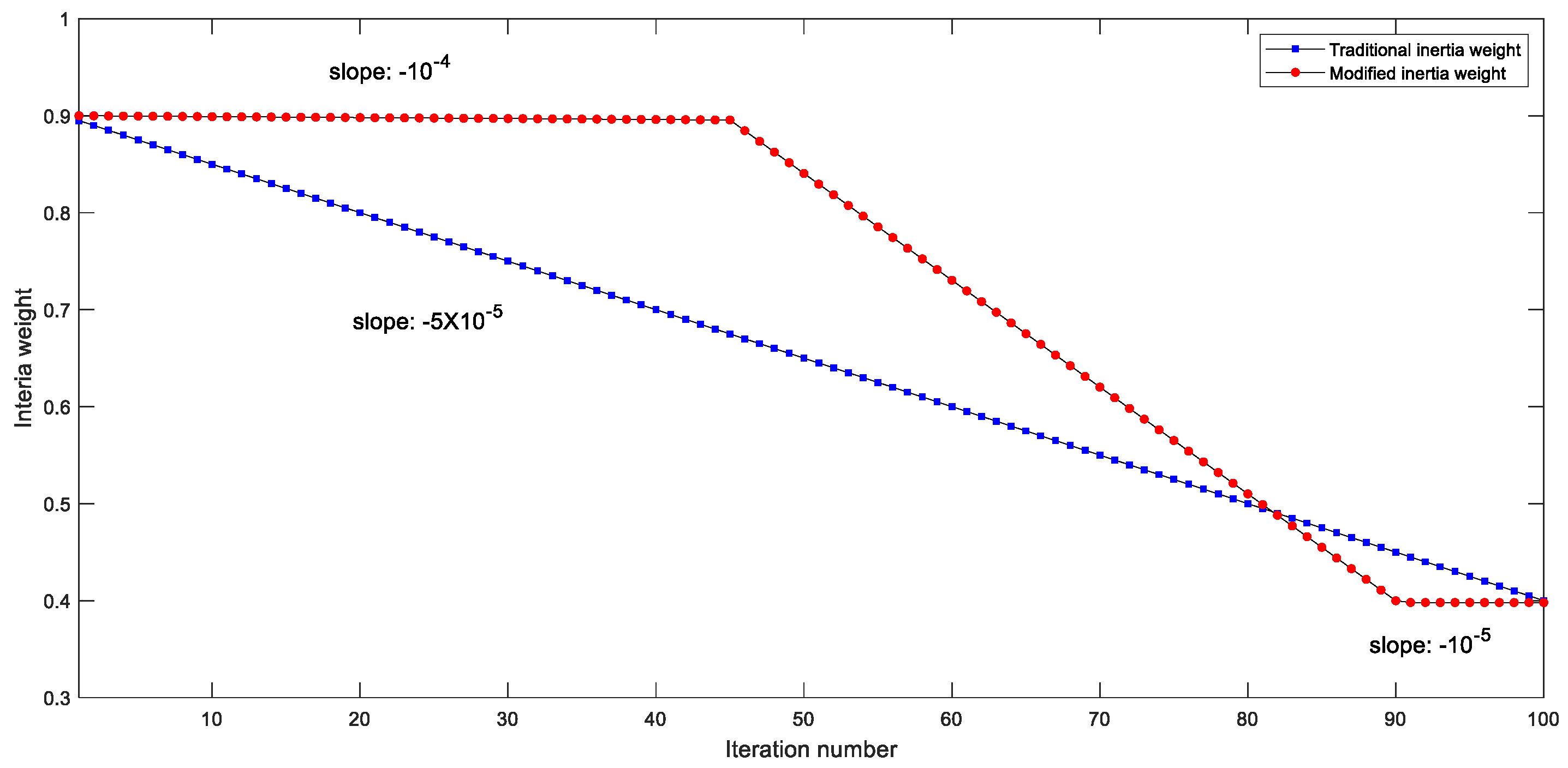
- The modified PSO (MSPO) is proposed to optimize the hyper-parameters in the SVM. The MPSO applies the piecewise inertial weight to enhance the global search ability to make the particle traverse all the space and also local search performance to increase the convergence speed.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| PV | photovoltaic |
| IF | selection method of relative modes |
| GA | genetic algorithm |
| SVM | support vector machine |
| EMD | empirical mode decomposition |
| EEMD | ensemble EMD |
| NA | amplitude of added white noise |
| IMFs | intrinsic mode functions |
| ICEEMDAN | improved CEEMDAN |
| Cr | crest factor |
| determination coefficient | |
| RMSE | root-mean-square error |
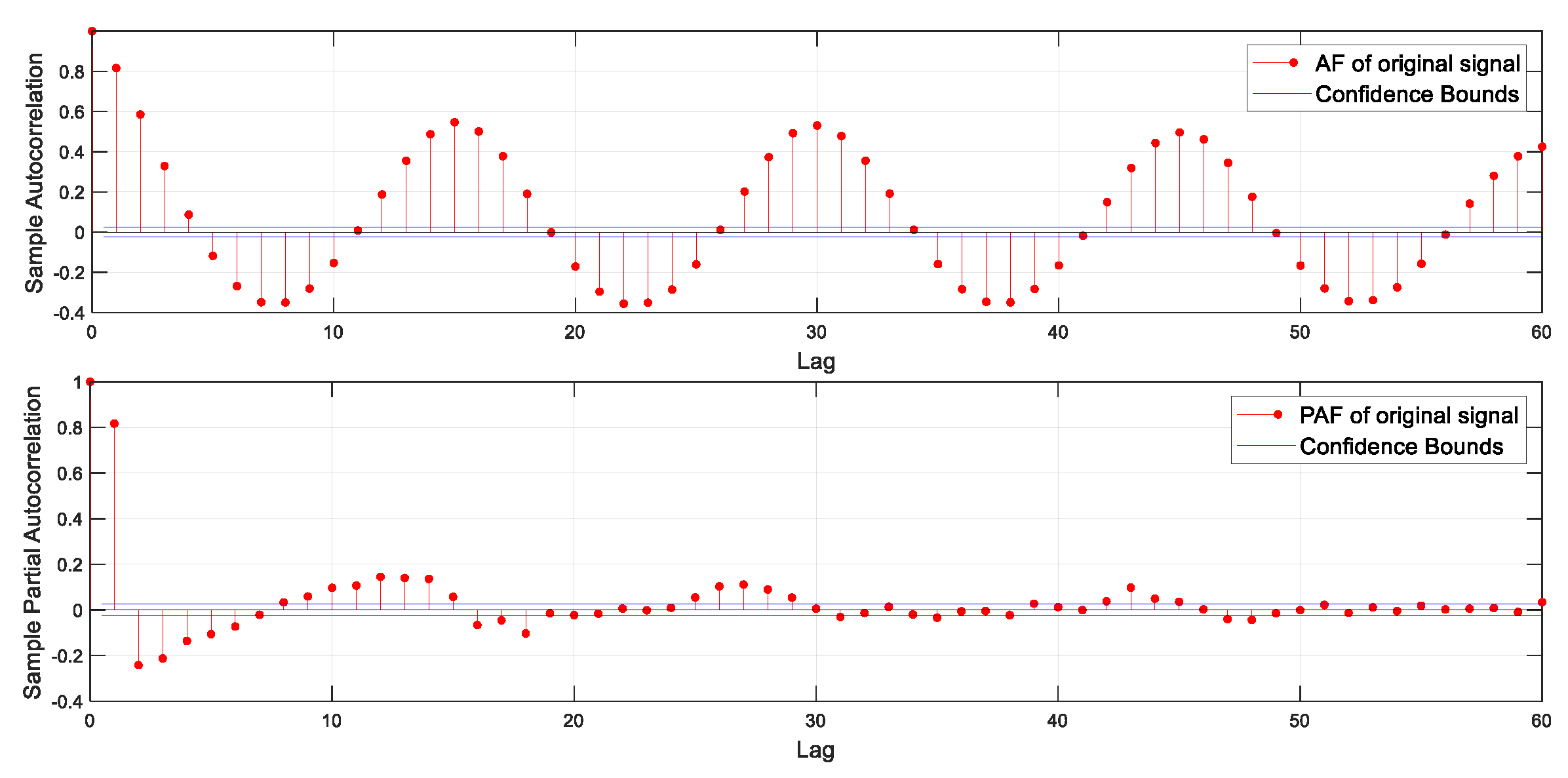
| PAF | partial autocorrelation function |
| PSO | particle swarm optimization |
| MPSO | modified particle swarm optimization |
| GS | grid search |
| ANN | artificial neural network |
| VMD | variational mode decomposition |
| CEEMDAN | complementary EEMD with adaptive noise (CEEMDAN) |
| EN | ensemble trials |
| IIMFs | identified IMFs |
| Sh | shape factor |
| Ku | kurtosis |
| CF | comprehensive factor |
| MRE | mean absolute error |
| AF | autocorrelation function |
| BP | back propagation neural network |
| RF | random forest |
References
- Kundur, P. Sustainable electric power systems in the 21st century: Requirements, challenges and the role of new technologies. In Proceedings of the IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004. [Google Scholar]
- Moro, A.; Holzer, A. A Framework to Predict Consumption Sustainability Levels of Individuals. Sustainability 2020, 12, 1423. [Google Scholar] [CrossRef]
- Ariyaratna, P.; Muttaqi, K.M.; Sutanto, D. A novel control strategy to mitigate slow and fast fluctuations of the voltage profile at common coupling Point of rooftop solar PV unit with an integrated hybrid energy storage system. J. Energy Storage 2018, 20, 409–417. [Google Scholar] [CrossRef]
- Huang, C.-J.; Kuo, P.-H. Multiple-Input Deep Convolutional Neural Network Model for Short-Term Photovoltaic Power Forecasting. IEEE Access 2019, 7, 74822–74834. [Google Scholar] [CrossRef]
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Idris, M.Y.I.; Mekhilef, S.; Horan, B.; Stojcevski, A. SVR-Based Model to Forecast PV Power Generation under Different Weather Conditions. Energies 2017, 10, 876. [Google Scholar] [CrossRef]
- Xu, D.; Kang, L.; Chang, L.; Chang, L.; Cao, B. Optimal sizing of standalone hybrid wind/PV power systems using genetic algorithms. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Saskatoon, SK, Canada, 1–4 May 2005; pp. 1722–1725. [Google Scholar]
- De Gooijer, J.G.; Hyndman, R.J. 25 years of time series forecasting. Int. J. Forecast. 2006, 22, 443–473. [Google Scholar] [CrossRef]
- Kim, J.; Jun, S.; Jang, D.; Park, S. Sustainable Technology Analysis of Artificial Intelligence Using Bayesian and Social Network Models. Sustainability 2018, 10, 115. [Google Scholar] [CrossRef]
- Chui, K.T.; Lytras, M.; Visvizi, A. Energy Sustainability in Smart Cities: Artificial Intelligence, Smart Monitoring, and Optimization of Energy Consumption. Energies 2018, 11, 2869. [Google Scholar] [CrossRef]
- Sodhro, A.H.; Pirbhulal, S.; De Albuquerque, V.H.C. Artificial Intelligence-Driven Mechanism for Edge Computing-Based Industrial Applications. IEEE Trans. Ind. Inform. 2019, 15, 4235–4243. [Google Scholar] [CrossRef]
- Chow, S.K.; Lee, E.W.; Li, D.H. Short-term prediction of photovoltaic energy generation by intelligent approach. Energy Build. 2012, 55, 660–667. [Google Scholar] [CrossRef]
- Jumaat, S.A.B.; Crocker, F.; Wahab, M.H.A.; Radzi, N.H.B.M. Investigate the photovoltaic (PV) module performance using Artificial Neural Network (ANN). In Proceedings of the 2016 IEEE Conference on Open Systems (ICOS), Langkawi, Malaysia, 10–12 October 2016; pp. 59–64. [Google Scholar]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Zendehboudi, A. Implementation of GA-LSSVM modelling approach for estimating the performance of solid desiccant wheels. Energy Convers. Manag. 2016, 127, 245–255. [Google Scholar] [CrossRef]
- Fayazi, A.; Arabloo, M.; Shokrollahi, A.; Zargari, M.H.; Ghazanfari, M.H. State-of-the-Art Least Square Support Vector Machine Application for Accurate Determination of Natural Gas Viscosity. Ind. Eng. Chem. Res. 2013, 53, 945–958. [Google Scholar] [CrossRef]
- Wang, F.; Li, K.; Wang, X.; Jiang, L.; Ren, J.; Mi, Z.; Shafie-Khah, M.; Catalao, J.P.S. A Distributed PV System Capacity Estimation Approach Based on Support Vector Machine with Customer Net Load Curve Features. Energies 2018, 11, 1750. [Google Scholar] [CrossRef]
- Niu, D.; Dai, S. A Short-Term Load Forecasting Model with a Modified Particle Swarm Optimization Algorithm and Least Squares Support Vector Machine Based on the Denoising Method of Empirical Mode Decomposition and Grey Relational Analysis. Energies 2017, 10, 408. [Google Scholar] [CrossRef]
- Pourbasheer, E.; Riahi, S.; Ganjali, M.R.; Norouzi, P. Application of genetic algorithm-support vector machine (GA-SVM) for prediction of BK-channels activity. Eur. J. Med. Chem. 2009, 44, 5023–5028. [Google Scholar] [CrossRef]
- Chen, P.; Yuan, L.; He, Y.; Luo, S. An improved SVM classifier based on double chains quantum genetic algorithm and its application in analogue circuit diagnosis. Neurocomputing 2016, 211, 202–211. [Google Scholar] [CrossRef]
- Duan, P.; Xie, K.; Guo, T.; Huang, X. Short-Term Load Forecasting for Electric Power Systems Using the PSO-SVR and FCM Clustering Techniques. Energies 2011, 4, 173–184. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE international conference on evolutionary computation proceedings. IEEE world congress on computational intelligence (Cat. No. 98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Bansal, J.C.; Singh, P.K.; Saraswat, M.; Verma, A.; Jadon, S.S.; Abraham, A. Inertia weight strategies in particle swarm optimization. In Proceedings of the 2011 Third World Congress on Nature and Biologically Inspired Computing, Salamanca, Spain, 19–21 October 2011; pp. 633–640. [Google Scholar]
- Ali, M.; Prasad, R.; Xiang, Y.; Deo, R.C. Near real-time significant wave height forecasting with hybridized multiple linear regression algorithms. Renew. Sustain. Energy Rev. 2020, 132, 110003. [Google Scholar] [CrossRef]
- Abedinia, O.; Amjady, N.; Ghadimi, N. Solar energy forecasting based on hybrid neural network and improved metaheuristic algorithm. Comput. Intell. 2017, 34, 241–260. [Google Scholar] [CrossRef]
- Yang, Y.; Dong, L. Short-term PV generation system direct power prediction model on wavelet neural network and weather type clustering. In Proceedings of the 2013 5th International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2013; Volume 1, pp. 207–211. [Google Scholar]
- Zhang, P.; Takano, H.; Murata, J. Daily solar radiation prediction based on wavelet analysis. In Proceedings of the SICE Annual Conference 2011, Tokyo, Japan, 13–18 September 2011; pp. 12–717. [Google Scholar]
- Li, F.-F.; Wang, S.-Y.; Wei, J. Long term rolling prediction model for solar radiation combining empirical mode decomposition (EMD) and artificial neural network (ANN) techniques. J. Renew. Sustain. Energy 2018, 10, 013704. [Google Scholar] [CrossRef]
- Nayak, N.; Pani, A.K. Short term PV power forecasting using empirical mode decomposition based orthogonal extreme learning machine technique. Indian J. Public Health Res. Dev. 2018, 9, 2170. [Google Scholar] [CrossRef]
- Abedinia, O.; Lotfi, M.; Bagheri, M.; Sobhani, B.; Shafie-Khah, M.; Catalao, J.P.S. Improved EMD-Based Complex Prediction Model for Wind Power Forecasting. IEEE Trans. Sustain. Energy 2020, 99, 1. [Google Scholar] [CrossRef]
- Abedinia, O.; Raisz, D.; Amjady, N. Effective prediction model for Hungarian small-scale solar power output. IET Renew. Power Gener. 2017, 11, 1648–1658. [Google Scholar] [CrossRef]
- Prasad, R.; Ali, M.; Kwan, P.; Khan, H. Designing a multi-stage multivariate empirical mode decomposition coupled with ant colony optimization and random forest model to forecast monthly solar radiation. Appl. Energy 2019, 236, 778–792. [Google Scholar] [CrossRef]
- Ali, M.; Deo, R.C.; Maraseni, T.; Downs, N.J. Improving SPI-derived drought forecasts incorporating synoptic-scale climate indices in multi-phase multivariate empirical mode decomposition model hybridized with simulated annealing and kernel ridge regression algorithms. J. Hydrol. 2019, 576, 164–184. [Google Scholar] [CrossRef]
- Prasad, R.; Ali, M.; Xiang, Y.; Khan, H. A double decomposition-based modelling approach to forecast weekly solar radiation. Renew. Energy 2020, 152, 9–22. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the Acoustics, Speech and Signal Processing (ICASSP), 2011 IEEE International Conference on IEEE, Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Ali, M.; Prasad, R. Significant wave height forecasting via an extreme learning machine model integrated with improved complete ensemble empirical mode decomposition. Renew. Sustain. Energy Rev. 2019, 104, 281–295. [Google Scholar] [CrossRef]
- Ali, M.; Prasad, R.; Xiang, Y.; Yaseen, Z.M. Complete ensemble empirical mode decomposition hybridized with random forest and kernel ridge regression model for monthly rainfall forecasts. J. Hydrol. 2020, 584, 124647. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, R.; Gao, R.X.; Feng, Z. Performance enhancement of ensemble empirical mode decomposition. Mech. Syst. Signal Process. 2010, 24, 2104–2123. [Google Scholar] [CrossRef]
- Niazy, R.K.; Beckmann, C.F.; Brady, J.M.; Smith, S.M. Performance Evaluation of Ensemble Empirical Mode Decomposition. Adv. Adapt. Data Anal. 2009, 1, 231–242. [Google Scholar] [CrossRef]
- Wang, H.; Sun, J.; Wang, W.-J. Photovoltaic Power Forecasting Based on EEMD and a Variable-Weight Combination Forecasting Model. Sustainability 2018, 10, 2627. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, W.; Zeng, J. A new short-term load forecasting method of power system based on EEMD and SS-PSO. Neural Comput. Appl. 2013, 24, 973–983. [Google Scholar] [CrossRef]
- Oneto, L.; Laureri, F.; Robba, M.; Delfino, F.; Anguita, D. Data-Driven Photovoltaic Power Production Nowcasting and Forecasting for Polygeneration Microgrids. IEEE Syst. J. 2017, 12, 2842–2853. [Google Scholar] [CrossRef]



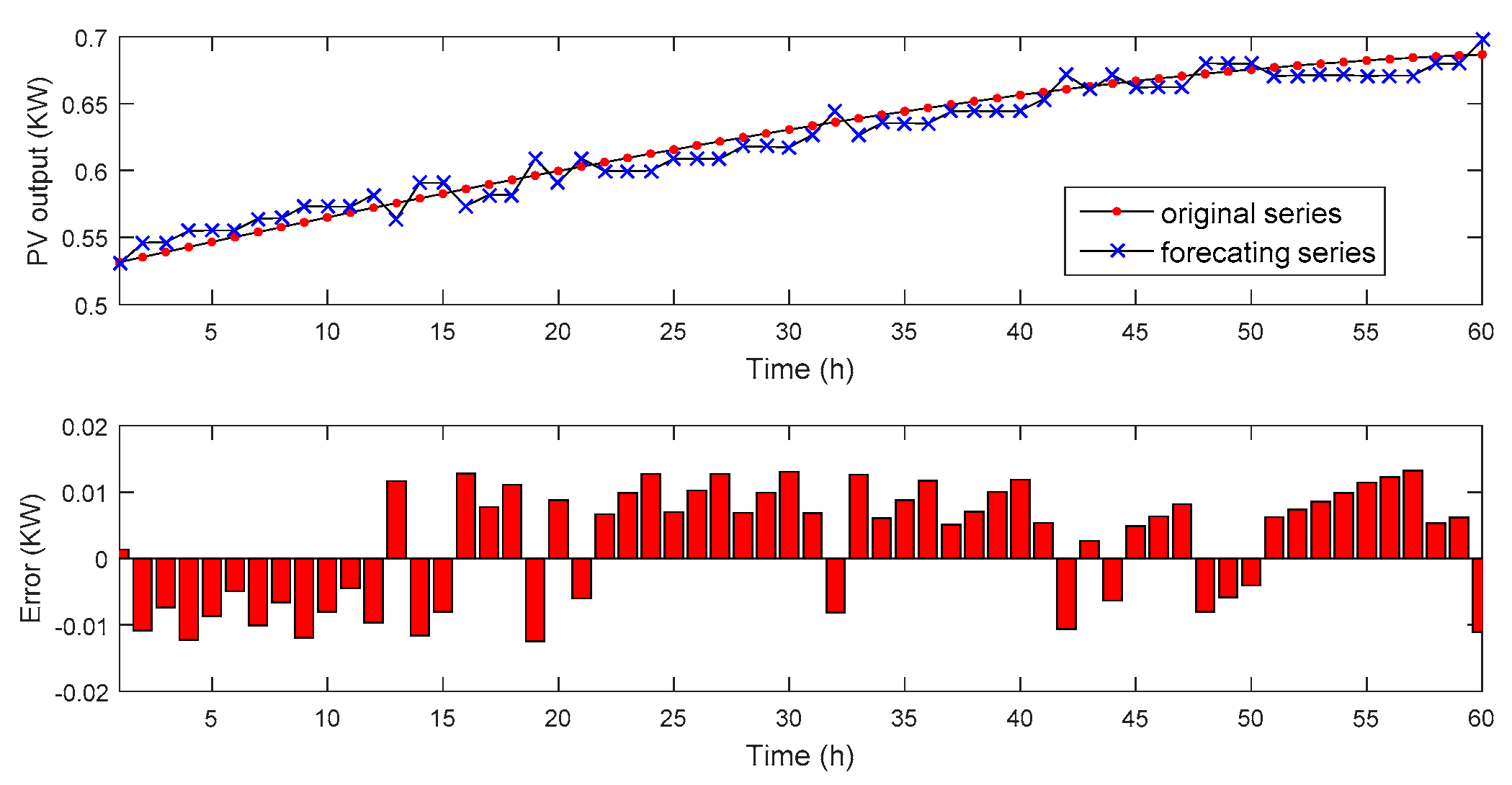
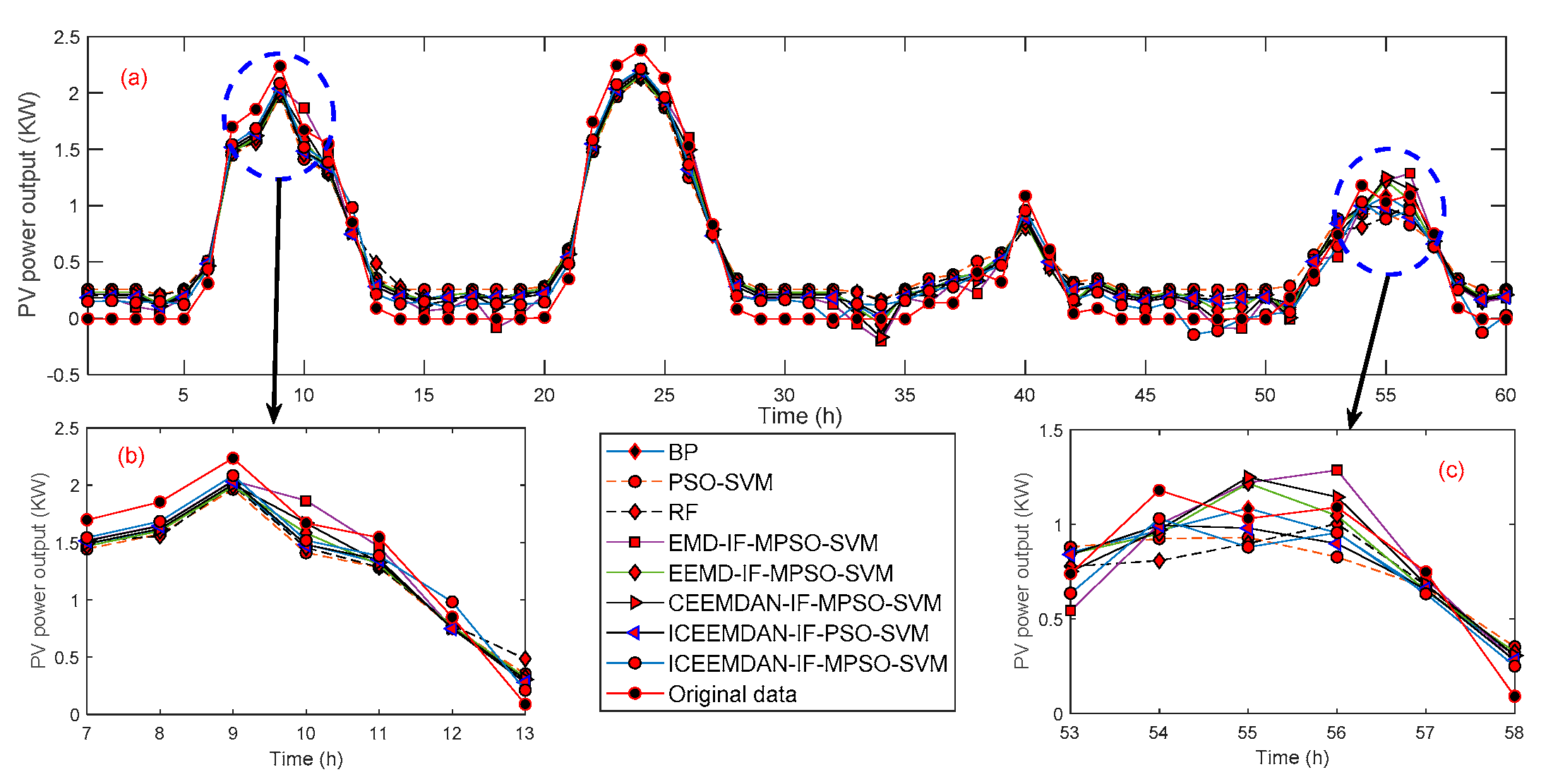
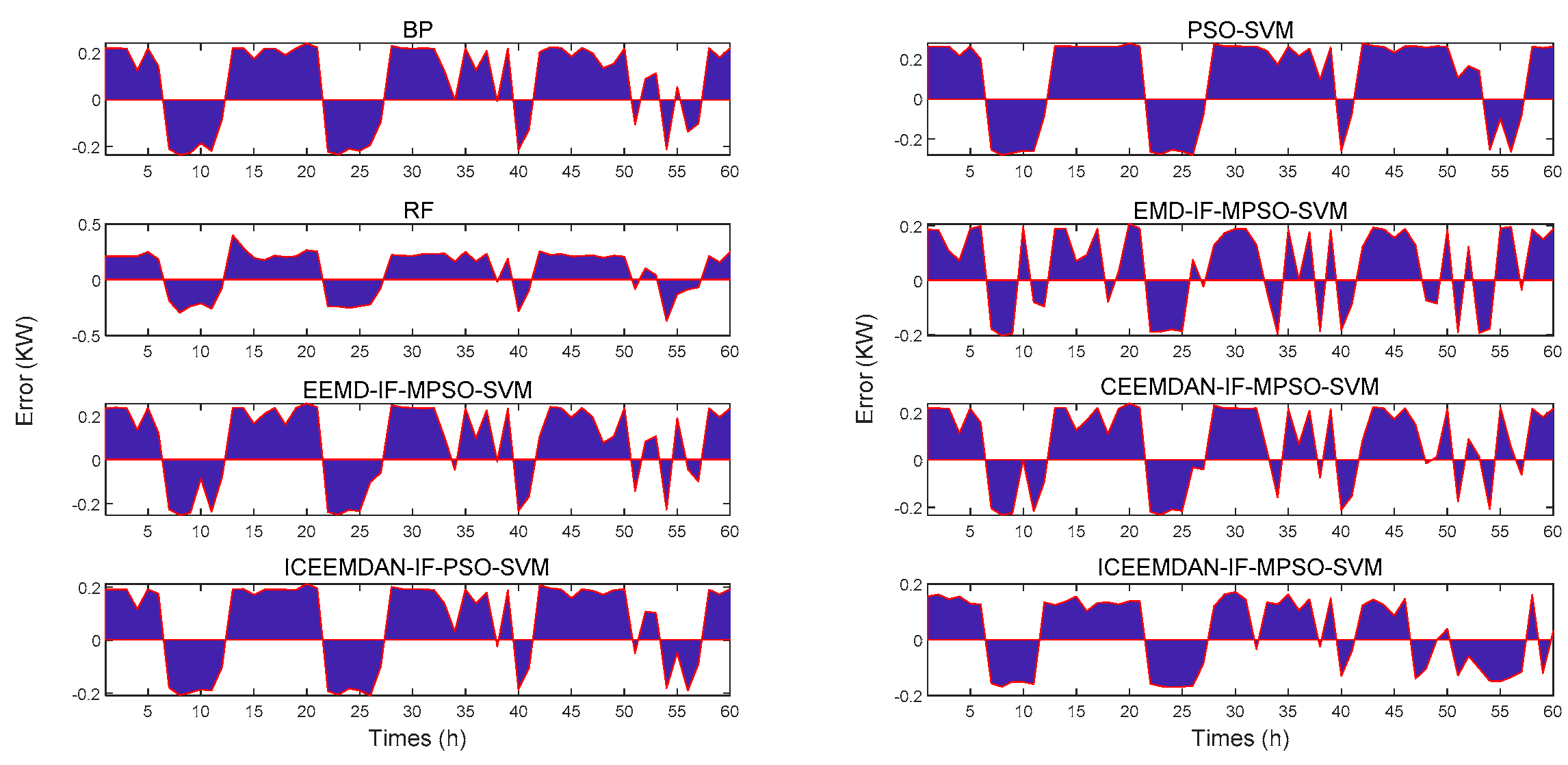

| Number | Statistical Parameter | Expression |
|---|---|---|
| 1 | Shape factor | |
| 2 | Crest factor | |
| 3 | Kurtosis |
| Group Order | First Group | Second Group | Three Group |
|---|---|---|---|
| Combined IMFs | IMF1 + IMF2 + IMF3 | IMF4 + IMF5 + IMF6 | IMF7 + IMF8 + IMF9 |
| Order | Name | Value | Order | Name | Value |
|---|---|---|---|---|---|
| 1 | Maximum iteration number | 100 | 6 | Iteration number | 45 |
| 2 | Start weight | 0.9 | 7 | Iteration number | 90 |
| 3 | End weight | 0.4 | 8 | Parameter C range | 0–100 |
| 4 | Slope | −10−4 | 9 | Parameter range | 0–100 |
| 5 | Slope | −10−5 | 10 | Population number | 20 |
| Model | MRE | RMSE | R2 |
|---|---|---|---|
| BP | 0.3764 | 0.1919 | 0.9279 |
| PSO-SVM | 0.4817 | 0.2417 | 0.8856 |
| RF | 0.4194 | 0.2157 | 0.9089 |
| EMD-IF-MPSO-SVM | 0.3076 | 0.1596 | 0.9501 |
| EEMD-IF-MPSO-SVM | 0.3829 | 0.1984 | 0.9299 |
| CEEMDAN-IF-MPSO-SVM | 0.3422 | 0.1813 | 0.9356 |
| ICEEMDAN-IF-PSO-SVM | 0.3453 | 0.1741 | 0.9406 |
| ICEEMDAN-IF-MPSO-SVM | 0.2607 | 0.1329 | 0.9654 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Liu, Y.; Li, T.; Xie, X.; Chang, C. The Short-Term Forecasting of Asymmetry Photovoltaic Power Based on the Feature Extraction of PV Power and SVM Algorithm. Symmetry 2020, 12, 1777. https://doi.org/10.3390/sym12111777
Wang L, Liu Y, Li T, Xie X, Chang C. The Short-Term Forecasting of Asymmetry Photovoltaic Power Based on the Feature Extraction of PV Power and SVM Algorithm. Symmetry. 2020; 12(11):1777. https://doi.org/10.3390/sym12111777
Chicago/Turabian StyleWang, Lishu, Yanhui Liu, Tianshu Li, Xinze Xie, and Chengming Chang. 2020. "The Short-Term Forecasting of Asymmetry Photovoltaic Power Based on the Feature Extraction of PV Power and SVM Algorithm" Symmetry 12, no. 11: 1777. https://doi.org/10.3390/sym12111777
APA StyleWang, L., Liu, Y., Li, T., Xie, X., & Chang, C. (2020). The Short-Term Forecasting of Asymmetry Photovoltaic Power Based on the Feature Extraction of PV Power and SVM Algorithm. Symmetry, 12(11), 1777. https://doi.org/10.3390/sym12111777




