A Fast Non-Linear Symmetry Approach for Guaranteed Consensus in Network of Multi-Agent Systems
Abstract
1. Introduction
2. Background and Methods
3. Theoretical Result
- is a non-linear model as well as DeGroot’s model, which means that it has fast convergence;
- is distinguished by a less complicated computation as well as the non-linear stochastic operators of CQSO, DSQO, and EDSQO; and,
- avoids the problem of periodic and non-changing initial values as in the case of EDSQO.
4. Discussion and Numerical Solution
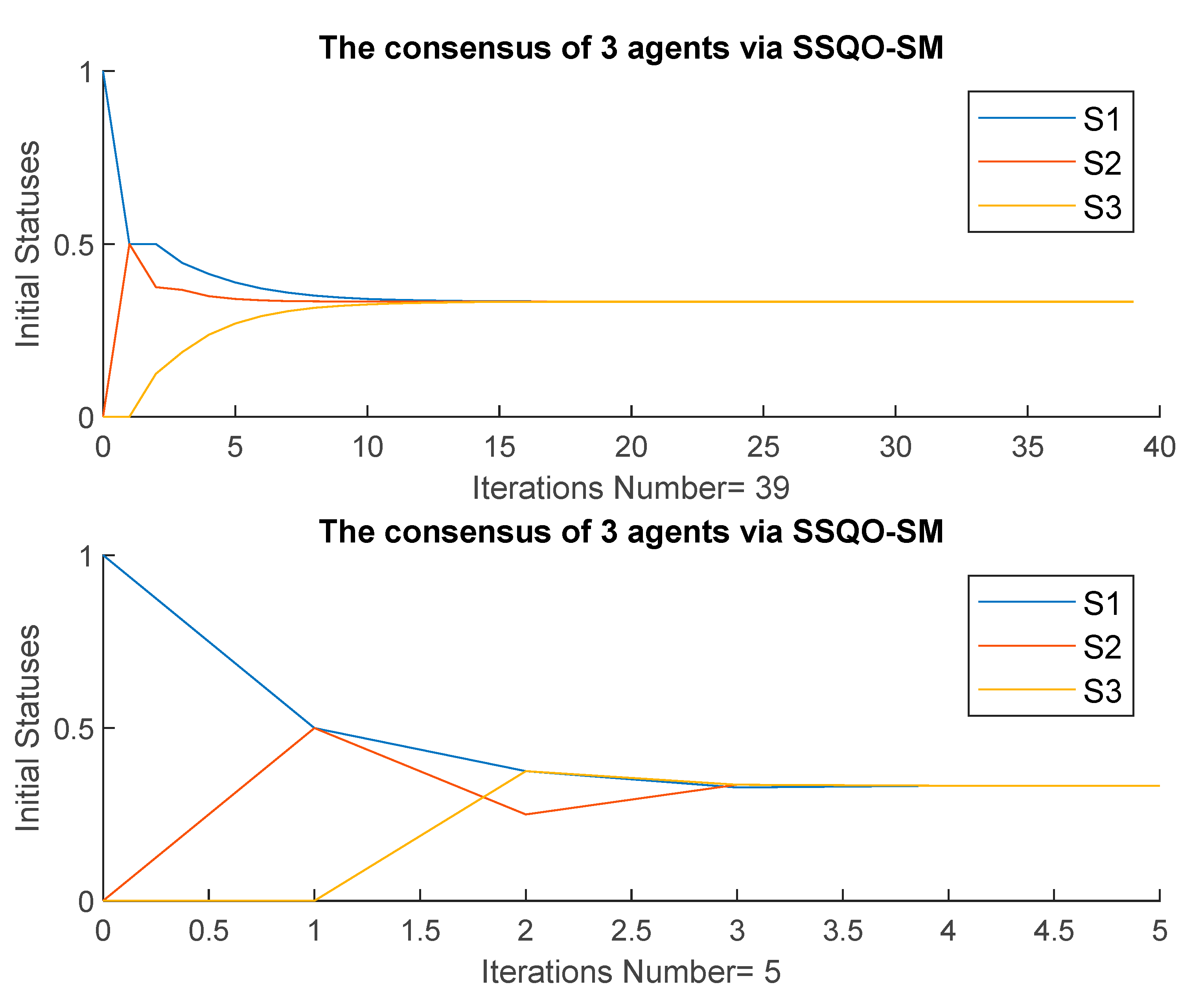
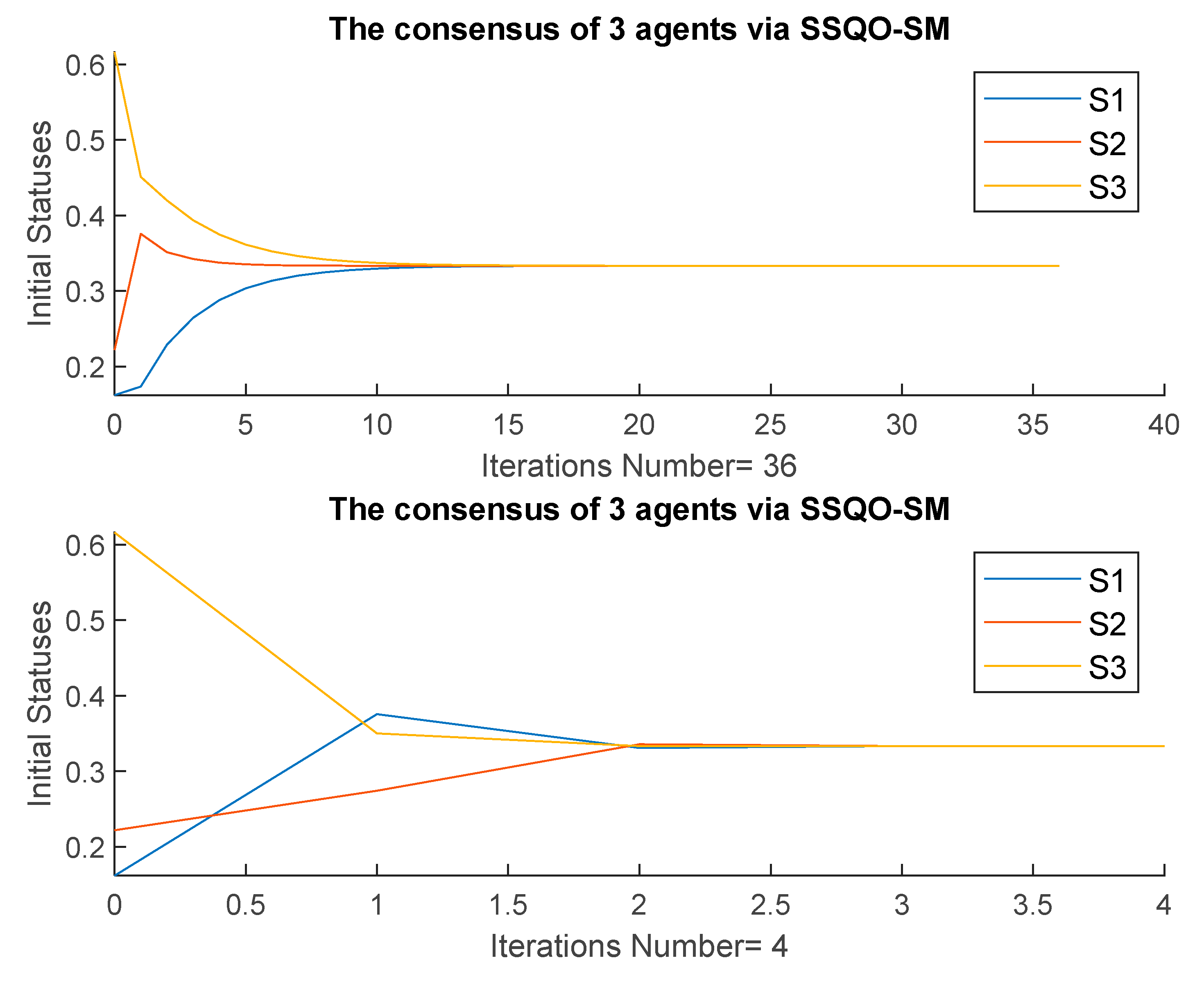
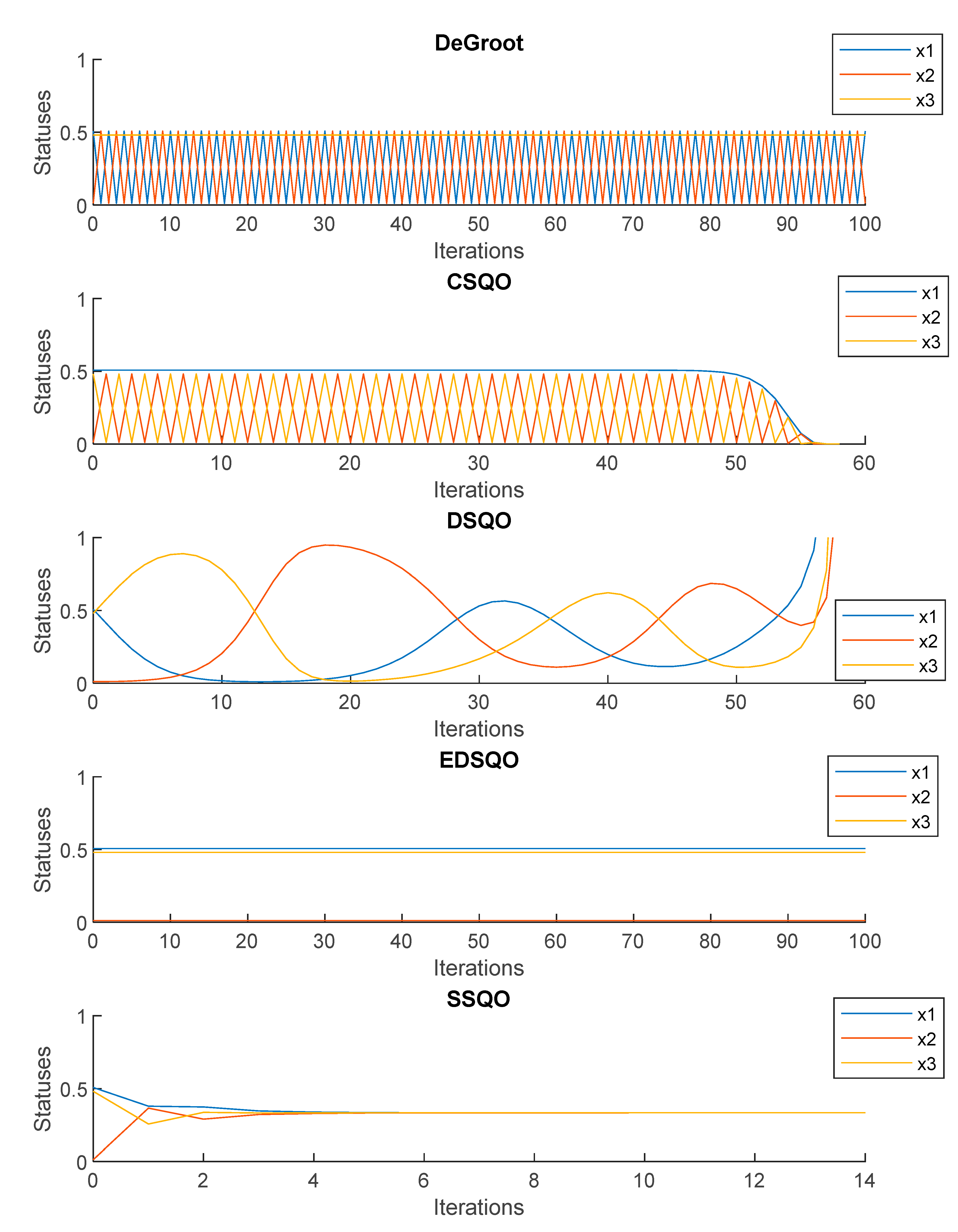
4.1. Three Agents
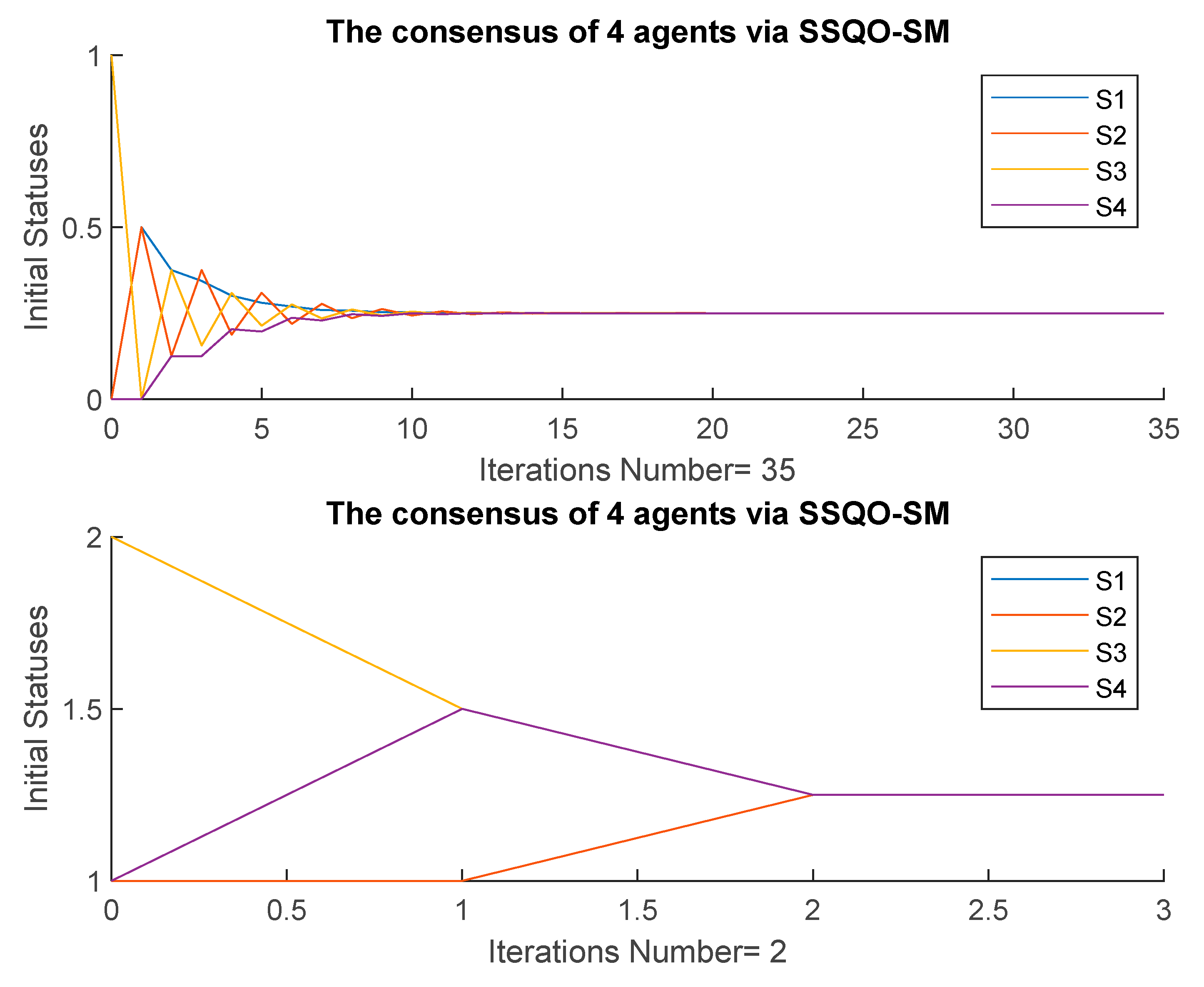
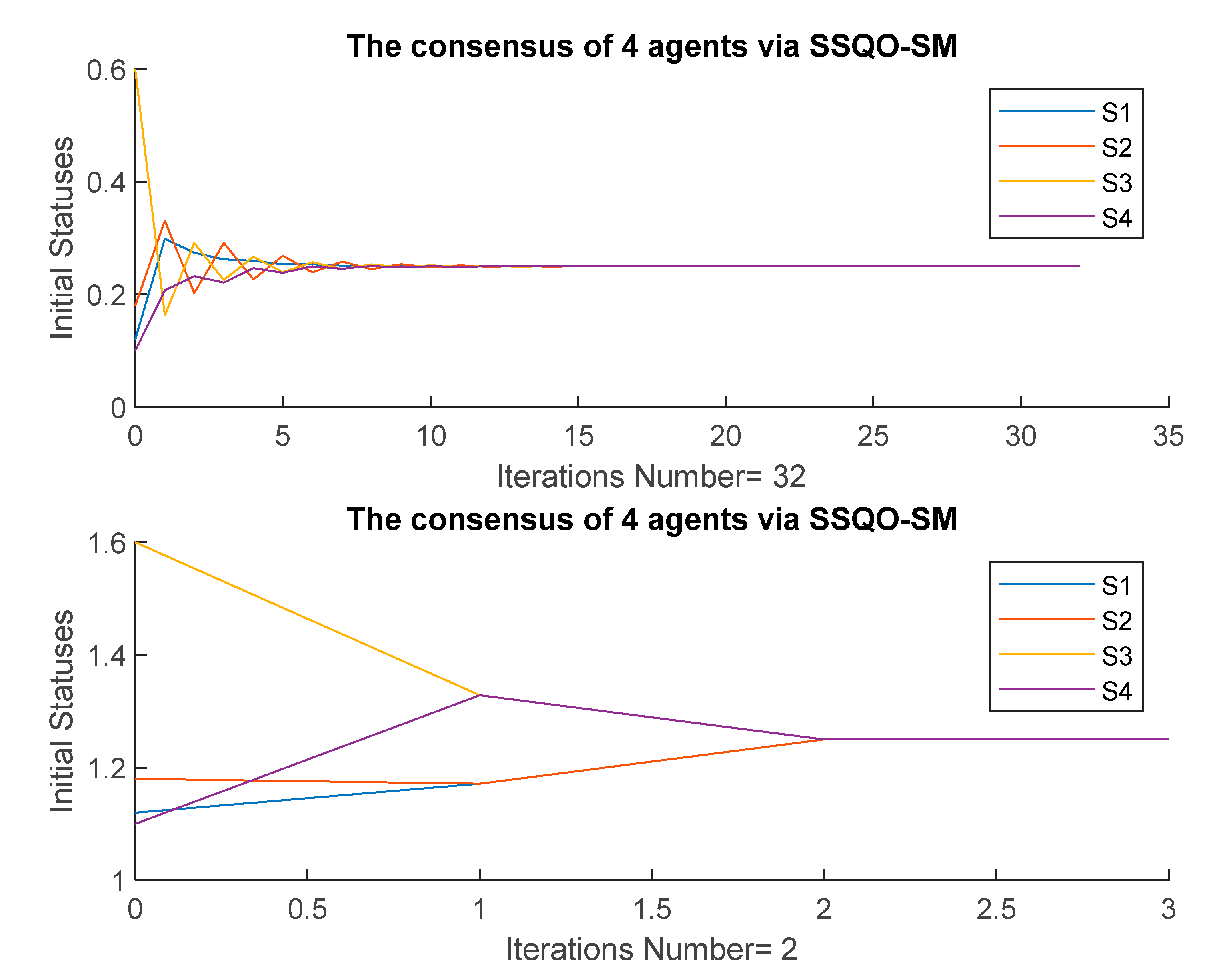
4.2. Four Agents
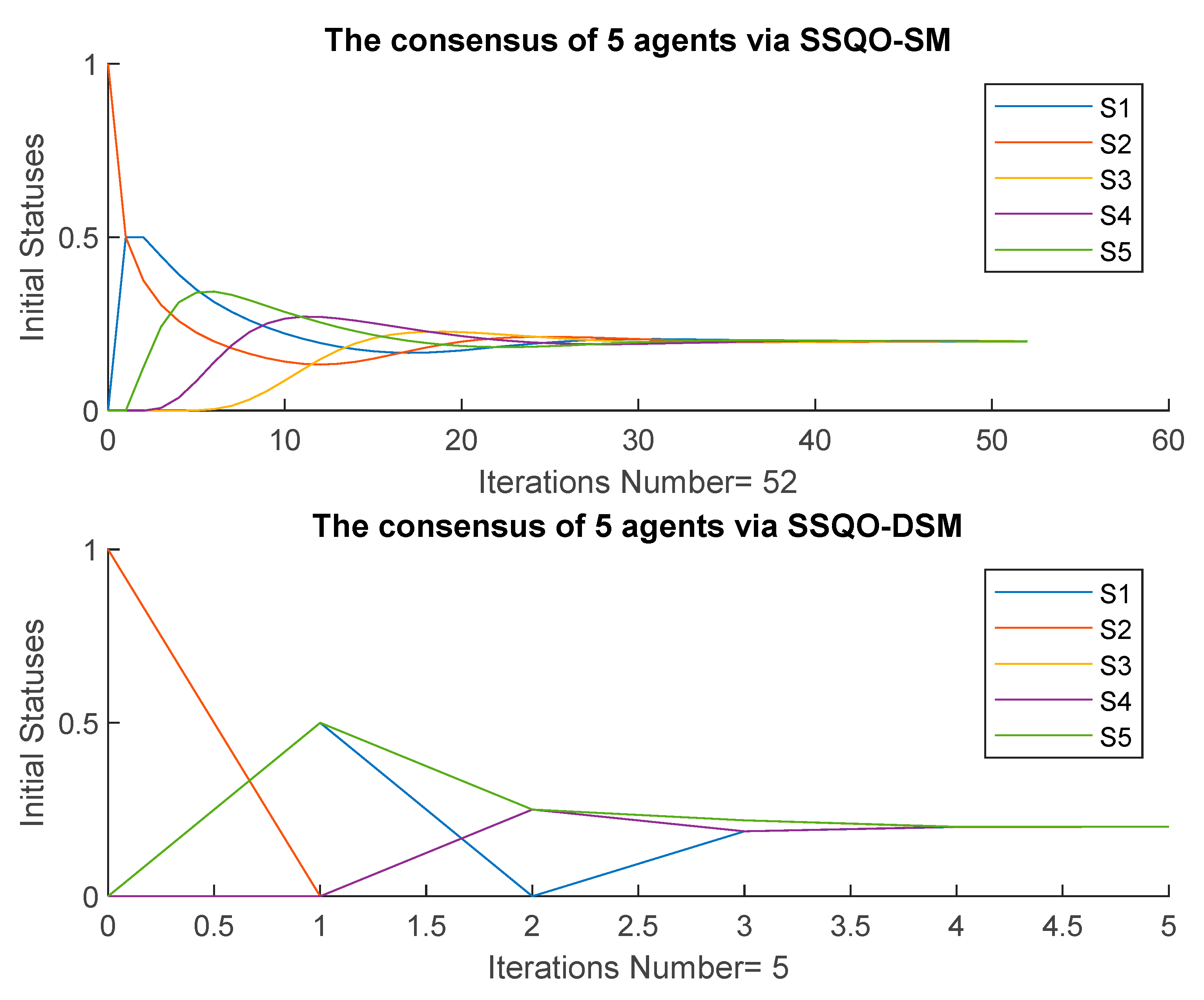
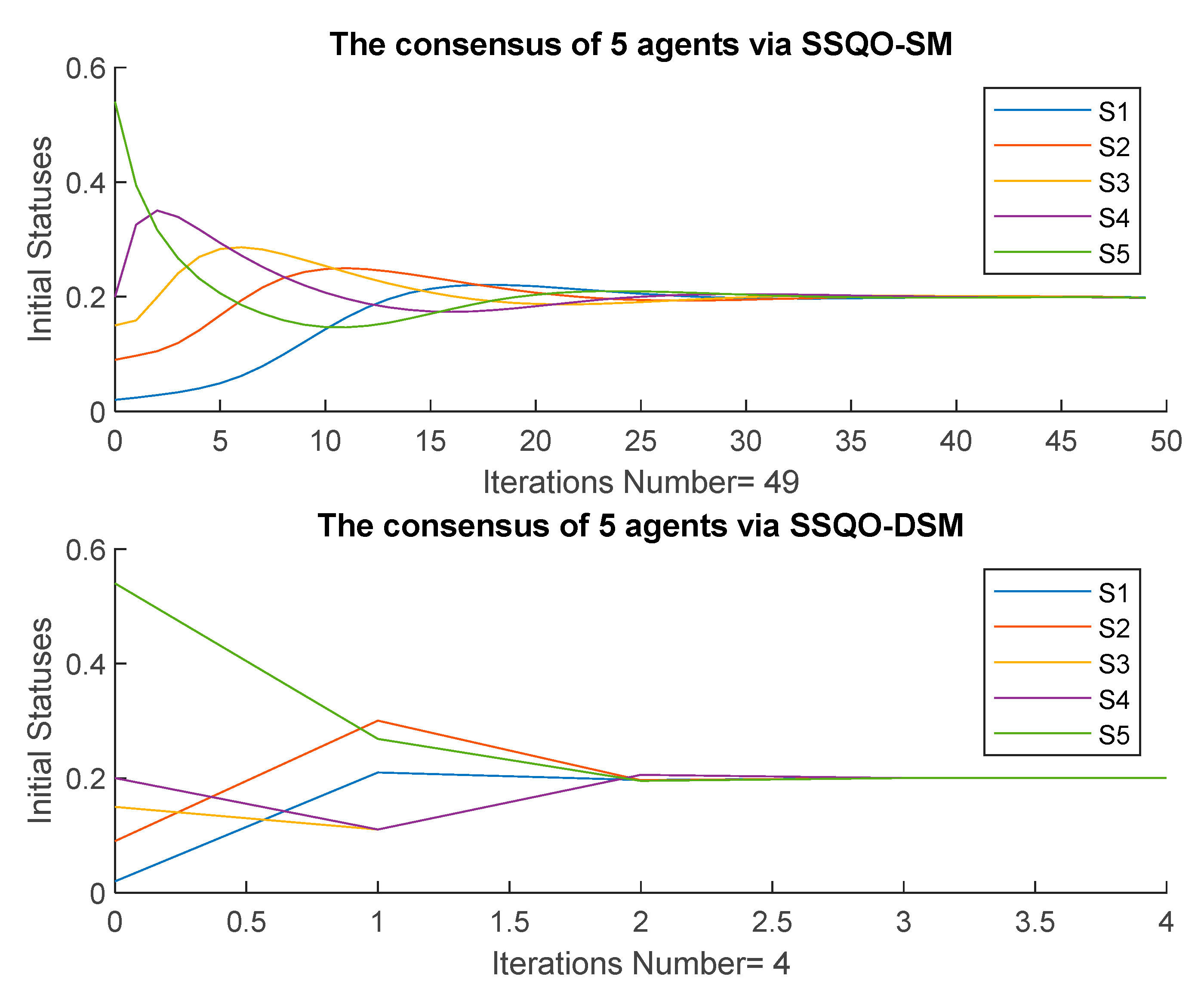
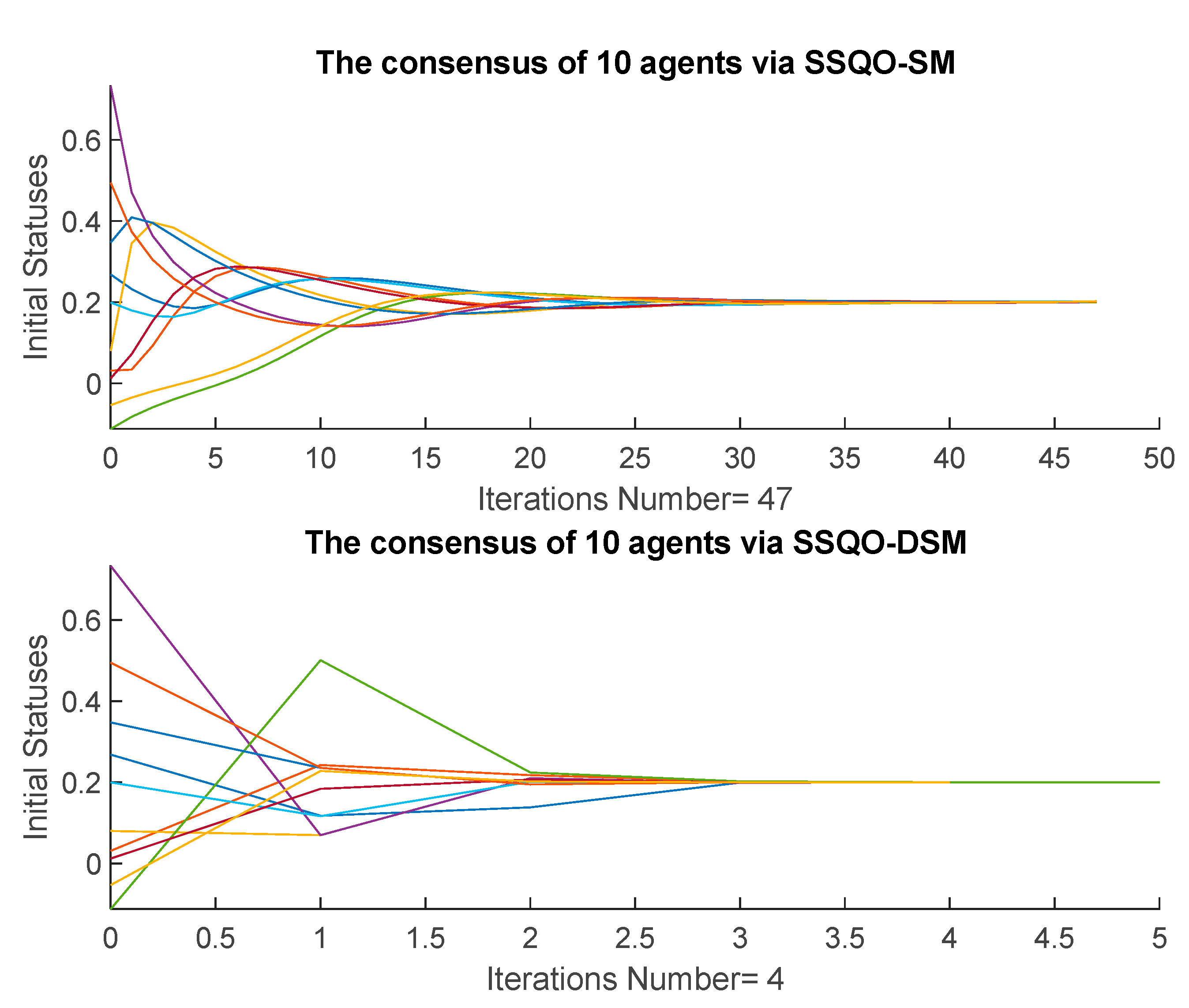
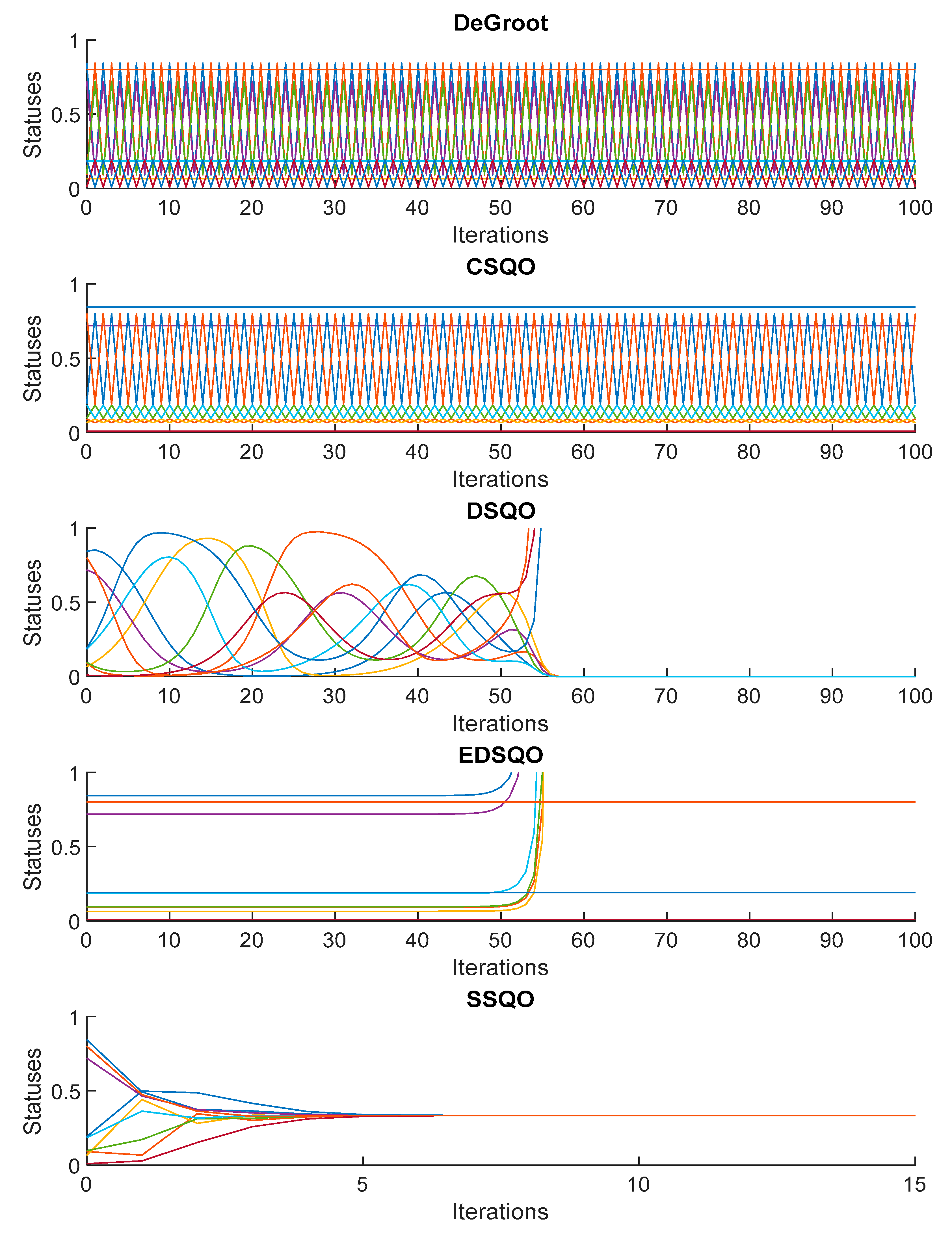
4.3. Five Agents
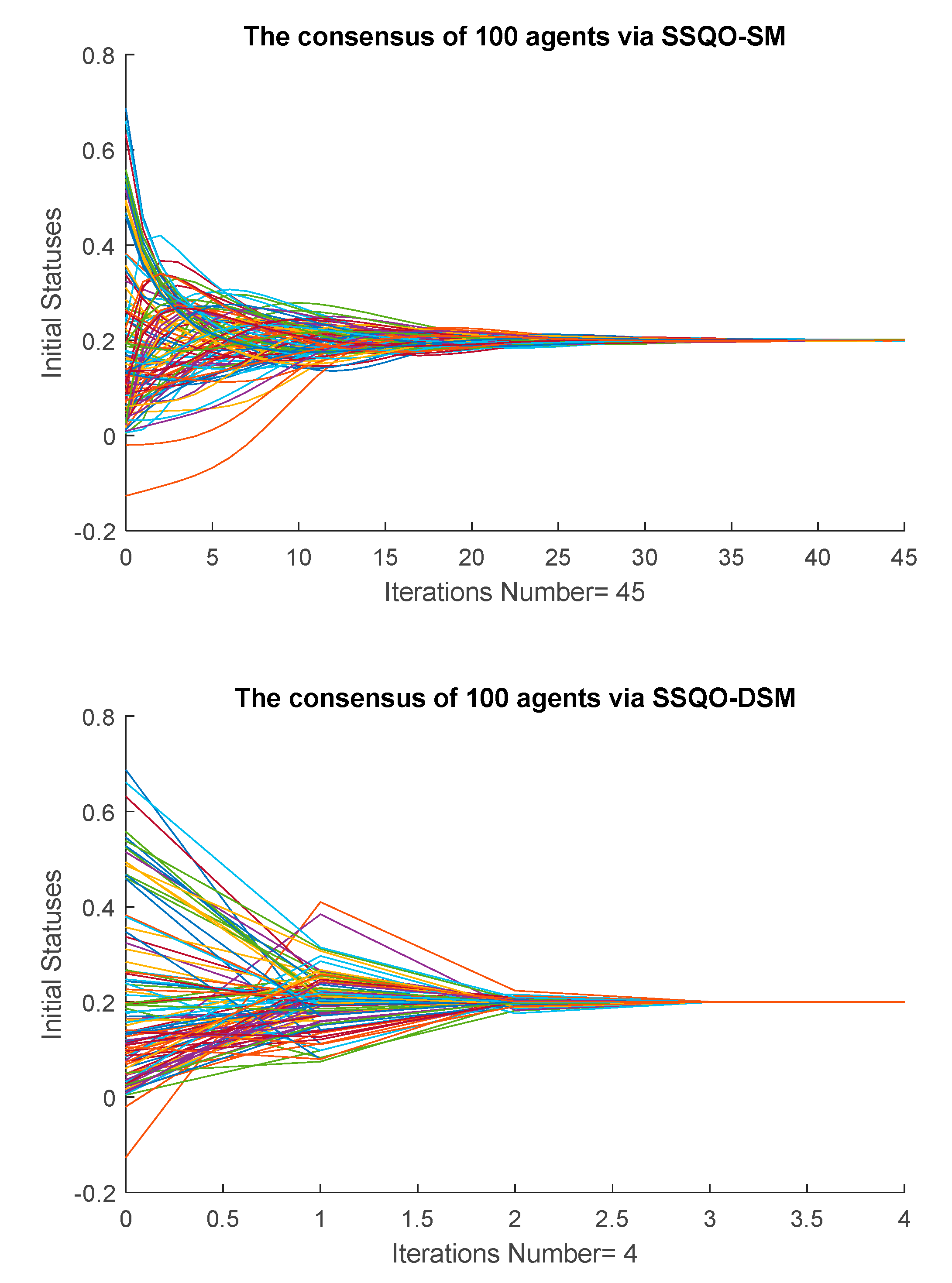
5. Comparison of the Consensus SSQO Model with Other Consensus Models
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abdulghafor, R.; Abdullah, S.S.; Turaev, S.; Othman, M. An overview of the consensus problem in the control of multi-agent systems. Automatika 2018, 59, 143–157. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S.; Zeki, A.; Al-Shaikhli, I. Reach a non-linear consensus for MAS via doubly stochastic quadratic operators. Int. J. Control. 2018, 91, 1431–1459. [Google Scholar] [CrossRef]
- Van der Hoek, W.; Wooldridge, M. Multi-agent systems. Found. Artif. Intell. 2008, 3, 887–928. [Google Scholar]
- Chen, Y.; Lu, J.; Yu, X.; Hill, D.J. Multi-Agent Systems with Dynamical Topologies: Consensus and Applications. IEEE Circuits Syst. Mag. 2013, 13, 21–34. [Google Scholar] [CrossRef]
- Bradley, R. Reaching a consensus. Soc. Choice Welf. 2007, 29, 609–632. [Google Scholar] [CrossRef]
- Berger, R.L. A Necessary and Sufficient Condition for Reaching a Consensus Using DeGroot’s Method. J. Am. Stat. Assoc. 1981, 76, 415–418. [Google Scholar] [CrossRef]
- Tsitsiklis, J.N.; Bertsekas, D.; Athans, M. Distributed asynchronous deterministic and stochastic gradient optimization algorithms. IEEE Trans. Autom. Control 1986, 31, 803–812. [Google Scholar] [CrossRef]
- Tsitsiklis, J.N. Problems in Decentralized Decision Making and Computation; MIT Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Lynch, N.A. Distributed Algorithms; Morgan Kaufmann: Burlington, MA, USA, 1996. [Google Scholar]
- Vicsek, T.; Czirok, A.; Ben-Jacob, E.; Cohen, I.; Shochet, O. Novel type of phase transition in a system of self-riven particles. Phys. Rev. Lett. 1995, 75, 1226–1229. [Google Scholar] [CrossRef]
- Bertsekas, D.P.; Tsitsiklis, J.N. Comments on “Coordination of Groups of Mobile Autonomous Agents Using Nearest Neighbor Rules. IEEE Trans. Autom. Control 2007, 52, 968–969. [Google Scholar] [CrossRef]
- Saber, R.; Murray, R. Consensus protocols for networks of dynamic agents. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; IEEE: New York, NY, USA, 2004; Volume 2, pp. 951–956. [Google Scholar]
- Ren, W.; Beard, R.W.; Atkins, E.M. A survey of consensus problems in multi-agent coordination. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; American Automatic Control Council: Evanston, IL, USA, 2005; pp. 1859–1864. [Google Scholar]
- Alex, O.; Tsitsiklis, J.N. Convergence Speed in Distributed Consensus and Control. SIAM Rev. SIAM 2006, 53, 747–772. [Google Scholar]
- Nedic, A.; Ozdaglar, A. Convergence rate for consensus with delays. J. Glob. Optim. 2008, 47, 437–456. [Google Scholar] [CrossRef]
- Duan, P.; Duan, Z.; Chen, G.; Shi, L. Distributed state estimation for uncertain linear systems: A regularized least-squares approach. Automatica 2020, 117, 109007. [Google Scholar] [CrossRef]
- Duan, P.; Liu, K.; Huang, N.; Duan, Z. Event-Based Distributed Tracking Control for Second-Order Multiagent Systems with Switching Networks. IEEE Trans. Syst. Man. Cybern. Syst. 2020, 50, 3220–3230. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Abdullah, S.S.; Turaev, S.; Zeki, A.; Al-Shaikhli, I. Linear and non-linear stochastic distribution for consensus problem in multi-agent systems. Neural. Comput. Appl. 2020, 32, 261–277. [Google Scholar] [CrossRef]
- Yu, W.; Chen, G.; Cao, M.; Kurths, J. Second-order consensus for multi-agent systems with directed topologies and non-linear dynamics. IEEE Trans. Syst. Man. Cybern. Part B 2020, 40, 881–891. [Google Scholar]
- Bishop, A.N.; Doucet, A. Consensus in the Wasserstein Metric Space of Probability Measures. arXiv 2014, arXiv:1404:0145. [Google Scholar]
- Zhu, M.; Martínez, S. Discrete-time dynamic average consensus. Automatica 2010, 46, 322–329. [Google Scholar] [CrossRef]
- Ajorlou, A.; Momeni, A.; Aghdam, A.G. Sufficient conditions for the convergence of a class of non-linear distributed consensus algorithms. Automatica 2011, 47, 625–629. [Google Scholar] [CrossRef]
- Bolouki, S. Linear Consensus Algorithms: Structural Properties and Connections with Markov Chains; Diss. École Polytechnique de Montréal: Montreal, QC, Canada, 2014. [Google Scholar]
- Schwarz, V.; Matz, G. Non-linear average consensus based on weight morphing. In Proceedings of the Acoustics, Speech and Signal Processing (ICASSP) 2012 IEEE International Conference, Kyoto, Japan, 27–29 March 2012; pp. 3129–3132. [Google Scholar]
- Bajovic, D.; Xavier, A.; Moura, E.F.; Sinopoli, B.; Xavier, J. Consensus and Products of Random Stochastic Matrices: Exact Rate for Convergence in Probability. IEEE Trans. Signal Process. 2013, 61, 2557–2571. [Google Scholar] [CrossRef]
- Meng, D.; Jia, Y.; Du, J.; Zhang, J. On iterative learning algorithms for the formation control of non-linear multi-agent systems. Automatica 2014, 50, 291–295. [Google Scholar] [CrossRef]
- Busoniu, L.; Morarescu, I.C. Consensus for black-box non-linear agents using optimistic optimization. Automatica 2014, 50, 1201–1208. [Google Scholar] [CrossRef]
- Ma, L.; Huo, X.; Zhao, X.; Zong, G. Adaptive fuzzy tracking control for a class of uncertain switched non-linear systems with multiple constraints: A small-gain approach. Int. J. Fuzzy Syst. 2019, 21, 2609–2624. [Google Scholar] [CrossRef]
- Song, J.-S.; Chang, X.-H. H∞ controller design of networked control systems with a new quantization structure. Appl. Math. Comput. 2020, 376, 125070. [Google Scholar] [CrossRef]
- Fagnani, F. Consensus dynamics over networks. Tech. Pap. 2014, 66, 1–25. [Google Scholar]
- Wang, H.; Liao, X.; Huang, T.; Li, C. Cooperative distributed optimization in multi-agent networks with delays. IEEE Trans. Syst. Man. Cybern. Syst. 2015, 45, 363–369. [Google Scholar] [CrossRef]
- Ghaderi, J.; Srikant, R. Opinion dynamics in social networks with stubborn agents: Equilibrium and convergence rate. Automatica 2014, 50, 3209–3215. [Google Scholar] [CrossRef]
- Priolo, A.; Gasparri, A.; Montijano, E.; Sagues, C. A distributed algorithm for average consensus on strongly connected weighted digraphs. Automatica 2014, 50, 946–951. [Google Scholar] [CrossRef]
- Hendrickx, J.M.; Shi, G.; Johansson, K.H. Finite-Time Consensus Using Stochastic Matrices with Positive Diagonals. IEEE Trans. Autom. Control 2014, 60, 1070–1073. [Google Scholar] [CrossRef]
- Lin, P.; Ren, W. Constrained Consensus in Unbalanced Networks with Communication Delays. IEEE Trans. Autom. Control 2013, 59, 775–781. [Google Scholar] [CrossRef]
- LeBlanc, H.J.; Zhang, H.; Sundaram, S.; Koutsoukos, X. Consensus of multi-agent networks in the presence of adversaries using only local information. In Proceedings of the 1st international conference on High Confidence Networked Systems, Beijing, China, 17–19 April 2012; Association for Computing Machinery: New York, NY, USA, 2012; pp. 1–10. [Google Scholar]
- Matei, I.; Baras, J.S.; Somarakis, C. Convergence Results for the Linear Consensus Problem under Markovian Random Graphs. SIAM J. Control Optim. 2013, 51, 1574–1591. [Google Scholar] [CrossRef]
- Moreau, L. Stability of multi-agent systems with time-dependent communication links. IEEE Trans. Automat. Contr. 2015, 50, 169–182. [Google Scholar] [CrossRef]
- Blondel, V.D.; Hendrickx, J.M.; Olshevsky, A.; Tsitsiklis, J.N. Convergence in multi-agent coordination, consensus, and flocking. In Proceedings of the 44th IEEE Conference, Seville, Spain, 12–15 December 2005; pp. 2996–3000. [Google Scholar]
- Fang, L.; Antsaklis, P. On Communication Requirements for Multi-agent Consensus Seeking. In Lecture Notes in Control and Information Science; Springer: Berlin/Heidelberg, Germany, 2006; pp. 53–67. [Google Scholar]
- Xiao, F.; Wang, L. Consensus protocols for discrete-time multi-agent systems with time-varying delays. Automatica 2008, 44, 2577–2582. [Google Scholar] [CrossRef]
- Jadbabaie, A.; Lin, J.; Morse, A.S. Coordination of groups of mobile autonomous agents using nearest neighbor rules. IEEE Trans. Autom. Control 2003, 48, 988–1001. [Google Scholar] [CrossRef]
- Moreau, L. Stability of continuous-time distributed consensus algorithms. In Proceedings of the 2004 43rd IEEE Conference on Decision and Control (CDC) (IEEE Cat. No.04CH37601), Nassau, Bahamas, 14–17 December 2004; Volume 4, pp. 3998–4003. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W. Consensus seeking in multi-agent systems under dynamically changing interaction topologies. IEEE Trans. Automat. Contr. 2005, 50, 655–661. [Google Scholar] [CrossRef]
- Ghabcheloo, R.; Aguiar, A.P.; Pascoal, A.M.; Silvestre, C.J. Synchronization in multi-agent systems with switching topologies and non-homogeneous communication delays. In Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 2327–2332. [Google Scholar]
- Münz, U.; Papachristodoulou, A.; Allgöwer, F. Consensus reaching in multi-agent packet-switched networks with non-linear coupling. Int. J. Control 2009, 82, 953–969. [Google Scholar] [CrossRef]
- Li, Z.; Duan, Z.; Chen, G.; Huang, L. Consensus of multi-agent systems and synchronization of complex networks: A unified viewpoint. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 57, 213–224. [Google Scholar]
- Li, Z.; Duan, Z.; Chen, G. Dynamic consensus of linear multi-agent systems. IET Control Theory Appl. 2011, 5, 19–28. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S. Consensus of fractional non-linear dynamics stochastic operators for multi-agent systems. Inf. Fusion 2018, 44, 1–21. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S.; Izzuddin, M. Non-linear Models for Distributed Consensus Modified from DSQO in Networks of Dynamic Agents. In Proceedings of the 4th International Conference on Mathematical Sciences, Putrajaya, Malaysia, 15–17 November 2016. [Google Scholar]
- Abdulghafor, R.; Almotairi, S.; Almohamedh, H.; Turaev, S.; Almutairi, B. Non-linear Consensus Protocol Modified from Doubly Stochastic Quadratic Operators in Networks of Dynamic Agents. Symmetry 2019, 11, 1519. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S.; Tamrin, I. Non-linear consensus for multi-agent systems using positive intractions of doubly stochastic quadratic operators. Int. J. Perceptive Cogn. Comput. 2016, 2, 19–22. [Google Scholar]
- Abdulghafor, R.; Turaev, S.; Zeki, A.; Abubaker, A. Non-linear convergence algorithm: Structural properties with doubly stochastic quadratic operators for multi-agent systems. J. Artif. Intell. Soft Comput. Res. 2018, 8, 49–61. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Almotairi, S.; Almohamedh, H.; Almutairi, B.; Bajahzar, A.; Almutairi, S.S. A Non-linear Convergence Consensus: Extreme Doubly Stochastic Quadratic Operators for Multi-Agent Systems. Symmetry 2020, 12, 1519. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S.; Zeki, A.; Shahidi, F. The convergence consensus of multi-agent systems controlled via doubly stochastic quadratic operators. In Proceedings of the 2015 International Symposium on Agents, Multi-Agent Systems and Robotics (ISAMSR), Putrajaya, Malaysia, 18–19 August 2015; Volume 22, pp. 59–64. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Shahidi, F.; Zeki, A.M.; Turaev, S. Dynamics of doubly stochastic quadratic operators on a finite-dimensional simplex. Open Math. 2016, 14, 509–519. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S.; Zeki, A. Necessary and Sufficient Conditions for Complementary Stochastic Quadratic Operators of Finite-Dimensional Simplex. Sukkur IBA J. Comput. Math. Sci. 2017, 1, 22–27. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Turaev, S.; Abubakar, A.; Zeki, A. The Extreme Doubly Stochastic Quadratic Operators on Two Dimensional Simplex. In Proceedings of the 4th International Conference on Advanced Computer Science Applications and Technologies (ACSAT), Kuala Lumpur, Malaysia, 8–10 December 2015; pp. 192–197. [Google Scholar]
- Shahidi, F.; Ganikhodzhaev, R.; Abdulghafor, R. The dynamics of some extreme doubly stochastic quadratic operators. Middle East J. Sci. Res. 2013, 13, 59–63. [Google Scholar]
- Abdulghafor, R.; Abdullah, S.S.; Turaev, S.; Hassan, R. The non-linear limit control of EDSQOs on finite dimensional simplex. Automatika 2019, 60, 404–412. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Shahidi, F.; Zeki, A.M.; Turaev, S. Dynamics Classifications of Extreme Doubly Stochastic Quadratic Operators on 2D Simplex. In Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2015; pp. 323–335. [Google Scholar]
- Bernstein, S. Solution of a Mathematical Problem Connected with the Theory of Heredity. Ann. Math. Stat. 1942, 13, 53–61. [Google Scholar] [CrossRef]
- DeGroot, M.H. Reaching a consensus. J. Am. Stat. Assoc. 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Abdulghafor, R.; Almohamedh, H.; Almutairi, B.; Wani, S.; Alharbi, A.; Almutairi, S.S.; Almotairi, S. EDSQ Operator on 2DS and Limit Behavior. Symmetry 2020, 12, 820. [Google Scholar] [CrossRef]
| Name | Advantages | Disadvantages | Evolutionary Operators | Transition Matrix | |
|---|---|---|---|---|---|
| 1 | DeGroot [63] |
|
| ||
| 2 | CSQO [18] |
|
| ||
| 3 | DSQO [2] |
|
| ||
| 4 | EDSQO [54] |
|
| ||
| 5 | SSQO proposed model |
|
| . |
| Name | Advantages | Disadvantages | |
|---|---|---|---|
| 1 | DeGroot [63] | This is a transition matrix under the rules of the DeGroot linear consensus model, which is the drawback that cannot reach to consensus. | |
| 2 | CSQO [18] | , , | This is a transition matrix under the rules of the CSQO non-linear consensus model, which is the drawback that cannot reach to consensus. |
| 3 | DSQO [2] | , , | This is a transition matrix under the rules of the DSQO non-linear consensus model, which is the drawback that cannot reach to consensus. |
| 4 | EDSQO [54] | , , | This is a transition matrix under the rules of the EDSQO non-linear consensus model, which is the drawback that cannot reach to consensus. |
| 5 | SSQO proposed model | , , | This is a transition matrix under the rules of the proposed SSQO non-linear consensus model, which avoids the drawback that cannot reach to consensus. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulghafor, R.; Almotairi, S. A Fast Non-Linear Symmetry Approach for Guaranteed Consensus in Network of Multi-Agent Systems. Symmetry 2020, 12, 1692. https://doi.org/10.3390/sym12101692
Abdulghafor R, Almotairi S. A Fast Non-Linear Symmetry Approach for Guaranteed Consensus in Network of Multi-Agent Systems. Symmetry. 2020; 12(10):1692. https://doi.org/10.3390/sym12101692
Chicago/Turabian StyleAbdulghafor, Rawad, and Sultan Almotairi. 2020. "A Fast Non-Linear Symmetry Approach for Guaranteed Consensus in Network of Multi-Agent Systems" Symmetry 12, no. 10: 1692. https://doi.org/10.3390/sym12101692
APA StyleAbdulghafor, R., & Almotairi, S. (2020). A Fast Non-Linear Symmetry Approach for Guaranteed Consensus in Network of Multi-Agent Systems. Symmetry, 12(10), 1692. https://doi.org/10.3390/sym12101692





