Abstract
The equation of state of SU(3) Yang–Mills theory can be modelled by an effective symmetric potential depending on the temperature and on a complex scalar field . Allowing to be dynamical opens the way to the study of spatially localized classical configurations of the scalar field. We first show that spherically symmetric static Q-balls exist in the range , being the deconfinement temperature. Then we argue that Q-holes solutions, if any, are unphysical within our framework. Finally, we couple our matter Lagrangian to Einstein gravity and show that spherically symmetric static boson stars exist in the same range of temperature. The Q-ball and boson-star solutions we find can be interpreted as “bubbles” of deconfined gluonic matter; their mean radius is always smaller than 10 fm.
1. Introduction
A fascinating feature of Yang–Mills theory is the existence of a deconfinement temperature, , above which free color charges (free gluons) may propagate without being confined into color singlets [1,2]. This deconfined phase can be thought as a “gluon plasma”, in analogy with the celebrated quark-gluon plasma experimentally created first at RHIC [3,4], i.e., the deconfined phase of full QCD.
In pure SU() Yang–Mills theory, deconfinement might be driven by the breaking of a global center symmetry, i.e., Z symmetry [5,6], exemplified by the behavior of the Polyakov loop at finite temperature T. The Polyakov loop is defined as , with the temporal component of the Yang–Mills field and the spatial coordinates. P is the path-ordering, g is the strong coupling constant and units where are used. Since gauge transformations belonging to the center of the gauge group only cause to be multiplied by an overall factor, the Polyakov loop is such that the spatial average when the Z symmetry is present (broken), hence when the theory is in a (de)confined phase [2,7]. Hence is commonly seen as an order parameter for Yang–Mills theory at finite T, although it may not be the best physical candidate. As shown in [8], distinct Z phases above do not actually label different physical states. Moreover, the value , giving the free energy of a static color source in the heath bath, may take unphysical complex values above . The real number may be a better candidate, with a free energy given by . It is also argued in [8] that the correlator at large distances may be a proper order parameter. Another relevant order parameter for pure Yang–Mills theory has finally been formulated in [9]: It is the spatial ’t Hooft loop [10], C being a closed spatial contour. shows a perimeter law in the confined phase and an area law in the deconfined phase: and respectively, with P and S the perimeter and the area of the closed contour.
In view of the above results we can safely assume that there exists one scalar field playing the role of an order parameter. Moreover, there should exist a Z temperature-dependent potential , whose global minimum is different at and , reproducing the equation of state computed in lattice QCD [11] in the mean-field approximation—recall that the pressure reads . In the case , the -symmetry should be present through terms in at the lowest-order in a power expansion of V [12]: The explicit form we will use is given in Section 2. In the following we go beyond mean-field theory and treat as a complex, position-dependent, scalar field: This dynamical field mimics the behavior of pure Yang–Mills theory at finite T. The value of being related to the phase of the gluonic matter, we can summarize the aim of our study as follows: We search for configurations describing localized regions of (de)confined gluonic matter, either in flat or curved 750/9.
On one hand we have already shown the existence of nontrivial solutions for , vanishing at infinity, at the deconfinement temperature in flat space-time and at large [13]. On the other hand, nontrivial static configurations in -symmetric potentials have already been found in [14,15]. Most of the effort in the field has been devoted to study the temporal evolution of such solutions in close relation with thermalization issues of experimentally observed quark-gluon-plasma [14,16,17,18,19]. In this work we search for spherically symmetric static Q-ball solutions with a focus on conditions constraining their existence: temperature range, radial nodes, etc. Less standard solitons as Q-holes [20], never studied up to now within that framework, are also discussed. Q-balls and Q-holes are discussed in Section 3 and Section 5.
Finally, we couple our Z3-symmetric Lagrangian to Einstein gravity. To our knowledge, very few attempts to describe to interplay between gravity and confinement/deconfinement phase transition can be found in the literature. One can quote [21,22], respectively discussing the loss of simultaneity between chiral restoration and deconfinement in curved space, and the possible existence of deconfined regions near a black hole horizon. Here we go one step further by building “particle-like” solutions for our scalar field that are known to appear in pure -dimensional Yang–Mills theory coupled to Einstein gravity, see the seminal paper [23]. Within our approach the Yang–Mills degrees of freedom are replaced by a complex scalar field, whose associated Q-balls, when coupled to gravity, are called boson stars—see the review [24] for more recent references. To our knowledge, such a problem has never been addressed at finite temperature although research devoted to “QCD boson stars” (at ) is currently ongoing [25]. We build gravitating solutions of static-boson-star-type, i.e., spherically symmetric localized configurations of the scalar field that lead to an asymptotically flat metric without singularity, see Section 5.
2. The Model
2.1. Z3-Symmetric Potential
Let us model SU(3) Yang–Mills theory at finite temperature by an effective Lagrangian based on a complex scalar field plus Z3−symmetry. We use the potential V of Ref. [26] which reads
with
and
We have retained the above parametrization because it to an optimal agreement with the equation of state of pure SU(3) Yang–Mills theory computed in lattice QCD [11], and also with the full lattice QCD equation of state at zero and nonzero chemical potential when coupled to a Nambu–Jona–Lasinio (NJL) model [26]. We note that the latter reference explicitly identifies the scalar field with the Polyakov loop. In fact, their result is more general since can be regarded as the actual order parameter of the model, not necessarily the Polyakov loop.
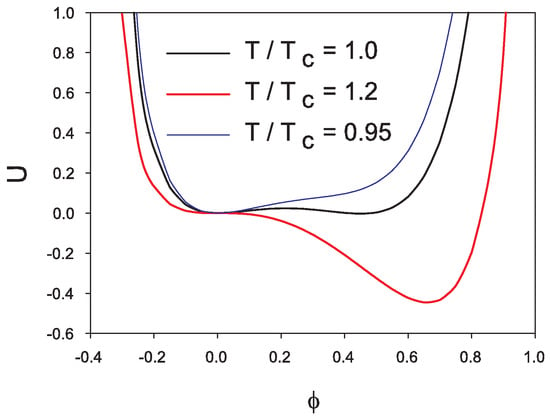
Potential (1) is displayed in Figure 1 for the values (3) of the parameters and for several temperatures. The change in minimum is clearly seen above and below : A (non)vanishing value for gives the minimum of U in the (de)confined phase. We notice that potential (1) is only Z3-symmetric and not U(1)-symmetric as is often the case in Lagrangians based on a complex scalar field, with typical potentials of the form [27]. A U(1)-symmetry can be recovered in the large- limit of Z-symmetric potentials, see [13,28].
According to the suggestion of e.g., Ref. [29], we choose for a kinetic part of the form , which has both the correct energy dimensions and the expected -scaling when the gauge group SU() is chosen. is the ’t Hooft coupling. Minkowski metric has signature . In our SU(3) case, recalling that , we can write our Lagrangian as
where , are the space-time coordinates. It is convenient to further define dimensionless variables related to the original (physical) ones by
so that the above Lagrangian can be replaced by the dimensionless one
where and where T is expressed in units of .
It is worth estimating the physical length used in the model. First, a typical value for the deconfinement temperature in pure gauge QCD is GeV [30]. Second, a way to estimate is to note that the short-range part of the static interaction between a quark and an antiquark scales as , at least from to . Lattice studies, performed at , favor up to [31], which is the value we retain here. We are then in position to estimate that, at ,
2.2. Coupling to Einstein Gravity
The coupling of the above Lagrangian to gravity can be performed by minimally coupling the scalar field to Einstein gravity: The action reads
with the effective coupling constant
The replacement of the partial derivatives by covariant ones in (6) must be performed.
3. Q-Balls
3.1. Ansatz and Existence Conditions
We begin by considering Lagrangian (6) where and are replaced by in order to recover the usual U(1)-symmetry needed to build Q-balls solutions.
The classical equations of motion in flat space-time with potential read
plus the complex conjugated equation. We then perform the usual Q-ball ansatz on the scalar field:
where and where . The solutions we will build can be characterized by their mas M and by a dimensionless conserved charge Q, respectively defined by
with and
The temporal component of the energy-momentum tensor represents the energy density, given by
The conserved charge Q finds its origin in the (artificially restored) U(1)-symmetry of the considered Lagrangian, leading to a conserved Noether current of the form , Q being the space integral of . Axially symmetric solutions with are spinning Q-balls whose angular momentum J is related to the charge Q according to [27]. Here we focus on non-spinning Q-balls.
We have studied the equations for generic values of although it is clear that only the solutions corresponding to are physically relevant for the potential under consideration: The original potential is Z3-symmetric, not U(1). Note also that if is a real solution of the equations of motion, with is also a solution because of the system’s symmetry.
The mass term of the potential plays a crucial role in the existence of the solutions. In a power expansion in ,
General results on Q-balls [27] state that the soliton exist for with
In particular, if the potential is negative in some interval of values of , the value belongs to the spectrum of the boson star. This turns out to be the case for . The condition also needs to be fulfilled; in terms temperature, this corresponds to . As a consequence, the general properties of Q-balls solutions suggest that Q-ball solutions with zero frequency will exist for .
The parametrization (2) of the potential is not unique. In particular, a power expansion of the form
is often used in effective YM theories at finite T, the choice , , leading to a good agreement with lattice QCD data [32]. Using this alternative choice would not forbid the existence of Q-ball solutions: The mass term is positive above and the criterion (16) leads to , so solitons are allowed also in this case.
3.2. Numerical Results
A numerical resolution of the equations (10) can now be performed. We use a collocation method for boundary-value ordinary differential equations, equipped with an adaptive mesh selection procedure [33]. The regularity of the solution at the origin implies , the finiteness of the energy and the charge impose . These are the boundary conditions.
We present in Figure 2 the spectrum of the Q-balls for . It can be observed that no Q-ball solution with can be found below : It is a nice feature of our model that it does not lead to solutions modelling deconfined matter below . In the range suggested by the above analysis however, such solutions can be found. From now on, we concentrate on the latter solutions. Our results are summarized in Figure 3 and Figure 4.
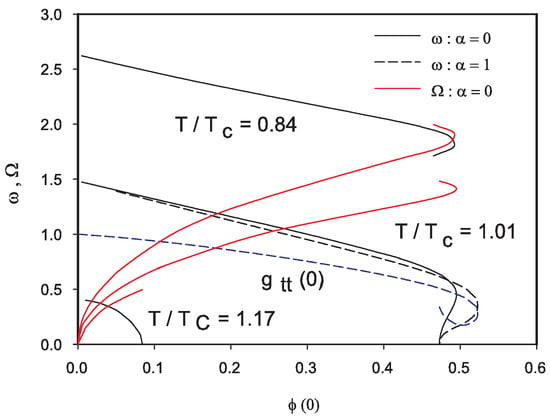
Figure 2.
Relation between and versus for three values of in flat space-time () (solid lines). The dotted lines represent and in the case for gravitating solutions ().
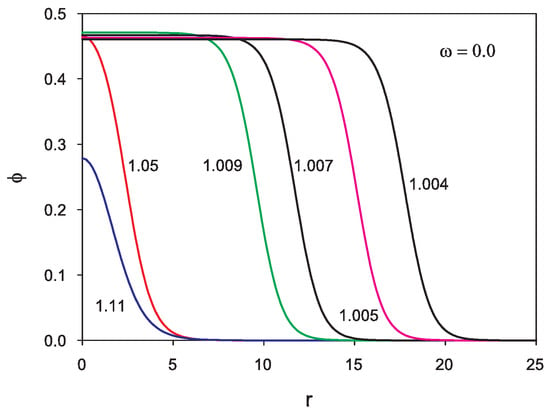
Figure 3.
Profiles of for several values of . Distances are in units of .
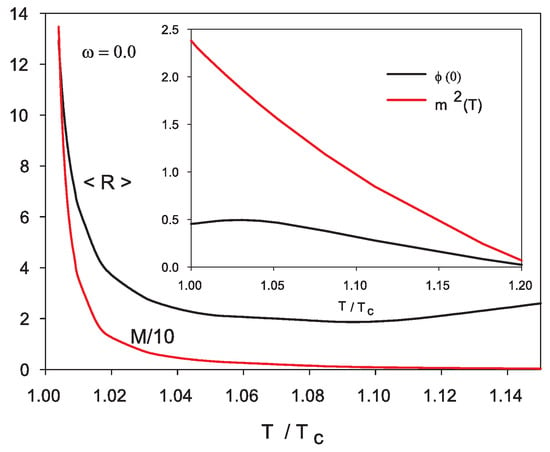
Figure 4.
Evolution of the mean radius as a function of , the insert contains and the mass (12) of the scalar field. Distances are in units of and masses are in units of .
Our numerical analysis shows that in the limit the scalar function approaches uniformly the null function as expected by the existence criterion discussed before. The limit reveals a peculiar behavior of the solitons: Their mean radius and mass increase considerably. In this limit the scalar function is closer and closer to a nonzero constant solution, leading to the observed increase in mass and mean radius.
All the Q-balls we find have a mean radius smaller than 14 fm and are lighter than GeV. Similar solutions were found in [14] with a simpler, power-law, symmetric potential of the form . At they find a soliton with a typical size of 1.5−2 fm while we find a Q-ball with mean radius 1.43 fm and mass 200 MeV at the same temperature. Other results are obtained in [14] but in dimensions so they cannot be compared to ours.
We have tried to construct radially excited solutions, i.e., solutions where the radial function presents one or more nodes, but so far, we cannot find any. The absence of solutions presenting nodes for our model can be explained by the following argument. In general, the existence of node solutions is closely related to the shape of the effective potential
Several conditions are necessary for node solutions to exist [27,34]: (i) should be a local maximum of , (ii) the effective potential should admit local minima for both signs of . It would be challenging to have a generic proof of the absence of node solutions with our potential but an inspection of the potential quickly reveals that no local minimum exist for when (see Figure 1), so the condition (ii) cannot be fulfilled when .
The spectrum of the fundamental Q-ball appears quite different with the present potential than in more conventional U(1)-symmetric potentials. For example, one of us previously studied Q-balls with the SUSY-inspired potential , with [35]. In contrast to our potential, solutions can be constructed for arbitrarily large values of the central density with the latter potential, and radially excited solitons can be obtained. We considered an effective potential consisting of a linear superposition of our potential and the SUSY-potential. The latter is known to admit node solutions: with . It turns out that when we progressively deform the SUSY-potential into our potential (say with a fixed value ) the zero-node solutions get continuously deformed and the frequency decreases with increasing the mixing parameter y. By contrast, for the one node solution, the quickly reaches and the solution becomes oscillating.
3.3. Symmetry Breaking
An obvious outlook is to include the matter sector of QCD in our approach. As discussed in [12], an immediate effect of quarks is the breaking of symmetry in the potential and the simplest way to mimic that symmetry breaking is to add a term proportional to or even to the potential. A more rigorous treatment of quark fields may be achieved by coupling to a NJL Lagrangian [15,36]. Within mean-field approximation for quarks, it has been show in [37] that complex-valued solutions of Q-ball-type still exist with broken -symmetry. A question arising at this stage is therefore: May the Q-balls we constructed “survive” to such a symmetry breaking?
We propose to perform the substitution with a real constant parameter. This ansatz breaks the -symmetry while still allowing analytical calculations. In a power expansion in on the real axis, the -term shifts the mass term: . Graphical inspection of the modified potential shows that there is always an interval of values in which is negative above if . Nevertheless a negative value of lowers and therefore lowers the maximal temperature at which Q-balls may be expected ( is indeed a decreasing function of T). If , there always exists an interval of temperatures above for which the existence of Q-balls is guaranteed. We can thus safely assume that the solutions we find will not necessarily disappear in a more realistic theory including quarks.
4. Q-Holes
Q-holes are configurations of the scalar field behaving like (11) but such that and , with a local minimum of the potential under study [20]. Are Q-holes solutions worth being constructed within the present approach?
A necessary condition for Q-holes to exist is that the second maximum of the effective potential (18) is lower than the maximum at the origin [38]. As illustrated in Figure 1, it can only happen below in our model since at vanishing . A configuration where is everywhere nonzero at a temperature below the deconfinement one is not physically relevant; although the problem is interesting from a technical point of view we have thus to discard Q-hole solutions in the present work. The same conclusion holds for the parameterization (17).
5. Boson Stars
The action (8) leads to the Einstein equation
where the energy-momentum tensor is given by . The metric defines and is the covariant derivative. An estimation of this coupling constant in the temperature range under study is . It is so small that no significant change of the solutions can be observed by numerical investigation. To appreciate more clearly the influence of gravity on the system we will construct solutions with and 1.
We search for boson-star solution. First, the ansatz (11) and the boundary conditions are kept for the scalar field. Second, we choose a spherically symmetric ansatz for the metric:
with the boundary conditions (asymptotically flat space-time) and (no singularity at origin). The gravitational mass of these gravitating objects is defined as usual according to . The explicit equations involving , f and l can be found in Appendix B of [34]; we do not recall them here for the sake of simplicity. The same numerical method as for Q-balls is used to construct boson-star solutions [33].
Even for such large values as , our results indicate that gravitating solutions with still exist on roughly the same interval of , see Figure 5. However, the numerical analysis turns out to be tricky in the limit likely because the local minimum of the potential disappears. Our results strongly suggest that the gravitational mass and mean radius increase considerably in the limit as shown by Figure 5, similarly as what is observed in the Q-ball case. As expected, the metric gets more deviated from the Minkowski metric in the central region of the soliton: for instance (see the blue line of Figure 5) and one can expect an essential singularity of the metric to be formed at .
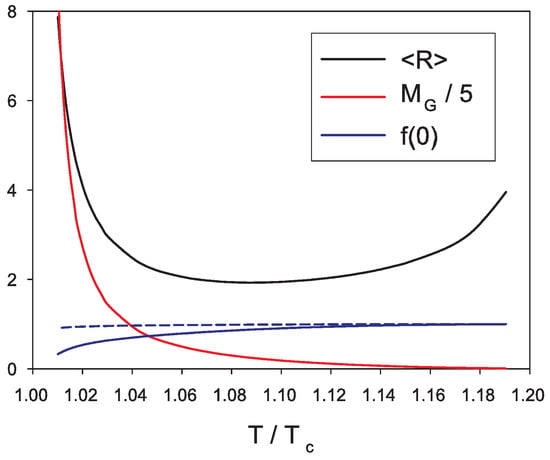
Figure 5.
Evolution of the mean radius (black line, in units of ) and of the gravitational mass (red lines, in units of ) as function of for boson stars. The metric component is represented by the solid (resp. dashed) blue lines for (resp. ). These values depend very weakly on and the curves are mostly superimposed.
The profiles of the solution corresponding to are presented in Figure 6 for (solid lines). This plot clearly demonstrates that the soliton splits the space into two distinct regions: an interior region where is practically constant and strongly curving space-time and a region with where space-time is essentially Minkowski. These regions are separated by a “wall” of the scalar field. The profile of a solution at an intermediate temperature is also shown in Figure 6; the same qualitative features are observed. The boson star finally presents different features for , i.e., the limit of vanishing . In this limit the scalar field approaches uniformly the null function and the Minkowski space-time is approached.
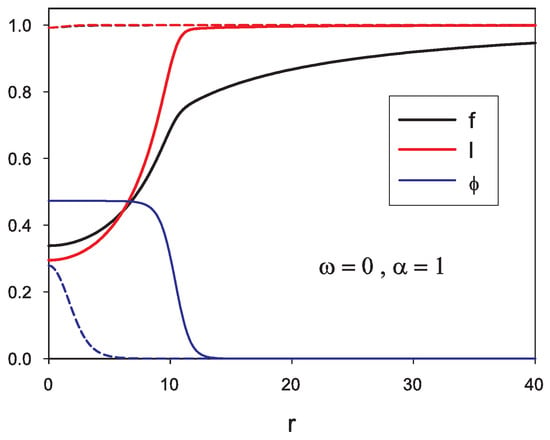
Figure 6.
Profiles of the metric functions and of the scalar field for and two values of the temperature: (solid lines) (dashed lines). The radial variable r is in units of .
The existence of boson-star configurations for implies the existence of such solutions for much smaller, “realistic”, values of the coupling constant around , see Figure 5. Since potential (17) will also lead to Q-balls above , we can state that boson stars also exist with that parameterization. We choose however not to perform full numerical computations since potential (2) leads to a more accurate modelling of QCD equation of state as computed on the lattice.
6. Summary and Outlook
We have built Q-balls and boson stars from a model with a complex scalar field plus a temperature-dependent -symmetric potential mimicking Yang–Mills theory at finite temperature. We have shown that static Q-balls only exist between 1 and 1.21 with a mean radius smaller than 10 fm and that they cannot have radial nodes. The solutions we find are spherically symmetric and the scalar field is such that and ; they can be interpreted as “bubbles” of deconfined gluonic matter. We also showed that Q-holes solutions should be discarded from a physical point of view since they are solutions modelling a deconfined phase, but that can only exist below within our approach. Static boson stars exist in roughly the same temperature range as Q-balls. Their qualitative features are almost independent on the value of the matter-Einstein gravity coupling constant .
To our knowledge, it is the first time that boson stars are constructed from an effective potential such as (2). Typical potentials used in boson-star-related studies are such that solutions exist for , see i.e., [35]. It is worth pointing out that the potential used here even allows the existence of static solutions with .
Computation of the QCD equation of state in curved space-time shows that the latter may affect the phase-diagram of the theory by increasing the splitting between the critical points for chiral and deconfinement transitions [21]. We hope to present generalizations of our boson-star configurations to the case of a nontrivial quark field in a future work; they could shed new light on the interplay between confinement, chiral symmetry and gravity.
Author Contributions
Conceptualization, F.B. and Y.B.; software, Y.B.; validation, F.B. and Y.B.; formal analysis, F.B. and Y.B.; writing—original draft preparation, F.B. and Y.B.; writing—review and editing, F.B. and Y.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Polyakov, A.M. Thermal Properties of Gauge Fields and Quark Liberation. Phys. Lett. B 1978, 72, 477–480. [Google Scholar] [CrossRef]
- Susskind, L. Lattice Models of Quark Confinement at High Temperature. Phys. Rev. D 1979, 20, 2610–2618. [Google Scholar] [CrossRef]
- Arsene, I.; Bearden, I.G.; Beavis, D.; Besliu, C.; Budick, B.; Bøggild, H.; Chasman, C.; Christensen, C.H.; Christiansen, P.; Cibor, J.; et al. Quark gluon plasma and color glass condensate at RHIC? The Perspective from the BRAHMS experiment. Nucl. Phys. A 2005, 757, 1–27. [Google Scholar] [CrossRef]
- Aidala, C.; Akiba, Y.; Alfred, M.; Andrieux, V.; Aoki, K.; Apadula, N.; Asano, H.; Ayuso, C.; Azmoun, B.; Babintsev, V.; et al. Creation of quark–gluon plasma droplets with three distinct geometries. Nat. Phys. 2019, 15, 214–220. [Google Scholar] [CrossRef]
- Yaffe, L.G.; Svetitsky, B. First Order Phase Transition in the SU(3) Gauge Theory at Finite Temperature. Phys. Rev. D 1982, 26, 963. [Google Scholar] [CrossRef]
- Svetitsky, B.; Yaffe, L.G. Critical Behavior at Finite Temperature Confinement Transitions. Nucl. Phys. B 1982, 210, 423–447. [Google Scholar] [CrossRef]
- Weiss, N. The Wilson Line in Finite Temperature Gauge Theories. Phys. Rev. D 1982, 25, 2667. [Google Scholar] [CrossRef]
- Smilga, A.V. Are Z(N) bubbles really there? Ann. Phys. 1994, 234, 1–59. [Google Scholar] [CrossRef]
- Korthals-Altes, C.; Kovner, A.; Stephanov, M.A. Spatial’t Hooft loop, hot QCD and Z(N) domain walls. Phys. Lett. B 1999, 469, 205–212. [Google Scholar] [CrossRef]
- Hooft, G.T. On the Phase Transition Towards Permanent Quark Confinement. Nucl. Phys. B 1978, 138, 1–25. [Google Scholar] [CrossRef]
- Boyd, G.; Engels, J.; Karsch, F.; Laermann, E.; Legeland, C.; Lutgemeier, M.; Petersson, B. Thermodynamics of SU(3) lattice gauge theory. Nucl. Phys. B 1996, 469, 419–444. [Google Scholar] [CrossRef]
- Sannino, F. Higher representations: Confinement and large N. Phys. Rev. D 2005, 72, 125006. [Google Scholar] [CrossRef]
- Brihaye, Y.; Buisseret, F. Q-ball formation at the deconfinement temperature in large-Nc QCD. Phys. Rev. D 2013, 87, 014020. [Google Scholar] [CrossRef]
- Gupta, U.S.; Mohapatra, R.K.; Srivastava, A.M.; Tiwari, V.K. Simulation of Z(3) walls and string production via bubble nucleation in a quark-hadron transition. Phys. Rev. D 2010, 82, 074020. [Google Scholar] [CrossRef]
- Jin, J.; Mao, H. Nontopological Soliton in the Polyakov Quark Meson Model. Phys. Rev. C 2016, 93, 015202. [Google Scholar] [CrossRef]
- Scavenius, O.; Dumitru, A.; Jackson, A.D. Explosive decomposition in ultrarelativistic heavy ion collision. Phys. Rev. Lett. 2001, 87, 182302. [Google Scholar] [CrossRef]
- Fraga, E.S.; Krein, G. Can dissipation prevent explosive decomposition in high-energy heavy ion collisions? Phys. Lett. B 2005, 614, 181–186. [Google Scholar] [CrossRef][Green Version]
- Gupta, U.S.; Mohapatra, R.K.; Srivastava, A.M.; Tiwari, V.K. Effects of Quarks on the Formation and Evolution of Z(3) Walls and Strings in Relativistic Heavy-Ion Collisions. Phys. Rev. D 2012, 86, 125016. [Google Scholar] [CrossRef]
- Mohapatra, R.K.; Srivastava, A.M. Domain growth and fluctuations during quenched transition to quark-gluon plasma in relativistic heavy-ion collisions. Phys. Rev. C 2013, 88, 044901. [Google Scholar] [CrossRef]
- Nugaev, E.; Shkerin, A.; Smolyakov, M. Q-holes. J. High Energy Phys. 2016, 12, 32. [Google Scholar] [CrossRef]
- Sasagawa, S.; Tanaka, H. The separation of the chiral and deconfinement phase transitions in the curved space-time. Prog. Theor. Phys. 2012, 128, 925–939. [Google Scholar] [CrossRef][Green Version]
- Flachi, A. Deconfinement transition and Black Holes. Phys. Rev. D 2013, 88, 041501. [Google Scholar] [CrossRef]
- Bartnik, R.; Mckinnon, J. Particle-Like Solutions of the Einstein Yang-Mills Equations. Phys. Rev. Lett. 1988, 61, 141–144. [Google Scholar] [CrossRef] [PubMed]
- Liebling, S.L.; Palenzuela, C. Dynamical Boson Stars. Living Rev. Relativ. 2012, 15, 6. [Google Scholar] [CrossRef] [PubMed]
- Kulshreshtha, U.; Kumar, S.; Kulshreshtha, D.S.; Kunz, J. Boson Stars and QCD Boson Stars. PoS 2020, LC2019, 054. [Google Scholar] [CrossRef]
- Ratti, C.; Roessner, S.; Thaler, M.A.; Weise, W. Thermodynamics of the PNJL model. Eur. Phys. J. C 2007, 49, 213–217. [Google Scholar] [CrossRef]
- Volkov, M.S.; Wohnert, E. Spinning Q balls. Phys. Rev. D 2002, 66, 085003. [Google Scholar] [CrossRef]
- Buisseret, F.; Lacroix, G. A large-Nc PNJL model with explicit ZNc symmetry. Phys. Rev. D 2012, 85, 016009. [Google Scholar] [CrossRef]
- Dumitru, A.; Pisarski, R.D. Event-by-event fluctuations from decay of a Polyakov loop condensate. Phys. Lett. B 2001, 504, 282–290. [Google Scholar] [CrossRef]
- Sarkar, S.; Satz, H.; Sinha, B. The Physics of the Quark-Gluon Plasma; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2010; Volume 785, pp. 1–369. [Google Scholar] [CrossRef]
- Kaczmarek, O.; Zantow, F. Static quark anti-quark interactions in zero and finite temperature QCD. I. Heavy quark free energies, running coupling and quarkonium binding. Phys. Rev. D 2005, 71, 114510. [Google Scholar] [CrossRef]
- Ratti, C.; Thaler, M.A.; Weise, W. Phases of QCD: Lattice thermodynamics and a field theoretical model. Phys. Rev. D 2006, 73, 014019. [Google Scholar] [CrossRef]
- Ascher, U.; Christiansen, J.; Russell, R. A Collocation Solver for Mixed Order Systems of Boundary Value Problems. Math. Comput. 1979, 33, 659–679. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; List, M. Rotating boson stars and Q-balls. Phys. Rev. D 2005, 72, 064002. [Google Scholar] [CrossRef]
- Brihaye, Y.; Diemer, V.; Hartmann, B. Charged Q-balls and boson stars and dynamics of charged test particles. Phys. Rev. D 2014, 89, 084048. [Google Scholar] [CrossRef]
- Fukushima, K. Chiral effective model with the Polyakov loop. Phys. Lett. B 2004, 591, 277–284. [Google Scholar] [CrossRef]
- Biswal, M.; Digal, S.; Saumia, P. Z3 meta-stable states in PNJL model. arXiv 2019, arXiv:1907.07981. [Google Scholar]
- Nugaev, E.Y.; Shkerin, A. Review of Nontopological Solitons in Theories with U(1)-Symmetry. J. Exp. Theor. Phys. 2020, 130, 301–320. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).