Solving the Asymmetry Multi-Objective Optimization Problem in PPPs under LPVR Mechanism by Bi-Level Programing
Abstract
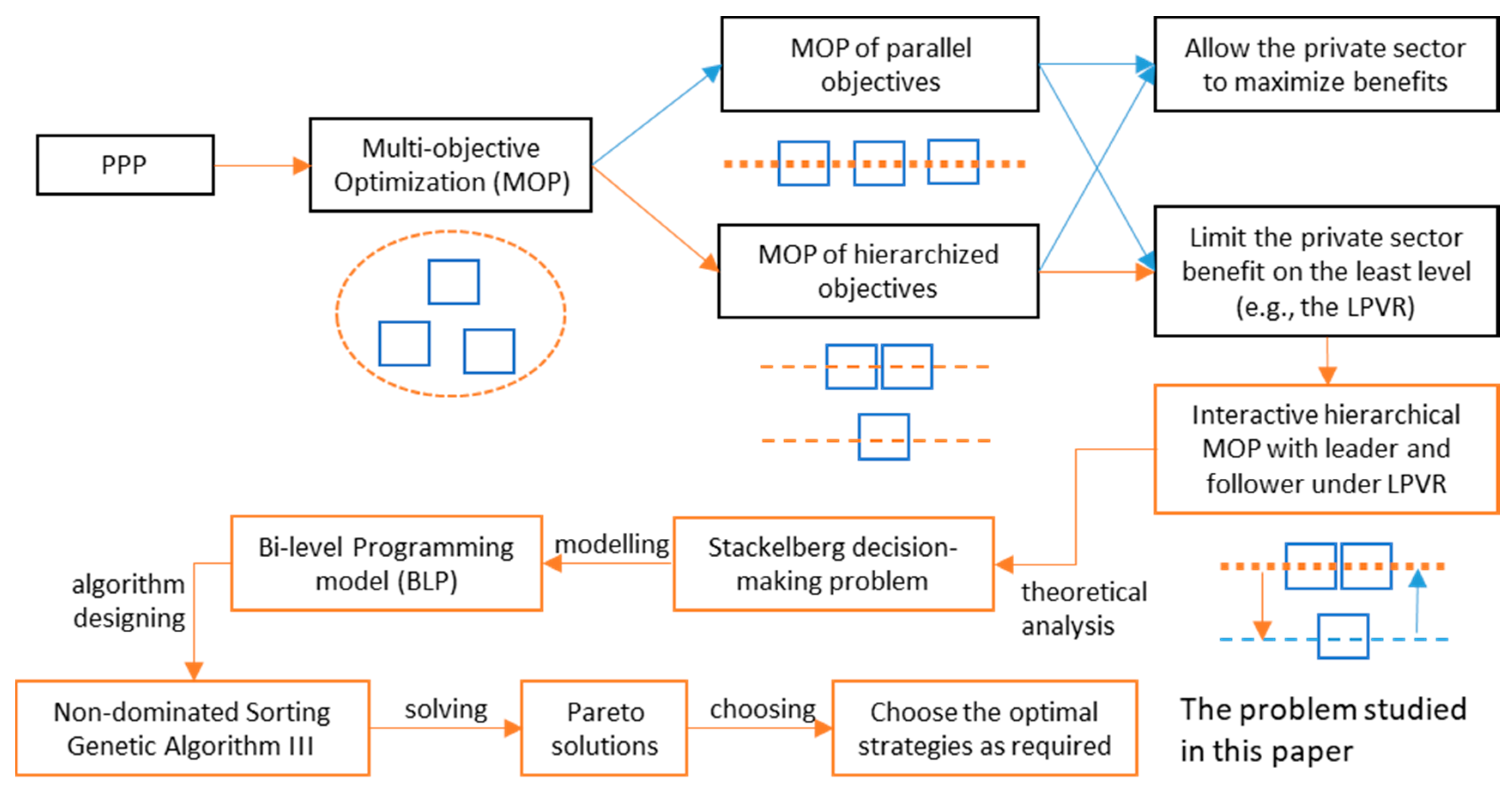
1. Introduction
2. Theoretical Analysis of the MOP under LPVR
2.1. The LPVR Mechanism
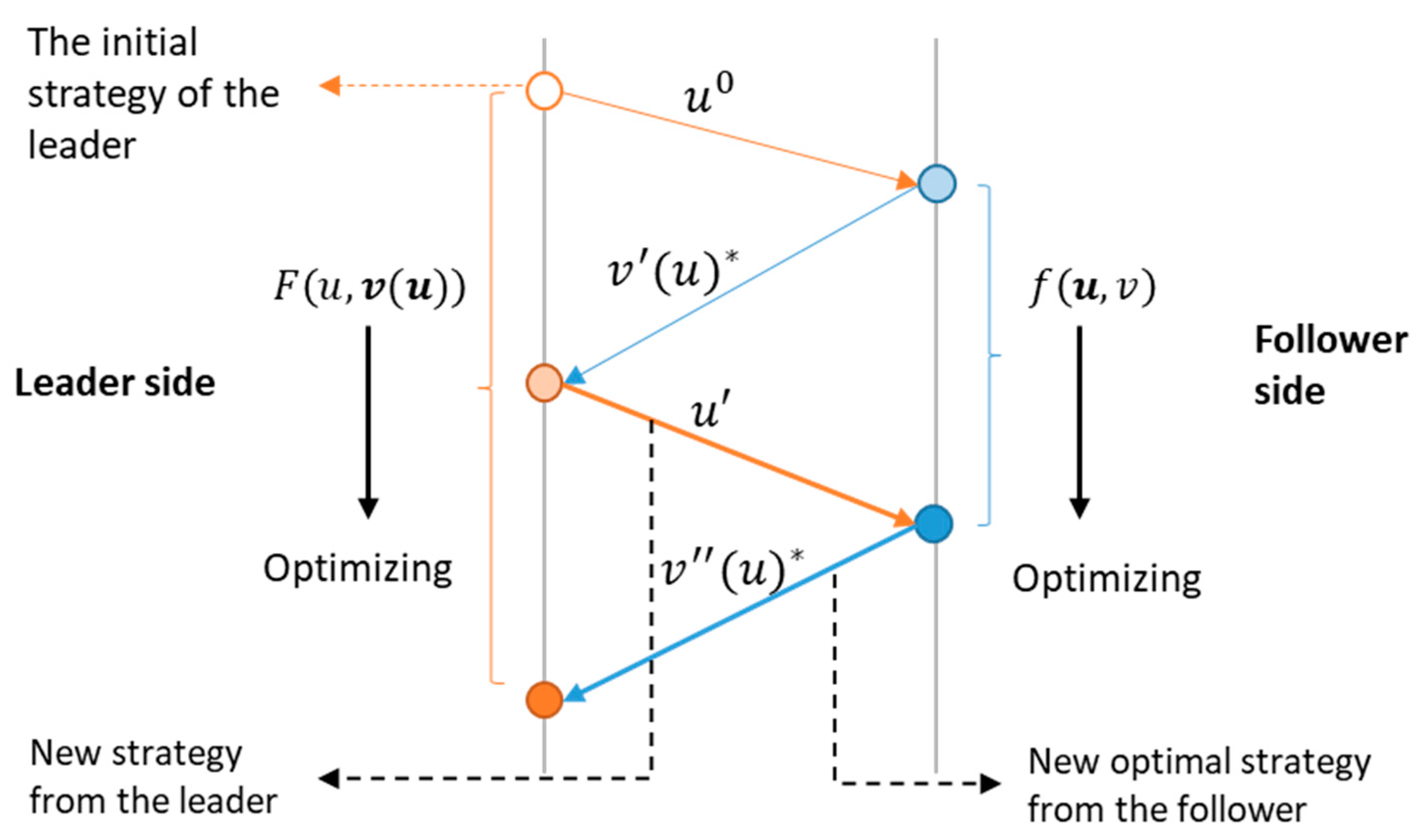
2.2. The Interactive Stackelberg Decision-Making Process
3. Modeling the Problem by Bi-Level Programing (BLP)
3.1. The Upper Programing (UP) Problem
3.2. The Lower Programing (LP) Problem
3.3. Optimization of Objectives in the BLP Model
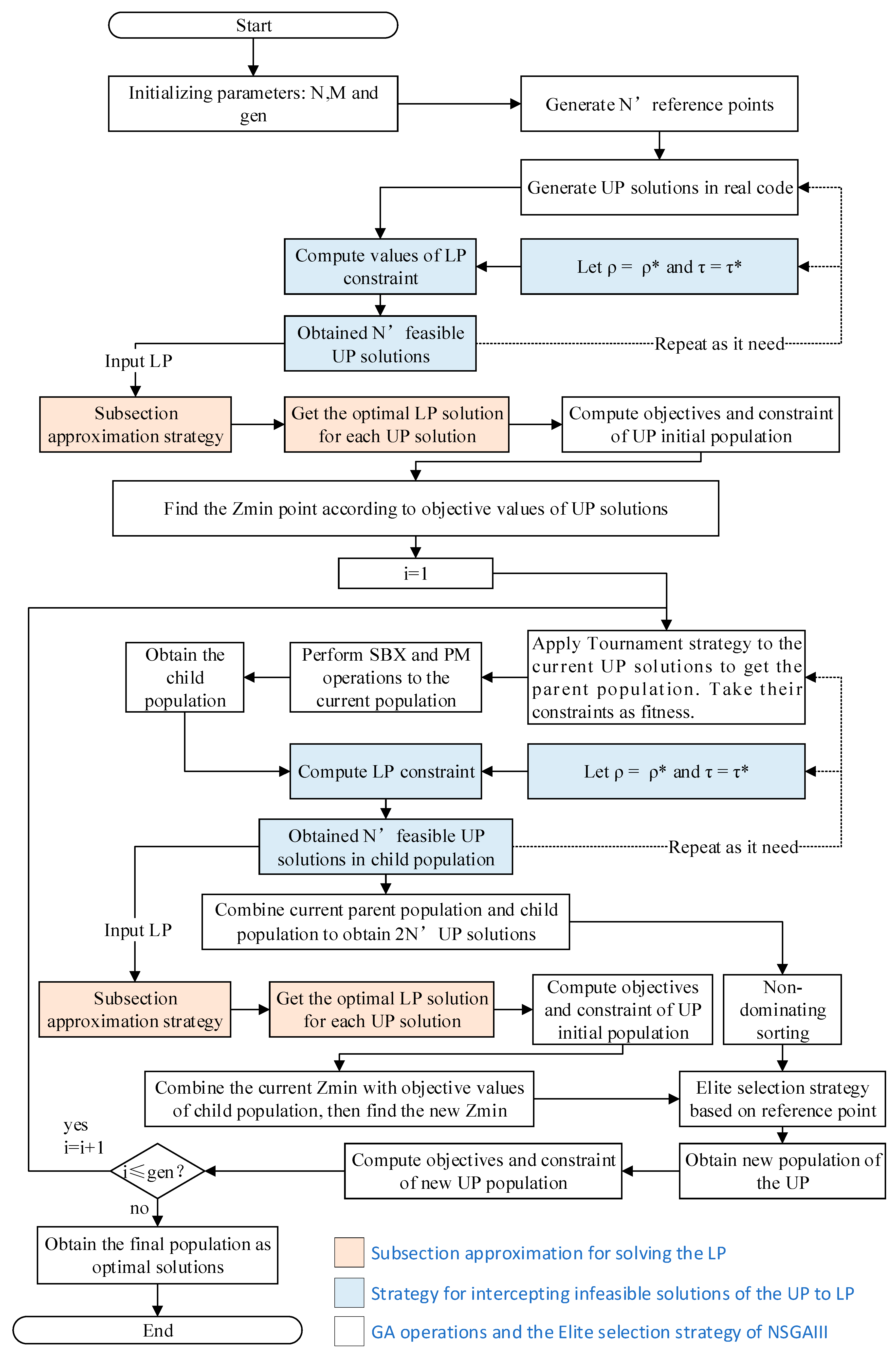
4. NSGAIII Framework-Based Algorithm for the BLP Model
4.1. Interception Strategy for Reparing Solutions of the UP Problem
4.2. Subsection Approximation Strategy for Optimizing the LP
4.3. Algorithm Design for the Complete BLP Model
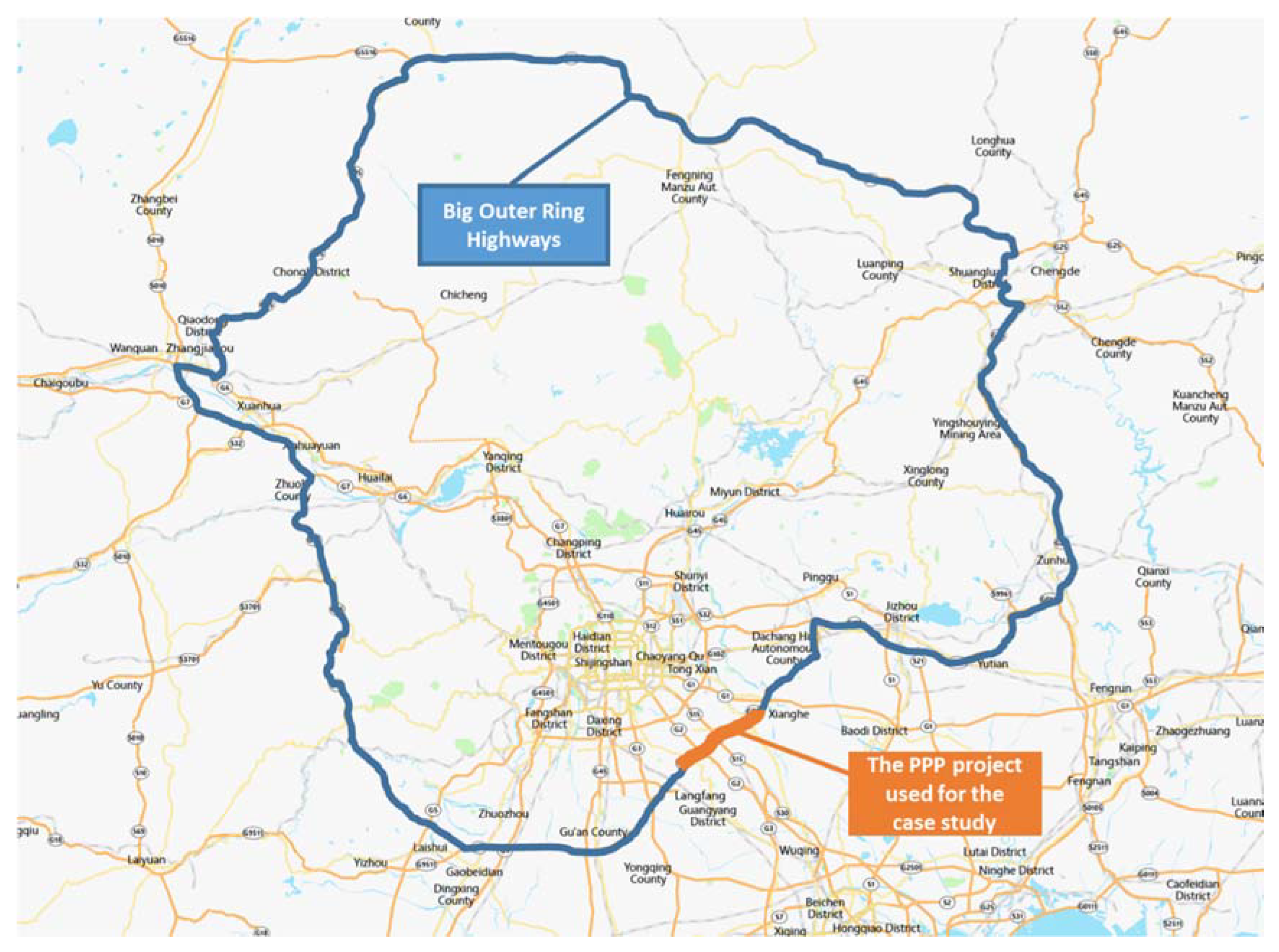
5. A case Study of the Big Outer Ring Highway PPP Project
5.1. The Big Outer Ring Highway PPP Project
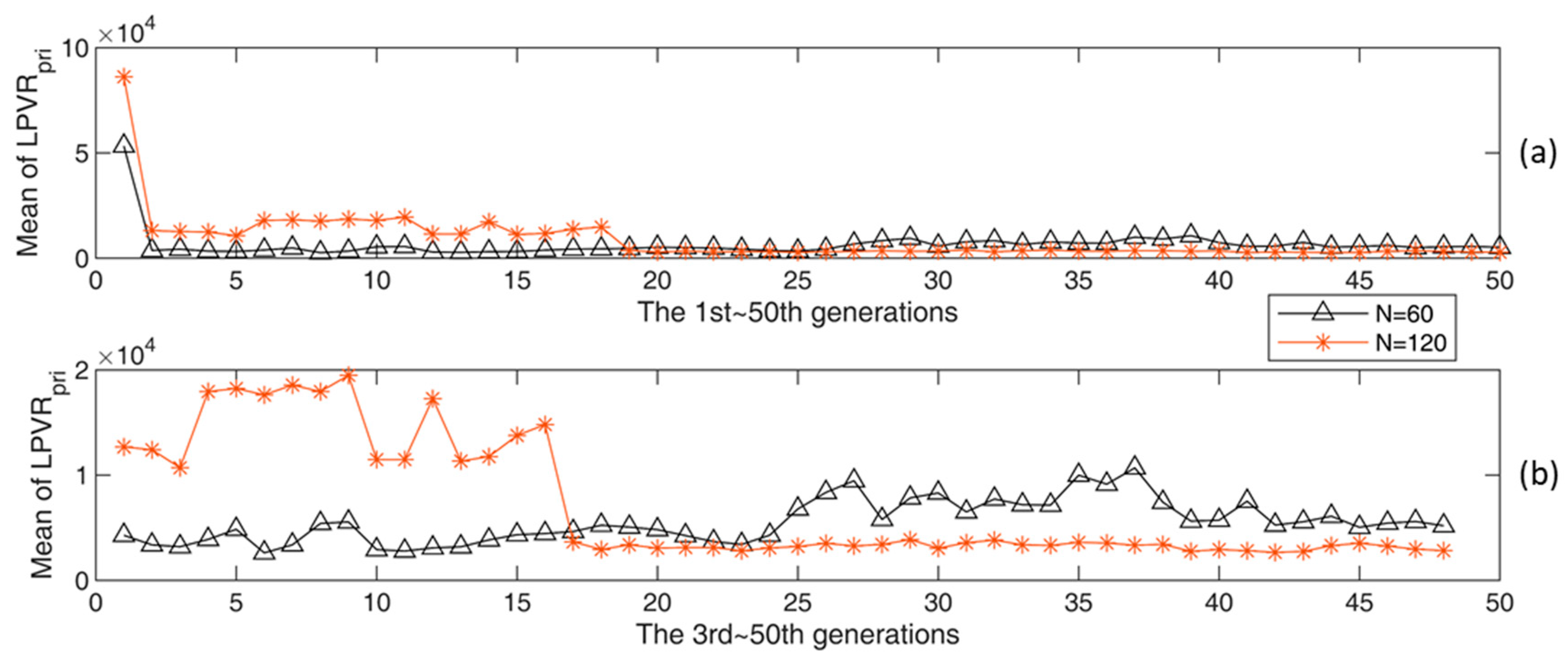
5.2. Evaluation Effects of Different Population Sizes
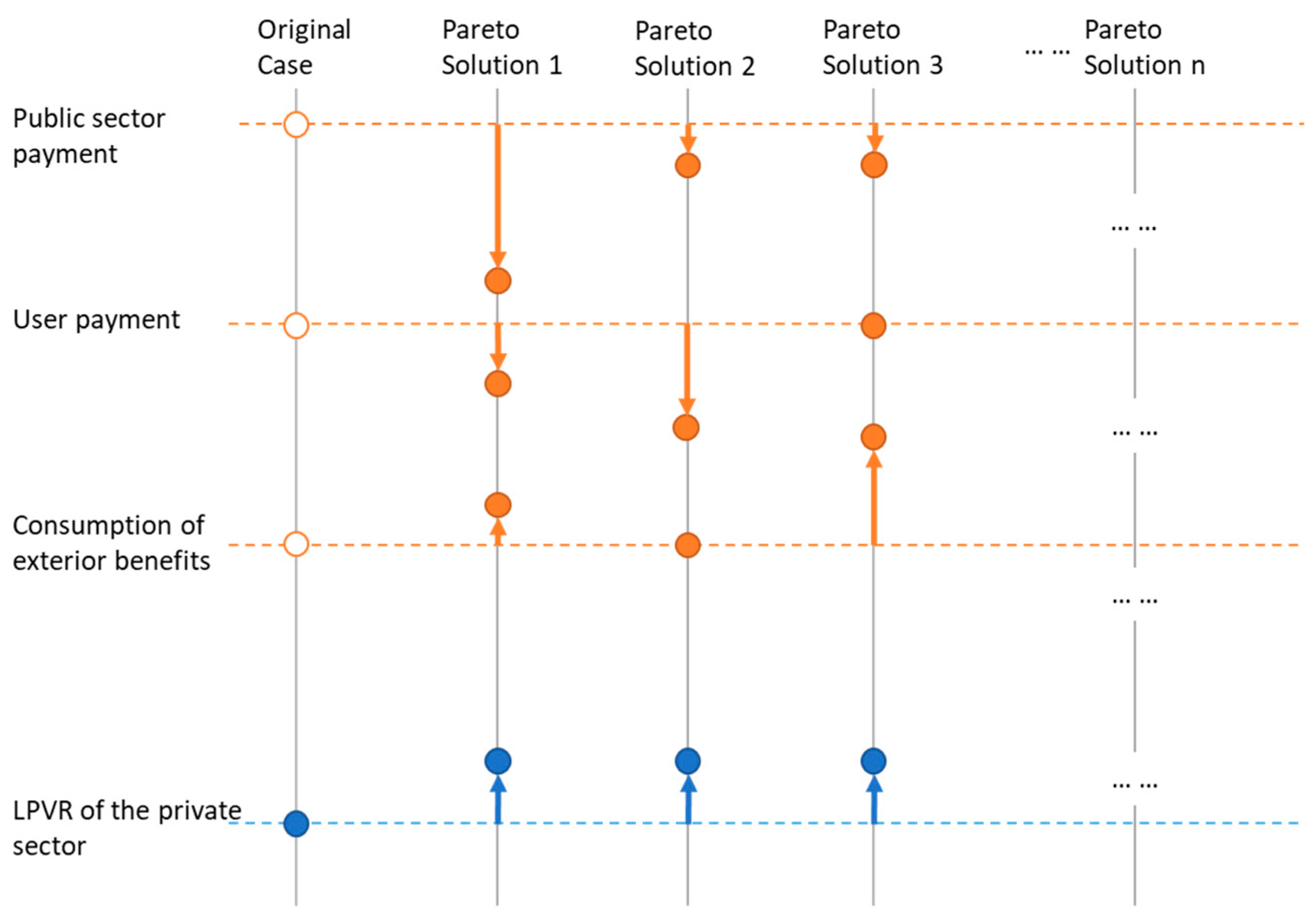
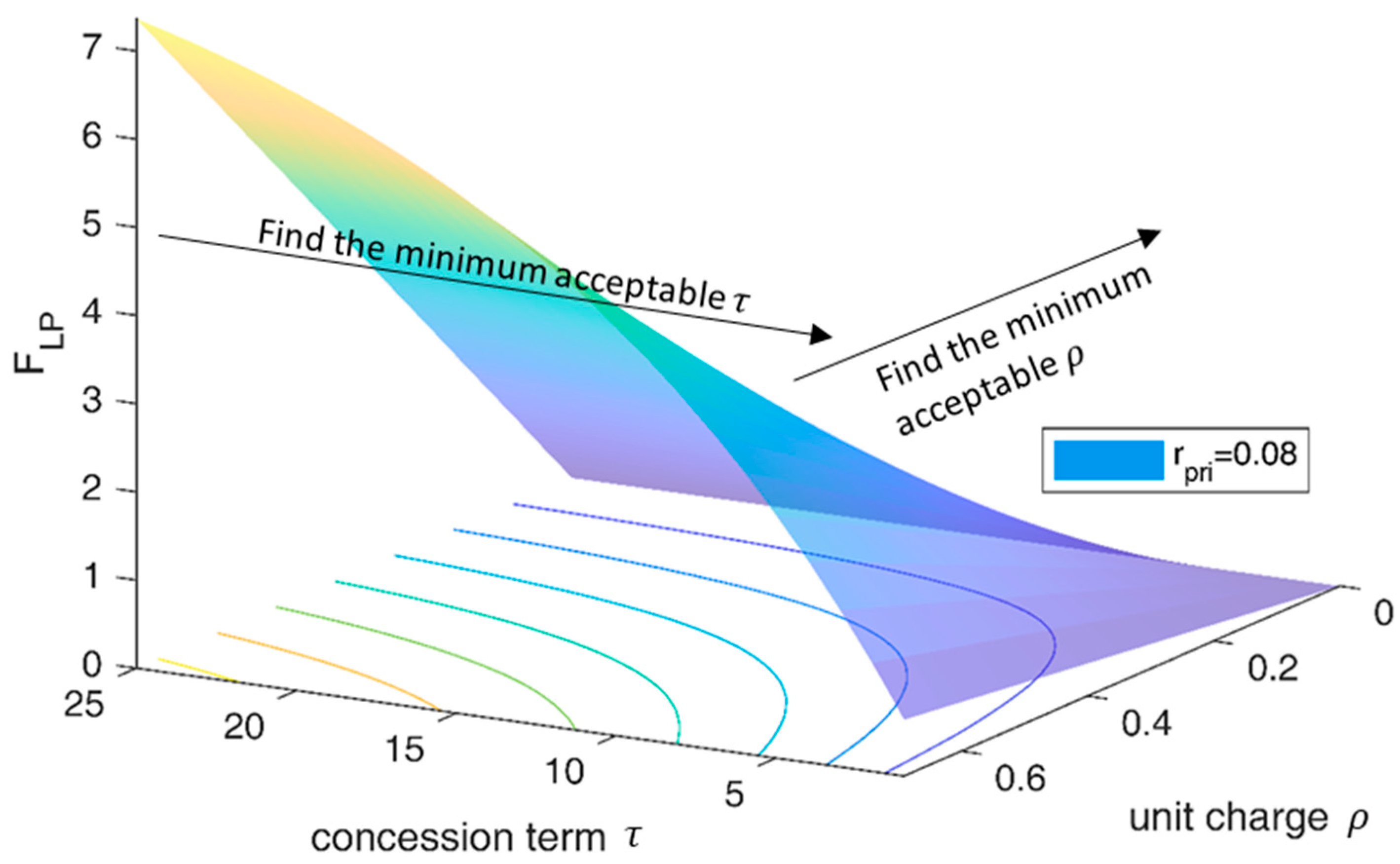
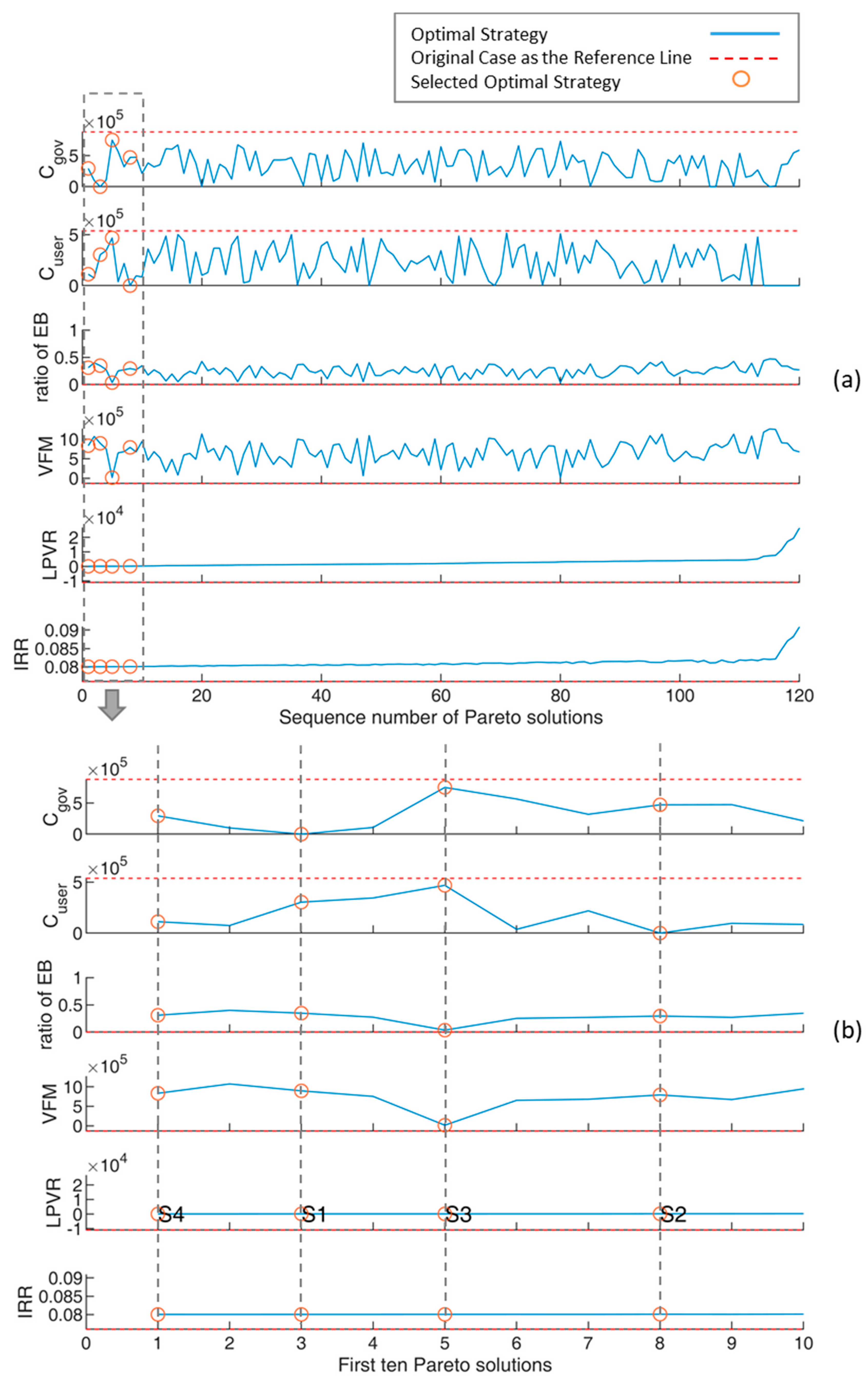
5.3. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Notation | Definition |
|---|---|
| Input Parameters | |
| Total investment of the project | |
| Extra direct investment that can be used to deduct loans, usually arising from a specific finance source such as a public transfer payment from the central government | |
| Construction term of the project | |
| Traffic volume of the i-th year in operation period | |
| Operation cost of the i-th year in operation period | |
| Montage paid of the i-th year in operation period | |
| The ratio of non-toll income making up to the toll income | |
| Ancillary services revenue; i.e., the non-toll incomes of the i-th year in concession term, such as refueling, parking and catering | |
| The proportion of equity capital funds | |
| The proportion of the funds invested in the j-th year of construction in the total investment | |
| Rate of the debt fund | |
| Discount rate of the public sector | |
| Discount rate of the private sector | |
| The exterior benefits generated from project implementation in the i-th year | |
| Decision Variables | |
| Initial investment for construction shared by the public sector. The private sector’s share is notated as . | |
| Subsidy per vehicle-kilometer | |
| Ratio of exterior benefits to be collected | |
| Toll of per vehicle-kilometer | |
| Concession term |
| Notation | Definition |
|---|---|
| NPV of the equity fund shared by the private sector | |
| NPV of the equity fund shared by the public sector | |
| NPV of the subsidy paid by the public sector as costs, discounted by | |
| Internal return rate (IRR) of the private sector over the project’s life | |
| NPV of the subsidy paid by the public sector and received by the private sector as revenue, discounted by | |
| NPV of toll collected by the private sector | |
| NPV of the exterior benefits transferred and taken by the private sector as extra revenue | |
| NPV of the operation costs paid by the private sector |
References
- Wang, H.; Xiong, W.; Wu, G.; Zhu, D. Public-private partnership in public administration discipline: A literature review. Public Manag. Rev. 2018, 20, 293–316. [Google Scholar] [CrossRef]
- Koppenjan, J.J.F. The formation of public-private partnerships: Lessons from nine transport infrastructure projects in The Netherlands. Public Admin. 2005, 83, 135–157. [Google Scholar] [CrossRef]
- Papajohn, D.; Cui, Q.; Bayraktar, M.E. Public-private partnerships in US transportation: Research overview and a path forward. J. Manag. Eng. 2011, 27, 126–135. [Google Scholar] [CrossRef]
- Garvin, M.J. Enabling development of the transportation public-private partnership market in the United States. J. Constr. Eng. Manag. 2010, 136, 402–411. [Google Scholar] [CrossRef]
- Xu, Y.; Yeung, J.F.; Jiang, S. Determining appropriate government guarantees for concession contract: Lessons learned from 10 PPP projects in China. Int. J. Strateg. Prop. Manag. 2014, 18, 356–367. [Google Scholar] [CrossRef]
- Kayhan, İ.E.; Jenkins, G.P. Determination of socially equitable guarantees for public-private partnerships: A toll-road case from Turkey. Turkish Stud. 2016, 17, 691–711. [Google Scholar] [CrossRef]
- Rouhani, O.M.; Gao, H.O.; Geddes, R.R. Policy lessons for regulating public-private partnership tolling schemes in urban environments. Transp. Policy 2015, 41, 68–79. [Google Scholar] [CrossRef]
- Song, J.; Zhao, Y.; Jin, L.; Sun, Y. Pareto optimization of public-private partnership toll road contracts with government guarantees. Transp. Res. Part A Policy Pract. 2018, 117, 158–175. [Google Scholar] [CrossRef]
- Button, K.; Daito, N. Sharing out the costs of a public-private partnership. Appl. Econ. Lett. 2014, 21, 383–386. [Google Scholar] [CrossRef]
- Vassallo, J.M. The role of the discount rate in tendering highway concessions under the LPVR approach. Transp. Res. Part A Policy Pract. 2010, 44, 806–814. [Google Scholar] [CrossRef][Green Version]
- Peng, W.; Cui, Q.; Chen, J. Option game model for optimizing concession length and public subsidies of public-private partnerships. Transp. Res. Rec. 2014, 109–117. [Google Scholar] [CrossRef]
- Liu, T.; Bennon, M.; Garvin, M.J.; Wang, S. Sharing the big risk: Assessment framework for revenue risk sharing mechanisms in transportation public-private partnerships. J. Constr. Eng. Manag. 2017, 143. [Google Scholar] [CrossRef]
- Sharafi, A.; Taleizadeh, A.A.; Amalnicka, M.S. Fair allocation in financial disputes between public-private partnership stakeholders using game theory. Serv. Sci. 2018, 10, 1–11. [Google Scholar] [CrossRef]
- South, A.; Eriksson, K.; Levitt, R. How Infrastructure public-private partnership projects change over project development phases. Proj. Manag. J. 2018, 49, 62–80. [Google Scholar] [CrossRef]
- Engel, E.; Fischer, R.; Galetovic, A. Privatizing Roads: A New Method for Auctioning Highways; The World Bank Group: Washington, DC, USA, 1997. [Google Scholar]
- Rouhani, O.M.; Geddes, R.R.; Do, W.; Gao, H.O.; Beheshtian, A. Revenue-risk-sharing approaches for public-private partnership provision of highway facilities. Case Stud. Transp. Policy 2018, 6, 439–448. [Google Scholar] [CrossRef]
- Engel, E.M.; Fischer, R.D.; Galetovic, A. Least-present-value-of-revenue auctions and highway franchising. J. Polit. Econ. 2001, 109, 993–1020. [Google Scholar] [CrossRef]
- Sharma, R.; Newman, P. Can land value capture make PPP’s competitive in fares? A Mumbai case study. Transp. Policy 2018, 64, 123–131. [Google Scholar] [CrossRef]
- Chen, C.L.; Cruz, J. Stackelburg solution for two-person games with biased information patterns. IEEE Trans. Automat. Control 1972, 17, 791–798. [Google Scholar] [CrossRef]
- Yang, H.; Bell, M.G.; Meng, Q. Modeling the capacity and level of service of urban transportation networks. Transp. Res. Part B Methodol. 2000, 34, 255–275. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, H.; Sun, H. Bi-level programming models, approaches and applications in urban transportation network design problems. Commun. Transp Syst. Eng. Inf. 2004, 4, 35–44. [Google Scholar]
- Liu, F.; Liu, J.; Yan, X. Quantifying the decision-making of PPPs in China by the entropy-weighted pareto front: A URT case from Guizhou. Sustainability 2018, 10, 1753. [Google Scholar] [CrossRef]
- Roghanian, E.; Aryanezhad, M.; Sadjadi, S.J. Integrating goal programming, Kuhn-Tucker conditions, and penalty function approaches to solve linear bi-level programming problems. Appl. Math. Comput. 2008, 195, 585–590. [Google Scholar] [CrossRef]
- Zhou, J.; Lam, W.H. A bi-level programming approach—Optimal transit fare under line capacity constraints. J. Adv. Transp. 2001, 35, 105–124. [Google Scholar] [CrossRef]
- Shang, L.; Aziz, A.M.A. Stackelberg game theory-based optimization model for design of payment mechanism in performance-based PPPs. J. Constr. Eng. Manag. 2020, 146. [Google Scholar] [CrossRef]
- Zhang, L.; Feng, X.; Chen, D.; Zhu, N.; Liu, Y. Designing a hazardous materials transportation network by a bi-level programming based on toll policies. Phys. A 2019, 534. [Google Scholar] [CrossRef]
- Jia, X.; He, R.; Zhang, C.; Chai, H. A Bi-level programming model of liquefied petroleum gas transportation operation for urban road network by period-security. Sustainability 2018, 10, 4714. [Google Scholar] [CrossRef]
- Assadipour, G.; Ke, G.Y.; Verma, M. A toll-based bi-level programming approach to managing hazardous materials shipments over an intermodal transportation network. Transp. Res. D Transp. Environ. 2016, 47, 208–221. [Google Scholar] [CrossRef]
- Fleming, P.J.; Purshouse, R.C.; Lygoe, R.J. Many-Objective Optimization: An Engineering Design Perspective; Springer: Berlin/Heidelberg, Germany, 2005; pp. 14–32. [Google Scholar]
- Tian, Y.; Xiang, X.; Zhang, X.; Cheng, R.; Jin, Y. Sampling Reference Points on the Pareto Fronts of Benchmark Multi-Objective Optimization Problems; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization. IEEE Comput. Intell. Manag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evolut. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Das, I.; Dennis, J.E. Normal-boundary intersection: A new method for generating the Pareto surface in nonlinear multicriteria optimization problems. SIAM J. Optimiz. 1998, 8, 631–657. [Google Scholar] [CrossRef]
- Yang, J.; Soh, C.K. Structural optimization by genetic algorithms with tournament selection. J. Comput. Civil Eng. 1997, 11, 195–200. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, R.B. Simulated binary crossover for continuous search space. Complex. Syst. 1995, 9, 115–148. [Google Scholar]
- Kumar, S.; Naresh, R. Nonconvex economic load dispatch using an efficient real-coded genetic algorithm. Appl. Soft Comput. 2009, 9, 321–329. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, Y.; Cheng, R.; Jin, Y. An efficient approach to nondominated sorting for evolutionary multiobjective optimization. IEEE Trans. Evolut. Comput. 2014, 19, 201–213. [Google Scholar] [CrossRef]

| Year | Operation Subsidy in Original Case ($ Million) | Unit Traffic Subsidy ($ Vehicle-km) | |||
|---|---|---|---|---|---|
| 2019 | 24.22 | 231.49 | 0.10462 | 27.19 | 111.57 |
| 2020 | 30.65 | 292.94 | 0.10462 | 28.28 | 220.54 |
| 2021 | 38.78 | 370.70 | 0.10462 | 29.42 | 265.32 |
| 2022 | 49.08 | 469.10 | 0.10462 | 30.61 | 301.64 |
| 2023 | 62.11 | 593.63 | 0.10462 | 31.85 | 332.97 |
| 2024 | 66.79 | 634.72 | 0.10523 | 33.15 | 385.35 |
| 2025 | 71.42 | 678.65 | 0.10523 | 34.51 | 439.89 |
| 2026 | 76.36 | 725.63 | 0.10523 | 35.93 | 496.65 |
| 2027 | 81.65 | 775.85 | 0.10524 | 37.42 | 555.69 |
| 2028 | 87.30 | 829.55 | 0.10523 | 38.97 | 617.05 |
| 2029 | 87.62 | 845.48 | 0.10363 | 40.60 | 638.83 |
| 2030 | 89.30 | 861.71 | 0.10363 | 42.30 | 661.38 |
| 2031 | 91.01 | 878.26 | 0.10363 | 44.08 | 684.73 |
| 2032 | 92.76 | 895.12 | 0.10363 | 45.94 | 708.90 |
| 2033 | 94.54 | 912.30 | 0.10363 | 47.89 | 733.94 |
| 2034 | 94.47 | 920.81 | 0.10259 | 49.93 | 759.88 |
| 2035 | 95.35 | 929.39 | 0.10259 | 52.06 | 786.76 |
| 2036 | 96.23 | 938.05 | 0.10259 | 54.29 | 814.61 |
| 2037 | 97.13 | 946.80 | 0.10259 | 56.63 | 842.78 |
| 2038 | 98.04 | 955.62 | 0.10259 | 59.08 | 871.33 |
| 2039 | 97.41 | 964.53 | 0.10100 | 61.64 | 876.72 |
| 2040 | 98.32 | 973.52 | 0.10100 | 64.32 | 899.72 |
| 2041 | 99.24 | 982.60 | 0.10099 | 67.12 | 923.68 |
| 2042 | 100.16 | 991.75 | 0.10100 | 70.06 | 948.55 |
| 2043 | 101.09 | 1001.01 | 0.10099 | 73.14 | 974.45 |
| (%) | ($ Vehicle-km) | (%) | ($ Vehicle-km) | (Years) | |
|---|---|---|---|---|---|
| Upper limit | |||||
| Lower limit |
| (%) | ($ Vehicle-km) | (%) | ($ Vehicle-km) | (Years) | |
|---|---|---|---|---|---|
| S0 | 49.00% | 0.1034 | 0.00% | 0.0976 | 25 |
| S1 | 0.00% | 0.0000 | 34.71% | 0.0820 | 15 |
| Δ1 | −49.00% | −100.00% | +34.71% | −15.94% | −40.00% |
| S2 | 48.22% | 0.0726 | 29.43% | 0.0000 | 15 |
| Δ2 | −0.78% | −29.84% | +29.43% | −100.00% | −40.00% |
| S3 | 47.30% | 0.1035 | 3.55% | 0.0993 | 20 |
| Δ3 | −1.70% | +0.05% | +3.55% | +1.75% | −20.00% |
| S4 | 45.05% | 0.0344 | 30.93% | 0.0302 | 15 |
| Δ4 | −3.95% | −66.69% | +30.93% | −69.03% | −40.00% |
($ Million) | PSC ($ Million) | VFM ($ Million) | ($ Million) | ($ Million) | |
|---|---|---|---|---|---|
| S0 | 1267.02 | 1071.83 | −195.19 | 238.00 | 1043.38 |
| S1 | 0.00 | 1289.00 | 1289.00 | 0.00 | 0.00 |
| Δ1 | −100.00% | +20.26% | +760.38% | −100.00% | −100.00% |
| S2 | 677.91 | 1816.86 | 1138.95 | 234.21 | 457.83 |
| Δ2 | −46.50% | +69.51% | +683.50% | −1.59% | −56.12% |
| S3 | 1080.09 | 1100.84 | 20.75 | 229.76 | 864.19 |
| Δ3 | −14.75% | +2.71% | +110.63% | −3.46% | −17.17% |
| S4 | 422.94 | 1622.39 | 1199.44 | 218.81 | 217.33 |
| Δ4 | −66.62% | +51.37% | +714.50% | −8.06% | −79.17% |
| LPVR ($ Million) | (%) | ($ Million) | ($ Million) | ($ Million) | ($ Million) | ($ Million) | |
|---|---|---|---|---|---|---|---|
| S0 | −15.82 | 7.60% | 630.23 | 606.52 | 0.00 | 247.71 | 360.58 |
| S1 | 0.20 | 8.00% | 0.00 | 364.98 | 1054.59 | 485.71 | 253.18 |
| Δ1 | +101.26% | +0.40% | −100.00% | −39.82% | - | +96.08% | −29.78% |
| S2 | 0.29 | 8.01% | 316.56 | 0.00 | 894.28 | 251.50 | 253.18 |
| Δ2 | +101.82% | +0.41% | −49.77% | −100.00% | - | +1.53% | −29.78% |
| S3 | 0.20 | 8.01% | 556.02 | 544.19 | 138.90 | 255.95 | 311.51 |
| Δ3 | +101.29% | +0.41% | −11.78% | −10.28% | - | +3.32% | −13.61% |
| S4 | 0.13 | 8.00% | 150.27 | 134.47 | 939.67 | 266.91 | 253.18 |
| Δ4 | +100.83% | +0.40% | −76.16% | −77.83% | - | +7.75% | −29.78% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Liu, J.; Yan, X. Solving the Asymmetry Multi-Objective Optimization Problem in PPPs under LPVR Mechanism by Bi-Level Programing. Symmetry 2020, 12, 1667. https://doi.org/10.3390/sym12101667
Liu F, Liu J, Yan X. Solving the Asymmetry Multi-Objective Optimization Problem in PPPs under LPVR Mechanism by Bi-Level Programing. Symmetry. 2020; 12(10):1667. https://doi.org/10.3390/sym12101667
Chicago/Turabian StyleLiu, Feiran, Jun Liu, and Xuedong Yan. 2020. "Solving the Asymmetry Multi-Objective Optimization Problem in PPPs under LPVR Mechanism by Bi-Level Programing" Symmetry 12, no. 10: 1667. https://doi.org/10.3390/sym12101667
APA StyleLiu, F., Liu, J., & Yan, X. (2020). Solving the Asymmetry Multi-Objective Optimization Problem in PPPs under LPVR Mechanism by Bi-Level Programing. Symmetry, 12(10), 1667. https://doi.org/10.3390/sym12101667





