1. Introduction
Nature-inspired optimization algorithms, such as swarm intelligence metaheuristics and evolutionary algorithms, have become increasingly popular in recent years for solving optimization problems in different domains, including, for instance, the firefly algorithm [
1,
2], crow search algorithm [
3], hybrid gray wolf optimizer–crow search algorithm [
4], elephant herding optimization and tree growth algorithm [
5], to name a few. The interested reader is encouraged to consult also [
6,
7,
8,
9,
10,
11] for recent works and applications of nature-inspired algorithms.
When the objective function is computationally expensive (taking a long time to evaluate) and black-box (neither the function expression nor its derivative function are explicitly known), Bayesian optimization (BO) is often employed. Relying on the expected improvement criterion, BO was first proposed by Mockus [
12,
13] and was popularized by Jones et al. when the framework called the Efficient Global Optimization (EGO) algorithm was introduced [
14]. Due to the ease of use and flexibility, the algorithm has been applied to solve different optimization problems in numerous research areas [
15,
16,
17,
18,
19]. Several modifications to the original EGO developed particularly for unconstrained problems have also been proposed in many works ever since [
20,
21,
22,
23,
24,
25].
Though not as widely used, Bayesian optimization has also been applied to solving constrained optimization problems over the past decade. We now briefly summarize past research on constrained Bayesian optimization (CBO). The method considered in [
26] combines the generalized expected improvement criterion with the probability of feasibility, while the expected feasible improvement criterion of [
27] combines the expected improvement with constraint functions. Good results were obtained both for simulated and real-world data of learning tasks based on locality sensitive hashing (LSH) hyperparameter tuning and support vector machine (SVM) model compression. The super-efficient global optimization proposed in [
28] also includes a feasibility criterion that prevents one from selecting from an infeasible region. Priem et al. [
29] proposed a method that uses the the confidence bound [
30] to improve the feasibility criterion for better exploring feasible regions in high-uncertainty regions.
Gramacy and Lee proposed a method called integrated expected conditional improvement [
31]. The method learns both the objective function and constraint functions at the same time by incorporating a constraint violation into the expected improvement criterion. It sequentially chooses a point whose expected reduction of expected improvement is below the current best observed value and satisfies the constraints. Gelbart et al. [
32] studied a criterion for constrained Bayesian optimization problems when noise may be present in the constraint functions and proposed a two-step approach for optimization when the objective and the constraints may be evaluated independently. The next point is selected by maximizing the expected feasible improvement. Then, either the objective or the constraint function will be chosen to evaluate based on the information gain metric. Hernández-Lobato et al. [
33] proposed a method called predictive entropy search with constraints, which is an extension of the predictive entropy search [
34]. It uses the information gain as a criterion to solve constrained optimization problems and does not require any feasible observation to initialize the algorithm. The rollout algorithm, an adaptation of the method often used in dynamic programming, sequentially selects the next points by maximizing the long-term feasible reduction of the objective function [
35]. Numerical results illuminated advantages of the algorithm especially when the objective function is multimodal and the feasible region has a complex topology.
Ariafar et al. [
36] proposed an approach that is based on the alternating direction method of multipliers. The method is separated into two solvable problems: the one that minimizes the objective function with a penalty term involving the solution being close to feasible regions and the other that minimizes penalized feasibility over an auxiliary variable that is closest to the solution found in the first step. Recently, Jiao et al. proposed a new sampling criterion for solving optimization problems with constraint functions [
37]. The new sampling criterion, called the constrained expected improvement, addressed the issue that the previous expected improvement criterion fails to work because the initial observations do not contain any feasible solutions. The results showed that the algorithm could exploit feasible regions locally as well as explore infeasible yet promising regions efficiently.
From another perspective, an optimization strategy based on stepwise uncertainty reduction principles was proposed for solving a multi-objective optimization [
38]. The strategy relies on a sequential reduction of the volume of the excursion sets below the current best solution. Using the same principle, a sampling criterion for a single objective optimization with constraint functions was introduced in [
39]. A combination of Gaussian process modeling and the augmented Lagrangian for Bayesian optimization with constraints was proposed by Gramacy et al. [
40]. Analytical formulas of the main criterion of the single expensive constraint and the cheap-to-evaluate objective function were subsequently derived in [
41], leading to a more efficient implementation of the infill sampling criterion for optimization framework.
Apparently, over the past decade, several Gaussian process (GP)-based infill sampling criteria have been developed and independently tested; however, none of these criteria were rigorously compared under the same umbrella and, in particular, under the BO setting when a very limited number of objective and constraint function evaluations are allowed. In this work, we therefore compare different infill sampling criteria developed for constraint optimization problems: expected feasible improvement [
26,
27], constrained expected improvement [
37], stepwise uncertainty reduction [
39], and augmented Lagrangian [
40]. The benchmark set consists of nine problems with features commonly found in engineering, as well as a constrained structural engineering design optimization problem. The comparison measurements include the quality of the best solution found, the efficiency to find a feasible region, and the overall number of feasible points being sampled. Different from the work in [
37] that compared different criteria under a GP surrogate-assisted evolutionary algorithm framework, this is the first attempt to compare the four infill sampling criteria under a unified constrained Bayesian optimization framework.
The remainder of this article is organized as follows. The related work and background are discussed in
Section 2. Numerical results comparing different infill sampling criteria under the CBO framework on benchmark problems are presented in
Section 3. Finally, conclusions and future work are discussed in
Section 4.
3. Empirical Experiments
3.1. Experimental Setup
We assume that the computation of both the objective and constraint functions are computationally expensive, and therefore a very limited number of objective and constraint function evaluations will be allowed. Computationally expensive means that the function evaluation completely dominates the cost of the optimization procedures. The term is linked not necessarily to the problem having high dimensionality or a large number of constraints. In fact, many practical optimization applications arising from expensive computer simulations have only a few number of decision variables.
3.1.1. Test Problem Description
We test the performance of CBO methods (Algorithm 1) with EFI, CEI, SUR, and AL criteria on the same benchmark suite as used in [
37]. It is worth noting that applying GP to higher dimensional settings (>10 dimensions) is generally difficult due to the curse of dimensionality for nonparametric regression. In addition, the higher the number of dimensions and constraints, the more computation time will be required for GP modeling as well as for optimizing the infill sampling criterion.
Details of the test problems including the number of decision variables
d, the characteristic of the objective function, known optimal value
, the number of constraint functions, the type of constraint functions, as well as the proportion of the feasible space to the whole search space (feasibility ratio) are given in
Table 1. Monte Carlo sampling with size
was used to estimate the last proportion of relative size of the feasible space to the size of the search space. The closer to 0 the value, the smaller the feasible region is. For problem definitions including the objective and constraint functions of these instances, see
Appendix A.
3.1.2. Experimental Settings
In order to separate the impact of the infill sampling criterion from the influence of model accuracy, the same GP model parameters were used for each criterion. At each step, a GP model with a Matérn 5/2 covariance function is fit to both the objective and constraint functions. The hyperparameters are re-estimated by Maximum Likelihood Estimation in every iteration using all points visited during all previous iterations. For problems with equality constraints (i.e., problems G03 and G11), a tolerance of 0.005 was used.
3.1.3. Comparison Metrics
We use the following measurements to examine the influence of different infill sampling criteria.
Quality of the final solution, represented by the mean and standard deviation of the best feasible solution found;
Efficiency and speed of finding a feasible region, represented by the count of the number of trials (out of 20) for which a feasible solution is found and how fast the first feasible solution is found;
Total number of feasible points being sampled, which is the proportion of feasible solutions to the total number of observations.
3.2. Results of Constrained Bayesian Optimization
The performance of constrained Bayesian optimization will depend on the locations of the points in the initial sample. In some cases, the initial design might contain a point already close to the global minimum. Therefore, to ensure the accurate representation of the algorithm’s capability, each experiment was repeated for 20 independent runs with different initial design points (but the same for all compared algorithms on a fixed run, to avoid the bias).
To test the efficiency of locating a feasible region, two scenarios of initial experimental design were investigated:
Scenario 1: 10 uniform points, all generated outside feasible regions;
Scenario 2: points of a Latin Hypercube Sampling Design (LHSD) [
45].
The first scenario, when all initial sample points were forced to be outside the feasible regions, was done to test the efficiency of the algorithm to enter feasible regions when no feasible solution is currently available. The second scenario, on the other hand, reflects a more realistic situation, i.e., the proportion of the feasible solutions generated in the initial design should, at least in practice, be proportional to the size of the feasible space to the search space.
Table 2 gives statistics of the number of feasible solutions found in the initial LHSD design when the size of the design is
over 20 trials. Problems with positive values of maximum and minimum in the table are those for which all of the 20 trials include at least one feasible solution in the initial design.
3.2.1. Scenario 1: Infeasible Initial Design Points
The average, standard deviation, and best feasible objective function values for the case when all initial design points were located outside the feasible regions obtained after 100 iterations are given in
Table 3. The numbers in the brackets of the row “mean” of the table represent the count of trials (out of 20) for which no feasible solution is found along the run. We can see that feasible solutions can be found by all algorithms in all runs except for problems G02 (AL missing 2 trials) and G06 (SUR missing 5 trials). When calculating the mean and standard deviation of the best values, we included only the values of those trials for which there is at least one feasible solution.
A Wilcoxon signed-rank test has been carried out to see whether the best feasible solutions found by each algorithm as reported are significantly different. For any two algorithms, the expression A1 ≈ A2 means that the final solutions found by A1 and A2 are not significantly different, while the expression A1 ≺ A2 means that A1 is significantly better than A2 at the 5% level of significance. The statistical results are summarized in
Table 4. We can see from the table that the performance we obtained for EFI and CEI were quite similar. Both algorithms performed best on 4 problems. As for AL, the algorithm performed best also on 4 problems, while SUR was best only on 1 problem.
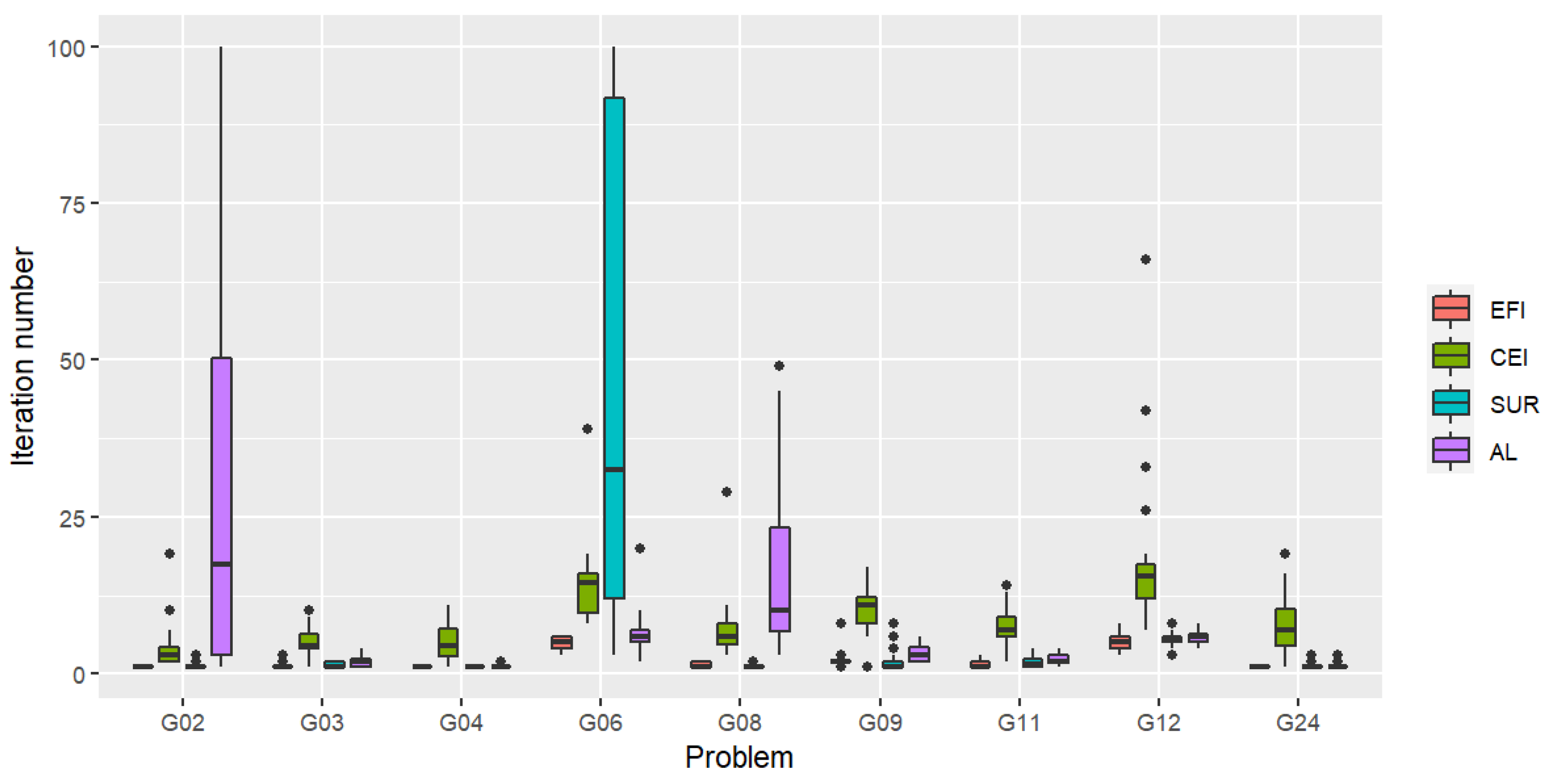
Figure 1 illustrates the distribution of the iteration numbers for which the first feasible solution was found. The value reflects how quickly the process will lead the search to reach feasible regions as the algorithm evolves from outside the feasible regions. From the boxplot, we can see that, overall, EFI could locate a first feasible solution fastest. Except for problems G02 and G06 (when AL and SUR had a problem locating a feasible solution in some trials), CEI found a first feasible solution slowest overall.
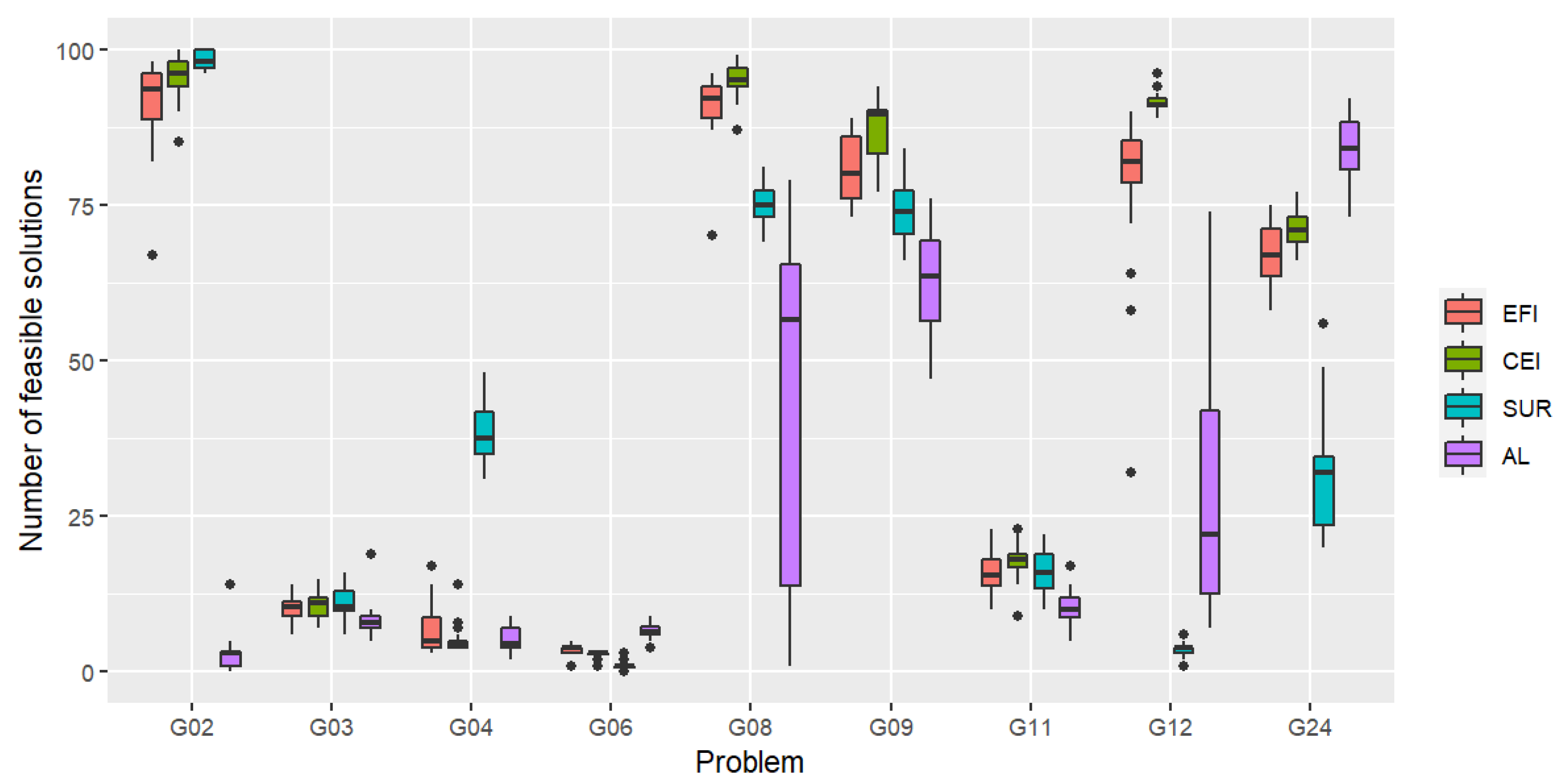
The distribution of the number of feasible solutions out of 100 observations is given in
Figure 2.
3.2.2. Scenario 2: Latin Hypercube Initial Design Points
For a more practical and realistic situation, LHSD is used to generate the initial points in the second scenario. In addition to the test problems used in Scenario 1, we also include a practical application of the pressure vessel design optimization problem with four constraints [
46]. We shall refer to this problem by the abbreviation P.V. The problem description can be found in
Appendix A.2. Results of the best solution found after 200 iterations are given in
Table 5. From the table, we can see that feasible solutions were found by all algorithms in all runs except for problems G02 and G08, where AL failed to locate a feasible solution on 4 and 2 trials, respectively.
In terms of the solution quality, results from a statistical test are reported in
Table 6. We can see that EFI and CEI performed quite similarly except for one case, G09, on which CEI is significantly better than EFI. CEI is best on 6 problems, EFI is best on 5 problems, and AL is best on 5 problems.
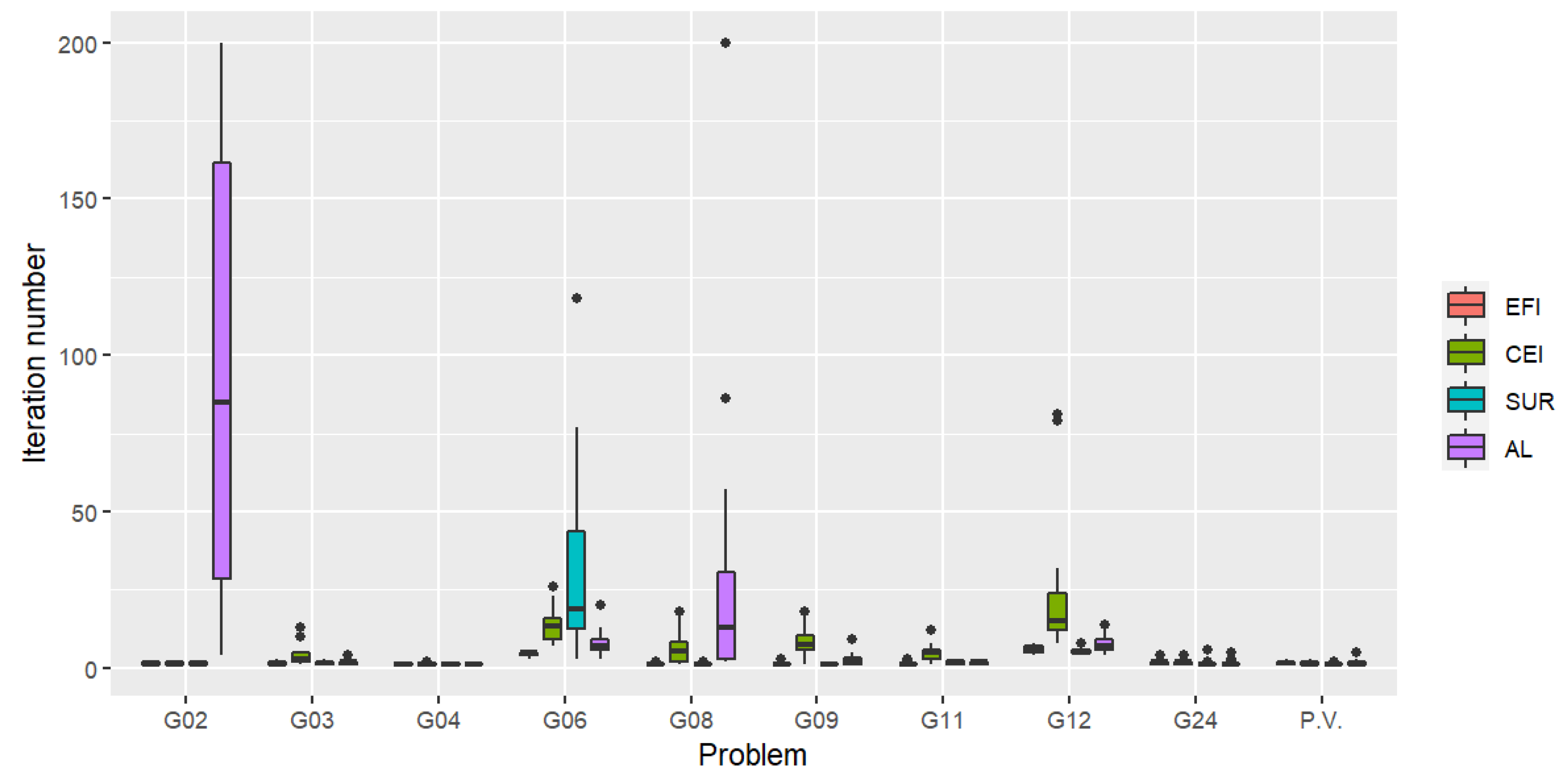
The iteration number for which the first feasible solution is found is shown in
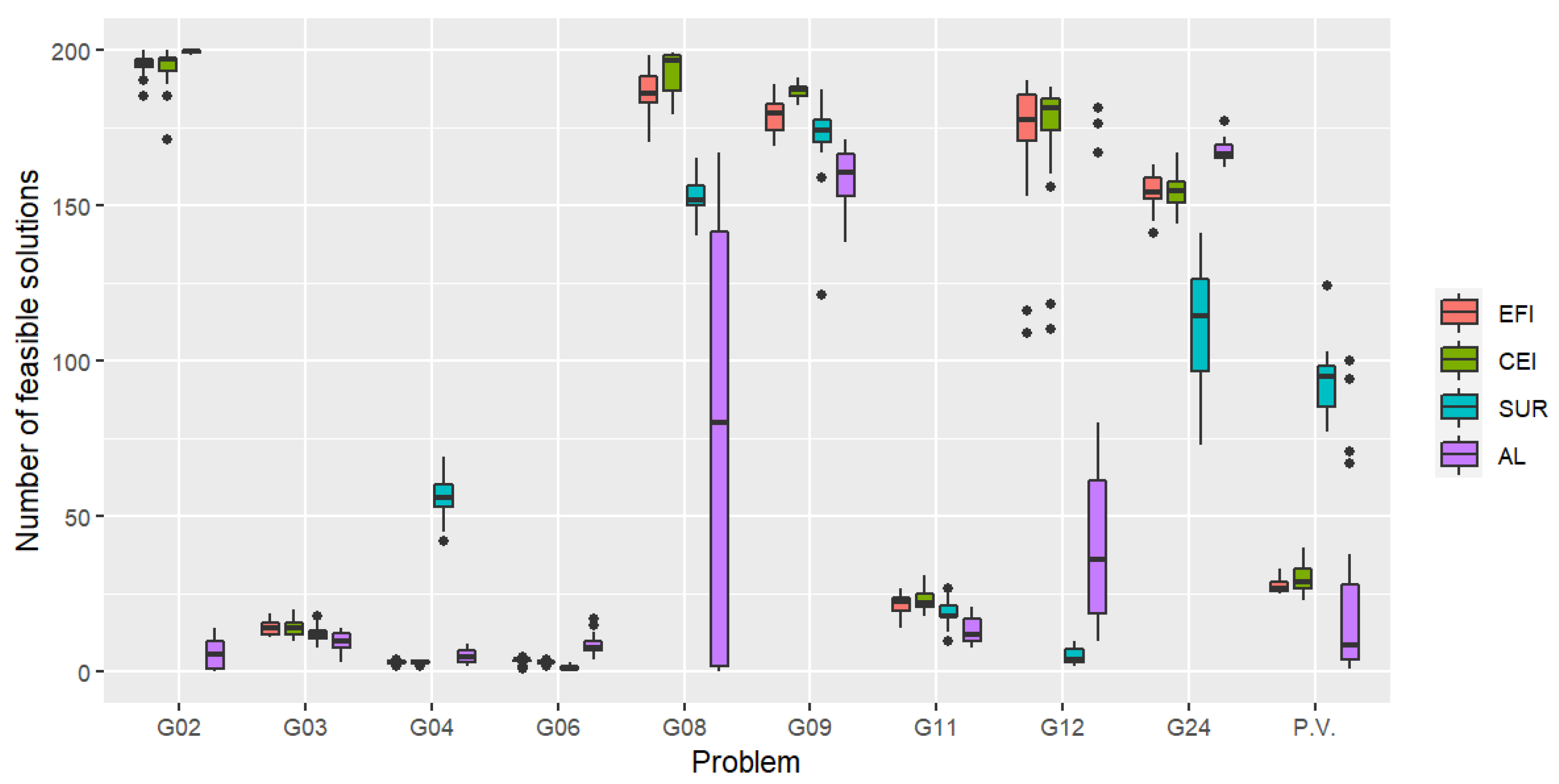
Figure 3. It is clear from these boxplots that overall, the fastest algorithm to find the first feasible point is again achieved by EFI. The number of feasible solutions (out of the total number of 200 observations) is given in
Figure 4. While AL performed best on 5 problems as mentioned, it did not find a feasible solution on some trials for 2 problems. In addition, AL performed significantly poorly on the pressure vessel problem.
Both EFI and CEI seem to work very well, but CEI tends to search over infeasible regions in the early stages of the algorithm before moving the search towards the feasible region afterwards, while EFI seems to behave in the opposite direction. Finally, although SUR did not fail to find a feasible solution in Scenario 2, none of its solutions is as good as that of other algorithms.
Finally, we summarize the best algorithm for each problem of the two scenarios in
Table 7.
4. Conclusions
In this article, we performed a study on the benchmarking of various CBO algorithms to test the capability of each infill sampling criterion. To that end, experiments with a set of benchmark problems were performed to investigate the impact of the choice of criteria on problems with varying shapes and sizes of feasible regions, ranges of the decision space, as well as initial number of feasible solutions. In light of the results obtained, SUR does not give a satisfactory performance on fast convergence when compared to other methods. AL performed best in several circumstances, but it could not locate a feasible solution on some problem trials. While the performances of EFI and CEI were quite similar, EFI seemed to locate a first feasible solution slightly faster. The obtained results indicate that EFI and CEI could better balance the exploration and exploitation of the objective space and at the same time explore feasible regions more efficiently.
Because of the inherent diversity of these methods, each compared method still has strengths and limitations that leave room for future improvement. Besides the issue of scaling to high-dimensional GPs, another important challenge associated with high-dimensional CBO and/or a large number of constraints is optimization of the infill sampling criterion, which often involves numerical integration methods. To apply CBO to high-dimensional problems, it is therefore necessary to develop methods that scale to high dimensional problems. Consequently, advanced methods on scalable/sparse GPs, local CBO, as well as the strategy used to optimize an infill sampling criterion can be potential research directions [
47,
48,
49,
50,
51].
In addition, the choice of the initial sampling strategy can also influence the overall quality of the BO [
52]. Variance reduction techniques such as those introduced in [
53] may also play an important role and affect the performance of algorithms. This can be a potential future direction for benchmarking the CBO algorithm’s performance.