A Joint Detection and Decoding Scheme for PC-SCMA System Based on Pruning Iteration
Abstract
1. Introduction
1.1. Related Work
1.2. Organization and Notation
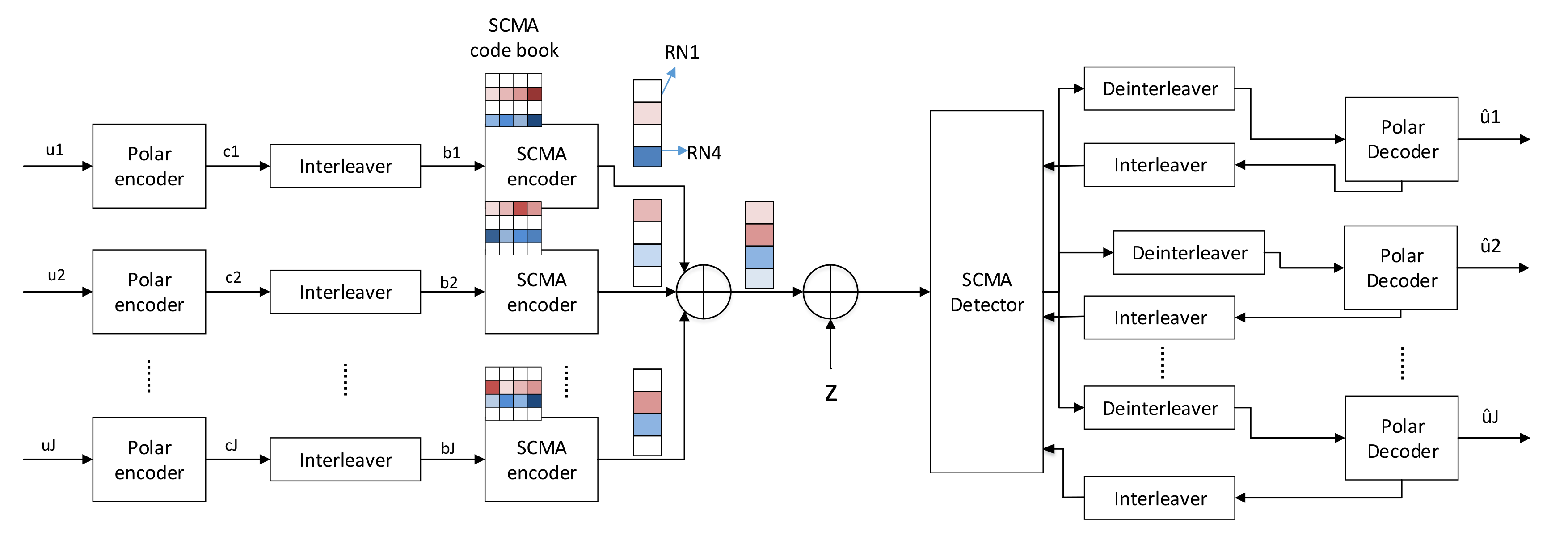
2. System Model
3. Proposed Algorithm for Joint Detection and Decoding
3.1. Joint Detection and Decoding Scheme Based on Pruning Iteration PI-JDD
3.1.1. RNs Update
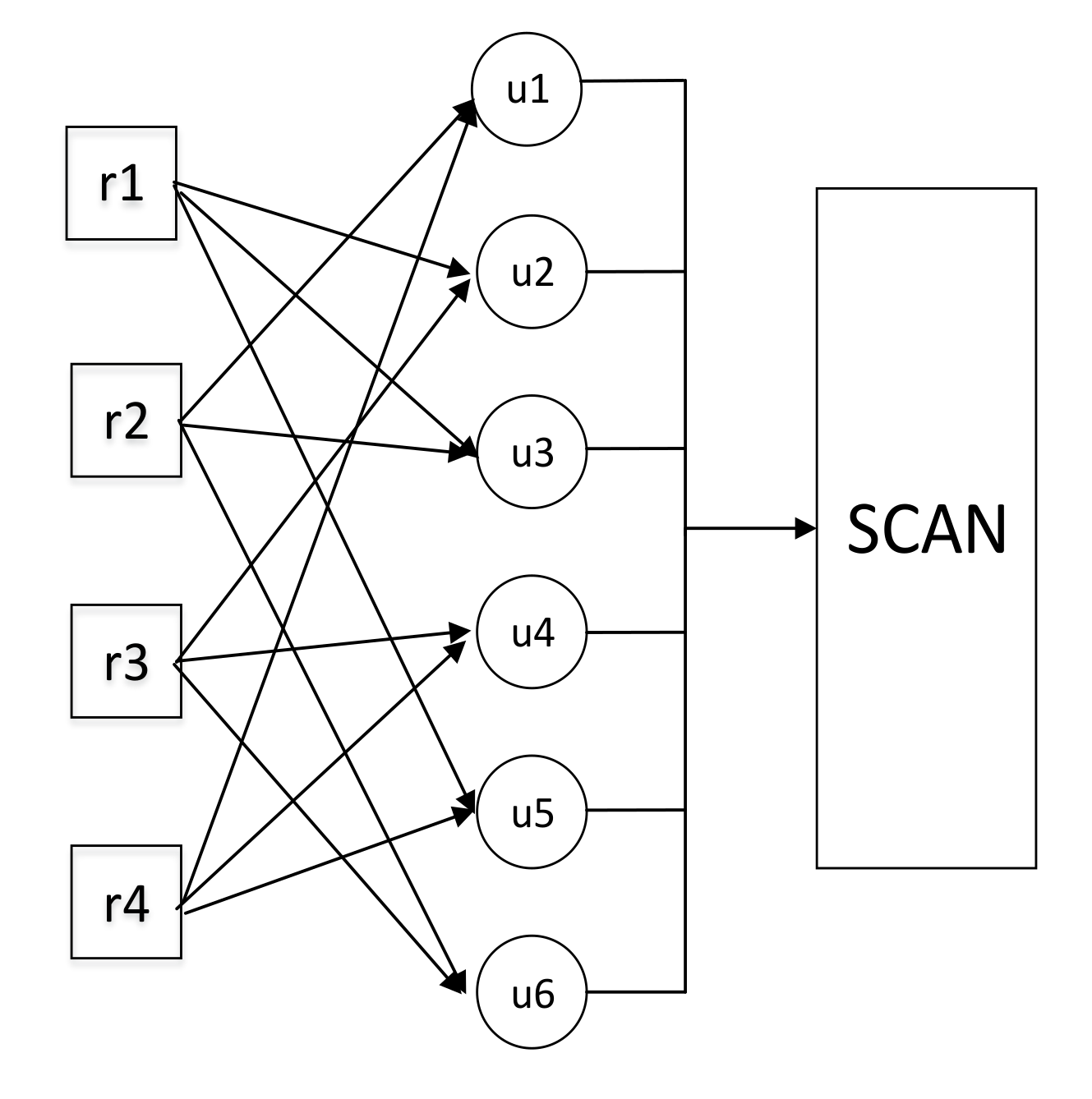
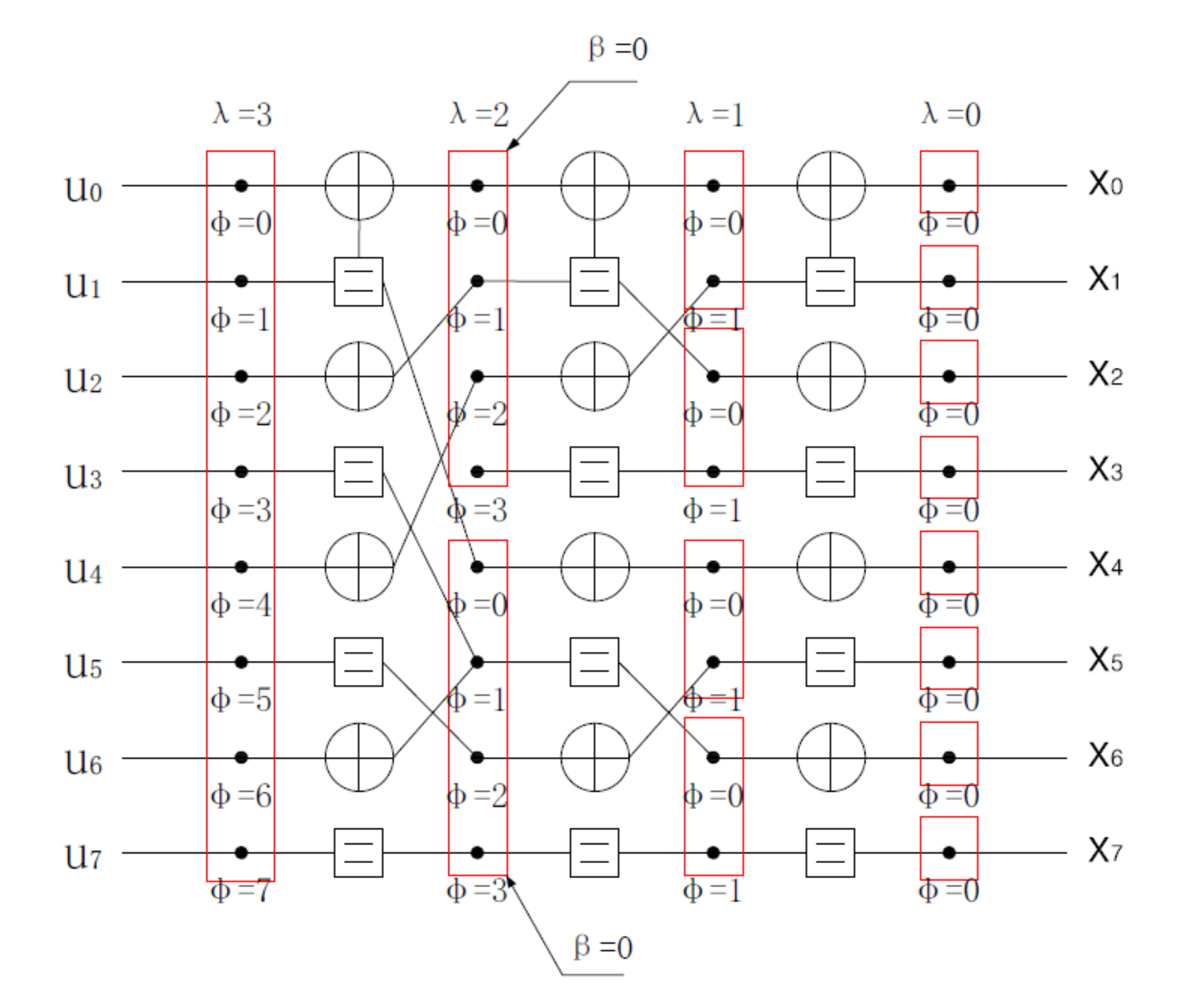
3.1.2. SCAN Decoding
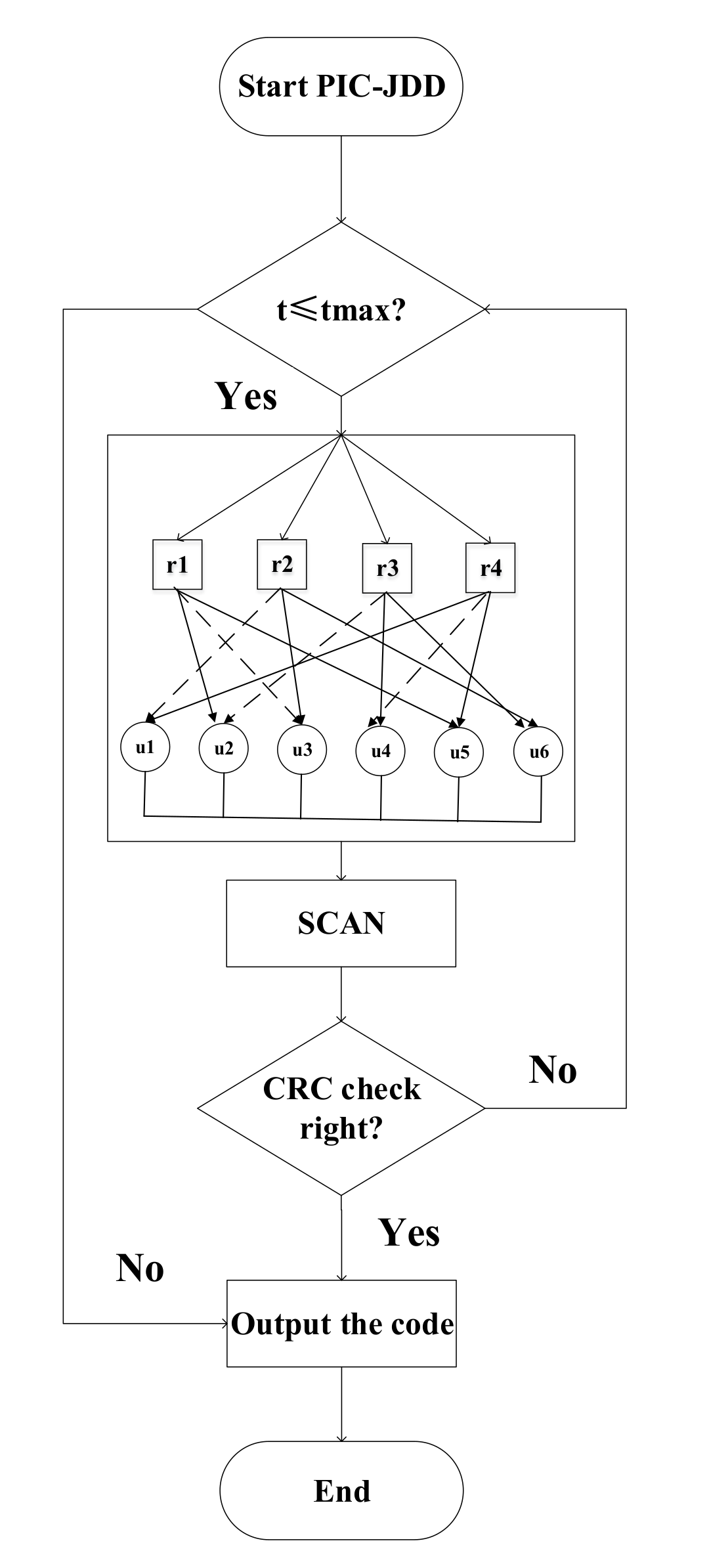
3.2. Joint Optimization Scheme for Joint Detection and Decoding PIC-JDD
4. Computational Complexity
5. Numerical Results
5.1. BER Performance Analysis of PI-JDD
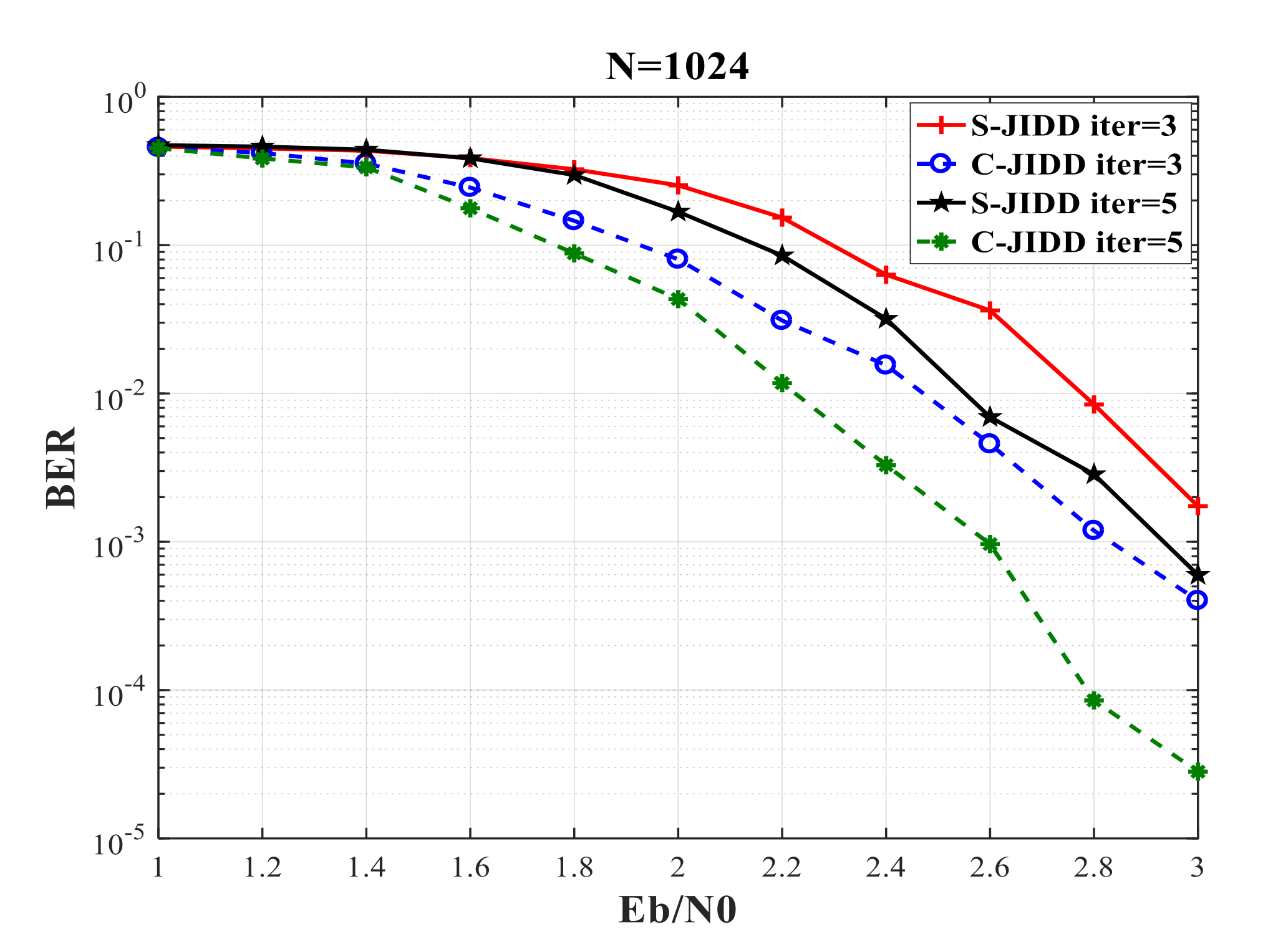
5.2. BER Performance Analysis of C-JIDD
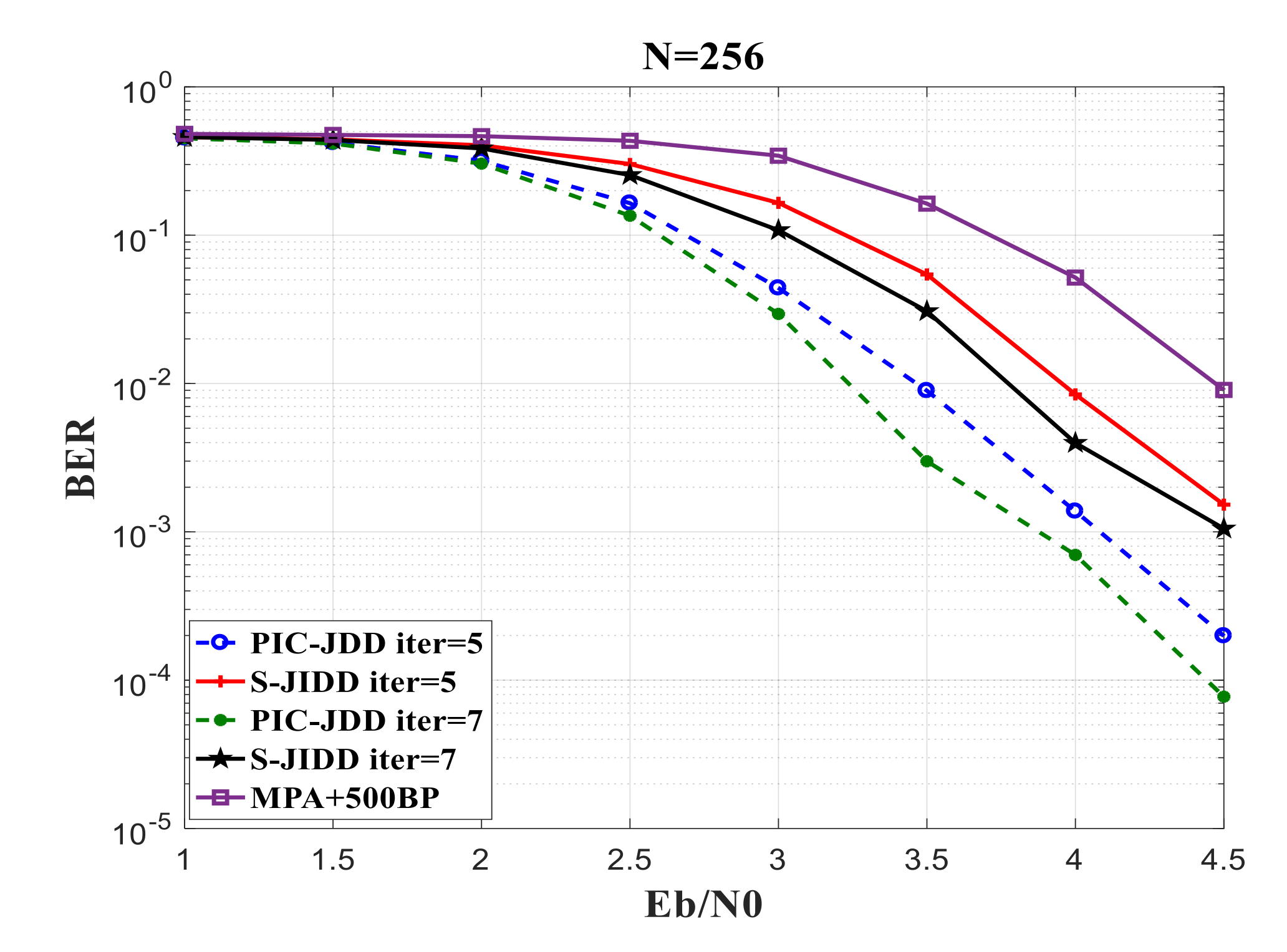
5.3. BER Performance Analysis of PIC-JDD
6. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Arikan, E. Channel Polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Nikopour, H.; Baligh, H. Sparse code multiple access. In Proceedings of the 2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013; pp. 332–336. [Google Scholar]
- Taherzadeh, M.; Nikopour, H.; Bayesteh, A.; Baligh, H. SCMA Codebook design. In Proceedings of the 2014 IEEE 80th Vehicular Technology Conference (VTC2014-Fall), Vancouver, BC, Canada, 14–17 September 2014; pp. 1–5. [Google Scholar]
- Peng, X.; Pan, Z.; Lai, K.; Wen, L.; Lei, J. Low complexity receiver of sparse code multiple access based on dynamic trellis. IET Commun. 2020, 14, 1420–1427. [Google Scholar] [CrossRef]
- Tan, Y.; Gao, Z.; Guo, S.; Gao, F. A dynamic multiuser detection scheme for uplink SCMA system. In Proceedings of the 2017 IEEE 17th International Conference on Communication Technology (ICCT), Chengdu, China, 27–30 October 2017; pp. 631–635. [Google Scholar]
- Du, Y.; Dong, B.; Wang, X. Multiuser detection scheme for SCMA systems based on serial strategy. Electron. Inf. Technol. 2016, 38, 1888–1893. [Google Scholar] [CrossRef]
- Arikan, E.; Telatar, E. On the rate of channel polarization. In Proceedings of the 2009 IEEE International Symposium on Information Theory, Seoul, Korea, 28 June–3 July 2009; pp. 1493–1495. [Google Scholar] [CrossRef]
- Hassani, S.H.; Urbanke, R. Polar codes: Robustness of the successive cancellation decoder with respect to quantization. In Proceedings of the 2012 IEEE International Symposium on Information Theory, Cambridge, MA, USA, 1–6 July 2012; pp. 1962–1966. [Google Scholar]
- Tal, I.; Vardy, A. List Decoding of polar codes. IEEE Trans. Inf. Theory 2015, 61, 2213–2226. [Google Scholar] [CrossRef]
- Niu, K.; Chen, K. Stack decoding of polar codes. Electron. Lett. 2012, 48, 695. [Google Scholar] [CrossRef]
- Chen, K.; Niu, K.; Lin, J. Improved successive cancellation decoding of polar codes. IEEE Trans. Commun. 2013, 61, 3100–3107. [Google Scholar] [CrossRef]
- Arkan, E. A performance comparison of polar codes and Reed-Muller codes. IEEE Commun. Lett. 2008, 12, 447–449. [Google Scholar] [CrossRef]
- Elkelesh, A.; Ebada, M.; Cammerer, S.; Brink, S.T. Belief propagation decoding of polar codes on permuted factor graphs. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; pp. 1–6. [Google Scholar]
- Lin, J.; Yan, Z.; Wang, Z. Efficient soft cancelation decoder architectures for polar codes. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2017, 25, 87–99. [Google Scholar] [CrossRef]
- Fayyaz, U.U.; Barry, J.R. Polar codes for partial response channels. In Proceedings of the 2013 IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; pp. 4337–4341. [Google Scholar]
- Fu, J.; Zhang, J.; Wang, J. Joint detection and decoding technology of SCMA and polarization code. Appl. Res. Comput. 2019, 36, 2739–2742. [Google Scholar] [CrossRef]
- Pan, Z.; Li, E.; Zhang, L.; Lei, J.; Tang, C.J. Design and optimization of joint iterative detection and decoding receiver for uplink polar coded SCMA system. IEEE Access 2018, 6, 52014–52026. [Google Scholar] [CrossRef]
- Zhang, Y.; Ge, W.; Zhang, P.; Gao, M. The optimization scheme for joint iterative detection and decoding of polar coded SCMA system. Opt. Fiber Technol. 2020, 58, 102283. [Google Scholar] [CrossRef]
- Miao, J.; Hu, X.; Zhao, Z. A Low Complexity Multiuser Detection Scheme with Dynamic Factor Graph for Uplink SCMA Systems. In Proceedings of the 2019 IEEE/CIC International Conference on Communications Workshops in China (ICCC Workshops), Changchun, China, 11–13 August 2019; pp. 846–851. [Google Scholar]
- Sun, S.; Cho, S.-G.; Zhang, Z. Error patterns in belief propagation decoding of polar codes and their mitigation methods. In Proceedings of the 2016 50th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 6–9 November 2016; pp. 1199–1203. [Google Scholar]
- Yuan, B.; Parhi, K.K. Early stopping criteria for energy-efficient low-latency belief-propagation polar code decoders. IEEE Trans. Signal. Process. 2014, 62, 6496–6506. [Google Scholar] [CrossRef]
- Nikopour, H.; Yi, E.; Bayesteh, A.; Au, K.; Hawryluck, M.; Baligh, H.; Ma, J. SCMA for downlink multiple access of 5G wireless networks. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 18–12 December 2014; pp. 3940–3945. [Google Scholar]
- Han, Y.; Zhou, W.; Zhao, M.; Zhou, S.; Zhoua, S. Enabling high order SCMA systems in downlink scenarios with a serial coding scheme. IEEE Access 2018, 6, 33796–33809. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Wang, D.; Zhang, Y.; Lan, Y. BER performance of multicast SCMA systems. IEEE Wirel. Commun. Lett. 2019, 8, 1073–1076. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, S.; Chen, Y. Iterative multiuser receiver in sparse code multiple access systems. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 2918–2923. [Google Scholar]
- Hagenauer, J.; Görtz, N. The turbo principle in joint source-channel coding. In Proceedings of the 2003 IEEE Information Theory Workshop (Cat. No.03EX674), Paris, France, 31 March–4 April 2003; pp. 275–278. [Google Scholar]
- Wang, X.; Poor, H. Iterative (turbo) soft interference cancellation and decoding for coded CDMA. IEEE Trans. Commun. 1999, 47, 1046–1061. [Google Scholar] [CrossRef]
- Sanderovich, A.; Peleg, M.; Shamai, S. LDPC coded MIMO multiple access with iterative joint decoding. IEEE Trans. Inf. Theory 2005, 51, 1437–1450. [Google Scholar] [CrossRef]
- Ren, B.; Han, S.; Meng, W.; Li, C.; Wu, X.; Sha, X. Enhanced turbo detection for SCMA based on information reliability. In Proceedings of the 2015 IEEE/CIC International Conference on Communications in China (ICCC), Shenzhen, China, 2–4 November 2015; pp. 1–5. [Google Scholar]
- Zhang, Z.; Han, K.; Hu, J.; Chen, J. Joint Detection and Decoding Schemes for Turbo Coded SCMA Systems. In Proceedings of the 2016 IEEE Globecom Workshops (GC Wkshps), Washington, DC, USA, 4–8 December; pp. 1–6. [CrossRef]
- Narasimhan, T.L.; Chockalingam, A. EXIT chart based design of irregular LDPC codes for large-MIMO systems. IEEE Commun. Lett. 2012, 17, 115–118. [Google Scholar] [CrossRef]
- Narasimhan, T.L.; Chockalingam, A.; Rajan, B.S. Factor graph based joint detection/decoding for LDPC coded large-MIMO systems. In Proceedings of the 2012 IEEE 75th Vehicular Technology Conference (VTC Spring), Yokohama, Japan, 6–9 May 2012; pp. 1–5. [Google Scholar]
- Kurkoski, B.; Siegel, P.; Wolf, J. Joint message-passing decoding of LDPC codes and partial-response channels. IEEE Trans. Inf. Theory 2002, 48, 1410–1422. [Google Scholar] [CrossRef]
- Wen, L.; Su, M. Joint sparse graph over GF (q) for code division multiple access systems. IET Commun. 2015, 9, 707–718. [Google Scholar] [CrossRef]
- Xiao, B.; Xiao, K.; Zhang, S.; Chen, Z.; Xia, B.; Liu, H.; Baicen, X.; Kexin, X.; Shutian, Z.; Zhiyong, C. Iterative detection and decoding for SCMA systems with LDPC codes. In Proceedings of the 2015 International Conference on Wireless Communications & Signal Processing (WCSP), Nanjing, China, 15–17 October 2015; pp. 1–5. [Google Scholar]
- Han, K.; Zhang, Z.; Hu, J.; Chen, J. A High performance joint detection and decoding scheme for LDPC coded SCMA system. In Proceedings of the 2016 IEEE Globecom Workshops (GC Wkshops), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Sun, W.-C.; Su, Y.-C.; Ueng, Y.-L.; Yang, C.-H. An LDPC-coded SCMA receiver with multi-user iterative detection and decoding. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 3571–3584. [Google Scholar] [CrossRef]
- Hao, Y.; Xiao, K.; Chen, Z.; Xia, B. Density evolution analysis of LDPC-coded SCMA systems. In Proceedings of the 2017 9th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 11–13 October 2017; pp. 1–6. [Google Scholar]
- Lai, K.; Wen, L.; Lei, J.; Xiao, P.; Maaref, A.; Imran, M. Sub-graph based joint sparse graph for sparse code multiple access systems. IEEE Access 2018, 6, 25066–25080. [Google Scholar] [CrossRef]
- Dai, J.; Niu, K.; Si, Z.; Lin, J. Evaluation and optimization of Gaussian approximation for polar codes. In Proceedings of the American Society for Information Science and Technology, St. Louis, MO, USA, 5–11 November 2015. [Google Scholar]








| Algorithm | ADD | MUL | COM |
| S-JIDD | |||
| PIC-JDD |
| Parameter | Value |
| Number of users J | 6 |
| Size of codebook M | 4 |
| Number of resources K | 4 |
| System load λ | 150% |
| a (N = 256) | 0.6 |
| a (N = 1024) | 0.4 |
| Code rate R (N = 256) | 0.47 |
| Code rate R (N = 1024) | 0.32 |
| Channel model | AWGN |
| Construction mode of polar code | Gaussian approximate |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Ge, W.; Zhang, P.; Gao, M.; Zhang, G. A Joint Detection and Decoding Scheme for PC-SCMA System Based on Pruning Iteration. Symmetry 2020, 12, 1624. https://doi.org/10.3390/sym12101624
Zhang Y, Ge W, Zhang P, Gao M, Zhang G. A Joint Detection and Decoding Scheme for PC-SCMA System Based on Pruning Iteration. Symmetry. 2020; 12(10):1624. https://doi.org/10.3390/sym12101624
Chicago/Turabian StyleZhang, Yongxing, Wenping Ge, Pengju Zhang, Mengyao Gao, and Gecheng Zhang. 2020. "A Joint Detection and Decoding Scheme for PC-SCMA System Based on Pruning Iteration" Symmetry 12, no. 10: 1624. https://doi.org/10.3390/sym12101624
APA StyleZhang, Y., Ge, W., Zhang, P., Gao, M., & Zhang, G. (2020). A Joint Detection and Decoding Scheme for PC-SCMA System Based on Pruning Iteration. Symmetry, 12(10), 1624. https://doi.org/10.3390/sym12101624




