Impact of Stair and Diagonal Matrices in Iterative Linear Massive MIMO Uplink Detectors for 5G Wireless Networks
Abstract
1. Introduction
2. Background
2.1. System Model
2.2. Definition of a Diagonal Matrix and a Stair Matrix
- -
- , where ,
- -
- , where .
3. Diagonal and Stair Matrices in Iterative Linear M-MIMO UL Detectors
3.1. Linear Detectors Based on Neumann Series and Newton Iteration
- , where is the diagonal matrix,
- , where is the stair matrix.
3.2. Linear Detectors Based on Iterative Methods
- Using a stair matrix: ,
- Using a diagonal matrix: .
4. Complexity Analysis
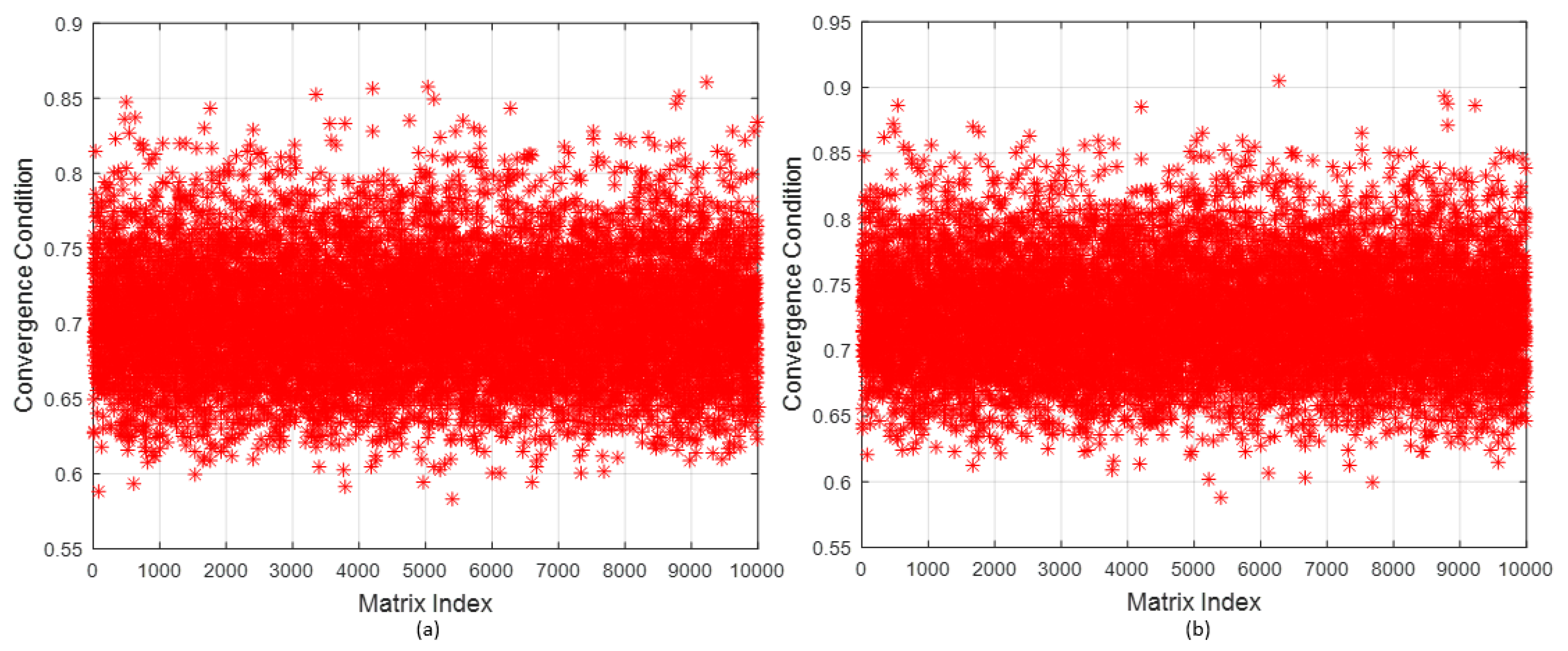
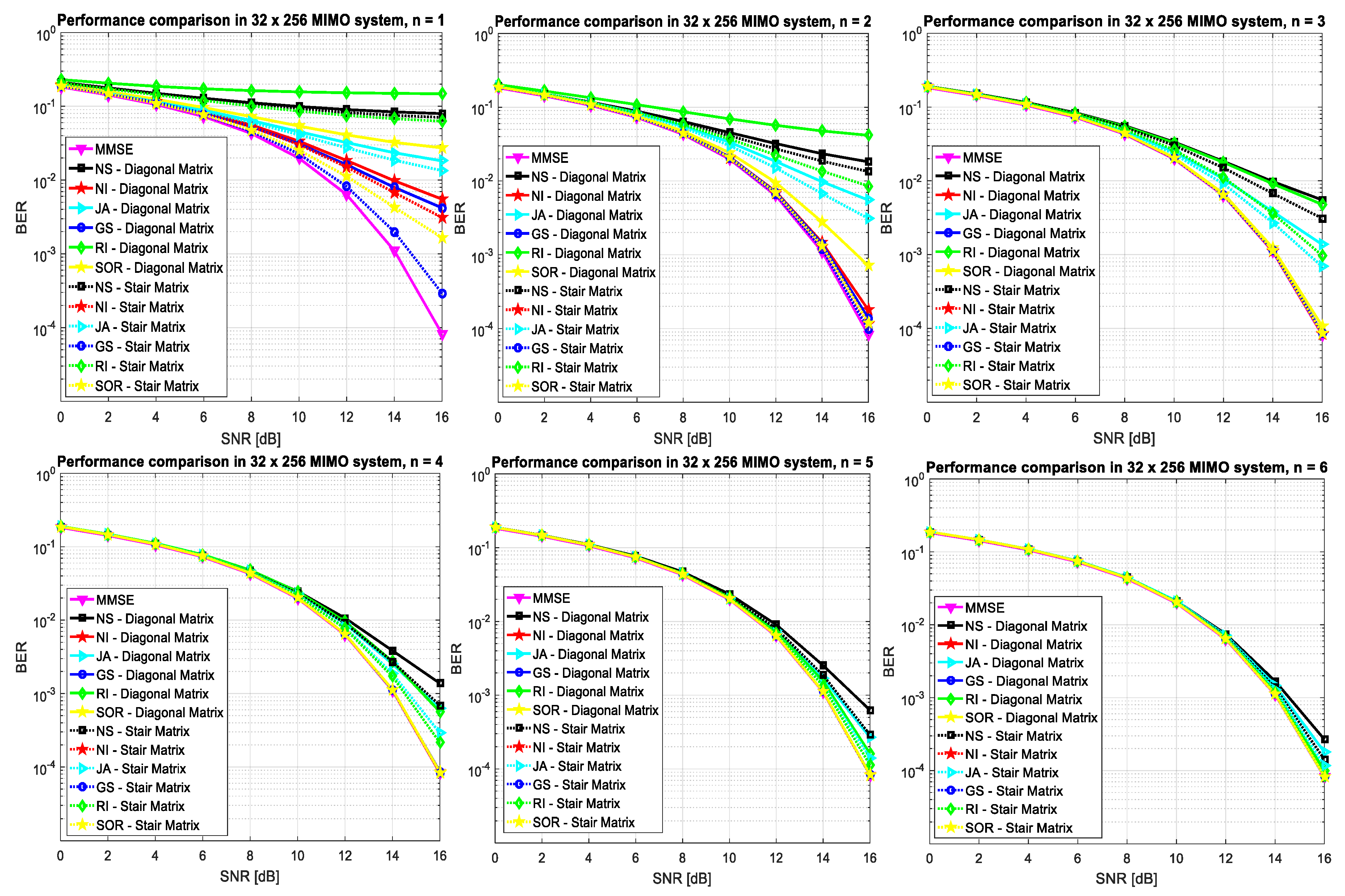
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Albreem, M.A.M. 5G wireless communication systems: Vision and challenges. In Proceedings of the 2015 International Conference on Computer, Communications, and Control Technology (I4CT) 2015, Kuching, Malaysia, 21–23 April 2015; pp. 493–497. [Google Scholar] [CrossRef]
- Mohammed, S.; Alsharif, M.; Gharghan, S.; Albreem, M. Beamforming Scheme for Millimeter-Wave Massive-MIMO 5G Wireless Networks. Symmetry 2019, 11, 1424. [Google Scholar] [CrossRef]
- Alsharif, M.; Kim, S.; Kuruoğlu, N. Energy Harvesting Techniques for Wireless Sensor Networks/Radio-Frequency Identification: A Review. Symmetry 2019, 11, 865. [Google Scholar] [CrossRef]
- Kim, H.; Kim, D.; Yang, S.; Son, Y.; Han, S. Mitigation of Inter-Cell Interference Utilizing Carrier Allocation in Visible Light Communication System. IEEE Commun. Lett. 2012, 16, 526–529. [Google Scholar] [CrossRef]
- Albreem, M.A.; Juntti, M.; Shahabuddin, S. Massive MIMO Detection Techniques: A Survey. IEEE Commun. Surv. Tutor. 2019, 21, 3109–3132. [Google Scholar] [CrossRef]
- Thian, B.S.; Goldsmith, A. Decoding for MIMO Systems with imperfect channel state information. In Proceedings of the 2010 IEEE Global Telecommunications Conference GLOBECOM, Miami, FL, USA, 6–10 December 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Albreem, M.; Salleh, M. Lattice Sphere Decoding for Block Data Transmission Systems. Wirel. Person. Commun. 2015, 82, 1833–1850. [Google Scholar] [CrossRef]
- Albreem, M.; Ismail, N. A Review: Detection Techniques For LTE System. Telecommun. Syst. 2015, 63, 153–168. [Google Scholar] [CrossRef]
- Chaudhary, M.; Meena, N.K.; Kshetrimayum, R.S. Local search based near optimal low complexity detection for large MIMO System. In Proceedings of the 2016 IEEE International Conference on Advanced Networks and Telecommunications Systems (ANTS), Bangalore, India, 6–9 November 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Takahashi, T.; Ibi, S.; Sampei, S. On Normalization of Matched Filter Belief in GaBP for Large MIMO Detection. In Proceedings of the 2016 IEEE 84th Vehicular Technology Conference (VTC-Fall), Montreal, QC, Canada, 18–21 September 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Xie, T.; Han, Q.; Xu, H.; Qi, Z.; Shen, W. A Low-Complexity Linear Precoding Scheme Based on SOR Method for Massive MIMO Systems. In Proceedings of the IEEE Vehicular Technology Conference, Glasgow, Scotland, 11–14 May 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Costa, H.; Roda, V. A Scalable Soft Richardson Method for Detection in a Massive MIMO System. Prz. Elektrotechniczny 2016, 92, 199–203. [Google Scholar] [CrossRef]
- Minango, J.; de Almeida, C. Optimum and quasi-optimum relaxation parameters for low-complexity massive MIMO detector based on Richardson method. IEE Electron. Lett. 2017, 53, 1114–1115. [Google Scholar] [CrossRef]
- Kong, B.Y.; Park, I.C. Low-complexity symbol detection for massive MIMO uplink based on Jacobi method. In Proceedings of the IEEE International Symposium on Personal, Indoor, and Mobile Radio Communications, Valencia, Spain, 4–8 September 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, C.; Liang, X.; Wu, Z.; Xu, S.; You, X. Efficient iterative soft detection based on polynomial approximation for massive MIMO. In Proceedings of the 2015 International Conference on Wireless Communications & Signal Processing, Nanjing, China, 15–17 October 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Dai, L.; Gao, X.; Su, X.; Han, S.; I, C.L.; Wang, Z. Low-Complexity Soft-Output Signal Detection Based on Gauss Seidel Method for Uplink Multiuser Large-Scale MIMO Systems. IEEE Trans. Veh. Technol. 2015, 64, 4839–4845. [Google Scholar] [CrossRef]
- Zhou, J.; Hu, J.; Chen, J.; He, S. Biased MMSE soft-output detection based on conjugate gradient in massive MIMO. In Proceedings of the 2015 IEEE 11th International Conference on ASIC, Chengdu, China, 3–6 November 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Jiang, F.; Li, C.; Gong, Z.; Su, R. Stair Matrix and its Applications to Massive MIMO Uplink Data Detection. IEEE Trans. Commun. 2018, 66, 2437–2455. [Google Scholar] [CrossRef]
- Prabhu, H.; Edfors, O.; Rodrigues, J.; Liu, L.; Rusek, F. Hardware efficient approximative matrix inversion for linear pre-coding in massive MIMO. In Proceedings of the 2014 IEEE International Symposium on Circuits and Systems, Melbourne, Australia, 1–5 June 2014; pp. 1700–1703. [Google Scholar] [CrossRef]

| Method | Stair Matrix (S) | Diagonal Matrix (D) |
|---|---|---|
| NI | ||
| RI | ||
| SOR | ||
| GS | ||
| JA | ||
| NS |
| Matrix | Mean | Median | Standard Deviation | Prob. Quadratic Convergence |
|---|---|---|---|---|
| Stair (S) | 0.7027 | 0.7007 | 0.2776 | 1 |
| Diagonal (D) | 0.7255 | 0.7233 | 0.2868 | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albreem, M.A.; Alsharif, M.H.; Kim, S. Impact of Stair and Diagonal Matrices in Iterative Linear Massive MIMO Uplink Detectors for 5G Wireless Networks. Symmetry 2020, 12, 71. https://doi.org/10.3390/sym12010071
Albreem MA, Alsharif MH, Kim S. Impact of Stair and Diagonal Matrices in Iterative Linear Massive MIMO Uplink Detectors for 5G Wireless Networks. Symmetry. 2020; 12(1):71. https://doi.org/10.3390/sym12010071
Chicago/Turabian StyleAlbreem, Mahmoud A., Mohammed H. Alsharif, and Sunghwan Kim. 2020. "Impact of Stair and Diagonal Matrices in Iterative Linear Massive MIMO Uplink Detectors for 5G Wireless Networks" Symmetry 12, no. 1: 71. https://doi.org/10.3390/sym12010071
APA StyleAlbreem, M. A., Alsharif, M. H., & Kim, S. (2020). Impact of Stair and Diagonal Matrices in Iterative Linear Massive MIMO Uplink Detectors for 5G Wireless Networks. Symmetry, 12(1), 71. https://doi.org/10.3390/sym12010071






