A Theoretical Analysis for Mixed Convection Flow of Maxwell Fluid between Two Infinite Isothermal Stretching Disks with Heat Source/Sink
Abstract
1. Introduction
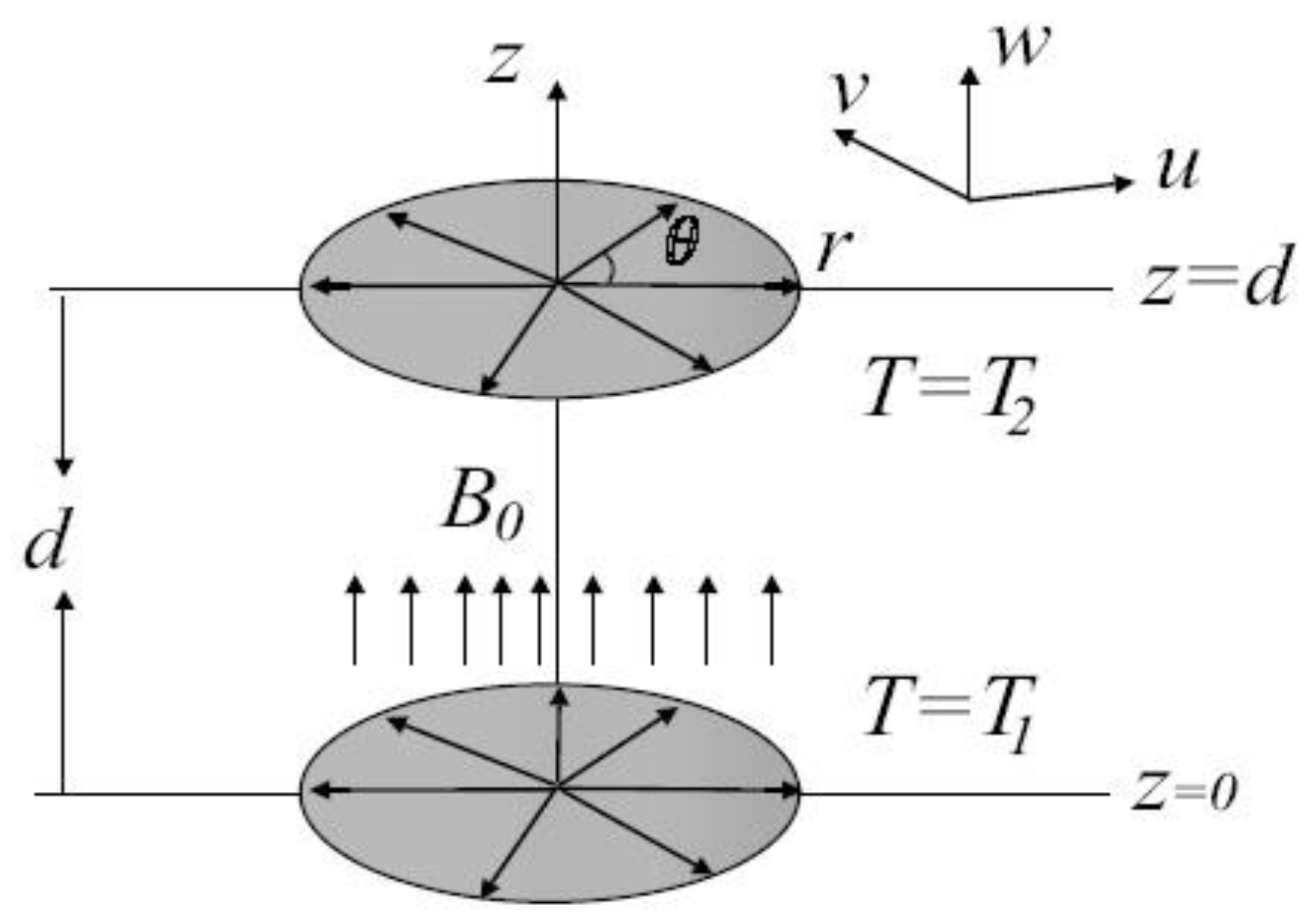
2. Mathematical Formulation
2.1. Skin Friction Coefficient
2.2. Local Nusselt Number
3. HomotopyAnalysis Method
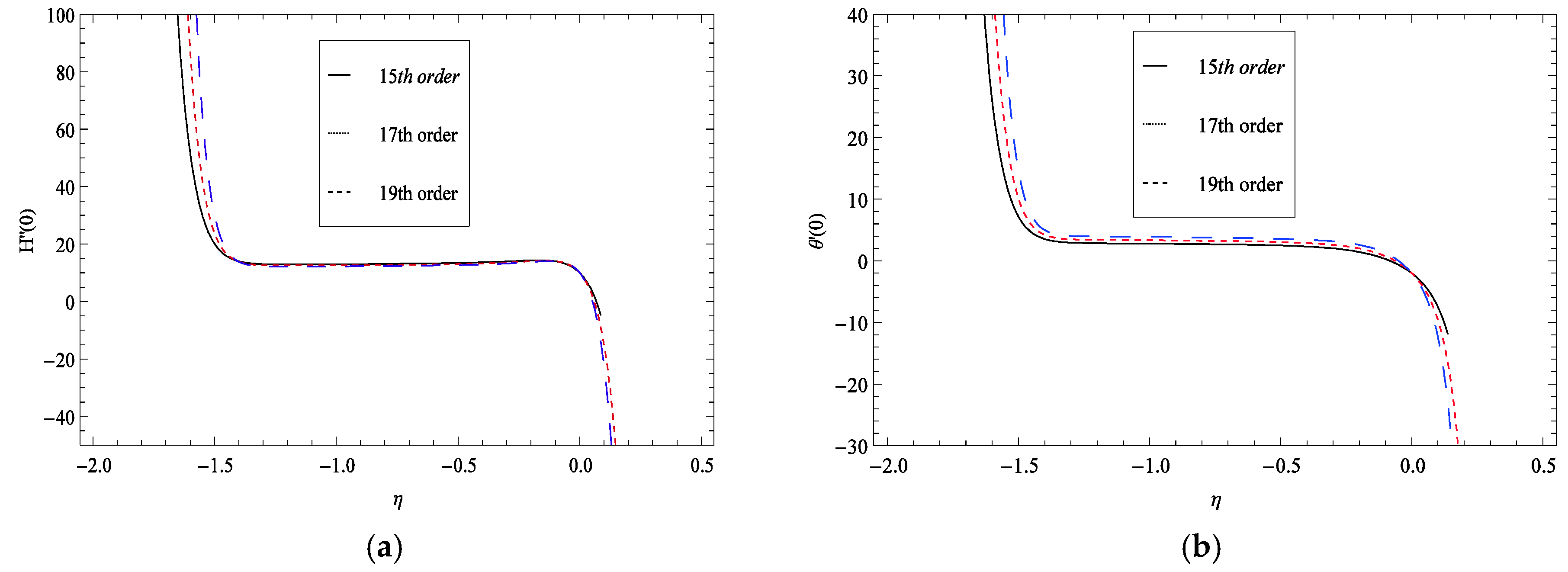
4. Convergence of Obtained Solution
5. Validation of Solution
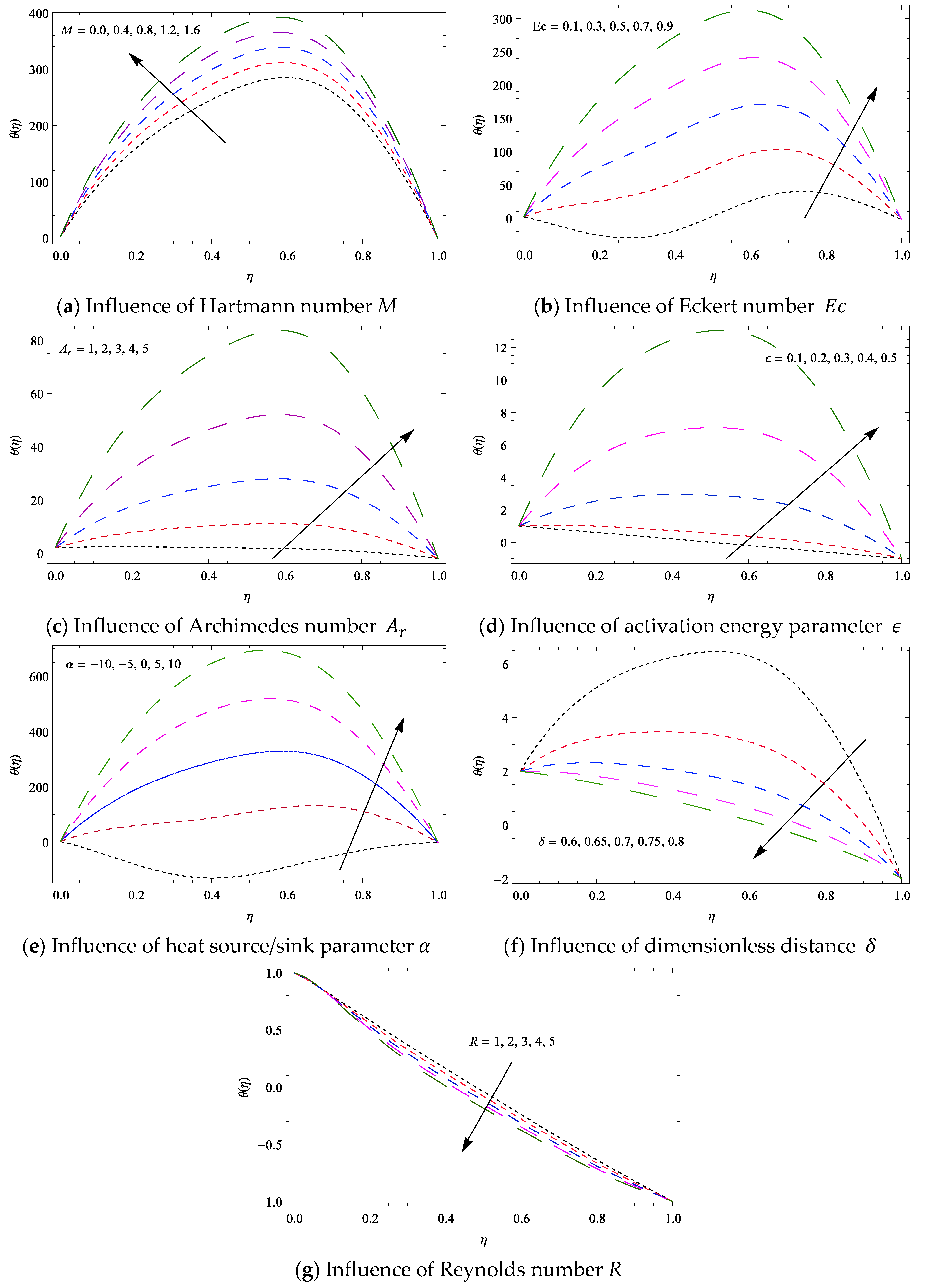
6. Results and Discussion
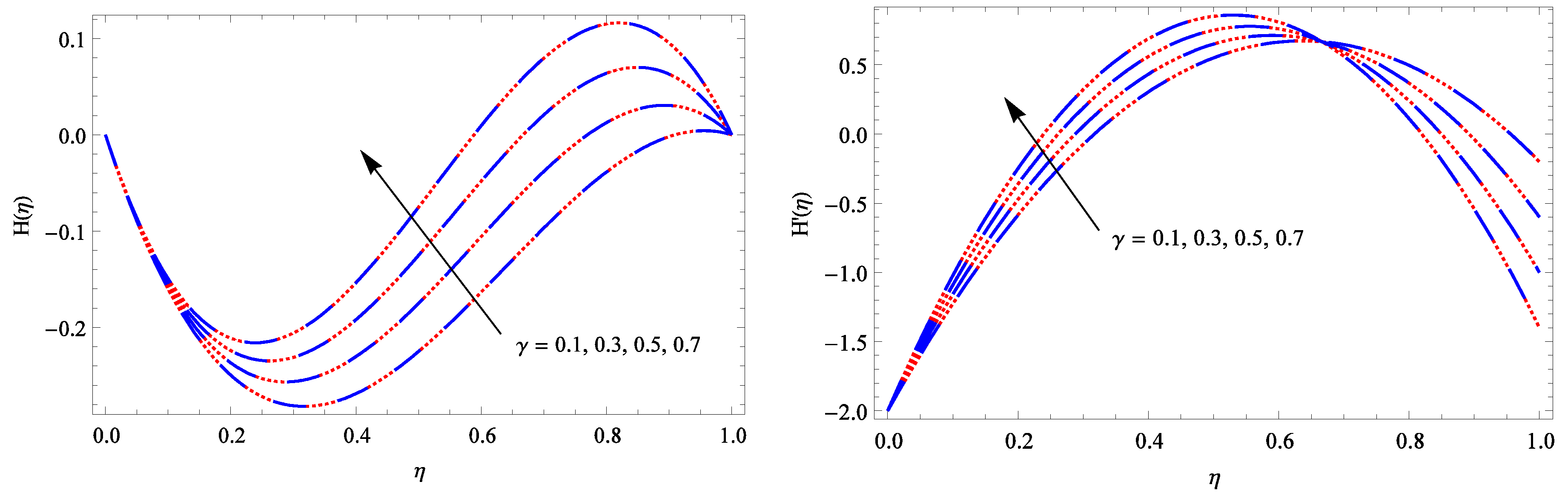
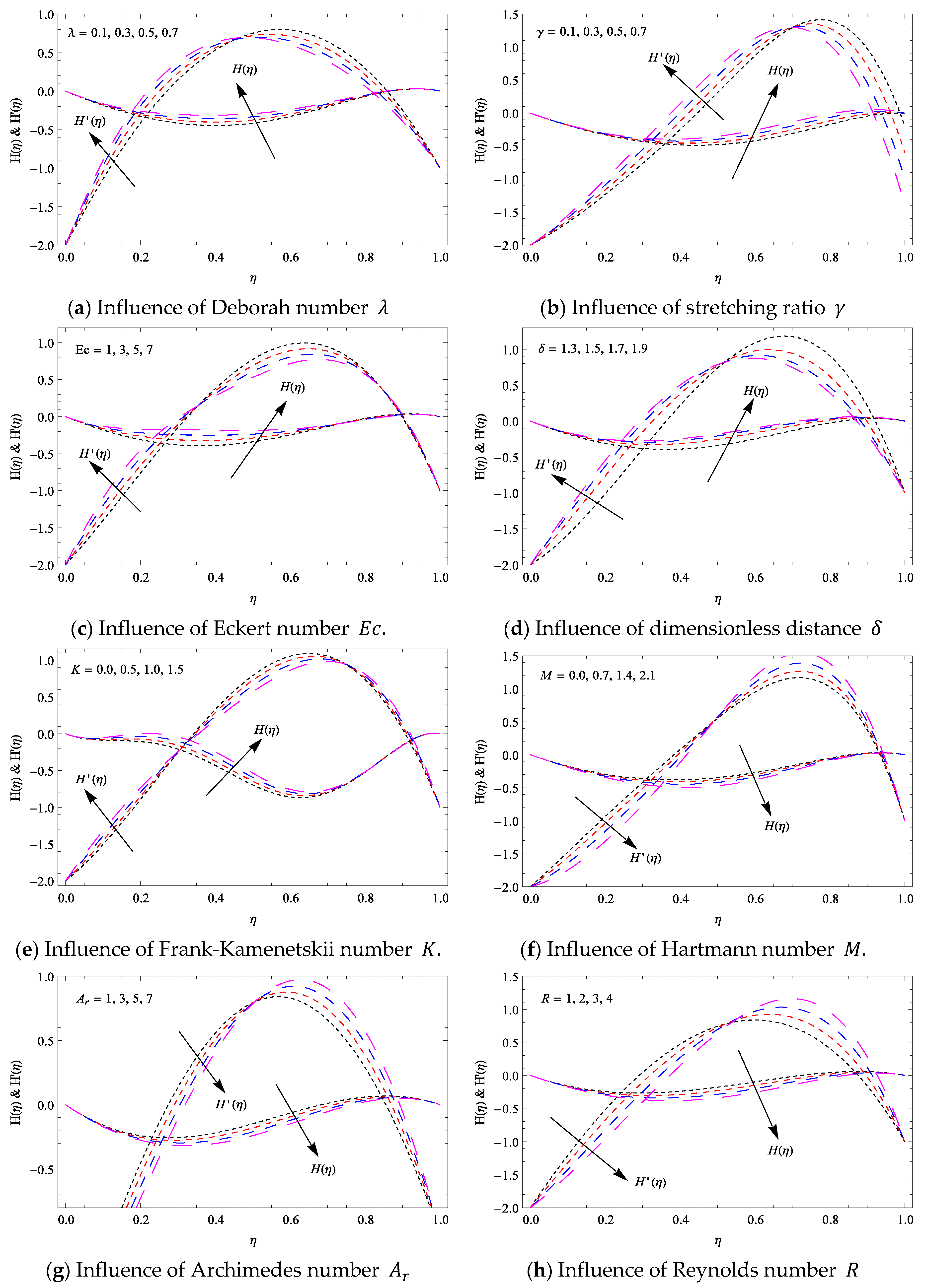
6.1. Velocity Distribution
6.2. Pressure Distribution
6.3. Temperature Distribution
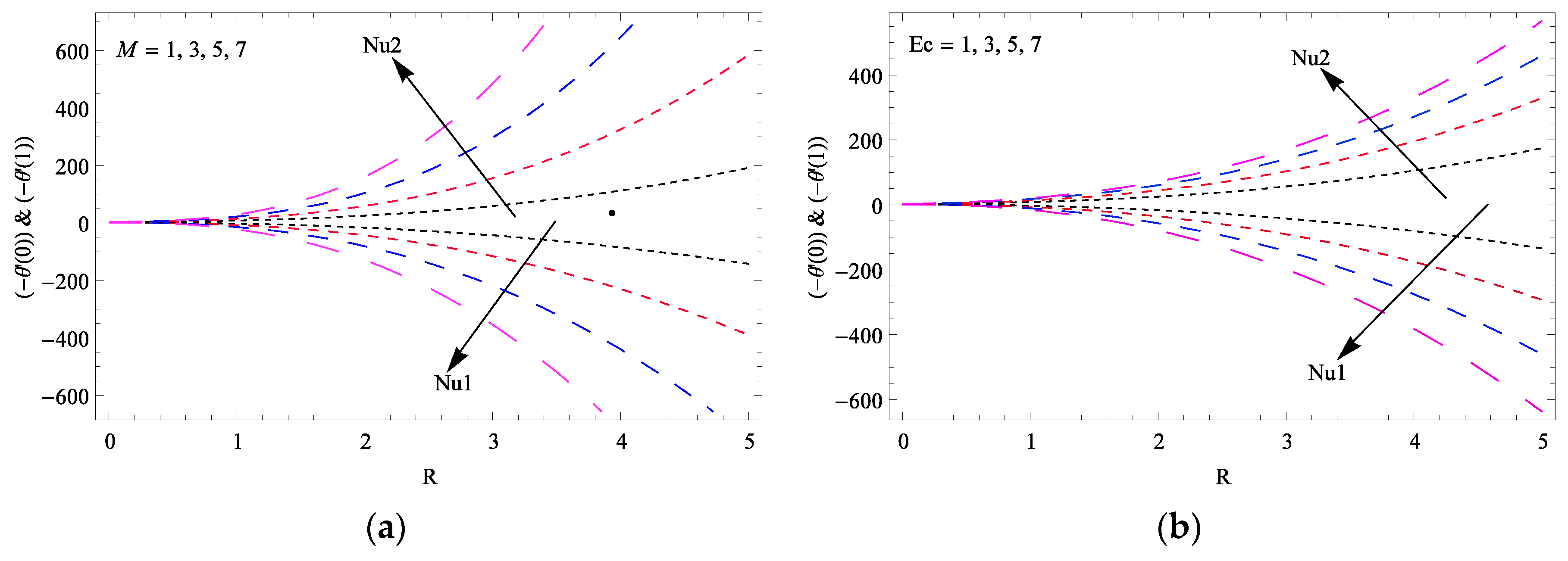
6.4. Physical Quantities of Interests
7. Conclusions
- The wall shear stress decreases by increasing stretching parameter, Hartmann number, Reynolds number, Deborah number, activation energy parameter and constant temperature parameter. It means that tangential stresses increase by increasing stretching the ratio parameter, Hartmann number and Reynolds number. While the behavior of dimensionless distance and Frank–Kamenetskii number are quite the opposite.
- The pressure distribution is increased with variation of theFrank–Kamenetskii number and stretching ratio parameter.
- When the Deborah number and Hartmann number increases, the wall shear stress at the lower disk increases while an opposite trend is found at the upper disk.
- It is observed that the surface heat transfer increases by increasing the stretching parameter and heat source/sink parameter.
- The rate of heat transfer decreases at the lower disk and increases at the upper disk by increasing the Hartmann number, Reynolds number, Archimedes number and activation energy parameter.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| cylindrical coordinate | |
| velocity components | |
| upper disk temperature | |
| E | activation energy |
| gas constant | |
| reactant concentration | |
| characteristic density | |
| is the kinematic viscosity | |
| thermal conductivity of fluid | |
| exothermicity factor | |
| stretching rate constant | |
| Hartmann number | |
| heat source/sink parameter | |
| Eckert number | |
| constant temperature parameter | |
| Archimedes number | |
| shear stress | |
| d | distance |
| T | is the fluid temperature |
| lower disk temperature | |
| B | product species |
| is chemical reaction | |
| is the relaxation time | |
| is the fluid pressure | |
| isreference temperature | |
| β | denotes the thermal expansion |
| heat generation/absorption coefficient | |
| Reynolds number | |
| Grashoff number | |
| Prandtl number | |
| Frank–Kamenetskii number | |
| activation energy parameter | |
| dimensionless distance |
References
- Maleque, K. Effects of exothermic/endothermic chemical reactions with Arrhenius activation energy on MHD free convection and mass transfer flow in presence of thermal radiation. J. Thermodyn. 2013, 2013, 692516. [Google Scholar] [CrossRef]
- Khan, M.I.; Hayat, T.; Khan, M.I.; Alsaedi, A. Activation energy impact in nonlinear radiative stagnation point flow of Cross nanofluid. Int. Commun. Heat Mass Transf. 2018, 91, 216–224. [Google Scholar] [CrossRef]
- Shafique, Z.; Mustafa, M.; Mushtaq, A. Boundary layer flow of Maxwell fluid in rotating frame with binary chemical reaction and activation energy. Results Phys. 2016, 6, 627–633. [Google Scholar] [CrossRef]
- Awad, F.G.; Motsa, S.; Khumalo, M. Heat and Mass Transfer in Unsteady Rotating Fluid Flow with Binary Chemical Reaction and Activation Energy. PLoS ONE 2014, 9, e107622. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, K.L. To promote radiation electrical MHD activation energy thermal extrusion manufacturing system efficiency by using Carreau-Nanofluid with parameters control method. Energy 2017, 130, 486–499. [Google Scholar] [CrossRef]
- Merkin, J.; Mahmood, T. Convective flows on reactive surfaces in porous media. Transp. Porous Media 1998, 47, 279–293. [Google Scholar] [CrossRef]
- Minto, B.J.; Ingham, D.B.; Pop, I. Free convection driven by an exothermic on a vertical surface embedded in porous media. Int. J. Heat Mass Trans. Transf. 1998, 41, 11–23. [Google Scholar] [CrossRef]
- Chou, S.F.; Tsern, I.P. Mixed convection heat transfer of horizontal channel flow over a heated block. Transp. Phenom. Heat Mass Trans. 1992, 2, 492–503. [Google Scholar]
- Nadeem, S.; Khan, M.R.; Khan, A.U. MHD stagnation point flow of viscous nanofluid over a curved surface. Phys. Scr. 2019, 94, 115207. [Google Scholar] [CrossRef]
- Ahmed, Z.; Al-Qahtani, A.; Nadeem, S.; Saleem, S. Computational Study of MHD Nanofluid Flow Possessing Micro-Rotational Inertia over a Curved Surface with Variable Thermophysical Properties. Processes 2019, 7, 387. [Google Scholar] [CrossRef]
- Khan, A.U.; Hussain, S.T.; Nadeem, S. Existence and stability of heat and fluid flow in the presence of nanoparticles along a curved surface by mean of dual nature solution. Appl. Math. Comput. 2019, 353, 66–81. [Google Scholar] [CrossRef]
- Sadiq, M.A.; Khan, A.U.; Saleem, S.; Nadeem, S. Numerical simulation of oscillatory oblique stagnation point flow of a magneto micropolar nanofluid. RSC Adv. 2019, 9, 4751–4764. [Google Scholar] [CrossRef]
- Harris, J. Rheology and Non-Newtonian Flow; Longman Inc.: New York, NY, USA, 1977. [Google Scholar]
- Hayat, T.; Abbas, Z.; Sajid, M. Series Solution for the Upper-Convected Maxwell Fluid over a Porous Stretching Plate. Phys. Lett. A 2006, 358, 396–403. [Google Scholar] [CrossRef]
- Aliakbar, V.; Pahlavan, A.A.; Sadeghy, K. The Influence of Thermal Radiation on MHD Flow of Maxwellian Fluid above Stretching Sheet. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 779–794. [Google Scholar] [CrossRef]
- Hayat, T.; Abbas, Z.; Sajid, M. MHD Stagnation-point Flow of an Upper-Convected Maxwell Fluid over a Stretching Surface. ChaosSolitons Fractals 2009, 39, 840–848. [Google Scholar] [CrossRef]
- Prasad, K.V.; Sujatha, A.; Vajravelu, K.; Pop, I. MHD Flow and Heat Transfer of a UCM Fluid over a Stretching Surface with Variable Thermophysical Properties. Meccanica 2012, 47, 1425–1439. [Google Scholar] [CrossRef]
- Khan, S.U.; Ali, N.; Sajid, M.; Hayat, T. Heat transfer characteristics in oscillatory hydromagnetic channel flow of Maxwell fluid using Cattaneo-Christov model. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2019, 89, 377–385. [Google Scholar] [CrossRef]
- Ahmed, J.; Khan, M.; Ahmad, L. MHD swirling flow and heat transfer in Maxwell fluid driven by two coaxially rotating disks with variable thermal conductivity. Chin. J. Phys. 2019, 60, 22–34. [Google Scholar] [CrossRef]
- Merkin, J.H.; Chaudhary, M.A. Free convection boundary layer driven by an exothermic surface reaction. Q. J. Mech. Appl. Math. 1994, 47, 405–428. [Google Scholar] [CrossRef]
- Gorder, R.A.V.; Sweet, E.; Vajravelu, K. Analytical solutions of a coupled nonlinear system arising in a flow between stretching disks. Appl. Math. Comput. 2010, 216, 1513–1523. [Google Scholar] [CrossRef]
- Khan, N.; Mahmood, T.; Sajid, M.; Hashmi, M.S. Heat and mass transfer on MHD mixed convection axisymmetric chemically reactive flow of Maxwell fluid driven by exothermal and isothermal stretching disks. Int. J. Heat Mass Transf. 2016, 92, 1090–1105. [Google Scholar] [CrossRef]
- Liao, S.J. On the analytic solution of magnetohydrodynamic flow of non-Newtonian fluids over a stretching sheet. J. Fluid Mech. 2003, 488, 189–212. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Solution of the Thomas–Fermi equation with a convergent approach. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4097–4103. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. ParametrizedAdomian decomposition method with optimum convergence. ACM Trans. Modeling Comput. Simul. 2017, 24, 21. [Google Scholar]
- Khan, S.U.; Ali, N.; Hayat, T. Analytical and Numerical Study of Diffusion of Chemically Reactive Species in Eyring-Powell Fluid over an Oscillatory Stretching Surface. Bulg. Chem. Commun. 2017, 49, 320–330. [Google Scholar]
- Ullah, I.; Waqas, M.; Hayat, T. Thermally radiated squeezed flow of magneto-nanofluid between two parallel disks with chemical reaction. J. Therm. Anal. Calorim. 2019, 135, 1021. [Google Scholar] [CrossRef]
- Khan, S.U.; Shehzad, S.A.; Ali, N. Darcy-Forchheimer MHD Couple Stress liquid flow by oscillatory stretched sheet with thermophoresis and heat generation/absorption. J. Porous Media 2018, 21, 1197–1213. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Aggregation effects on water base Al2O3—Nano fluid over permeable wedge in mixed convection. Asia-Pac. J. Chem. Eng. 2016, 11, 179–186. [Google Scholar] [CrossRef]
- Hassan, M.; Ellahi, R.; Zeeshan, A.; Bhatti, M.M. Analysis of natural convective flow of non-Newtonian fluid under the effects of nanoparticles of different materials. J. Process Mech. Eng. 2019, 233, 643–652. [Google Scholar] [CrossRef]
- Ambreen, A.K.; Bukhari, S.R.; Marin, M.; Ellahi, R. Effects of chemical reaction on third grade magnetohydrodynamics fluid flow under the influence of heat and mass transfer with variable reactive index. Heat Transf. Res. 2019, 50, 1061–1080. [Google Scholar]
- Sajjad, R.; Hayat, T.; Ellahi, R.; Muhammad, T.; Alsaedi, A. Darcy–Forchheimer flow of nanofluid due to a curved stretching surface. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 2–20. [Google Scholar]
- Hassan, M.; Ellahi, R.; Bhatti, M.M.; Zeeshan, A. A comparitive study of magnetic and non-magnetic particles in nanofluidpropigating over over a wedge. Can. J. Phys. 2019, 97, 277–285. [Google Scholar] [CrossRef]
- Hussain, F.; Ishtiaq, F.; Hussain, A. Peristaltic transport of Jeffrey fluid in a rectangular duct through a porous medium under the effect of partial slip: An application to upgrade industrial sieves/filters. Pramana J. Phys. 2019, 93, 34. [Google Scholar]
- Ellahi, R.; Hassan, M.; Zeeshan, A. A study of heat transfer in power law nanofluid. Therm. Sci. J. 2016, 20, 2015–2026. [Google Scholar] [CrossRef]
- Zeeshan, A.; Hassan, M.; Ellahi, R.; Nawaz, M. Shape effect of nanosize particles in unsteady mixed convection flow of nanofluid over disk with entropy generation. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2017, 231, 871–879. [Google Scholar] [CrossRef]


| Order of Approximation | ||
|---|---|---|
| 11 | 9.79594 | −1.91738 |
| 14 | 9.79619 | −1.91686 |
| 16 | 9.79643 | −1.91634 |
| 18 | 9.79667 | −1.91582 |
| 20 | 9.79717 | −1.91461 |
| 25 | 9.79717 | −1.91461 |
| 30 | 9.79717 | −1.91461 |
| Gorder et al. [21] | Present Result (HAM) | |||
|---|---|---|---|---|
| 0.0 | 0.000 | −2.00 | 0.000 | −2.00 |
| 0.2 | −0.224 | −0.360 | −0.224 | −0.360 |
| 0.4 | −0.192 | 0.560 | −0.192 | 0.560 |
| 0.6 | −0.048 | 0.760 | −0.048 | 0.760 |
| 0.8 | 0.064 | 0.240 | 0.064 | 0.240 |
| 1.0 | 0.000 | −1.00 | 0.000 | −1.000 |
| Lower Disk | Upper Disk | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −116.204 | −252.335 |
| 0.4 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −129.404 | −262.989 |
| 0.6 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −142.249 | −272.563 |
| 0.5 | 1.0 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −135.869 | −267.915 |
| 0.5 | 1.5 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −149.413 | −273.824 |
| 0.5 | 2.0 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −162.905 | −281.867 |
| 0.5 | 01 | 1.0 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −1.63619 | −38.7856 |
| 0.5 | 01 | 2.0 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −22.2454 | −67.5845 |
| 0.5 | 01 | 3.0 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −44.9617 | −108.970 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −135.869 | −267.915 |
| 0.5 | 01 | 05 | 2.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −102.816 | −437.258 |
| 0.5 | 01 | 05 | 3.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −69.7624 | −606.601 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −135.869 | −267.915 |
| 0.5 | 01 | 05 | 1.0 | 1.5 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | 115.683 | −430.368 |
| 0.5 | 01 | 05 | 1.0 | 2.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | 367.236 | −592.821 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −135.869 | −267.915 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.4 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −195.891 | −369.982 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.6 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −255.476 | −472.018 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −135.869 | −267.915 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.6 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −62.2384 | −77.8090 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.7 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −23.2608 | −44.7235 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.1 | 0.5 | 02 | 2.0 | 0.1 | −130.344 | −270.583 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.3 | 0.5 | 02 | 2.0 | 0.1 | −133.108 | −269.244 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −135.869 | −267.915 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.1 | 02 | 2.0 | 0.1 | −14.4518 | −37.1367 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.3 | 02 | 2.0 | 0.1 | −52.1849 | −61.3395 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −89.1381 | −99.7870 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 3.5 | 2.0 | 0.1 | 24.7854 | −1205.14 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 4.0 | 2.0 | 0.1 | 195.575 | −1786.25 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 4.5 | 2.0 | 0.1 | 445.195 | −2541.17 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −135.869 | −267.915 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.3 | 0.1 | −185.374 | −345.966 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.6 | 0.1 | −247.552 | −440.297 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −155.783 | −257.838 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.2 | −154.907 | −257.367 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.3 | −154.003 | −256.903 |
| Lower Disk | Upper Disk | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −43.2173 | 62.2902 |
| 0.4 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −43.1456 | 64.2379 |
| 0.6 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −43.1225 | 66.2978 |
| 0.5 | 1.0 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −43.1714 | 65.2526 |
| 0.5 | 1.5 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −49.2164 | 71.3174 |
| 0.5 | 2.0 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −55.2913 | 77.3855 |
| 0.5 | 01 | 2.0 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −1.93260 | 10.9702 |
| 0.5 | 01 | 3.0 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −9.76591 | 20.5937 |
| 0.5 | 01 | 4.0 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −20.8434 | 35.8615 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −34.5174 | 58.1590 |
| 0.5 | 01 | 05 | 2.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −59.2591 | 126.626 |
| 0.5 | 01 | 05 | 3.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −70.4176 | 209.251 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −34.5174 | 58.1590 |
| 0.5 | 01 | 05 | 1.0 | 1.5 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −65.0929 | 88.3373 |
| 0.5 | 01 | 05 | 1.0 | 2.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −95.5317 | 118.241 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −37.1562 | 59.1911 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.4 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −35.3967 | 58.5028 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.6 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −33.6384 | 57.8153 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −34.5174 | 58.1590 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.6 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −4.57816 | 17.6285 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.7 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −2.16759 | 8.23666 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.1 | 0.5 | 02 | 2.0 | 0.1 | −32.5620 | 56.3592 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.3 | 0.5 | 02 | 2.0 | 0.1 | −33.5476 | 57.2673 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −34.5174 | 58.1590 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.1 | 02 | 1.0 | 0.1 | −4.03154 | 4.78376 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.3 | 02 | 1.0 | 0.1 | −7.31547 | 21.5100 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 1.0 | 0.1 | −34.5174 | 58.1590 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 3.5 | 1.0 | 0.1 | −128.255 | 180.574 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 4.0 | 1.0 | 0.1 | −171.887 | 236.943 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 4.5 | 1.0 | 0.1 | −221.713 | 301.095 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.0 | 0.1 | −34.5174 | 58.1590 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.3 | 0.1 | −43.9555 | 76.6222 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 2.6 | 0.1 | −53.7965 | 97.8575 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 1.0 | 0.1 | −35.1337 | 58.7998 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 1.0 | 0.2 | −35.8183 | 59.5099 |
| 0.5 | 01 | 05 | 1.0 | 1.0 | 0.2 | 0.5 | 0.5 | 0.5 | 02 | 1.0 | 0.3 | −36.5027 | 60.2180 |
| 0.3 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.8144 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.8151 |
| 0.7 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.8170 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.8151 |
| 0.5 | 03 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.7897 |
| 0.5 | 05 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.7400 |
| 0.5 | 01 | 01 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.6770 |
| 0.5 | 01 | 02 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.6946 |
| 0.5 | 01 | 03 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.7235 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.8151 |
| 0.5 | 01 | 05 | 02 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.9559 |
| 0.5 | 01 | 05 | 03 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −11.0960 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.8151 |
| 0.5 | 01 | 05 | 01 | 02 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.8064 |
| 0.5 | 01 | 05 | 01 | 03 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.7978 |
| 0.5 | 01 | 05 | 01 | 01 | 2.0 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.5643 |
| 0.5 | 01 | 05 | 01 | 01 | 2.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.4735 |
| 0.5 | 01 | 05 | 01 | 01 | 3.0 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.3631 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.3 | 0.01 | 02 | 2.0 | 1.2 | −10.6729 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.2 | −10.8151 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.7 | 0.01 | 02 | 2.0 | 1.2 | −10.9575 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.1 | 02 | 2.0 | 1.2 | −12.1179 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.2 | 02 | 2.0 | 1.2 | −14.0721 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.3 | 02 | 2.0 | 1.2 | −16.1551 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 10 | 2.0 | 1.2 | −11.3132 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 50 | 2.0 | 1.2 | −15.1132 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 100 | 2.0 | 1.2 | −20.1335 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 01 | 1.2 | −10.4104 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 02 | 1.2 | −10.3151 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 03 | 1.2 | −11.2584 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 0.5 | −10.8071 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.0 | −10.8127 |
| 0.5 | 01 | 05 | 01 | 01 | 0.5 | 0.5 | 0.01 | 02 | 2.0 | 1.5 | −10.8189 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, N.; Nabwey, H.A.; Hashmi, M.S.; Khan, S.U.; Tlili, I. A Theoretical Analysis for Mixed Convection Flow of Maxwell Fluid between Two Infinite Isothermal Stretching Disks with Heat Source/Sink. Symmetry 2020, 12, 62. https://doi.org/10.3390/sym12010062
Khan N, Nabwey HA, Hashmi MS, Khan SU, Tlili I. A Theoretical Analysis for Mixed Convection Flow of Maxwell Fluid between Two Infinite Isothermal Stretching Disks with Heat Source/Sink. Symmetry. 2020; 12(1):62. https://doi.org/10.3390/sym12010062
Chicago/Turabian StyleKhan, Nargis, Hossam A. Nabwey, Muhammad Sadiq Hashmi, Sami Ullah Khan, and Iskander Tlili. 2020. "A Theoretical Analysis for Mixed Convection Flow of Maxwell Fluid between Two Infinite Isothermal Stretching Disks with Heat Source/Sink" Symmetry 12, no. 1: 62. https://doi.org/10.3390/sym12010062
APA StyleKhan, N., Nabwey, H. A., Hashmi, M. S., Khan, S. U., & Tlili, I. (2020). A Theoretical Analysis for Mixed Convection Flow of Maxwell Fluid between Two Infinite Isothermal Stretching Disks with Heat Source/Sink. Symmetry, 12(1), 62. https://doi.org/10.3390/sym12010062








