Serious Solutions for Unsteady Axisymmetric Flow over a Rotating Stretchable Disk with Deceleration
Abstract
:1. Introduction
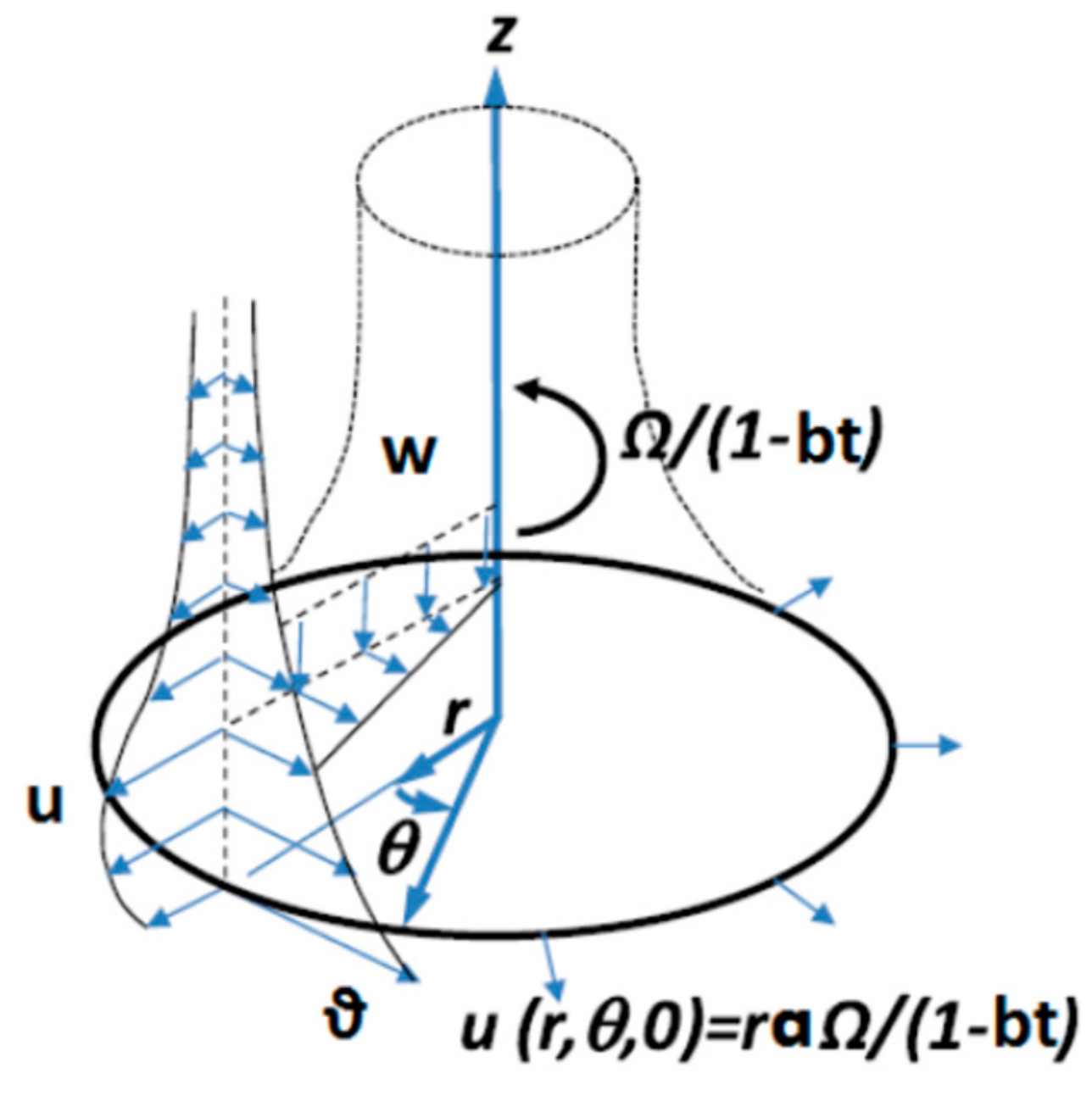
2. Formulation of the Problem
3. Homotopy Analysis Method
3.1. Zeroth-Order Deformation Equation
3.2. Mth-Order Deformation
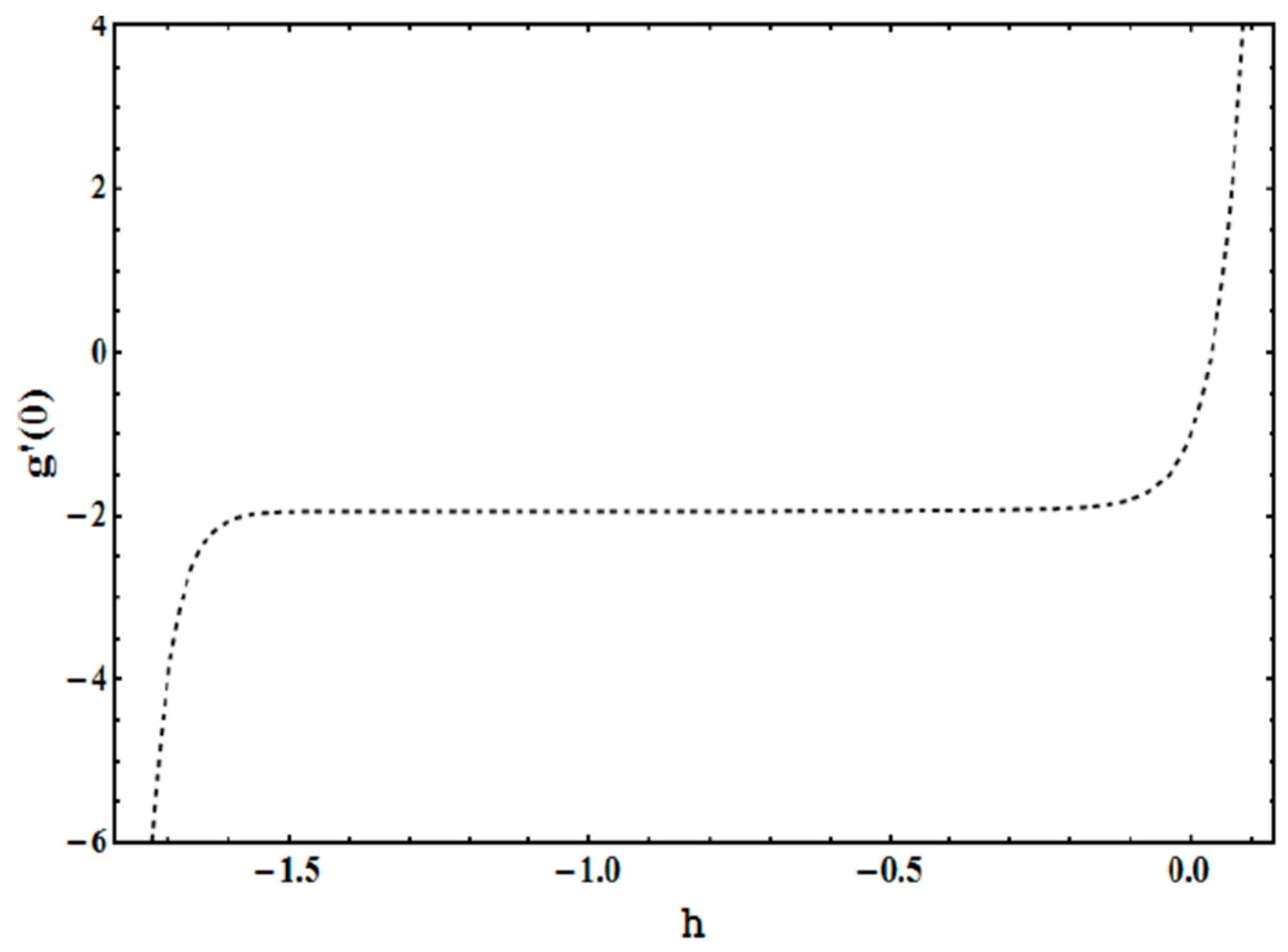
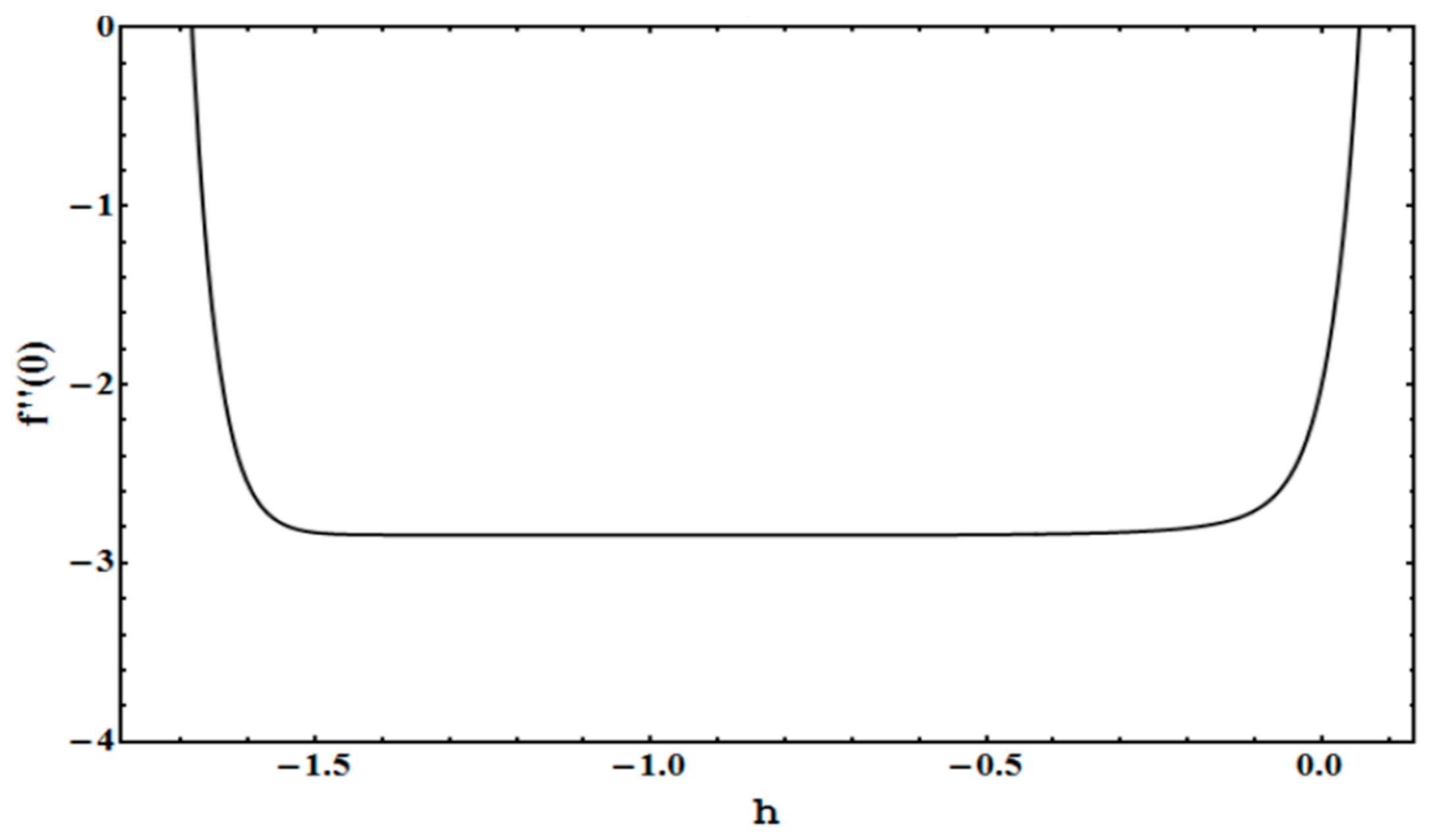
4. Convergence of the HAM Solution
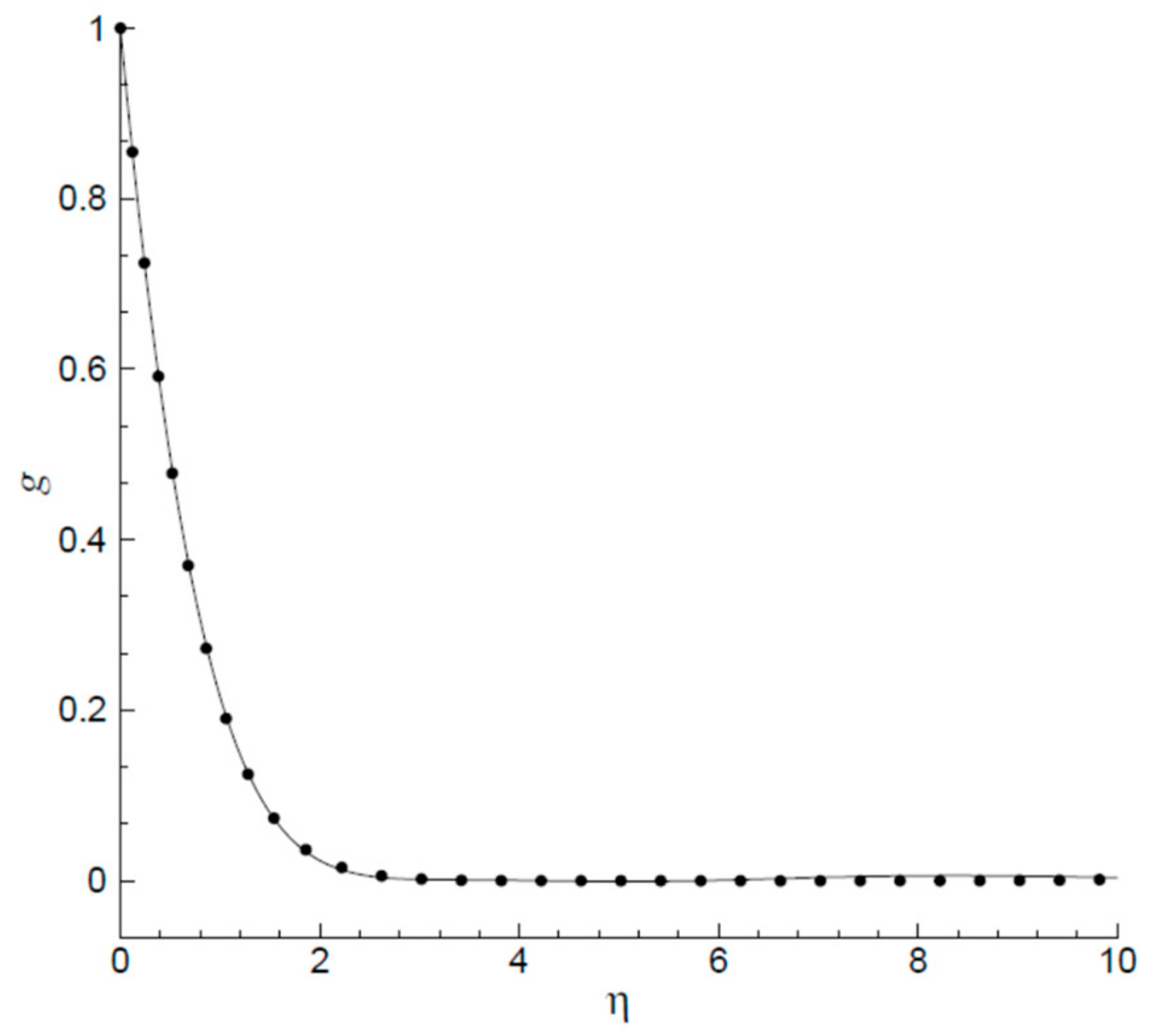
5. Results and Discussion
6. Conclusions
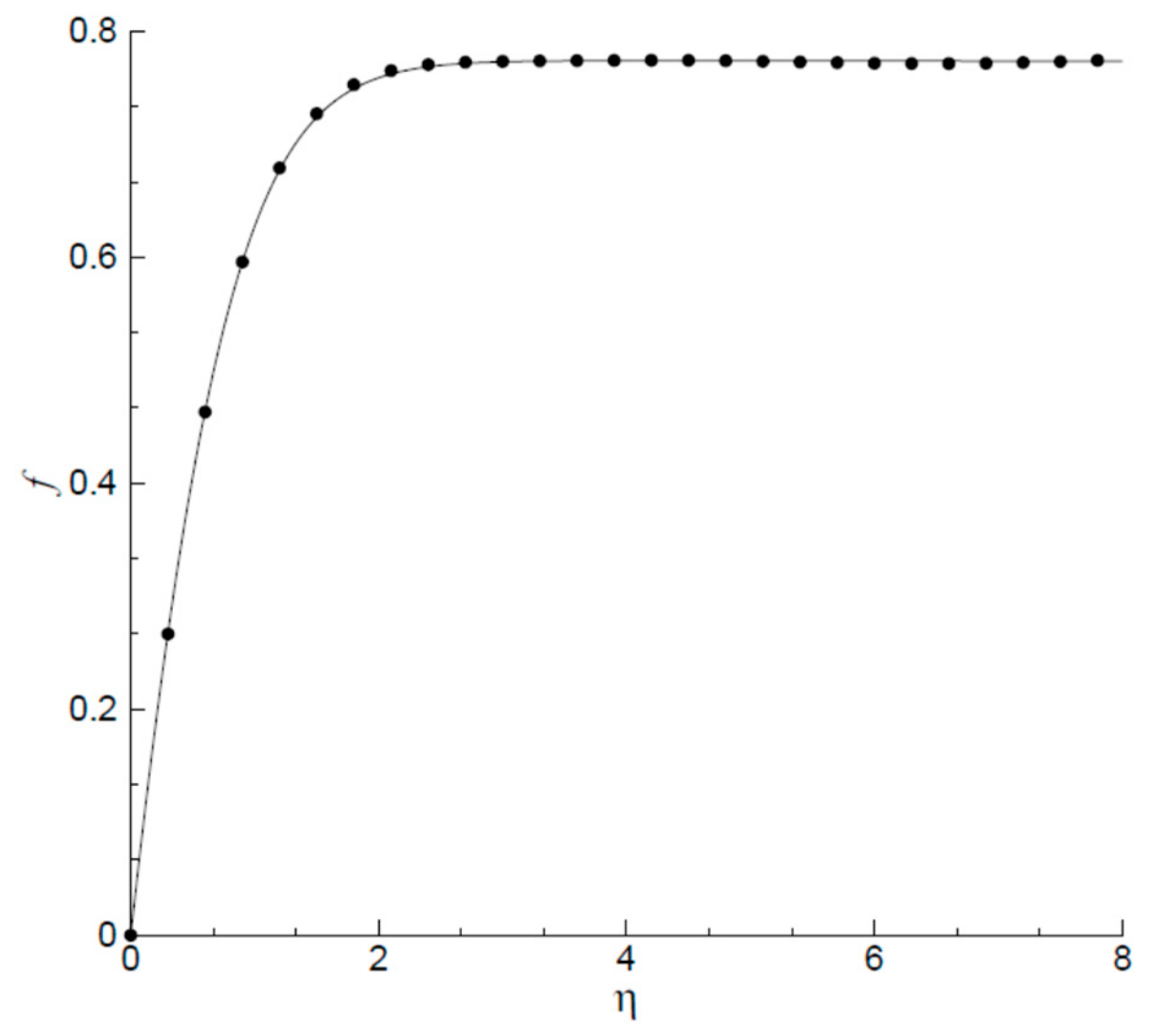
- Results obtained by homotopy analysis method are in good agreement with existing numerical results;
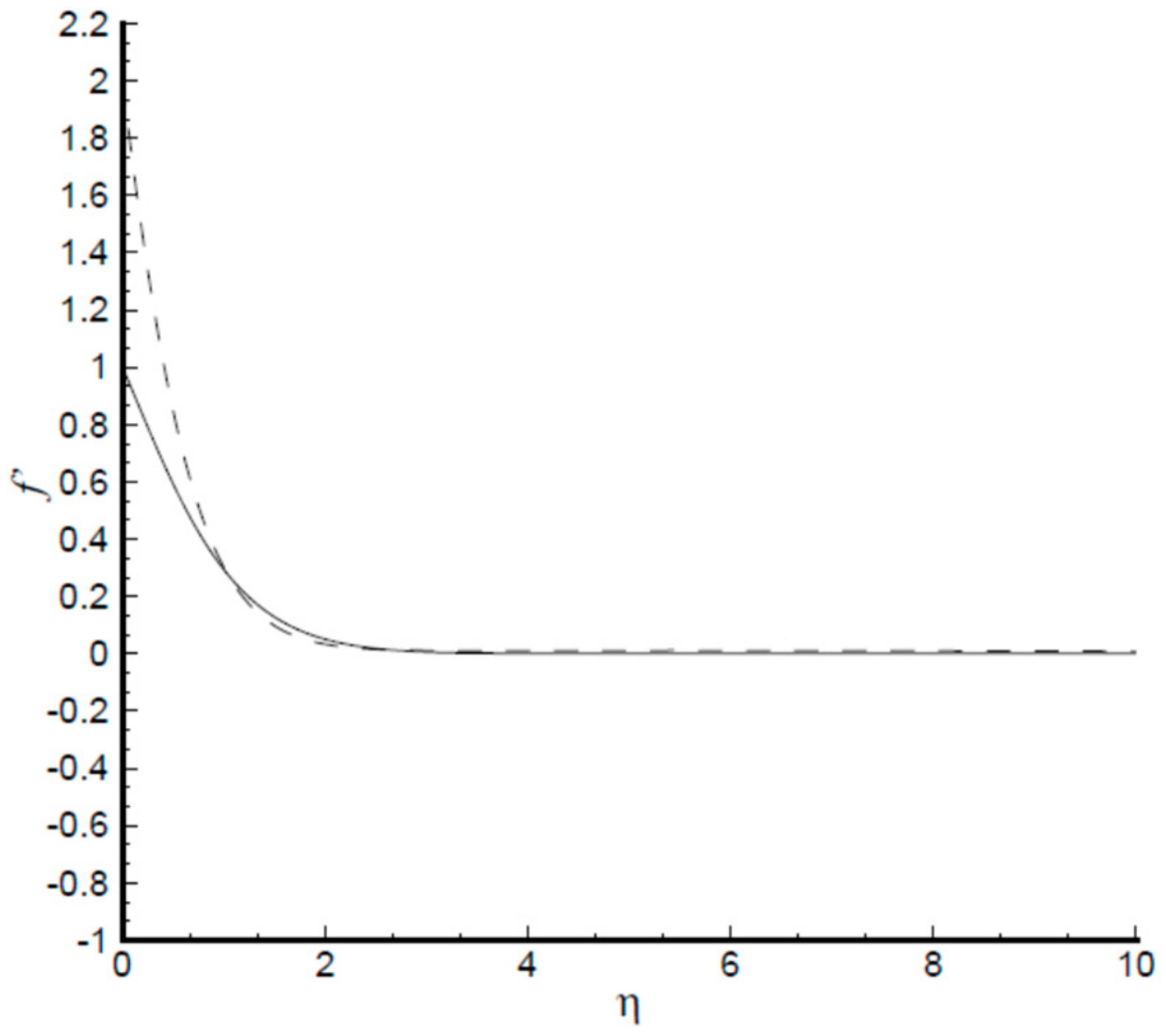
- All the velocity profiles decrease with an increase in unsteadiness parameter ;
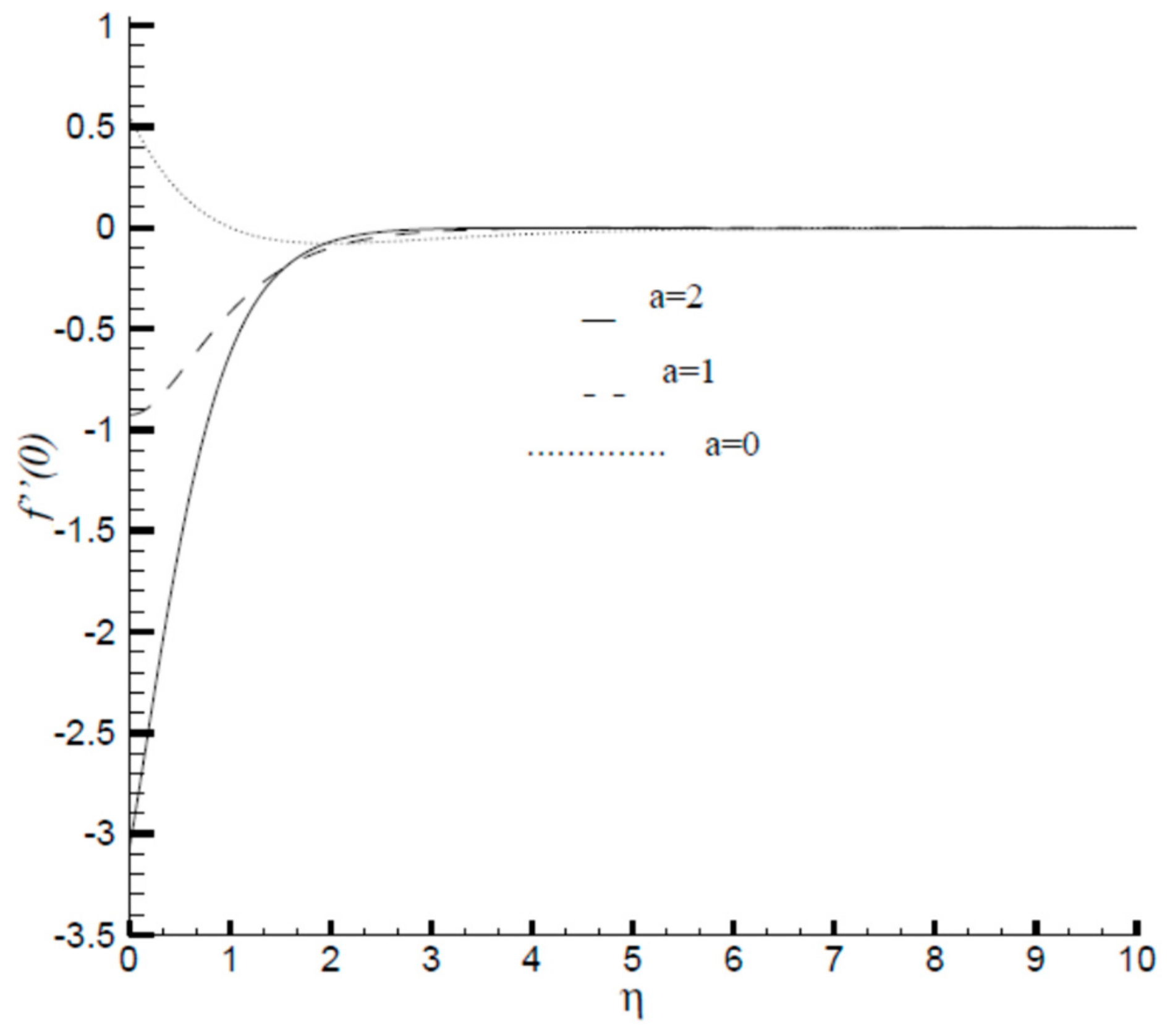
- Radial and axial velocity of the flow increases with the increase in disk stretching parameter , whereas tangential velocity shows a decreasing trend with an increase in ;
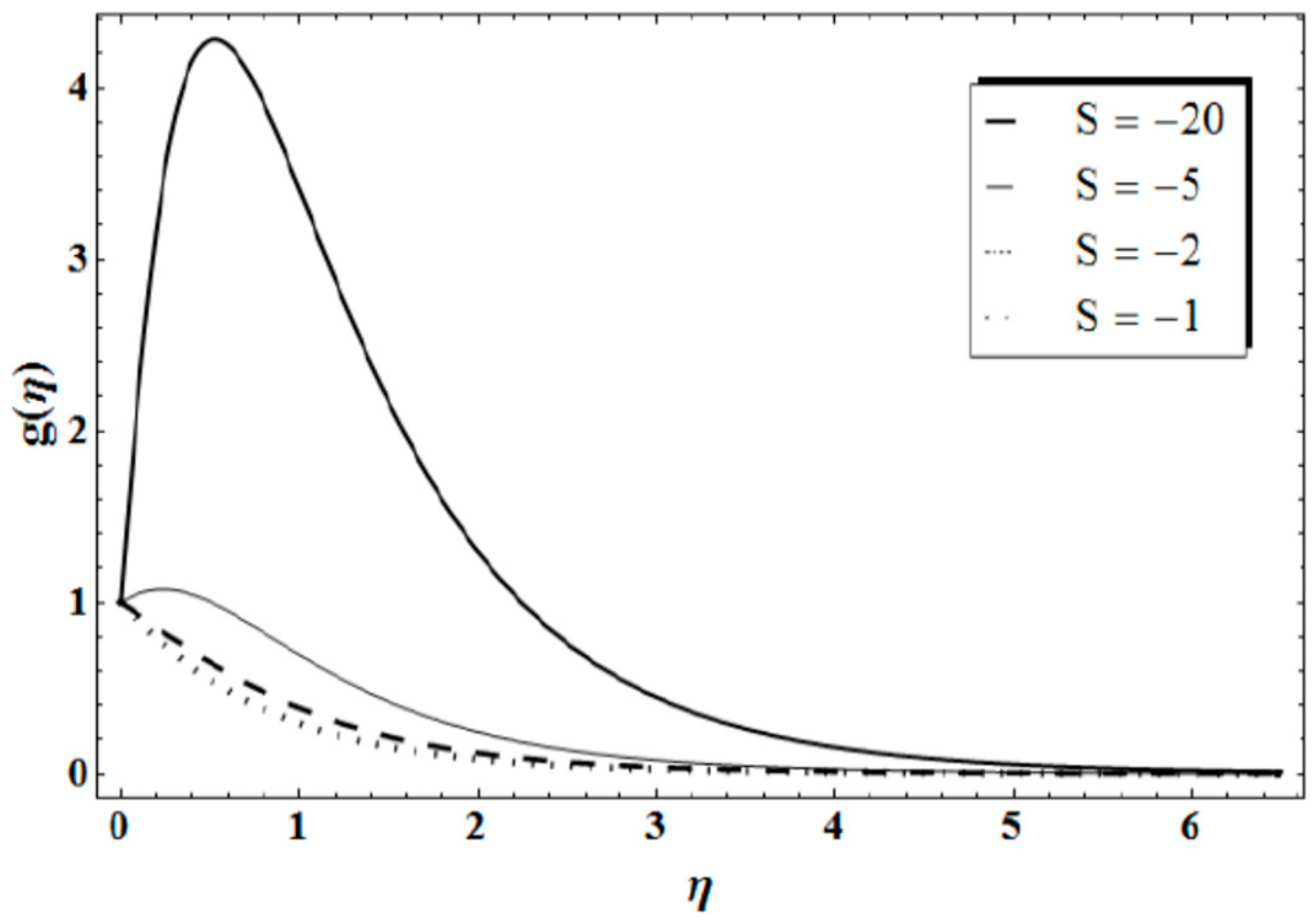
- Variation trend decays with faster velocity to the ambient for fast deceleration as compared to the slow deceleration of the disk.
Funding
Acknowledgments
Conflicts of Interest
References
- Turkyilmazoglu, M. Three-dimensional MHD stagnation flow due to a stretchable rotating disk. Int. J. Heat Mass Transf. 2012, 55, 6959–6965. [Google Scholar] [CrossRef]
- Von Kármán, T. Über Laminar Und Turbulente Reibung. J. Appl. Math. Mech. 1921, 1, 233–252. [Google Scholar]
- Fang, T.; Zhang, J. Flow between two stretchable disks-An exact solution of the NavierStokes equations. Int. Commun. Heat Mass Transf. 2008, 35, 892–895. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ali, M.; Freidoonimehr, N.; Nazari, F. Parametric analysis and optimization of entropy generation in unsteady MHD flow over a stretching rotating disk using articial neural network and particle swarm optimization algorithm. Energy 2013, 55, 1–14. [Google Scholar] [CrossRef]
- Fang, T.; Hua, T. Unsteady viscous flow over a rotating stretchable disk with deceleration. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 5064–5072. [Google Scholar] [CrossRef]
- Liao, S. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Nadeem, S.; Awais, M. Thin film flow of an unsteady shrinking sheet through porous medium with variable viscosity. Phys. Lett. A 2008, 372, 4965–4972. [Google Scholar] [CrossRef]
- Nadeem, S.; Ali, M. Analytical solutions for pipe flow of a fourth grade fluid with Reynold and Vogel’s models of viscosities. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2073–2090. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbasbandy, S.; Hussain, M. Series solutions of boundary layer flow of a Micropolar fluid near the stagnation point towards a shrinking sheet. Z. Fur Nat. 2009, 64, 575–582. [Google Scholar] [CrossRef]
- Nadeem, S. Thin film flow of a third grade fluid with variable viscosity. Z. Fur Nat. 2009, 64, 553–558. [Google Scholar] [CrossRef]
- Nadeem, S.; Hussain, A. MHD flow of a viscous fluid on a non-linear porous shrinking sheet by Homotopy analysis method. Appl. Math. Mech. 2009, 30, 1569–1578. [Google Scholar] [CrossRef]
- Khan, H.; Ram, N.M.; Vajravelu, K.; Liao, S.J. The explicit Series Solution of SIR and SIS Epidemic Models. Appl. Math. Comput. 2009, 215, 653–669. [Google Scholar] [CrossRef]
- Khan, H.; Liao, S.J.; Ram, N.M.; Vajravelu, K. An analytical solution for a nonlinear time delay model in Biology. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3141–3148. [Google Scholar] [CrossRef]
- Khan, H.; Xu, H. Series Solution of Thomas Fermi Atom Model. Phys. Lett. A 2007, 365, 111–115. [Google Scholar] [CrossRef]
- Liao, S. A short review on the homotopy analysis method in fluid mechanics. J. Hydrodyn. 2010, 22, 882–884. [Google Scholar] [CrossRef]

| Order | ||||
|---|---|---|---|---|
| 2nd | −0.7673 | −1.196 | 0.311 | 0.044 |
| 4th | −0.6945 | −1.246 | 0.021 | 0.0067 |
| 6th | −0.6681 | −1.264 | 0.0046 | 0.0021 |
| 8th | −0.6581 | −1.270 | 0.00091 | 0.000715 |
| 10th | −0.6543 | −1.271 | 0.00014 | 0.00023 |
| Order | ||||
|---|---|---|---|---|
| 2nd | −0.9642 | −1.3321 | 0.031 | 0.379 |
| 4th | −0.9374 | −1.4162 | 0.0047 | 0.0055 |
| 6th | −0.9262 | −1.446 | 0.00075 | 0.00091 |
| 8th | −0.9217 | −1.458 | 0.00012 | 0.00016 |
| 10th | −0.9200 | −1.4627 | 0.000018 | 0.000033 |
| Order | ||||
|---|---|---|---|---|
| 2nd | −2.779 | −1.658 | 0.408 | 0.543 |
| 4th | −2.9729 | −1.847 | 0.0876 | 0.136 |
| 6th | −3.044 | −1.924 | 0.0234 | 0.0437 |
| 8th | −3.072 | −1.953 | 0.0071 | 0.018 |
| 10th | −3.082 | −1.958 | 0.0024 | 0.012 |
| Order | ||||
|---|---|---|---|---|
| 2nd | −0.9062 | −1.2760 | 0.1051 | 0.0221 |
| 4th | −0.8592 | −1.3424 | 0.0283 | 0.0037 |
| 6th | −0.8319 | −1.3654 | 0.0077 | 0.00082 |
| 8th | −0.8172 | −1.3741 | 0.0021 | 0.00021 |
| 10th | −0.8093 | −1.3774 | 0.00058 | 0.00006 |
| Order | Err | Err | ||
|---|---|---|---|---|
| 2nd | −0.9007 | 0.1062 | −0.9243 | 0.1405 |
| 4th | −0.8535 | 0.0283 | −0.8826 | 0.0514 |
| 6th | −0.8282 | 0.0076 | −0.8658 | 0.0312 |
| 8th | −0.8149 | 0.0021 | −0.8325 | 0.0069 |
| 10th | −0.8080 | 0.0005 | −0.8201 | 0.0025 |
| Order | Err | Err | ||
|---|---|---|---|---|
| 2nd | −1.2345 | 0.03718 | −1.2786 | 0.022 |
| 4th | −1.3157 | 0.0087 | −1.3445 | 0.0036 |
| 6th | −1.3502 | 0.0024 | −1.3578 | 0.0016 |
| 8th | −1.366 | 0.0007 | −1.3737 | 0.00021 |
| 10th | −1.3734 | 0.0002 | −1.3768 | 0.00006 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadiq, M.A. Serious Solutions for Unsteady Axisymmetric Flow over a Rotating Stretchable Disk with Deceleration. Symmetry 2020, 12, 96. https://doi.org/10.3390/sym12010096
Sadiq MA. Serious Solutions for Unsteady Axisymmetric Flow over a Rotating Stretchable Disk with Deceleration. Symmetry. 2020; 12(1):96. https://doi.org/10.3390/sym12010096
Chicago/Turabian StyleSadiq, Muhammad Adil. 2020. "Serious Solutions for Unsteady Axisymmetric Flow over a Rotating Stretchable Disk with Deceleration" Symmetry 12, no. 1: 96. https://doi.org/10.3390/sym12010096
APA StyleSadiq, M. A. (2020). Serious Solutions for Unsteady Axisymmetric Flow over a Rotating Stretchable Disk with Deceleration. Symmetry, 12(1), 96. https://doi.org/10.3390/sym12010096




