Keller-Box Analysis of Buongiorno Model with Brownian and Thermophoretic Diffusion for Casson Nanofluid over an Inclined Surface
Abstract
:1. Introduction
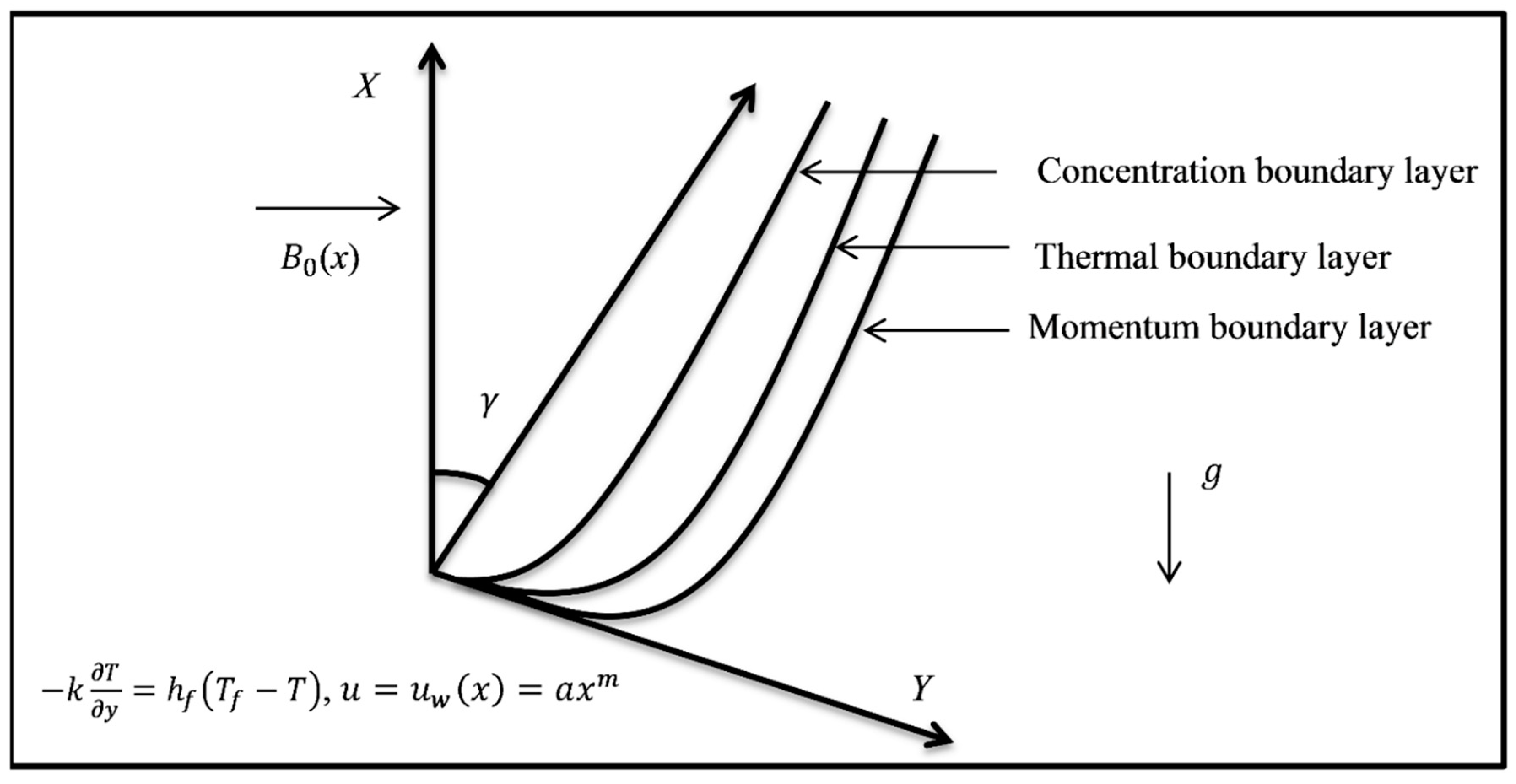
2. Problem Formulation
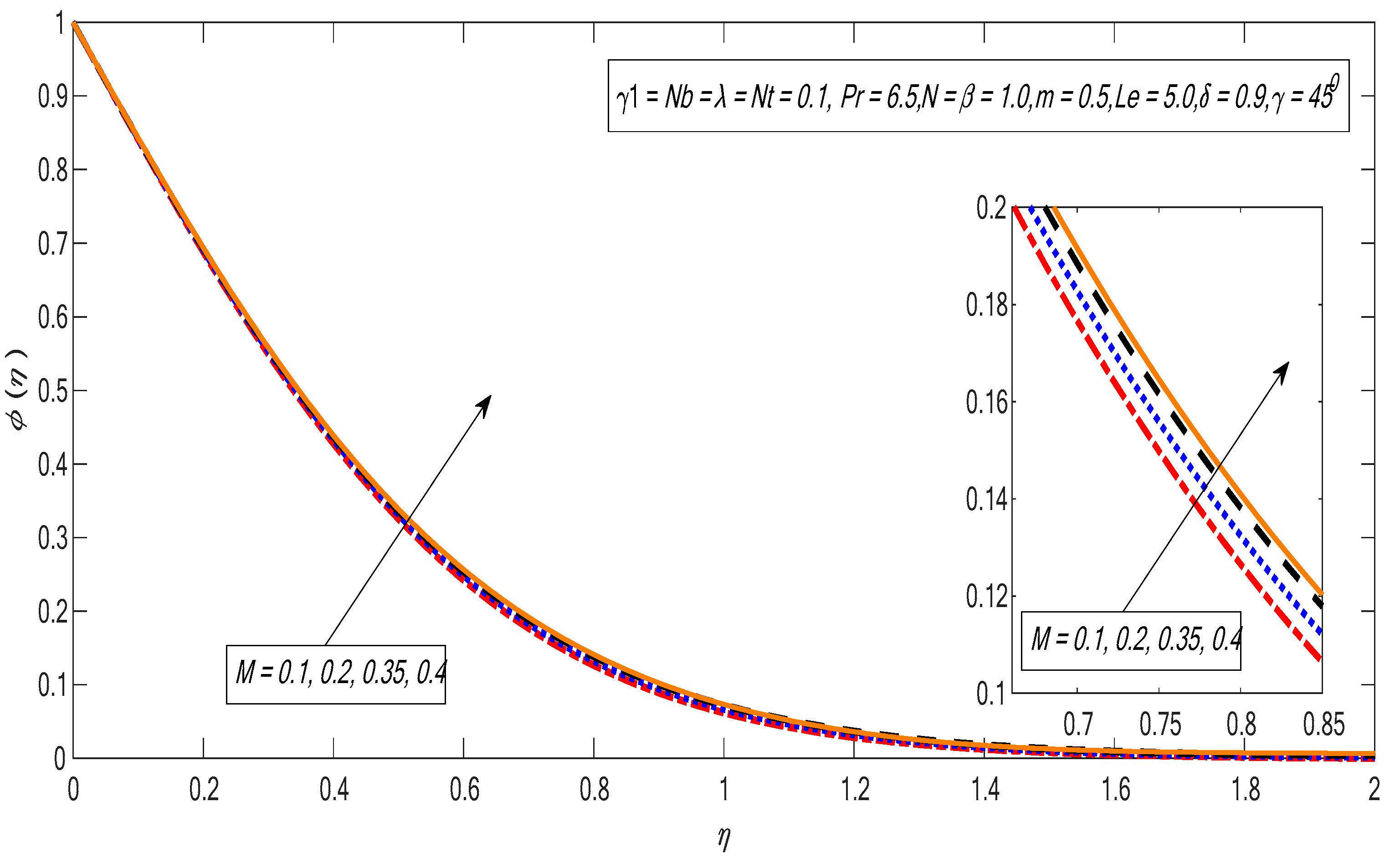
3. Results and Discussion
4. Conclusions
- ➢
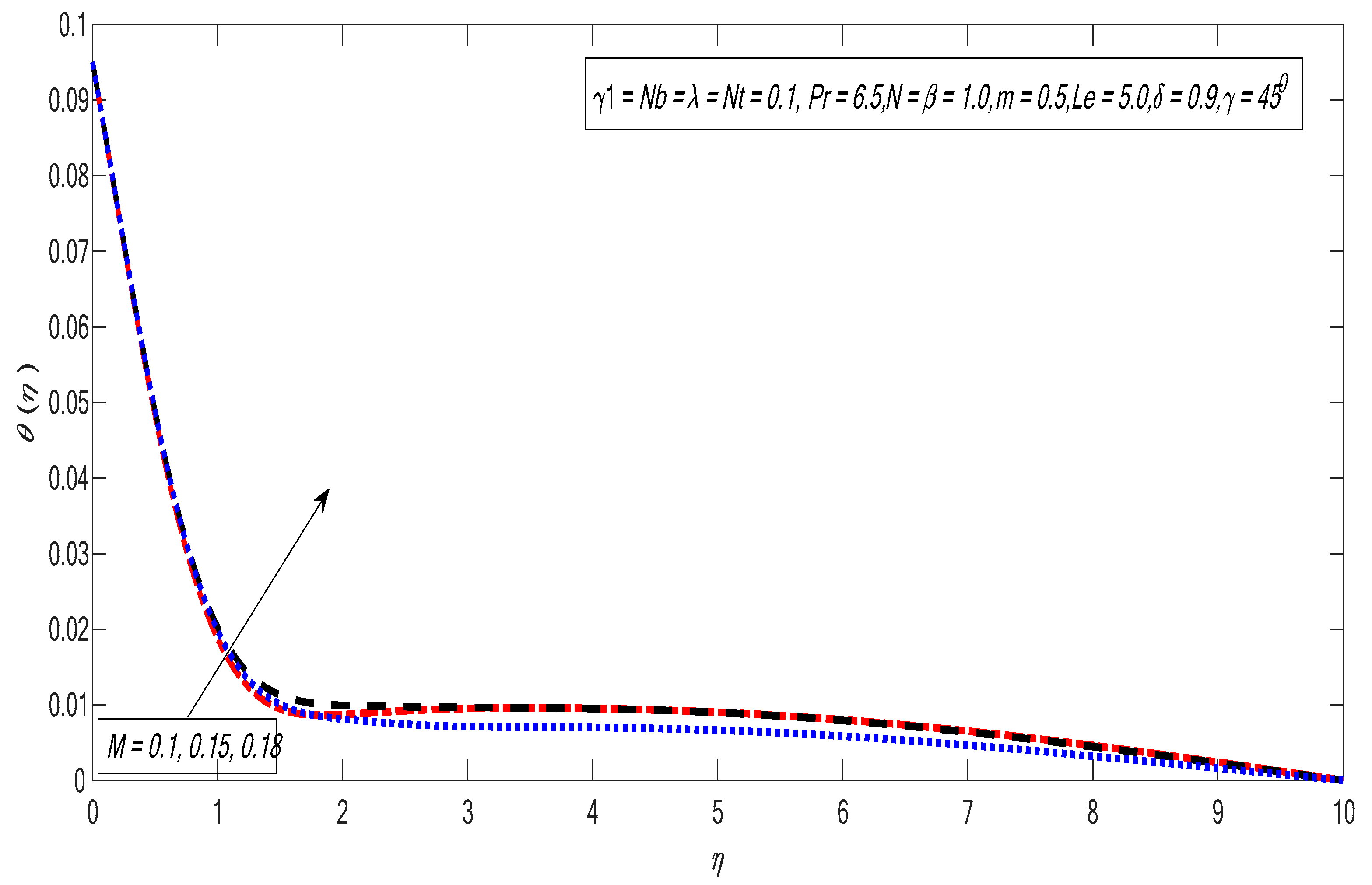
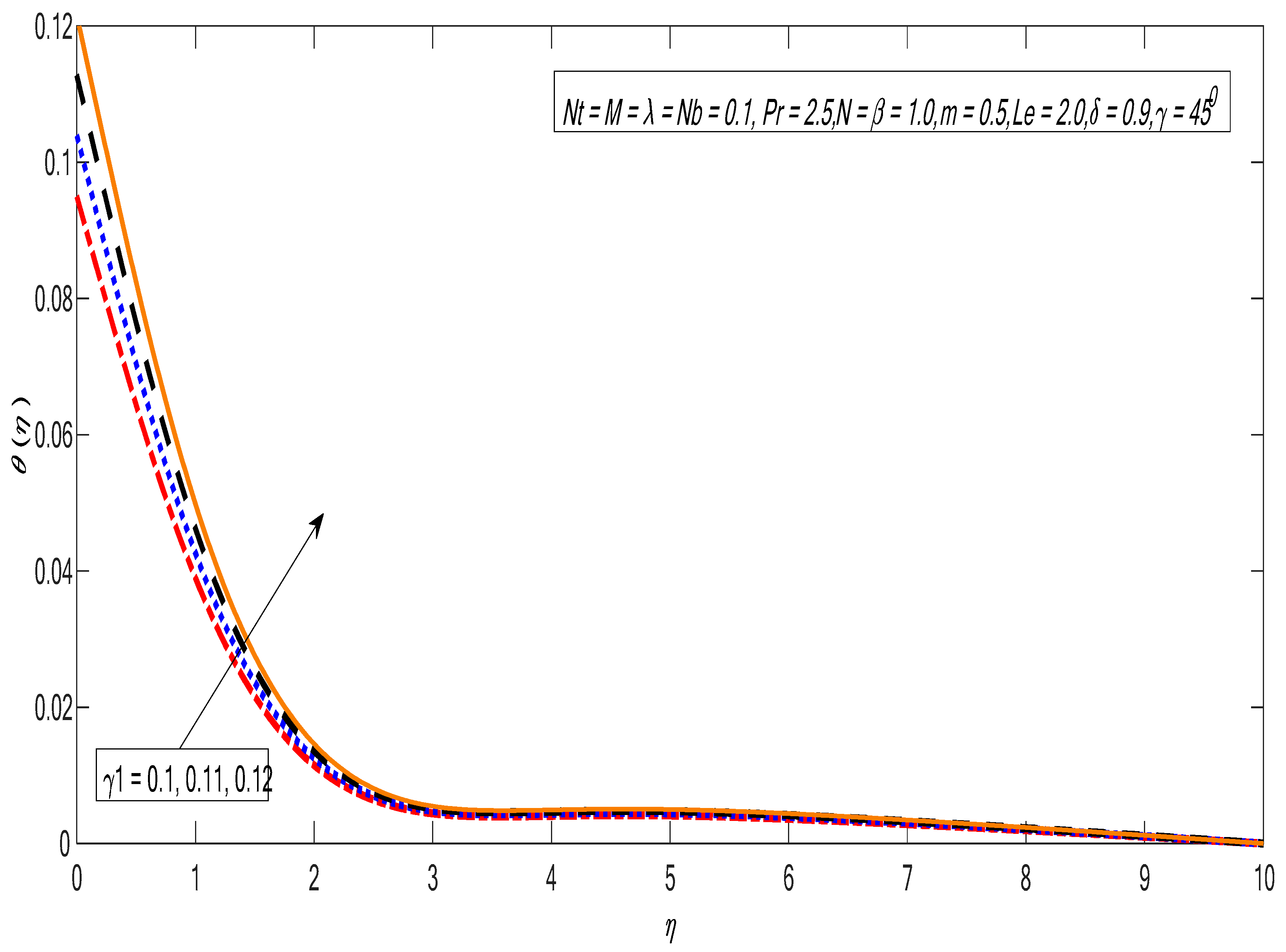
- The temperature profile increases near the boundary layer by improving the Biot number.
- ➢
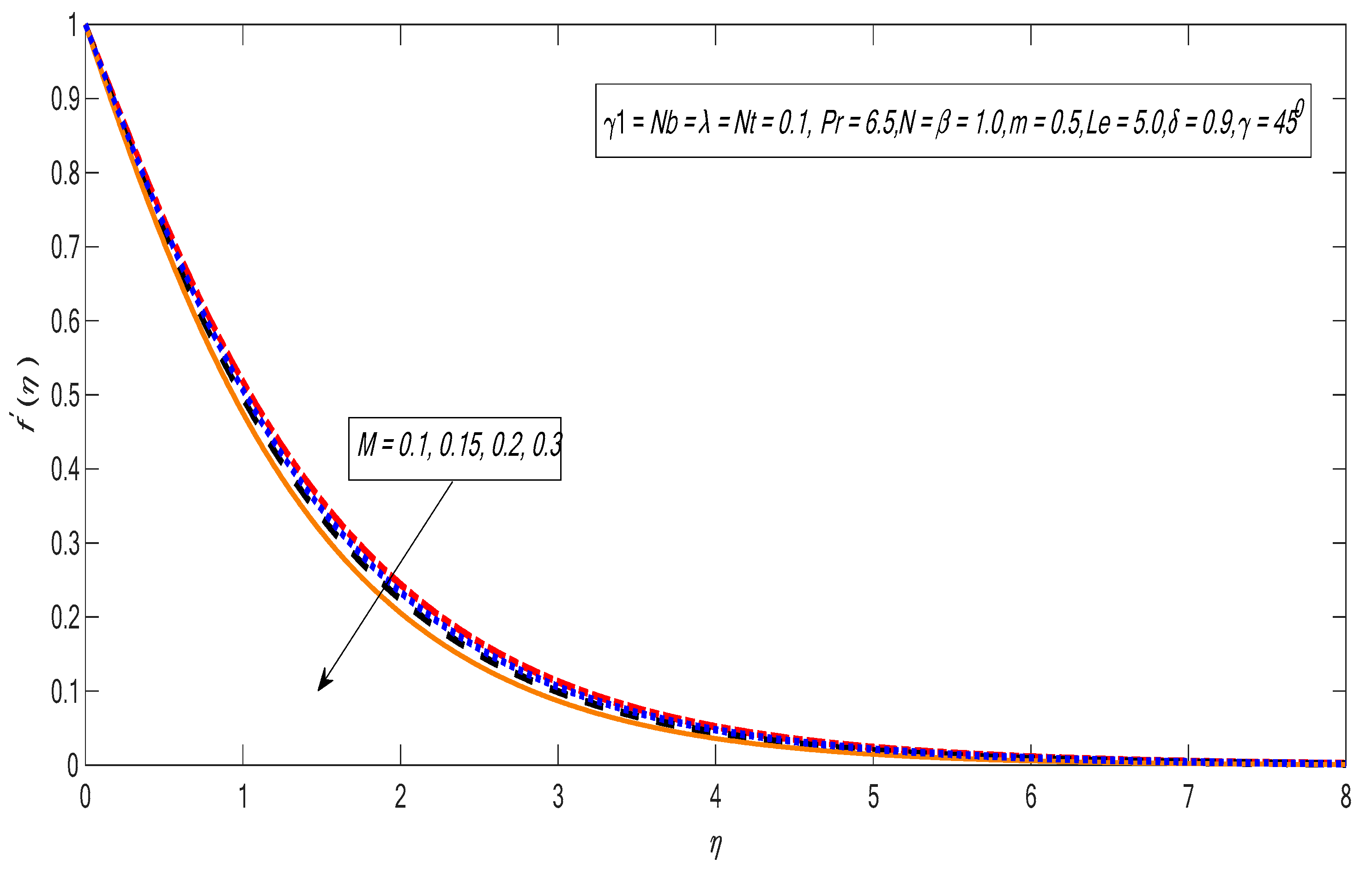
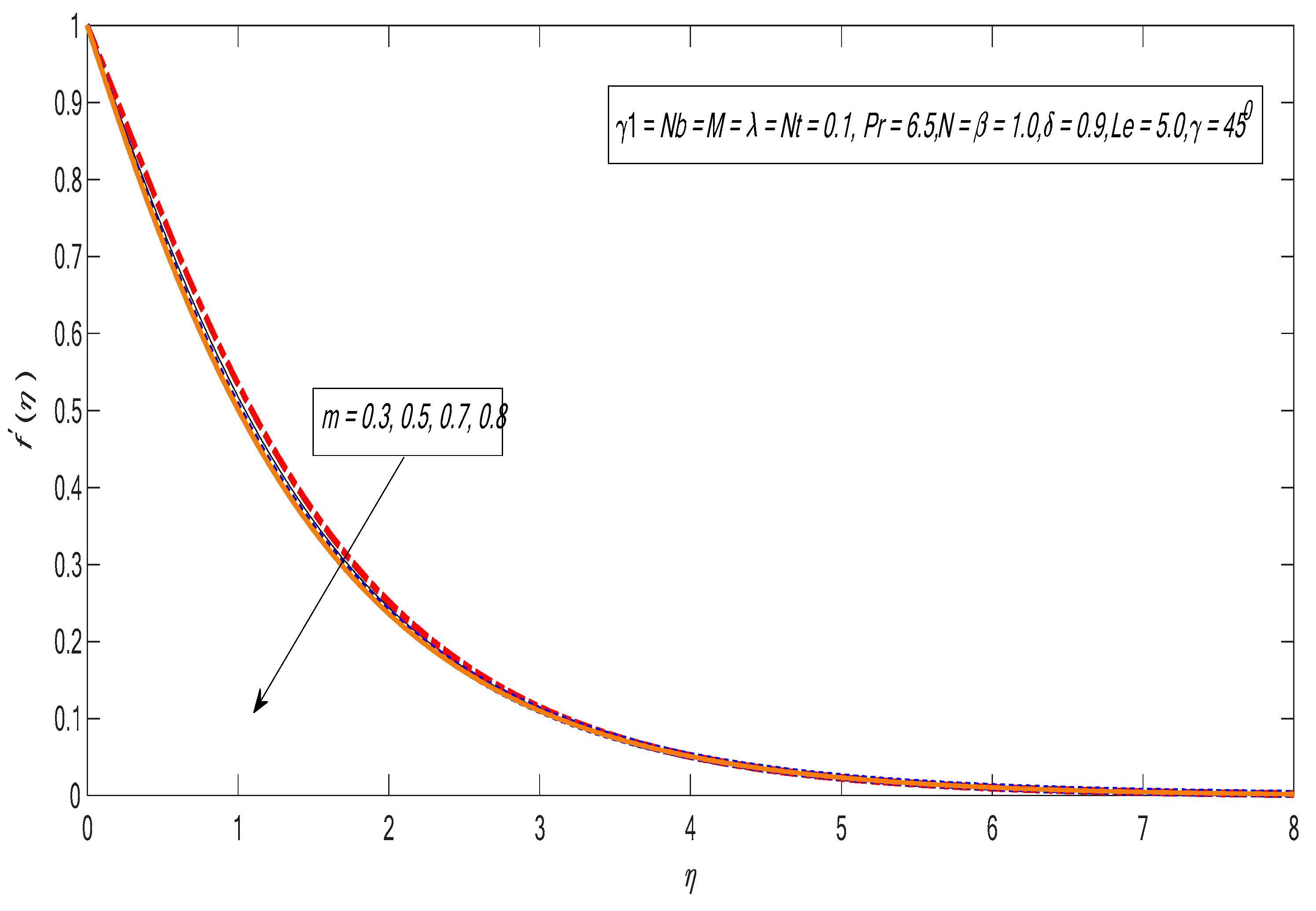
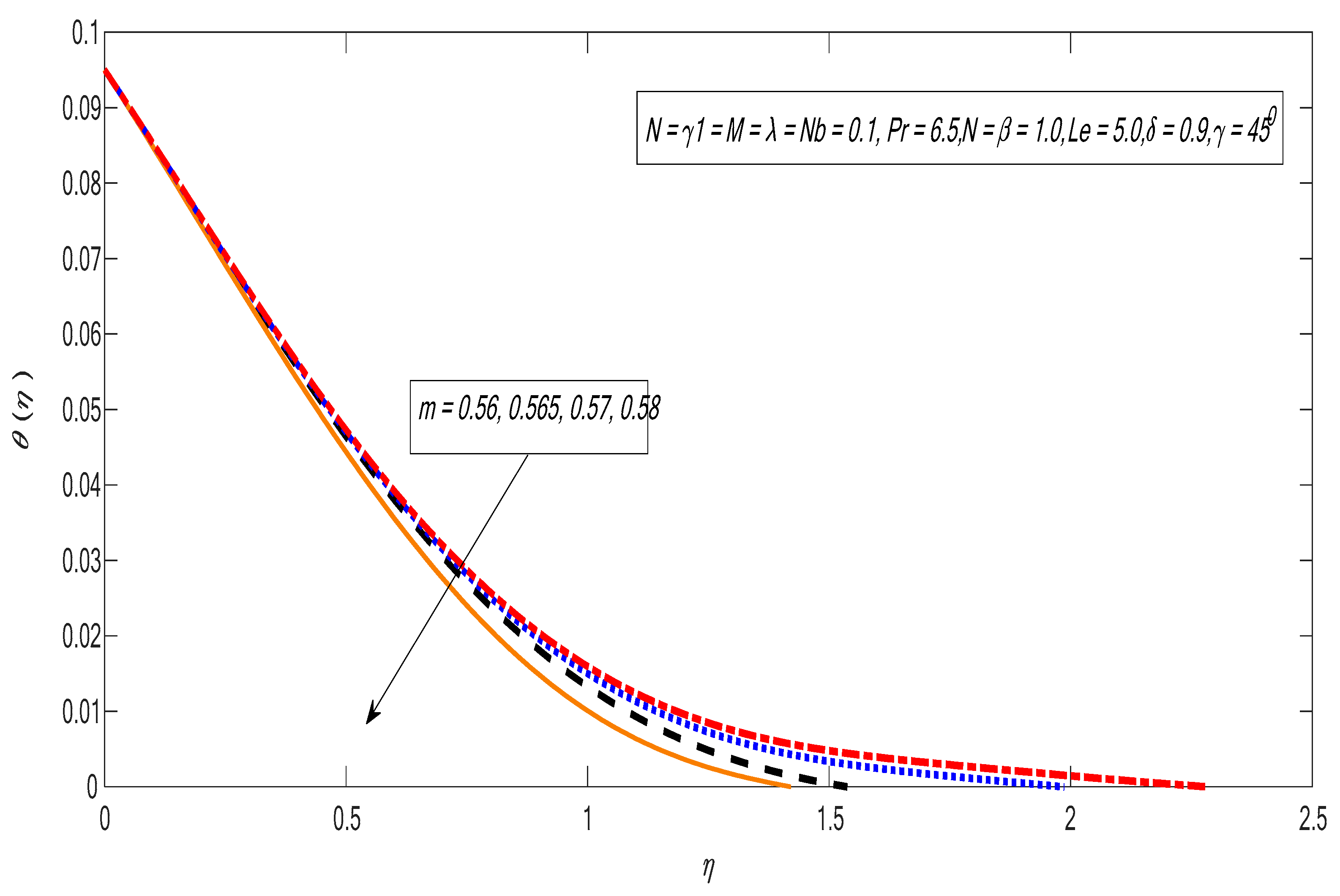
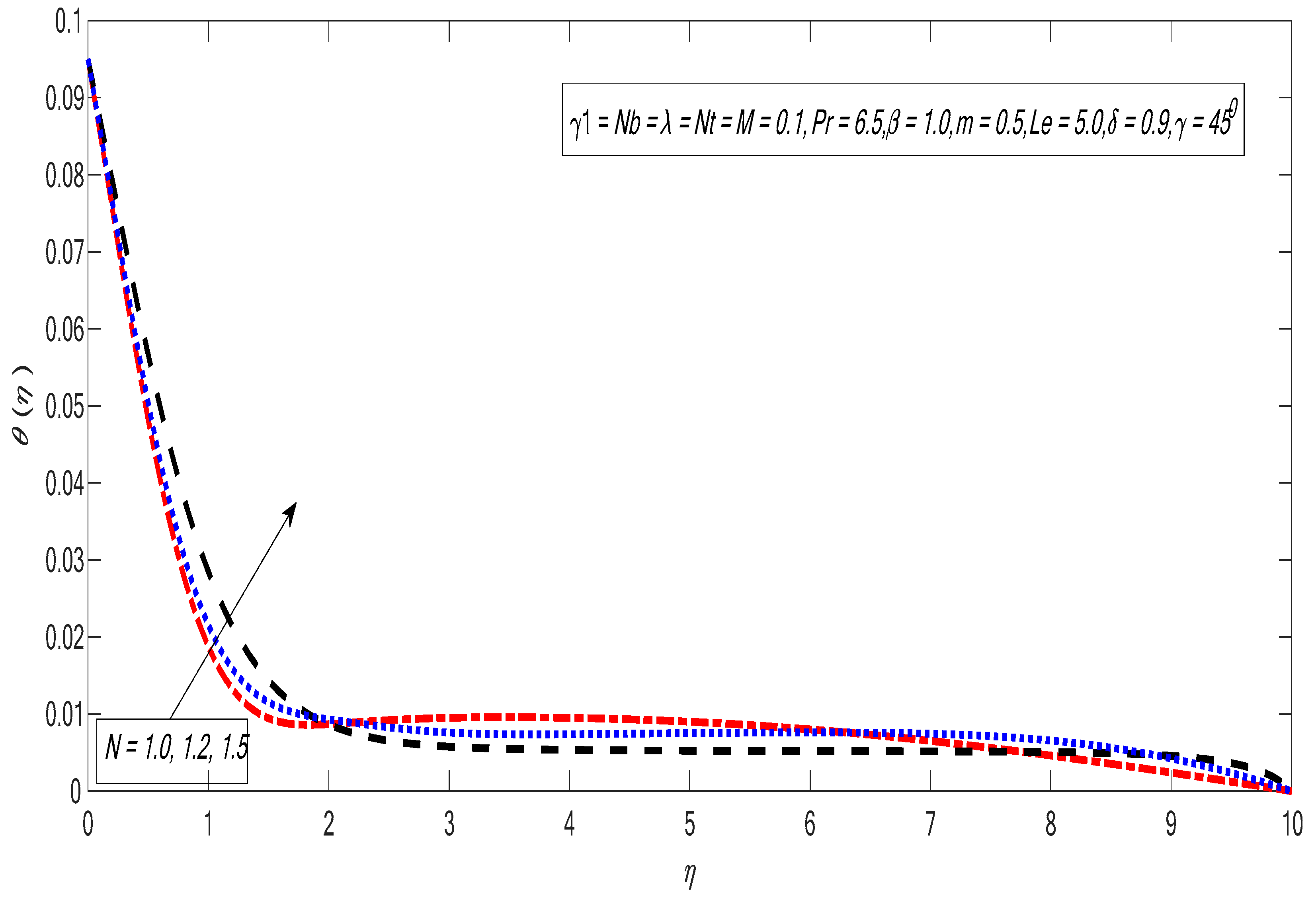
- The velocity and temperature profiles drop by improving the nonlinear power index.
- ➢
- The heat exchange improved upon improving the radiation parameter.
- ➢
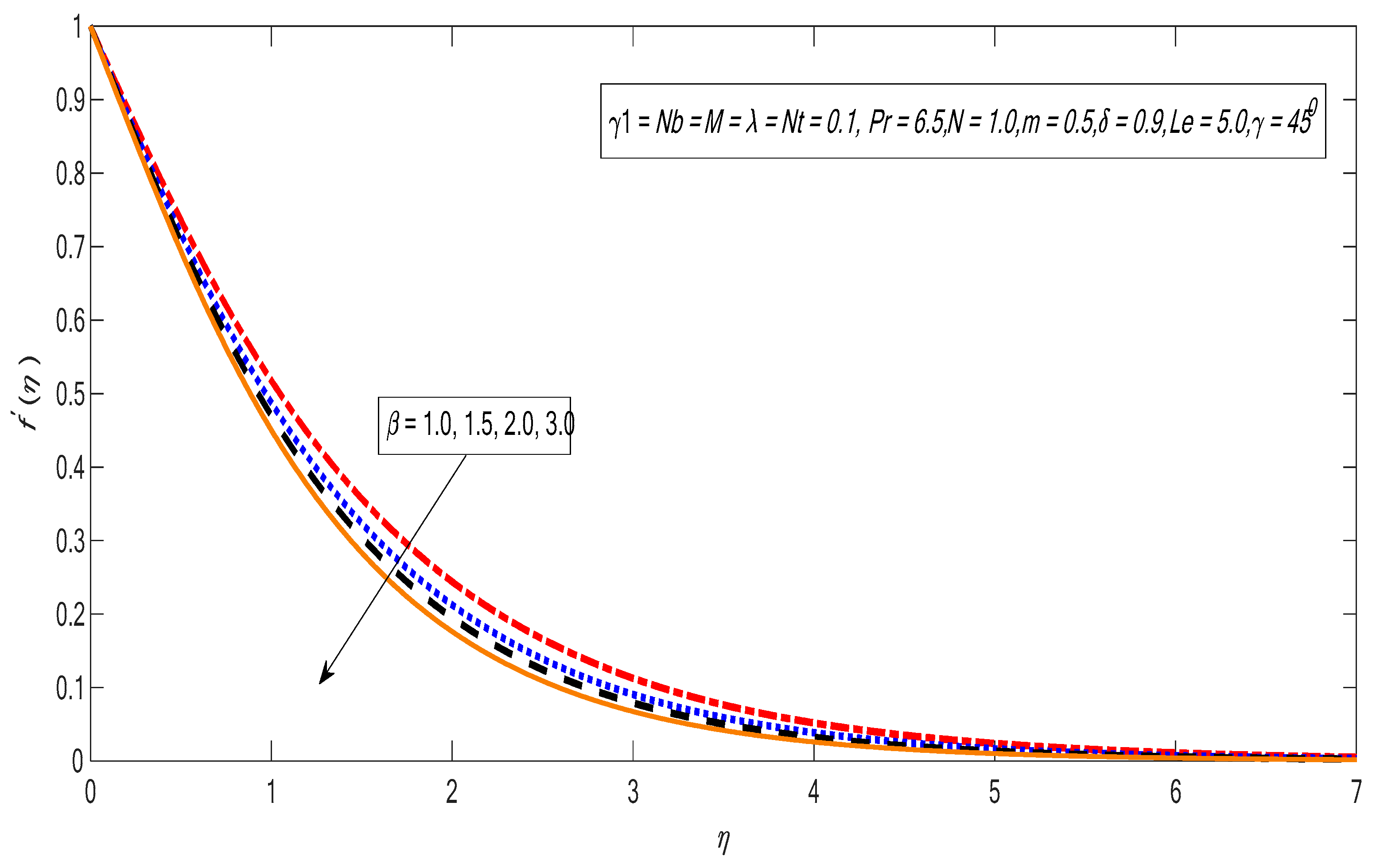
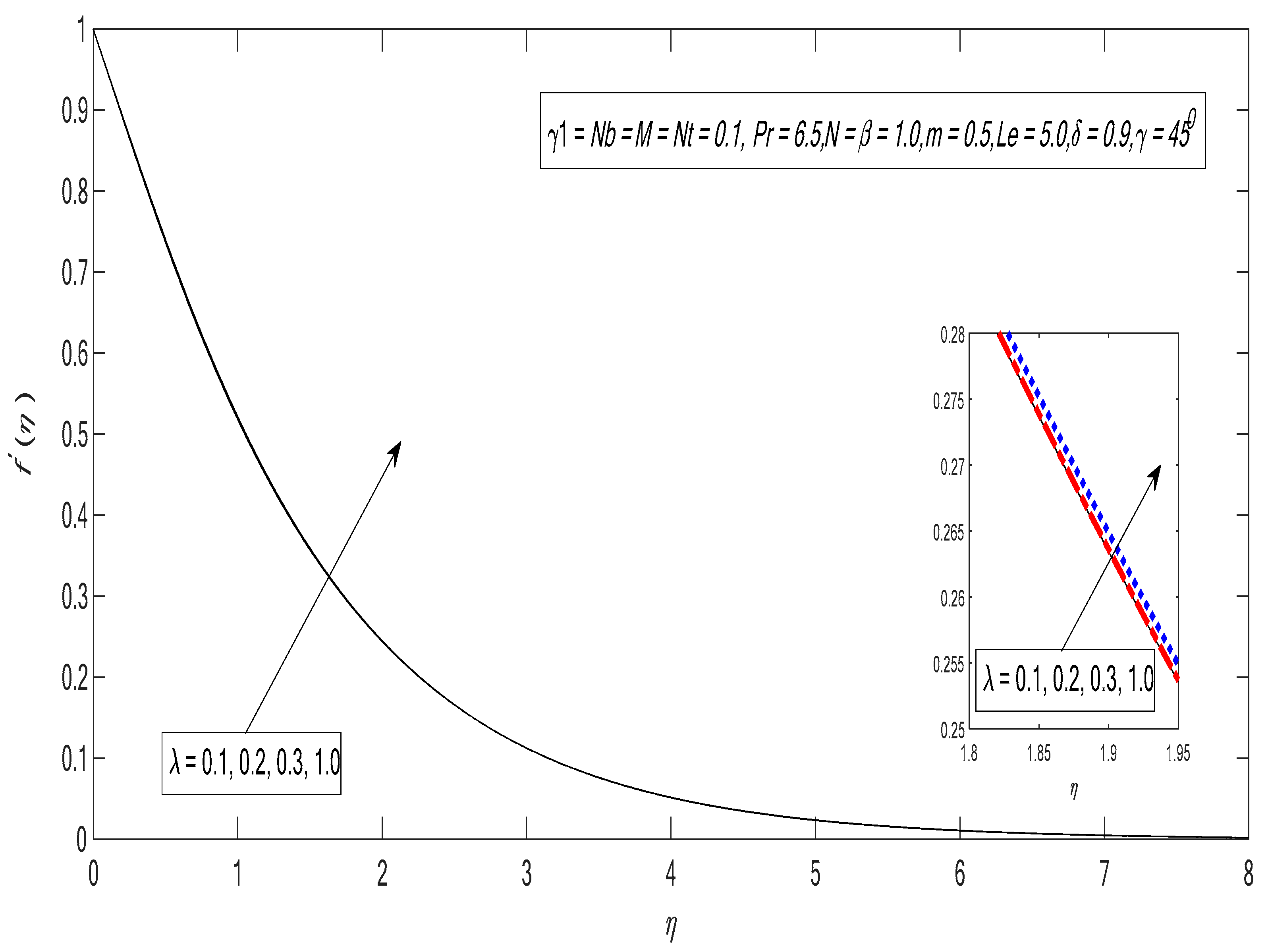
- The velocity distribution retards by increasing the Casson parameter.
- ➢
- The Nuselt number decreases by increasing the Casson parameter.
- ➢
- The skin friction declines by improving the Biot number.
- ➢
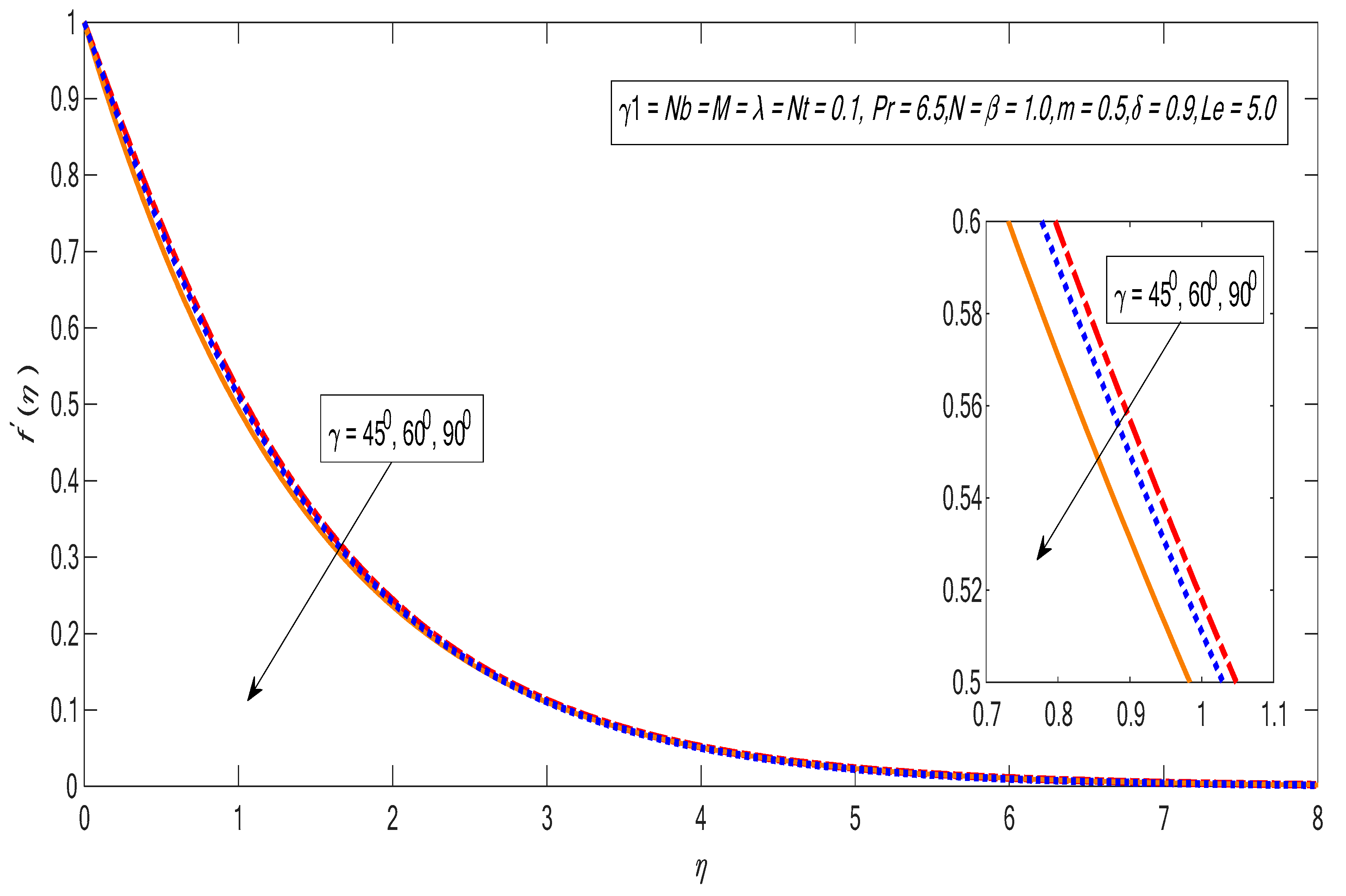
- The velocity profile shows an inverse relation with the inclination factor.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Anwar, M.I.; Tanveer, N.; Salleh, M.Z.; Shafie, S. Diffusive effects on hydrodynamic Casson nanofluid boundary layer flow over a stretching surface. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2017; Volume 890, p. 012047. [Google Scholar]
- Afify, A.A. The influence of slip boundary condition on Casson nanofluid flow over a stretching sheet in the presence of viscous dissipation and chemical reaction. Math. Probl. Eng. 2017, 2017, 3804751. [Google Scholar] [CrossRef]
- Souayeh, B.; Reddy, M.G.; Sreenivasulu, P.; Poornima, T.; Rahimi-Gorji, M.; Alarifi, I.M. Comparative analysis on non-linear radiative heat transfer on MHD Casson nanofluid past a thin needle. J. Mol. Liq. 2019, 284, 163–174. [Google Scholar] [CrossRef]
- Rashidi, S.; Esfahani, J.; Ellahi, R. Convective heat transfer and particle motion in an obstructed duct with two side by side obstacles by means of DPM model. Appl. Sci. 2017, 7, 431. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Zeeshan, A.; Ellahi, R. Electromagnetohydrodynamic (EMHD) peristaltic flow of solid particles in a third-grade fluid with heat transfer. Mech. Ind. 2017, 18, 314. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Study of shiny film coating on multi-fluid flows of a rotating disk suspended with nano-sized silver and gold particles: A comparative analysis. Coatings 2018, 8, 422. [Google Scholar] [CrossRef]
- Anwar, M.I.; Shafie, S.; Hayat, T.; Shehzad, S.A.; Salleh, M.Z. Numerical study for MHD stagnation-point flow of a micropolar nanofluid towards a stretching sheet. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 89–100. [Google Scholar] [CrossRef]
- Mustafa, M.; Khan, J.A. Model for flow of Casson nanofluid past a non-linearly stretching sheet considering magnetic field effects. AIP Adv. 2015, 5, 077148. [Google Scholar] [CrossRef] [Green Version]
- Anwar, M.I.; Shafie, S.; Khan, I.; Ali, A.; Salleh, M.Z. Dufour and Soret effects on free convection flow of Nanofluid past a power law stretching sheet. Int. J. Appl. Maths Stats 2013, 43. [Google Scholar]
- Anwar, M.I.; Khan, I.; Sharidan, S.; Salleh, M.Z. Conjugate effects of heat and mass transfer of nanofluids over a nonlinear stretching sheet. Int. J. Phys. Sci. 2012, 7, 4081–4092. [Google Scholar] [CrossRef]
- Qing, J.; Bhatti, M.; Abbas, M.; Rashidi, M.; Ali, M. Entropy generation on MHD Casson nanofluid flow over a porous stretching/shrinking surface. Entropy 2016, 18, 123. [Google Scholar] [CrossRef]
- Abbas, T.; Bhatti, M.M.; Ayub, M. Aiding and opposing of mixed convection Casson nanofluid flow with chemical reactions through a porous Riga plate. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2018, 232, 519–527. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Singer, D.A.; Wang, H.P. Developments and applications of non-Newtonian flows. ASME FED 1995, 66, 99–105. [Google Scholar] [CrossRef]
- Asma, K.; Khan, I.; Arshad, K.; Sharidan, S.; Tlili, I. Case study of MHD blood flow in a porous medium with CNTS and thermal analysis. Case Stud. Therm. Eng. 2018, 12, 374–380. [Google Scholar]
- Suriyakumar, P.; Devi, S.A. Effects of Suction and Internal Heat Generation on Hydromagnetic Mixed Convective Nanofluid Flow over an Inclined Stretching Plate. Eur. J. Adv. Eng. Technol. 2015, 2, 51–58. [Google Scholar]
- Khan, M.; Shahid, A.; Malik, M.Y.; Salahuddin, T. Thermal and concentration diffusion in Jeffery nanofluid flow over an inclined stretching sheet: A generalized Fourier’s and Fick’s perspective. J. Mol. Liq. 2018, 251, 7–14. [Google Scholar] [CrossRef]
- Thumma, T.; Beg, O.A.; Kadir, A. Numerical study of heat source/sink effects on dissipative magnetic nanofluid flow from a non-linear inclined stretching/shrinking sheet. J. Mol. Liq. 2017, 232, 159–173. [Google Scholar] [CrossRef]
- Prakash, J.; Tripathi, D.; Triwari, A.K.; Sait, S.M.; Ellahi, R. Peristaltic Pumping of Nanofluids through a Tapered Channel in a Porous Environment: Applications in Blood Flow. Symmetry 2019, 11, 868. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Abbas, T.; Ellahi, R. Effects of radiative electro-magnetohydrodynamics diminishing internal energy of pressure-driven flow of titanium dioxide-water nanofluid due to entropy generation. Entropy 2019, 21, 236. [Google Scholar] [CrossRef]
- Shehzad, N.; Zeeshan, A.; Ellahi, R.; Rashidi, S. Modelling study on internal energy loss due to entropy generation for non-darcy poiseuille flow of silver-water nanofluid: An application of purification. Entropy 2018, 20, 851. [Google Scholar] [CrossRef]
- Hussain, F.; Ellahi, R.; Zeeshan, A. Mathematical models of electro-magnetohydrodynamic multiphase flows synthesis with nano-sized hafnium particles. Appl. Sci. 2018, 8, 275. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Thermally Charged MHD Bi-phase Flow Coatings with non-Newtonian Nanofluid and Hafnium Particles along Slippery Walls. Coatings 2019, 9, 300. [Google Scholar] [CrossRef]
- Rashad, A. Unsteady nanofluid flow over an inclined stretching surface with convective boundary condition and anisotropic slip impact. Int. J. Heat Technol. 2017, 35, 82–90. [Google Scholar] [CrossRef]
- Govindarajan, A. Radiative fluid flow of a nanofluid over an inclined plate with non-uniform surface temperature. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2018; Volume 1000, p. 12173. [Google Scholar]
- Hatami, M.; Jing, D.; Yousif, M.A. Three-dimensional analysis of condensation nanofluid film on an inclined rotating disk by efficient analytical methods. Arab J. Basic Appl. Sci. 2018, 25, 28–37. [Google Scholar] [CrossRef] [Green Version]
- Cimpean, D.S.; Pop, I. Fully developed mixed convection flow of a nanofluid through an inclined channel filled with a porous medium. Int. J. Heat Mass Transf. 2012, 55, 907–914. [Google Scholar] [CrossRef]
- Reddy, P.B.A. Magnetohydrodynamic flow of a Casson fluid over an exponentially inclined permeable stretching surface with thermal radiation and chemical reaction. Ain Shams Eng. J. 2016, 7, 593–602. [Google Scholar] [CrossRef] [Green Version]
- Hakeem, A.A.; Renuka, P.; Ganesh, N.V.; Kalaivanan, R.; Ganga, B. Influence of inclined Lorentz forces on boundary layer flow of Casson fluid over an impermeable stretching sheet with heat transfer. J. Magn. Magn. Mater. 2016, 401, 354–361. [Google Scholar] [CrossRef]
- Rawi, N.A.; Ilias, M.R.; Lim, Y.J.; Isa, Z.M.; Shafie, S. Unsteady mixed convection flow of Casson fluid past an inclined stretching sheet in the presence of nanoparticles. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2017; Volume 890, p. 012048. [Google Scholar]
- Jain, S.; Parmar, A. Multiple slip effects on inclined MHD Casson fluid flow over a permeable stretching surface and a melting surface. Int. J. Heat Technol. 2018, 36, 585–594. [Google Scholar] [CrossRef]
- Ali, M.; Alim, M.A.; Alam, M.S. Similarity solution of heat and mass transfer flow over an inclined stretching sheet with viscous dissipation and constant heat flux in presence of magnetic field. Procedia Eng. 2015, 105, 557–569. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Asadollahi, A. Peristaltic blood flow of couple stress fluid suspended with nanoparticles under the influence of chemical reaction and activation energy. Symmetry 2019, 11, 276. [Google Scholar] [CrossRef]
- Bohra, S. Heat and mass transfer over a three-dimensional inclined non-linear stretching sheet with convective boundary conditions. Indian J. Pure Appl. Phys. (IJPAP) 2017, 55, 847–856. [Google Scholar]
- Khan, M.; Sardar, H.; Gulzar, M.M.; Alshomrani, A.S. On multiple solutions of non-Newtonian Carreau fluid flow over an inclined shrinking sheet. Results Phys. 2018, 8, 926–932. [Google Scholar] [CrossRef]
- Alam, M.S.; Islam, M.R.; Ali, M.; Alim, M.A.; Alam, M.M. Magnetohydrodynamic boundary layer flow of non-Newtonian fluid and combined heat and mass transfer about an inclined stretching sheet. Open J. Appl. Sci. 2015, 5, 279. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M. Numerical Study on Micropolar Nanofluid Flow over an Inclined Surface by Means of Keller-Box. Asian J. Probab. Stat. 2019, 1–21. [Google Scholar] [CrossRef]
- Bognár, G.; Gombkötő, I.; Hriczó, K. Non-Newtonian fluid flow down an inclined plane. In Proceedings of the 9th ASME/WSEAS International Conference on Fluid Mechanics and Aerodynamics, Florence, Italy, August 2011; pp. 23–25. [Google Scholar]
- Reddy, V.R.; REDDY, M.S.; Nagendra, N.; Rao, A.S.; Reddy, M.S. Radiation Effect on Boundary Layer Flow of a Non Newtonian Jeffrey Fluid Past an Inclined Vertical Plate. i-Manag. J. Math. 2017, 6, 34. [Google Scholar]
- Rafique, K.; Anwar, M.I.; Misiran, M. Keller-box Study on Casson Nano Fluid Flow over a Slanted Permeable Surface with Chemical Reaction. Asian Res. J. Math. 2019, 14, 1–17. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Two-Phase Couette Flow of Couple Stress Fluid with Temperature Dependent Viscosity Thermally Affected by Magnetized Moving Surface. Symmetry 2019, 11, 647. [Google Scholar] [CrossRef]
- Benos, L.T.; Mahabaleshwar, U.S.; Sakanaka, P.H.; Sarris, I.E. Thermal analysis of the unsteady sheet stretching subject to slip and magnetohydrodynamic effects. Therm. Sci. Eng. Prog. 2019, 13, 100367. [Google Scholar] [CrossRef]
- Mastroberardino, A.; Mahabaleshwar, U.S. Mixed convection in viscoelastic flow due to a stretching sheet in a porous medium. J. Porous Media 2013, 16, 483–500. [Google Scholar] [CrossRef]
- Ghadikolaei, S.S.; Hosseinzadeh, K.; Ganji, D.D.; Jafari, B. Nonlinear thermal radiation effect on magneto Casson nanofluid flow with Joule heating effect over an inclined porous stretching sheet. Case Stud. Therm. Eng. 2018, 12, 176–187. [Google Scholar] [CrossRef]
- Saidulu, N.; Gangaiah, T.; Lakshmi, A.V. Radiation Effect on Mhd Flow of a Tangent Hyperbolic Nanofluid over an Inclined Exponentially Stretching Sheet. Int. J. Fluid Mech. Res. 2019, 46. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Hussanan, A.; Salleh, M.Z.; Alkasasbeh, H.T.; Khan, I. MHD flow and heat transfer in a Casson fluid over a nonlinearly stretching sheet with Newtonian heating. Heat Transf. Res. 2018, 49. [Google Scholar] [CrossRef]
- Ullah, A.; Shah, Z.; Kumam, P.; Ayaz, M.; Islam, S.; Jameel, M. Viscoelastic MHD Nanofluid Thin Film Flow over an Unsteady Vertical Stretching Sheet with Entropy Generation. Processes 2019, 7, 262. [Google Scholar] [CrossRef]
- Oyelakin, I.S.; Mondal, S.; Sibanda, P. Unsteady Casson nanofluid flow over a stretching sheet with thermal radiation, convective and slip boundary conditions. Alex. Eng. J. 2016, 55, 1025–1035. [Google Scholar] [CrossRef] [Green Version]
| Nb | Nt | Khan and Pop [45] | Present Results | ||
|---|---|---|---|---|---|
| 0.1 | 0.1 | 0.9524 | 2.1294 | 0.9524 | 2.1294 |
| 0.2 | 0.2 | 0.3654 | 2.5152 | 0.3654 | 2.5152 |
| 0.3 | 0.3 | 0.1355 | 2.6088 | 0.1355 | 2.6088 |
| 0.4 | 0.4 | 0.0495 | 2.6038 | 0.0495 | 2.6038 |
| 0.5 | 0.5 | 0.0179 | 2.5731 | 0.0179 | 2.5731 |
| Nb | Nt | Pr | Le | M | N | λ | δ | m | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.1 | 6.5 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.9 | 0.1 | 0.5 | 45° | 0.0936 | 1.6159 | 0.5417 |
| 0.5 | 0.1 | 6.5 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.9 | 0.1 | 0.5 | 45° | 0.0447 | 1.6541 | 0.5449 |
| 0.1 | 0.13 | 6.5 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.9 | 0.1 | 0.5 | 45° | 0.0961 | 1.6038 | 0.5406 |
| 0.1 | 0.1 | 10.0 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.9 | 0.1 | 0.5 | 45° | 0.0563 | 1.7133 | 0.6235 |
| 0.1 | 0.1 | 6.5 | 10.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.9 | 0.1 | 0.5 | 45° | 0.0919 | 2.3622 | 0.5785 |
| 0.1 | 0.1 | 6.5 | 5.0 | 0.3 | 1.0 | 1.0 | 0.1 | 0.9 | 0.1 | 0.5 | 45° | 0.0957 | 1.5958 | 0.6332 |
| 0.1 | 0.1 | 6.5 | 5.0 | 0.1 | 5.0 | 1.0 | 0.1 | 0.9 | 0.1 | 0.5 | 45° | 0.0527 | 1.6374 | 0.5421 |
| 0.1 | 0.1 | 6.5 | 5.0 | 0.1 | 1.0 | 5.0 | 0.1 | 0.9 | 0.1 | 0.5 | 45° | 0.0916 | 1.5833 | 0.6563 |
| 0.1 | 0.1 | 6.5 | 5.0 | 0.1 | 1.0 | 1.0 | 1.0 | 0.9 | 0.1 | 0.5 | 45° | 0.0952 | 1.6184 | 0.5250 |
| 0.1 | 0.1 | 6.5 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 2.0 | 0.1 | 0.5 | 45° | 0.0949 | 1.6376 | 0.3809 |
| 0.1 | 0.1 | 6.5 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.9 | 0.2 | 0.5 | 45° | 0.1779 | 1.5828 | 0.5363 |
| 0.1 | 0.1 | 6.5 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.9 | 0.1 | 1.5 | 45° | 0.1253 | 1.5763 | 0.6968 |
| 0.1 | 0.1 | 6.5 | 5.0 | 0.1 | 1.0 | 1.0 | 0.1 | 0.9 | 0.1 | 0.5 | 60° | 0.0968 | 1.6098 | 0.5818 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafique, K.; Imran Anwar, M.; Misiran, M.; Khan, I.; Alharbi, S.O.; Thounthong, P.; Nisar, K.S. Keller-Box Analysis of Buongiorno Model with Brownian and Thermophoretic Diffusion for Casson Nanofluid over an Inclined Surface. Symmetry 2019, 11, 1370. https://doi.org/10.3390/sym11111370
Rafique K, Imran Anwar M, Misiran M, Khan I, Alharbi SO, Thounthong P, Nisar KS. Keller-Box Analysis of Buongiorno Model with Brownian and Thermophoretic Diffusion for Casson Nanofluid over an Inclined Surface. Symmetry. 2019; 11(11):1370. https://doi.org/10.3390/sym11111370
Chicago/Turabian StyleRafique, Khuram, Muhammad Imran Anwar, Masnita Misiran, Ilyas Khan, Sayer O. Alharbi, Phatiphat Thounthong, and Kottakkaran Sooppy Nisar. 2019. "Keller-Box Analysis of Buongiorno Model with Brownian and Thermophoretic Diffusion for Casson Nanofluid over an Inclined Surface" Symmetry 11, no. 11: 1370. https://doi.org/10.3390/sym11111370
APA StyleRafique, K., Imran Anwar, M., Misiran, M., Khan, I., Alharbi, S. O., Thounthong, P., & Nisar, K. S. (2019). Keller-Box Analysis of Buongiorno Model with Brownian and Thermophoretic Diffusion for Casson Nanofluid over an Inclined Surface. Symmetry, 11(11), 1370. https://doi.org/10.3390/sym11111370







