Dark Matter as a Result of Field Oscillations in the Modified Theory of Induced Gravity
Abstract
1. Introduction
2. Centrally Symmetric Solutions
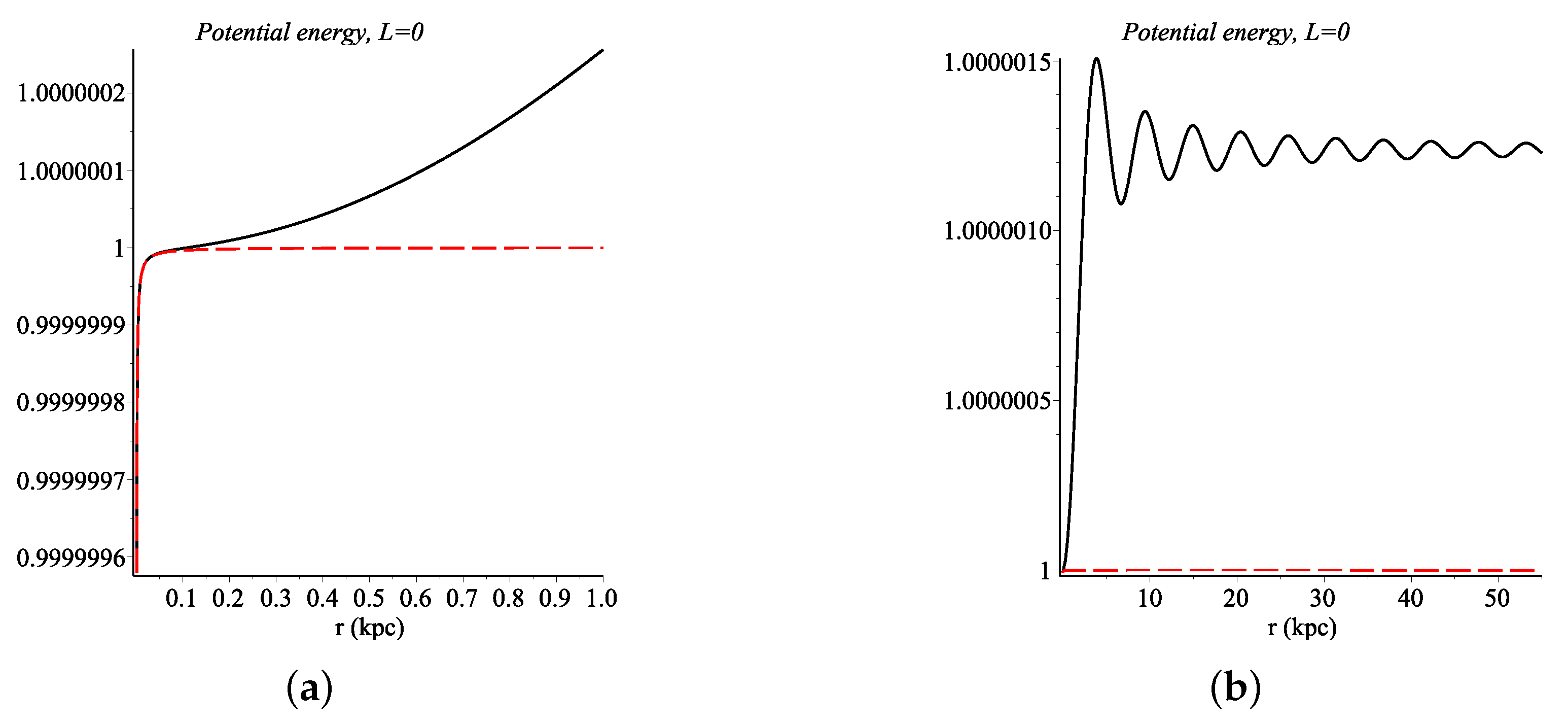
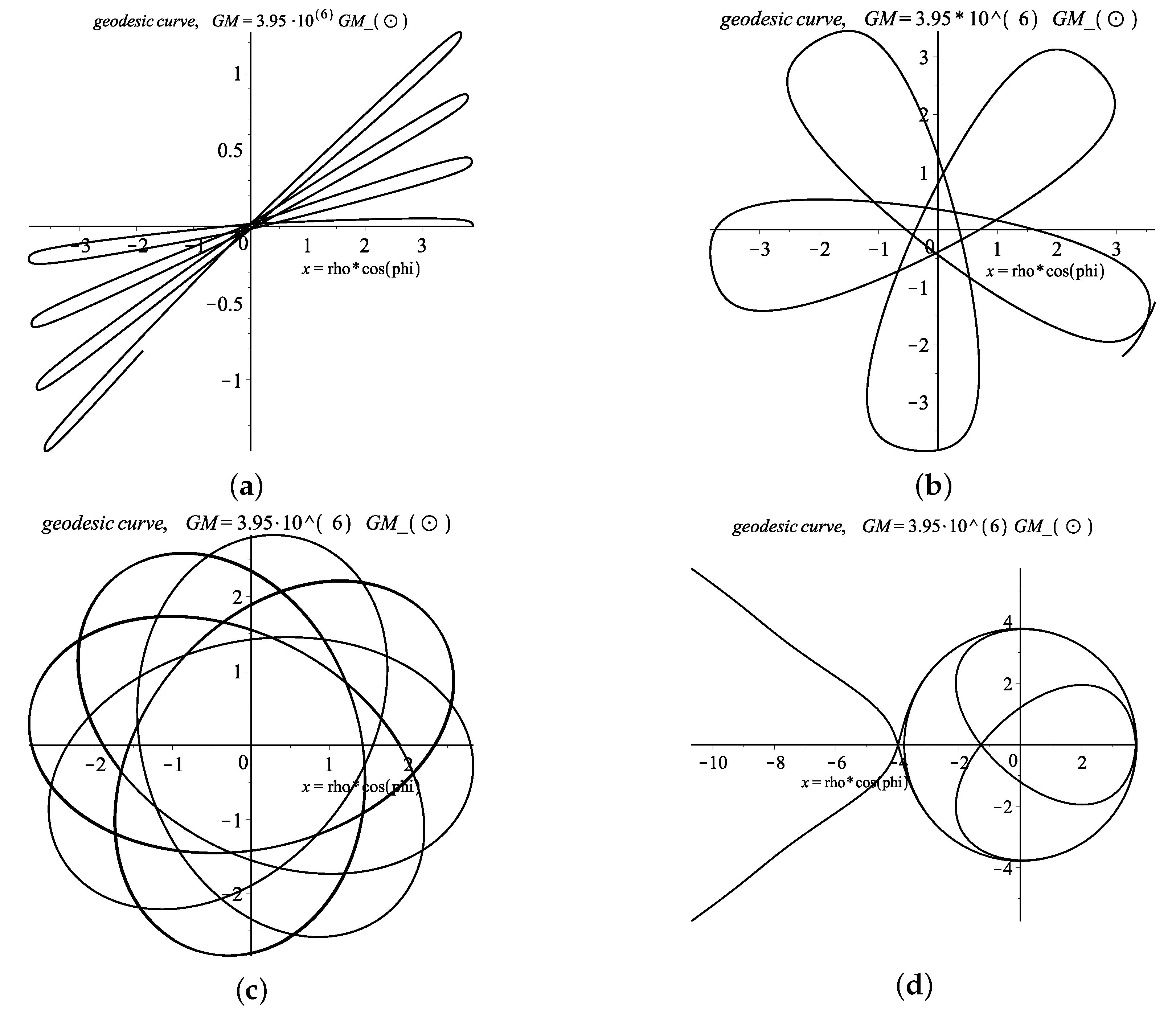
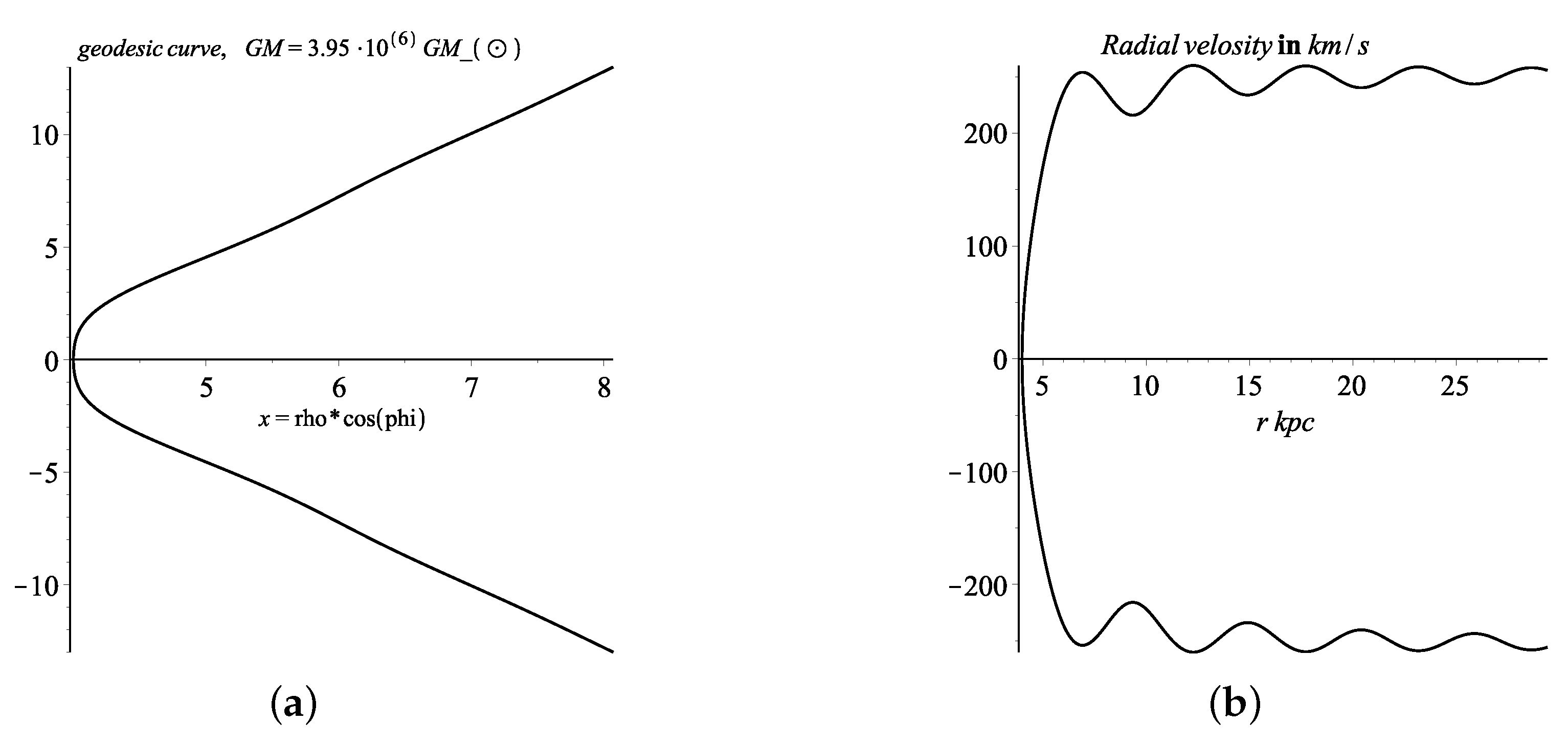
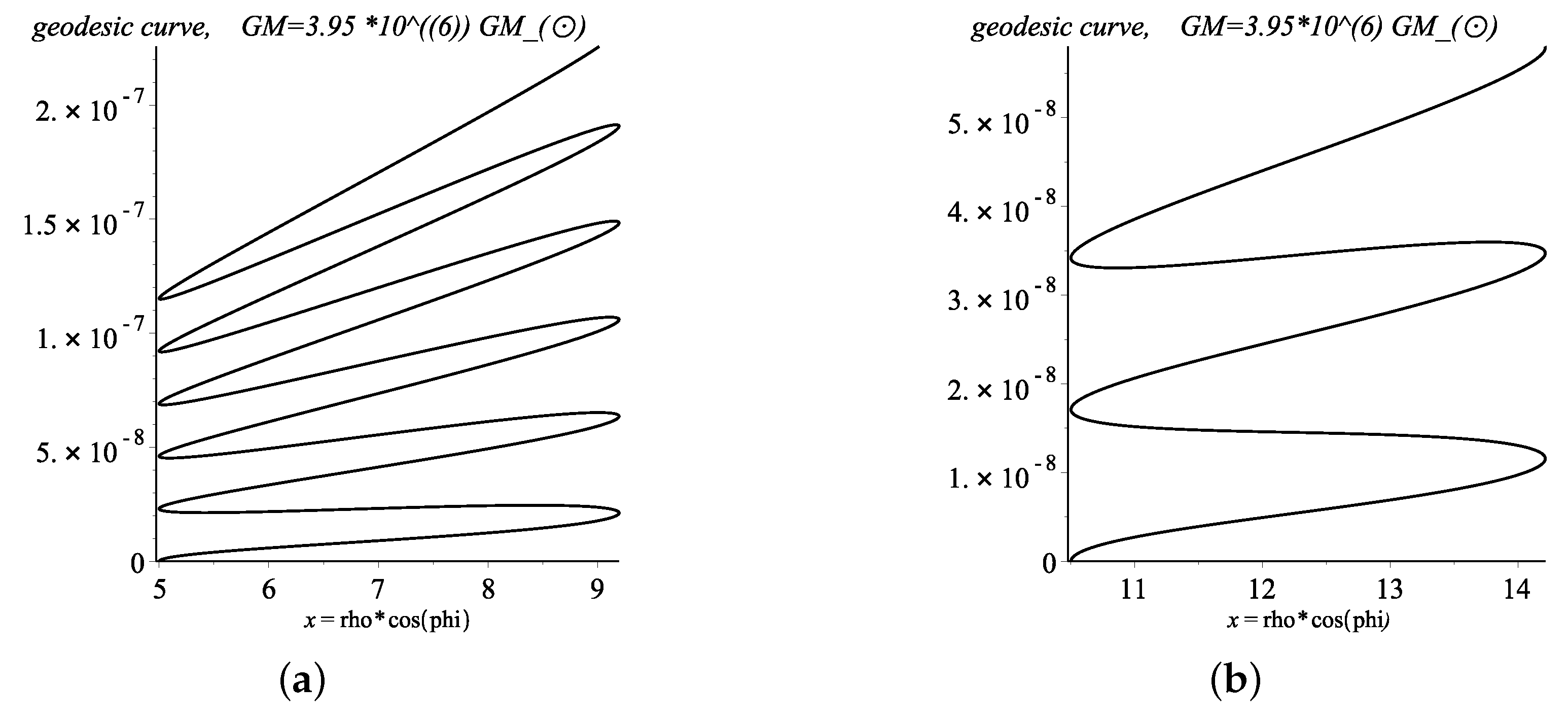
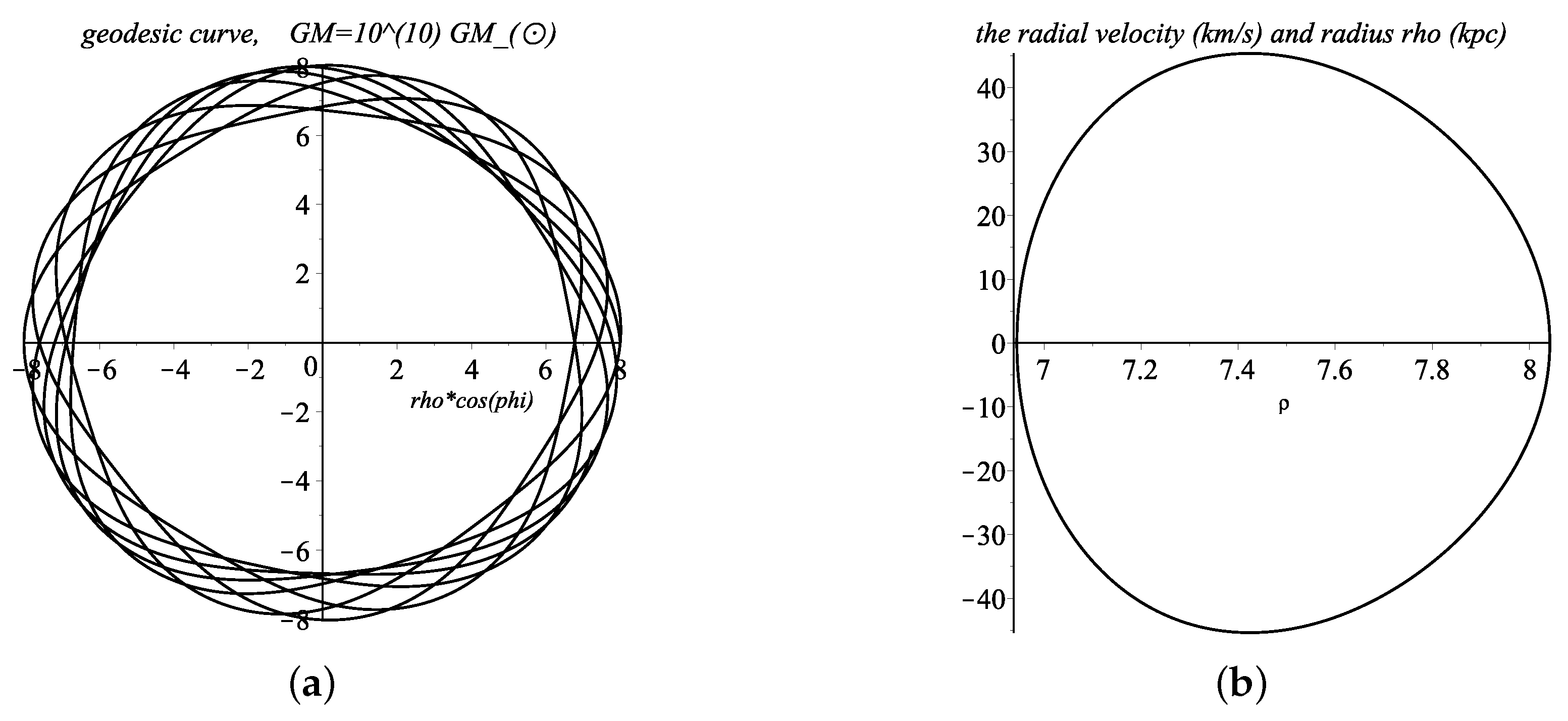
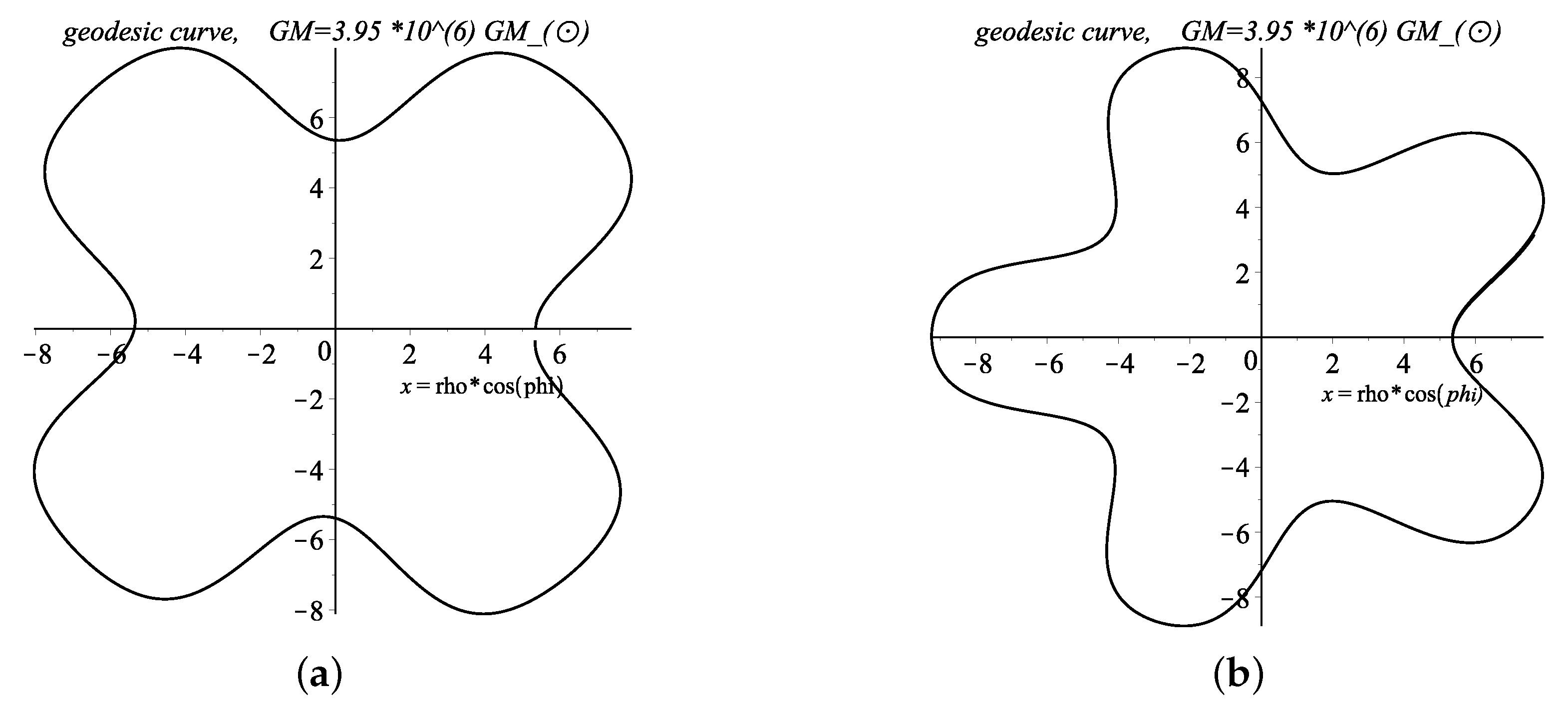
Numerical Solutions for Geodesic Lines
3. Conclusions and Discussion
Funding
Conflicts of Interest
Abbreviations
| GR | General relativity |
| MTIG | Modified Theory of Induced Gravity |
References
- Zasov, A.V.; Saburova, A.S.; Khoperskov, A.V.; Khoperskov, S.A. Dark matter in galaxies. Phys. Usp. 2017, 60, 3–40. [Google Scholar] [CrossRef]
- Speake, C.; Quinn, T. The search for Newton’s constant. Phys. Today 2014, 67, 27–33. [Google Scholar] [CrossRef]
- Rosi, G.; Sorrentino, F.; Cacciapuoti, L.; Prevedelli, M.; Tino, G.M. Precision measurement of the Newtonian gravitational constant using cold atoms. Nature 2014, 510, 518–521. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Chao, X.; Liu, J.-P.; Wu, J.-F.; Yang, S.-Q.; Shao, C.-G.; Quan, L.-D.; Tan, W.-H.; Tu, L.-C.; Liu, Q.; et al. Measurements of the gravitational constant using two independent method. Nature 2018, 560, 582–588. [Google Scholar] [CrossRef] [PubMed]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. Determination of the Local Value of the Hubble Constant. Astrophys. J. 2016. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.; Anderson, J.; Mackenty, J.W.; Bowers, J.B.; Clubb, K.I.; Filippenko, A.V.; Jones, D.O.; et al. New Parallaxes of Galactic Cepheids from Spatially Scanning the Hubble Space Telescope: Implications for the Hubble Constant. arXiv 2018, arXiv:1801.01120. [Google Scholar] [CrossRef]
- Zaripov, F. The Ambiguity in the Definition and Behavior of the Gravitational and Cosmological ‘Coupling Constants’ in the Theory of Induced Gravity. Symmetry 2019, 11, 81. [Google Scholar] [CrossRef]
- Zaripov, F. Oscillating Cosmological Solutions in the Modified Theory of Induced Gravity. Adv. Astron. 2019, 2019, 15. [Google Scholar] [CrossRef]
- Bizon, P.; Rostworowski, A. On weakly turbulent instability of anti-de Sitter space. Phys. Rev. Lett. 2011, 107, 031102. [Google Scholar] [CrossRef]
- Maliborski, M.; Rostworowski, A. Lecture notes on turbulent instability of anti-de Sitter spacetime. Int. J. Mod. Phys. A 2013, 28, 1340020. [Google Scholar] [CrossRef]
- Craps, B.; Evninb, O.; Vanhoof, J. Ultraviolet asymptotics and singular dynamics of AdS perturbations. JHEP 2015, 1510. [Google Scholar] [CrossRef]
- Dias, O.J.C.; Horowitz, G.T.; Santos, J.E. Gravitational Turbulent Instability of Anti-de Sitter Space. Class. Quant. Grav. 2012, 29, 194002. [Google Scholar] [CrossRef]
- Zaripov, F.S. A conformally invariant generalization of string theory to higher-dimensional objects. Hierarchy of coupling constants. Gravit. Cosmol. 2007, 13, 273–281. [Google Scholar]
- Zaripov, F. Modified equations in the theory of induced gravity. Astr. Space Sci. 2014, 352, 289–305. [Google Scholar] [CrossRef]
- Zaripov, F.S. Phenomenological Model of Multiphase Cosmological Scenario in Theory of Induced Gravity. Russ. Phys. J. 2017, 59, 1834–1841. [Google Scholar] [CrossRef]
- Sakharov, A.D. Vacuum Quantum Fluctuations in Curved Space and the Theory of Gravitation. Sov. Phys. Dokl. 1968, 12, 1040, Reprinted in Gen. Rel. Grav. 2000, 32, 365–367. [Google Scholar] [CrossRef]
- Visser, M. Sakharov’s Induced Gravity: A Modern Perspective. Mod. Phys. Lett. 2002, 17, 977. [Google Scholar] [CrossRef]
- Andrianov, A.A.; Andrianov, V.A.; Giacconi, P.; Soldati, R. Induced gravity and universe creation on the domain wall in five-dimensional space-time. Theor. Math. Phys. 2006, 148, 880. [Google Scholar] [CrossRef]
- Linnemann, N.S.; Visser, M.R. Hints towards the Emergent Nature of Gravity. arXiv 2018, arXiv:1711.10503v2. [Google Scholar] [CrossRef]
- Verlinde, E. On the origin of gravity and the laws of Newton. J. High Energy Phys. 2011, 2011, 1. [Google Scholar] [CrossRef]
- Verlinde, E. Emergent gravity and the dark universe. SciPost Phys. 2017. [Google Scholar] [CrossRef]
- Zaripov, F.S. Generalized equations of induced gravity. The evolution of coupling constants. Vestnik TGGPU 2010, 4, 23–28. (In Russian) [Google Scholar]
- Brans, C.; Dicke, R.H. Mach’s principle and relativistic theory of gravitation. Phys. Rev. 1961, 124, 925. [Google Scholar] [CrossRef]
- Jordan, P. Schwerkraft and Weltall; Friedrich Vieweg und Sohn: Braunschweig, Germany, 1955. [Google Scholar]
- Narlikar, J.V. Lepton creation and the Dirac relationship between fundamental constants. Nature 1974, 247, 99–100. [Google Scholar] [CrossRef]
- Scholz, E. Weyl geometry in late 20th century physics. arXiv 2011, arXiv:1111.3220v1. [Google Scholar]
- Aviles, A.; Gruber, C.; Luongo, O.; Quevedo, H. Cosmography and constraints on the equation of state of the Universe in various parametrizations. Phys. Rev. D 2012, 86, 123516. [Google Scholar] [CrossRef]
- Aalbers, J. Conformal Symmetry in Classical Gravity. 2013. Available online: http://dspace.library.uu.nl/handle/1874/280136 (accessed on 20 November 2018).
- Carballo-Rubio, R. Longitudinal diffeomorphisms obstruct the protection of vacuum energy. Phys. Rev. D 2015, 91, 124071. [Google Scholar] [CrossRef]
- Dengiz, S.; Tekin, B. Higgs Mechanism for New Massive Gravity and Weyl Invariant Extensions of Higher Derivative Theories. Phys. Rev. D 2011, 84, 024033. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D. Introduction to Modified Gravity and Gravitational Alternative for Dark Energy. Int. J. Geom. Methods Mod. Phys. 2007, 4, 115–145. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: the equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Sahoo, P.K. Wormholes in exponential f(R, T) gravity. Eur. Phys. J. 2019, 79. [Google Scholar] [CrossRef]
- Nojiri, S.I.; Odintsov, S.D. Accelerating cosmology in modified gravity: From convenient F(R) or string-inspired theory to bimetric F(R) gravityInt. J. Geom. Methods Mod. Phys. 2014, 11, 1–24. [Google Scholar] [CrossRef]
- De Rham, C.; Dvali, G.; Hofmann, S.; Khoury, J.; Pujolàs, O.; Redi, M.; Tolley, A.J. Cascading Gravity: Extending the Dvali-Gabadadze-Porrati Model to Higher Dimension. Phys. Rev. Lett. 2008, 100, 251603. [Google Scholar] [CrossRef] [PubMed]
- Luongo, O.; Muccino, M. Speeding up the Universe using dust with pressure. Phys. Rev. D 2018, 98, 103520. [Google Scholar] [CrossRef]
- Peter, K.; Dunsby, S.; Luongo, O.; Reverberi, L. Dark Energy and Dark Matter from an additional adiabatic fluid. Phys. Rev. D 2016, 94, 083525. [Google Scholar]
- De Felice, A.; Tsujikawa, S. f(R) theories. Liv. Rev. Relativ. 2010. [Google Scholar] [CrossRef]
- Capozziello, S.; Luongo, O.; Pincak, R.; Ravanpak, A. Cosmic acceleration in non-flat f(T) cosmology. arXiv 2018, arXiv:1804.03649. [Google Scholar] [CrossRef]
- Ringermacher, H.I.; Mead, L.R. Observation of Discrete Oscillations in a Model-Independent Plot of Cosmological Scale Factor versus Lookback Time and Scalar Field Model. Astron. J. 2015, 149, 137. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K.; Sebastianie, L. Unification of constant-roll inflation and dark energy with logarithmic R2-corrected and exponential F(R) gravity. Nucl. Phys. 2017, 923, 608–632. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Pozdeeva, E.O.; Starobinsky, A.A.; Tronconi, A.; Venturi, G.; Vernov, S.Y. Transformations between Jordan and Einstein frames: Bounces, antigravity, and crossing singularities. Phys. Rev. D 2016, 94, 063510. [Google Scholar] [CrossRef]
- Bars, I.; James, A. Physical interpretation of antigravity. Phys. Rev. D 2016, 93, 044029. [Google Scholar] [CrossRef]
- Matsunaga, N.; Feast, M.W.; Bono, G.; Kobayashi, N.; Inno, L.; Nagayama, T.; Nishiyama, S.; Matsuoka, Y.; Nagata, T. A lack of classical Cepheids in the inner part of the Galactic disc. MNRAS 2016, 462, 414–420. [Google Scholar] [CrossRef]
- Van Dokkum, P.; Abraham, R.; Romanowsky, A.J.; Brodie, J.; Conroy, C.; Danieli, S.; Zhang, J. Extensive globular cluster systems associated with ultra diffuse galaxies in the Coma cluster. Astrophys. J. Lett. 2017, 844, L11. [Google Scholar] [CrossRef]
- Van Dokkum, P.; Cohen, Y.; Danieli, S.; Kruijssen, J.M.D.; Romanowsky, A.J.; Merritt, A.; Abraham, R.; Brodie, J.; Conroy, C.; Lokhorst, D.; et al. A galaxy lacking dark matter. Nature 2018, 555, 629–632. [Google Scholar] [CrossRef] [PubMed]
- Van Dokkum, P.; Cohen, Y.; Danieli, S.; Kruijssen, J.M.D.; Romanowsky, A.J.; Merritt, A.; Abraham, R.; Brodie, J.; Conroy, C.; Lokhorst, D.; et al. An Enigmatic Population of Luminous Globular Clusters in a Galaxy Lacking Dark Matter. Astrophys. J. Lett. 2018, 856, L30. [Google Scholar] [CrossRef]
- Van Dokkum, P.; Abraham, R.; Brodie, J.; Conroy, C.; Danieli, S.; Merritt, A.; Mowla, L.; Romanowsky, A.; Zhang, J. A High Stellar Velocity Dispersion and 100 Globular Clusters for the Ultra Diffuse Galaxy Dragonfly 44. Astrophys. J. Lett. 2016, 828, L6. [Google Scholar] [CrossRef]
- Anderson, J.D.; Laing, P.A.; Lau, E.L.; Nieto, M.M.; Turyshev, S.G. Search for a Standard Explanation of the Pioneer Anomaly. Mod. Phys. Lett. A 2002, 17, 875–885. [Google Scholar] [CrossRef]
- Nieto, M.M.; Anderson, J.D. Using Early Data to Illuminate the Pioneer Anomaly. Class. Quant. Grav. 2005, 22, 5343–5354. [Google Scholar] [CrossRef]
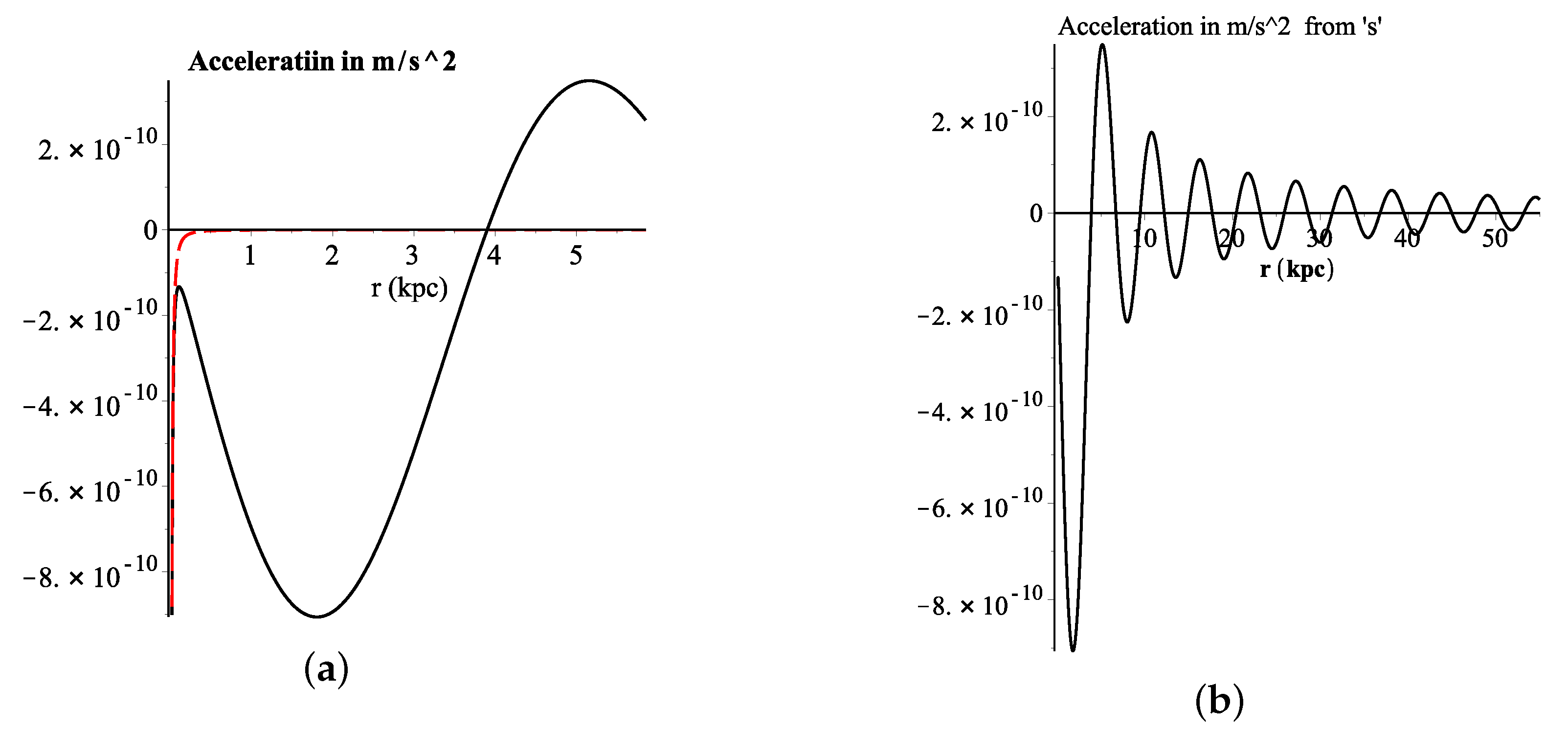

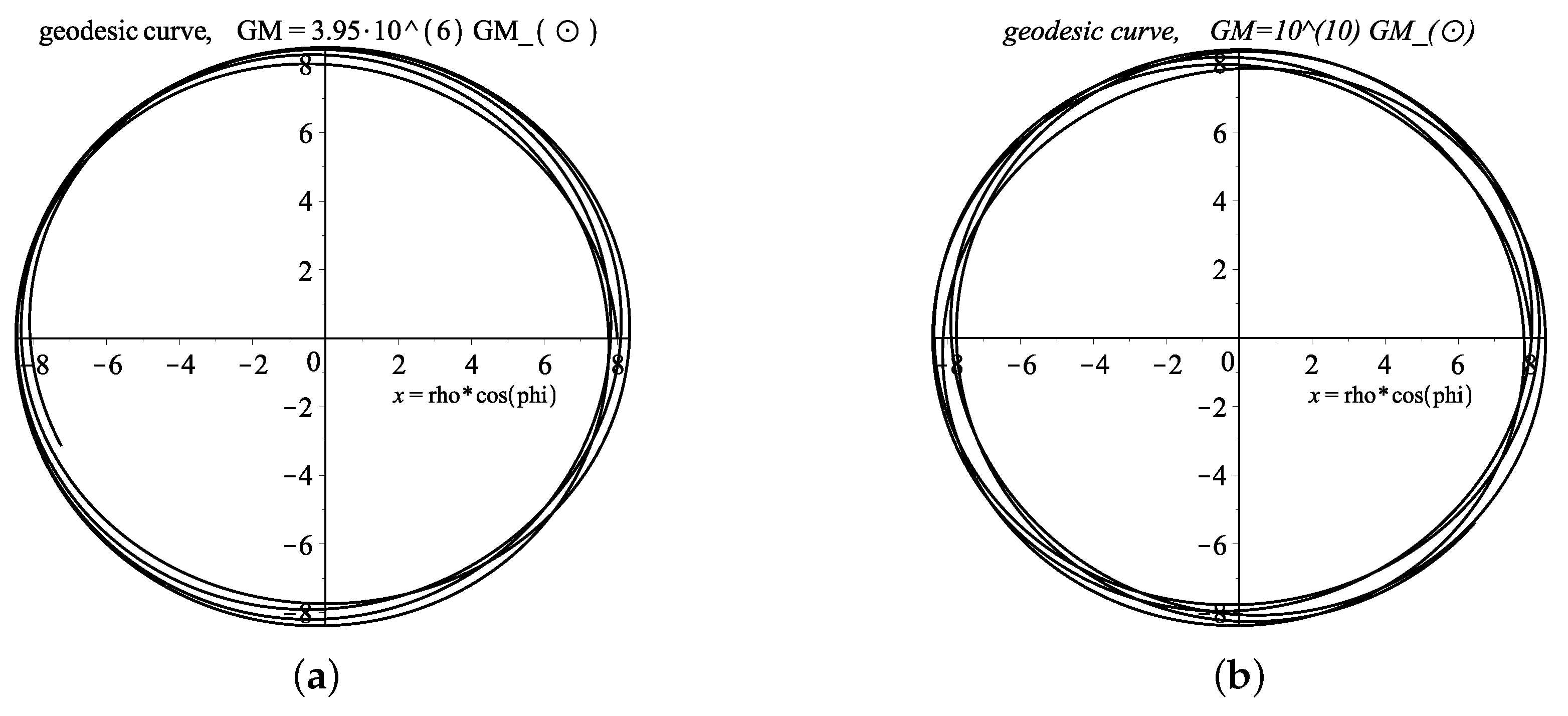
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaripov, F. Dark Matter as a Result of Field Oscillations in the Modified Theory of Induced Gravity. Symmetry 2020, 12, 41. https://doi.org/10.3390/sym12010041
Zaripov F. Dark Matter as a Result of Field Oscillations in the Modified Theory of Induced Gravity. Symmetry. 2020; 12(1):41. https://doi.org/10.3390/sym12010041
Chicago/Turabian StyleZaripov, Farkhat. 2020. "Dark Matter as a Result of Field Oscillations in the Modified Theory of Induced Gravity" Symmetry 12, no. 1: 41. https://doi.org/10.3390/sym12010041
APA StyleZaripov, F. (2020). Dark Matter as a Result of Field Oscillations in the Modified Theory of Induced Gravity. Symmetry, 12(1), 41. https://doi.org/10.3390/sym12010041




