Constraints on the String T-Duality Propagator from the Hydrogen Atom
Abstract
1. Introduction
2. Hydrogen Atom Energy Levels
2.1. Conventional Description
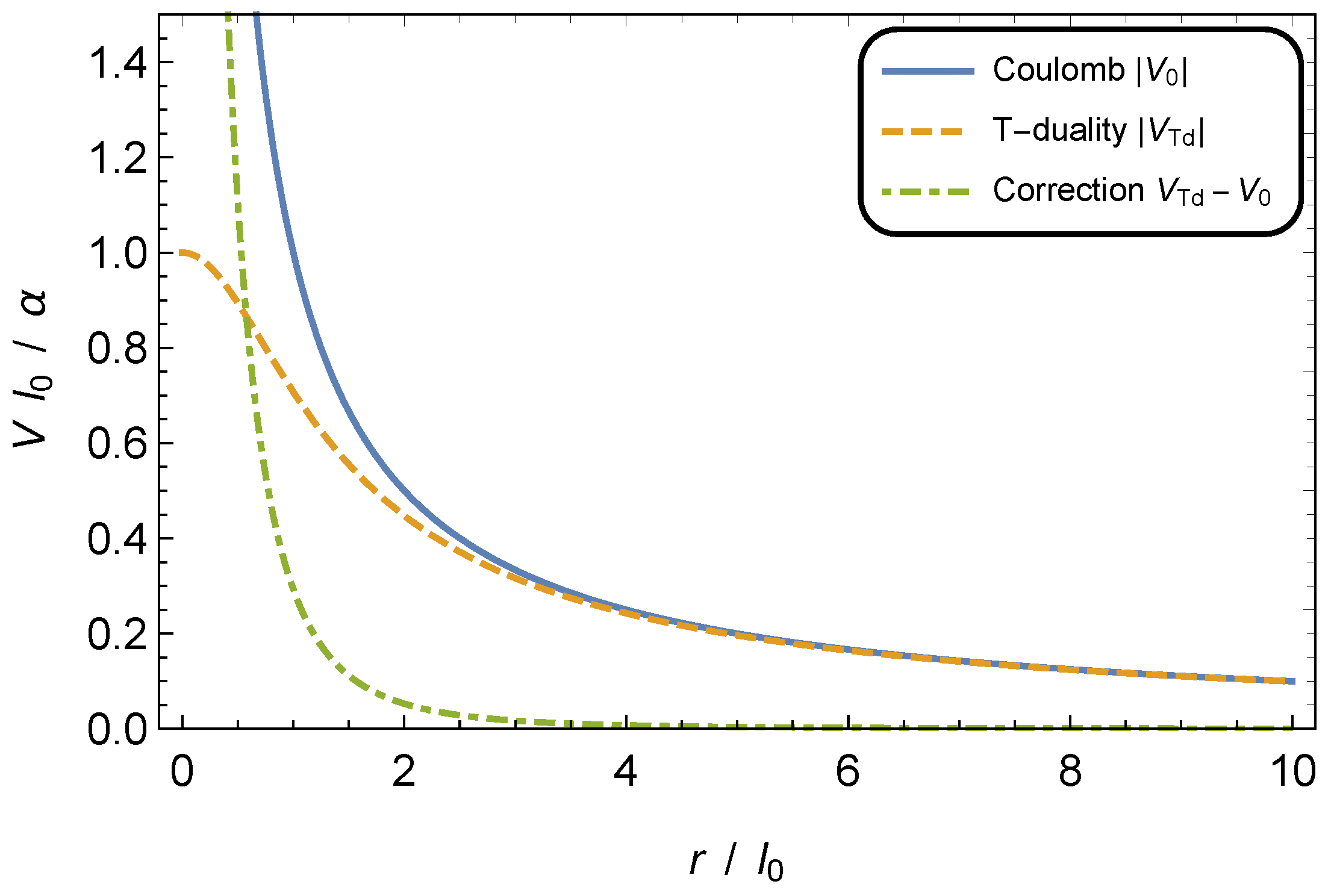
2.2. Contribution from T-Duality Propagator
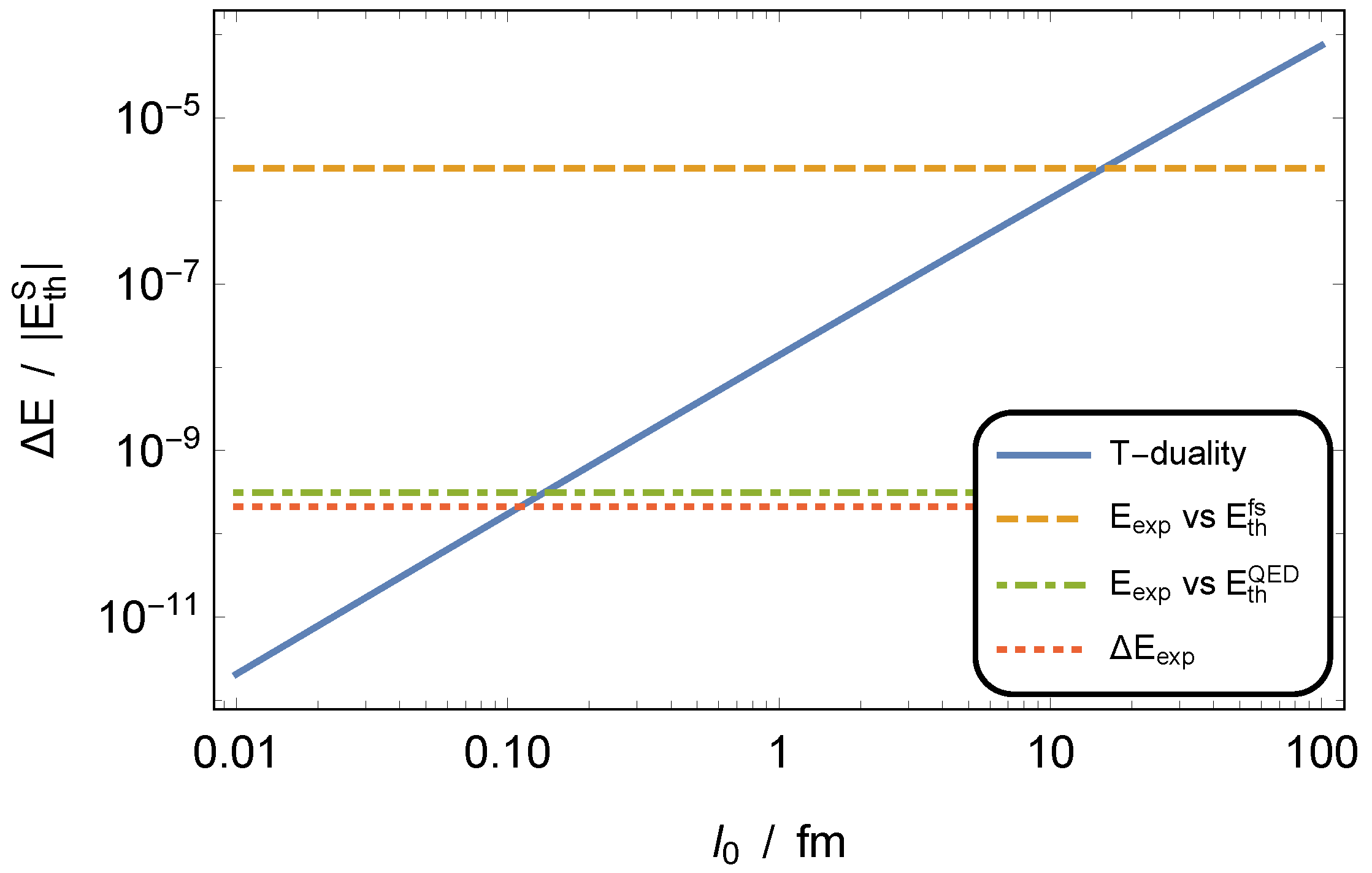
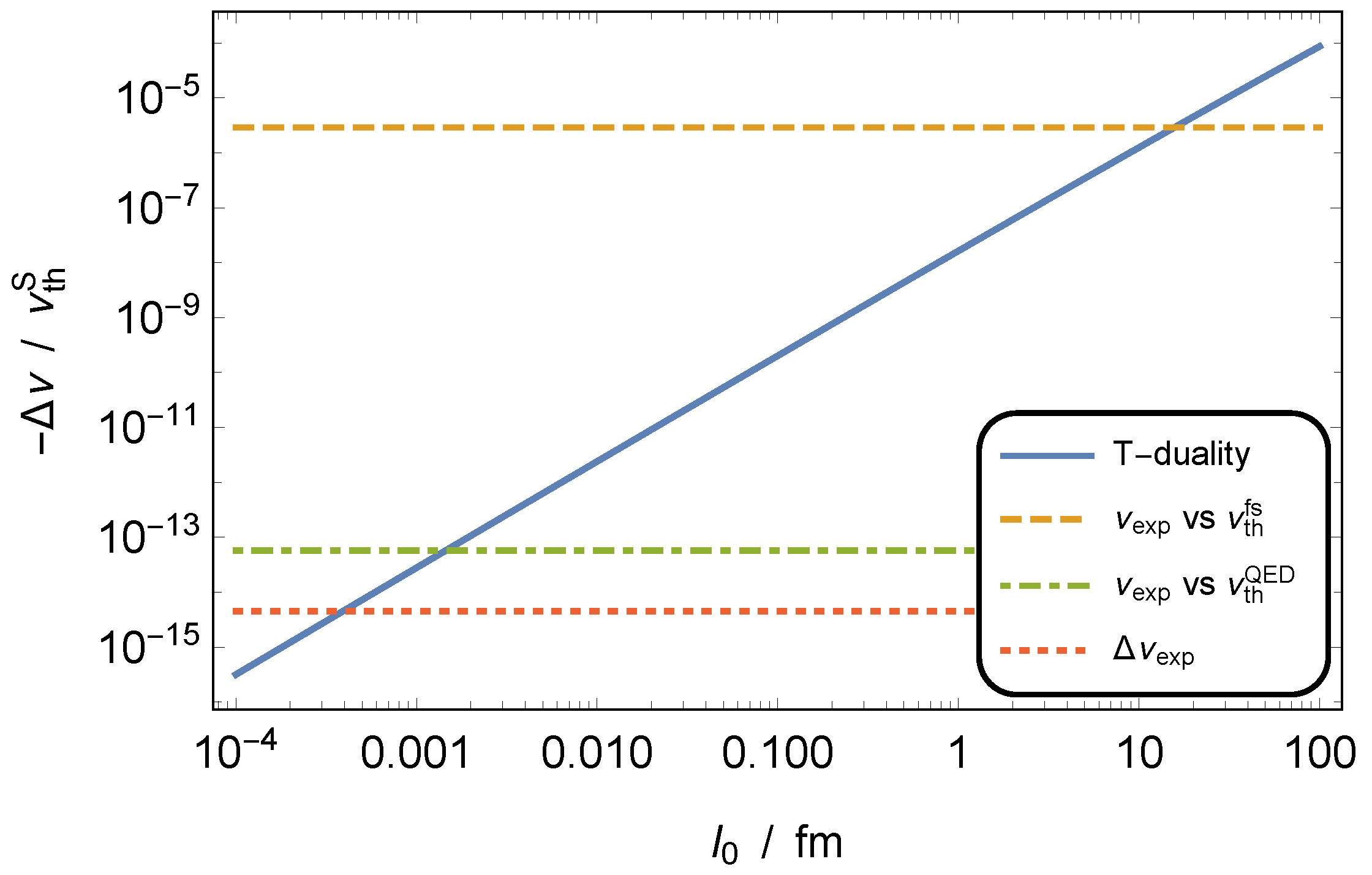
3. Constraints on the Zero-Point Length
3.1. Ground State Energy
3.2. Transition Frequency
4. Discussion
5. Summary
Author Contributions
Funding
Conflicts of Interest
Appendix A. Useful Identities
References
- Weinberg, S. The Quantum Theory of Fields; Volume II. Modern Applications; Cambridge University Press: Cambridge, UK, 2015; pp. 305–318. [Google Scholar]
- De Rham, C. Massive Gravity. Living Rev. Rel. 2014, 17, 7. [Google Scholar] [CrossRef] [PubMed]
- Maggiore, M. Gravitational Waves; Volume 1. Theory and Experiments; Oxford University Press: Oxford, UK, 2017; pp. 7–12, 70–74. [Google Scholar]
- Fontanini, M.; Spallucci, E.; Padmanabhan, T. Zero-point length from string fluctuations. Phys. Lett. B 2006, 633, 627–630. [Google Scholar] [CrossRef]
- Smailagic, A.; Spallucci, E.; Padmanabhan, T. String theory T duality and the zero point length of space-time. arXiv 2003, arXiv:hep-th/0308122. [Google Scholar]
- Spallucci, E.; Fontanini, M. Zero-point length, extra-dimensions and string T-duality. In New Developments in String Theory Research; Grece, S.A., Ed.; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2006; pp. 245–270. [Google Scholar]
- Nicolini, P.; Spallucci, E.; Wondrak, M.F. Quantum Corrected Black Holes from String T-Duality. Phys. Lett. B 2019, 797, 134888. [Google Scholar] [CrossRef]
- Padmanabhan, T. Duality and Zero-Point Length of Spacetime. Phys. Rev. Lett. 1997, 78, 1854–1857. [Google Scholar] [CrossRef]
- Padmanabhan, T. Hypothesis of path integral duality. I. Quantum gravitational corrections to the propagator. Phys. Rev. D 1998, 57, 6206–6215. [Google Scholar] [CrossRef]
- Srinivasan, K.; Sriramkumar, L.; Padmanabhan, T. The Hypothesis of path integral duality. II: Corrections to quantum field theoretic results. Phys. Rev. D 1998, 58, 044009. [Google Scholar] [CrossRef]
- Sriramkumar, L.; Shankaranarayanan, S. Path integral duality and Planck scale corrections to the primordial spectrum in exponential inflation. J. High Energy Phys. 2006, 12, 050. [Google Scholar] [CrossRef]
- Kothawala, D.; Sriramkumar, L.; Shankaranarayanan, S.; Padmanabhan, T. Path integral duality modified propagators in spacetimes with constant curvature. Phys. Rev. D 2009, 80, 044005. [Google Scholar] [CrossRef]
- Kothawala, D.; Shankaranarayanan, S.; Sriramkumar, L. Quantum gravitational corrections to the stress-energy tensor around the BTZ black hole. J. High Energy Phys. 2008, 09, 095. [Google Scholar] [CrossRef]
- Padmanabhan, T. A Measure for Quantum Paths, Gravity and Spacetime Microstructure. arXiv 2019, arXiv:gr-qc/1908.10872. [Google Scholar]
- Shankaranarayanan, S.; Padmanabhan, T. Hypothesis of path integral duality: Applications to QED. Int. J. Mod. Phys. D 2001, 10, 351–366. [Google Scholar] [CrossRef]
- Ohanian, H.C. Finite quantum electrodynamics with a gravitationally smeared propagator. Phys. Rev. D 1997, 55, 5140–5146. [Google Scholar] [CrossRef]
- Ohanian, H.C. Finite quantum electrodynamics and gauge invariance. Nuovo Cim. A 1997, 110, 751–756. [Google Scholar]
- Ohanian, H.C. Smearing of propagators by gravitational fluctuations on the Planck scale. Phys. Rev. D 1999, 60, 104051. [Google Scholar] [CrossRef]
- Mohr, P.J.; Newell, D.B.; Taylor, B.N. CODATA Recommended Values of the Fundamental Physical Constants: 2014. Rev. Mod. Phys. 2016, 88, 035009. [Google Scholar] [CrossRef]
- Brau, F. Minimal length uncertainty relation and hydrogen atom. J. Phys. A 1999, 32, 7691–7696. [Google Scholar] [CrossRef]
- Akhoury, R.; Yao, Y.P. Minimal length uncertainty relation and the hydrogen spectrum. Phys. Lett. B 2003, 572, 37–42. [Google Scholar] [CrossRef][Green Version]
- Hossenfelder, S.; Bleicher, M.; Hofmann, S.; Ruppert, J.; Scherer, S.; Stöcker, H. Signatures in the Planck regime. Phys. Lett. B 2003, 575, 85–99. [Google Scholar] [CrossRef]
- Antonacci Oakes, T.L.; Francisco, R.O.; Fabris, J.C.; Nogueira, J.A. Ground State of the Hydrogen Atom via Dirac Equation in a Minimal Length Scenario. Eur. Phys. J. C 2013, 73, 2495. [Google Scholar] [CrossRef]
- Wondrak, M.F.; Nicolini, P.; Bleicher, M. Unparticle contribution to the hydrogen atom ground state energy. Phys. Lett. B 2016, 759, 589–592. [Google Scholar] [CrossRef]
- Kramida, A.E. A critical compilation of experimental data on spectral lines and energy levels of hydrogen, deuterium, and tritium. Atom. Data Nucl. Data Tables 2010, 96, 586–644, Erratum in 2019, 126, 295. [Google Scholar] [CrossRef]
- Greiner, W. Quantenmechanik. Einführung; Wissenschaftlicher Verlag Harri Deutsch: Frankfurt am Main, Germany, 2005; pp. 219–234. [Google Scholar]
- Schwabl, F. Quantenmechanik (QM I); Eine Einführung; Springer: Berlin, Germany, 2007; pp. 121–142, 217–227. [Google Scholar]
- Blumenhagen, R.; Cvetic, M.; Langacker, P.; Shiu, G. Toward realistic intersecting D-brane models. Annu. Rev. Nucl. Part. Sci. 2005, 55, 71–139. [Google Scholar] [CrossRef]
- Jentschura, U.D.; Kotochigova, S.; LeBigot, E.O.; Mohr, P.J.; Taylor, B.N. The Energy Levels of Hydrogen and Deuterium (Version 2.1); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2005. Available online: http://physics.nist.gov/HDEL (accessed on 30 August 2019).
- Matveev, A.; Parthey, C.G.; Predehl, K.; Alnis, J.; Beyer, A.; Holzwarth, R.; Udem, T.; Wilken, T.; Kolachevsky, N.; Abgrall, M.; et al. Precision Measurement of the Hydrogen 1S-2S Frequency via a 920-km Fiber Link. Phys. Rev. Lett. 2013, 110, 230801. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Series, and Products, 7th ed.; Elsevier Academic Press: London, UK, 2007. [Google Scholar]
| Energy | Description | Value |
|---|---|---|
| Schrödinger | ||
| Schrödinger, incl. fine-structure | ||
| current theoretical value [29] | ||
| current experimental value [25] | ||
| Frequency | Description | Value |
|---|---|---|
| Schrödinger | ||
| Schrödinger, incl. fine-structure | ||
| current theoretical value [29] | ||
| current experimental value [30] |
| Reference Value | Upper Bound on | Reference Value | Upper Bound on |
|---|---|---|---|
| m | m | ||
| m | m | ||
| m | m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wondrak, M.F.; Bleicher, M. Constraints on the String T-Duality Propagator from the Hydrogen Atom. Symmetry 2019, 11, 1478. https://doi.org/10.3390/sym11121478
Wondrak MF, Bleicher M. Constraints on the String T-Duality Propagator from the Hydrogen Atom. Symmetry. 2019; 11(12):1478. https://doi.org/10.3390/sym11121478
Chicago/Turabian StyleWondrak, Michael F., and Marcus Bleicher. 2019. "Constraints on the String T-Duality Propagator from the Hydrogen Atom" Symmetry 11, no. 12: 1478. https://doi.org/10.3390/sym11121478
APA StyleWondrak, M. F., & Bleicher, M. (2019). Constraints on the String T-Duality Propagator from the Hydrogen Atom. Symmetry, 11(12), 1478. https://doi.org/10.3390/sym11121478




