Abstract
Similar to other fluids (Newtonian and non-Newtonian), micropolar fluid also exhibits symmetric flow and exact symmetric solution similar to the Navier–Stokes equation; however, it is not always realizable. In this article, the Buongiorno mathematical model of hydromagnetic micropolar nanofluid is considered. A joint phenomenon of heat and mass transfer is studied in this work. This model indeed incorporates two important effects, namely, the Brownian motion and the thermophoretic. In addition, the effects of magnetohydrodynamic (MHD) and chemical reaction are considered. The fluid is taken over a slanted, stretching surface making an inclination with the vertical one. Suitable similarity transformations are applied to develop a nonlinear transformed model in terms of ODEs (ordinary differential equations). For the numerical simulations, an efficient, stable, and reliable scheme of Keller-box is applied to the transformed model. More exactly, the governing system of equations is written in the first order system and then arranged in the forms of a matrix system using the block-tridiagonal factorization. These numerical simulations are then arranged in graphs for various parameters of interest. The physical quantities including skin friction, Nusselt number, and Sherwood number along with different effects involved in the governing equations are also justified through graphs. The consequences reveal that concentration profile increases by increasing chemical reaction parameters. In addition, the Nusselt number and Sherwood number decreases by decreasing the inclination.
1. Introduction
In the last couple of decades, fast advances in nanotechnology have prompted the development of new age coolants called nanofluids. Nanofluids are designed by interrupting nanoparticles with normal sizes of less than 100 nm in conventional heat exchange liquids such as ethylene glycol, water, and oil. These are the current heat exchange specialists that trigger the thermal conductivity of the base fluids, and they have been a fundamental subject for experts and researchers in the course of the last few years due to their fluctuated design and modern applications Choi [1]. Eastman et al. [2] reported in a study that thermal conductivity is enhanced up to 60% when CuO nanoparticles are added into a base liquid (water) with volume fraction 5%. Furthermore, they reported that the thermal conductivity increased up to 40% by adding the copper nanoparticles with volume fraction 1% into the conventional fluid. Buongiorno [3] discussed in his study that there are seven mechanisms, which are important to enhance the thermal conductivity of the base fluid. Among these mechanisms, Brownian motion and thermophoresis are the more substantial. Currently, nanofluids are used relatively commonly in electronic engineering, physical processing, communication, etc. Several research articles on the flow of nanofluids are reported in the relevant literature. Further, nanofluids have prominent application in welding equipment, in cooling high energy flux devices including high power wave tubes and in cooling automobile engines, etc. [4]. The heat transfer of nanofluid over a nonlinear porous sheet is numerically discussed by Zaimi et al. [5]. Moreover, the flow of nanofluid over a porous slanted surface is discussed by Sandeep and Kumar [6]. Chakraborty et al. [7] examined the nanofluid flow over a permeable inclined plate with solar radiations. Rashad [8] studied nanofluid flow by considering convective boundaries and the anisotropic slip effect. Mitra [9] investigated computational modeling of nanofluid flow over a heated inclined plate.
The energy and mass transport with chemical reactions over an inclined stretching plate has garnered considerable interest because of its many applications in engineering. In processes such as drying, evaporation of surface water, the flow in a desert cooler, and heat transport in a wet cooling tower, energy and mass transport occur. Shit and Majee [10] scrutinized the flow of magnetohydrodynamic (MHD) fluid on a slanted surface. Eid [11] discussed the mixed convection flow by incorporating effects of chemical reactions. Jain and Bohra [12] scrutinized the effect of chemical reactions on three dimensional incompressible flows over an inclined surface. The flow of free convection fluid through a slanted sheet was elucidated by Sheri and Modugula [13]. Recently, different researchers studied the heat and mass exchange phenomenon with different impacts, see [14,15,16,17,18].
The idea of micropolar fluid has attained great importance, because conventional Newtonian liquids cannot precisely match the properties of fluid flow in numerous industrial uses, namely, polymeric fluids, biology, colloidal solutions, and paints. Fluids that are rigid, accidentally concerned with elements adjourned in a sticky medium, and with microstructure atoms are termed as micropolar fluids, in which the element distortion is unnoticed, see Eringen [19]. Rahman et al. [20] studied the heat exchange procedure in micropolar fluid flow by incorporating different fluid properties over a permeable inclined plate. Micropolar fluid flow, by taking different effects over an inclined sheet, was studied by Das [21]. Kasim et al. [22] investigated magnetohydrodynamic (MHD) micropolar fluid flow towards an inclined plate. Srinivasacharya and Bindu [23] discussed entropy generation of micropolar fluid flow on an inclined channel with parallel plates. Anwar et al. [24] conducted a numerical study of micropolar nanofluid flow by incorporating the thermophoresis effects. Magnetomicropolar flow over a slanted channel with parallel plates was investigated by Hazbavi and Sharhani [25]. Srinivasacharya et al. [26] explored the double diffusive effect on the flow of micropolar fluid on a slanted sheet. Other similar studies on the different aspects of fluids are given in [27,28,29,30,31]. The flow symmetry of fluids in general has been studied using theoretical methods, various experiment methods, and different numerical techniques, in various fields such as the field of fluid mechanics, the field of thermal engineering, etc., due to their several benefits and relevance in terms of flow control and heat transfer enhancement. However, symmetric flows of non-Newtonian fluids have not been sufficiently elucidated due to their nonlinear characteristics.
Energy and mass exchange has attracted the attention of contemporary researchers due to its diverse uses such as in cancer therapy, sensors, drying processes, MHD generators, the cooling of nuclear reactors, high temperature plasmas, etc. Recently, Ellahi et al. [32] investigated the magnetohydrodynamic flow of nanofluid with entropy generation numerically. Moreover, numerical simulation of MHD mixed convection nanofluid flow was conducted by Khan et al. [33].
Motivated by the above cited literature, we have decided to study the flow of micropolar nanofluid over an inclined surface with Brownian motion and thermophoretic impacts. In view of industrial and engineering applications, in this study, the chemical reaction and heat generation or absorption effects are considered. Moreover, a lot of work on non-Newtonian nanofluids’ flow by considering different geometries has been done, but no one scholar to date has considered the inclined surface geometry combined with micropolar nanofluid by incorporating the considered effects, i.e., chemical reaction and suction or injection, with the Keller-box technique. Therefore, in order to fill this gap in the literature, we conducted this research. The inclined stretching geometry with MHD impacts have important applications in automobiles, MHD generators, extrusion of sheets, etc.
2. Problem Formulation
Our main purpose is to study the micropolar-type nanofluid flow over a permeable inclined plate with an angle . The velocities taken in account are, and , respectively; here, ‘x’ is the coordinate measured along the stretching surface and ‘a’ is a constant. The transverse magnetic field is taken perpendicular to the extending surface. It is supposed that the magnetic and electric field effects are very minor as the magnetic Reynolds number is less, see Mishra et al. [27].The micropolar finite size particles along with nanoparticles are constantly distributed in the base fluids. The fluid particles have extra space to travel about, formerly hitting other fluid particles, where these particles revolve in the fluid field and fallouts for spinning effects in the micropolar nanofluid. The temperature and nanoparticle fraction take the constant values and whereas and are the nanofluid temperature and mass fractions, respectively.
The flow equations for current problem are given by Khan and Pop [28]:
where the components of velocity along and are denoted by and , is the heat generation or absorption coefficient, is the chemical reaction coefficient, the thermal diffusivity parameter is denoted by , and the ratio between the effective heat capacity of the nanoparticle and heat capacity of the liquid is represented by .
The boundary settings are
The stream function for that purpose is given as
where Equation (1) is fulfilled identically. For this problem, transformations are demarcated as
On substituting Equation (8), the system of Equations (2)–(5) is
where
Here, denotes the local Grashof number, signifies the modified local Grashof number, the chemical reaction parameter is denoted by , heat generation or absorption factor, and is the dimensionless vertex viscosity. To achieve the true similarity solution, the parameters must be constant. This condition is achieved if the thermal expansion coefficient and concentration expansion coefficient are proportional to x1. Hence, we assume that (see [34,35,36,37])
where and are constants. Substituting Equation (14) into the parameters and , we get
The transformed boundary conditions are
It is found that by eliminating the vertex viscosity, i.e., = 0, the nanofluid model is deprived of micropolar impacts. The Sherwood number, skin friction, and Nusselt number are defined by
The associated terms for , and are defined as
where is the local Reynolds number.
3. Results and Discussion
This section deals with the mathematical results of converted nonlinear ordinary differential Equations (9)–(12) with boundary settings (16) elucidated via finite difference scheme (Keller-box scheme). This method is very fast, easy to program, and easy to use for highly nonlinear ordinary differential equations. In this problem, the step size with boundary layer thickness is considered. Moreover, convergence criteria in this problem depend on the difference between current and previous iterations. When the convergence criterion is satisfied for all points in the -direction, the iteration process was terminated. For statistical outcomes of physical factors such as (Brownian motion factor), (thermophoresis factor), chemical reaction constraint , magnetic parameter , local Grashof number , (heat generation or absorption parameter), i.e., , modified local Grashof number , inclination factor , (Prandtl number), (Lewis number), suction or injection constraint and material parameter , different figures are plotted.
In Table 1, due to the lack of , , , , , and with = 90°, and outcomes for and are compared with published outcomes of Khan and Pop [38]. Table 2 shows that decreases for a growth in the magnitudes of , , , , and on decreasing the factor , whereas it increases with the increase of , , , and . Further, is boosted by various magnitudes of , , and drops for greater magnitudes of , and on decreasing magnitudes of . In addition, rises with increasing magnitudes of , , , , , and drops with the higher magnitudes of , , , , and on decreasing .

Table 1.
Contrast of the reduced Nusselt number and the reduced Sherwood number when, and with .

Table 2.
Values of the and .
Figure 1 indicates that the velocity profile decelerated by enhancing the values of the inclination parameter . This is because enhancing the value of the inclination parameter retards the strength of the bouncy force by a factor due to thermal variation. We also found that the influence of the bouncy force (which is highest for ) exceeds the main stream velocity significantly. Figure 2 indicates that the velocity profile increases for large values of modified local Grashof number . Physically, the viscosity of the liquid falls with the growth of , and the concentration upturns which causes the increment in the velocity contour. Moreover, Figure 3 displays that enlarges with increasing values of . Here, presents the features of the buoyancy forces, which offers a direct relation with . Increase of buoyancy forces diminishes the viscous force, which is favorable to the fluid motion. Figure 4 depicts impacts of on . It is found that retards as we upturn the factor . This is because the application of a magnetic field produces Lorentz force, which create retardation in the speed of the fluid. The same effect is seen in the case of angular velocity for changed values of in Figure 5. The angular velocity shows an inverse relation with the magnetic field strength, which matches with the result of Rafique et al. [31].
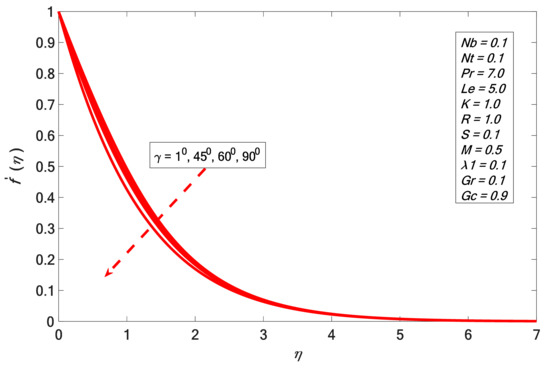
Figure 1.
Velocity profile against .
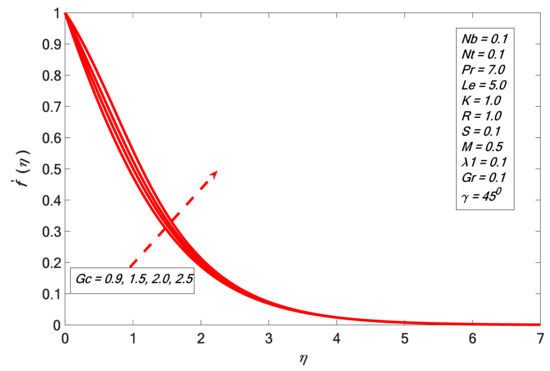
Figure 2.
Velocity profile against .
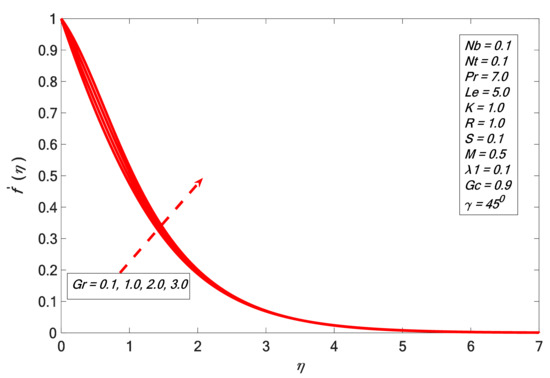
Figure 3.
Velocity profile against .
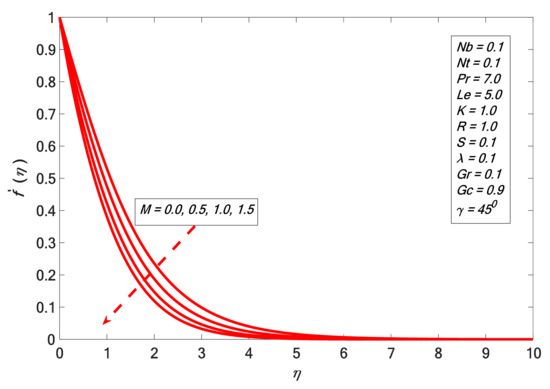
Figure 4.
Velocity profile against .
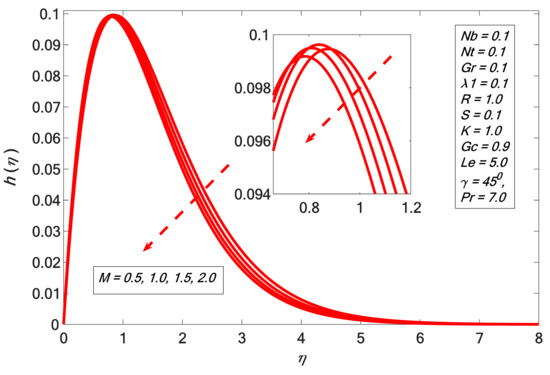
Figure 5.
Angular velocity against .
It is noticed in Figure 6 that increases with the increment of . The angular velocity profile upsurge corresponding with higher magnitudes of is indicated in Figure 7, and it emulates the result of Rafique et al. [31]. The boundary layer thickness declines by enhancing the magnitudes of . Figure 8 indicates the result of the suction factor on the velocity profile. The velocity contour decreases against the growth of . It is noted that the enrichment of porosity decreases the permeability, which causes the retardation of the fluid velocity. As we increase porosity, the velocity will be increasingly retarded. Figure 9 presents the effect of heat generation on . The temperature profile increases by growing . The velocity of the liquid is enhanced by increasing ; therefore, heat is generated in the flow area and the temperature increases within the thermal boundary layer. Figure 10 and Figure 11 depict the outcome of Brownian motion on temperature and concentration outline. It is observed that increases versus ; the opposite reaction is shown in the case of concentration profile. The movement of the nanoparticles increases due to the irregular motion which acts to heat up the boundary layer. Hence, the concentration of the nanoparticles decreases. The effects of the thermophoresis constraint on and are presented in Figure 12 and Figure 13 respectively. It is observed that and are directly proportional to . Figure 14 depicts the effect of the Prandtl number on . It indicates that decreases the higher the Prandtl number. The boundary layer thickness shortens by enhancing the values of the Prandtl number. Figure 15 shows that the concentration profile decreases for higher values of . The Lewis number reduces the boundary layer thickness. Figure 16 indicates a direct correspondence between the concentration profile and chemical reaction parameter .
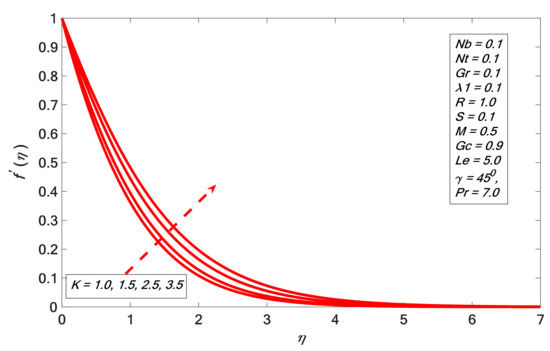
Figure 6.
Velocity profile against .
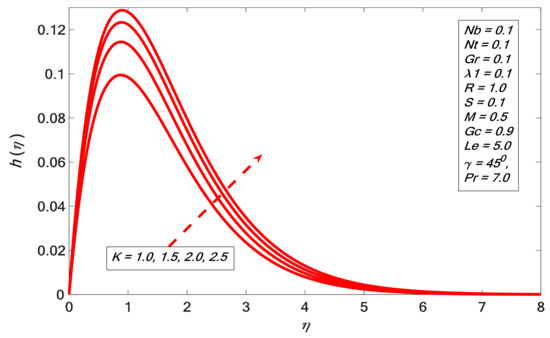
Figure 7.
Angular velocity against .
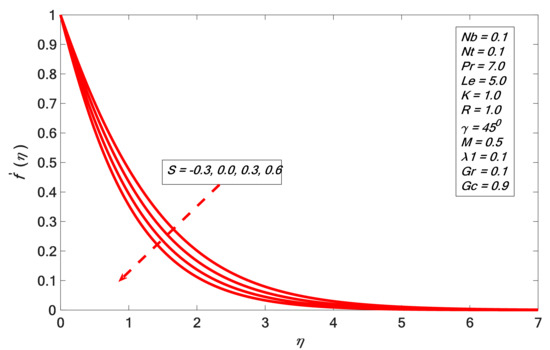
Figure 8.
Velocity profile against .
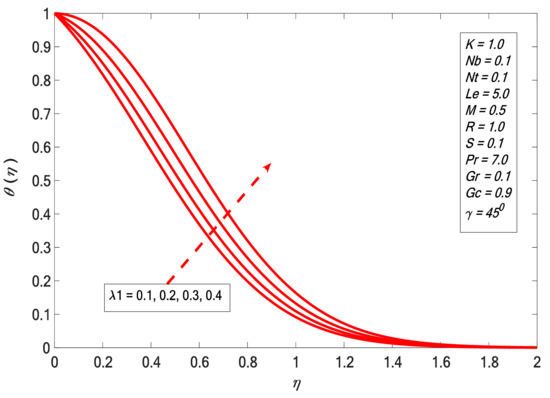
Figure 9.
Temperature profile against .
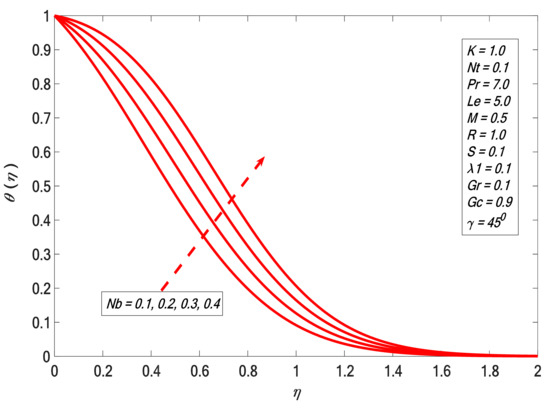
Figure 10.
Temperature profile against .
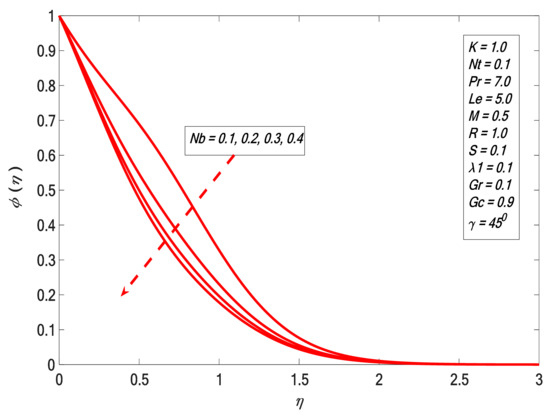
Figure 11.
Concentration profile against .
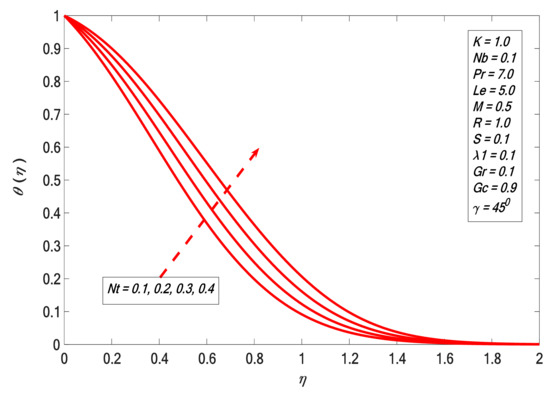
Figure 12.
Temperature profile against .
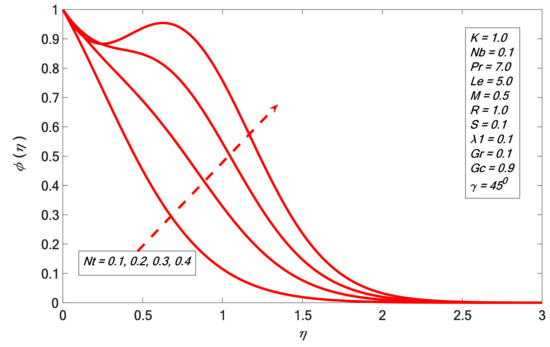
Figure 13.
Concentration profile against .
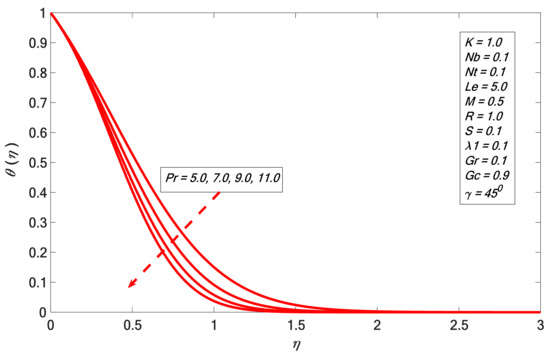
Figure 14.
Temperature profile against .
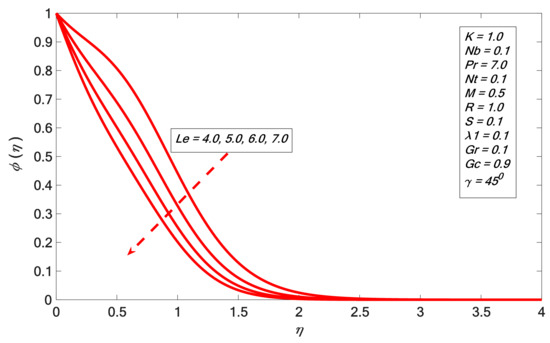
Figure 15.
Concentration profile against .
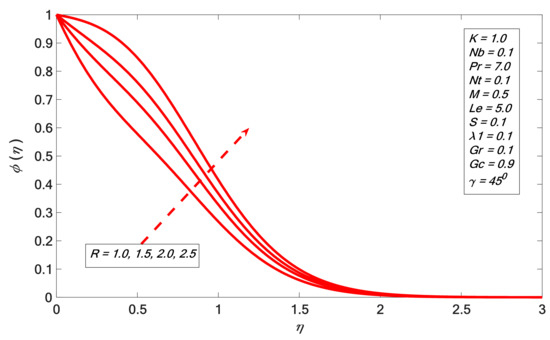
Figure 16.
Concentration profile against .
4. Conclusions
The investigation of micropolar-type nanofluid flow over a permeable inclined surface with the impact of inclination factor has been studied in this article. The effects of chemical reaction and suction or injection are incorporated in the flow field. The main findings of this study are the following:
- ⮚
- The temperature profile falls by improving .
- ⮚
- The Nusselt number enhances with the increase of the chemical reaction effect.
- ⮚
- The Nusselt number improves the higher the magnitude of inclination.
- ⮚
- The Sherwood number upturns by improving the inclination parameter.
- ⮚
- The Sherwood number decreases by improving the chemical reaction impact.
- ⮚
- The Sherwood number reduces the larger the value of .
- ⮚
- The skin friction decreases for higher values of .
- ⮚
- Skin friction decreases with the enhancement of the chemical reaction parameter.
Author Contributions
Formulation done by K.R. and M.M. Problem solved by K.R. and M.I.A. Results computed by K.R.; I.K. and D.B. Results discussed by E.-S.M.S.; A.H.S. and K.S.N. All authors contributed equally in writing manuscript.
Acknowledgments
The authors would like to extend their sincere appreciation to the Deanship of Scientific Research at King Saud University for its funding of this research through the Research Group Project No. RGP-160.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Fluid concentration | Heat generation or absorption | Chemical reaction | |||
| Skin friction coefficient | Thermal diffusivity | Reynolds number | |||
| Ambient nanoparticle volume fraction | Lewis number | Sherwood number | |||
| Surface volume fraction | Brownian motion parameter | Fluid temperature | |||
| Specific heat at constant pressure | Thermophoretic parameter | Wall temperature | |||
| Brownian diffusion coefficient | Nusselt number | Ambient temperature | |||
| Thermophoretic diffusion coefficient | Prandtle number | wall velocity | |||
| Similarity function for velocity | Gravitational acceleration | ambient velocity | |||
| Volume heat capacity | Kinematic viscosity | Dynamic viscosity | |||
| Dimensionless solid volume fraction | Condition at the wall | Ambient condition | |||
| Local Grashof number | Thermal expansion coefficient | Concentration expansion coefficient | |||
| Electric conductivity | Spin gradient viscosity | Vertex viscosity | |||
| Micro inertia per unit mass | Inclination parameter | Differentiation with respect to | |||
| Velocity in direction | Velocity in direction | Cartesian coordinate | |||
| Dimensionless temperature | Suction or injection parameter | Thermal conductivity | |||
| Fluid density | Bouncy parameter | Uniform magnetic field strength | |||
| Material parameter | Similarity independent variable | ||||
| Non-dimensional angular velocity | Stretching rate |
References
- Choi, S.U.S.; Singer, D.A.; Wang, H.P. Developments and applications of non-Newtonian flows. ASME FED 1995, 66, 99–105. [Google Scholar]
- Eastman, J.A.; Choi, U.S.; Li, S.; Thompson, L.J.; Lee, S. Enhanced thermal conductivity through the development of nanofluids. MRS Online Proc. Libr. Arch. 1996, 457. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Sivashanmugam, P. Application of nanofluids in heat transfer. In An Overview of Heat Transfer Phenomena; InTech: Rijeka, Croatia, 2012; Volume 16. [Google Scholar]
- Zaimi, K.; Ishak, A.; Pop, I. Boundary layer flow and heat transfer over a nonlinearly permeable stretching/shrinking sheet in a nanofluid. Sci. Rep. 2014, 4, 4404. [Google Scholar] [CrossRef]
- Sandeep, N.; Kumar, M.S. Heat and Mass Transfer in Nanofluid Flow over an Inclined Stretching Sheet with Volume Fraction of Dust and Nanoparticles. J. Appl. Fluid Mech. 2014, 9, 2205–2215. [Google Scholar] [CrossRef]
- Chakraborty, T.; Das, K.; Kundu, P.K. Ag-water nanofluid flow over an inclined porous plate embedded in a non-Darcy porous medium due to solar radiation. J. Mech. Sci. Technol. 2017, 31, 2443–2449. [Google Scholar] [CrossRef]
- Rashad, A. Unsteady nanofluid flow over an inclined stretching surface with convective boundary condition and anisotropic slip impact. Int. J. Heat Technol. 2017, 35, 82–90. [Google Scholar] [CrossRef]
- Mitra, A. Computational Modelling of Boundary-Layer Flow of a Nano fluid Over a Convective Heated Inclined Plate. J. Mech. Contin. Math. Sci. 2018, 13, 88–94. [Google Scholar] [CrossRef]
- Shit, G.C.; Majee, S. Hydromagnetic Flow over an Inclined Non-Linear Stretching Sheet with Variable Viscosity in the Presence of Thermal Radiation and Chemical Reaction. J. Appl. Fluid Mech. 2014, 7, 239–247. [Google Scholar]
- Eid, M.R. Chemical reaction effect on MHD boundary-layer flow of two-phase nano fluid model over an exponentially stretching sheet with a heat generation. J. Mol. Liq. 2016, 220, 718–725. [Google Scholar] [CrossRef]
- Jain, S.; Bohra, S. Heat and mass transfer over a three-dimensional inclined non-linear stretching sheet with convective boundary conditions. Indian J. Pure Appl. Phys. 2017, 55, 847–856. [Google Scholar]
- Sheri, S.R.; Modugula, P. Thermal-diffusion and diffusion-thermo effects on MHD flow through porous medium past an exponentially accelerated inclined plate with variable temperature. ARPN J. Eng. Appl. Sci. 2017, 12, 5518–5526. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M. Keller-box Study on Casson Nano Fluid Flow over a Slanted Permeable Surface with Chemical Reaction. Asian Res. J. Math. 2019, 14, 1–17. [Google Scholar] [CrossRef][Green Version]
- Bhatti, M.M.; Mishra, S.R.; Abbas, T.; Rashidi, M.M. A mathematical model of MHD nanofluid flow having gyrotactic microorganisms with thermal radiation and chemical reaction effects. Neural Comput. Appl. 2018, 30, 1237–1249. [Google Scholar] [CrossRef]
- Abbas, T.; Bhatti, M.M.; Ayub, M. Aiding and opposing of mixed convection Casson nanofluid flow with chemical reactions through a porous Riga plate. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2018, 232, 519–527. [Google Scholar] [CrossRef]
- Qing, J.; Bhatti, M.; Abbas, M.; Rashidi, M.; Ali, M. Entropy generation on MHD Casson nanofluid flow over a porous stretching/shrinking surface. Entropy 2016, 18, 123. [Google Scholar] [CrossRef]
- Mishra, S.R.; Baag, S.; Bhatti, M.M. Study of heat and mass transfer on MHD Walters B′ nanofluid flow induced by a stretching porous surface. Alex. Eng. J. 2018, 57, 2435–2443. [Google Scholar] [CrossRef]
- Eringen, A.C. Simple microfluids. Int. J. Eng. Sci. 1964, 2, 205–217. [Google Scholar] [CrossRef]
- Rahman, M.M.; Aziz, A.; Al-Lawatia, M.A. International Journal of Thermal Sciences Heat transfer in micropolar fluid along an inclined permeable plate with variable fluid properties. Int. J. Therm. Sci. 2010, 49, 993–1002. [Google Scholar] [CrossRef]
- Das, K. Slip effects on heat and mass transfer in MHD micropolar fluid flow over an inclined plate with thermal radiation and chemical reaction. Int. J. Numer. Methods Fluids 2012, 70, 96–113. [Google Scholar] [CrossRef]
- Kasim AR, M.; Mohammad, N.F.; Shafie, S. Unsteady MHD mixed convection flow of a micropolar fluid along an inclined stretching plate. Heat Transf. Asian Res. 2013, 42, 89–99. [Google Scholar]
- Srinivasacharya, D.; Bindu, K.H. Entropy generation in a micropolar fluid flow through an inclined channel. Alex. Eng. J. 2016, 55, 973–982. [Google Scholar] [CrossRef]
- Anwar, M.I.; Shafie, S.; Hayat, T.; Shehzad, S.A.; Salleh, M.Z. Numerical study for MHD stagnation-point flow of a micropolar nanofluid towards a stretching sheet. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 89–100. [Google Scholar] [CrossRef]
- Hazbavi, A.; Sharhani, S. IMECE2017-72528 Micropolar Fluid Flow between Two Inclined Parallel Plates. In Proceedings of the ASME 2017 International Mechanical Engineering Congress and Exposition, Tampa, FL, USA, 3–9 November 2017; pp. 1–6. [Google Scholar]
- Srinivasacharya, D.; RamReddy, C.; Naveen, P. Double dispersion effect on nonlinear convective flow over an inclined plate in a micropolar fluid saturated non-Darcy porous medium. Eng. Sci. Technol. Int. J. 2018, 21, 984–995. [Google Scholar] [CrossRef]
- Mishra, S.R.; Baag, S.; Mohapatra, D.K. Engineering Science and Technology, an International Journal Chemical reaction and Soret effects on hydromagnetic micropolar fluid along a stretching sheet. Eng. Sci. Technol. Int. J. 2016, 19, 1919–1928. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M.; Khan, I.; Sherif, E.S.M. The Implicit Keller Box Scheme for Combined Heat and Mass Transfer of Brinkman-Type Micropolar Nanofluid with Brownian Motion and Thermophoretic Effect Over an Inclined Surface. Appl. Sci. 2020, 10, 280. [Google Scholar] [CrossRef]
- Prakash, J.; Tripathi, D.; Tiwari, A.K.; Sait, S.M.; Ellahi, R. Peristaltic Pumping of Nanofluids through a Tapered Channel in a Porous Environment: Applications in Blood Flow. Symmetry 2019, 11, 868. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M.; Khan, I.; Seikh, A.H.; Sherif, E.S.M.; Nisar, K.S. Brownian Motion and Thermophoretic Diffusion Effects on Micropolar Type Nanofluid Flow with Soret and Dufour Impacts over an Inclined Sheet: Keller-Box Simulations. Energies 2019, 12, 4191. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M. Numerical Study on Micropolar Nanofluid Flow over an Inclined Surface by Means of Keller-Box. Asian J. Probab. Stat. 2019, 4, 1–21. [Google Scholar] [CrossRef]
- Ellahi, R.; Sait, S.M.; Shehzad, N.; Mobin, N. Numerical simulation and mathematical modeling of electro-osmotic Couette–Poiseuille flow of MHD power-law nanofluid with entropy generation. Symmetry 2019, 11, 1038. [Google Scholar] [CrossRef]
- Khan, U.; Abbasi, A.; Ahmed, N.; Alharbi, S.O.; Noor, S.; Khan, I.; Mohyud-Din, S.T.; Khan, W.A. Modified MHD Radiative Mixed Convective Nanofluid Flow Model with Consideration of the Impact of Freezing Temperature and Molecular Diameter. Symmetry 2019, 11, 833. [Google Scholar] [CrossRef]
- Makinde, O.D.; Olanrewaju, P.O. Buoyancy effects on thermal boundary layer over a vertical plate with a convective surface boundary condition. J. Fluids Eng. 2010, 132, 044502. [Google Scholar] [CrossRef]
- Ilias, M.R.; Rawi, N.A.; Shafie, S. MHD Free Convection Flow and Heat Transfer of Ferrofluids over a Vertical Flat Plate with Aligned and Transverse Magnetic Field. Indian J. Sci. Technol. 2016, 9, 7. [Google Scholar] [CrossRef]
- Olanrewaju, P.O.; Hayat, T. The effects of buoyancy and transpiration on the flow and heat transfer over a moving permeable surface in a parallel stream in the presence of radiation. Int. J. Comput. Methods Eng. Sci. Mech. 2014, 15, 330–336. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M.; Khan, I.; Seikh, A.H.; Sherif, E.S.M.; Sooppy Nisar, K. Keller-Box Simulation for the Buongiorno Mathematical Model of Micropolar Nanofluid Flow over a Nonlinear Inclined Surface. Processes 2019, 7, 926. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).