Mechanical Behaviors of a Symmetrical Bolt Fasten Wedge Active Joint for Braced Excavations
Abstract
1. Introduction
2. Design of the BFW Active Joint
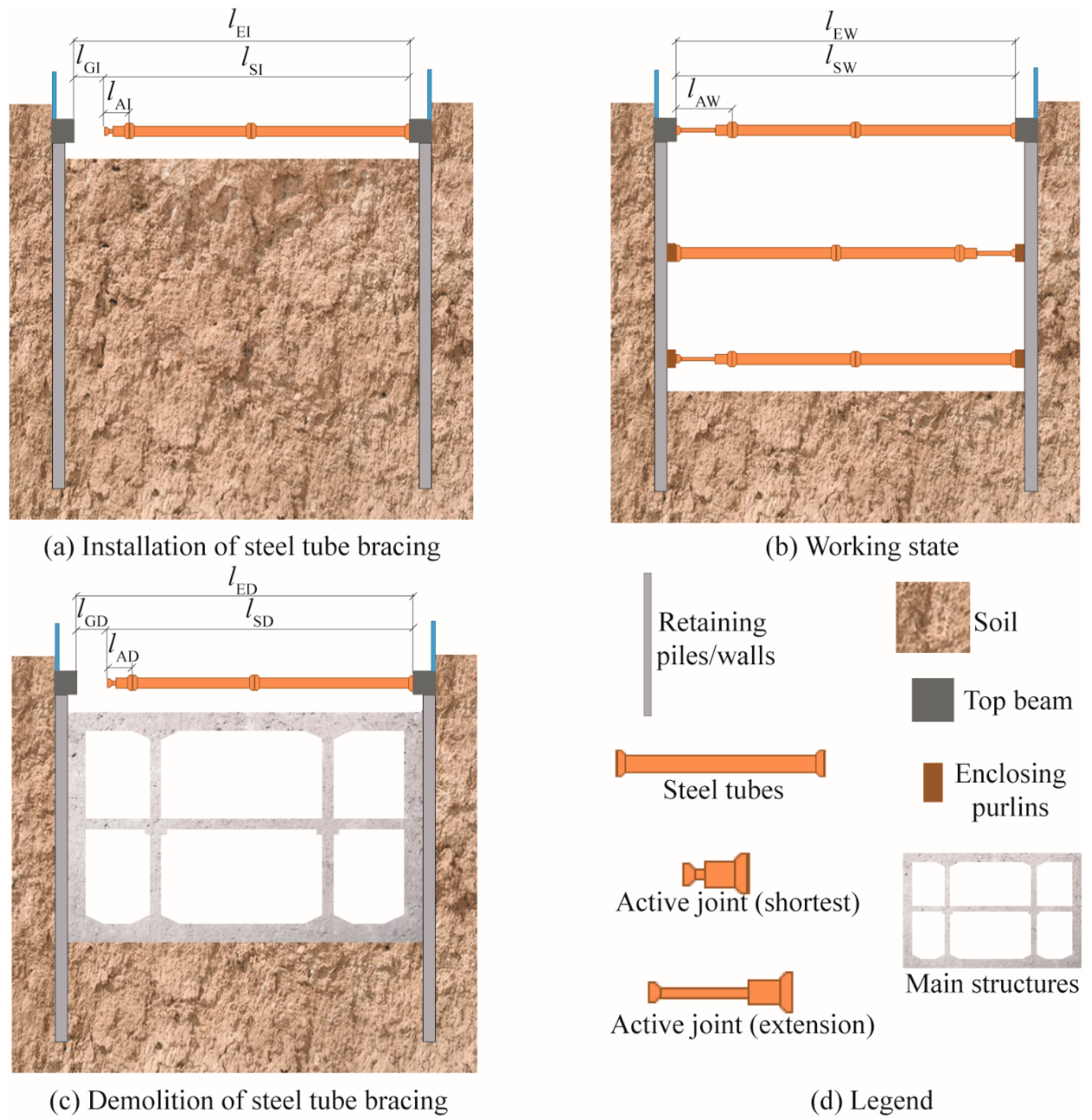
2.1. Basic Function of Active Joints
- Before deformation (installation): lEI—excavation width, lSI—total length of the steel tube, lAI—length of the active joint, and lGI—length of the reserved gap.
- In deformation (working): lEW—excavation width, lSW—total length of the steel tube, and lAW—length of the active joint.
- After deformation (demolition): lED—excavation width, lSD—total length of the steel tube, lAD—length of the active joint, and lGD—length of the demolition required gap.
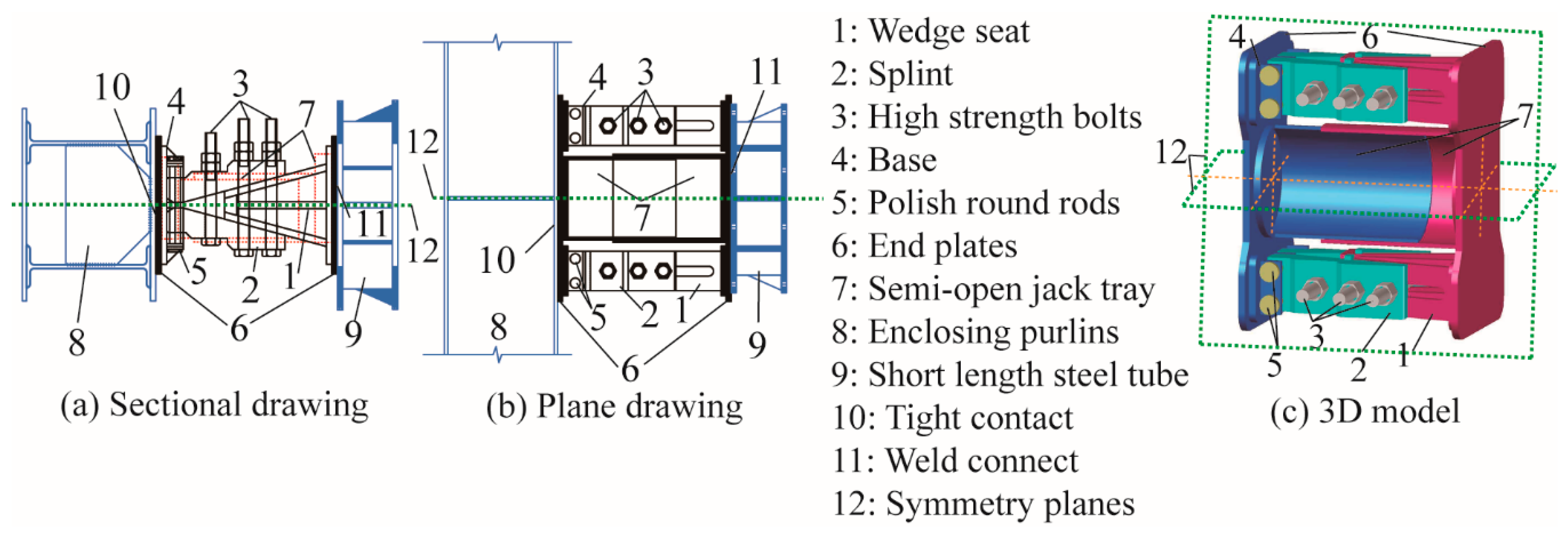
2.2. Components and Composition
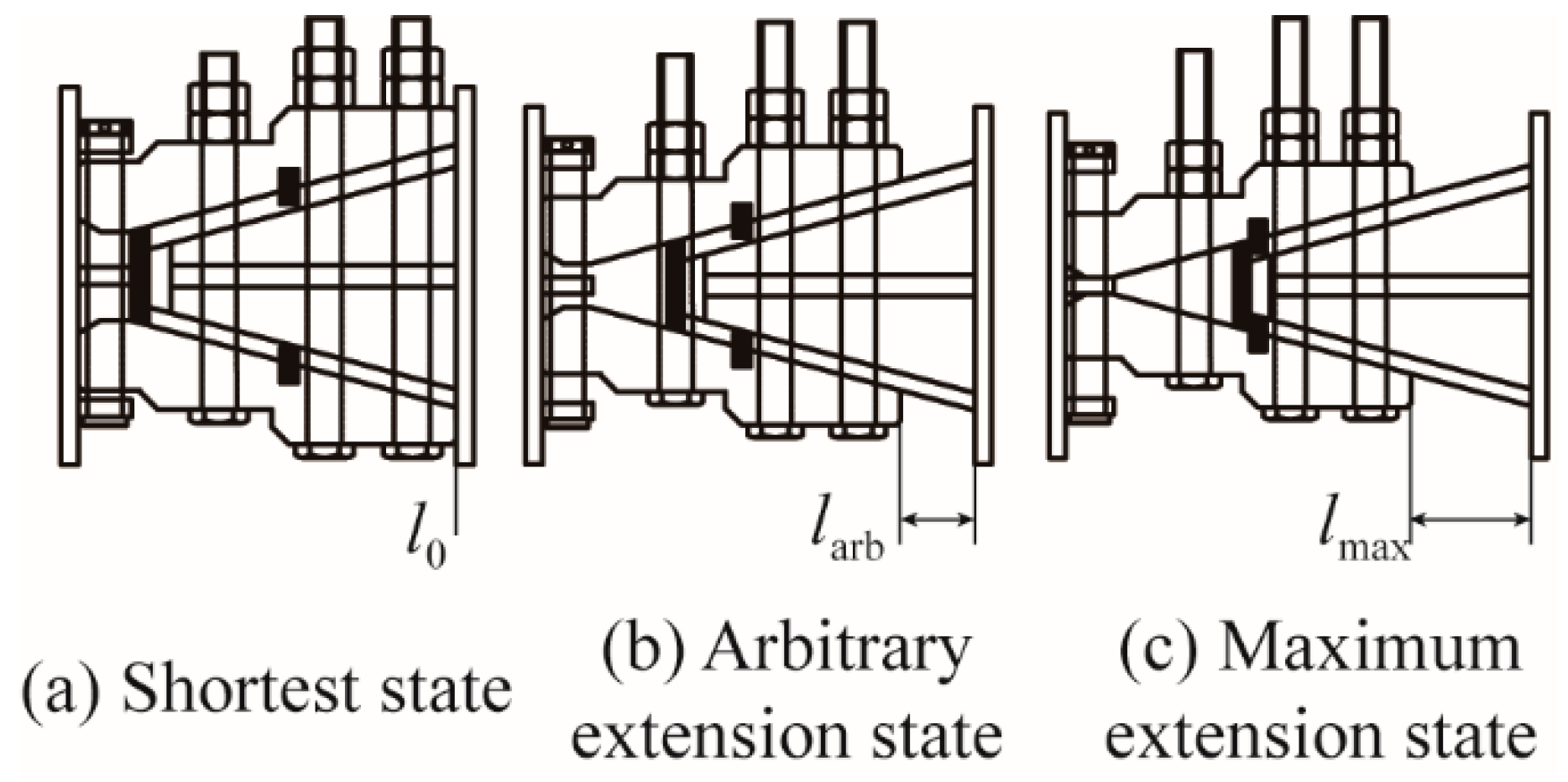
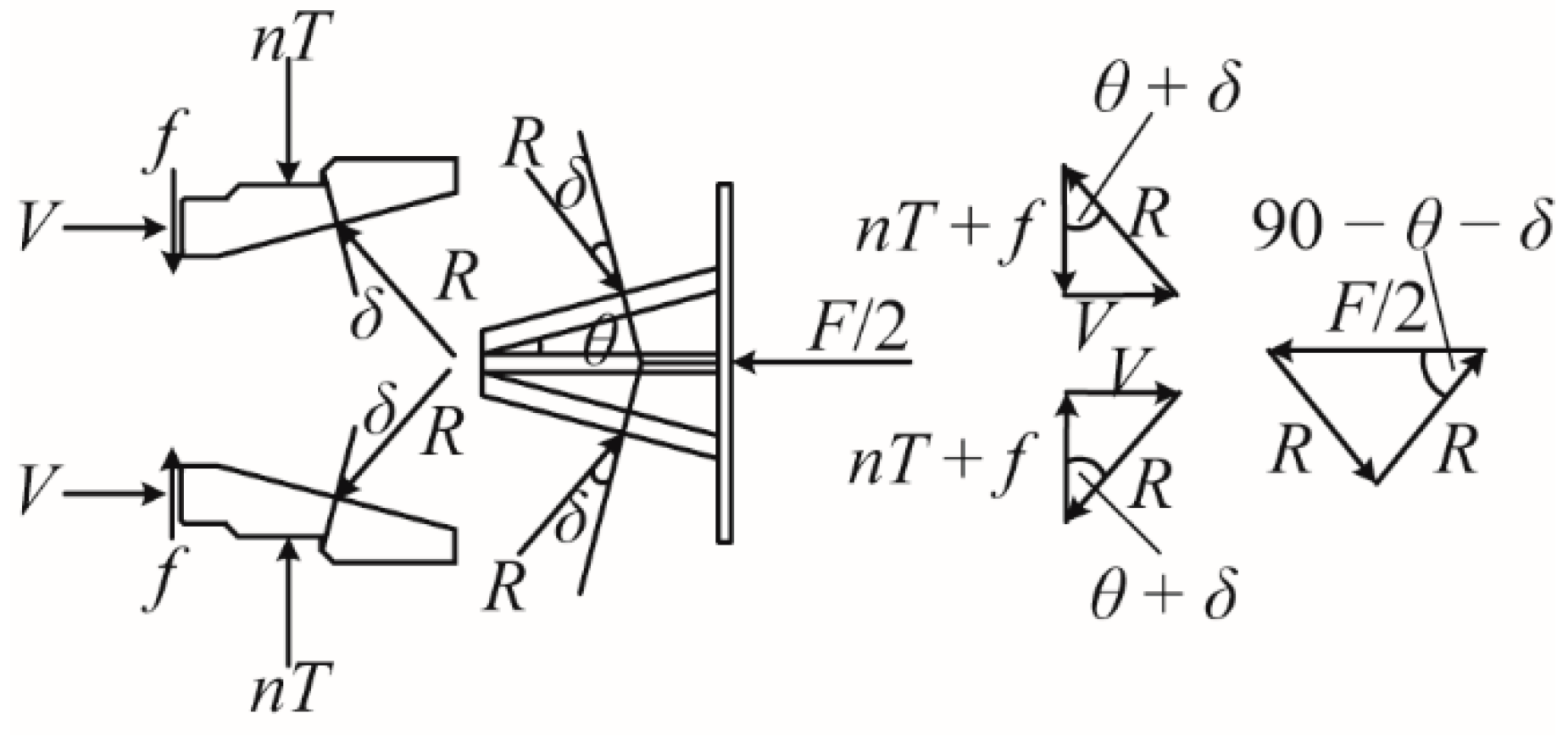
2.3. Working Mechanism
- F/2: the axial force transferred by the steel tube to each side.
- T: the tension provided by a high-strength bolt, where n is the number of the bolts on one side, and a BFW active joint contains 2n bolts.
- R: the resistance between the splints and the wedge seat.
- V: the supporting force between the splints and the base.
- f: the friction between the bottom of the splints and the base.
- δ: the steel friction angle, where μ is the steel static friction coefficient, and tan δ = μ.
- θ: the angle between the direction of the axial force F/2 and the direction of the contact surface, where the contact surface is between the wedge seat and the splints.
- Vi—the volume of a component of the BFW active joint.
- Ad—the cross-sectional area of the column.
- h—the length of the BFW active joint.
- m—the number of the components of the BFW active joint.
- i—the component number.
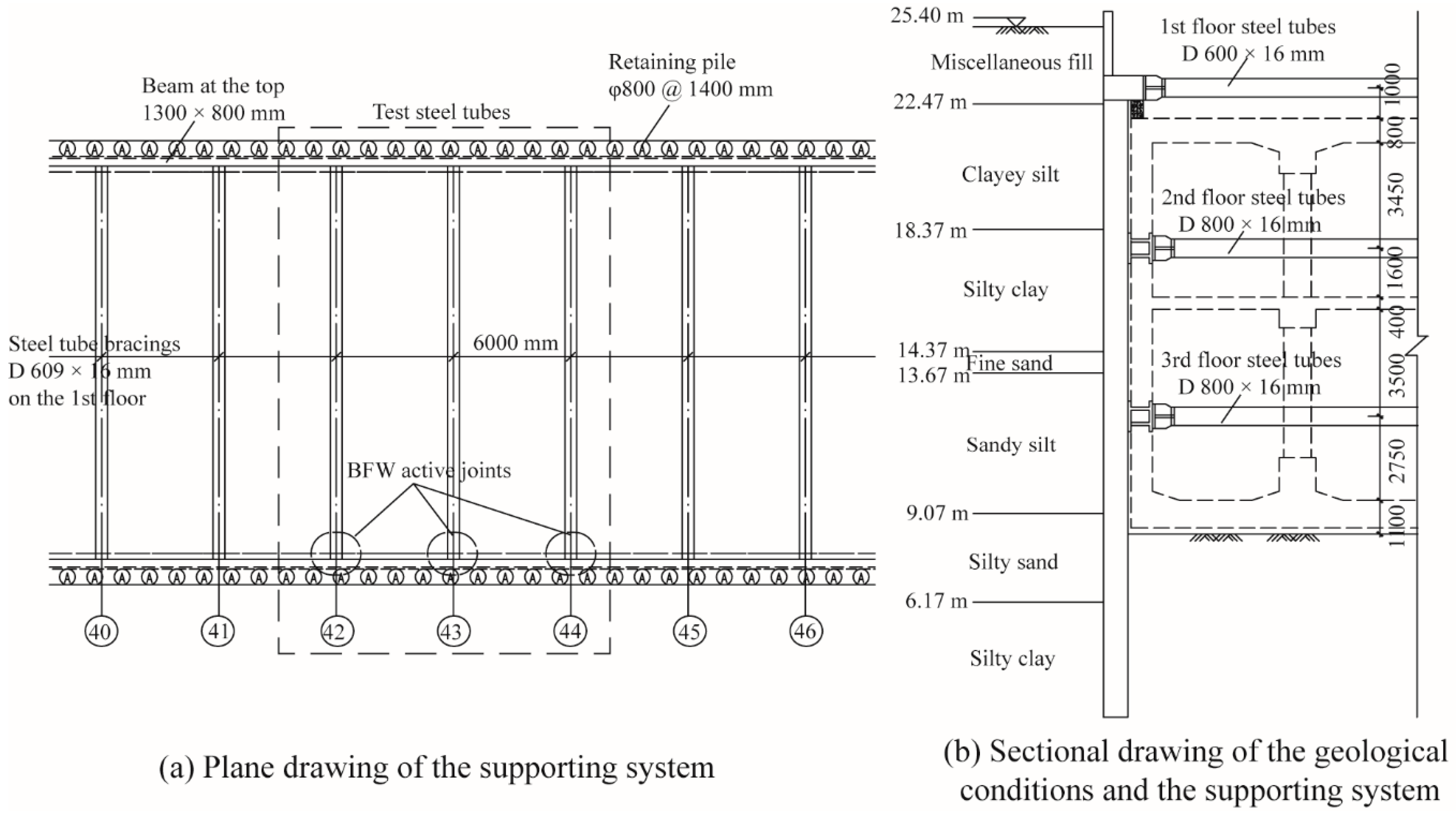
3. Field Operation Tests
3.1. Design of Specimens
3.2. Test Site and Preparation
3.3. Operation Process
- (1)
- The gap was filled with fillers like steel wedges or cement, as shown in Figure 8a. It should be noted that the end plate near the splints must be kept parallel to the vertical plate of the buried tray. If there exists an angle between the two plates, it is necessary to fill the gap with fillers like steel wedges or cement.
- (2)
- The bolts were tightened step-by-step in the process of the jack force application, as shown in Figure 8b. The jack force application consists of three loading stages using a jack pressure gauge, i.e., 5 MPa, 12 MPa, and 25 MPa. Six bolts were fastened one-by-one on each stage. The jack force application was stopped when the loading using the jack pressure gauge reached 25 MPa which met the intended pre-axial force. All the bolts should be fastened at the same level, and the fastened torque should be 4111 Nm. No space should be left between the wedge seat and the splints.
- (3)
- The jack was unloaded and moved away, as shown in Figure 8c, and the BFW active joint started working. The earth pressure transmitted by the lateral walls of the foundation pit were borne by the steel tube bracings with the BFW active joints. The BFW active joints were connected with steel tubes in a series connection and they bore the same axial force as the steel tubes.
- (4)
- The steel tube bracing with the BFW active joint was demolished. The bolts were loosened after the axial force was applied by the jack, as shown in Figure 8d. Then, the BFW active joints were shortened and they were moved out of the pit with the steel tube bracings.
3.4. Analysis of the Field Operation Results
- (a)
- It is important to weld the BFW active joint concentrically with the short steel tube in the pre-processing at the test site.
- (b)
- The total length of the BFW active joint and steel tube is a little smaller than the excavated width of the foundation pit, so a gap of 30–130 mm will be formed. At this time, since the BFW active joint is in the zero-extension state, it can be extended to eliminate the gap during jack force application.
- (c)
- It is necessary to keep the contact surface of the purlin or the diaphragm retaining walls flat and vertical.
- (d)
- It is important to ensure that the loading process is uniform and slow, and that the bolts are tightened to the same tightening torque (4111 Nm for the M39 type). Both the whole loading process and tightening process should be divided into three steps, step-by-step, which can provide a good loading effect. The bolts need to finally be fastened to a tightening torque of 4111 Nm.
- (e)
- The jack is used to supplement the axial force and then the bolts will be tightened according to the above steps once the axial force loss occurs with the variation of soil excavation and earth pressure change.
4. Laboratory Axial Compression Experiments
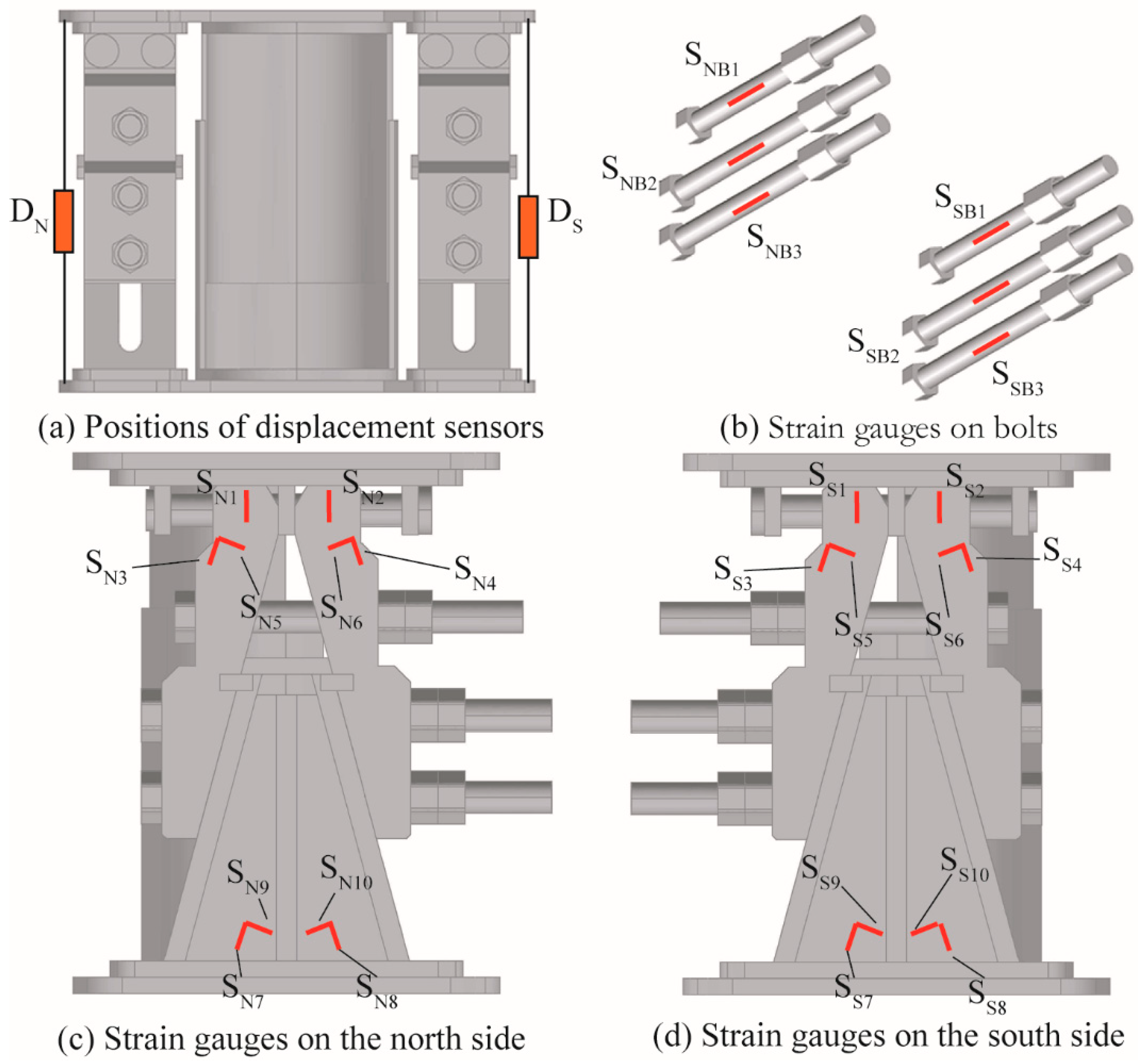
4.1. Measurement Scheme of Displacements and Strains
4.2. Loading Schemes
- (a)
- The specimens were loaded from 0 kN to 500 kN and unloaded back to 0 kN, where the loading rate was 30 kN/min. Gaps in the specimens could be closed in this stage of preloading.
- (b)
- Formal loading and data collection were applied under force control, where the loading rate was 50 kN/min. The loading started from 0 kN. When the bearing capacity of the specimens could no longer rise or had a large deformation or failure, loading was stopped. Then, unloading was slowed down and the test ended.
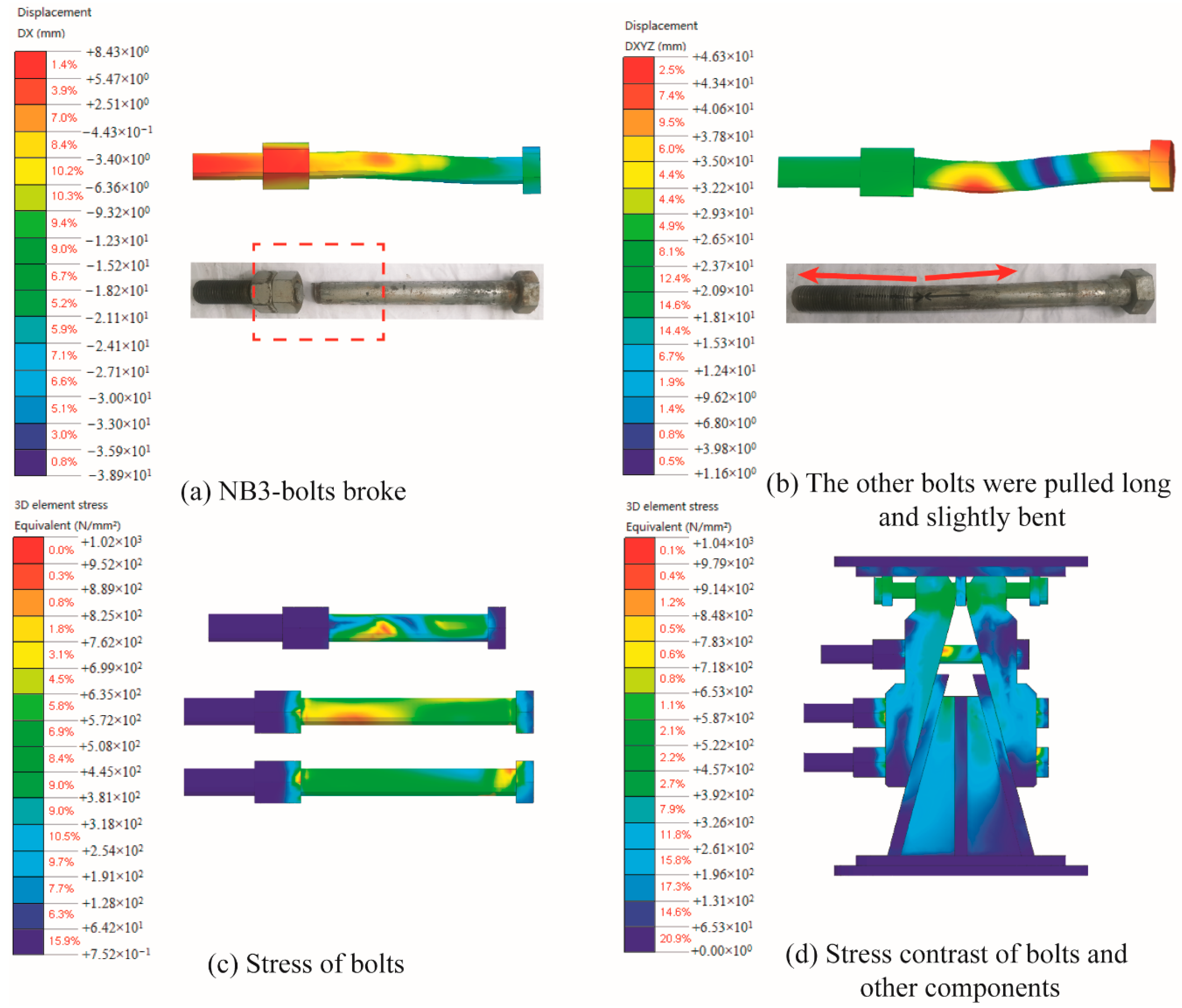
4.3. Experimental Phenomena and Failure Modes
4.4. Bearing Capacities and Stiffness
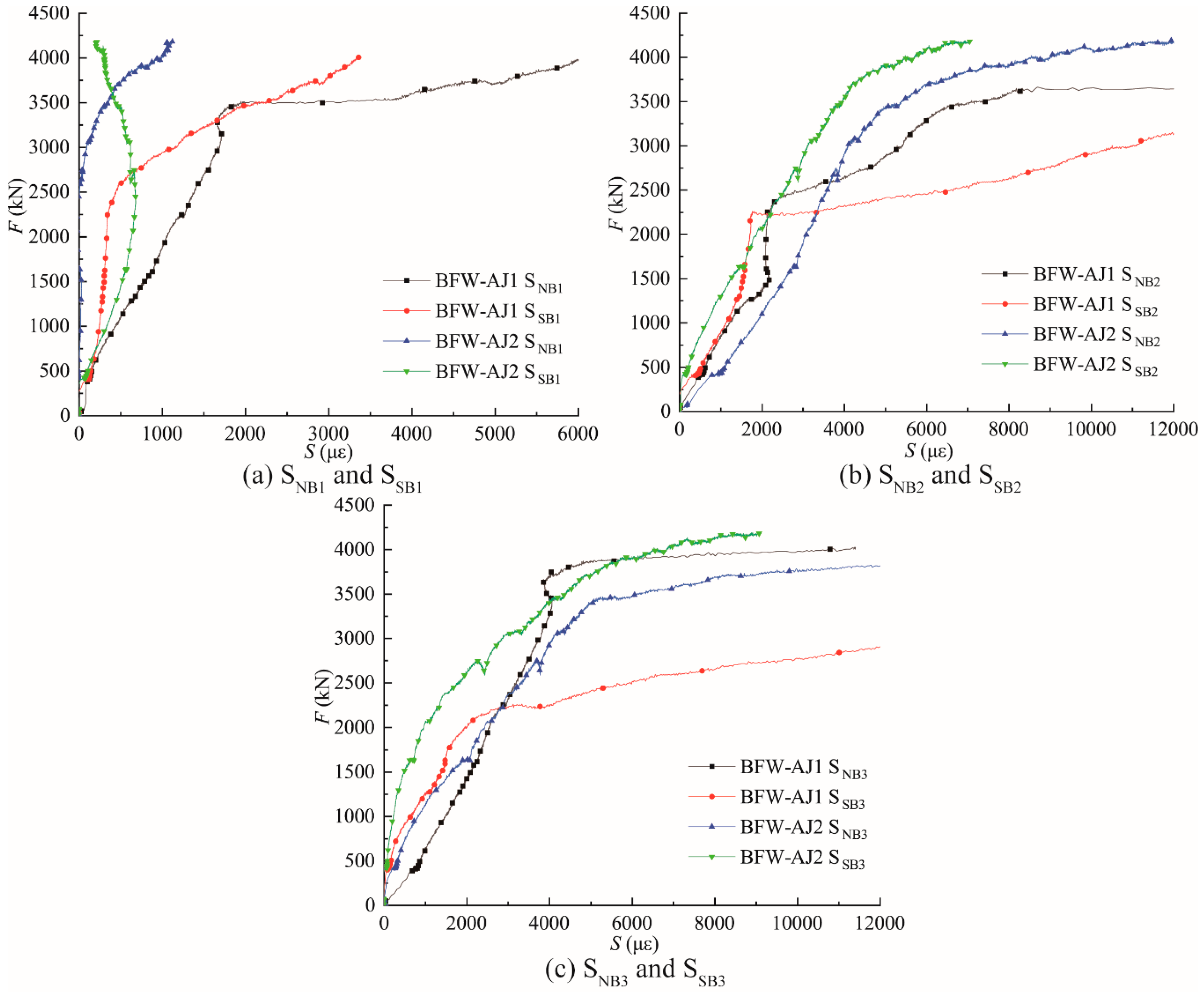
4.5. Strain Distributions
5. Numerical Simulation and Validation
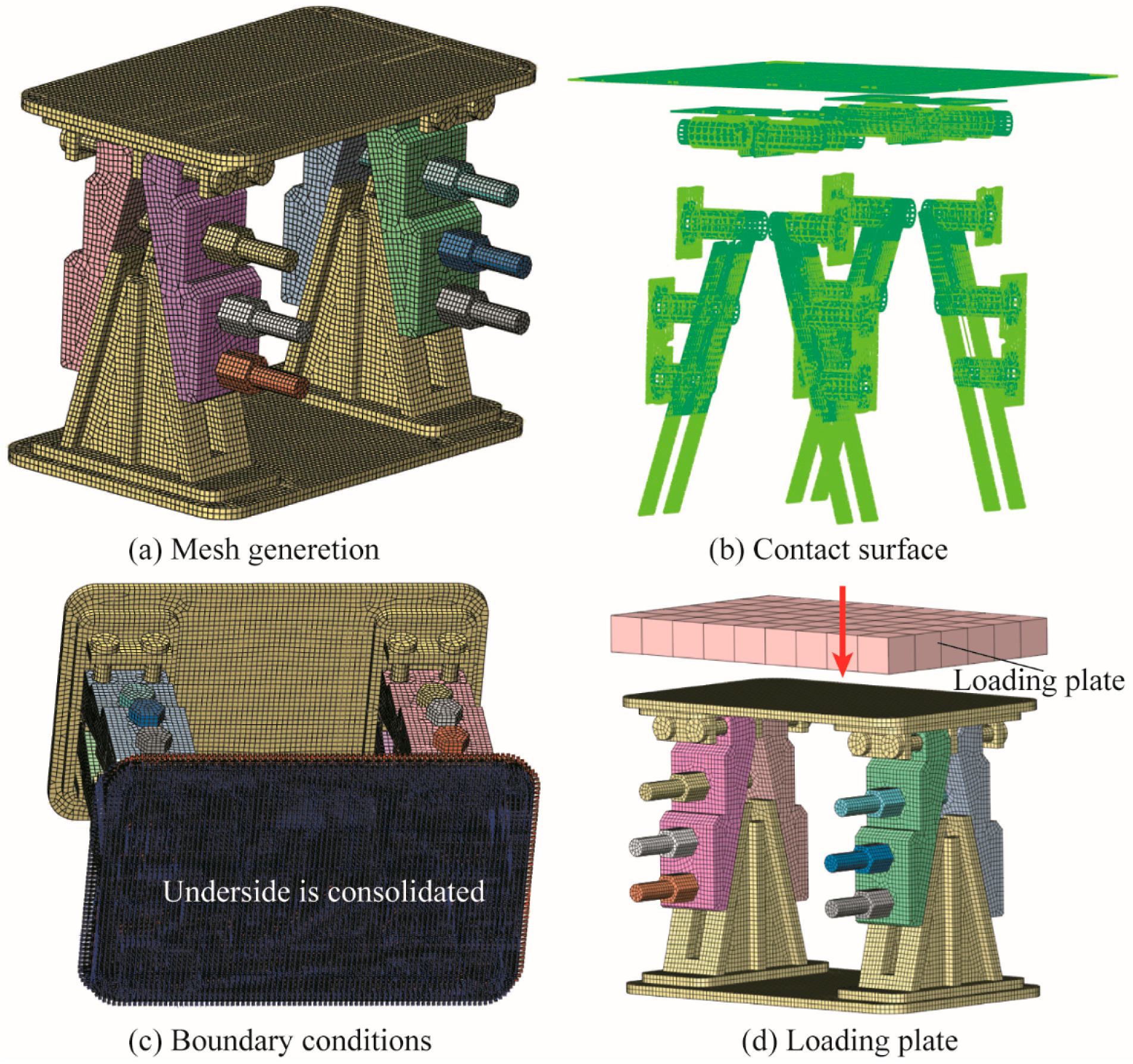
5.1. Numerical Model
5.2. Comparisons of Numerical and Experimental Results
5.2.1. Failure Modes
5.2.2. Load–Displacement Curves
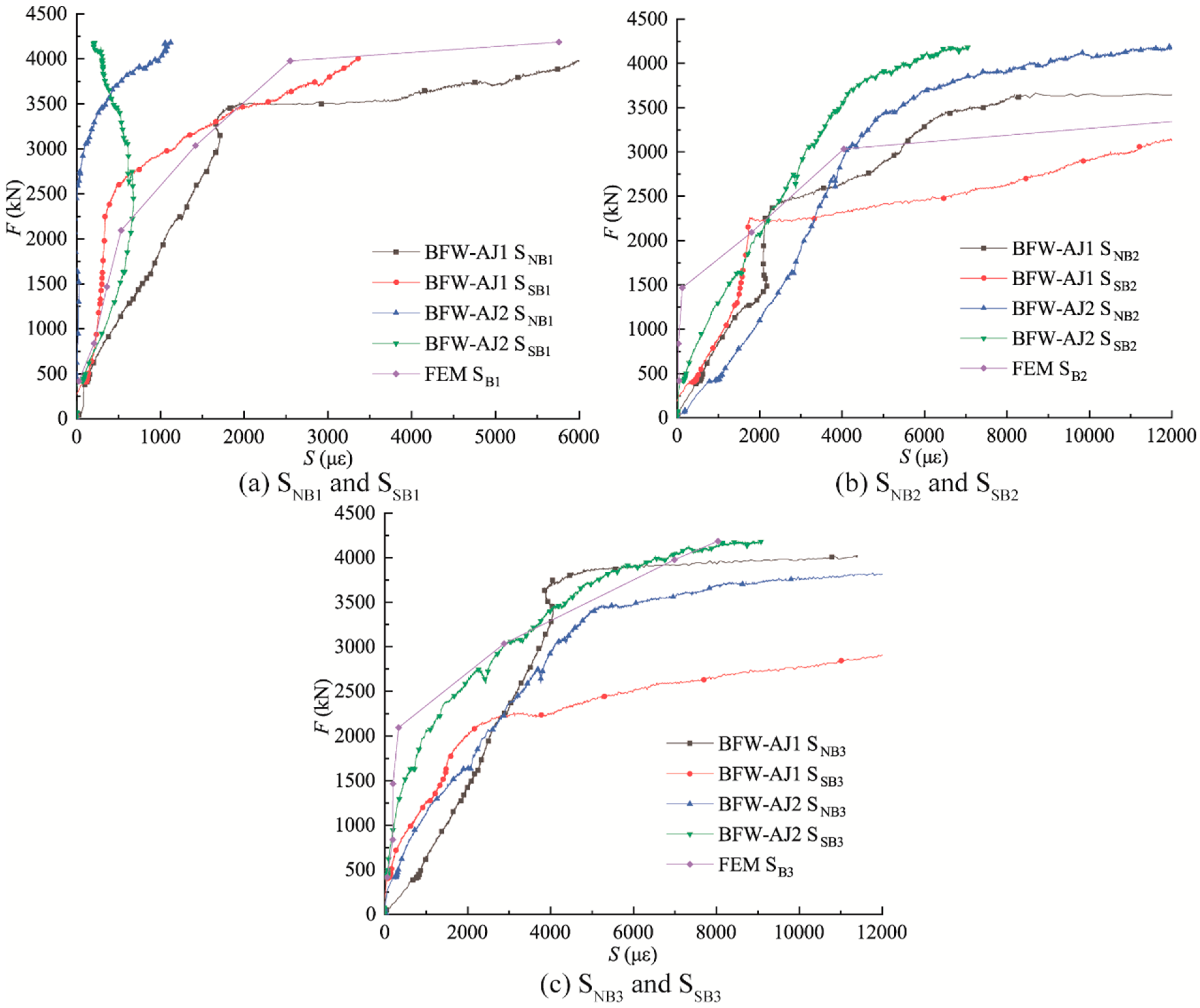
5.2.3. Load–Strain Curves
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tan, Y.; Li, M. Measured performance of a 26 m deep top-down excavation in downtown Shanghai. Can. Geotech. J. 2011, 48, 704–719. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, M.; Li, P.; Lu, D. An innovative bolt fastener for steel tube bracing in deep excavations. In Proceedings of the China-Europe Conference on Geotechnical Engineering, Vienna, Austria, 13–16 August 2018. [Google Scholar]
- El-Sawy, K.M. Inelastic stability of liners of cylindrical conduits with local imperfection under external pressure. Tunn. Undergr. Space Technol. 2013, 33, 98–110. [Google Scholar] [CrossRef]
- Feng, R.; Lin, J.; Mou, X. Experiments on hybrid tubular K-joints with circular braces and square chord in stainless steel. Eng. Struct. 2019, 190, 52–65. [Google Scholar] [CrossRef]
- Lam, E.S.S.; Li, B.; Xue, Z.H.; Leung, K.T.; Lam, J.Y.K. Experimental studies on reinforced concrete interior beam-column joints strengthened by unsymmetrical chamfers. Eng. Struct. 2019, 191, 575–582. [Google Scholar] [CrossRef]
- Puzrin, A.M.; Alonso, E.E.; Pinyol, N.M. Braced excavation collapse: Nicoll Highway, Singapore. In Geomechanics of Failures; Springer: Dordrecht, The Netherlands, 2010; pp. 151–181. [Google Scholar]
- Endicott, J. Lessons learned from the collapse of the Nicoll Highway in Singapore April 2004; IABSE Symposium Report; International Association for Bridge and Structural Engineering: Zurich, Switzerland, 2013; Volume 101, pp. 1–6. [Google Scholar]
- Li, H.; Wang, G. Causes and suggestion on deep foundation excavation accident in some. Constr. Technol. 2010, 39, 57. [Google Scholar]
- Zhang, K.; Li, J. Accident analysis for “08.11.15” foundation pit collapse of Xianghu station of Hangzhou metro. Chin. J. Geotech. Eng. 2010, 32, 338–342. [Google Scholar]
- Costa, R.; Valdez, J.; Oliveira, S.; da Silva, L.S.; Bayo, E. Experimental behaviour of 3D end-plate beam-to-column bolted steel joints. Eng. Struct. 2019, 188, 277–289. [Google Scholar] [CrossRef]
- Gil-Martín, L.M.; Hernández-Montes, E.; Shin, M.; Aschheim, M. Developments in excavation bracing systems. Tunn. Undergr. Space Technol. 2012, 31, 107–116. [Google Scholar] [CrossRef]
- Ataei, A.; Bradford, M.A.; Valipour, H.R.; Liu, X. Experimental study of sustainable high strength steel flush end plate beam-to-column composite joints with deconstructable bolted shear connectors. Eng. Struct. 2016, 123, 124–140. [Google Scholar] [CrossRef]
- Grimsmo, E.L.; Clausen, A.H.; Langseth, M.; Aalberg, A. An experimental study of static and dynamic behaviour of bolted end-plate joints of steel. Int. J. Impact Eng. 2015, 85, 132–145. [Google Scholar] [CrossRef]
- Iwicki, P.; Wójcik, M.; Tejchman, J. Failure of cylindrical steel silos composed of corrugated sheets and columns and repair methods using a sensitivity analysis. Eng. Fail. Anal. 2011, 18, 2064–2083. [Google Scholar] [CrossRef]
- Peng, L.; Guo, X.; Huang, Z.; Xiong, Z.; Yang, S. Experimental studies on behaviour of bolted ball-cylinder joints under axial force. Steel Compos. Struct. 2016, 21, 137–156. [Google Scholar]
- Guo, X.; Huang, Z.; Xiong, Z.; Yang, S.; Peng, L. Numerical studies on behaviour of bolted ball-cylinder joint under axial force. Steel Compos. Struct. 2016, 20, 1323–1343. [Google Scholar] [CrossRef]
- Zeng, Q.; Guo, X.; Huang, Z.; Zong, S. Uniaxial compression bearing capacity of bolted ball-cylinder joint. Eng. Struct. 2019, 183, 976–986. [Google Scholar] [CrossRef]
- Guo, X.; Xiong, Z.; Luo, Y.; Qiu, L.; Liu, J. Experimental investigation on the semi-rigid behaviour of aluminium alloy gusset joints. Thin Walled Struct. 2015, 87, 30–40. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; L, J. Field test verification of new flexible head steel support and deep foundation excavation support effect. Constr. Technol. 2019, 48, 72–77. [Google Scholar]
- Zhang, M.; Xie, Z.; Liu, Y. Mechanical properties and improvement measures of the active node in steel braced foundation pit engineering for subway. J. Beijing Jiaotong Univ. 2019, 43, 66–73. [Google Scholar]
- Zhang, M.; Yang, M.; Wang, X. Innovative study on active node of steel tube bracing system for braced excavations. Eng. Mech. 2018, 35, 88–94. [Google Scholar]
- Editorial Group. GB 50017-2017, Code for Design of Steel Structures; Ministry of Housing and Urbanrural Development of the People’s Republic of China: Beijing, China; General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2017.
- Zhang, M.; Yang, M.; Li, P. Field application and experimental verification of dismountable double-section BFW active nodes for braced excavations. In Proceedings of the 13th Chinese National Conference on Soil Mechanics and Geotechnical Engineering (CNCSMGE), Tianjin, China, 18–21 July 2019; Volume 2, pp. 437–446. [Google Scholar]
- Editorial Group. GB T699-2015, Quality Carbon Structure Steels; General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China; Standardization Administration of the People’s Republic of China: Beijing, China, 2015.
- Cheng, D. Handbook of Mechanical Design; Chemical Industry Press: Beijing, China, 2016. [Google Scholar]
- Sultan, A.; John, P.; Nikolaos, N. Time-dependent behaviour of cracked, partially bonded reinforced concrete beams under repeated and sustained loads. Eng. Struct. 2018, 163, 267–280. [Google Scholar]
- Li, P.; Zou, H.; Wang, F.; Xiong, H. An analytical mechanism of limit support pressure on cutting face for deep tunnels in the sand. Comput. Geotech. 2020, 119, 103372. [Google Scholar] [CrossRef]
- Zhang, M.; Li, S.; Li, P. Numerical analysis of ground displacement and segmental stress and influence of yaw excavation loadings for a curved shield tunnel. Comput. Geotech. 2020, 118, 103325. [Google Scholar] [CrossRef]




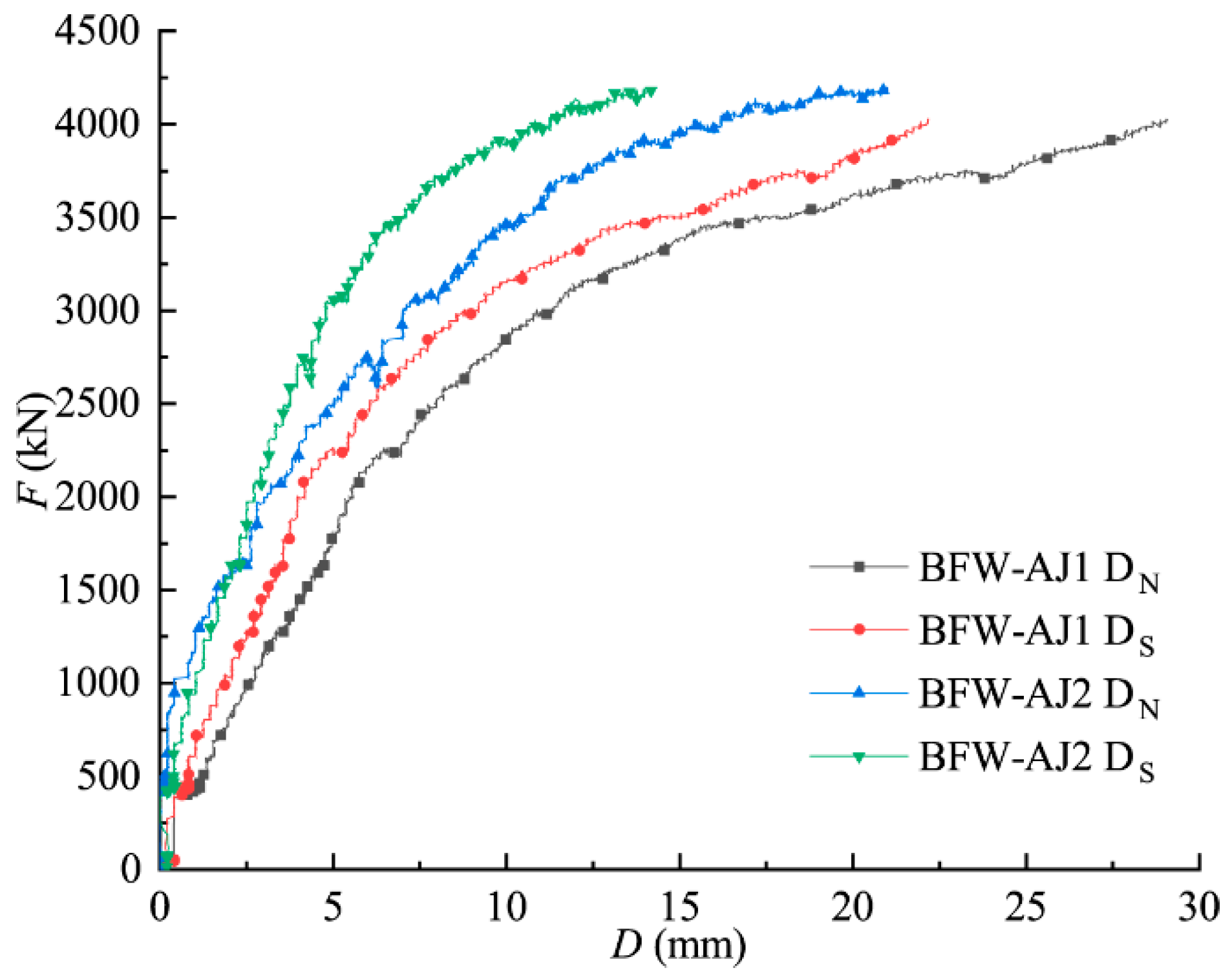
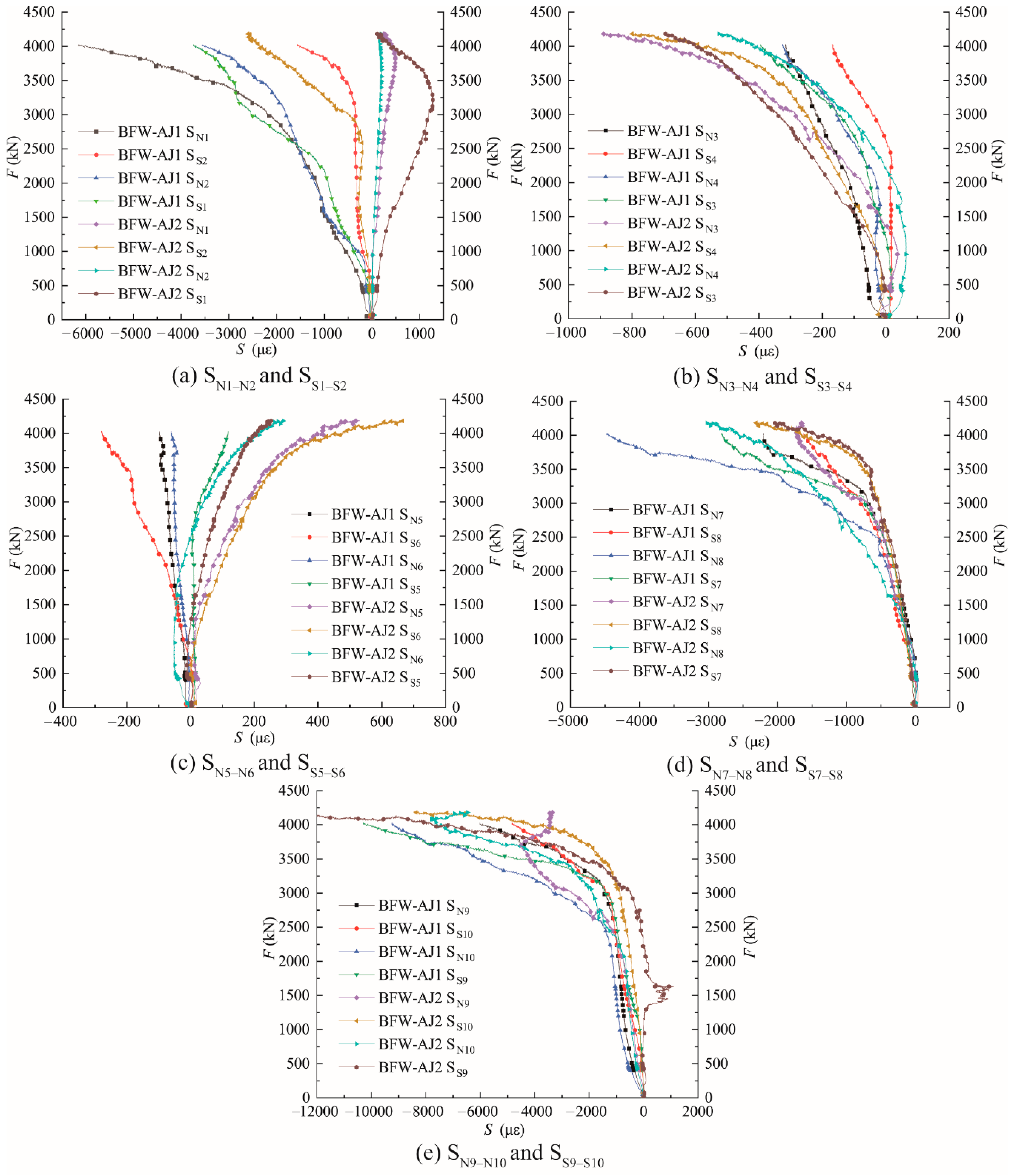
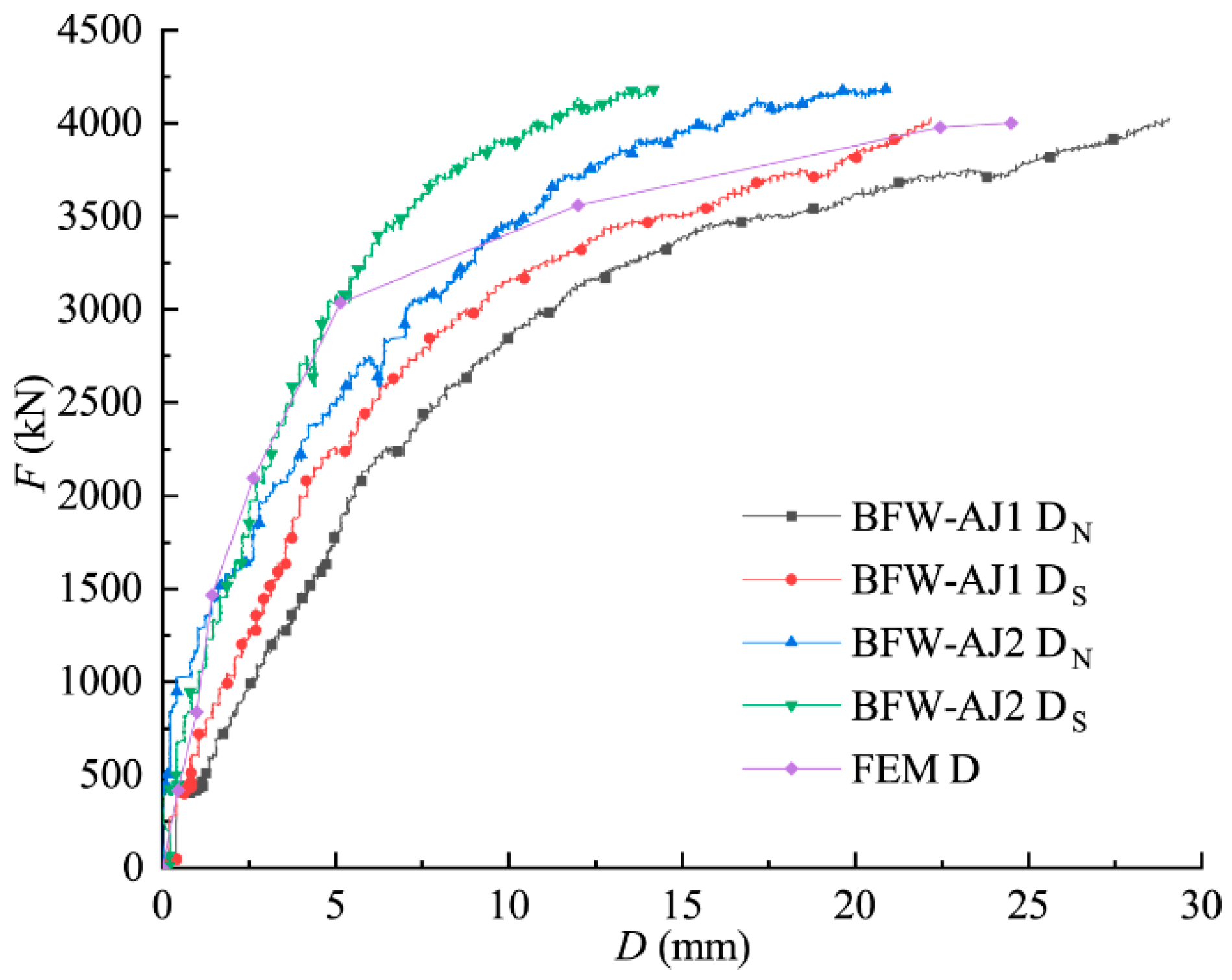
| Specimen | BCmax of EP (kN) | Δe (mm) | BCult (kN) | Δu (mm) | YScon (kN) | Stiffness (kN/mm) |
|---|---|---|---|---|---|---|
| BFW-AJ1 | 2625 | 8.87 | 4021 | 26.76 | 2952 | 295.9 |
| BFW-AJ2 | 3065 | 8.67 | 4195 | 17.57 | 3376 | 353.5 |
| High-Strength Bolts | Other Components | |
|---|---|---|
| Young’s modulus E | 2.06 × 105 N/mm2 | 2.06 × 105 N/mm2 |
| Gravimetric density | 7.70 × 10−5 N/mm3 | 7.70 × 10−5 N/mm3 |
| Poisson ratio ν | 0.3 | 0.3 |
| Constitutive model | von Mises | von Mises |
| Initial yield stress fy | 355 N/mm2 | 900 N/mm2 |
| Ultimate yield stress fu | 600 N/mm2 | 1080 N/mm2 |
| No. | Master Surface to Slave Surface | Type |
|---|---|---|
| 1 | Wedge seat to splints | Surface-to-surface |
| 2 | Splints’ heels to base | Surface-to-surface |
| 3 | Splints to bolts | Surface-to-surface |
| 4 | Splints to polish round rods | Surface-to-surface |
| 5 | Base to polish round rods | Surface-to-surface |
| 6 | Loading plate to end plate | Surface-to-surface |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Yang, M.; Li, P.; Gao, Y. Mechanical Behaviors of a Symmetrical Bolt Fasten Wedge Active Joint for Braced Excavations. Symmetry 2020, 12, 140. https://doi.org/10.3390/sym12010140
Zhang M, Yang M, Li P, Gao Y. Mechanical Behaviors of a Symmetrical Bolt Fasten Wedge Active Joint for Braced Excavations. Symmetry. 2020; 12(1):140. https://doi.org/10.3390/sym12010140
Chicago/Turabian StyleZhang, Mingju, Meng Yang, Pengfei Li, and Yunhao Gao. 2020. "Mechanical Behaviors of a Symmetrical Bolt Fasten Wedge Active Joint for Braced Excavations" Symmetry 12, no. 1: 140. https://doi.org/10.3390/sym12010140
APA StyleZhang, M., Yang, M., Li, P., & Gao, Y. (2020). Mechanical Behaviors of a Symmetrical Bolt Fasten Wedge Active Joint for Braced Excavations. Symmetry, 12(1), 140. https://doi.org/10.3390/sym12010140





