On the Crossing Numbers of the Joining of a Specific Graph on Six Vertices with the Discrete Graph

Abstract

In the paper, we extend known results concerning crossing numbers of join products of small graphs of order six with discrete graphs. The crossing number of the join product $G^{\ast }+D_n$ for the graph $G^{\ast }$ on six vertices consists of one vertex which is adjacent with three non-consecutive vertices of the 5-cycle. The proofs were based on the idea of establishing minimum values of crossings between two different subgraphs that cross the edges of the graph $G^{\ast }$ exactly once. These minimum symmetrical values are described in the individual symmetric tables.

1. Introduction

An investigation on the crossing number of graphs is a classical and very difficult problem. Garey and Johnson [1] proved that this problem is NP-complete. Recall that the exact values of the crossing numbers are known for only a few families of graphs. The purpose of this article is to extend the known results concerning this topic. In this article, we use the definitions and notation of the crossing numbers of graphs presented by Klešč in [2]. Kulli and Muddebihal [3] described the characterization for all pairs of graphs which join product of a planar graph. In the paper, some parts of proofs are also based on Kleitman’s result [4] on the crossing numbers for some complete bipartite graphs. More precisely, he showed that

$$\mathrm{cr}\left(K_{m,n}\right)=⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋,\mathrm{for}m\le 6.$$

Again, by Kleitman’s result [4], the crossing numbers for the join of two different paths, the join of two different cycles, and also for the join of path and cycle, were established in [2]. Further, the exact values for crossing numbers of $G+D_n$ and of $G+P_n$ for all graphs G on less than five vertices were determined in [5]. At present, the crossing numbers of the graphs $G+D_n$ are known only for few graphs G of order six in [6,7,8,9]. In all these cases, the graph G is usually connected and includes at least one cycle.

The methods in the paper mostly use the combinatorial properties of cyclic permutations. For the first time, the idea of configurations is converted from the family of subgraphs which do not cross the edges of the graph $G^{\ast }$ of order six onto the family of subgraphs whose edges cross the edges of $G^{\ast }$ just once. According to this algebraic topological approach, we can extend known results for the crossing numbers of new graphs. Some of the ideas and methods were used for the first time in [10]. In [6,8,9], some parts of proofs were done with the help of software which is described in detail in [11]. It is important to recall that the methods presented in [5,7,12] do not suffice to determine the crossing number of the graph $G^{\ast }+D_n$. Also in this article, some parts of proofs can be simplified by utilizing the work of the software that generates all cyclic permutations in [11]. Its C++ version is located also on the website http://web.tuke.sk/fei-km/coga/, and the list with all short names of 120 cyclic permutations of six elements have already been collected in Table 1 of [8].

2. Cyclic Permutations and Corresponding Configurations of Subgraphs

Let $G^{\ast }$ be the connected graph on six vertices consisting of one vertex which is adjacent with three non-consecutive vertices of the 5-cycle. We consider the join product of the graph $G^{\ast }$ with the discrete graph $D_n$ on n vertices. It is not difficult to see that the graph $G^{\ast }+D_n$ consists of just one copy of the graph $G^{\ast }$ and of n vertices $t_1,\dots ,t_n$, where any vertex $t_j$, $j=1,\dots ,n$, is adjacent to every vertex of the graph $G^{\ast }$. Let $T^j$, $j=1,\dots ,n$, denote the subgraph which is uniquely induced by the six edges incident with the fixed vertex $t_j$. This means that the graph $T^1\cup \cdots \cup T^n$ is isomorphic with $K_{6,n}$ and

$$G^{\ast }+D_n=G^{\ast }\cup K_{6,n}=G^{\ast }\cup \left({\displaystyle \bigcup _{j=1}^n}{T}^j\right).$$

(1)

In the paper, the definitions and notation of the cyclic permutations and of the corresponding configurations of subgraphs for a good drawing D of the graph $G^{\ast }+D_n$ presented in [8] are used. The rotation ${\mathrm{rot}}_D\left(t_j\right)$ of a vertex $t_j$ in the drawing D is the cyclic permutation that records the (cyclic) counter-clockwise order in which the edges leave $t_j$, see [10]. We use the notation $\left(123456\right)$ if the counterclockwise order of the edges incident with the vertex $t_j$ is $t_j{v}_1$, $t_j{v}_2$, $t_j{v}_3$, $t_j{v}_4$, $t_j{v}_5$, and $t_j{v}_6$. Recall that a rotation is a cyclic permutation. Moreover, as we have already mentioned, we separate all subgraphs $T^j$, $j=1,\dots ,n$, of the graph $G^{\ast }+D_n$ into three mutually-disjoint families depending on how many times the edges of $G^{\ast }$ are crossed by the edges of the considered subgraph $T^j$ in D. This means, for $j=1,\dots ,n$, let $R_D=\{T^j:{\mathrm{cr}}_D(G^{\ast },T^j)=0\}$ and $S_D=\{T^j:{\mathrm{cr}}_D(G^{\ast },T^j)=1\}$. The edges of $G^{\ast }$ are crossed by each other subgraph $T^j$ at least twice in D. For $T^j\in R_D\cup S_D$, let $F^j$ denote the subgraph $G^{\ast }\cup T^j$, $j\in \{1,2,\dots ,n\}$, of $G^{\ast }+D_n$, and let $D\left(F^j\right)$ be its subdrawing induced by D.

If we would like to obtain an optimal drawing D of $G^{\ast }+D_n$, then the set $R_D\cup S_D$ must be nonempty provided by the arguments in Theorem 1. Thus, we only consider drawings of the graph $G^{\ast }$ for which there is a possibility of obtaining a subgraph $T^j\in R_D\cup S_D$. Since the graph $G^{\ast }$ contains the 6-cycle as a subgraph (for brevity, we can write $C_6\left(G^{\ast }\right)$), we have to assume only crossings between possible subdrawings of the subgraph $C_6\left(G^{\ast }\right)$ and two remaining edges of $G^{\ast }$. Of course, the edges of the cycle $C_6\left(G^{\ast }\right)$ can cross themselves in the considered subdrawings. The vertex notation of $G^{\ast }$ will be substantiated later in all drawings in Figure 1.

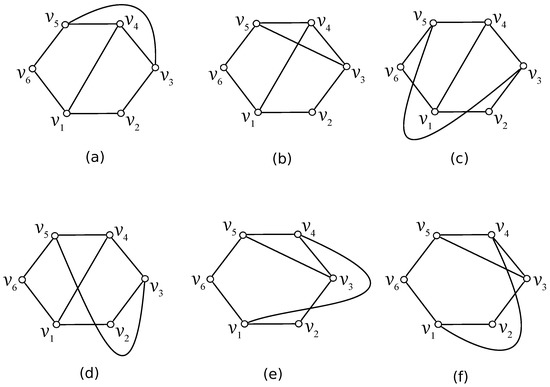
Figure 1. Six possible drawings of $G^{\ast }$ with no crossing among edges of $C_6\left(G^{\ast }\right)$. (a): the planar drawing of $G^{\ast }$; (b): the drawing of $G^{\ast }$ with ${\mathrm{cr}}_D\left(G^{\ast }\right)=1$ and without crossing on edges of $C_6\left(G^{\ast }\right)$; (c): the drawing of $G^{\ast }$ only with two crossings on edges of $C_6\left(G^{\ast }\right)$; (d): the drawing of $G^{\ast }$ with ${\mathrm{cr}}_D\left(G^{\ast }\right)=2$ and with one crossing on edges of $C_6\left(G^{\ast }\right)$; (e): the drawing of $G^{\ast }$ only with one crossing on edges of $C_6\left(G^{\ast }\right)$; (f): the drawing of $G^{\ast }$ with ${\mathrm{cr}}_D\left(G^{\ast }\right)=2$ and with one crossing on edges of $C_6\left(G^{\ast }\right)$.

First, assume a good drawing D of $G^{\ast }+D_n$ in which the edges of $G^{\ast }$ do not cross each other. In this case, without loss of generality, we can consider the drawing of $G^{\ast }$ with the vertex notation like that in Figure 1a. Clearly, the set $R_D$ is empty. Our aim is to list all possible rotations ${\mathrm{rot}}_D\left(t_j\right)$ which can appear in D if the edges of $G^{\ast }$ are crossed by the edges of $T^j$ just once. There is only one possible subdrawing of $F^j\setminus \left\{v_4\right\}$ represented by the rotation $\left(16532\right)$, which yields that there are exactly five ways of obtaining the subdrawing of $G\cup T^j$ depending on which edge of the graph $G^{\ast }$ can be crossed by the edge $t_j{v}_4$. We denote these five possibilities by ${\mathcal{A}}_k$, for $k=1,\dots ,5$. For our considerations over the number of crossings of $G^{\ast }+D_n$, it does not play a role in which of the regions is unbounded. So we can assume the drawings shown in Figure 2. Thus, the configurations ${\mathcal{A}}_1$, ${\mathcal{A}}_2$, ${\mathcal{A}}_3$, ${\mathcal{A}}_4$, and ${\mathcal{A}}_5$ are represented by the cyclic permutations $\left(165324\right)$, $\left(165432\right)$, $\left(146532\right)$, $\left(165342\right)$, and $\left(164532\right)$, respectively. Of course, in a fixed drawing of the graph $G^{\ast }+D_n$, some configurations from $\mathcal{M}=\{{\mathcal{A}}_1,{\mathcal{A}}_2,{\mathcal{A}}_3,{\mathcal{A}}_4,{\mathcal{A}}_5\}$ need not appear. We denote by ${\mathcal{M}}_D$ the set of all configurations that exist in the drawing D belonging to the set $\mathcal{M}$.

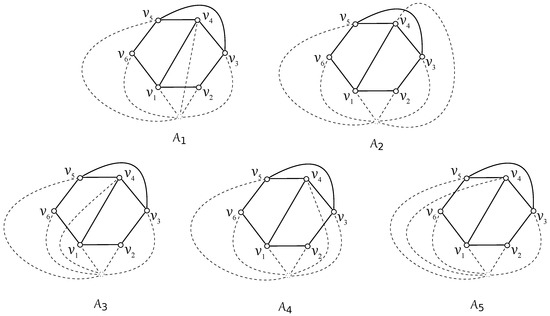
Figure 2. Drawings of five possible configurations from $\mathcal{M}$ of the subgraph $F^j$.

Recall that we are able to extend the idea of establishing minimum values of crossings between two different subgraphs onto the family of subgraphs which cross the edges of $G^{\ast }$ exactly once. Let $\mathcal{X}$ and $\mathcal{Y}$ be the configurations from ${\mathcal{M}}_D$. We denote by ${\mathrm{cr}}_D(\mathcal{X}$ and $\mathcal{Y})$ the number of crossings in D between $T^i$ and $T^j$ for different $T^i,T^j\in S_D$ such that $F^i$ and $F^j$ have configurations $\mathcal{X}$ and $\mathcal{Y}$, respectively. Finally, let $\mathrm{cr}(\mathcal{X},\mathcal{Y})=\min \left\{{\mathrm{cr}}_D(\mathcal{X},\mathcal{Y})\right\}$ over all possible good drawings of $G^{\ast }+D_n$ with $\mathcal{X},\mathcal{Y}\in {\mathcal{M}}_D$. Our aim is to determine $\mathrm{cr}(\mathcal{X},\mathcal{Y})$ for all such pairs $\mathcal{X},\mathcal{Y}\in \mathcal{M}$. In particular, the configurations ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$ are represented by the cyclic permutations $\left(165324\right)$ and $\left(165432\right)$, respectively. Since the minimum number of interchanges of adjacent elements of $\left(165324\right)$ required to produce cyclic permutation $\left(165432\right)$ is two, we need at least four interchanges of adjacent elements of $\left(165432\right)$ to produce cyclic permutation $\overline{\left(165324\right)}=\left(142356\right)$. (Let $T^x$ and $T^y$ be two different subgraphs represented by their $\mathrm{rot}\left(t_x\right)$ and $\mathrm{rot}\left(t_y\right)$ of length m, $m\ge 3$. If the minimum number of interchanges of adjacent elements of $\mathrm{rot}\left(t_x\right)$ required to produce $\mathrm{rot}\left(t_y\right)$ is at most z, then ${\mathrm{cr}}_D(T^x,T^y)\ge ⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋-z$. Details have been worked out by Woodall [13].) So any subgraph $T^j$ with the configuration ${\mathcal{A}}_2$ of $F^j$ crosses the edges of $T^i$ with the configuration ${\mathcal{A}}_1$ of $F^i$ at least four times; that is, $\mathrm{cr}({\mathcal{A}}_1,{\mathcal{A}}_2)\ge 4$. The same reasoning gives $\mathrm{cr}({\mathcal{A}}_1,{\mathcal{A}}_3)\ge 5$, $\mathrm{cr}({\mathcal{A}}_1,{\mathcal{A}}_4)\ge 5$, $\mathrm{cr}({\mathcal{A}}_1,{\mathcal{A}}_5)\ge 4$, $\mathrm{cr}({\mathcal{A}}_2,{\mathcal{A}}_3)\ge 4$, $\mathrm{cr}({\mathcal{A}}_2,{\mathcal{A}}_4)\ge 5$, $\mathrm{cr}({\mathcal{A}}_2,{\mathcal{A}}_5)\ge 5$, $\mathrm{cr}({\mathcal{A}}_3,{\mathcal{A}}_4)\ge 4$, $\mathrm{cr}({\mathcal{A}}_3,{\mathcal{A}}_5)\ge 5$, and $\mathrm{cr}({\mathcal{A}}_4,{\mathcal{A}}_5)\ge 4$. Clearly, also $\mathrm{cr}({\mathcal{A}}_i,{\mathcal{A}}_i)\ge 6$ for any $i=1,\dots ,5$. All resulting lower bounds for the number of crossings of two configurations from $\mathcal{M}$ are summarized in the symmetric Table 1 (here, ${\mathcal{A}}_k$ and ${\mathcal{A}}_l$ are configurations of the subgraphs $F^i$ and $F^j$, where $k,l\in \{1,2,3,4,5\}$).

Table 1. The necessary number of crossings between $T^i$ and $T^j$ for the configurations ${\mathcal{A}}_k$, ${\mathcal{A}}_l$.

-	${\mathcal{A}}_1$	${\mathcal{A}}_2$	${\mathcal{A}}_3$	${\mathcal{A}}_4$	${\mathcal{A}}_5$
${\mathcal{A}}_1$	6	4	5	5	4
${\mathcal{A}}_2$	4	6	4	5	5
${\mathcal{A}}_3$	5	4	6	4	5
${\mathcal{A}}_4$	5	5	4	6	4
${\mathcal{A}}_5$	4	5	5	4	6

Assume a good drawing D of the graph $G^{\ast }+D_n$ with just one crossing among edges of the graph $G^{\ast }$ (in which there is a possibility of obtaining of subgraph $T^j\in R_D\cup S_D$). At first, without loss of generality, we can consider the drawing of $G^{\ast }$ with the vertex notation like that in Figure 1b. Of course, the set $R_D$ can be nonempty, but our aim will be also to list all possible rotations ${\mathrm{rot}}_D\left(t_j\right)$ which can appear in D if the edges of $G^{\ast }$ are crossed by the edges of $T^j$ just once. Since the edges $v_1{v}_2$, $v_2{v}_3$, $v_1{v}_6$, and $v_5{v}_6$ of $G^{\ast }$ can be crossed by the edges $t_j{v}_3$, $t_j{v}_1$, $t_j{v}_5$, and $t_j{v}_1$, respectively, these four ways under our consideration can be denoted by ${\mathcal{B}}_k$, for $k=1,2,3,4$. Based on the aforementioned arguments, we assume the drawings shown in Figure 3.

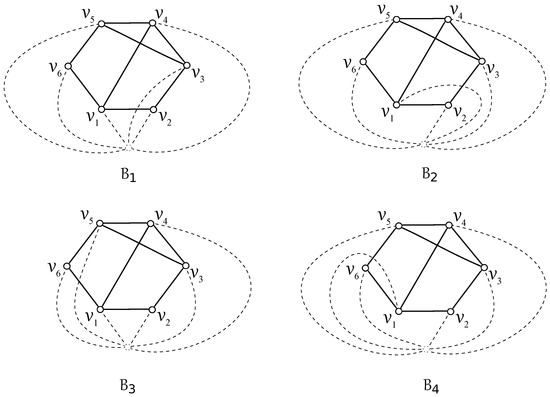
Figure 3. Drawings of four possible configurations from $\mathcal{N}$ of the subgraph $F^j$.

Thus, the configurations ${\mathcal{B}}_1$, ${\mathcal{B}}_2$, ${\mathcal{B}}_3$, and ${\mathcal{B}}_4$ are uniquely represented by the cyclic permutations $\left(165423\right)$, $\left(126543\right)$, $\left(156432\right)$, and $\left(154326\right)$, respectively. Because some configurations from $\mathcal{N}=\{{\mathcal{B}}_1,{\mathcal{B}}_2,{\mathcal{B}}_3,{\mathcal{B}}_4\}$ may not appear in a fixed drawing of $G^{\ast }+D_n$, we denote by ${\mathcal{N}}_D$ the subset of $\mathcal{N}$ consisting of all configurations that exist in the drawing D. Further, due to the properties of the cyclic rotations, we can easily verify that $\mathrm{cr}({\mathcal{B}}_i,{\mathcal{B}}_j)\ge 4$ for any $i,j\in \{1,2,3,4\}$, $i\ne j$. (Let us note that this idea was used for an establishing the values in Table 1)

In addition, without loss of generality, we can consider the drawing of $G^{\ast }$ with the vertex notation like that in Figure 1e. In this case, the set $R_D$ is also empty. Hence, our aim is to list again all possible rotations ${\mathrm{rot}}_D\left(t_j\right)$ which can appear in D if $T^j\in S_D$. Since there is only one subdrawing of $F^j\setminus \left\{v_3\right\}$ represented by the rotation $\left(16542\right)$, there are four ways to obtain the subdrawing of $F^j$ depending on which edge of $G^{\ast }$ is crossed by the edge $t_j{v}_3$. These four possibilities under our consideration are denoted by ${\mathcal{E}}_k$, for $k=1,2,3,4$. Again, based on the aforementioned arguments, we assume the drawings shown in Figure 4.

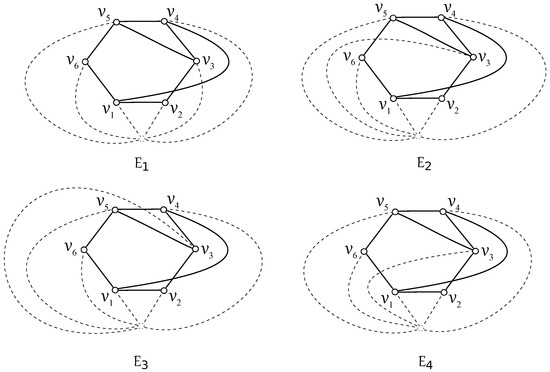
Figure 4. Drawings of four possible configurations from $\mathcal{O}$ of the subgraph $F^j$.

Thus, the configurations ${\mathcal{E}}_1$, ${\mathcal{E}}_2$, ${\mathcal{E}}_3$, and ${\mathcal{E}}_4$ are represented by the cyclic permutations $\left(165432\right)$, $\left(163542\right)$, $\left(165342\right)$, and $\left(136542\right)$, respectively. Again, we denote by ${\mathcal{O}}_D$ the subset of $\mathcal{O}=\{{\mathcal{E}}_1,{\mathcal{E}}_2,{\mathcal{E}}_3,{\mathcal{E}}_4\}$ consisting of all configurations that exist in the drawing D. Further, due to the properties of the cyclic rotations, all lower-bounds of number of crossings of two configurations from $\mathcal{O}$ can be summarized in the symmetric Table 2 (here, ${\mathcal{E}}_k$ and ${\mathcal{E}}_l$ are configurations of the subgraphs $F^i$ and $F^j$, where $k,l\in \{1,2,3,4\}$).

Table 2. The necessary number of crossings between $T^i$ and $T^j$ for the configurations ${\mathcal{E}}_k$, ${\mathcal{E}}_l$.

-	${\mathcal{E}}_1$	${\mathcal{E}}_2$	${\mathcal{E}}_3$	${\mathcal{E}}_4$
${\mathcal{E}}_1$	6	4	5	4
${\mathcal{E}}_2$	4	6	5	5
${\mathcal{E}}_3$	5	5	6	4
${\mathcal{E}}_4$	4	5	4	6

Finally, without loss of generality, we can consider the drawing of $G^{\ast }$ with the vertex notation like that in Figure 1f. In this case, the set $R_D$ is also empty. So our aim will be to list again all possible rotations ${\mathrm{rot}}_D\left(t_j\right)$ which can appear in D if $T^j\in S_D$. Since there is only one subdrawing of $F^j\setminus \left\{v_2\right\}$ represented by the rotation $\left(16543\right)$, there are three ways to obtain the subdrawing of $F^j$ depending on which edge of $G^{\ast }$ is crossed by the edge $t_j{v}_2$. These three possibilities under our consideration are denoted by ${\mathcal{F}}_k$, for $k=1,2,3$. Again, based on the aforementioned arguments, we assume the drawings shown in Figure 5.

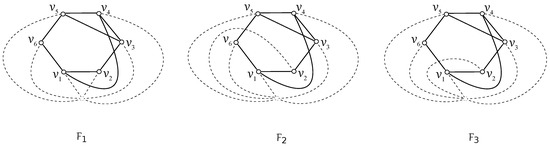
Figure 5. Drawings of three possible configurations from $\mathcal{P}$ of the subgraph $F^j$.

Thus, the configurations ${\mathcal{F}}_1$, ${\mathcal{F}}_2$, and ${\mathcal{F}}_3$ are represented by the cyclic permutations $\left(165432\right)$, $\left(162543\right)$, and $\left(126543\right)$, respectively. Again, we denote by ${\mathcal{P}}_D$ the subset of $\mathcal{P}=\{{\mathcal{F}}_1,{\mathcal{F}}_2,{\mathcal{F}}_3\}$ consisting of all configurations that exist in the drawing D. Further, due to the properties of the cyclic rotations, all lower-bounds of number of crossings of two configurations from $\mathcal{P}$ can be summarized in the symmetric Table 3 (here, ${\mathcal{F}}_k$ and ${\mathcal{F}}_l$ are configurations of the subgraphs $F^i$ and $F^j$, where $k,l\in \{1,2,3\}$).

Table 3. The necessary number of crossings between $T^i$ and $T^j$ for the configurations ${\mathcal{F}}_k$ and ${\mathcal{F}}_l$.

-	${\mathcal{F}}_1$	${\mathcal{F}}_2$	${\mathcal{F}}_3$
${\mathcal{F}}_1$	6	4	5
${\mathcal{F}}_2$	4	6	5
${\mathcal{F}}_3$	5	5	6

3. The Crossing Number of ${\mathit{G}}^{\ast }+{\mathit{D}}_{\mathit{n}}$

Recall that two vertices $t_i$ and $t_j$ of $G^{\ast }+D_n$ are antipodal in a drawing D of $G^{\ast }+D_n$ if the subgraphs $T^i$ and $T^j$ do not cross. A drawing is antipodal-free if it has no antipodal vertices. For easier and more accurate labeling in the proofs of assertions, let us define notation of regions in some subdrawings of $G^{\ast }+D_n$. The unique drawing of $G^{\ast }$ as shown in Figure 1a contains four different regions. Let us denote these four regions by ${\omega }_{1,2,3,4}$, ${\omega }_{1,4,5,6}$, ${\omega }_{3,4,5}$, and ${\omega }_{1,2,3,5,6}$ depending on which of vertices are located on the boundary of the corresponding region.

Lemma 1.

Let D be a good and antipodal-free drawing of$G^{\ast }+D_n$, for$n>3$, with the drawing of$G^{\ast }$with the vertex notation like that in Figure 1a. If$T^u,T^v,T^t\in S_D$are three different subgraphs such that$F^u,F^v$, and$F^t$have three different configurations from the set$\{{\mathcal{A}}_i,{\mathcal{A}}_j,{\mathcal{A}}_k\}\subseteq {\mathcal{M}}_D$with$i+2\equiv j+1\equiv k\left(\mathrm{mod}5\right)$, then

$${\mathrm{cr}}_D(G^{\ast }\cup T^u\cup T^v\cup T^t,T^m)\ge 6forany{T}^m\notin S_D.$$

Proof of Lemma 1.

Let us assume the configurations ${\mathcal{A}}_1$ of $F^u$, ${\mathcal{A}}_2$ of $F^v$, and ${\mathcal{A}}_3$ of $F^t$. It is obvious that ${\mathrm{cr}}_D(T^u\cup T^v\cup T^t,T^m)\ge 3$ holds for any subgraph $T^m$, $m\ne u,v,t$. Further, if ${\mathrm{cr}}_D(G^{\ast },T^m)>2$, then we obtain the desired result ${\mathrm{cr}}_D(G^{\ast }\cup T^u\cup T^v\cup T^t,T^m)\ge 3+3=6$. To finish the proof, let us suppose that there is a subgraph $T^m\notin S_D$ such that $T^m$ crosses exactly once the edges of each subgraph $T^u$, $T^v$, and $T^t$, and let also consider ${\mathrm{cr}}_D(G^{\ast },T^m)=2$. As ${\mathrm{cr}}_D(T^u,T^m)=1$, the vertex $t_m$ must be placed in the quadrangular region with four vertices of $G^{\ast }$ on its boundary; that is, $t_m\in {\omega }_{1,4,5,6}$. Similarly, the assumption ${\mathrm{cr}}_D(T^t,T^m)=1$ enforces that $t_m\in {\omega }_{1,2,3,4}$. Since the vertex $t_m$ cannot be placed simultaneously in both regions, we obtain a contradiction. The proof proceeds in the similar way also for the remaining possible cases of the configurations of subgraphs $F^u$, $F^v$, and $F^t$, and the proof is done. □

Now we are able to prove the main result of the article. We can calculate the exact values of crossing numbers for small graphs using an algorithm located on a website http://crossings.uos.de/. It uses an ILP formulation based on Kuratowski subgraphs. The system also generates verifiable formal proofs like those described in [14]. Unfortunately, the capacity of this system is limited.

Lemma 2.

$\mathrm{cr}(G^{\ast }+D_1)=1$and$\mathrm{cr}(G^{\ast }+D_2)=3$.

Theorem 1.

$\mathrm{cr}(G^{\ast }+D_n)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋$for$n\ge 1$.

Proof of Theorem 1.

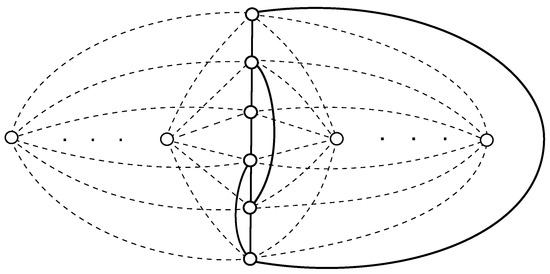
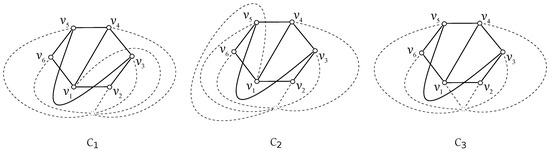
Figure 6 offers the drawing of $G^{\ast }+D_n$ with exactly $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋$ crossings. Thus, $\mathrm{cr}(G^{\ast }+D_n)\le 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋$. We prove the reverse inequality by induction on n. By Lemma 2, the result is true for $n=1$ and $n=2$. Now suppose that, for some $n\ge 3$, there is a drawing D with

$${\mathrm{cr}}_D(G^{\ast }+D_n)<6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋$$

(2)

and that

$$\mathrm{cr}(G^{\ast }+D_m)\ge 6⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋+m+⌊\frac{m}{2}⌋\mathrm{for}\mathrm{any}\mathrm{integer}m<n.$$

(3)

Figure 6. The good drawing of $G^{\ast }+D_n$ with $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋$ crossings.

Let us first show that the considered drawing D must be antipodal-free. For a contradiction, suppose, without loss of generality, that ${\mathrm{cr}}_D(T^{n-1},T^n)=0$. If at least one of $T^{n-1}$ and $T^n$, say $T^n$, does not cross $G^{\ast }$, it is not difficult to verify in Figure 1 that $T^{n-1}$ must cross $G^{\ast }\cup T^n$ at least trice; that is, ${\mathrm{cr}}_D(G^{\ast },T^{n-1}\cup T^n)\ge 3$. From [4], we already know that $\mathrm{cr}\left(K_{6,3}\right)=6$, which yields that the edges of the subgraph $T^{n-1}\cup T^n$ are crossed by any $T^k$, $k=1,2,\dots ,n-2$, at least six times. So, for the number of crossings in D we have:

$$\begin{array}{c}{\mathrm{cr}}_D(G^{\ast }+D_n)={\mathrm{cr}}_D\left(G^{\ast }+D_{n-2}\right)+{\mathrm{cr}}_D(T^{n-1}\cup T^n)+{\mathrm{cr}}_D(K_{6,n-2},T^{n-1}\cup T^n)+{\mathrm{cr}}_D(G^{\ast },T^{n-1}\cup T^n)\\ \ge 6⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+n-2+⌊\frac{n-2}{2}⌋+6(n-2)+3=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋.\end{array}$$

This contradiction with the assumption (2) confirms that D is antipodal-free. Moreover, if $r=\left|R_D\right|$ and $s=\left|S_D\right|$, the assumption (3) together with $\mathrm{cr}\left(K_{6,n}\right)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋$ imply that, in D, if $r=0$, then there are at least $⌈\frac{n}{2}⌉+1$ subgraphs $T^j$ for which the edges of $G^{\ast }$ are crossed just once by them. More precisely:

$${\mathrm{cr}}_D\left(G^{\ast }\right)+{\mathrm{cr}}_D(G^{\ast },K_{6,n})\le {\mathrm{cr}}_D\left(G^{\ast }\right)+0r+1s+2(n-r-s)<n+⌊\frac{n}{2}⌋;$$

that is,

$$s+2(n-r-s)<n+⌊\frac{n}{2}⌋.$$

(4)

This enforces that $2r+s\ge n-⌊\frac{n}{2}⌋+1$, and if $r=0$, then $s\ge n-⌊\frac{n}{2}⌋+1=⌈\frac{n}{2}⌉+1$. Now, for $T^j\in R_D\cup S_D$, we discuss the existence of possible configurations of subgraphs $F^j=G^{\ast }\cup T^j$ in D.

Case 1:${\mathrm{cr}}_D\left(G^{\ast }\right)=0$. Without loss of generality, we can consider the drawing of $G^{\ast }$ with the vertex notation like that in Figure 1a. It is obvious that the set $R_D$ is empty; that is, $r=0$. Thus, we deal with only the configurations belonging to the nonempty set ${\mathcal{M}}_D$ and we discuss over all cardinalities of the set ${\mathcal{M}}_D$ in the following subcases:

i.

$\left|{\mathcal{M}}_D\right|\ge 3$. We consider two subcases. Let us first assume that $\{{\mathcal{A}}_i,{\mathcal{A}}_j,{\mathcal{A}}_k\}\subseteq {\mathcal{M}}_D$ with $i+2\equiv j+1\equiv k\left(\mathrm{mod}5\right)$. Without lost of generality, let us consider three different subgraphs $T^{n-2},T^{n-1},T^n\in S_D$ such that $F^{n-2}$, $F^{n-1}$ and $F^n$ have configurations ${\mathcal{A}}_i$, ${\mathcal{A}}_j$, and ${\mathcal{A}}_k$, respectively. Then, ${\mathrm{cr}}_D(T^{n-2}\cup T^{n-1}\cup T^n,T^m)\ge 14$ holds for any $T^m\in S_D$ with $m\ne n-2,n-1,n$ by summing the values in all columns in the considered three rows of Table 1. Moreover, ${\mathrm{cr}}_D(G^{\ast }\cup T^{n-2}\cup T^{n-1}\cup T^n,T^m)\ge 6$ is fulfilling for any subgraph $T^m\notin S_D$ by Lemma 1. ${\mathrm{cr}}_D(T^{n-2}\cup T^{n-1}\cup T^n)\ge 13$ holds by summing of three corresponding values of Table 1 between the considered configurations ${\mathcal{A}}_i$, ${\mathcal{A}}_j$, and ${\mathcal{A}}_k$, by fixing the subgraph $G^{\ast }\cup T^{n-2}\cup T^{n-1}\cup T^n$,

$$\begin{array}{c}{\mathrm{cr}}_D(G^{\ast }+D_n)={\mathrm{cr}}_D\left(K_{6,n-3}\right)+{\mathrm{cr}}_D(K_{6,n-3},G^{\ast }\cup T^{n-2}\cup T^{n-1}\cup T^n)+{\mathrm{cr}}_D(G^{\ast }\cup T^{n-2}\cup T^{n-1}\cup T^n)\\ \ge 6⌊\frac{n-3}{2}⌋⌊\frac{n-4}{2}⌋+15(s-3)+6(n-s)+13+3=6⌊\frac{n-3}{2}⌋⌊\frac{n-4}{2}⌋+6n+9s-29\\ \ge 6⌊\frac{n-3}{2}⌋⌊\frac{n-4}{2}⌋+6n+9\left(⌈\frac{n}{2}⌉+1\right)-29\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋.\end{array}$$

In addition, let us assume that ${\mathcal{M}}_D=\{{\mathcal{A}}_i,{\mathcal{A}}_j,{\mathcal{A}}_k\}$ with $i+1\equiv j\left(\mathrm{mod}5\right)$, $j+1\not\equiv k\left(\mathrm{mod}5\right)$, and $k+1\not\equiv i\left(\mathrm{mod}5\right)$. Without lost of generality, let us consider two different subgraphs $T^{n-1},T^n\in S_D$ such that $F^{n-1}$ and $F^n$ have mentioned configurations ${\mathcal{A}}_i$ and ${\mathcal{A}}_j$, respectively. Then, ${\mathrm{cr}}_D(G^{\ast }\cup T^{n-1}\cup T^n,T^m)\ge 1+10=11$ holds for any $T^m\in S_D$ with $m\ne n-1,n$ also, by summing the values in Table 1. Hence, by fixing the subgraph $G^{\ast }\cup T^{n-1}\cup T^n$,

$$\begin{array}{c}{\mathrm{cr}}_D(G^{\ast }+D_n)={\mathrm{cr}}_D\left(K_{6,n-2}\right)+{\mathrm{cr}}_D(K_{6,n-2},G^{\ast }\cup T^{n-1}\cup T^n)+{\mathrm{cr}}_D(G^{\ast }\cup T^{n-1}\cup T^n)\\ \ge 6⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+11(s-2)+4(n-s)+4+2=6⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+4n+7s-16\\ \ge 6⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+4n+7\left(⌈\frac{n}{2}⌉+1\right)-16\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋.\end{array}$$

ii.

$\left|{\mathcal{M}}_D\right|=2$; that is, ${\mathcal{M}}_D=\{{\mathcal{A}}_i,{\mathcal{A}}_j\}$ for some $i,j\in \{1,\dots ,5\}$ with $i\ne j$. Without lost of generality, let us consider two different subgraphs $T^{n-1},T^n\in S_D$ such that $F^{n-1}$ and $F^n$ have mentioned configurations ${\mathcal{A}}_i$ and ${\mathcal{A}}_j$, respectively. Then, ${\mathrm{cr}}_D(G^{\ast }\cup T^{n-1}\cup T^n,T^m)\ge 1+10=11$ holds for any $T^m\in S_D$ with $m\ne n-1,n$ also by Table 1. Thus, by fixing the subgraph $G^{\ast }\cup T^{n-1}\cup T^n$, we are able to use the same inequalities as in the previous subcase.

iii.

$\left|{\mathcal{M}}_D\right|=1$; that is, ${\mathcal{M}}_D=\left\{{\mathcal{A}}_j\right\}$ for only one $j\in \{1,\dots ,5\}$. Without lost of generality, let us assume that $T^n\in S_D$ with the configuration ${\mathcal{A}}_j\in {\mathcal{M}}_D$ of the subgraph $F^n$. As ${\mathcal{M}}_D=\left\{{\mathcal{A}}_j\right\}$, we have ${\mathrm{cr}}_D(G^{\ast }\cup T^n,T^k)\ge 1+6=7$ for any $T^k\in S_D$, $k\ne n$ provided that ${\mathrm{rot}}_D\left(t_n\right)={\mathrm{rot}}_D\left(t_k\right)$, for more see [13]. Hence, by fixing the subgraph $G^{\ast }\cup T^n$,

$$\begin{array}{c}{\mathrm{cr}}_D(G^{\ast }+D_n)={\mathrm{cr}}_D\left(K_{6,n-1}\right)+{\mathrm{cr}}_D(K_{6,n-1},G^{\ast }\cup T^n)+{\mathrm{cr}}_D(G^{\ast }\cup T^n)\\ \ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+7(s-1)+3(n-s)+1=6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+3n+4s-6\\ \ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+3n+4\left(⌈\frac{n}{2}⌉+1\right)-6\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋.\end{array}$$

Case 2:${\mathrm{cr}}_D\left(G^{\ast }\right)=1$ with ${\mathrm{cr}}_D\left(C_6\left(G^{\ast }\right)\right)=0$. At first, without loss of generality, we can consider the drawing of $G^{\ast }$ with the vertex notation like that in Figure 1b. Since the set $R_D$ can be nonempty, two possible subcases may occur:

i.

Let $R_D$ be the nonempty set; that is, there is a subgraph $T^i\in R_D$. Now, for a $T^i\in R_D$, the reader can easily see that the subgraph $F^i=G^{\ast }\cup T^i$ is uniquely represented by ${\mathrm{rot}}_D\left(t_i\right)=\left(165432\right)$, and ${\mathrm{cr}}_D(T^i,T^j)\ge 6$ for any $T^j\in R_D$ with $j\ne i$ provided that ${\mathrm{rot}}_D\left(t_i\right)={\mathrm{rot}}_D\left(t_j\right)$; for more see [13]. Moreover, it is not difficult to verify by a discussion over all possible drawings D that ${\mathrm{cr}}_D(G^{\ast }\cup T^i,T^k)\ge 5$ holds for any subgraph $T^k\in S_D$, and ${\mathrm{cr}}_D(G^{\ast }\cup T^i,T^k)\ge 4$ is also fulfilling for any subgraph $T^k\notin R_D\cup S_D$. Thus, by fixing the subgraph $G^{\ast }\cup T^i$,

$$\begin{array}{c}{\mathrm{cr}}_D(G^{\ast }+D_n)\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+6(r-1)+5s+4(n-r-s)+1=6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋\\ +4n+(2r+s)-5\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+4n+\left(n-⌊\frac{n}{2}⌋+1\right)-5\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋.\end{array}$$

ii.

Let $R_D$ be the empty set; that is, each subgraph $T^j$ crosses the edges of $G^{\ast }$ at least once in D. Thus, we deal with the configurations belonging to the nonempty set ${\mathcal{N}}_D$. Let us consider a subgraph $T^j\in S_D$ with the configuration ${\mathcal{B}}_i\in {\mathcal{N}}_D$ of $F^j$, where $i\in \{1,2,3,4\}$. Then, the lower-bounds of number of crossings of two configurations from $\mathcal{N}$ confirm that ${\mathrm{cr}}_D(G^{\ast }\cup T^j,T^k)\ge 1+4=5$ holds for any $T^k\in S_D$, $k\ne j$. Moreover, one can also easily verify over all possible drawings D that ${\mathrm{cr}}_D(G^{\ast }\cup T^j,T^k)\ge 4$ is true for any subgraph $T^k\notin S_D$. Hence, by fixing the subgraph $G^{\ast }\cup T^j$,

$$\begin{array}{c}{\mathrm{cr}}_D(G^{\ast }+D_n)\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+5(s-1)+4(n-s)+1+1=6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋\hfill \\ +4n+s-3\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+4n+\left(⌈\frac{n}{2}⌉+1\right)-3\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋.\hfill \end{array}$$

In addition, without loss of generality, we can consider the drawing of $G^{\ast }$ with the vertex notation like that in Figure 1e. It is obvious that the set $R_D$ is empty; that is, the set $S_D$ cannot be empty. Thus, we deal with the configurations belonging to the nonempty set ${\mathcal{O}}_D$. Note that the lower-bounds of number of crossings of two configurations from $\mathcal{O}$ were already established in Table 2. Since there is a possibility to find a subdrawing of $G^{\ast }\cup T^j\cup T^k$, in which ${\mathrm{cr}}_D(G^{\ast }\cup T^j,T^k)=3$ with $T^j\in S_D$ and $T^k\notin S_D$, we discuss four following subcases:

i.

${\mathcal{E}}_4\in {\mathcal{O}}_D$. Without lost of generality, let us assume that $T^n\in S_D$ with the configuration ${\mathcal{E}}_4\in {\mathcal{O}}_D$ of $F^n$. Only for this subcase, one can easily verify over all possible drawings D for which ${\mathrm{cr}}_D(G^{\ast }\cup T^n,T^k)\ge 4$ is true for any subgraph $T^k\notin S_D$. Thus, by fixing the subgraph $G^{\ast }\cup T^n$,

$$\begin{array}{c}{\mathrm{cr}}_D(G^{\ast }+D_n)\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+5(s-1)+4(n-s)+1+1=6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋\hfill \\ +4n+s-3\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+4n+\left(⌈\frac{n}{2}⌉+1\right)-3\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋.\hfill \end{array}$$

ii.

${\mathcal{E}}_4\notin {\mathcal{O}}_D$ and ${\mathcal{E}}_3\in {\mathcal{O}}_D$. Without lost of generality, let us assume that $T^n\in S_D$ with the configuration ${\mathcal{E}}_3\in {\mathcal{O}}_D$ of $F^n$. In this subcase, ${\mathrm{cr}}_D(G^{\ast }\cup T^n,T^k)\ge 1+5=6$ holds for any subgraph $T^k\in S_D$, $k\ne n$ by the remaining values in the third row of Table 2. Hence, by fixing the subgraph $G^{\ast }\cup T^n$,

$$\begin{array}{c}{\mathrm{cr}}_D(G^{\ast }+D_n)\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+6(s-1)+3(n-s)+1+1=6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋\\ +3n+3s-4\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+3n+3\left(⌈\frac{n}{2}⌉+1\right)-4\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋.\end{array}$$

iii.

${\mathcal{O}}_D=\{{\mathcal{E}}_1,{\mathcal{E}}_2\}$. Without lost of generality, let us consider two different subgraphs $T^{n-1},T^n\in S_D$ such that $F^{n-1}$ and $F^n$ have mentioned configurations ${\mathcal{E}}_1$ and ${\mathcal{E}}_2$, respectively. Then, ${\mathrm{cr}}_D(G^{\ast }\cup T^{n-1}\cup T^n,T^k)\ge 1+10=11$ holds for any $T^k\in S_D$ with $k\ne n-1,n$ also by Table 2. Thus, by fixing the subgraph $G^{\ast }\cup T^{n-1}\cup T^n$,

$$\begin{array}{c}{\mathrm{cr}}_D(G^{\ast }+D_n)\ge 6⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+11(s-2)+4(n-s)+4+2=6⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋\\ +4n+7s-16\ge 6⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+4n+7\left(⌈\frac{n}{2}⌉+1\right)-16\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋.\end{array}$$

iv.

${\mathcal{O}}_D=\left\{{\mathcal{E}}_i\right\}$ for only one $i\in \{1,2\}$. Without lost of generality, let us assume that $T^n\in S_D$ with the configuration ${\mathcal{E}}_1$ of $F^n$. In this subcase, ${\mathrm{cr}}_D(G^{\ast }\cup T^n,T^k)\ge 1+6=7$ holds for any $T^k\in S_D$, $k\ne n$ provided that ${\mathrm{rot}}_D\left(t_n\right)={\mathrm{rot}}_D\left(t_k\right)$. Hence, by fixing the subgraph $G^{\ast }\cup T^n$,

$$\begin{array}{c}{\mathrm{cr}}_D(G^{\ast }+D_n)\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+7(s-1)+3(n-s)+1=6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋\\ +3n+4s-6\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+3n+4\left(⌈\frac{n}{2}⌉+1\right)-6\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋.\end{array}$$

Case 3:${\mathrm{cr}}_D\left(G^{\ast }\right)=2$ with ${\mathrm{cr}}_D\left(C_6\left(G^{\ast }\right)\right)=0$. At first, without loss of generality, we can consider the drawing of $G^{\ast }$ with the vertex notation like that in Figure 1c. It is obvious that the set $R_D$ is empty, that is, the set $S_D$ cannot be empty. Our aim is to list again all possible rotations ${\mathrm{rot}}_D\left(t_j\right)$ which can appear in D if a subgraph $T^j\in S_D$. Since there is only one subdrawing of $F^j\setminus \left\{v_1\right\}$ represented by the rotation $\left(26543\right)$, there are three ways to obtain the subdrawing of $F^j$ depending on which edge of $G^{\ast }$ is crossed by the edge $t_j{v}_1$. These three possible ways under our consideration can be denoted by ${\mathcal{C}}_k$, for $k=1,2,3$. Based on the aforementioned arguments, we assume the drawings shown in Figure 7.

Figure 7. Drawings of three possible configurations of the subgraph $F^j$.

Thus the configurations ${\mathcal{C}}_1$, ${\mathcal{C}}_2$, and ${\mathcal{C}}_3$ are represented by the cyclic permutations $\left(132654\right)$, $\left(143265\right)$, and $\left(165432\right)$, respectively. Further, due to the properties of the cyclic rotations we can easily verify that $\mathrm{cr}({\mathcal{C}}_i,{\mathcal{C}}_j)\ge 4$ for any $i,j\in \{1,2,3\}$. Moreover, one can also easily verify over all possible drawings D that ${\mathrm{cr}}_D(G^{\ast }\cup T^j,T^k)\ge 4$ holds for any subgraph $T^k\notin S_D$, where $T^j\in S_D$ with some configuration ${\mathcal{C}}_i$ of $F^j$. As there is a $T^j\in S_D$, by fixing the subgraph $G^{\ast }\cup T^j$,

$$\begin{array}{c}{\mathrm{cr}}_D(G^{\ast }+D_n)\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+5(s-1)+4(n-s)+2+1=6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋\hfill \\ +4n+s-2\ge 6⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+4n+\left(⌈\frac{n}{2}⌉+1\right)-2\ge 6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋.\hfill \end{array}$$

In addition, without loss of generality, we can consider the drawing of $G^{\ast }$ with the vertex notation like that in Figure 1d. In this case, by applying the same process, we obtain two possible forms of rotation ${\mathrm{rot}}_D\left(t_j\right)$ for $T^j\in S_D$. Namely, the rotations $\left(165423\right)$ and $\left(165432\right)$ if the edge $t_j{v}_2$ crosses either the edge $v_3{v}_4$ or the edge $v_3{v}_5$ of $G^{\ast }$, respectively. Further, they satisfy also the same properties like in the previous subcase, i.e., the same lower bounds of numbers of crossings on the edges of the subgraph $G^{\ast }\cup T^j$ by any $T^k$, $k\ne j$. Hence, we are able to use the same fixing of the subgraph $G^{\ast }\cup T^j$ for obtaining a contradiction with the number of crossings in D.

Finally, without loss of generality, we can consider the drawing of $G^{\ast }$ with the vertex notation like that in Figure 1f. In this case, the set $R_D$ is empty; that is, the set $S_D$ cannot be empty. Thus, we can deal with the configurations belonging to the nonempty set ${\mathcal{P}}_D$. Recall that the lower-bounds of number of crossings of two configurations from $\mathcal{P}$ were already established in Table 3. Further, we can apply the same idea and also the same arguments as for the configurations ${\mathcal{E}}_i\in {\mathcal{O}}_D$, with $i=1,2,3$, in the subcases ii.–iv. of Case 2.

Case 4:${\mathrm{cr}}_D\left(G^{\ast }\right)\ge 1$ with ${\mathrm{cr}}_D\left(C_6\left(G^{\ast }\right)\right)\ge 1$. For all possible subdrawings of the graph $G^{\ast }$ with at least one crossing among edges of $C_6\left(G^{\ast }\right)$, and also with the possibility of obtaining a subgraph $T^j$ that crosses the edges of $G^{\ast }$ at most once, one of the ideas of the previous subcases can be applied.

We have shown, in all cases, that there is no good drawing D of the graph $G^{\ast }+D_n$ with fewer than $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋$ crossings. This completes the proof of the main theorem.  □

4. Conclusions

Determining the crossing number of a graph $G+D_n$ is an essential step in establishing the so far unknown values of the numbers of crossings of graphs $G+P_n$ and $G+C_n$, where $P_n$ and $C_n$ are the path and the cycle on n vertices, respectively. Using the result in Theorem 1 and the optimal drawing of $G^{\ast }+D_n$ in Figure 6, we are able to postulate that $\mathrm{cr}(G^{\ast }+P_n)$ and $\mathrm{cr}(G^{\ast }+C_n)$ are at least one more than $\mathrm{cr}(G^{\ast }+D_n)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n+⌊\frac{n}{2}⌋$.