Low-Rank Multi-Channel Features for Robust Visual Object Tracking
Abstract
:1. Introduction
2. Related Work
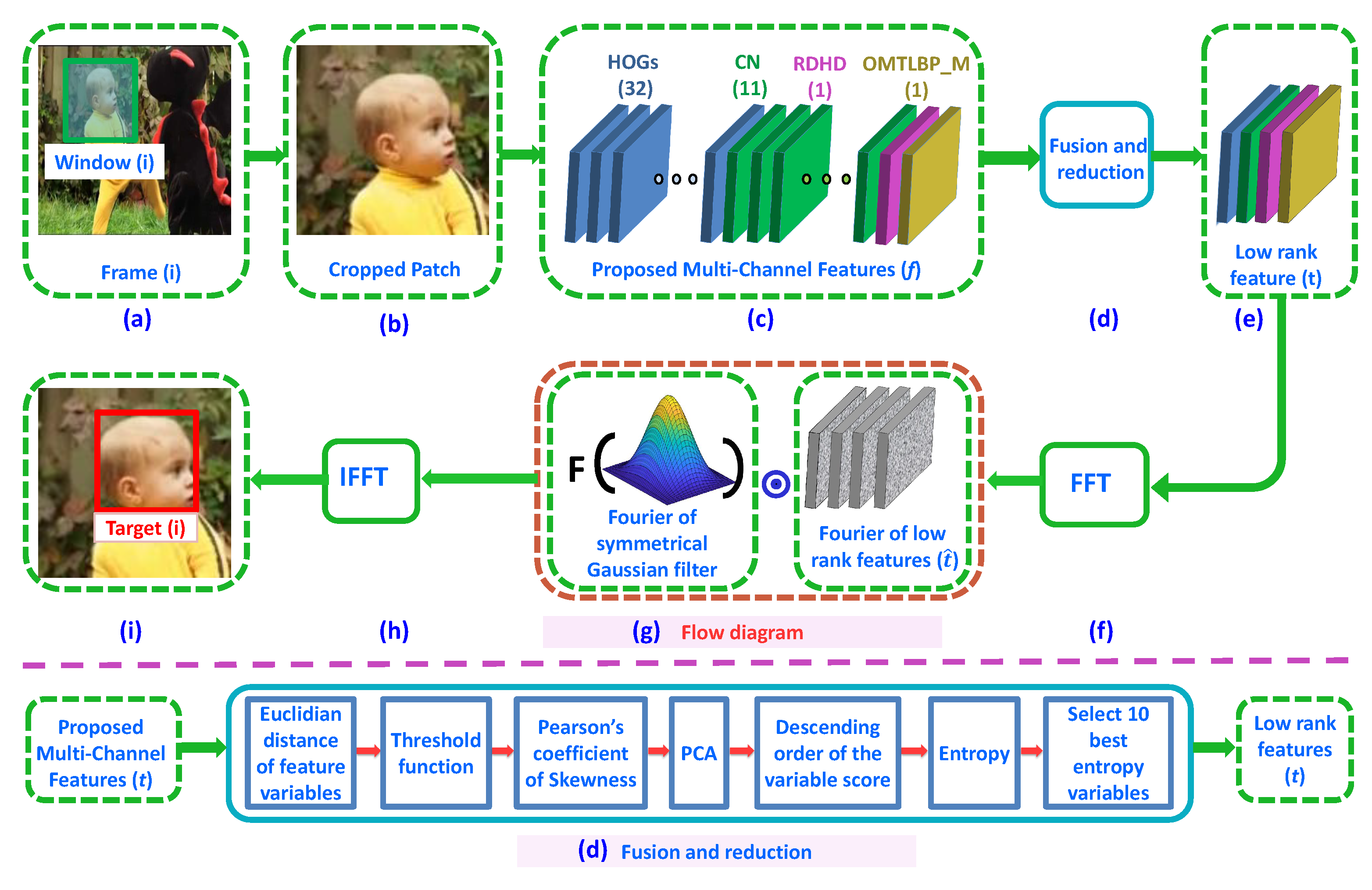
3. Proposed Method
3.1. Multi-Channel Feature
Fusion and Reduction
4. Experimental Setup
4.1. Dataset and Evaluated Trackers
4.2. Evaluation Procedure
4.3. Parameter Setting
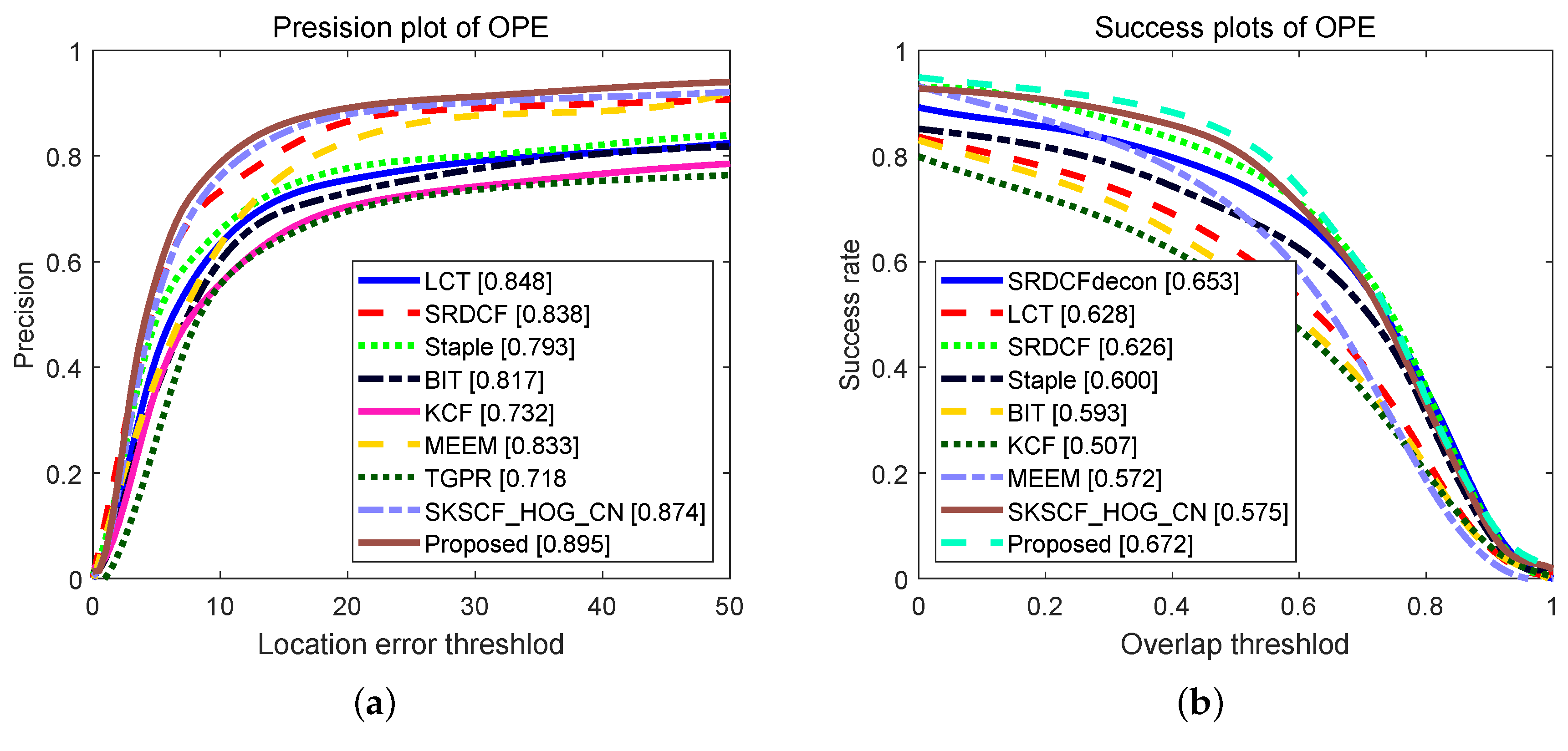
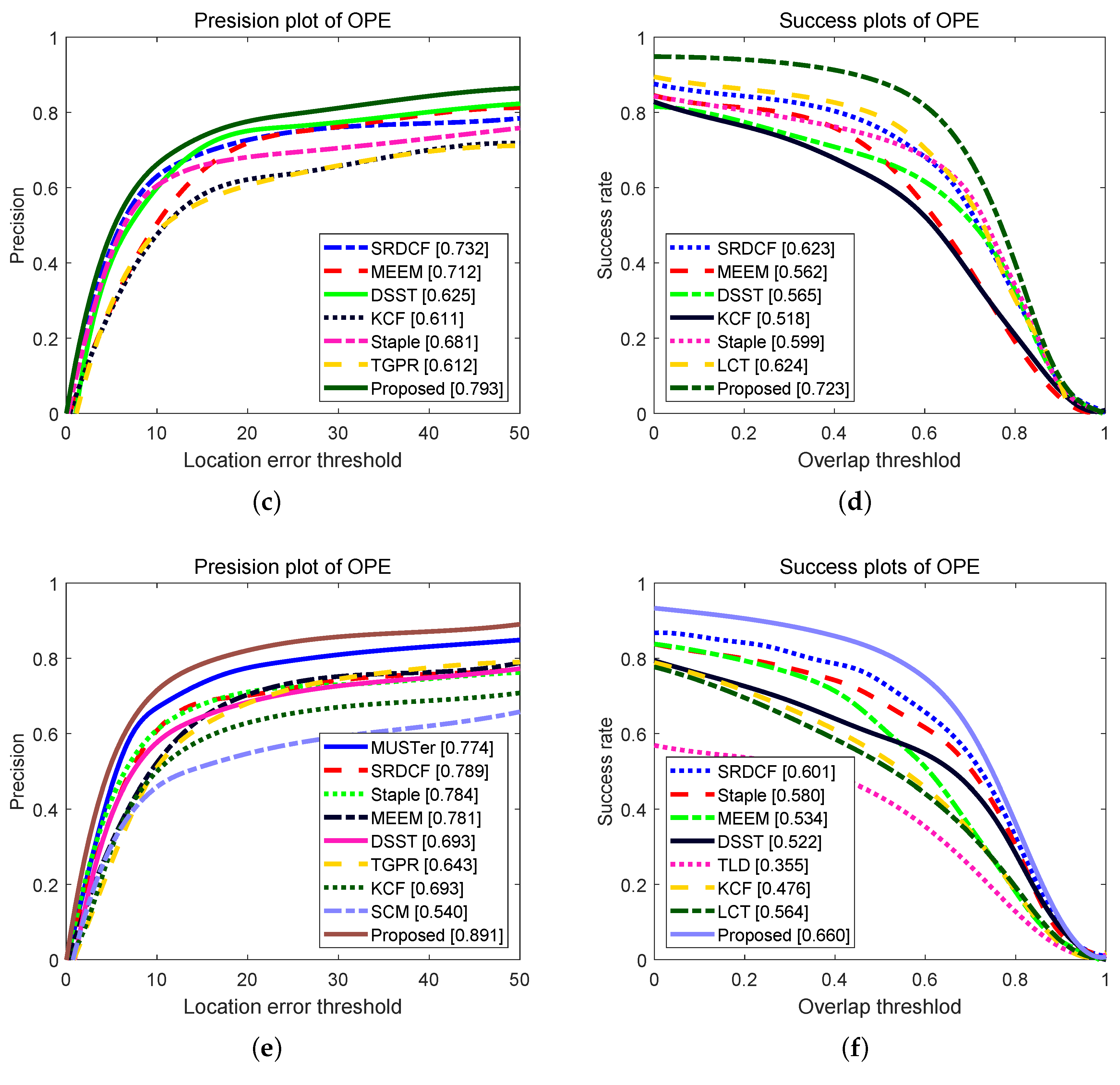
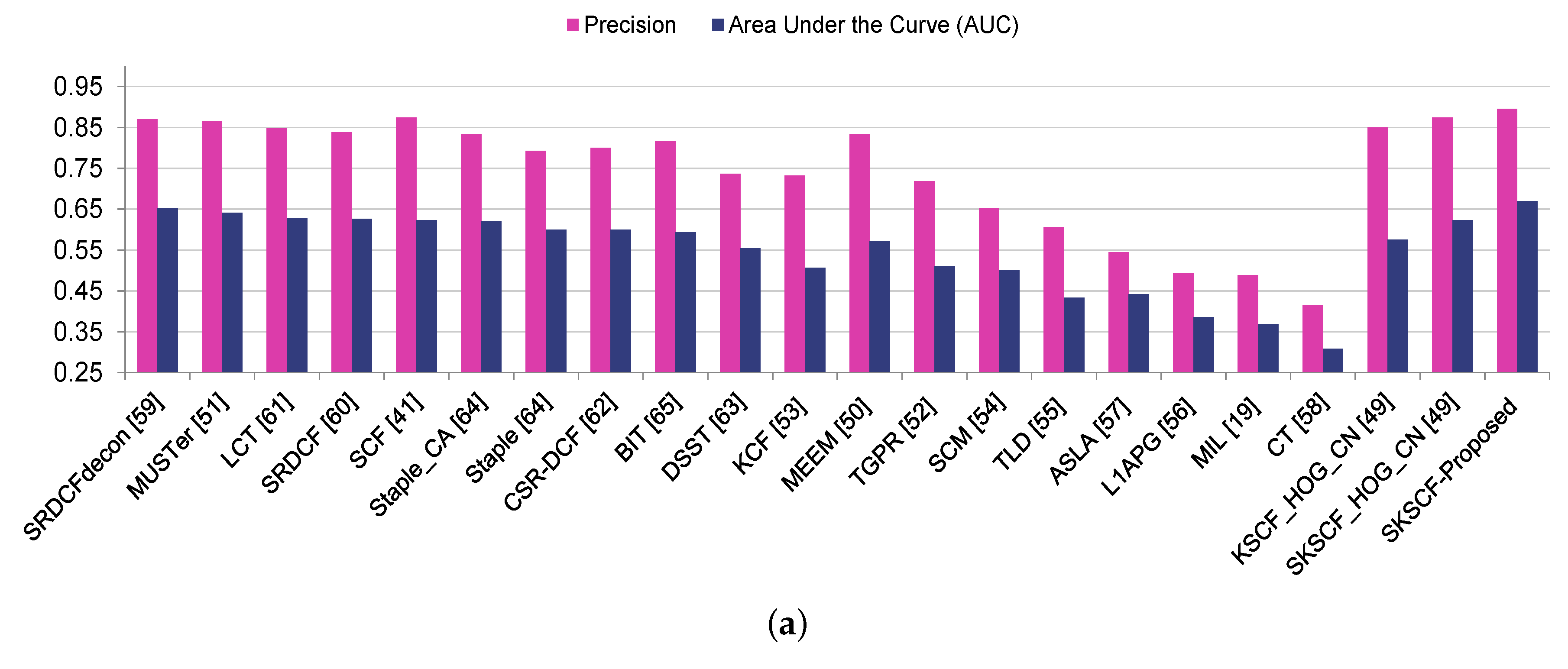
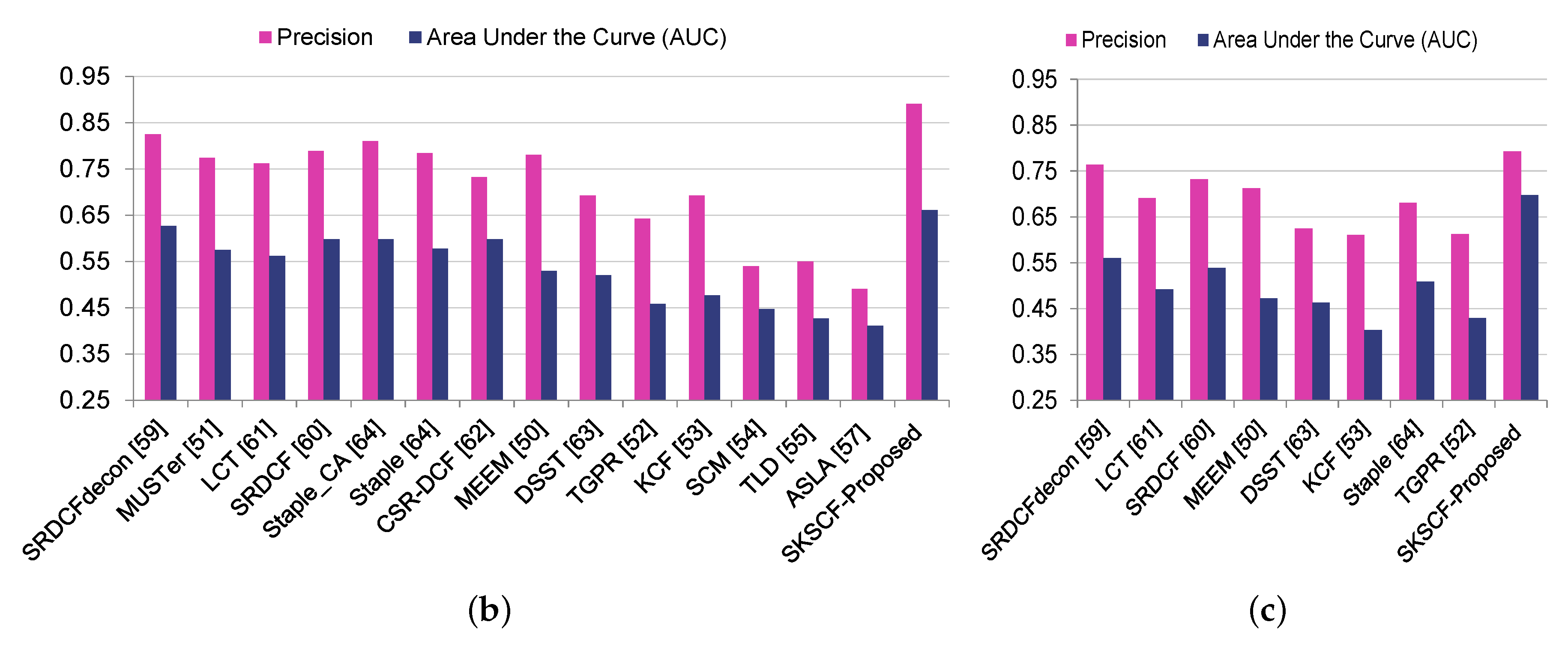
4.4. Overall Performance
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aggarwal, J.K.; Xia, L. Human activity recognition from 3d data: A review. Pattern Recognit. Lett. 2014, 48, 70–80. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, H.; Fang, J. Multiple vehicle tracking in aerial video sequence using driver behavior analysis and improved deterministic data association. J. Appl. Remote. Sens. 2018, 12, 016014. [Google Scholar] [CrossRef]
- Sivanantham, S.; Paul, N.N.; Iyer, R.S. Object tracking algorithm implementation for security applications. Far East J. Electron. Commun. 2016, 16, 1. [Google Scholar] [CrossRef]
- Yun, X.; Sun, Y.; Yang, X.; Lu, N. Discriminative Fusion Correlation Learning for Visible and Infrared Tracking. Math. Probl. Eng. 2019. [Google Scholar] [CrossRef]
- Li, P.; Wang, D.; Wang, L.; Lu, H. Deep visual tracking: Review and experimental comparison. Pattern Recognit. 2018, 76, 323–338. [Google Scholar] [CrossRef]
- Yazdi, M.; Bouwmans, T. New trends on moving object detection in video images captured by a moving camera: A survey. Comput. Sci. Rev. 2018, 28, 157–177. [Google Scholar] [CrossRef]
- Pan, Z.; Liu, S.; Fu, W. A review of visual moving target tracking. Multimed. Tools Appl. 2017, 76, 16989–17018. [Google Scholar] [CrossRef]
- Wu, Y.; Lim, J.; Yang, M.H. Online object tracking: A benchmark. In Proceedings of the IEEE conference on computer vision and pattern recognition, Portland, OR, USA, 23–28 June 2013; pp. 2411–2418. [Google Scholar]
- Liu, F.; Gong, C.; Huang, X.; Zhou, T.; Yang, J.; Tao, D. Robust visual tracking revisited: From correlation filter to template matching. IEEE Trans. Image Process. 2018, 27, 2777–2790. [Google Scholar] [CrossRef] [PubMed]
- Ross, D.A.; Lim, J.; Lin, R.S.; Yang, M.H. Incremental learning for robust visual tracking. Int. J. Comput. Vis. 2008, 77, 125–141. [Google Scholar] [CrossRef]
- Hare, S.; Golodetz, S.; Saffari, A.; Vineet, V.; Cheng, M.M.; Hicks, S.L.; Torr, P.H. Struck: Structured output tracking with kernels. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 2096–2109. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zhang, L.; Liu, Q.; Zhang, D.; Yang, M.H. Fast visual tracking via dense spatio-temporal context learning. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Zuo, W.; Wu, X.; Lin, L.; Zhang, L.; Yang, M.H. Learning support correlation filters for visual tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 1158–1172. [Google Scholar] [CrossRef] [PubMed]
- Kristan, M.; Matas, J.; Leonardis, A.; Vojir, T.; Pflugfelder, R.; Fernandez, G.; Cehovin, L. A novel performance evaluation methodology for single-target trackers. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2137–2155. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Lin, M.; Wu, Y.; Yang, M.H.; Yan, S. Nus-pro: A new visual tracking challenge. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 335–349. [Google Scholar] [CrossRef] [PubMed]
- Fan, H.; Lin, L.; Yang, F.; Chu, P.; Deng, G.; Yu, S.; Ling, H. Lasot: A high-quality benchmark for large-scale single object tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 5374–5383. [Google Scholar]
- Kim, D.Y.; Vo, B.N.; Vo, B.T.; Jeon, M. A labeled random finite set online multi-object tracker for video data. Pattern Recognit. 2019, 90, 377–389. [Google Scholar] [CrossRef]
- Babenko, B.; Yang, M.H.; Belongie, S. Visual tracking with online multiple instance learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 983–990. [Google Scholar]
- Grabner, H.; Grabner, M.; Bischof, H. Real-time tracking via on-line boosting. Bmvc 2006, 1, 6. [Google Scholar]
- Nam, H.; Han, B. Learning multi-domain convolutional neural networks for visual tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June– 1 July 2016; pp. 4293–4302. [Google Scholar]
- Li, H.; Li, Y.; Porikli, F. Deeptrack: Learning discriminative feature representations online for robust visual tracking. IEEE Trans. Image Process. 2016, 25, 1834–1848. [Google Scholar] [CrossRef] [PubMed]
- Zhong, W.; Lu, H.; Yang, M.H. Robust object tracking via sparse collaborative appearance model. IEEE Trans. Image Process. 2014, 23, 2356–2368. [Google Scholar] [CrossRef]
- Lan, X.; Zhang, S.; Yuen, P.C.; Chellappa, R. Learning common and feature-specific patterns: A novel multiple-sparse-representation-based tracker. IEEE Trans. Image Process. 2018, 27, 2022–2037. [Google Scholar] [CrossRef]
- Zhong, W.; Lu, H.; Yang, M.-H. Robust object tracking via sparsity based collaborative model. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 1838–1845. [Google Scholar]
- Jia, X.; Lu, H.; Yang, M.H. Visual tracking via adaptive structural local sparse appearance model. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 16–21 June 2012; pp. 1822–1829. [Google Scholar]
- Hong, Z.; Chen, Z.; Wang, C.; Mei, X.; Prokhorov, D.; Tao, D. Multi-store tracker (muster): A cognitive psychology inspired approach to object tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 749–758. [Google Scholar]
- Zhang, J.; Ma, S.; Sclaroff, S. MEEM: Robust tracking via multiple experts using entropy minimization. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 188–203. [Google Scholar]
- Bolme, D.S.; Beveridge, J.R.; Draper, B.A.; Lui, Y.M. Visual object tracking using adaptive correlation filters. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 2544–2550. [Google Scholar]
- Wang, L.; Lu, H.; Yang, M.H. Constrained superpixel tracking. IEEE Trans. Cybern. 2018, 48, 1030–1041. [Google Scholar] [CrossRef]
- Lukezic, A.; Zajc, L.C.; Kristan, M. Deformable parts correlation filters for robust visual tracking. IEEE Trans. Cybern. 2018, 48, 1849–1861. [Google Scholar] [CrossRef]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. Exploiting the circulant structure of tracking-by-detection with kernels. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 702–715. [Google Scholar]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. High-speed tracking with kernelized correlation filters. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 583–596. [Google Scholar] [CrossRef] [PubMed]
- Montero, A.S.; Lang, J.; Laganiere, R. Scalable kernel correlation filter with sparse feature integration. In Proceedings of the IEEE International Conference on Computer Vision Workshop (ICCVW), Santiago, Chile, 7–13 December 2015; pp. 587–594. [Google Scholar]
- Galoogahi, H.K.; Sim, T.; Lucey, S. Correlation filters with limited boundaries. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 4630–4638. [Google Scholar]
- Danelljan, M.; Hager, G.; Khan, F.S.; Felsberg, M. Learning spatially regularized correlation filters for visual tracking. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 4310–4318. [Google Scholar]
- Bibi, A.; Mueller, M.; Ghanem, B. Target response adaptation for correlation filter tracking. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 419–433. [Google Scholar]
- Xu, T.; Feng, Z.H.; Wu, X.J.; Kittler, J. Learning Adaptive Discriminative Correlation Filters via Temporal Consistency preserving Spatial Feature Selection for Robust Visual Object Tracking. IEEE Trans. Image Process. 2019, 28, 5596–5609. [Google Scholar] [CrossRef] [PubMed]
- Lukei, A.; Voj, T.; Zajc, L.E.; Matas, J.; Kristan, M. Discriminative correlation filter with channel and spatial reliability. CVPR 2017, 126, 6309–6318. [Google Scholar]
- Danelljan, M.; Häger, G.; Khan, F.S.; Felsberg, M. Discriminative scale space tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1561–1575. [Google Scholar] [CrossRef] [PubMed]
- Danelljan, M.; Hager, G.; Khan, F.S.; Felsberg, M. Adaptive decontamination of the training set: A unified formulation for discriminative visual tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1430–1438. [Google Scholar]
- Tu, Z.; Guo, L.; Li, C.; Xiong, Z.; Wang, X. Minimum Barrier Distance-Based Object Descriptor for Visual Tracking. Appl. Sci. 2018, 8, 2233. [Google Scholar] [CrossRef]
- Felzenszwalb, P.F.; Girshick, R.B.; McAllester, D.; Ramanan, D. Object detection with discriminatively trained part-based models. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1627–1645. [Google Scholar] [CrossRef] [PubMed]
- Danelljan, M.; Khan, F.S.; Felsberg, M.; Weijer, J.V.D. Adaptive color attributes for real-time visual tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1090–1097. [Google Scholar]
- Possegger, H.; Mauthner, T.; Bischof, H. In defense of color-based model-free tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 2113–2120. [Google Scholar]
- Lukezic, A.; Vojir, T.; Zajc, L.C.; Matas, J.; Kristan, M. Discriminative correlation filter with channel and spatial reliability. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6309–6318. [Google Scholar]
- Song, T.; Li, H.; Meng, F.; Wu, Q.; Cai, J. Letrist: Locally encoded transform feature histogram for rotation-invariant texture classification. IEEE Trans. Circuits Syst. Video Techol. 2018, 28, 1565–1579. [Google Scholar] [CrossRef]
- Saeed, A.; Fawad; Khan, M.J.; Riaz, M.A.; Shahid, H.; Khan, M.S.; Amin, Y.; Loo, J.; Tenhunen, H. Robustness-Driven Hybrid Descriptor for Noise-Deterrent Texture Classification. IEEE Access 2019, 7, 110116–110127. [Google Scholar] [CrossRef]
- Khan, M.J.; Riaz, M.A.; Shahid, H.; Khan, M.S.; Amin, Y.; Loo, J.; Tenhunen, H. Texture Representation through Overlapped Multi-oriented Tri-scale Local Binary Pattern. IEEE Access 2019, 7, 66668–66679. [Google Scholar]
- Khan, M.A.; Sharif, M.; Javed, M.Y.; Akram, T.; Yasmin, M.; Saba, T. License number plate recognition system using entropy-based features selection approach with SVM. IET Image Process. 2017, 12, 200–209. [Google Scholar] [CrossRef]
- Xiong, W.; Zhang, L.; Du, B.; Tao, D. Combining local and global: Rich and robust feature pooling for visual recognition. Pattern Recognit. 2017, 62, 225–235. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Q.; Zhang, L.; Tao, D.; Huang, X.; Du, B. Ensemble manifold regularized sparse low-rank approximation for multiview feature embedding. Pattern Recognit. 2015, 48, 3102–3112. [Google Scholar] [CrossRef]
- Arsalan, M.; Hong, H.; Naqvi, R.; Lee, M.; Kim, M.D.; Park, K. Deep learning-based iris segmentation for iris recognition in visible light environment. Symmetry 2017, 9, 263. [Google Scholar] [CrossRef]
- Masood, H.; Rehman, S.; Khan, A.; Riaz, F.; Hassan, A.; Abbas, M. Approximate Proximal Gradient-Based Correlation Filter for Target Tracking in Videos: A Unified Approach. Arab. J. Sci. Eng. 2019, 1–18. [Google Scholar] [CrossRef]
- Qi, Y.; Zhang, S.; Qin, L.; Yao, H.; Huang, Q.; Lim, J.; Yang, M.H. Hedged deep tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 4303–4311. [Google Scholar]
- Hare, S.; Saffari, A.; Struck, P.H.T. Structured output tracking with kernels. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 263–270. [Google Scholar]
- Cai, B.; Xu, X.; Xing, X.; Jia, K.; Miao, J.; Tao, D. Bit: Biologically inspired tracker. IEEE Trans. Image Process. 2016, 25, 1327–1339. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zhang, L.; Yang, M.H. Real-time compressive tracking. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 864–877. [Google Scholar]
- Ma, C.; Yang, X.; Zhang, C.; Yang, M.H. Long-term correlation tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5388–5396. [Google Scholar]
- Bao, C.; Wu, Y.; Ling, H.; Ji, H. Real time robust l1 tracker using accelerated proximal gradient approach. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 1830–1837. [Google Scholar]
- Kalal, Z.; Mikolajczyk, K.; Matas, J. Tracking-learning-detection. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1409–1422. [Google Scholar] [CrossRef] [PubMed]
- Dinh, T.B.; Vo, N.; Medioni, G. Context tracker: Exploring supporters and distracters in unconstrained environments. CVPR 2011, 1177–1184. [Google Scholar] [CrossRef]
- Bertinetto, L.; Valmadre, J.; Golodetz, S.; Miksik, O.; Torr, P.H. Staple: Complementary learners for real-time tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1401–1409. [Google Scholar]
- Gao, J.; Ling, H.; Hu, W.; Xing, J. Transfer learning based visual tracking with gaussian processes regression. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 188–203. [Google Scholar]
| Kernels | Linear | Polynomial | Gaussian | |
|---|---|---|---|---|
| Mean DP (%) | 83.89 | 85.91 | 87.04 | |
| SKSCF | Mean AUC (%) | 59.33 | 60.82 | 62.30 |
| Mean FPS (%) | 14 | 11 | 8 | |
| Mean DP (%) | 82.00 | 84.20 | 85.00 | |
| KSCF | Mean AUC (%) | 56.20 | 57.10 | 57.50 |
| Mean FPS (%) | 94 | 55 | 35 |
| Attributes | FM | BC | MB | DEF | IV | IPR | LR | OCC | OPR | OV | SV | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Precision | SKSCF-Proposed | 0.798 | 0.829 | 0.835 | 0.899 | 0.853 | 0.811 | 0.598 | 0.890 | 0.865 | 0.815 | 0.800 |
| SKSCF_HoG_CN [13] | 0.779 | 0.859 | 0.802 | 0.893 | 0.841 | 0.810 | 0.596 | 0.872 | 0.857 | 0.800 | 0.809 | |
| KSCF_HoG_CN [13] | 0.680 | 0.825 | 0.761 | 0.854 | 0.805 | 0.816 | 0.555 | 0.852 | 0.836 | 0.697 | 0.768 | |
| MEEM [27] | 0.745 | 0.802 | 0.721 | 0.856 | 0.771 | 0.796 | 0.529 | 0.801 | 0.840 | 0.726 | 0.795 | |
| TGPR [63] | 0.579 | 0.763 | 0.570 | 0.760 | 0.695 | 0.683 | 0.567 | 0.668 | 0.693 | 0.535 | 0.637 | |
| KCF [32] | 0.564 | 0.752 | 0.599 | 0.747 | 0.687 | 0.692 | 0.379 | 0.735 | 0.718 | 0.589 | 0.680 | |
| SCM [24] | 0.346 | 0.578 | 0.358 | 0.589 | 0.613 | 0.613 | 0.305 | 0.646 | 0.621 | 0.429 | 0.672 | |
| TLD [60] | 0.557 | 0.428 | 0.523 | 0.495 | 0.540 | 0.588 | 0.349 | 0.556 | 0.593 | 0.576 | 0.606 | |
| ASLA [25] | 0.255 | 0.496 | 0.283 | 0.473 | 0.529 | 0.521 | 0.156 | 0.479 | 0.535 | 0.333 | 0.552 | |
| L1APG [59] | 0.367 | 0.425 | 0.379 | 0.398 | 0.341 | 0.524 | 0.460 | 0.475 | 0.490 | 0.329 | 0.472 | |
| MIL [18] | 0.415 | 0.456 | 0.381 | 0.493 | 0.359 | 0.465 | 0.171 | 0.448 | 0.484 | 0.393 | 0.471 | |
| CT [57] | 0.330 | 0.339 | 0.314 | 0.463 | 0.365 | 0.361 | 0.152 | 0.429 | 0.405 | 0.336 | 0.448 | |
| SRDCFdecon [40] | 0.686 | 0.597 | 0.704 | 0.543 | 0.593 | 0.563 | 0.605 | 0.585 | 0.606 | 0.643 | 0.633 | |
| SRDCF [35] | 0.728 | 0.641 | 0.734 | 0.697 | 0.665 | 0.674 | 0.696 | 0.694 | 0.724 | 0.734 | 0.694 | |
| LCT [58] | 0.541 | 0.504 | 0.559 | 0.537 | 0.572 | 0.558 | 0.508 | 0.525 | 0.566 | 0.595 | 0.555 | |
| CSRDCF [38] | 0.728 | 0.859 | 0.838 | 0.839 | 0.792 | 0.782 | 0.879 | 0.790 | 0.806 | 0.827 | 0.808 | |
| STAPLE [62] | 0.550 | 0.654 | 0.553 | 0.573 | 0.617 | 0.596 | 0.530 | 0.581 | 0.624 | 0.621 | 0.593 | |
| BIT [56] | 0.492 | 0.562 | 0.531 | 0.498 | 0.539 | 0.508 | 0.493 | 0.546 | 0.565 | 0.560 | 0.491 | |
| Success | SKSCF-Proposed | 0.734 | 0.796 | 0.755 | 0.870 | 0.759 | 0.710 | 0.581 | 0.794 | 0.762 | 0.813 | 0.679 |
| SKSCF_HoG_CN [13] | 0.729 | 0.795 | 0.757 | 0.863 | 0.743 | 0.720 | 0.542 | 0.788 | 0.757 | 0.808 | 0.682 | |
| KSCF_HoG_CN [13] | 0.629 | 0.741 | 0.689 | 0.779 | 0.649 | 0.690 | 0.389 | 0.696 | 0.697 | 0.705 | 0.540 | |
| MEEM [27] | 0.706 | 0.747 | 0.692 | 0.711 | 0.653 | 0.648 | 0.470 | 0.694 | 0.694 | 0.742 | 0.594 | |
| TGPR [63] | 0.542 | 0.713 | 0.570 | 0.711 | 0.632 | 0.601 | 0.501 | 0.592 | 0.603 | 0.546 | 0.505 | |
| KCF [32] | 0.516 | 0.669 | 0.539 | 0.668 | 0.534 | 0.575 | 0.358 | 0.593 | 0.587 | 0.589 | 0.477 | |
| SCM [24] | 0.348 | 0.550 | 0.358 | 0.566 | 0.586 | 0.574 | 0.308 | 0.602 | 0.576 | 0.449 | 0.635 | |
| TLD [60] | 0.475 | 0.388 | 0.485 | 0.434 | 0.461 | 0.477 | 0.327 | 0.455 | 0.489 | 0.516 | 0.494 | |
| ASLA [25] | 0.261 | 0.468 | 0.284 | 0.485 | 0.514 | 0.496 | 0.163 | 0.469 | 0.509 | 0.359 | 0.544 | |
| L1APG [59] | 0.359 | 0.404 | 0.363 | 0.398 | 0.298 | 0.445 | 0.458 | 0.437 | 0.423 | 0.341 | 0.407 | |
| MIL [18] | 0.353 | 0.414 | 0.261 | 0.440 | 0.300 | 0.339 | 0.157 | 0.378 | 0.369 | 0.416 | 0.335 | |
| CT [57] | 0.327 | 0.323 | 0.262 | 0.420 | 0.308 | 0.290 | 0.143 | 0.360 | 0.325 | 0.405 | 0.342 | |
| SRDCFdecon [40] | 0.533 | 0.457 | 0.558 | 0.402 | 0.458 | 0.424 | 0.447 | 0.430 | 0.452 | 0.481 | 0.469 | |
| SRDCF [35] | 0.564 | 0.461 | 0.591 | 0.503 | 0.503 | 0.484 | 0.463 | 0.511 | 0.519 | 0.537 | 0.502 | |
| LCT [58] | 0.413 | 0.369 | 0.437 | 0.374 | 0.398 | 0.391 | 0.294 | 0.371 | 0.389 | 0.418 | 0.364 | |
| CSRDCF [38] | 0.592 | 0.616 | 0.627 | 0.574 | 0.585 | 0.556 | 0.567 | 0.572 | 0.573 | 0.589 | 0.558 | |
| STAPLE [62] | 0.437 | 0.485 | 0.446 | 0.433 | 0.490 | 0.440 | 0.335 | 0.453 | 0.459 | 0.467 | 0.431 | |
| BIT [56] | 0.386 | 0.392 | 0.409 | 0.378 | 0.377 | 0.368 | 0.285 | 0.394 | 0.390 | 0.398 | 0.333 |
| Attributes | FM | BC | MB | DEF | IV | IPR | LR | OCC | OPR | OV | SV | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Precision | SKSCF-Proposed | 0.878 | 0.837 | 0.809 | 0.846 | 0.847 | 0.811 | 0.872 | 0.798 | 0.828 | 0.698 | 0.804 |
| MBD [41] | 0.780 | 0.783 | 0.757 | 0.813 | 0.765 | 0.801 | 0.808 | 0.783 | 0.816 | 0.713 | 0.799 | |
| HDT [54] | 0.833 | 0.844 | 0.789 | 0.835 | 0.819 | 0.844 | 0.846 | 0.783 | 0.815 | 0.633 | 0.817 | |
| MEEM [27] | 0.781 | 0.746 | 0.731 | 0.786 | 0.746 | 0.794 | 0.631 | 0.769 | 0.813 | 0.685 | 0.757 | |
| Struck [55] | 0.633 | 0.550 | 0.577 | 0.549 | 0.558 | 0.628 | 0.671 | 0.546 | 0.604 | 0.468 | 0.611 | |
| KCF [32] | 0.630 | 0.712 | 0.600 | 0.627 | 0.713 | 0.693 | 0.560 | 0.631 | 0.678 | 0.498 | 0.641 | |
| TLD [60] | 0.582 | 0.515 | 0.530 | 0.515 | 0.571 | 0.606 | 0.531 | 0.558 | 0.588 | 0.463 | 0.584 | |
| CXT [61] | 0.568 | 0.444 | 0.545 | 0.415 | 0.511 | 0.599 | 0.509 | 0.454 | 0.538 | 0.388 | 0.538 | |
| SCM [24] | 0.331 | 0.578 | 0.269 | 0.572 | 0.608 | 0.544 | 0.602 | 0.574 | 0.582 | 0.425 | 0.577 | |
| Staple [62] | 0.659 | 0.560 | 0.597 | 0.569 | 0.588 | 0.648 | 0.634 | 0.566 | 0.674 | 0.494 | 0.675 | |
| SRDCF [35] | 0.677 | 0.580 | 0.600 | 0.579 | 0.598 | 0.665 | 0.645 | 0.579 | 0.683 | 0.510 | 0.683 | |
| Success | SKSCF-Proposed | 0.595 | 0.589 | 0.596 | 0.559 | 0.616 | 0.538 | 0.515 | 0.621 | 0.545 | 0.534 | 0.560 |
| MBD [41] | 0.595 | 0.577 | 0.592 | 0.558 | 0.553 | 0.562 | 0.457 | 0.557 | 0.573 | 0.483 | 0.526 | |
| HDT [54] | 0.568 | 0.578 | 0.574 | 0.543 | 0.409 | 0.555 | 0.401 | 0.528 | 0.510 | 0.472 | 0.486 | |
| MEEM [27] | 0.542 | 0.530 | 0.522 | 0.489 | 0.516 | 0.513 | 0.367 | 0.504 | 0.465 | .0475 | 0.502 | |
| Struck [55] | 0.408 | 0.416 | 0.447 | 0.452 | 0.373 | 0.382 | 0.372 | 0.328 | 0.389 | 0.333 | 0.374 | |
| KCF [32] | 0.459 | 0.497 | 0.468 | 0.436 | 0.401 | 0.468 | 0.388 | 0.443 | 0.457 | 0.396 | 0.394 | |
| TLD [60] | 0.392 | 0.438 | 0.399 | 0.420 | 0.369 | 0.355 | 0.399 | 0.306 | 0.368 | 0.300 | 0.349 | |
| SCM [24] | 0.355 | 0.409 | 0.442 | 0.397 | 0.421 | 0.386 | 0.407 | 0.345 | 0.396 | 0.432 | 0.406 | |
| Staple [62] | 0.537 | 0.574 | 0.546 | 0.554 | 0.598 | 0.552 | 0.422 | 0.548 | 0.534 | 0.481 | 0.525 | |
| SRDCF [35] | 0.597 | 0.583 | 0.594 | 0.544 | 0.613 | 0.544 | 0.514 | 0.599 | 0.550 | 0.463 | 0.561 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fawad; Jamil Khan, M.; Rahman, M.; Amin, Y.; Tenhunen, H. Low-Rank Multi-Channel Features for Robust Visual Object Tracking. Symmetry 2019, 11, 1155. https://doi.org/10.3390/sym11091155
Fawad, Jamil Khan M, Rahman M, Amin Y, Tenhunen H. Low-Rank Multi-Channel Features for Robust Visual Object Tracking. Symmetry. 2019; 11(9):1155. https://doi.org/10.3390/sym11091155
Chicago/Turabian StyleFawad, Muhammad Jamil Khan, MuhibUr Rahman, Yasar Amin, and Hannu Tenhunen. 2019. "Low-Rank Multi-Channel Features for Robust Visual Object Tracking" Symmetry 11, no. 9: 1155. https://doi.org/10.3390/sym11091155
APA StyleFawad, Jamil Khan, M., Rahman, M., Amin, Y., & Tenhunen, H. (2019). Low-Rank Multi-Channel Features for Robust Visual Object Tracking. Symmetry, 11(9), 1155. https://doi.org/10.3390/sym11091155






