Optical Helicity and Optical Chirality in Free Space and in the Presence of Matter
Abstract
1. Introduction
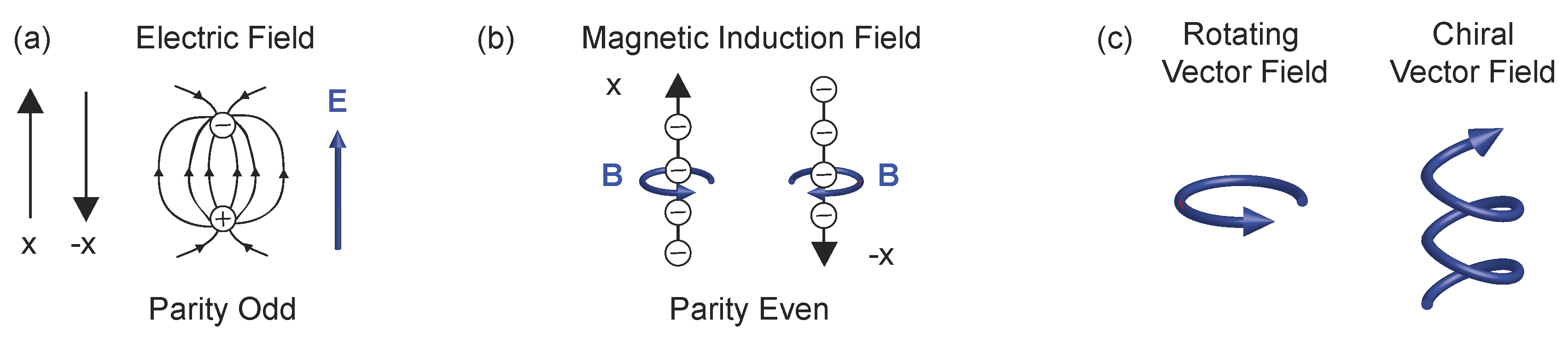
2. Rotating and Handed Vector Fields
3. Physical Significance of Optical Helicity and Optical Chirality in Free Space
Chiral Symmetries in Electromagnetism
4. Physical Significance of Optical Helicity and Chirality upon Interaction with Matter
4.1. Observables Derived from Chiral Electromagnetism
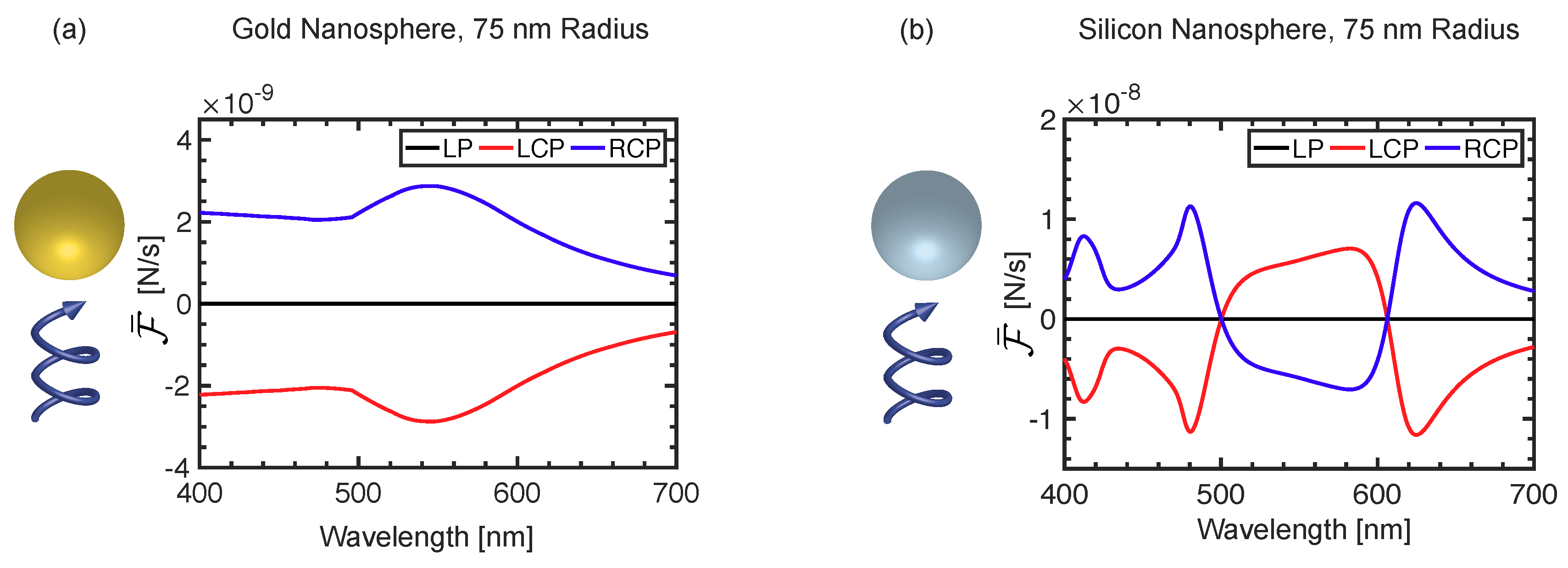
5. Chiral Light–Matter Interactions in Artificial Nanostructures
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Richardson, G. The Foundations of Stereo Chemistry: Memoirs by Pasteur, Van’t Hoff, Lebel and Wislicenus; American Book Company: New York, NY, USA, 1901. [Google Scholar]
- Eriksson, T.; Björkman, S.; Höglund, P. Clinical pharmacology of thalidomide. Eu. J. Clin. Pharmacol. 2001, 57, 365–376. [Google Scholar] [CrossRef] [PubMed]
- Seo, J.S.; Whang, D.; Lee, H.; Im Jun, S.; Oh, J.; Jeon, Y.J.; Kim, K. A homochiral metal-organic porous material for enantioselective separation and catalysis. Nature 2000, 404, 982. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Abney, C.; Lin, W. Enantioselective catalysis with homochiral metal-organic frameworks. Chem. Soc. Rev. 2009, 38, 1248–1256. [Google Scholar] [CrossRef] [PubMed]
- Blaser, H.U.; Federsel, H.J. Asymmetric Catalysis on Industrial Scale: Challenges, Approaches and Solutions; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2004. [Google Scholar]
- Tang, Y.; Cohen, A.E. Enhanced enantioselectivity in excitation of chiral molecules by superchiral light. Science 2011, 332, 333–336. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Saleh, A.A.; van de Haar, M.A.; Baum, B.; Briggs, J.A.; Lay, A.; Reyes-Becerra, O.A.; Dionne, J.A. Nanoscopic control and quantification of enantioselective optical forces. Nat. Nanotechnol. 2017, 12, 1055. [Google Scholar] [CrossRef] [PubMed]
- Petersen, J.; Volz, J.; Rauschenbeutel, A. Chiral nanophotonic waveguide interface based on spin-orbit interaction of light. Science 2014, 346, 67–71. [Google Scholar] [CrossRef]
- Le Feber, B.; Rotenberg, N.; Kuipers, L. Nanophotonic control of circular dipole emission. Nat. Commun. 2015, 6, 6695. [Google Scholar] [CrossRef]
- Papakostas, A.; Potts, A.; Bagnall, D.; Prosvirnin, S.; Coles, H.; Zheludev, N. Optical manifestations of planar chirality. Phys. Rev. Lett. 2003, 90, 107404. [Google Scholar] [CrossRef]
- Gansel, J.K.; Thiel, M.; Rill, M.S.; Decker, M.; Bade, K.; Saile, V.; von Freymann, G.; Linden, S.; Wegener, M. Gold helix photonic metamaterial as broadband circular polarizer. Science 2009, 325, 1513–1515. [Google Scholar] [CrossRef]
- Hendry, E.; Carpy, T.; Johnston, J.; Popland, M.; Mikhaylovskiy, R.; Lapthorn, A.; Kelly, S.; Barron, L.; Gadegaard, N.; Kadodwala, M. Ultrasensitive detection and characterization of biomolecules using superchiral fields. Nat. Nanotechnol. 2010, 5, 783–787. [Google Scholar] [CrossRef]
- Hentschel, M.; Schäferling, M.; Weiss, T.; Liu, N.; Giessen, H. Three-dimensional chiral plasmonic oligomers. Nano Lett. 2012, 12, 2542–2547. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Belkin, M.; Alù, A. Twisted optical metamaterials for planarized ultrathin broadband circular polarizers. Nat. Commun. 2012, 3, 870. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Schäferling, M.; Metzger, B.; Giessen, H. Interpreting chiral nanophotonic spectra: The plasmonic Born-Kuhn model. Nano Lett. 2013, 13, 6238–6243. [Google Scholar] [CrossRef] [PubMed]
- Mark, A.G.; Gibbs, J.G.; Lee, T.C.; Fischer, P. Hybrid nanocolloids with programmed three-dimensional shape and material composition. Nat. Mater. 2013, 12, 802. [Google Scholar] [CrossRef] [PubMed]
- Schamel, D.; Pfeifer, M.; Gibbs, J.G.; Miksch, B.r.; Mark, A.G.; Fischer, P. Chiral Colloidal Molecules and Observation of the Propeller Effect. J. Am. Chem. Soc. 2013, 135, 12353–12359. [Google Scholar] [CrossRef] [PubMed]
- Schäferling, M.; Yin, X.; Engheta, N.; Giessen, H. Helical plasmonic nanostructures as prototypical chiral near-field sources. ACS Photonics 2014, 1, 530–537. [Google Scholar] [CrossRef]
- McPeak, K.M.; van Engers, C.D.; Blome, M.; Park, J.H.; Burger, S.; Gosalvez, M.A.; Faridi, A.; Ries, Y.R.; Sahu, A.; Norris, D.J. Complex Chiral Colloids and Surfaces via High-Index Off-Cut Silicon. Nano Lett. 2014, 14, 2934–2940. [Google Scholar] [CrossRef]
- Yeom, J.; Yeom, B.; Chan, H.; Smith, K.W.; Dominguez-Medina, S.; Bahng, J.H.; Zhao, G.; Chang, W.S.; Chang, S.J.; Chuvilin, A.; et al. Chiral templating of self-assembling nanostructures by circularly polarized light. Nat. Mater. 2015, 14, 66. [Google Scholar] [CrossRef]
- Wang, L.Y.; Smith, K.W.; Dominguez-Medina, S.; Moody, N.; Olson, J.M.; Zhang, H.; Chang, W.S.; Kotov, N.; Link, S. Circular Differential Scattering of Single Chiral Self-Assembled Gold Nanorod Dimers. ACS Photonics 2015, 2, 1602–1610. [Google Scholar] [CrossRef]
- McPeak, K.M.; van Engers, C.D.; Bianchi, S.; Rossinelli, A.; Poulikakos, L.V.; Bernard, L.; Herrmann, S.; Kim, D.K.; Burger, S.; Blome, M.; et al. Ultraviolet plasmonic chirality from colloidal aluminum nanoparticles exhibiting charge-selective protein detection. Adv. Mater. 2015, 27, 6244–6250. [Google Scholar] [CrossRef]
- Tullius, R.; Karimullah, A.S.; Rodier, M.; Fitzpatrick, B.; Gadegaard, N.; Barron, L.D.; Rotello, V.M.; Cooke, G.; Lapthorn, A.; Kadodwala, M. “Superchiral” spectroscopy: Detection of protein higher order hierarchical structure with chiral plasmonic nanostructures. J. Am. Chem. Soc. 2015, 137, 8380–8383. [Google Scholar] [CrossRef] [PubMed]
- Kosters, D.; De Hoogh, A.; Zeijlemaker, H.; Acar, H.; Rotenberg, N.; Kuipers, L. Core-shell plasmonic nanohelices. ACS Photonics 2017, 4, 1858–1863. [Google Scholar] [CrossRef] [PubMed]
- Hentschel, M.; Schäferling, M.; Duan, X.; Giessen, H.; Liu, N. Chiral plasmonics. Sci. Adv. 2017, 3, e1602735. [Google Scholar] [CrossRef] [PubMed]
- Karst, J.; Strohfeldt, N.; Schäferling, M.; Giessen, H.; Hentschel, M. Single plasmonic oligomer chiral spectroscopy. Adv. Opt. Mater. 2018, 6, 1800087. [Google Scholar] [CrossRef]
- Lee, H.E.; Ahn, H.Y.; Mun, J.; Lee, Y.Y.; Kim, M.; Cho, N.H.; Chang, K.; Kim, W.S.; Rho, J.; Nam, K.T. Amino-acid-and peptide-directed synthesis of chiral plasmonic gold nanoparticles. Nature 2018, 556, 360. [Google Scholar] [CrossRef] [PubMed]
- Karst, J.; Cho, N.H.; Kim, H.; Lee, H.E.; Nam, K.T.; Giessen, H.; Hentschel, M. Chiral scatterometry on chemically synthesized single plasmonic nanoparticles. ACS Nano 2019. [Google Scholar] [CrossRef] [PubMed]
- García-Etxarri, A.; Dionne, J.A. Surface-enhanced circular dichroism spectroscopy mediated by nonchiral nanoantennas. Phys. Rev. B 2013, 87, 235409. [Google Scholar] [CrossRef]
- Ho, C.S.; Garcia-Etxarri, A.; Zhao, Y.; Dionne, J. Enhancing enantioselective absorption using dielectric nanospheres. ACS Photonics 2017, 4, 197–203. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, T.; Wang, R.; Zhang, X. Amplification of the molecular chiroptical effect by low-loss dielectric nanoantennas. Nanoscale 2017, 9, 5701–5707. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, E.; Tsakmakidis, K.L.; Askarpour, A.N.; Dehkhoda, P.; Tavakoli, A.; Altug, H. Nanophotonic platforms for enhanced chiral sensing. ACS Photonics 2018, 5, 2669–2675. [Google Scholar] [CrossRef]
- Solomon, M.L.; Hu, J.; Lawrence, M.; García-Etxarri, A.; Dionne, J.A. Enantiospecific optical enhancement of chiral sensing and separation with dielectric metasurfaces. ACS Photonics 2018, 6, 43–49. [Google Scholar] [CrossRef]
- Yao, K.; Liu, Y. Enhancing circular dichroism by chiral hotspots in silicon nanocube dimers. Nanoscale 2018, 10, 8779–8786. [Google Scholar] [CrossRef] [PubMed]
- Graf, F.; Feis, J.; Garcia-Santiago, X.; Wegener, M.; Rockstuhl, C.; Fernandez-Corbaton, I. Achiral, helicity preserving, and resonant structures for enhanced sensing of chiral molecules. ACS Photonics 2019, 6, 482–491. [Google Scholar] [CrossRef]
- Hanifeh, M.; Capolino, F. Helicity density enhancement in a planar array of achiral high-density dielectric nanoparticles. arXiv 2019, arXiv:1905.03387. [Google Scholar]
- Zhao, X.; Reinhard, B.M. Switchable Chiroptical Hot-Spots in Silicon Nanodisk Dimers. ACS Photonics 2019. [Google Scholar] [CrossRef]
- Mohammadi, E.; Tavakoli, A.; Dehkhoda, P.; Jahani, Y.; Tsakmakidis, K.L.; Tittl, A.; Altug, H. Accessible superchiral near-fields driven by tailored electric and magnetic resonances in all-dielectric nanostructures. ACS Photonics 2019. [Google Scholar] [CrossRef]
- Govorov, A.O.; Gun’ko, Y.K.; Slocik, J.M.; Gérard, V.A.; Fan, Z.; Naik, R.R. Chiral nanoparticle assemblies: Circular dichroism, plasmonic interactions, and exciton effects. J. Mater. Chem. 2011, 21, 16806–16818. [Google Scholar] [CrossRef]
- Valev, V.K.; Baumberg, J.J.; Sibilia, C.; Verbiest, T. Chirality and chiroptical effects in plasmonic nanostructures: fundamentals, recent progress, and outlook. Adv. Mater. 2013, 25, 2517–2534. [Google Scholar] [CrossRef]
- Ben-Moshe, A.; Maoz, B.M.; Govorov, A.O.; Markovich, G. Chirality and chiroptical effects in inorganic nanocrystal systems with plasmon and exciton resonances. Chem. Soc. Rev. 2013, 42, 7028–7041. [Google Scholar] [CrossRef]
- Smith, K.W.; Link, S.; Chang, W.S. Optical characterization of chiral plasmonic nanostructures. J. Photochem. Photobiol. C Photochem. Rev. 2017, 32, 40–57. [Google Scholar] [CrossRef]
- Barnett, S.M.; Cameron, R.P.; Yao, A.M. Duplex symmetry and its relation to the conservation of optical helicity. Phys. Rev. A 2012, 86, 013845. [Google Scholar] [CrossRef]
- Crimin, F.; Mackinnon, N.; Götte, J.; Barnett, S. Optical helicity and chirality: Conservation and sources. Appl. Sci. 2019, 9, 828. [Google Scholar] [CrossRef]
- Tung, W.K. Group Theory in Physics: An Introduction to Symmetry Principles, Group Representations, and Special Functions in Classical and Quantum Physics; World Scientific Publishing Company: Singapore, 1985. [Google Scholar]
- Schwartz, M.D. Quantum Field Theory and the Standard Model; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Moffatt, H.K. The degree of knottedness of tangled vortex lines. J. Fluid Mech. 1969, 35, 117–129. [Google Scholar] [CrossRef]
- Berger, M.A. Introduction to magnetic helicity. Plasma Phys. Control. Fusion 1999, 41, B167. [Google Scholar] [CrossRef]
- Cameron, R.P. On the “second potential” in electrodynamics. J. Opt. 2013, 16, 015708. [Google Scholar] [CrossRef]
- Fernandez-Corbaton, I.; Zambrana-Puyalto, X.; Tischler, N.; Vidal, X.; Juan, M.L.; Molina-Terriza, G. Electromagnetic duality symmetry and helicity conservation for the macroscopic maxwells equations. Phys. Rev. Lett. 2013, 111, 060401. [Google Scholar] [CrossRef] [PubMed]
- Cameron, R.P.; Barnett, S.M.; Yao, A.M. Optical helicity, optical spin and related quantities in electromagnetic theory. New J. Phys. 2012, 14, 053050. [Google Scholar] [CrossRef]
- Candlin, D. Analysis of the New Conservation Law in Electromagnetic Theory. Il Nuovo Cimento (1955–1965) 1965, 37, 1390–1395. [Google Scholar] [CrossRef]
- Kibble, T. Conservation laws for free fields. J. Math. Phys. 1965, 6, 1022–1026. [Google Scholar] [CrossRef]
- Tang, Y.; Cohen, A.E. Optical chirality and its interaction with matter. Phys. Rev. Lett. 2010, 104, 163901. [Google Scholar] [CrossRef]
- Lipkin, D.M. Existence of a New Conservation Law in Electromagnetic Theory. J. Math. Phys. 1964, 5, 696–700. [Google Scholar] [CrossRef]
- Noether, E. Invariante variations probleme. Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Gottingen (Royal Society of Sciences, Gottingen) 1918, 235–257, 1918. [Google Scholar]
- Calkin, M.G. An Invariance Property of the Free Electromagnetic Field. Am. J. Phys. 1965, 33, 958–960. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Bekshaev, A.Y.; Nori, F. Dual electromagnetism: Helicity, spin, momentum and angular momentum. New J. Phys. 2013, 15, 033026. [Google Scholar] [CrossRef]
- Sayir, M.; Dual, J.; Kaufmann, S. Ingenieurmechanik 1; Springer: Wiesbaden, Germany, 2008. [Google Scholar]
- Hafner, C. (ETH Zürich, Zürich, ZH, Switzerland). Personal Communication, 2016. [Google Scholar]
- Poulikakos, L.V. Chiral Light–Matter Interactions in the Near and Far Field. Ph.D. Thesis, ETH Zürich, Zürich, Switzerland, 2018. [Google Scholar]
- Guasti, M.F. Chirality, helicity and the rotational content of electromagnetic fields. Phys. Lett. A 2019, 383, 3180–3186. [Google Scholar] [CrossRef]
- Barron, L. Chirality at the Nanoscale; Wiley-VCH Verlag: Weinheim, BW, Germany; GmbH and Co. KGaA: Dusseldorf, Germany, 2009. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1999. [Google Scholar]
- Hafner, C. Numerische Berechnung Elektromagnetischer Felder, Grundlagen, Methoden, Anwendungen; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Poulikakos, L.V.; Gutsche, P.; McPeak, K.M.; Burger, S.; Niegemann, J.; Hafner, C.; Norris, D.J. Optical chirality flux as a useful far-field probe of chiral near fields. ACS Photonics 2016, 3, 1619–1625. [Google Scholar] [CrossRef]
- Vázquez-Lozano, J.E.; Martínez, A. Optical chirality in dispersive and lossy media. Phys. Rev. Lett. 2018, 121, 043901. [Google Scholar] [CrossRef]
- Philbin, T.G. Lipkin’s conservation law, noether’s theorem, and the relation to optical helicity. Phys. Rev. A 2013, 87, 043843. [Google Scholar] [CrossRef]
- Van Kruining, K.; Götte, J.B. The conditions for the preservation of duality symmetry in a linear medium. J. Opt. 2016, 18, 085601. [Google Scholar] [CrossRef]
- Nienhuis, G. Conservation laws and symmetry transformations of the electromagnetic field with sources. Phys. Rev. A 2016, 93, 023840. [Google Scholar] [CrossRef]
- Alpeggiani, F.; Bliokh, K.; Nori, F.; Kuipers, L. Electromagnetic helicity in complex media. Phys. Rev. Lett. 2018, 120, 243605. [Google Scholar] [CrossRef] [PubMed]
- Zambrana-Puyalto, X.; Vidal, X.; Juan, M.L.; Molina-Terriza, G. Dual and anti-dual modes in dielectric spheres. Opt. Express 2013, 21, 17520–17530. [Google Scholar] [CrossRef] [PubMed]
- Zambrana-Puyalto, X.; Fernandez-Corbaton, I.; Juan, M.; Vidal, X.; Molina-Terriza, G. Duality symmetry and Kerker conditions. Opt. Lett. 2013, 38, 1857–1859. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.K.; Aizpurua, J.; Zambrana-Puyalto, X.; Vidal, X.; Molina-Terriza, G.; Sáenz, J.J. Isotropically polarized speckle patterns. Phys. Rev. Lett. 2015, 114, 113902. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.; Woerdman, J. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185. [Google Scholar] [CrossRef] [PubMed]
- Simpson, N.; Dholakia, K.; Allen, L.; Padgett, M. Mechanical equivalence of spin and orbital angular momentum of light: An optical spanner. Opt. Lett. 1997, 22, 52–54. [Google Scholar] [CrossRef]
- Padgett, M.; Courtial, J.; Allen, L. Light’s orbital angular momentum. Phys. Today 2004, 57, 35–40. [Google Scholar] [CrossRef]
- Garcia-Etxarri, A. Optical polarization mobius strips on all-dielectric optical scatterers. ACS Photonics 2017, 4, 1159–1164. [Google Scholar] [CrossRef]
- Olmos-Trigo, J.; Sanz-Fernández, C.; García-Etxarri, A.; Molina-Terriza, G.; Bergeret, F.S.; Sáenz, J.J. Enhanced spin-orbit optical mirages from dual nanospheres. Phys. Rev. A 2019, 99, 013852. [Google Scholar] [CrossRef]
- Olmos-Trigo, J.; Sanz-Fernández, C.; Abujetas, D.R.; García-Etxarri, A.; Molina-Terriza, G.; Sánchez-Gil, J.; Bergeret, S.F.; Saénz, J.J. Role of the absorption on the spin-orbit interactions of light with Si nano-particles. arXiv 2019, arXiv:1903.03816. [Google Scholar] [CrossRef]
- Fernandez-Corbaton, I.; Zambrana-Puyalto, X.; Molina-Terriza, G. Helicity and angular momentum: A symmetry-based framework for the study of light-matter interactions. Phys. Rev. A 2012, 86, 042103. [Google Scholar] [CrossRef]
- Nieto-Vesperinas, M. Optical theorem for the conservation of electromagnetic helicity: Significance for molecular energy transfer and enantiomeric discrimination by circular dichroism. Phys. Rev. A 2015, 92, 023813. [Google Scholar] [CrossRef]
- Poulikakos, L.V.; Thureja, P.; Stollmann, A.; De Leo, E.; Norris, D.J. Chiral light design and detection inspired by optical antenna theory. Nano Lett. 2018, 18, 4633–4640. [Google Scholar] [CrossRef] [PubMed]
- Gutsche, P.; Poulikakos, L.V.; Hammerschmidt, M.; Burger, S.; Schmidt, F. Time-harmonic optical chirality in inhomogeneous space. In Opto, Photonic and Phononic Properties of Engineered Nanostructures VI; International Society for Optics and Photonics: San Francisco, CA, USA, 2016; Volume 9756. [Google Scholar]
- Collett, E. Field Guide to Polarization; SPIE Press: Bellingham, WA, USA, 2005; Volume FG05. [Google Scholar]
- Schnoering, G.; Poulikakos, L.V.; Rosales-Cabara, Y.; Canaguier-Durand, A.; Norris, D.J.; Genet, C. Three-dimensional enantiomeric recognition of optically trapped single chiral nanoparticles. Phys. Rev. Lett. 2018, 121, 023902. [Google Scholar] [CrossRef] [PubMed]
- Schäferling, M.; Dregely, D.; Hentschel, M.; Giessen, H. Tailoring enhanced optical chirality: Design principles for chiral plasmonic nanostructures. Phys. Rev. X 2012, 2, 031010. [Google Scholar] [CrossRef]
- Choi, J.S.; Cho, M. Limitations of a Superchiral Field. Phys. Rev. A 2012, 86, 063834. [Google Scholar] [CrossRef]
- Canaguier-Durand, A.; Genet, C. Chiral near fields generated from plasmonic optical lattices. Phys. Rev. A 2014, 90, 023842. [Google Scholar] [CrossRef]
- Hanifeh, M.; Albooyeh, M.; Capolino, F. Helicity maximization of structured light to empower nanoscale chiral matter interaction. arXiv 2018, arXiv:1809.04119. [Google Scholar]
- Hanifeh, M.; Albooyeh, M.; Capolino, F. Empowering Structured Light to Enhance Chirality Detection and Characterization at Nanoscale. In Opto, Complex Light and Optical Forces XIII; International Society for Optics and Photonics: San Francisco, CA, USA, 2019; Volume 10935, p. 1093504. [Google Scholar]
- Novotny, L.; Hecht, B. Principles of Nano-Optics, 2nd ed.; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Moffatt, H.K. Helicity and Singular Structures in Fluid Dynamics. Proc. Natl. Acad. Sci. USA 2014, 111, 3663–3670. [Google Scholar] [CrossRef] [PubMed]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Aspnes, D.E.; Studna, A.A. Dielectric functions and optical parameters of Si, Ge, GaP, GaAs, GaSb, InP, InAs, and InSb from 1.5 to 6.0 Ev. Phys. Rev. B 1983, 27, 985. [Google Scholar] [CrossRef]
- Hashiyada, S.; Narushima, T.; Okamoto, H. Imaging chirality of optical fields near achiral metal nanostructures excited with linearly polarized light. ACS Photonics 2018, 5, 1486–1492. [Google Scholar] [CrossRef]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Capolino, F. Theory and Phenomena of Metamaterials; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2009. [Google Scholar]

| Optical Helicity Conservation in Free Space | Optical Chirality Conservation in Free Space |
|---|---|
| Physical Significance | Fundamental | → | Observable |
|---|---|---|---|
| Classical Mechanics | |||
| Linear Motion: | Linear Momentum [] | Force [N] | |
| Rotational Motion: | Angular Momentum [] | Torque [] | |
| Classical Electrodynamics | |||
| Handed Motion: | Optical Helicity Density [] | Optical Chirality Density [] |
| Physical Quantity | Tensor Rank | Parity Symmetry | Time Symmetry |
|---|---|---|---|
| Optical Chirality Density | 3 | Odd (pseudoscalar) | Even |
| Optical Chirality Flux Density | 1 | Even (pseudovector) | Even |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poulikakos, L.V.; Dionne, J.A.; García-Etxarri, A. Optical Helicity and Optical Chirality in Free Space and in the Presence of Matter. Symmetry 2019, 11, 1113. https://doi.org/10.3390/sym11091113
Poulikakos LV, Dionne JA, García-Etxarri A. Optical Helicity and Optical Chirality in Free Space and in the Presence of Matter. Symmetry. 2019; 11(9):1113. https://doi.org/10.3390/sym11091113
Chicago/Turabian StylePoulikakos, Lisa V., Jennifer A. Dionne, and Aitzol García-Etxarri. 2019. "Optical Helicity and Optical Chirality in Free Space and in the Presence of Matter" Symmetry 11, no. 9: 1113. https://doi.org/10.3390/sym11091113
APA StylePoulikakos, L. V., Dionne, J. A., & García-Etxarri, A. (2019). Optical Helicity and Optical Chirality in Free Space and in the Presence of Matter. Symmetry, 11(9), 1113. https://doi.org/10.3390/sym11091113






