Abstract
In this review, a short description of exceptional field theory and its application is presented. Exceptional field theories provide a U-duality covariant description of supergravity theories, allowing addressing relevant phenomena, such as non-geometricity. Some applications of the formalism are briefly described.
1. Introduction
The notion of symmetry has been one of the most important drivers for theoretical physics in recent decades. Recently, of most interest have been duality symmetries relating different theories or different regimes of the same theory. The most well-known example of the former is the renowned AdS/CFT correspondence of Maldacena [1], and more generally gauge-gravity duality. This correspondence relates string theory on at small coupling and the quantum SYM at strong coupling. This is based on equivalence between two descriptions of the same near-horizon region of the D3-brane in terms of the open and closed strings, and allows addressing phenomena in CFT at strong coupling in terms of gravitational degrees of freedom at weak coupling.
String theory also possesses symmetries, called T- and S-dualities, which relate different regimes of the same theory. These allowed unifying five string theories, Type IIA/B, Type I, heterotic and , into a duality web and to understand all these as different regimes of a single theory, usually addressed as M-theory [2,3]. T-duality is a perturbative symmetry of the fundamental string and is the oldest known duality in string theory. It manifests itself in the amazing fact that Type IIA and Type IIB string theories compactified on a 1-torus are equivalent at quantum level. Most transparently this can be seen when looking at the mass spectrum of the closed string on a background with one circular direction of radius R
Here n is the number of discrete momenta of the string along the circular direction and m is the number of windings of the string around the cycle, N and correspond to the numbers of higher level left and right modes on the string. One immediately notices that the mass spectrum is symmetric under the following replacement
The symmetry relates backgrounds with radii R and upon switching string momentum and winding modes. More generally T-duality mixes metric and 2-form gauge field degrees of freedom, thus potentially completely messing up structure of space-time. In particular, the symmetry allows consistently defining string dynamics on such backgrounds, given by explicit metric and the Kalb-Ramond field that cannot be consistently described in terms of manifolds. Instead, these are related to as T-folds, which are defined as a set of patches glued by T-duality transformations, rather than diffeomorphisms [4]. Such backgrounds are called non-geometric and are of huge interest for cosmological model building as string vacua potentially capable of completely stabilizing scalar moduli ending up with a dS-like space with small cosmological constant.
T-duality is a perturbative symmetry of string theory seen already in the mass spectrum of string excitations. S-duality of Type IIB string theory provides an example of non-perturbative string symmetry. This relates strong and weak coupled regimes of the theory, and in addition relates heterotic SO and Type I strings. The net of dualities between five string theories allows understanding them as different approximations to a single 11-dimensional theory called M-theory. The 11th direction arises in the strong coupling limit of Type IIA theory.
M-theory describes dynamics of M2 and M5 branes, which are fundamental 2 and 5 dimensional objects interacting with 3-form and 6-form gauge potentials dual to each other [3]. Low-energy limit of the theory is captured by 11-dimensional maximal supergravity, whose algebra of central charges is nicely interpreted in terms of M2 and M5 brane charges [3]. M-theory compactified on a circle gives Type IIA theory with the fundamental string arising from wrapped M2 brane. Compactifying M-theory on a 2-torus one recovers either Type IIA or Type IIB depending on the reduction scheme, which is the fundamental precursor for T-duality symmetry between these theory. In addition, modular symmetry of the torus gives rise to S-duality symmetry of Type IIB as will be explained in more details below. Together, T- and S-duality of the string combine into a set of U-duality symmetries, which appears to be a powerful tool for investigating properties and the internal structure of M-theory. This review is focused on duality symmetries of string and M-theory and in particular at approaches to supergravity covariant with respect to these symmetries.
1.1. Dualities in String Theory
S-duality is a hidden symmetry of the Type IIB string theory which relates strong and weak coupling regimes. On the field theory level this can be recovered by inspecting spectrum of massless modes of the Type IIB string, which includes
where g is the metric, is the scalar field called the dilaton and the 4-form gauge field is defined to have self-dual field strength. With the action of the S-duality group SL the fields drop into irreducible representations with g being a scalar, the 2-forms combine into a doubled and the scalar fields combine into the so-called axio-dilaton defined as
Axio-dilaton transforms non-linearly under S-duality
The existence of this hidden symmetry of the Type IIB massless string spectrum suggests that the supergravity action can be rewritten in an SL-covariant form, which is indeed possible and results in the following (see e.g., [5]):
where the indices label the fundamental representation of and
One may notice that the transformation (5) has the form that of the transformation of complex structure of a 2-torus. This observation leads to the geometrical picture which is behind F-theory, a 12-dimensional field theory, whose compactification on a 2-torus gives an orientifold reduction of Type IIB theory (for more details see e.g., [6,7]). Freedom in definition of a complex structure on the 2-torus of F-theory is equivalent to the S-duality symmetry of the 10-dimensional theory. Such geometric interpretation of a symmetry of a theory goes along the line of the old Kaluza-Klein idea, where the U(1) gauge symmetry of Maxwell theory is lifted into reparametrisations of a small circle (1-torus) of a 5-dimensional gravitational theory with no electromagnetic degrees of freedom. In this short review we highlight basic features and list some applications of the so-called Doubled (Exceptional) Field Theory, which does the same to T(U)-dualities of string (M-)theory, i.e., provides a geometric interpretation of the duality symmetries in terms of geometry of an especially constructed higher dimensional space.
T-duality is a hidden symmetry of the 2-dimensional non-linear sigma model (string theory) which relates the theory on a torus with radius of a given direction x and the same theory on a torus with radius of the same direction. Under T-duality transformation of the string background, given by the metric, Kalb-Ramond 2-form field, the dilaton and the RR fields, partition function of the string does not change. Consider the action for the closed string on a background with one circular direction in the conformal gauge and adopt the light cone world-sheet coordinates
Here label all ten space-time directions, parametrizes the compact direction and parametrize the rest. For the background fields we define . To see that the action above is invariant under replacing the circle of radius R by a circle of the inverse radius parametrized by , one used the global symmetry and turns it into a local one. The gauging is performed by introducing a world-volume 1-form gauge field and replacing normal derivatives by covariant e . To turn back to the correct counting of the degrees of freedom in the theory one must introduce a Lagrange multiplier to restrict the gauge field to pure gauge. Hence, one arrives at the following action
where is the field strength for the gauge field A. Integrating the Lagrange multiplier out of the partition function one return back to the action . Alternatively, integrating out vector degrees of freedom A one arrives at (for more details see [8])
with the new background defined by the so-called Buscher rules
Since the partition function did not change during the above procedure, the physics of the string on two background related by the T-duality transformation (11) is the same. Taking into account the transformation of measure of the functional integral one supplements the above rules by the following transformation of the dilaton:
In the more general case of the string on a background with d compact isometric directions the group of T-duality transformations can be shown to be O. The most convenient tool for that is the so-called Duff’s procedure [9,10] which exploits hidden symmetry between equations of motion and Bianchi identities following from the action for the non-linear sigma model
For the metric and the B-field equations of motion and Bianchi identities can be rewritten in explicitly O-covariant form
Here we define combinations
of derivatives of the normal coordinates and the dual coordinates . The equation (14) can be considered to be self-duality constraints, which remove half of the fields of the full doubled set . The matrix parametrizes the background fields in a T-duality covariant manner
The invariant tensor of the O group is taken in the block-skew-diagonal form
At the level of string theory T-duality is a proper symmetry of the theory, which does not change physics upon a transformation. When reducing to the low-energy dynamics governed by 10-dimensional half-maximal supergravity, T-duality turns into a solution-generating symmetry, as it transforms a given string theory background into another one. In this case, the symmetry group O is defined over rational numbers rather than only integers. In what follows, we will always denote this group simply by O, and add explicitly when needed.
1.2. U-duality in Maximal Supergravity
When combined into the web of dualities five string theories become a single 11-dimensional M-theory, encoded in dynamics of M2 and M5 branes. T- and S-duality symmetries lift into U-dualities of the membranes; however, these are much more complicated for a sigma model analysis. In the seminal paper by Cremmer, Julia, Lu and Pope [11,12] it has been shown that 11-dimensional supergravity compactified on a d-torus possesses hidden symmetry . This is reflected in the fact that all bosonic field of the reduced theory can be collected into irreducible representations of the U-duality group, while fermionic fields transform under maximal compact subgroup of . Here the notation means that one takes maximal real subgroup of complexification of the group .
The most transparent way to see the symmetry is to analyse spectrum of fields in the lower dimensional theory obtained by reduction of the 11-dimensional fields say to 4 dimensions.
As it is shown in Figure 1 the resulting fields can be collected into the vector fields transforming in the of , scalar coset , scalars and a constant . Vector degrees of freedom coming from the metric and the 3-form field correspond 28 electric gauge potentials. To compose the irrep of , which is representation of the lowest dimension, one adds magnetic potentials and imposes self-duality condition on the U-duality covariant field strength
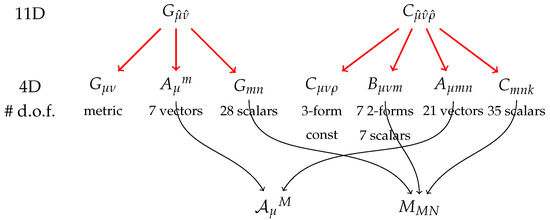
Figure 1.
Reduction of 11D fields into four dimensions, dualization into the lowest possible rank tensor and recollection into the multiplet in the and the coset space . Both magnetic and electric vectors potentials are included in the counting (see the text).
Here is the symmetric invariant tensor of and is the scalar matrix which parametrizes the coset space and the antisymmetric tensor is usually chosen to be . The field strength is defined as usual as . As it has been explicitly shown in detail in [11], to end up with irreducible representations of the U-duality group one must dualize all tensor fields to the lowest possible rank. For the 2-form field one constructs gauge invariant 3-form field strength, whose Bianchi identities and equations of motion can be swapped by Hodge dualization to a 1-form field strength. This is associated with scalar fields. To keep covariancy and to recover tensor hierarchy one must add the same amount of 2-form fields and impose duality condition.
Finally, equations of motion for the 3-form field in 4 dimensions imply that the field strength is constant. It appears that this constant is not a scalar under the U-duality group, and one must either set it to zero or to turn on all constant belonging to its representation. This can be done consistently in embedding tensor formalism, which results in a deformed theory with non-abelian gauge symmetry [13].
In conventional supergravity U-duality symmetry is a global symmetry of the theory similar to the U(1) duality symmetry of equations of motion of electrodynamics. In exceptional field theories this symmetry receives a geometric interpretation as a symmetry of the underlying space-time. To carry a proper representation of a U-duality group space-time coordinates must be extended following a special rule based on winding of branes, both standard and exotic. In Section 2.1 the construction and local symmetries of the extended space will be explained in more details, in Section 2.3 field spectrum and action of exceptional field theories will be reviewed for a general U-duality group and for as an explicit example. We will show that this theory reproduces the full 11D supergravity, Type IIA/B, D = 4 gauged and ungauged supergravities depending on the choice of solution of a special constraint called section condition. In Section 3.1 non-conventional solutions of this condition will be shown to lead to non-geometric backgrounds, i.e., such field configurations which are not globally or even locally well defined in terms of differential geometry. Finally, in Section 3.2 we consider exotic branes as T(U)-duality partners of the standard branes of string and M-theory, and review their description in terms of extended space and non-geometry in exceptional field theories.
2. Duality-Covariant Field Theories
2.1. Local Symmetries of Extended Space
Duality symmetries appear in toroidal reductions of supergravity and combine geometric symmetries of the torus (diffeomorphisms), gauge transformations and actual duality transformations mixing space-time and gauge degrees of freedom. To proceed with construction of a duality covariant theory, one understands the group of duality symmetries or more fundamentally as descending from geometrical structure of the underlying space. Since d coordinates of the d-torus do not fit into an irreducible representation of the duality group, one has to consider an extended space.
In the previous section, we saw that T-duality symmetries relate winding and momentum modes of the string, and for the string on a torus the mass spectrum can be covariantly written as
where is the generalized metric and combines the momentum and winding of the string in an O-covariant vector
The first term contains momenta in “external” non-toroidal directions . Recalling Duff’s procedure, that operates with normal and dual scalar fields on the world-volume of the string, it is natural to consider backgrounds, not necessarily toroidal that depend on the full set of T-duality covariant coordinates . Note that the generalized metric in the mass formula is constant since the background is toroidal, this is relaxed in exceptional field theory and the toroidal case is understood as the most symmetric background preserving all duality symmetries.
At the level of the non-linear sigma model extra degrees of freedom encoded by the dual scalar fields are removed by the self-duality condition (14). Similarly, T-covariant field theory with fields depending on the doubled amount of coordinates must be augmented by a constraint that reduces the number of space-time direction. Apart from reference to the sigma model, this is necessary for further supersymmetric completion of the theory to avoid higher spin fields, which normally appear in supersymmetric theories in dimensions higher than 11. The condition naturally follows from construction of local diffeomorphism symmetry on the extended space parametrized by the coordinates which is defined by the so-called generalized Lie derivative
where is a generalized vector combining a GL vector and a 1-form , the same for the transformation parameter . The tensor encoding deformation of the generalized Lie derivative away from the conventional GL Lie derivative is subject to constraints following from consistency of algebra of transformation . These constraints have been analysed in [14] and can be summarized as
Here d is the number of compact dimensions and is the projector on the adjoint representation of the corresponding duality group. It is defined as and . The coefficients and depend on the duality group and for the cases in question take numerical values , , . These conditions imply that the Y-tensor must be constructed from invariant tensors of the corresponding T- and U-duality groups (see Table 1).

Table 1.
Y-tensor for different T(U)-duality groups for string and M-theory on a d-torus. Here the Greek indices label the representation of and the index i labels the of , n denotes dimension of the representation generalized vectors of the theory transform in.
The above still does not guarantee the algebra of transformations is closed. Indeed, one writes
where the bracket is a generalisation of the Courant bracket of the Hitchin’s generalised geometry. The obstruction =for the algebra to close is proportional to terms of the type , hence one naturally imposes the so-called section constraint
where bullets stand for any combination of any fields. Similarly, one shows that the very same condition ensures satisfaction of the Jacobi identity for .
The most natural and transparent solution of the section constraint is , which is simply the condition that nothing depends on . This drops the generalized Lie derivative back to the conventional undoubled space-time and splits it into the usual Lie derivative and gauge transformations. More generally one can solve the section constraint by dropping dependence on all apart a given , and drop in addition dependence on the corresponding normal coordinate . Now one can use the set to measure distances, and hence these will correspond to geometric coordinates of the new frame. These two frames are related by a T-duality transformation along the direction d
In the next subsection we construct Exceptional Field Theories, which do not distinguish between such frames, hence providing a local T(U)-duality covariant approach to supergravity.
2.2. Winding Modes and Exotic Branes
Before proceeding with the field theory construction it is suggestive to follow the logic of counting of winding modes of M-branes in M-theory in details. In contrast to the string, where the winding mode is always parametrized by a 1-form irrespective of the number of compact directions, winding modes of branes follows more complicated pattern. To start with, one notices that winding modes of a p-brane can be parametrized by a p-form. Spectrum of M-theory contains M2, M5-branes, KK6-monopole and various additional (exotic) branes, whose counting will be useful for U-duality groups and larger. Table 2 lists irreducible representations of U-duality groups for each dimension d of compact torus, governing transformation of extended coordinates and the corresponding generalized momentum . The normal geometric coordinates correspond to the usual momentum P of a state. Windings of M2 and M5 branes are given by 2- and 5-forms respectively and give and number of winding states, where is the binomial coefficient. Hence, the M5 brane contributes only starting from dimension , since it simply cannot wrap spaces of lower dimensions.

Table 2.
Counting of winding modes of branes of M-theory on a background of the form with being a four-dimensional manifold. The first column contains dimensions of the compact torus, the second column lists the corresponding U-duality group, and the last column lists representations of G under which coordinates of the extended space transform.
The Kaluza-Klein monopole is an object with 6 + 1-dimensional worldvolume and one Taub-NUT direction corresponding to the Hopf cycle. This is magnetic dual of the graviton. Hence, it windings are represented by a mixed-symmetry tensor , which is a 7-form taking values in 1-forms and traceless. In components this is represented by the following tensor
where b must be equal to one of ’s for non-vanishing components. For winding direction this amounts in 7 independent winding modes, while for the case is is suggestive to contract with Levi-Civita tensor as
In total has components and the condition removes 8 more leaving only 56.
The important observation here is that the total number of momentum and winding modes for a d-torus with sums up to dimension of an irreducible representation of the corresponding U-duality symmetry group. For this apparently does not work, as summing winding modes of all branes up to the KK6 one obtains 148, while dimension of the smallest irrep is 248. To cure the result one first recalls that the spectrum of both string and M-theory contains exotic branes in addition to the normal (standard) branes. These are T(U)-duality partners of the normal branes and can be understood as sources of non-geometric backgrounds. Such backgrounds cannot be defined in terms of manifolds, instead these are described in terms of T(U)-folds [4,15,16], whose patches are glued by T(U)-duality transformations. At the level of field configurations this is realized as a monodromy when going around the point the exotic brane is placed [17].
It is convenient to label exotic branes in the same way as states of the 3D maximal supergravity are classified [3,17]. Hence, for any brane of string theory one adopts the notation , where gives the number of world-volume directions, denote the number of special (quadratic, cubic etc.) directions and n gives the power of the string coupling constant in tension of the brane. Such brane completely wrapped on a torus would have tension given by
where denote radius of the i-th toroidal direction and is the string length. For example, for the NS5-brane, which has 6 world-volume directions, no special circles and whose tension scales as , one would use the notation . Kaluza-Klein monopole is denoted as and has 6 worldvolume directions, one special circle corresponding to the Hopf fibre and its tension scales as . In these notations duality symmetries of string theory act on such states as follows
The well-known example of a T-duality orbit containing exotic branes has been investigated in [18] (see also [19] for a review) and reads
The orbit starts with the NS5-brane, which is completely geometric and whose background can be consistently described both locally and globally in terms of the metric and the gauge field. Performing T-duality transformations along smeared transverse directions one obtains KK5-monopole and then the exotic -brane. The background of the -brane cannot be described globally as it has non-trivial monodromy and is glued by T-duality. Going further along the orbit one recovers -branes, whose background is not well defined even locally, and -brane which is object of co-dimension-0. These branes, the corresponding backgrounds and their description in terms of T-duality covariant field theory will be considered in more details in Section 3.1.
Branes of M-theory completely wrapped on d compact direction with radii are in correspondence with massive BPS states of maximal -dimensional supergravity, and can be labelled similarly to the branes of string theory. Tension of -brane, or equivalently mass of the corresponding state, is then given by
where is the 11-dimensional Planck mass. In these notations the M2-brane is denotes as , the KK6-monopole is denoted as .
The exotic branes and whose winding modes contribute counting for the U-duality group, have three, six and 7 special Hopf-fiber-like direction. In addition, the brane has one cubic special circle. Interpretation of cubic circles is more subtle that that of the quadratic ones, some discussion of these for branes of the Type II theories can be found in [20]. Windings modes for these branes correspond to components of the following mixed symmetry tensors
where indices to the right after commas must be equal to the those to the left, i.e., for the last line we have and b’s = a’s. One immediately notices the reason these branes are the ones which are able to contribute the counting of winding for the theory. Indeed, this U-duality group corresponds to toroidal directions, hence 8 is the maximal number of antisymmetric indices one can have in a winding mode. Say for the brane with 3 special directions this provides room for 5 longitudinal directions, while for the one is left with none, hence a 0-brane.
It is important to note that although one includes windings of exotic branes into the counting for the case, components of the generalized momentum still do not sum up to 248, the smallest possible irrep being rather 240. This cannot be cured by adding more exotic branes, since no other such brane is able to fit the 8-torus. More importantly, as it will be clear from analysis of the field spectrum of exceptional field theory, the problem is much more than just counting of extra coordinates, a huge part of which would be dropped anyway. Vector fields of the theory must be in the same irrep as the generalized momentum to add up to a covariant derivative, hence one needs extra 8 field to build up an irrep. This is indeed what happens in the ExFT: one introduces extra tensor fields and imposes conditions on them similar to the section constraint [21]. For , which is an affine algebra with infinite-dimensional representations, one has to add infinitely many coordinates and fields. For larger U-duality groups the problem is even more complicated as first one encounters , which is an extension of the by two imaginary roots, and then , which must encode timelike direction as well. Some progress in the construction of such infinitely dimensional extended spaces and the corresponding theories has been made in [22,23,24,25].
2.3. Exceptional Field Theories
Consider a general exceptional field theory defined on D-dimensional space-time parametrized by coordinates , which we will call “external” and N-dimensional extended space, which we will call “internal” parametrized by . It is important to note, however, that no compactification is assumed in formulation of the theory. Toroidal reductions of supergravity described in the previous subsection have been used exclusively for counting winding modes. In the framework of exceptional field theories, toroidal backgrounds represent a solution, which preserves the maximal amount of U-duality. In this respect, toroidal backgrounds for ExFT are the same as Minkowski for General Relativity. In what follows, all fields are allowed to depend on the whole set of coordinates .
On this space the following field content is defined: external metric , N vector fields , generalized metric and various external tensors transforming under an irrep of G the U-duality group. Generalized metric parametrized the coset space , where K is the maximal compact subgroup of G. For supersymmetric theories one in addition defines fermions, transforming under an irrep of K.
Locally geometry of the extended space parametrized by is represented by the generalized Lie derivative , which defines generalized diffeomorphism transformations of generalized tensors along a generalized vector . Since, the vector depends both on the external and internal coordinates, partial derivative of a generalized tensor does not transform covariantly. To fix that one introduces long derivative following the usual approach of the Yang-Mills theory
Hence, the vector fields play the role of gauge connection in the theory. The corresponding field strength is defined in the usual way
One however faces a subtlety here noticing that such defined field strength is not a generalized tensor. This situation is familiar from the construction of maximal gauged supergravities, where one has to add p-form gauge field to a p-form field strength to build covariant expressions. Eventually, this leads to tensor hierarchy of the theory [26]. Hence, one defines
using that up to the section constraint. In general, one shows that generalized vectors of the form for any do not induce generalized diffeomorphisms when the section constraint is satisfied (for details see [27]). Hence, the 2-forms of the theory came from reduction of the 3-form of 11-dimensional supergravity are utulized in the covariant field strength.
If the 2-forms are dynamical, one needs to construct a covariant field strength for them, which will enter the fully covariant Lagrangian. For that, one considers Bianchi identity for the 2-form field strength, which can be written as
As before, such recovered field strength is covariant only when contracted with the Y-tensor, and hence needs additional contributions. One invokes 3-form potential , for whose field strength one needs a 4-form and so on. This tower of p-forms and their field strengths is called tensor hierarchy of exceptional field theories and drops to that of maximal gauged supergravities upon the Scherk-Schwarz reduction ansatz (see below). In principle, the hierarchy can go up to the top form; however it ends much earlier since at some point one no longer needs to construct yet another field strength since the corresponding gauge field is non-dynamical and does not enter the Lagrangian. Although the ExFT is more suitable for phenomenological applications, it has short tensor hierarchy and issues with self-duality. Hence, let us consider the construction of the SL(5) ExFT in more detail to illustrate the general idea.
Covariant field strength for the gauge field that is recovered from the commutator of long derivatives and then shifted by a derivative of , takes the following form [28]
where is the fully antisymmetric invariant tensor of SL(5). Explicit check shows that under generalized transformations of the fundamental fields and such defined field strength transforms covariantly, i.e., .
Bianchi identity for the 2-form field strength has non-trivial RHS and which can be written as a full derivative of a tensor
This tensor however has a freedom in adding of terms of the type
Indeed, in the Bianchi identity such term will give , which vanishes upon the section constraint of the theory
To match tensor hierarchy of the maximal gauged supergravity [29] one fixes a coefficient in front of the term and the covariant 3-form field strength reads
Now one notices by looking at the Figure 2 that there are too little degrees of freedom to compose both the 2-form and the 3-form gauge potentials. On the other hand, according to the prescription of [11] the three form should be dualized into a two form to complete the irrep of SL(5). Speaking about covariant theories, one would like to keep information about the 3-form, which is done by taking into account an alternative prescription, which is to dualize the 2-forms into 3-forms to complete the irrep of SL(5). Hence, one ends up with the same degrees of freedom encoded in the fields and . The duality relation between these potentials can be written in the following covariant form
where is the Levi-Civita tensor in the external 7 directions and is the inverse of the generalized metric .
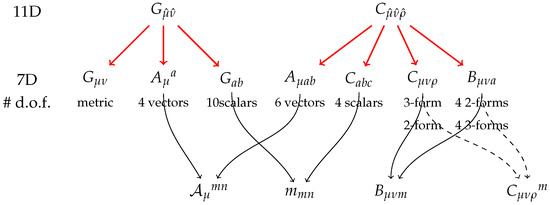
Figure 2.
Reduction of 11D fields into seven dimensions, dualization into the lowest possible rank tensor and recollection into SL(5) multiplets. Dashed lines correspond to an alternative combination of the 2- and 3-forms into the 3-form dual to in 7 dimensions (see the text). Here the small Latin indices label the fundamental irrep of SL(5) and small Latin indices from the beginning of the alphabet label the fundamental irrep of GL(4).
Since the 3-form field strength contains the same information as the 4-form field strength, the latter is considered to be non-physical and is not included into the Lagrangian. It appears only in the corresponding Bianchi identity
and is needed to ensure invariance of the Lagrangian with respect to external diffeomorphisms. Note that the 3-form gauge potential containing in the 4-form field strength has been already used for construction of the 3-form covariant field strength (see Figure 2).
Lagrangian of the theory is schematically the same as the one for the maximal gauged supergravity
Here the kinetic part is given by the Einstein-Hilbert term, scalar kinetic term, and vector and tensor kinetic terms respectively. In addition, one includes the “scalar potential” V, which contains only terms with derivatives along extended coordinates, and the topological term which does not contain contractions with the metric. Explicitly the expressions read
Here the modified Riemann curvature transforms covariantly under both generalized and external diffeomorphisms. The potential V is written in terms of the 10 × 10 generalized metric which is related to the metric by
i.e., each capital index M labelling the is represented by an antisymmetric pair of indices each labelling the fundamental of SL(5). In addition, one halves each contraction of capital indices when turning to pairs to avoid extra counting.
The topological part cannot be written in a covariant form, precisely as in the gauged supergravity case; however its variation can
Transformations of the fields denote external diffeomorphisms parametrized by a vector , generalized diffeomorphisms parametrized by a generalized vector and gauge transformations of the fields :
The amazing feature of exceptional field theories observed already in [30] is that the form of the Lagrangian is completely fixed by demanding invariance with respect to the above transformations. In contrast, in gauged supergravities one has to impose supersymmetry to fix all coefficients, although the general structure of the Lagrangian is completely the same. The non-trivial check is that supersymmetry works well for the Lagrangian of exceptional field theory fixed in such a way. This has been checked explicitly for and in [31,32], and is expected to work for all other cases as well.
2.4. The Section Constraint
Exceptional field theories are formulated on a space-time parametrized by d external (conventional) coordinates and D “internal” extended coordinates . Since no reduction is assumed, these are theories on a -dimensional space-time, which always has dimension greater than 11. To reduce the amount of degrees of freedom, and to ensure consistency of algebra of generalized diffeomorphism one has to impose condition, the section constraint, which is
where • stands for any field or combination of fields. Y-tensors for different U-duality groups are listed in Table 1.
This condition restricts dependence of fields of the theory on the extended coordinates and can be solved in various ways. Consider as an example the theory for which the condition is
where is the invariant symplectic form of and are generators of the group. In [33] it has been shown that this condition has precisely two algebraic types of solutions: corresponding to embeddings of the D = 11 maximal supergravity and of Type IIB supergravity. All other follow from this two. In addition, there is a special way to relax this constraint by imposing the so-called Scherk-Schwarz ansatz.
Consider first the algebraic solution of the section constraint corresponding to embedding of the 11D maximal supergravity. In this case, one decomposes the fundamental of E7 under the action of the subgroup as
where subscripts denote the GL(1) weight. For the coordinates this implies
Here and further in this subsection
The section constraint then can be satisfied by imposing
hence fields depend only on 7 coordinates and 4 coordinates , in total 11. Field content of the E7 theory decomposed under the GL(7) subgroup apparently fits the field content of the 11 dimensional supergravity in the 7 + 4 split form, as the former was constructed from the latter initially. Type IIA supergravity is obtain from this theory by further reduction in the usual way.
The alternative solution of the section constraint is associated with decomposition under the embedding , which implies for the fundamental irrep
For components of the extended coordinates this reads
and the field content will be decomposed accordingly, The SL(2) subgroup transforming subsets of dual coordinates correspond to S-duality symmetry of Type IIB supergravity. The section constraint implies
and the fields depend on 6 coordinates and 4 coordinates , in total 10. After reduction, the SL(2) S-duality symmetry can be kept manifestly at the cost of the full 10-dimensional Lorenz symmetry. To restore the latter, one has to break the former.
A special solution to the section constraint trivially embedded into the above two classes is , i.e., all fields do not depend on extended coordinates. This corresponds simply to d-dimensional maximal ungauged supergravity, i.e., a reduction of the 11-dimensional supergravity on a torus . These are known to allow deformations, gaugings, producing a class of theories corresponding to various reductions of the initial 11-dimensional theory [26]. Exceptional field theories are able to reproduce such gauged supergravities as well under a special ansatz, which relaxes the differential section condition to an algebraic constraint. These will be considered in more detail in Section 3.1.
2.5. Double Field Theory
Double field theory, which is a T-duality covariant formulation of supergravity, also fits the above scheme. The duality group is O(n,n) with , the Y-tensor then becomes , where for any n. Since algebraic structure of the theory does not depend on the number of “internal” dimensions, it is natural to extend all 10 coordinates of Type II supergravity. The generalized metric then
and the rest of the construction is repeated identically.
Important remark here concerns the section constraint, which is
where we introduce notation for extended coordinates. The above implies that for any pair of a normal coordinate and the corresponding dual coordinate fields are allowed do depend on one or another, but not on both. The choices are related by a T-duality transformation precisely as in the Duff’s procedure
Hence, such defined T-duality means that one translates all upper indices * into lower indices *, and the coordinates becomes normal geometric coordinate in the new T-duality frame. Note however a different possibility, where one simply replaces dependence of background fields on by , still counting the latter as a non-geometric dual coordinate. This will turn a solution of supergravity equations of motion into a proper string background, which however (i) does not solve e.o.m.s, (ii) is non-geometric. This way DFT and ExFT allow addressing exotic branes and the corresponding non-geometric backgrounds. See further Section 3.2 for more details.
3. Applications
3.1. Non-Geometric Compactifications
Choosing a solution of the section constraint of exceptional field theory can be understood as a dimensional reduction as it drops dependence of fields of the theory on a subset of coordinates. E.g., the trivial solution when all fields depend only on D external coordinates corresponds to reduction of the 11-dimensional supergravity on a -torus. Other toroidal reductions can as well be obtained in such a way by choosing a smaller subset of the extended coordinates to be dropped. However, exceptional field theory is able to incorporate more general reductions, in fact all parametrized in terms of embedding tensor.
Taking the general idea of twisted dimensional reduction of Scherk and Schwarz [34] one introduces the following generalized Scherk-Schwarz ansatz
where is usually referred to as the twist matrix. The ansatz tells that all information about dependence on the extended coordinates is contained in the twist matrix. Inserting this into the definition of generalised Lie derivative one obtains
which can be thought of as a definition of the tensor
where . In principle, this tensor depends on as it is constructed out of twist matrices and their derivatives; however, for now we will assume . Certainly this implies restrictions on the twist matrices which will be discussed in a moment.
Upon the generalised Scherk-Schwarz ansatz the closure constraint (23) and the condition for to transform covariantly boil down to the following simple algebraic constraint
Here we understand as a matrix labelled by A. The above looks as a commutation relation for an algebra with generators ; however, since is not necessarily antisymmetric, such simple interpretation does not work. Instead, one recognizes here the structure of gauged supergravities, with being the embedding tensor. Hence, the main line of the subsection is that Scherk-Schwarz reduction of exceptional field theories replaces the differential section constraint by the algebraic condition (64), which has precisely the same form as the quadratic constraint of gauged supergravity. Moreover, performing the reduction at the level of the action one reproduces precisely action of the corresponding D-dimensional gauged supergravity. This has been shown first for DFT in [35] and then for exceptional field theories SL(5), SO(5,5), , and the enhanced O(d,d) exceptional field theory in [36,37,38,39]. Let us now briefly describe structure of gauged supergravities and their relation to generalized Scherk-Shwarz reductions.
Gauged supergravities most straightforwardly can be described in the so-called embedding tensor formalism first developed in the context of three dimensional theories [40,41] and then constructed for other maximal supergravities (for review see [26,42,43]). When dimensionally reduced on a d-torus 11-dimensional supergravity produces maximally supersymmetric theory in dimensions, which contains vector fields , with . The vector fields descent from the metric and the 3-form C-field in 11 dimensions precisely in the same way as the generalized vector fields of exceptional field theory (see Figure 1 and Figure 2). For toroidal reductions the resulting theory is abelian with the gauge group and gauge transformations
In addition, the lower dimensional theory has U-duality symmetry group G and the vector multiplet transforms under an irrep of dimension dim. Reductions on more complicated manifolds endowed with torsion and/or curvature, and reductions in the presence of fluxes of gauge fields result in theories with less symmetry, and with vector multiplets belonging to adjoint representation of a non-abelian gauge group. Such reductions correspond to the diagonal arrow on Figure 3, while toroidal reductions correspond to the vertical arrow. Hence, it is natural to deform the abelian maximal theory introducing non-abelian interactions between the vector fields, preserving supersymmetry and local symmetries of the theory. A self-consistent algorithm for such a procedure is based on the notion of embedding tensor , which defines embedding of the desired local gauge group into the full global U-duality group G
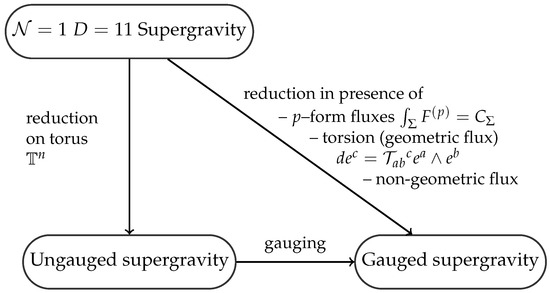
Figure 3.
Relations between toroidal reductions of supergravity, gaugings and more complicated dimensional reductions involving geometric and non-geometric fluxes.
One writes deformation of the gauge transformation rule for vector multiplets as follows
where g is the deformation parameter. The “structure constants” can be written in terms of the embedding tensor as
where is basis of generators of the global U-duality group G, and Z and are symmetric and antisymmetric in respectively. Hence, the embedding tensor indeed selects a subset of these generators to construct the constants , which define the non-abelian gauge transformation.
Certainly, such a deformation of the ungauged D-dimensional theory cannot be done in an arbitrary way and has rather to satisfy certain constraints. The first one is the linear constraint and comes from the condition that the resulting deformed equations of motion are still invariant under the full set of supersymmetries, i.e., the deformed gauged supergravity is a maximally supersymmetric theory. The linear constraint projects certain representations of G in the decomposition of the embedding tensor , which can be schematically written as
As an example, one may consider the theory constructed in [13,44], for which , , and
The linear constraint tells that for the theory to be maximally supersymmetric the embedding tensor cannot have the part
Please note that the duality group to be gauged contains a part, which correspond to global rescalings of the external metric. After the gauging procedure the corresponding generators correspond to the so-called trombone gauging. Certainly, theories with non-zero trombone part of the embedding tensor cannot be written in terms of an action, as rescalings are symmetries of equations of motion, rather than the action [44].
In addition to the linear constraint the embedding tensor must respect the so-called quadratic constraint, which follows from the condition of covariancy of the tensor under global transformations. These are nothing but (64)
Note that the LHS does not have the part symmetric in , while the tensor has no symmetry in the lower indices in general. Hence, the above implies constraint on the symmetric part . This condition is essential for the Jacobi identity for gauge transformations. Indeed, one discovers that the Jacobiator of gauge transformations has the conventional form
However, the commutation relations (64) restricted for the antisymmetric part only do imply the RHS of the above expression to vanish, which is usually the case for a conventional Lie algebraic structure constants. Instead one again finds the symmetric part
hence, the Jacobi identity is satisfied upon similarly to the closure constraint.
Such rich algebraic structure of the deformations means that one is not simply dealing with a single gauge group, but rather with a set of gauge groups inside the full duality group G, defined by choosing the embedding tensor. Gauged supergravities for different dimensions have been constructed in the series of papers [13,29,44,45,46,47] which contain detailed analysis of the constraint briefly described above, construction of the corresponding effective action including the fermionic sector and analysis of some examples.
Solving the linear and quadratic constraints for the embedding tensor one ends up with a theory which can be in principle obtained as a dimensional reduction of the 11-dimensional supergravity on some manifold. For example, a particular choice of gaugings for the theory correspond to embedding , which gives reduction on a sphere considered in [48,49]. In this case, components of the embedding tensor are equal to the integral value of the flux of the 7-form field strength on the sphere.
Such gaugings, which can be interpreted in terms of dimensional reductions are called geometric and are said to have higher dimensional origin. However, the full set of solutions to the quadratic and linear constraint contains gaugings which do not have apparent higher dimensional origin, moreover one can show that some cannot have any [50]. Although these still define consistent theories in lower dimensions and give masses and couplings for lower dimensional fields, one cannot come up with a dimensional reduction scheme starting from the 11D supergravity and ending up with these theories.
At this point, one turns back to the beginning of this subsection, where Scherk-Schwarz reduction of exceptional field theories have been shown to produce algebraic structures of the same type as those of gauged supergravities. In principle, since any gauging is given as an expression written in terms of twist matrices and their derivatives, as in (63), one may hope that it is possible to solve these equations and present twist matrices explicitly for each type of gauging. This has been shown to be true for half-maximal gaugings and maximal gaugings in [50], where full classification of the corresponding twist matrices was obtained. The most outstanding output of such analysis is that the so-called non-geometric gaugings, i.e., those which do not have higher standard dimensional origin, can be constructed out of generalized twist matrices. Moreover, the set of non-geometric gaugings itself is divided into normal and genuine non-geometric subsets. The former is defined to belong to a U-duality orbit of a geometric gauging, and hence the theory can be rotated to a frame, where no non-geometry is present. On the other hand, the latter do not belong to such an orbit and hence the theory is always non-geometric. At least for some examples, genuine non-geometric gaugings were shown to descent from twist matrices which break the section constraint.
At this point it is suggestive to return to the constraint (64) and recall that for that to satisfy one does not need to impose any conditions on dependence of twist matrices on the extended coordinates. Hence, in principle it is possible to break the section constraint, while satisfying the quadratic constraint that has been shown explicitly in [50]. Certainly, such twist matrices cannot be understood as defining a reduction of the conventional supergravity. Whether such configurations can be understood as proper string backgrounds is not clear, as all duality-covariant setups so far imply the section condition. However, genuine non-geometric gaugings look very promising for cosmological model building as these provide extra parameters in scalar potential of the lower dimensional theory, which may help to stabilize its moduli. Indeed, if one considers a setup with geometric gaugings which fails to stabilize certain subset of scalar moduli, any gaugings belonging to duality orbits of the initial ones would also fail to do so, since the physics must be duality invariant. In contrast, genuine non-geometric gaugings do not suffer from such constraints and hence can enhance the realm of possible models. This approach has been taken to analyse cosmological implications of exceptional field theories in application to some toy-model examples in [51,52,53,54,55].
3.2. Exotic Brane Backgrounds
Geometric gaugings of lower dimensional supergravities are equal to integral values of fluxes on the internal manifold, and hence, naturally acquire interpretation in terms of branes. Wrapped around cycles of the internal space, these source fluxes of gauge p-form fields, which then are subject of the usual Dirac quantisation condition (see e.g., [56] for review). Similarly, non-geometric fluxes can be interpreted as integrated values of field strengths of mixed symmetry potentials sourced by exotic branes. Algebraic-wise one finds good correspondence between mixed allowed symmetry potentials of lower dimensional supergravity (equivalently, exotic branes) and gaugings [57,58,59]. However, the conventional supergravity is known to be unable to properly describe backgrounds of such exotic branes and to provide a technique for calculating the corresponding non-geometric fluxes.
The well-known example comes from the T-duality orbit of the NS5-brane, starting with the H-flux [18,19]. This is known to contain non-geometric Q- and R-fluxes via the relation
where denotes T-duality transformation in the corresponding isometry direction. Since in the conventional supergravity T-duality transformation is defined only along a Killing direction and T-duality along the world-volume direction of the NS5-brane do not change the background, one has to smear on the four transverse directions to perform the transformation. The full NS5-brane background is characterized by the harmonic function in four Euclidean dimensions
To have flat asymptotics at spatial infinity as one defines the harmonic function as
where . To smear along say the direction one considers harmonic function which has apparent isometry along z and solves the equations of motion of supergravity with the same amount of flux. This procedure gives the following background of the smeared NS5-brane which we refer to as the H-monopole
where and the 1-form is defined to be of a magnetic configuration
hence the name “H-monopole”. Performing T-duality along the compact direction z by simply applying the Buscher rules (11) one arrives at the background of KK-monopole
This background has vanishing B-field and the magnetic monopole configuration is given by the metric components . In three transverse directions such background behaves as the gravitational magnetic monopole.
Already at this step the backgrounds start to get tricky. Indeed, the Gross-Perry monopole solution, which describes the part of the KK5 background, is topologically a Hopf fibration with the special cycle given by the z direction [60]. Moving around this cycle one observes periodicity in and glues the background by a diffeomorphisms transformation. This non-trivial topological structure is reflected by non-vanishing geometric flux , defined as structure constants of the algebra of local vielbeins
where and the vielbein is defined in the usual lower-triangular gauge as
To T-dualize further, one has to smear one more direction, say , which brings us to the set of co-dimension-2 solutions. These are not well defined field configurations as one cannot satisfy proper conditions at space infinity asymptotics. Formally, the harmonic function in two dimensions is , where , and diverges both at the core and at the infinity. For that renormalization procedure introduces a dimensionful parameters , which somehow run when one approaches the singularity points [17]. In what follows, we will drop these parameters for simplicity and always assume the harmonic function of the form
Performing T-duality transformation of the KK5-background smeared in such a way one arrives at the following background
where are the polar coordinates in the transverse plane . One immediately notices the non-trivial monodromy: when going around the brane the background is glued by a T-duality transformation in the directions . Such non-geometric configurations are believed to be sourced by exotic branes and are properly described on the language of T-folds [15,16,61]. In terms of the classification (28) the background (84) is sourced by the -brane. Now it is easy to see that the two ”quadratic” directions in the mass formula correspond to the two special directions of the brane.
The monodromy gluing the torus can be conveniently represented as a linear transformation of the corresponding generalized metric
where the matrix encodes the non-geometric -transform
with . This suggests that it is more natural to use the -frame of DFT [62] where the generalized metric parametrized by the space-time metric and a bi-vector field instead of the 2-form Kalb-Ramond field. In these variables the background becomes
This form naturally reflects the fact that the -brane electrically interacts with the bi-vector field as was shown explicitly in [20,63,64]. Indeed, the bi-vector is actually an 8-form taking values in two-vectors, which can be written in 10-dimensions as
with additional condition that all components with any of the upper indices repeating any of the lower indices vanish [58]. Hence, the corresponding Wess-Zumino term for the -brane has the following structure
where are the world-volume coordinates.
Turning to the -frame allows defining the corresponding flux explicitly as , which in 10 dimensions is represented by a mixed symmetry tensor. Smearing one more direction one obtains linearly growing harmonic function, and T-dualising along arrives at the s-called R-monopole, the -brane. This is a co-dimension-1 solution, a domain wall, which is even more peculiar. Non-vanishing R-flux of the background reflects non-associativity of the closed string coordinates on such background [65,66].
One concludes that exotic brane backgrounds in the approach of the conventional supergravity are solutions fo equations of motion of co-dimension , i.e., domain strings, walls and space-time filling objects. Co-dimension-2 solutions are characterized by non-trivial monodromy around the core of the object, which glues the background by a T-duality transformation. In the T-duality covariant approach of DFT one expects to describe a whole duality orbit as a single field configuration. This is indeed possible and has been shown explicitly for the orbit of the NS5-brane in [67,68] and for backgrounds of exotic branes of M-theory in [69,70,71] (for review see [72]).
In [67,68] it has been shown that all branes, both geometric and exotic, of the T-duality orbit starting with the NS5-brane are just different faces of a single object called DFT monopole. This background is a solution of DFT equations of motion, characterized by the generalized metric written in the form of a quasi-interval (note that this is not an invariant expression and cannot be understood as a definition for distance in the doubled space) and the invariant dilaton d
Here the harmonic function and the vector are that of the H-monopole
Of crucial importance here is the understanding of the coordinate dependence of the fields. First, one notes that the section condition is satisfied since the fields depend only on and do not depend on their duals . Second, the form of the solution as written above does not tell us which coordinates are geometric, i.e., used for measuring physical distances, and which are not. This is additional information which is given upon fixing position of the DFT monopole in the doubled space. Since nothing changes when replacing by , equivalently, when T-dualizing along the world-volume directions, one has five possible choices for geometric coordinates listed in Table 3. Consider the Q-monopole, the brane, for which the geometric set of transverse coordinates is . This implies that the harmonic function, which is always of the form (91), depends on one dual coordinate that is in this case. Hence, one has properly defined harmonic function with nice asymptotic behaviour, which however is allowed to depend on dual coordinates. Please note that instead of the H-monopole background one may start with the full NS5-brane background and the harmonic function
which would imply that a -brane background is characterized by fields which depend on r dual coordinates. This number if also equal to the number of special circles.

Table 3.
Possible choices for orientation of DFT monopole in the doubled space.
The orbit starting at the NS5-brane was also considered in [67], where the background of the localised Kaluza-Klein monopole has been recovered from the DFT monopole. Such a background has been known before these results and was recovered from the usual Kaluza-Klein monopole background by taking into account backreaction from worldsheet instantons in the two-dimensional linear sigma model [73,74,75,76]. Similarly, worldsheet instanton corrections have been shown to localize the background of the co-dimension-2 brane in dual space [77]. In Figure 4 relations between monopoles and their localized versions are shown schematically.
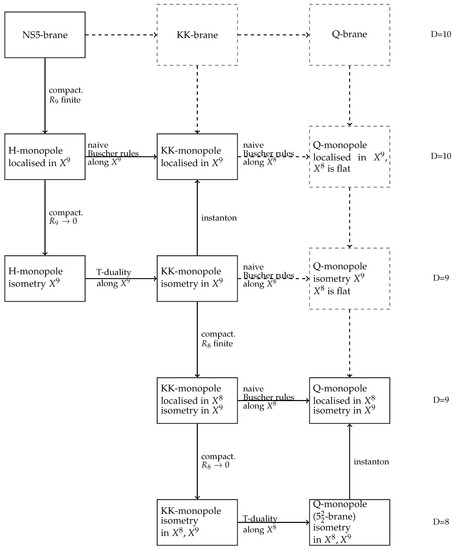
Figure 4.
Systematics of backgrounds with H, geometric f and Q fluxes and their relations. Note that in [77] Q-monopole localised in both and has been constructed with both these directions being compact.
3.3. Deformations of Supergravity Backgrounds
Backgrounds of DFT depending on a dual coordinate and the possibility to parametrize the generalized metric in terms of exotic degrees of freedom, such as the bi-vector , open a window to investigate issues related to integrability of the 2-dimensional sigma model. It is known that kappa symmetry of the two-dimensional sigma model does not imply strictly equations of motion of 10-dimensional supergravity, but leads to a more general setup. This has been elaborated in a series of paper (see e.g., [78,79,80,81]) and is usually referred to as the generalized supergravity. In this theory the degree of freedom represented by the dilaton and its derivative is replaced by a set of vectors , and the equations of motion of generalized supergravity drop to the conventional ones upon . The most amazing feature of this theory is that (at least some) solutions of its equations of motion can be obtained as integrable deformations of backgrounds of the conventional sugra.
Integrability of the two-dimensional sigma model on the background has been shown in [82] by explicit construction of the corresponding Lax pair. Such sigma model gain the expected interpretation as Type II string theory living on the background supported by non-vanishing flux of 5-form. In [83] a deformed version of the sigma-model has been considered, which appeared to be also integrable for the so-called -deformations. The -deformed sigma model is very peculiar when understood as theory of string on a classical background. In this case, the corresponding background, which is commonly referred to as , does not satisfy equations of motion of 10-dimensional supergravity [84]. However, it still defines a proper background for string propagation due to Weyl invariance, and moreover the corresponding model is integrable. Such a deformed background was shown to satisfy equations of motion of generalized supergravity [81,85,86].
At the level of field theory, generalized supergravity can be obtained from the conventional Type II supergravity by considering equations of motion for background with one isometry direction and with dilaton, linearly depending on the isometry direction . T-dualizing solutions along by formally applying Buscher rules one obtains solutions of generalized supergravity. In Double Field Theory such procedure is reflected by just changing the role as a geometric coordinate to become non-geometric, as has been shown explicitly in [86,87]. Alternatively, one is able to reproduce generalized supergravity equations of motion by generalized Scherk-Schwarz reduction of exceptional field theory with twist matrices depending on one dual coordinate. This was explicitly shown for the ExFT in [88]; however, similar procedure can be performed for ExFTs with any U-duality group.
In addition to the nice incorporation of both generalized and normal supergravities in a single picture, DFT provides a simple and straightforward algorithm for generating deformed backgrounds from a given solution. This procedure has been mainly developed in [89,90,91,92,93,94] and is based on the so-called -frame of DFT [95]. The basic idea of Bvs frame is that the generalized metric of DFT as an element of the coset space can be parametrized in terms of the fields or alternatively
This is equivalent to choosing the generalized vielbein to be of lower-triangular or upper-triangular form. In principle, one may keep both and fields in the metric; however this will duplicate gauge degrees of freedom and require either an additional constraint or change in the status of one of the fields. When substituted into the full action of DFT
the generalized metric in -frame provides the action of the so-called -supergravity. This theory has been initially developed to address non-geometric fluxes Q and R, which are more naturally written in terms of the bivector field, as in the previous subsection.
The matrix equality (93) can be written in terms of the fundamental fields in the following simple form
In the above one immediately recognizes the open-closed string map [96] that relates backgrounds as seen by the closed string to that seen by the open string. In this interpretation the field on the RHS is understood as the non-commutativity parameter, usually denoted .
The relation (93) can be understood as a deformation of a solution given by the metric background by a coordinate-dependent parameter (see Figure 5). One starts with a background with vanishing B-field, parametrized only by metric degrees of freedom and the dilaton . Since , the corresponding generalized metric can be understood in either B or -frame. Consider now a deformed generalized metric, which contains the metric that solves conventional equations of motion, and the field . Then, written in the B-frame this generalized metric encodes a solution of equations of motion of the conventional supergravity. Equivalently, this implies that the generalized metric solves equations of motion of DFT given the section constraint is satisfied. In the -frame, given is a solution, these equations of motion impose constraints on the bi-vector field for the deformation to give a solution. In [93] these constraints have been obtained explicitly from equations of motion of -supergravity of [97]. Given a general solution of these equations one is guaranteed to recover solutions of generalized supergravity after deformation, and in the special case, when , these boil down to solutions of the conventional supergravity.
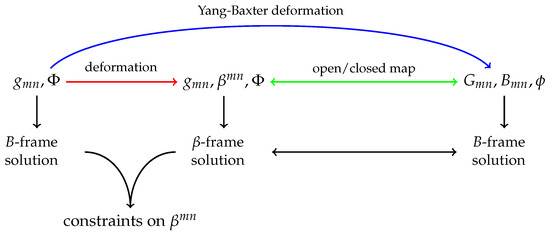
Figure 5.
Relationships between the relevant theories and their solutions. b-frame refers to the standard supergravity (possibly generalised), while -frame is the theory of [98]. Yang-Baxter deformation acts within usual supergravity, but we interpret it as a composition of the open/closed string map with a deformation by . This leads to the constraints for (essentially the CYBE) arising from supergravity field equations.
Of special interest are backgrounds with a set of isometries encoded by Killing vectors , which form an algebra upon
For these the deformation parameter can be chosen in the bi-Killing form
where is a constant antisymmetric matrix. Such deformed backgrounds satisfy equations of motion of supergavity if the r-matrix satisfied classical Yang-Baxter equation, which is the semi-classical limit of the quantum Yang-Baxter equation
A particular example of such deformation is given by the -background discussed above, which corresponds to deformations with r-matrix . The non-vanishing vector is a sign of the generalized supergravity equations of motion, and indeed .
The constraint imposed on couplings of the two-dimensional sigma-model by Weyl invariance has been uplifted to the full T-duality covariant sigma-model in [94,99] and proper local counter-terms have been constructed. The covariant approach implies a generalization of the bi-vector deformations described above into a full -shift. This is a local transformation inside DFT, which can be applied to a solution with non-vanishing H-flux. The general procedure is as follows, one starts with a generalized metric and a set of generalized Killing vectors , the deformation then is given by
where is a constant parameter of deformation. The generalized Killing vector should satisfy the algebraic section constraint (cf. that of [64])
This ensures the matrix to be a T-duality transformation, i.e., . In the usual duality frame one chooses and the above transformation reduces to a -deformation.
4. Conclusions and Discussion
In this short review, we have briefly described the structure of exceptional field theories (ExFT’s), which provide a (T)U-duality covariant approach to supergravity. These are based on symmetries of toroidally reduced supergravity; however are defined on a general background. From the point of view of ExFT the toroidal background is a maximally symmetric solution preserving all U-duality symmetries. In this sense the approach is similar to the embedding tensor technique, which is used to define gauge supergravity in a covariant and supersymmetry invariant form. Although any particular choice of gauging breaks certain amount of supersymmetry, the formalism itself is completely invariant. Similarly the U-duality covariant approach is transferred to dynamics of branes in both string and M-theory, whose construction has not been covered here.
In the text, we described construction of the field content of exceptional field theories from fields of dimensionally reduced 11-dimensional supergravity, and local and global symmetries of the theories. Various solutions of the section constraint giving Type IIA/B, 11D and lower-dimensional gauged supergravities have been discussed without going deep into technical details. For readers’ convenience references for the original works are present.
As a formalism exceptional field theory has found essential number of application, some of which have been described in this review in more details. In particular, we have covered generalized twist reductions of ExFTs, which reproduce lower-dimensional gauged supergravities, description of non-geometric brane backgrounds and an algorithm for generating deformations of supergravity backgrounds based on frame change inside DFT. However, many fascinating applications of the DFT and ExFT formalisms have been left aside. Among these are non-abelian T-dualities in terms of Poisson-Lie transformations inside DFT [100,101]; generating supersymmetric vacua and consistent truncations of supergravity into lower dimensions [102,103,104] (for review see [105]); compactifications on non-geometric (Calabi-Yau) backgrounds and construction of cosmological models [54,55,106,107].
Funding
This work was funded by the Russian state grant Goszadanie 3.9904.2017/8.9 and by the Foundation for the Advancement of Theoretical Physics and Mathematics “BASIS”.
Conflicts of Interest
The author declares no conflict of interest.
References
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
- Witten, E. String theory dynamics in various dimensions. Nucl. Phys. 1995, B443, 85–126. [Google Scholar] [CrossRef]
- Obers, N.; Pioline, B. U duality and M theory. Phys. Rept. 1999, 318, 113–225. [Google Scholar] [CrossRef]
- Hull, C. Global aspects of T-duality, gauged sigma models and T-folds. JHEP 2007, 0710, 057. [Google Scholar] [CrossRef]
- Bohm, R.; Gunther, H.; Herrmann, C.; Louis, J. Compactification of type IIB string theory on Calabi-Yau threefolds. Nucl. Phys. 2000, B569, 229–246. [Google Scholar] [CrossRef]
- Morrison, D.R.; Vafa, C. Compactifications of F theory on Calabi-Yau threefolds. 2. Nucl. Phys. 1996, B476, 437–469. [Google Scholar] [CrossRef]
- Sen, A. F theory and orientifolds. Nucl. Phys. 1996, B475, 562–578. [Google Scholar] [CrossRef]
- Musaev, E. U-Dualities in Type II String Theories and M-Theory. Ph.D. Thesis, Queen Mary, University of London, London, UK, 2013. [Google Scholar]
- Duff, M. Duality rotations in string theory. Nucl. Phys. 1990, B335, 610–620. [Google Scholar] [CrossRef]
- Duff, M.; Lu, J. Duality rotations in membrane theory. Nucl. Phys. 1990, B347, 394–419. [Google Scholar] [CrossRef]
- Cremmer, E.; Julia, B.; Lu, H.; Pope, C. Dualization of dualities. 1. Nucl. Phys. 1998, B523, 73–144. [Google Scholar] [CrossRef]
- Cremmer, E.; Julia, B.; Lu, H.; Pope, C.N. Dualization of dualities. 2. Twisted self-duality of doubled fields, and superdualities. Nucl. Phys. 1998, B535, 242–292. [Google Scholar] [CrossRef]
- De Wit, B.; Samtleben, H.; Trigiante, M. The Maximal D = 4 supergravities. JHEP 2007, 0706, 049. [Google Scholar] [CrossRef]
- Berman, D.S.; Cederwall, M.; Kleinschmidt, A.; Thompson, D.C. The gauge structure of generalised diffeomorphisms. JHEP 2013, 1301, 064. [Google Scholar] [CrossRef]
- Hull, C.M. A Geometry for non-geometric string backgrounds. JHEP 2005, 10, 065. [Google Scholar] [CrossRef]
- Hull, C.M. Doubled geometry and T-folds. JHEP 2007, 0707, 080. [Google Scholar] [CrossRef]
- De Boer, J.; Shigemori, M. Exotic Branes in String Theory. Phys. Rep. 2012, 532, 65–118. [Google Scholar] [CrossRef]
- Shelton, J.; Taylor, W.; Wecht, B. Nongeometric flux compactifications. JHEP 2005, 0510, 085. [Google Scholar] [CrossRef]
- Wecht, B. Lectures on Nongeometric Flux Compactifications. Class. Quant. Grav. 2007, 24, S773–S794. [Google Scholar] [CrossRef]
- Bergshoeff, E.; Kleinschmidt, A.; Musaev, E.T.; Riccioni, F. The different faces of branes in Double Field Theory. arXiv 2019, arXiv:1903.05601. [Google Scholar]
- Hohm, O.; Samtleben, H. Exceptional field theory. III. E8(8). Phys. Rev. 2014, D90, 066002. [Google Scholar] [CrossRef]
- Kleinschmidt, A.; Nicolai, H. Higher spin representations of K(E10). In Proceedings of the International Workshop on Higher Spin Gauge Theories, Singapore, 4–6 November 2015; World Scientific: Singapore, 2017; pp. 25–38. [Google Scholar] [CrossRef]
- Bossard, G.; Cederwall, M.; Kleinschmidt, A.; Palmkvist, J.; Samtleben, H. Generalized diffeomorphisms for E9. Phys. Rev. 2017, D96, 106022. [Google Scholar] [CrossRef]
- Bossard, G.; Ciceri, F.; Inverso, G.; Kleinschmidt, A.; Samtleben, H. E9 exceptional field theory. Part I. The potential. JHEP 2019, 03, 089. [Google Scholar] [CrossRef]
- Cederwall, M.; Palmkvist, J. L∞ algebras for extended geometry. J. Phys. Conf. Ser. 2019, 1194, 012021. [Google Scholar] [CrossRef]
- Samtleben, H. Lectures on Gauged Supergravity and Flux Compactifications. Class. Quant. Grav. 2008, 25, 214002. [Google Scholar] [CrossRef]
- Abzalov, A.; Bakhmatov, I.; Musaev, E.T. Exceptional field theory: SO(5,5). JHEP 2015, 06, 088. [Google Scholar] [CrossRef]
- Musaev, E.T. Exceptional field theory: SL(5). JHEP 2016, 02, 012. [Google Scholar] [CrossRef]
- Samtleben, H.; Weidner, M. The Maximal D = 7 supergravities. Nucl. Phys. 2005, B725, 383–419. [Google Scholar] [CrossRef]
- Hohm, O.; Samtleben, H. Exceptional Field Theory I: E6(6) covariant Form of M-Theory and Type IIB. Phys. Rev. 2014, D89, 066016. [Google Scholar] [CrossRef]
- Godazgar, H.; Godazgar, M.; Hohm, O.; Nicolai, H.; Samtleben, H. Supersymmetric E7(7) Exceptional Field Theory. JHEP 2014, 1409, 044. [Google Scholar] [CrossRef]
- Musaev, E.; Samtleben, H. Fermions and supersymmetry in E6(6) exceptional field theory. JHEP 2015, 1503, 027. [Google Scholar] [CrossRef]
- Hohm, O.; Samtleben, H. Exceptional field theory. II. E7(7). Phys. Rev. 2014, D89, 066017. [Google Scholar] [CrossRef]
- Scherk, J.; Schwarz, J.H. How to Get Masses from Extra Dimensions. Nucl. Phys. 1979, B153, 61–88. [Google Scholar] [CrossRef]
- Graña, M.; Marqués, D. Gauged Double Field Theory. JHEP 2012, 1204, 020. [Google Scholar] [CrossRef]
- Berman, D.S.; Musaev, E.T.; Thompson, D.C. Duality Invariant M-theory: Gauged supergravities and Scherk-Schwarz reductions. JHEP 2012, 1210, 174. [Google Scholar] [CrossRef]
- Musaev, E.T. Gauged supergravities in 5 and 6 dimensions from generalised Scherk-Schwarz reductions. JHEP 2013, 1305, 161. [Google Scholar] [CrossRef]
- Baron, W.H. Gaugings from E7(7) extended geometries. Phys. Rev. 2015, D91, 024008. [Google Scholar] [CrossRef]
- Hohm, O.; Musaev, E.T.; Samtleben, H. O(d + 1, d + 1) enhanced double field theory. JHEP 2017, 10, 086. [Google Scholar] [CrossRef]
- Nicolai, H.; Samtleben, H. Maximal gauged supergravity in three-dimensions. Phys. Rev. Lett. 2001, 86, 1686–1689. [Google Scholar] [CrossRef]
- De Wit, B.; Samtleben, H.; Trigiante, M. On Lagrangians and gaugings of maximal supergravities. Nucl. Phys. 2003, B655, 93–126. [Google Scholar] [CrossRef]
- De Wit, B.; Nicolai, H.; Samtleben, H. Gauged supergravities in three-dimensions: A Panoramic overview. arXiv 2004, arXiv:hep-th/0403014. [Google Scholar]
- Trigiante, M. Gauged Supergravities. Phys. Rept. 2017, 680, 1–175. [Google Scholar] [CrossRef]
- Le Diffon, A.; Samtleben, H. Supergravities without an Action: Gauging the Trombone. Nucl. Phys. 2009, B811, 1–35. [Google Scholar] [CrossRef][Green Version]
- De Wit, B.; Nicolai, H.; Samtleben, H. Gauged Supergravities, Tensor Hierarchies, and M-Theory. JHEP 2008, 0802, 044. [Google Scholar] [CrossRef]
- De Wit, B.; Samtleben, H.; Trigiante, M. The Maximal D = 5 supergravities. Nucl. Phys. 2005, B716, 215–247. [Google Scholar] [CrossRef]
- Bergshoeff, E.; Samtleben, H.; Sezgin, E. The Gaugings of Maximal D=6 Supergravity. JHEP 2008, 0803, 068. [Google Scholar] [CrossRef]
- Cremmer, E.; Julia, B. The SO(8) supergravity. Nucl. Phys. 1979, B159, 141–212. [Google Scholar] [CrossRef]
- De Wit, B.; Nicolai, H. N = 8 Supergravity with Local SO(8) × SU(8) Invariance. Phys. Lett. 1982, B108, 285–290. [Google Scholar] [CrossRef]
- Dibitetto, G.; Fernandez-Melgarejo, J.; Marques, D.; Roest, D. Duality orbits of non-geometric fluxes. Fortsch. Phys. 2012, 60, 1123–1149. [Google Scholar] [CrossRef]
- Danielsson, U.; Dibitetto, G. On the distribution of stable de Sitter vacua. JHEP 2013, 03, 018. [Google Scholar] [CrossRef]
- Damian, C.; Loaiza-Brito, O.; Rey, L.; Sabido, M. Slow-Roll Inflation in Non-geometric Flux Compactification. J. High Energy Phys. 2013, 2013, 109. [Google Scholar] [CrossRef]
- Blabäck, J.; Danielsson, U.; Dibitetto, G. Fully stable dS vacua from generalised fluxes. JHEP 2013, 08, 054. [Google Scholar] [CrossRef]
- Hassler, F.; Lust, D.; Massai, S. On Inflation and de Sitter in Non-Geometric String Backgrounds. arXiv 2014, arXiv:1405.2325. [Google Scholar] [CrossRef]
- Ma, C.T.; Shen, C.M. Cosmological Implications from O(D,D). Fortsch. Phys. 2014, 62, 921–941. [Google Scholar] [CrossRef]
- Blumenhagen, R.; Kors, B.; Lust, D.; Stieberger, S. Four-dimensional String Compactifications with D-Branes, Orientifolds and Fluxes. Phys. Rept. 2007, 445, 1–193. [Google Scholar] [CrossRef]
- Riccioni, F.; West, P.C. E(11)-extended spacetime and gauged supergravities. JHEP 2008, 0802, 039. [Google Scholar] [CrossRef]
- Kleinschmidt, A. Counting supersymmetric branes. JHEP 2011, 10, 144. [Google Scholar] [CrossRef]
- Lombardo, D.M.; Riccioni, F.; Risoli, S. P fluxes and exotic branes. JHEP 2016, 12, 114. [Google Scholar] [CrossRef]
- Gross, D.J.; Perry, M.J. Magnetic Monopoles in Kaluza-Klein Theories. Nucl. Phys. 1983, B226, 29–48. [Google Scholar] [CrossRef]
- Hull, C. Generalised geometry for M-theory. JHEP 2007, 0707, 079. [Google Scholar] [CrossRef]
- Andriot, D.; Hohm, O.; Larfors, M.; Lust, D.; Patalong, P. Non-Geometric Fluxes in Supergravity and Double Field Theory. Fortsch. Phys. 2012, 60, 1150–1186. [Google Scholar] [CrossRef]
- Chatzistavrakidis, A.; Gautason, F.F.; Moutsopoulos, G.; Zagermann, M. Effective actions of nongeometric five-branes. Phys. Rev. 2014, D89, 066004. [Google Scholar] [CrossRef]
- Blair, C.D.A.; Musaev, E.T. Five-brane actions in double field theory. JHEP 2018, 03, 111. [Google Scholar] [CrossRef]
- Andriot, D.; Larfors, M.; Lust, D.; Patalong, P. (Non-)commutative closed string on T-dual toroidal backgrounds. JHEP 2013, 06, 021. [Google Scholar] [CrossRef]
- Blair, C.D.A. Non-commutativity and non-associativity of the doubled string in non-geometric backgrounds. JHEP 2015, 06, 091. [Google Scholar] [CrossRef]
- Berman, D.S.; Rudolph, F.J. Branes are Waves and Monopoles. JHEP 2015, 05, 015. [Google Scholar] [CrossRef]
- Bakhmatov, I.; Kleinschmidt, A.; Musaev, E.T. Non-geometric branes are DFT monopoles. JHEP 2016, 10, 076. [Google Scholar] [CrossRef]
- Bakhmatov, I.; Berman, D.; Kleinschmidt, A.; Musaev, E.; Otsuki, R. Exotic branes in Exceptional Field Theory: The SL(5) duality group. JHEP 2018, 08, 021. [Google Scholar] [CrossRef]
- Fernández-Melgarejo, J.J.; Kimura, T.; Sakatani, Y. Weaving the Exotic Web. JHEP 2018, 09, 072. [Google Scholar] [CrossRef]
- Berman, D.S.; Musaev, E.T.; Otsuki, R. Exotic Branes in Exceptional Field Theory: E7(7) and Beyond. JHEP 2018, 12, 053. [Google Scholar] [CrossRef]
- Berman, D.S.; Musaev, E.T.; Otsuki, R. Exotic Branes in M-Theory. In Proceedings of the Dualities and Generalized Geometries, Corfu, Greece, 9–16 September 2018. arXiv 2019, arXiv:hep-th/1903.10247. [Google Scholar]
- Jensen, S. The KK-Monopole/NS5-Brane in Doubled Geometry. JHEP 2011, 1107, 088. [Google Scholar] [CrossRef]
- Gregory, R.; Harvey, J.A.; Moore, G.W. Unwinding strings and t duality of Kaluza-Klein and h monopoles. Adv. Theor. Math. Phys. 1997, 1, 283–297. [Google Scholar] [CrossRef]
- Tong, D. NS5-branes, T duality and world sheet instantons. JHEP 2002, 07, 013. [Google Scholar] [CrossRef]
- Harvey, J.A.; Jensen, S. Worldsheet instanton corrections to the Kaluza-Klein monopole. JHEP 2005, 10, 028. [Google Scholar] [CrossRef]
- Kimura, T.; Sasaki, S. Worldsheet instanton corrections to -brane geometry. JHEP 2013, 08, 126. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Tseytlin, A.A. Effective Field Theory from Quantized Strings. Phys. Lett. 1985, 158B, 316–322. [Google Scholar] [CrossRef]
- Callan, C.G., Jr.; Martinec, E.J.; Perry, M.J.; Friedan, D. Strings in Background Fields. Nucl. Phys. 1985, B262, 593–609. [Google Scholar] [CrossRef]
- Hull, C.M.; Townsend, P.K. Finiteness and Conformal Invariance in Nonlinear σ Models. Nucl. Phys. 1986, B274, 349–362. [Google Scholar] [CrossRef]
- Wulff, L.; Tseytlin, A.A. Kappa-symmetry of superstring sigma model and generalized 10d supergravity equations. JHEP 2016, 06, 174. [Google Scholar] [CrossRef]
- Bena, I.; Polchinski, J.; Roiban, R. Hidden symmetries of the AdS(5) x S**5 superstring. Phys. Rev. 2004, D69, 046002. [Google Scholar] [CrossRef]
- Delduc, F.; Magro, M.; Vicedo, B. An integrable deformation of the AdS5xS5 superstring action. Phys. Rev. Lett. 2014, 112, 051601. [Google Scholar] [CrossRef]
- Arutyunov, G.; Borsato, R.; Frolov, S. Puzzles of η-deformed AdS5 × S5. JHEP 2015, 12, 049. [Google Scholar] [CrossRef]
- Arutyunov, G.; Frolov, S.; Hoare, B.; Roiban, R.; Tseytlin, A.A. Scale invariance of the η-deformed AdS5 × S5 superstring, T-duality and modified type II equations. Nucl. Phys. 2016, B903, 262–303. [Google Scholar] [CrossRef]
- Sakamoto, J.i.; Sakatani, Y.; Yoshida, K. Weyl invariance for generalized supergravity backgrounds from the doubled formalism. PTEP 2017, 2017, 053B07. [Google Scholar] [CrossRef]
- Sakatani, Y.; Uehara, S.; Yoshida, K. Generalized gravity from modified DFT. JHEP 2017, 04, 123. [Google Scholar] [CrossRef]
- Baguet, A.; Magro, M.; Samtleben, H. Generalized IIB supergravity from exceptional field theory. JHEP 2017, 03, 100. [Google Scholar] [CrossRef]
- Araujo, T.; Bakhmatov, I.; Colgáin, E.Ó.; Sakamoto, J.I.; Sheikh-Jabbari, M.M.; Yoshida, K. Conformal twists, Yang–Baxter σ-models & holographic noncommutativity. J. Phys. 2018, A51, 235401. [Google Scholar] [CrossRef]
- Araujo, T.; Ó Colgáin, E.; Sakamoto, J.; Sheikh-Jabbari, M.M.; Yoshida, K. I in generalized supergravity. Eur. Phys. J. 2017, C77, 739. [Google Scholar] [CrossRef]
- Sakamoto, J.I.; Sakatani, Y.; Yoshida, K. Homogeneous Yang-Baxter deformations as generalized diffeomorphisms. J. Phys. 2017, A50, 415401. [Google Scholar] [CrossRef]
- Bakhmatov, I.; Ó Colgáin, E.; Sheikh-Jabbari, M.M.; Yavartanoo, H. Yang-Baxter Deformations Beyond Coset Spaces (a slick way to do TsT). JHEP 2018, 06, 161. [Google Scholar] [CrossRef]
- Bakhmatov, I.; Musaev, E.T. Classical Yang-Baxter equation from β-supergravity. JHEP 2019, 01, 140. [Google Scholar] [CrossRef]
- Sakamoto, J.I.; Sakatani, Y. Local β-deformations and Yang-Baxter sigma model. JHEP 2018, 06, 147. [Google Scholar] [CrossRef]
- Andriot, D.; Hohm, O.; Larfors, M.; Lust, D.; Patalong, P. A geometric action for non-geometric fluxes. Phys. Rev. Lett. 2012, 108, 261602. [Google Scholar] [CrossRef]
- Seiberg, N.; Witten, E. String theory and noncommutative geometry. JHEP 1999, 9909, 032. [Google Scholar] [CrossRef]
- Andriot, D.; Betz, A. NS-branes, source corrected Bianchi identities, and more on backgrounds with non-geometric fluxes. JHEP 2014, 07, 059. [Google Scholar] [CrossRef]
- Andriot, D.; Betz, A. β-supergravity: A ten-dimensional theory with non-geometric fluxes, and its geometric framework. JHEP 2013, 12, 083. [Google Scholar] [CrossRef]
- Fernández-Melgarejo, J.J.; Sakamoto, J.I.; Sakatani, Y.; Yoshida, K. Weyl Invariance of String Theories in Generalized Supergravity Backgrounds. Phys. Rev. Lett. 2019, 122, 111602. [Google Scholar] [CrossRef]
- Catal-Ozer, A. Non-Abelian T-duality as a Transformation in Double Field Theory. arXiv 2019, arXiv:1904.00362. [Google Scholar]
- Hassler, F. Poisson-Lie T-Duality in Double Field Theory. arXiv 2017, arXiv:707.08624. [Google Scholar]
- Baguet, A.; Hohm, O.; Samtleben, H. Consistent Type IIB Reductions to Maximal 5D Supergravity. Phys. Rev. 2015, D92, 065004. [Google Scholar] [CrossRef]
- Malek, E.; Samtleben, H.; Vall Camell, V. Supersymmetric AdS7 and AdS6 vacua and their minimal consistent truncations from exceptional field theory. Phys. Lett. 2018, B786, 171–179. [Google Scholar] [CrossRef]
- Malek, E.; Samtleben, H.; Vall Camell, V. Supersymmetric AdS7 and AdS6 vacua and their consistent truncations with vector multiplets. JHEP 2019, 04, 088. [Google Scholar] [CrossRef]
- Hohm, O.; Samtleben, H. The many facets of exceptional field theory. In Proceedings of the Dualities and Generalized Geometries, Corfu, Greece, 9–16 September 2018. arXiv 2019, arXiv:1905.08312. [Google Scholar]
- Blumenhagen, R.; Font, A.; Plauschinn, E. Relating Double Field Theory to the Scalar Potential of N = 2 Gauged Supergravity. arXiv 2015, arXiv:1507.08059. [Google Scholar] [CrossRef]
- Bosque, P.d.; Hassler, F.; Lust, D. Flux Formulation of DFT on Group Manifolds and Generalized Scherk-Schwarz Compactifications. arXiv 2015, arXiv:1509.04176. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).