1. Introduction
Arrangement of decision alternatives is necessary for any rational decision-making process. Therefore, decision alternatives are ordered before making the actual decision. Because decision alternatives are characterized by various attributes, multi-criteria techniques are useful for ordering these alternatives [
1]. The decision alternatives are ordered with the use of a chosen multi-criteria technique which takes into account the decision-maker’s preferences with respect to all given issues as well as their relative importance. Among the different multi-criteria techniques, we have some scoring techniques which determine a ranking of decision alternatives as order of assigned scoring values. The most popular scoring techniques are:
The Simple Additive Weighting method (SAW) [
2,
3];
Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) [
4].
The SAW method is also known as the Simple Multi Attribute Rating Technique [
2,
3].
In real decision-making problems, the criteria are usually assessed in a qualitative form. This implies the linguistic approach for decision assessing. Then, any criterion is evaluated by linguistic values which are words or sentences in a natural language. Therefore, the meaning of any linguistic value is imprecise. For these reason, linguistic values may be represented with use of fuzzy set theory [
5,
6,
7]. In line with suggestions given in [
8], any criterion evaluation is approximated by some kind of imprecise number.
A commonly used model of an imprecise number is fuzzy number (FN) [
9]. An important disadvantage of FN theory is that subtraction of FNs is the inverse operator to addition of FNs. The notion of OFN is proposed by Kosiński et al [
10] as a model of such an imprecise number that subtraction of OFNs is the inverse operator to addition of OFNs. Therefore, OFNs can help with the interpretation of specific improper fuzzy arithmetic results. The major drawback of Kosiński’s theory is the existence of OFNs which are not linked to any membership function [
11]. Therefore, the Kosiński’s theory is revised in [
12]. From the point-view of symmetry theory, the space of all OFNs may be considered as centrally symmetric closure of an isomorphic image of the space of all FNs.
Any criteria may be valued by OFNs. The main goal of our article is to examine the impact of criteria ranking orientation on a decision-making process. Thus we focus on such scoring techniques which use scoring function with arguments’ values given by OFNs.
To our best knowledge, OFNs are so far only used in the scoring functions describing the SAW method or TOPSIS [
13]. In TOPSIS, we always used a scoring function valued with crisp real numbers. For this reason, the values of the TOPSIS scoring function always are ordered in a natural way like real numbers. Thanks to this, if we order decision alternatives with the use of TOPSIS then the obtained arrangement is independent of the orientation of values of scoring function arguments. On the other hand, the SAW scoring method uses a weighted average of criterion ratings. Therefore, if arguments of SAW scoring function are valued by OFNs then any SAW scoring function is also valued by OFNs. Only then we can obtain a decision alternatives arrangement which may be dependent on an orientation of values of scoring function arguments. Thus, our focus should be restricted to effects of applications of the SAW method equipped with scoring function determined for argument valued by OFN.
The basic SAW method is related to scoring function with arguments evaluated by real numbers. The fuzzy SAW method is introduced by Chou and Chang [
8] in such way that each argument of scoring function is valued by Trapezoidal FN (TrFN). This proposition is justified in this way that TrOFNs are more realistic representation of linguistic assessments. For the needs of the scoring negotiation offers, Roszkowska and Kacprzak [
13] tentatively introduced the Oriented Fuzzy SAW (OF-SAW) with arguments of scoring function valued by trapezoidal OFN (TrOFN). The replacement of TrFN by TrOFN is justified by the fact that TrOFNs contain more information than TrFN. In [
14], the OF-SAW method is modified in a way that is compatible with revised theory of OFNs [
12]. In [
15] it is justified that the OF-SAW method equipped with the fuzzy initial preorder is significantly better than the OF-SAW methods equipped with any crisp initial preorder outlined with the use of any defuzzification method. There it is shown that the use of defuzzification procedures can totally blur the true picture of a real order of decision alternatives. So, we should avoid the defuzzification stage in ordering decision alternatives.
Summing up, since the main goal of our paper is to examine the impact of criteria ranking orientation on a decision-making process, our focus will be on the OF-SAW equipped with fuzzy initial preorder. In this way, we can compare linguistically evaluated decision alternatives without losing information about the imprecision and orientation of linguistic evaluation. This approach is more realistic.
This paper is organized as follows.
Section 2 describes the elements of fuzzy sets theory. We restrict our considerations to the case of TrOFNs. There, FNs, TrFNs, OFNs, TrOFNs, disorientation map, and fuzzy order relations between TrFNs or between TrOFNs are discussed. Moreover, the central symmetry phenomenon of the space of all TrOFNs is explained there. The OF-SAW method equipped with fuzzy initial preorder is presented in
Section 3. In
Section 4, we discuss disorientation impact on ordering of decision alternatives. Original mathematical theorems show that an orientation omission can result in increase in risk of choosing the right decision alternative.
Section 5 presents here some new results obtained for the example of the OF-SAW empirical application for ranking negotiation offers. Here we study the effects of replacing the oriented criteria raking with a disoriented one. In with way we show that an orientation omitting causes noticeable increase in risk burdening the decision making process.
Section 6 contains final conclusions. For the convenience of readers, all acronyms used are defined in Nomenclature section.
Appendix A and
Appendix B contain full proofs of applied original mathematical theorems.
Appendix C presents membership functions of initial preorders considered in
Section 5.
2. Elements of Fuzzy Sets Theory
Let be given space of all considered states. The symbol denotes the family of all crisp sets in the space . Any precise information about considered states may be described by crisp set .
A fuzzy subset
is determined as the set of ordered pairs
where
is its membership function. Multi-valued logic interprets the membership function in this way that each value
is equal to the ‘truth value’ of the sentence
. The symbol
denotes the family of all fuzzy subsets of the space
. Any imprecise information about considered states may be described by fuzzy set
.
Basic set theory operations and relations are defined in the usual way, suggested by Zadeh [
16]. Among other things, we have here the inclusion relation
After Klir [
17] we understand ambiguity as a lack of an explicit recommendation between one alternative amongst various others. Therefore, if condition (2) is met then we say that the fuzzy set
is more ambiguous than the fuzzy set
.
For any fuzzy set
we can distinguish its support
, determined as follows:
2.1. Fuzzy Numbers
An usually applied model of imprecise number is a fuzzy number (FN) which is most generally defined as a some kind of a fuzzy set in the real line
[
9]. In the fuzzy SAW method [
8], the FN applications are restricted to following their kind.
Definition 1. For any non-decreasing sequence, the trapezoidal FN (TrFN) is the fuzzy set determined by its membership functions as follows: We denote the space of all TrFNs by the symbol . The TrFN represents the crisp number . In this way we get . For any TrFN is a formal model of linguistic variable “about ”.
Let us take into account any arithmetic operation
defined on
. By
we denote an extension of arithmetic operation
to
. In [
9], arithmetic operations on FN are introduced with use of the Zadeh’s Extension Principle. In line with it, for any pair
represented by their membership functions
, the FN
is described by its membership function
determined by means of the identity:
In line with above, the dot product
and the sum
determined on
are given as follows
All above arithmetic operations are executed in the standard order. Moreover, let us note that
We can argue about these TrFNs, that is more ambiguous than .
2.2. Ordered Fuzzy Numbers
The notion of OFN is intuitively introduced by Kosiński [
10] as a model of such an imprecise number that the subtraction of OFNs is the inverse operator to the addition of OFNs. Therefore, OFNs can contribute to specific problems concerning the solution of fuzzy linear equations of the form or help with the interpretation of specific improper fuzzy arithmetic results. The main disadvantage of Kosiński’s theory is the existence of OFNs which cannot be linked to any membership function [
11]. For this reason, the Kosiński’s theory is revised in [
12]. Due to high complexity of arithmetic operations, an application of OF-SAW method [
13] restricts the use of OFNs only to their kind distinguished below.
Definition 2 [
12]
. For any monotonic sequence, the trapezoidal ordered fuzzy number (TrOFN) is the pair of the orientation and fuzzy subset determined explicitly by its membership functions as follows The identity (9) additionally describes numerical intervals in way which is applied in this paper.
The symbol
denotes the space of all TrOFNs. Any TrOFN describes an imprecise number with additional information about the location of the approximated number. This information is given as orientation of TrOFN. If
then TrOFN
has the positive orientation
. For any
the positively oriented TrOFN
is a formal model of linguistic variable “about or slightly above
”. The symbol
denotes the space of all positively oriented TrOFN. If
, then TrOFN
has the negative orientation
. For any
the negatively oriented TrOFN
is a formal model of linguistic variable “about or slightly below
”. The symbol
denotes the space of all negatively oriented TrOFN. If
, OFN
TrOFN describes an unoriented number
. Summing up, we see that
The arithmetic operations on
are not consistent with Zadeh’s Extension Principle. Kosiński [
1] formulated the postulate that the subtraction of OFNs is the inverse operator to the addition of OFNs. For this reason, Kosiński [
10] introduces the arithmetic operators of dot product
for TrOFNs by the identity
Then, the unary minus operator
on
is extended to the minus operator
on
in the following way
Kosiński defines OFNs addition with use of formulas proven by Goetschel and Voxman [
18] for FNs addition. Furthermore, Kosiński [
11] have shown that there exists such pair of OFNs that their sum does not exist. Therefore, Kosiński’s addition is replaced by addition
defined on
by the identity [
12]
In [
12], the definition of addition operator
is justified in detail. The difference
between OFNs is defined in usual way
All above arithmetic operations are executed in the standard order. In [
19] it is proven that the subtraction
is the inverse operator for the addition operators
. Therefore, we can say that revised theory of OFNs meet the intuitive postulate put forward by Kosiński.
On the other hand, the additive semigroup
and the additive semigroup
cannot be considered as homomorphic algebraic structures [
19]. Therefore, any theorems on FNs cannot automatically extended to the case of OFNs.
2.3. Disorientation Map
For the case
the membership function of TrFN
is equal to the membership function of TrOFN
. This fact implies the existence of isomorphism
given for any nondecreasing sequence
by the identity
This isomorphism may be extended to the space
by disorientation map
given by the identity
The disorientation map
may be equivalently determined by the identity
Moreover, it is very easy to check that for any pair
we have
Let us examine the disorientation map property that interests us. At the beginning, let’s follow the example below.
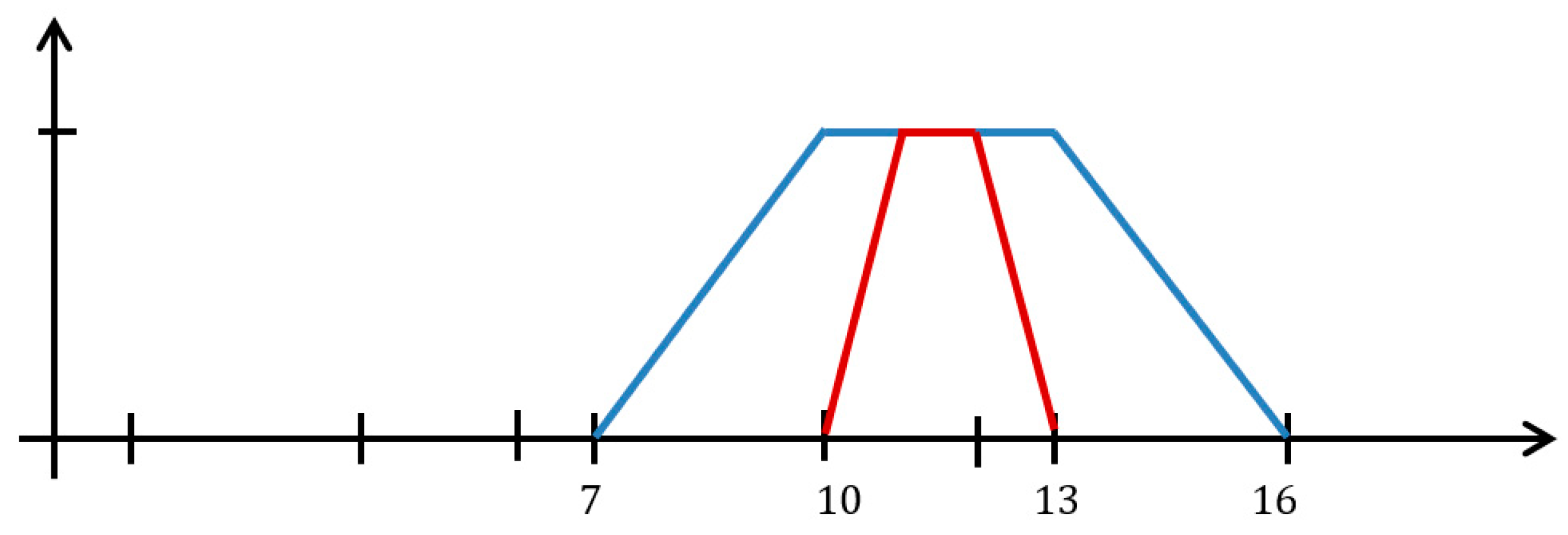
Example 1. We compare the effect of “disorientation before addition” and the effect of “disorientation after addition”. Let us look on the following numerical caseFigure 1 presents the diagram of the membership functions of above results. We see that we have In this case, the the sum of disoriented OFNs is more ambigous than disoriented sum of the same OFNs. It implies that the actions of disorientating and additing are not permutable. □
The above conclusions can be generalized to the following theorem proven in
Appendix A.
Theorem 1. For any sequences and we have We see that the disorientation map is subadditive.
The space of all TrOFNs may be equivalently defined with use of basic notions of the symmetry theory. We take into account the space of all TrFNs and isomorphism determined by (16). The central symmetric relation is determined by the unary minus operator defined on by (12). Then space is the centrally symmetric closure of the set . This fact may be useful in proving some mathematical theorems about TrOFNs.
2.4. Relation “Greater than or Equal to” for Trapezoidal Fuzzy Numbers
We consider the pair
of TrFNs described by their membership functions
. On the set
, we determine the relation
read as follows:
In agreement with the Zadeh’s Extension Principle, the relation (24) is a fuzzy preorder
described by its membership function
given as follows [
20]:
Theorem 2 [
19]
. For any TrFNs we have 2.5. Relation “Greater than or Equal to” for Trapezoidal Oriented Fuzzy Numbers
For any pair
, the symbol
denotes the relation
which is introduced in [
19]. This relation is a fuzzy preorder
defined by its membership function
. In [
19], it is additionally assumed that any membership function
meets the following well-known conditions:
for any pair
, the extension principle
for any pair
, the sign exchange law
for any pair
, the law of subtraction of parties of inequality
Theorem 4 [
19]
. For any pair we have Finally, when taken together, we get the dependency
3. Oriented Fuzzy SAW vs. Disoriented Fuzzy SAW
In decision-making, we meet situations dealing with imprecision resulting from linguistic assessment of decision alternatives. This assessment is made with use fixed Linguistic Order Scale (LOS) which contains ordered words of natural language. In information science, natural language words are considered as values of related linguistic variable. From the perspective of decision-making processes, the linguistic variable evaluation methodologies are reviewed in [
1,
21,
22,
23].
Understanding linguistic variables depends on the applied pragmatics of the natural language. Due this, the semantic meaning of linguistic values may be imprecise. Thus, any linguistic variable can be described by fuzzy sets [
5,
6,
7,
8]. In line with suggestions given in [
8], any linguistic value is represented by some type of FN. Then, each decision alternative is evaluated with the use of the Numerical Order Scale (NOS) given as a sequence of some type of FNs.
In this paper, we will consider any NOS given as a sequence of TrOFNs. Such NOS is denoted by o-NOS. An example of o-NOS is constructed and justified in [
13].
Originally, the SAW method uses a NOS given as a finite subset of positive real numbers. The SAW method was first associated with o-NOS in [
13]. In this way, we obtain Oriented Fuzzy SAW (OF-SAW). Then in [
14], the OF-SAW method has been adapted to the requirements of the revised OFNs’ theory.
On the other hand, all elements of o-NOS may be disoriented by means of the disorientation map (17). In this way we can obtain disoriented NOS (d-NOS). If we replace o-NOS by d-NOS then by reducing the whole of our analysis to FN. The SAW method associated with d-NOS is denoted by the acronym d-SAW. Using d-SAW method, we evaluate a decision alternative with losing information about the orientation of criterion ratings.
We will compare results obtained by use of OF-SAW method with results obtained by use of d-SAW method. In this way, we will examine impact of NOS orientation on a decision making process.
We consider here a multi-criteria decision-making problem with evaluation criteria and decision alternatives , where is an assumed evaluation template. The OF-SAW and d-SAW methods are described by the following procedure:
Procedure 1:
Step 1: Define the set of evaluation criteria;
Step 2: Define the weight vector fulfilling the conditionwhere weight describes the importance of this criterion in the evaluation of the alternatives. Step 3: For each evaluation criterion , determine its scope ;
Step 4: Determine the evaluation template ;
Step 5: Define the o-NOS ;
Step 6: Define the evaluation function fulfilling for each the condition Step 7: Determine the set of evaluated decision alternatives;
Step 8: For the OF-SAW method, determine the scoring function given for any as an aggregated evaluation indexwhere ; Step 9: Using OF-SAW method, evaluate each alternative by a scoring valuewhere Step 10: For the d-SAW method, determine the scoring function given for any as an aggregated evaluation index Step 11: Using d-SAW method, evaluate each alternative by a scoring value From Equations (23), (36), and (39), we immediately obtain that
It proves that if we omit the information about the orientation of criterion rating then it can increase in the ambiguity of the calculated scoring value.
We understand the term risk as a possibility of negative consequences of performed actions [
24,
25]. The increase in the scoring value ambiguity suggests a higher number of decision alternatives to choose from. This leads to an increase in the risk of choosing an incorrect alternative from recommended ones. This may result in making a decision, which will be ex post associated with a profit lower than maximal one, that is with a loss of chance. Described risk is called the ambiguity risk. In conclusion, omitting information about criterion rating orientation can result in increase in ambiguity risk when choosing the right alternative.
In the next sections, we will examine in more detail the impact of omission of NOS orientation on a decision-making process.
4. Disorientation Impact on Decisions Ordering
Decision-making consists of choosing exactly one decision alternative. Therefore, every decision made is precise. For this reason, the main goal of the application of any SAW method is to determine crisp partial order
, which reads as follows:
Let be given the set
of decision alternatives. To preserve the generality of our discussion, we will consider generalized SAW (g-SAW) method determined by fixed scoring function
. Each g-SAW method is pre-equipped with the initial preorder given for each pair
by the equivalency
The preorder (43) is a fuzzy relation
described by membership function
given as follows
For any nonempty set
, we set the best alternative
given as follows:
The best alternative
is described by membership function
, given by the identity
Identity (45) defines the best alternative as an alternative characterized by the maximal value of scoring function . For any , the support is always nonempty.
In this paper, we study the OF-SAW method pre-equipped with the initial preorder given for each pair
by the equivalency
It, together with (32), implies that the preorder (46) is a fuzzy relation
determined by membership function
given in the following way:
It means that the OF-SAW method may be equivalently described as g-SAW method determined by the scoring function . Then OF-SAW method is equivalently equipped with initial preorder . This preorder includes all the gathered information on the imprecision and orientation of linguistic evaluation. Thanks to that, it is the most faithful order of linguistic evaluated alternatives. The fuzzy subset may be used as an imprecise recommendation of the best alternative.
We compare OF-SAW method with d-SAW method which equivalently defined as g-SAW method equipped with scoring function . The below theorem describes an important relationship between OF-SAW and d-SAW methods.
Proof. Let the fixed set be given as
. For any
, the inequalities (27) and (41) imply that
The above theorem confirms our suspicions that omitting orientation of criterion ratings can result in increase in ambiguity risk when choosing the right alternative.
For any g-SAW method, the initial preorder
is applied to determine an induced partial order
. Any induced preorder may be used as order (42). An example of induced partial order is faithful order
introduced in [
15] for OF-SAW method.
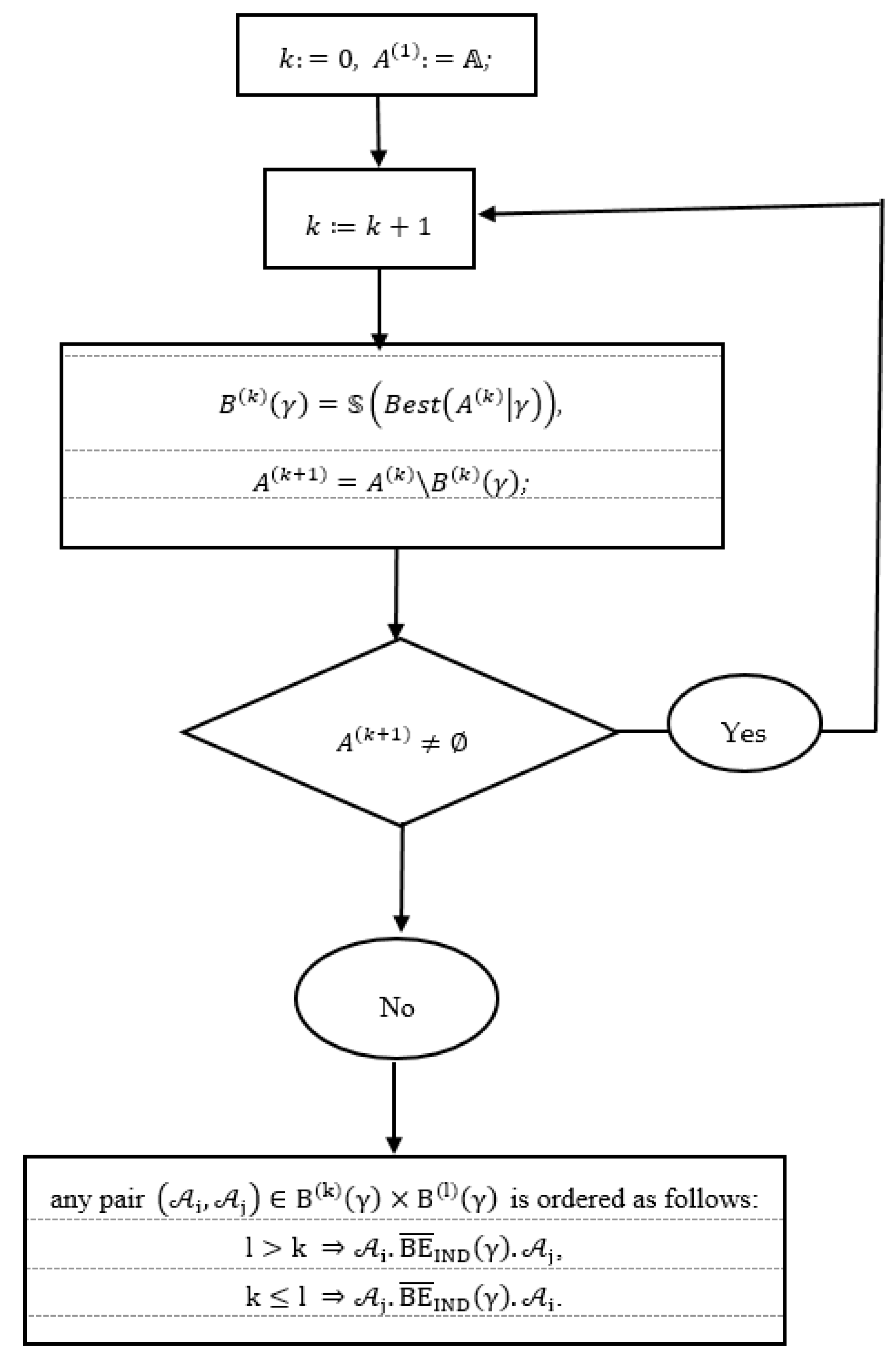
In this section, the faithful order will be generalized for the case of any g-SAW method equipped with a scoring function . Then the generalized faithful order is determined with use the following procedure:
Procedure 2:
Step 1: Perform the substitutions , ;
Step 2: Perform the substitutions ;
Step 3:
Perform the substitutions Step 4:
If the conditionis satisfied then go back to Step 2. Otherwise, go to Step 5. Step 5:
We have a sequence in which each recommendation belongs only to one set . For any given numbers , the value dominates the values Thanks to that, any pair is ordered as follows:In this way, the partially ordered set is uniquely determined. Let us notice that for any pair
we have
which is denoted as
For better help audience to understand the modelling this procedure, it is additionally described by flowchart given on Figure 2.We see that any subset is an equivalence class determined by a partial order . Summing up all the above considerations, the sequence of equivalence classes uniquely determines the partially ordered set . This approach is especially useful in negotiating problems when each negotiating party uses an opposite order.
In this paper, an amount of information is expressed in bits. A more numerous sequence of equivalence classes sets a more detailed order on the set
of decision alternatives. This means that along with the increase in the number
of elements of the sequence
, the amount of information described by the partially ordered set
grows. Therefore, the number
will be used in comparing the individual g-SAW methods equipped with different scoring function
. In [
15], the same approach was used for comparisons of individual OF-SAW methods with different initial preorder.
The main goal of this chapter is to study the effects of replacing the OF-SAW method by the d-SAW method. In this way, we examine the consequences of omitting information about orientation of criterion ratings. Above it is shown that the OF-SAW method is equivalently represented by the g-SAW method equipped with scoring function
. The d-SAW method may be equivalently defined as g-SAW method with scoring function
. Moreover, Theorem 5 implies that
It means that omitting orientation of criterion ratings can result in decrease in amount of information described by inducted partial order. This can indirectly impact on a risk burdening the decision-making process.
In the last two sections, we show the possibility that omitting orientation of criterion ratings can result in increase in risk when choosing the right alternative. For this reason, we recommend the partially ordered set as a proper tool for analyzing decision-making alternatives. The order includes all the gathered information on the imprecision and orientation of linguistic evaluation. Therefore, we can say that partial order is the best crisp approximation of real order of considered decision alternatives. Thanks to that, it is the faithful order of linguistically evaluated decision alternatives. In the next section we intend to show the significance of the effects of omitting the orientation of criterion ratings.
5. Case Study
In this section, we consider an example of applications of OF-SAW methods for evaluation of negotiation offers. The considered negotiation problem is fully described by Roszkowska and Kacprzak [
13] who tentatively introduced the OF-SAW in scoring negotiation offers. In this way, they determine NOS as a sequence of TrOFNs. In [
14], the considered negotiation offers are evaluated by an OF-SAW method which is compatible with the revised theory of OFN [
14]. In both papers, initial preorders are crisp partial orders between defuzzified values [
26] of scoring function. In this way, we lose a lot of information about evaluated negotiation offers. Thus, in [
15], considered negotiation offers are arranged by initial preorder obtained without a defuzzification procedure.
The discussed negotiation problem was determined independently of later studies. This fact raised the credibility of the subsequent case studies. Therefore, in this paper, we will apply a considered negotiation problem for investigating the significance of the effects of omitting the orientation of criterion ratings. In order to accomplish this task, we will evaluate all negotiation offers simultaneously using OF-SAW and d-SAW methods. Comparison of the results obtained by both methods will allow us to evaluate the effects of orientation omitting. To clarify our considerations, all calculations associated with the use of OF-SAW method will be indicated in red. For the same reason, all calculations related to the use of d-SAW method will be indicated in blue.
In this section, all negotiation offers are always evaluated using LOS and
o-NOS introduced in [
13]. Moreover, using the disorientation map (17), we designate
d-NOS. All these ordered scales are presented in
Table 1.
Let us consider the negotiation problem introduced in [
13]. This negotiation problem is described by decision making task with decision alternatives
given as negotiation packages. There an evaluation criterion is called a negotiation issue.
The Seller takes into account 15 negotiation packages discussed in detail in [
13]. All these packages are evaluated with the following negotiation issues:
—unit price expressed in €,
—complaint conditions described verbally,
—time of payment determined in days.
The Seller’s linguistic rating of all negotiations packages is given in
Table 2.
Using the content of
Table 1, we transform linguistic rating into numeric rating expressed in o-NOS and d-NOS. The results of this transformation are presented in
Table 3.
Seller determines the validity of each of the negotiation issues using the following weight vector
In the next step, we evaluate all negotiations packages with use OF-SAW and d-SAW methods. All obtained values of scoring function are presented in
Table 4.
We observe that the condition (41) is met for any negotiation package
. Moreover, for negotiation packages
we have
It proves that the omitting information about criterion rating orientation noticeably increases ambiguity risk of choosing the right negotiation offer.
The identities (44), (32), and (26), determine the initial preorders
and
. The membership functions of these preorders are explicitly described in
Appendix C. Then we distinguish the set
of the best negotiation packages. In the considered case, this set is crisp one. We have
In the face of a low number of the set
, we proceed to the determination of induced partial order
of negotiation packages. To do so, we use Procedure 2 to determine the following equivalence classes:
The sequence
explicitly determines the partial order
which describes the negotiating Seller’s preferences. These preferences are presented in
Table 4 by means of tired ranks [
27]. In order to highlight the results of our considerations, the rows of
Table 4 are ordered by determined partial order.
We will compare partial order
with induced partial order
. Using Procedure 2, we obtain the following equivalence classes:
The sequence
explicitly determines the partial order
described in
Table 4 by tired ranks [
27]. We notice that for amounts of equivalence classes we get
It means that in considered case orientation omitting noticeable decreases the amount of information about negotiating Seller’s preferences. It impacts on a risk burdening the negotiation process.
In considered case, applied tired ranks are not random. Therefore, we cannot use statistical tests for Spearman’s coefficient rho [
27]. Nevertheless, we observe that the orders
and
noticeably differ from each other. Look, for example, on the positions of offers
and
. We conclude that orientation omitting noticeably blurs the best approximation of a real order of negotiation packages. It significantly increases the hazard of accepting wrong negotiation offer.
Summing up, in the analyzed case, orientation omitting noticeable increases the risk of accepting wrong negotiation offer. In this way, we show that the OF-SAW method is more reliable than d-SAW method.
6. Final Conclusions
In our approach, each decision criterion is evaluated with the use of the predefined o-NOS given as a sequence of TrOFNs. In this paper we evaluate decision alternatives by the OF-SAW method associated with o-NOS. In line with results obtained in [
15], our attention was paid to OF-SAW methods equipped with fuzzy initial preorder described by its membership function (48). In
Section 3, we justified the view that this preorder is the most faithful order of linguistic evaluation alternatives.
We examined impact of criterion rating orientation on decision-making processes. For this reason, we also took into account d-NOS determined as the sequence of disoriented elements of o-NOS. If we associate a SAW method with d-NOS, then we obtain d-SAW method. Using d-SAW method, we evaluate a decision alternative with losing information about the orientation of criterion ratings. Therefore, comparison of results obtained with OF-SAW with the results obtained by means of d-SAW allowed us to examine the impact orientation omitting on ordering of decision alternatives.
In
Section 3, using mathematical deduction we concluded that omitting information about criterion rating orientation can result in increase in risk when choosing the right alternative. This is just an application about the possibility of the impact of the orientation omission on the risk burdening a decision-making process. Nevertheless, this application proves that omitting information about criterion rating orientation does not decrease in decision-maker’s risk.
In
Section 4, thanks to the use of mathematical deduction, we confirmed our suspicions that omitting orientation of criterion ratings can result in increase in ambiguity risk when choosing the right alternative. For analogous reasons, we concluded here that orientation omission may result in decrease in amount of information about partial order of decisions alternatives. Of course, it means that orientation omission does not increase in information about arrangement of decision alternatives. It impacts on a risk burdening the negotiation process.
Moreover, in
Section 4 we proposed to accept Procedure 2 determining induced order of decision alternatives. This is the same order as the decision alternatives order proposed in [
15]. We justified the view that if this induced order is determined with use of OF-SAW method then it is the best approximation of real order of considered decision alternatives. Thanks to that, it is the faithful order of linguistically evaluated decision alternatives.
In
Section 5, we considered an example of applications of OF-SAW methods for evaluation of negotiation offers. We applied considered negotiation problem for investigation the significance of the effects of omitting the orientation of criterion ratings. In order to accomplish this task, we evaluated all negotiation offers simultaneously using OF-SAW and d-SAW methods. Comparison of the results obtained by both methods allowed us to evaluate the effects of orientation omitting. We noticed that:
omitting information about criterion rating orientation noticeable increases ambiguity risk of choosing the right negotiation offer;
the orientation omission noticeable decreases the amount of information about negotiating Seller’s preferences;
the orientation omission noticeably blurs the best approximation of a real order of negotiation packages.
So we found the case when the orientation omitting noticeable increases risk burdening decision making process.
Taking into account all the results of our research, we formulate the final conclusion:
For this reason, we can say that the OF-SAW associated with o-NOS is significantly better than d-SAW associated with d-NOS. Oriented Numerical Scale cannot be replaced by disoriented Numerical Order Scale.
Obtained in this paper results cannot be automatically generalized to other scoring techniques. It is necessary to undertake separate studies for each technique.
At present, the main disadvantage of OF-SAW method is the lack of well-justified o-NOS that would be empirically verified. Such empirical verification should be carried out for substantively different decision problems. We hope that further research progress on OF-SAW applications will solve this problem.
Further, we should generalize OF-SAW method for the case of imprecise weights which may be applicable in group decision making. We suppose that such imprecise weights will be represented by FN. Then we should to discuss the product TrFN by TrOFN. This is a new original mathematical problem. Its solution is a necessary condition for the correct generalization of the OF-SAW method for imprecise weighing instruments.
It is advisable to undertake research on various orders induced by the OF-SAW method equipped with fuzzy initial preorder. Then we should to propose different procedures determining induced order of decision alternatives. Obtained in this way, induced orders and the faithful order will have to be compared using the methodology used in this work.