Effect of Landscape Elements on the Symmetry and Variance of the Spatial Distribution of Individual Birds within Foraging Flocks of Geese
Abstract
1. Introduction
1.1. Behavioural Instability
1.2. Environmental Stressors of Geese
1.3. Behavioural Instability of Symmetry
1.4. Behavioural Instability of Variance
1.5. Aims of the Investigation
2. Materials and Methods
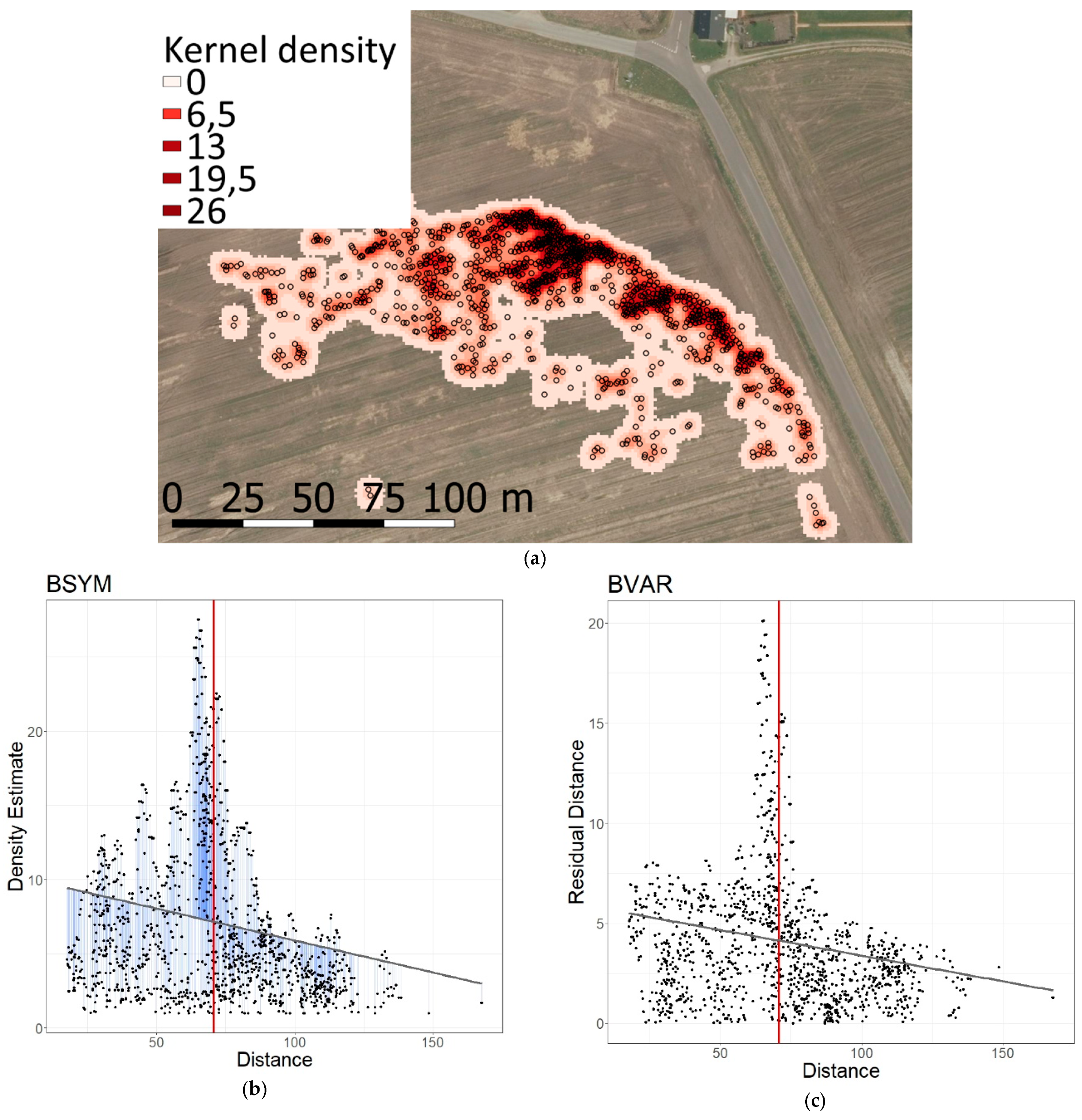
2.1. Data Collection
2.2. Data Extraction
2.3. Data Analysis
3. Results
3.1. Correlation between Distance to Landscape Elements and Behavioural Instability of Symmetry (BSYM)
3.1.1. Wind Turbines
3.1.2. Roads
3.1.3. Hedgerows
3.2. Correlation between Distance to Landscape Elements and Behavioural Instability of Variance (BVAR)
3.2.1. Wind Turbines
3.2.2. Roads
3.2.3. Hedgerows
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pertoldi, C.; Bahrndorff, S.; Novicic, Z.K.; Rohde, P.D. The Novel Concept of “Behavioural Instability” and Its Potential Applications. Symmetry 2016, 8, 135. [Google Scholar] [CrossRef]
- Rees, E.C. Impacts of wind farms on swans and geese: A review. Wildfowl 2012, 62, 37–72. [Google Scholar]
- Madsen, J. Impact of Disturbance on Field Utilization of Pink-footed Geese in West Jutland, Denmark. Biol. Conserv. 1985, 33, 53–63. [Google Scholar] [CrossRef]
- Larsen, J.K.; Madsen, J. Effects of wind turbines and other physical elements on field utilization by pink-footed geese (Anser brachyrhynchus): A landscape perspective. Landsc. Ecol. 2000, 15, 755–764. [Google Scholar] [CrossRef]
- Chudziǹska, M.E.; van Best, F.M.; Madsen, J.; Nabe-Nielsen, J. Using habitat selection theories to predict the spatiotemporal distribution of migratory birds during stopover—A case study of pink-footed geese Anser brachyrhynchus. Oikos 2015, 124, 854–860. [Google Scholar] [CrossRef]
- Harrison, A.L.; Petkov, N.; Mitev, D.; Popgeorgiev, G.; Gove, B.; Hilton, G.M. Scale-dependent habitat selection by wintering geese: Implications for landscape management. Biodivers. Conserv. 2018, 27, 167–188. [Google Scholar] [CrossRef]
- Hötker, H. Birds: Displacement. In Wildlife and Wind Farms, Conflicts and Solutions; Volume 1 Onshore: Potential Effects; Perrow, M.R., Ed.; Pelagic Publishing: Exeter, UK, 2017; pp. 119–154. [Google Scholar]
- Roberts, G. Why individual vigilance declines as group size increases. Anim. Behav. 1996, 51, 1077–1086. [Google Scholar] [CrossRef]
- Bech-Hansen, M.; Kallehauge, R.M.; Lauritzen, J.M.S.; Sørensen, M.H.; Pertoldi, C.; Bruhn, D.; Laubek, B.; Jensen, L.F. Evaluation of disturbance effect on geese and swans (Anserinae) caused by an approaching unmanned aerial vehicle. Bird Conserv. Int. under review.
- Silverman, B. Density Estimation for Statistics and Data Analysis; Chapman & Hall: London, UK, 1986; pp. 9–13. [Google Scholar]
- Lazarus, J. Vigilance, flock size and domain of danger size in the White-fronted Goose. Wildfowl 1978, 29, 135–145. [Google Scholar]
- Gill, J.A. Habitat Choice in Pink-Footed Geese: Quantifying the Constraints Determining Winter Site Use. J. Appl. Ecol. 1996, 33, 884–892. [Google Scholar] [CrossRef]
- Black, M.J.; Carbone, C.; Wells, R.L.; Owen, M. Foraging dynamics in goose flocks: The cost of living on the edge. Anim. Behav. 1992, 44, 41–50. [Google Scholar] [CrossRef]
- Carbone, C.; Thompson, W.A.; Zadorina, L.; Rowcliffe, J.M. Competition, predation risk and patterns of flock expansion in barnacle geese (Branta leucopsis). J. Zool. Lond. 2003, 259, 301–308. [Google Scholar] [CrossRef]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry: Measurement, analysis, patterns. Annu. Rev. Ecol. Syst. 1986, 17, 391–421. [Google Scholar] [CrossRef]
- Pertoldi, C.; Kristensen, T.N.; Andersen, D.H.; Loeschcke, V. Developmental instability as an estimator of genetic stress. Heredity 2006, 96, 122–127. [Google Scholar] [CrossRef] [PubMed]
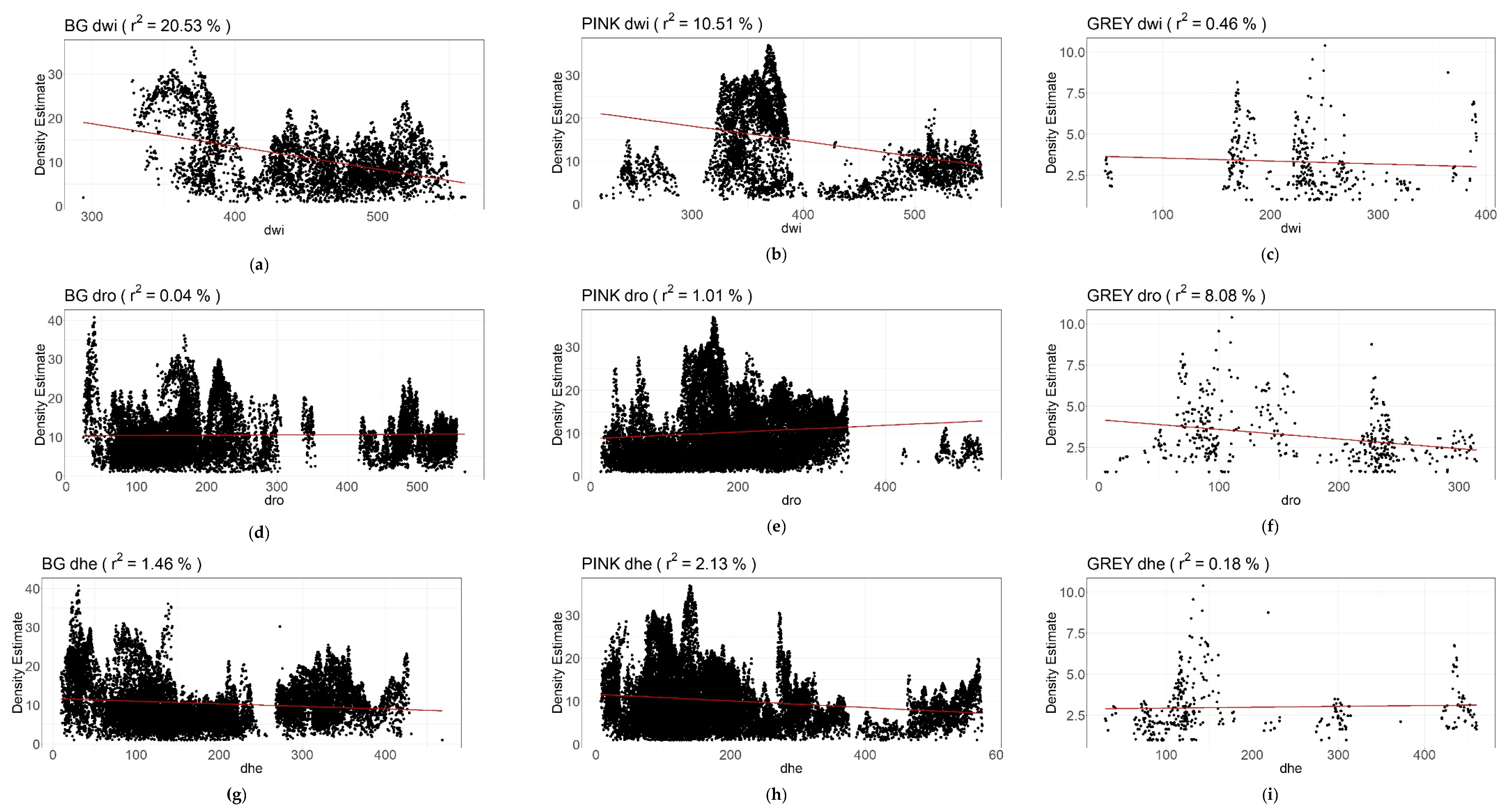
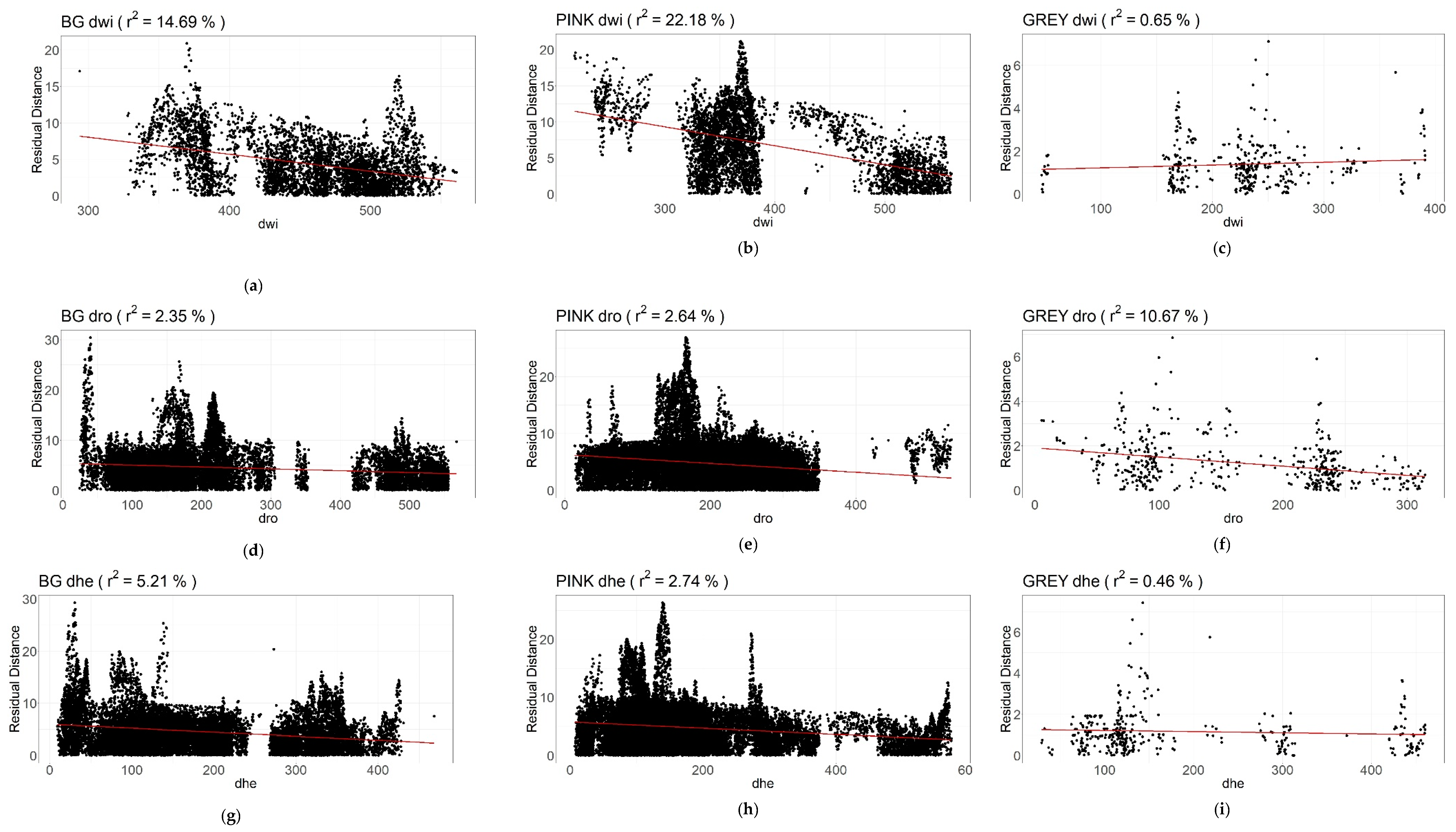
| Species Dist. from Obstacles | n (Number of Measurements) | LRD r2 | LRD a & b | LRD p | LRR r2 | LRR a & b | LRR p | |||
|---|---|---|---|---|---|---|---|---|---|---|
| BG | dwi | 4872 | 20.53% | Slope a: Intercept b: | −0.052 34.182 | *** | 14.69% | Slope a: Intercept b: | −0.023 15.038 | *** |
| dro | 18925 | 0.04% | Slope a: Intercept b: | 0.001 10.258 | ** | 2.35% | Slope a: Intercept b: | −0.004 5.394 | ** | |
| dhe | 18925 | 1.46% | Slope a: Intercept b: | −0.007 11.610 | *** | 5.20% | Slope a: Intercept b: | −0.008 5.968 | *** | |
| PINK | dwi | 4894 | 10.51% | Slope a: Intercept b: | −0.035 28.681 | *** | 22.18% | Slope a: Intercept b: | −0.026 17.196 | *** |
| dro | 26394 | 1.01% | Slope a: Intercept b: | −0.008 8.744 | *** | 2.64% | Slope a: Intercept b: | −0.008 6.301 | *** | |
| dhe | 26313 | 2.13% | Slope a: Intercept b: | 0.008 11.588 | *** | 2.74% | Slope a: Intercept b: | −0.005 5.734 | *** | |
| GREY | dwi | 361 | 0.45% | Slope a: Intercept b: | −0.002 3.720 | n.s. | 0.65% | Slope a: Intercept b: | 0.001 1.090 | n.s. |
| dro | 458 | 8.08% | Slope a: Intercept b: | −0.006 4.176 | *** | 10.67% | Slope a: Intercept b: | −0.004 1.910 | *** | |
| dhe | 353 | 0.18 | Slope a: Intercept b: | 0.001 2.873 | n.s. | 0.46% | Slope a: Intercept b: | −0.001 1.22 | n.s. | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bech-Hansen, M.; M. Kallehauge, R.; Bruhn, D.; H. Funder Castenschiold, J.; Beltoft Gehrlein, J.; Laubek, B.; F. Jensen, L.; Pertoldi, C. Effect of Landscape Elements on the Symmetry and Variance of the Spatial Distribution of Individual Birds within Foraging Flocks of Geese. Symmetry 2019, 11, 1103. https://doi.org/10.3390/sym11091103
Bech-Hansen M, M. Kallehauge R, Bruhn D, H. Funder Castenschiold J, Beltoft Gehrlein J, Laubek B, F. Jensen L, Pertoldi C. Effect of Landscape Elements on the Symmetry and Variance of the Spatial Distribution of Individual Birds within Foraging Flocks of Geese. Symmetry. 2019; 11(9):1103. https://doi.org/10.3390/sym11091103
Chicago/Turabian StyleBech-Hansen, Mads, Rune M. Kallehauge, Dan Bruhn, Johan H. Funder Castenschiold, Jonas Beltoft Gehrlein, Bjarke Laubek, Lasse F. Jensen, and Cino Pertoldi. 2019. "Effect of Landscape Elements on the Symmetry and Variance of the Spatial Distribution of Individual Birds within Foraging Flocks of Geese" Symmetry 11, no. 9: 1103. https://doi.org/10.3390/sym11091103
APA StyleBech-Hansen, M., M. Kallehauge, R., Bruhn, D., H. Funder Castenschiold, J., Beltoft Gehrlein, J., Laubek, B., F. Jensen, L., & Pertoldi, C. (2019). Effect of Landscape Elements on the Symmetry and Variance of the Spatial Distribution of Individual Birds within Foraging Flocks of Geese. Symmetry, 11(9), 1103. https://doi.org/10.3390/sym11091103






