Extended Convergence Analysis of the Newton–Hermitian and Skew–Hermitian Splitting Method

Abstract

Many problems in diverse disciplines such as applied mathematics, mathematical biology, chemistry, economics, and engineering, to mention a few, reduce to solving a nonlinear equation or a system of nonlinear equations. Then various iterative methods are considered to generate a sequence of approximations converging to a solution of such problems. The goal of this article is two-fold: On the one hand, we present a correct convergence criterion for Newton–Hermitian splitting (NHSS) method under the Kantorovich theory, since the criterion given in Numer. Linear Algebra Appl., 2011, 18, 299–315 is not correct. Indeed, the radius of convergence cannot be defined under the given criterion, since the discriminant of the quadratic polynomial from which this radius is derived is negative (See Remark 1 and the conclusions of the present article for more details). On the other hand, we have extended the corrected convergence criterion using our idea of recurrent functions. Numerical examples involving convection–diffusion equations further validate the theoretical results.

1. Introduction

Numerous problems in computational disciplines can be reduced to solving a system of nonlinear equations with n equations in n variables like

$$F\left(x\right)=0$$

(1)

using Mathematical Modelling [1,2,3,4,5,6,7,8,9,10,11]. Here, F is a continuously differentiable nonlinear mapping defined on a convex subset $\mathsf{\Omega }$ of the $n-$dimensional complex linear space ${\mathbb{C}}^n$ into ${\mathbb{C}}^n.$ In general, the corresponding Jacobian matrix $F^{\prime }\left(x\right)$ is sparse, non-symmetric and positive definite. The solution methods for the nonlinear problem $F\left(x\right)=0$ are iterative in nature, since an exact solution $x^{*}$ could be obtained only for a few special cases. In the rest of the article, some of the well established and standard results and notations are used to establish our results (See [3,4,5,6,10,11,12,13,14] and the references there in). Undoubtedly, some of the well known methods for generating a sequence to approximate $x^{*}$ are the inexact Newton (IN) methods [1,2,3,5,6,7,8,9,10,11,12,13,14]. The IN algorithm involves the steps as given in the following:

Algorithm IN [6]

• Step 1: Choose initial guess $x_0$, tolerance value $tol$; Set $k=0$
• Step 2: While $F\left(x_k\right)>tol\times F\left(x_0\right)$, Do
  • Choose ${\eta }_k\in [0,1)$. Find $d_k$ so that $\parallel F\left(x_k\right)+F^{\prime }\left(x_k\right)d_k\parallel \le {\eta }_k\parallel F\left(x_k\right)\parallel$.
  • Set $x_{k+1}=x_k+d_k$; $k=k+1$

Furthermore, if A is sparse, non-Hermitian and positive definite, the Hermitian and skew-Hermitian splitting (HSS) algorithm [4] for solving the linear system $Ax=b$ is given by,

Algorithm HSS [4]

• Step 1: Choose initial guess $x_0$, tolerance value $tol$ and $\alpha >0$; Set $l=0$
• Step 2: Set $H=\frac{1}{2}(A+A^{*})\mathrm{and}S=\frac{1}{2}(A-A^{*})$, where H is Hermitian and S is skew-Hermitian parts of A.
• Step 3: While $\parallel b-A{x}_{\mathsf{ł}}\parallel >tol\times \parallel b-A{x}_0\parallel$, Do
  • Solve $(\alpha I+H)x_{l+1/2}=(\alpha I-S)x_l+b$
  • Solve $(\alpha I+S)x_l=(\alpha I-H)x_{\mathsf{ł}+1/2}+b$
  • Set $l=l+1$

Newton–HSS [5] algorithm combines appropriately both IN and HSS methods for the solution of the large nonlinear system of equations with positive definite Jacobian matrix. The algorithm is as follows:

Algorithm NHSS (The Newton–HSS method [5])

• Step 1: Choose initial guess $x_0$, positive constants $\alpha$ and $tol$; Set $k=0$
• Step 2: While $\parallel F\left(x_k\right)\parallel >tol\times \parallel F\left(x_0\right)\parallel$

  -

  Compute Jacobian $J_k=F^{\prime }\left(x_k\right)$

  -

  Set

  $$H_k\left(x_k\right)=\frac{1}{2}(J_k+J_k^{*})\mathrm{and}{S}_k\left(x_k\right)=\frac{1}{2}(J_k-J_k^{*}),$$

  (2)

  where $H_k$ is Hermitian and $S_k$ is skew-Hermitian parts of $J_k$.

  -

  Set $d_{k,0}=0;l=0$

  -

  While

  $$\parallel F\left(x_k\right)+J_k{d}_{k,\mathsf{ł}}\parallel \ge {\eta }_k\times \parallel F\left(x_k\right)\parallel ({\eta }_k\in [0,1))$$

  (3)

  Do

  {

  • Solve sequentially:

    $$\begin{array}{c}\hfill (\alpha I+H_k)d_{k,l+1/2}=(\alpha I-S_k)d_{k,l}+b\end{array}$$

    (4)

    $$\begin{array}{c}\hfill (\alpha I+S_k)d_{k,l}=(\alpha I-H_k)d_{k,l+1/2}+b\end{array}$$

    (5)
  • Set $l=l+1$

  }

  -

  Set

  $$x_{k+1}=x_k+d_{k,l};k=k+1$$

  (6)

  -

  Compute $J_k$, $H_k$ and $S_k$ for new $x_k$

Please note that ${\eta }_k$ is varying in each iterative step, unlike a fixed positive constant value in used in [5]. Further observe that if $d_{k,{\ell }_k}$ in (6) is given in terms of $d_{k,0}$, we get

$$d_{k,{\ell }_k}=(I-T_k^{\ell }){(I-T_k)}^{-1}{B}_k^{-1}F\left(x_k\right)$$

(7)

where $T_k:=T(\alpha ,k),B_k:=B(\alpha ,k)$ and

$$\begin{array}{ccc}\hfill T(\alpha ,x)& =& B{(\alpha ,x)}^{-1}C(\alpha ,x)\hfill \\ \hfill B(\alpha ,x)& =& \frac{1}{2\alpha }(\alpha I+H\left(x\right))(\alpha I+S\left(x\right))\hfill \\ \hfill C(\alpha ,x)& =& \frac{1}{2\alpha }(\alpha I-H\left(x\right))(\alpha I-S\left(x\right)).\hfill \end{array}$$

(8)

Using the above expressions for $T_k$ and $d_{k,{\ell }_k}$, we can write the Newton–HSS in (6) as

$$x_{k+1}=x_k-{(I-T_k^{\ell })}^{-1}F{\left(x_k\right)}^{-1}F\left(x_k\right).$$

(9)

A Kantorovich-type semi-local convergence analysis was presented in [7] for NHSS. However, there are shortcomings:

(i)

The semi-local sufficient convergence criterion provided in (15) of [7] is false. The details are given in Remark 1. Accordingly, Theorem 3.2 in [7] as well as all the followings results based on (15) in [7] are inaccurate. Further, the upper bound function $g_3$ (to be defined later) on the norm of the initial point is not the best that can be used under the conditions given in [7].

(ii)

The convergence domain of NHSS is small in general, even if we use the corrected sufficient convergence criterion (12). That is why, using our technique of recurrent functions, we present a new semi-local convergence criterion for NHSS, which improves the corrected convergence criterion (12) (see also Section 3 and Section 4, Example 4.4).

(iii)

Example 4.5 taken from [7] is provided to show as in [7] that convergence can be attained even if these criteria are not checked or not satisfied, since these criteria are not sufficient too. The convergence criteria presented here are only sufficient.

Moreover, we refer the reader to [3,4,5,6,7,8,9,10,11,13,14] and the references therein to avoid repetitions for the importance of these methods for solving large systems of equations.

The rest of the note is organized as follows. Section 2 contains the semi-local convergence analysis of NHSS under the Kantorovich theory. In Section 3, we present the semi-local convergence analysis using our idea of recurrent functions. Numerical examples are discussed in Section 4. The article ends with a few concluding remarks.

2. Semi-Local Convergence Analysis

To make the paper as self-contained as possible we present some results from [3] (see also [7]). The semi-local convergence of NHSS is based on the conditions ($\mathcal{A}$). Let $x_0\in {\mathbb{C}}^n$ and $F:\mathsf{\Omega }\subset {\mathbb{C}}^n⟶{\mathbb{C}}^n$ be $G-$differentiable on an open neighborhood ${\mathsf{\Omega }}_0\subset \mathsf{\Omega }$ on which $F^{\prime }\left(x\right)$ is continuous and positive definite. Suppose $F^{\prime }\left(x\right)=H\left(x\right)+S\left(x\right)$ where $H\left(x\right)$ and $S\left(x\right)$ are as in (2) with $x_k=x.$

$\mathrm{(𝒜}$₁)

There exist positive constants $\beta ,\gamma$ and $\delta$ such that

$$max\{\parallel H\left(x_0\right)\parallel ,\parallel S\left(x_0\right)\parallel \}\le \beta ,\parallel F^{\prime }{\left(x_0\right)}^{-1}\parallel \le \gamma ,\parallel F\left(x_0\right)\parallel \le \delta ,$$

(10)

$\mathrm{(𝒜}$₂)

There exist nonnegative constants $L_h$ and $L_s$ such that for all $x,y\in U(x_0,r)\subset {\mathsf{\Omega }}_0,$

$$\begin{array}{ccc}\hfill \parallel H\left(x\right)-H\left(y\right)\parallel & \le & L_h\parallel x-y\parallel \hfill \\ \hfill \parallel S\left(x\right)-S\left(y\right)\parallel & \le & L_s\parallel x-y\parallel .\hfill \end{array}$$

(11)

Next, we present the corrected version of Theorem 3.2 in [7].

Theorem 1.

Assume that conditions ($\mathcal{A}$) hold with the constants satisfying

$$\delta {\gamma }^{2}L\le {\overline{g}}_3\left(\eta \right)$$

(12)

where ${\overline{g}}_3\left(t\right):=\frac{{(1-t)}^2}{2(2+t+2t^2-t^3)},$ $\eta =max\left\{{\eta }_k\right\}<1,r=max\{r_1,r_2\}$ with

$$\begin{array}{ccc}\hfill r_1& =& \frac{\alpha +\beta }{L}\left(\sqrt{1+\frac{2\alpha \tau \theta }{(2\gamma +\gamma \tau \theta ){(\alpha +\beta )}^2}}-1\right)\hfill \\ \hfill r_2& =& \frac{b-\sqrt{b^2-2ac}}{a}\hfill \\ \hfill a& =& \frac{\gamma L(1+\eta )}{1+2{\gamma }^2\delta L\eta },b=1-\eta ,c=2\gamma \delta ,\hfill \end{array}$$

(13)

and with ${\ell }_{*}=lim{inf}_{k⟶\infty }{\ell }_k$ satisfying ${\ell }_{*}>\lfloor \frac{ln\eta }{ln\left(\right(\tau +1)\theta }\rfloor ,$ (Here $\lfloor .\rfloor$ represents the largest integer less than or equal to the corresponding real number) $\tau \in (0,\frac{1-\theta }{\theta })$ and

$$\theta \equiv \theta (\alpha ,x_0)=\parallel T(\alpha ,x_0)\parallel <1.$$

(14)

Then, the iteration sequence ${\left\{x_k\right\}}_{k=0}^{\infty }$ generated by Algorithm NHSS is well defined and converges to $x_{*},$ so that $F\left(x_{*}\right)=0.$

Proof. 

We simply follow the proof of Theorem 3.2 in [7] but use the correct function ${\overline{g}}_3$ instead of the incorrect function $g_3$ defined in the following remark. □

Remark 1.

The corresponding result in [7] used the function bound

$$g_3\left(t\right)=\frac{1-t}{2(1+t^2)}$$

(15)

instead of ${\overline{g}}_3$ in (12) (simply looking at the bottom of first page of the proof in Theorem 3.2 in [7]), i.e., the inequality they have considered is,

$$\delta {\gamma }^{2}L\le g_3\left(\eta \right).$$

(16)

However, condition (16) does not necessarily imply $b^2-4ac\ge 0,$ which means that $r_2$ does not necessarily exist (see (13) where $b^2-2ac\ge 0$ is needed) and the proof of Theorem 3.2 in [7] breaks down. As an example, choose $\eta =\frac{1}{2},$ then $g_3\left(\frac{1}{2}\right)=\frac{1}{5},{\overline{g}}_3\left(\frac{1}{2}\right)=\frac{1}{23}$ and for ${\overline{g}}_3\left(\frac{1}{2}\right)=\delta {\gamma }^{2}L<g_3\left(\frac{1}{2}\right),$ we have $b^2-4ac<0.$ Notice that our condition (12) is equivalent to $b^2-4ac\ge 0.$ Hence, our version of Theorem 3.2 is correct. Notice also that

$${\overline{g}}_3\left(t\right)<g_3\left(t\right)\mathrm{for}\mathrm{each}t\ge 0,$$

(17)

so (12) implies (16) but not necessarily vice versa.

3. Semi-Local Convergence Analysis II

We need to define some parameters and a sequence needed for the semi-local convergence of NHSS using recurrent functions.

Let $\beta ,\gamma ,\delta ,L_0,L$ be positive constants and $\eta \in [0,1).$ Then, there exists $\mu \ge 0$ such that $L=\mu L_0.$ Set $c=2\gamma \delta .$ Define parameters $p,q,{\eta }_0$ and ${\delta }_0$ by

$$p=\frac{(1+\eta )\mu \gamma L_0}{2},q=\frac{-p+\sqrt{p^2+4\gamma L_{0}p}}{2\gamma L_0},$$

(18)

$${\eta }_0=\sqrt{\frac{\mu }{\mu +2}}$$

(19)

and

$$\xi =\frac{\mu }{2}min\{\frac{2(q-\eta )}{(1+\eta )\mu +2q},\frac{(1+\eta )q-\eta -q^2}{(1+\eta )q-\eta }\}.$$

(20)

Moreover, define scalar sequence $\left\{s_k\right\}$ by

$$\begin{array}{ccc}\hfill s_0& =& 0,s_1=c=2\gamma \delta \mathrm{and} \mathrm{for} \mathrm{each}k=1,2,\dots \hfill \\ \hfill s_{k+1}& =& s_k+\frac{1}{1-\gamma L_0{s}_k}[p(s_k-s_{k-1})+\eta (1-\gamma L_0{s}_{k-1})](s_k-s_{k-1}).\hfill \end{array}$$

(21)

We need to show the following auxiliary result of majorizing sequences for NHSS using the aforementioned notation.

Lemma 1.

Let $\beta ,\gamma ,\delta ,L_0,L$ be positive constants and $\eta \in [0,1).$ Suppose that

$${\gamma }^{2}L\delta \le \xi$$

(22)

and

$$\eta \le {\eta }_0,$$

(23)

where ${\eta }_0,\xi$ are given by (19) and (20), respectively. Then, sequence $\left\{s_k\right\}$ defined in (21) is nondecreasing, bounded from above by

$$s^{**}=\frac{c}{1-q}$$

(24)

and converges to its unique least upper bounds $s^{*}$ which satisfies

$$c\le s^{*}\le s^{**}.$$

(25)

Proof. 

Notice that by (18)–(23) $q\in (0,1),q>\eta ,{\eta }_0\in [\frac{\sqrt{3}}{3},1),c>0,$ $(1+\eta )q-\eta >0,$ $(1+\eta )q-\eta -q^2>0$ and $\xi >0.$ We shall show using induction on k that

$$0<s_{k+1}-s_k\le q(s_k-s_{k-1})$$

(26)

or equivalently by (21)

$$0\le \frac{1}{1-\gamma L_0{s}_k}[p(s_k-s_{k-1})+\eta (1-\gamma L_0{s}_{k-1})]\le q.$$

(27)

Estimate (27) holds true for $k=1$ by the initial data and since it reduces to showing $\delta \le \frac{\eta }{{\gamma }^{2}L}\frac{q-\eta }{(1+\eta )\mu +2q},$ which is true by (20). Then, by (21) and (27), we have

$$0<s_2-s_1\le q(s_1-s_0),\gamma L_0{s}_1<1$$

and

$$s_2\le s_1+q(s_1-s_0)=\frac{1-q^2}{1-q}(s_1-s_0)<\frac{s_1-s_0}{1-q}=s^{**}.$$

Suppose that (26),

$$\gamma L_0{s}_k<1$$

(28)

and

$$s_{k+1}\le \frac{1-q^{k+1}}{1-q}(s_1-s_0)<s^{**}$$

(29)

hold true. Next, we shall show that they are true for k replaced by $k+1.$ It suffices to show that

$$0\le \frac{1}{1-\gamma L_0{s}_{k+1}}(p(s_{k+1}-s_k)+\eta (1-\gamma L_0{s}_k))\le q$$

or

$$p(s_{k+1}-s_k)+\eta (1-\gamma L_0{s}_k)\le q(1-\gamma L_0{s}_{k+1})$$

or

$$p(s_{k+1}-s_k)+\eta (1-\gamma L_0{s}_k)-q(1-\gamma L_0{s}_{k+1})\le 0$$

or

$$p(s_{k+1}-s_k)+\eta (1-\gamma L_0{s}_1)+\gamma q{L}_0{s}_{k+1})-q\le 0$$

(since $s_1\le s_k$) or

$$2\gamma \delta p{q}^k+2{\gamma }^{2}q{L}_0\delta (1+q+\dots +q^k)+\eta (1-2{\gamma }^2{L}_0\delta )-q\le 0.$$

(30)

Estimate (30) motivates us to introduce recurrent functions $f_k$ defined on the interval $[0,1)$ by

$$f_k\left(t\right)=2\gamma \delta p{t}^k+2{\gamma }^2{L}_0\delta (1+t+\dots +t^k)t-t+\eta (1-2{\gamma }^2{L}_0\delta ).$$

(31)

Then, we must show instead of (30) that

$$f_k\left(q\right)\le 0.$$

(32)

We need a relationship between two consecutive functions $f_k:$

$$\begin{array}{ccc}\hfill f_{k+1}\left(t\right)& =& f_{k+1}\left(t\right)-f_k\left(t\right)+f_k\left(t\right)\hfill \\ \hfill & =& 2\gamma \delta p{t}^{k+1}+2{\gamma }^2{L}_0\delta (1+t+\dots t^{k+1})t-t\hfill \\ \hfill & & +\eta (1-2{\gamma }^2{L}_0\delta )-2\gamma \delta p{t}^k-2{\gamma }^2{L}_0\delta (1+t+\dots +t^k)t\hfill \\ \hfill & & +t-\eta (1-2{\gamma }^2{L}_0\delta )+f_k\left(t\right)\hfill \\ \hfill & =& f_k\left(t\right)+2\gamma \delta g\left(t\right)t^k,\hfill \end{array}$$

(33)

where

$$g\left(t\right)=\gamma L_0{t}^2+pt-p.$$

(34)

Notice that $g\left(q\right)=0.$ It follows from (32) and (34) that

$$f_{k+1}\left(q\right)=f_k\left(q\right)\mathrm{for}\mathrm{each}k.$$

(35)

Then, since

$$f_{\infty }\left(q\right)=\underset{k⟶\infty }{lim}{f}_k\left(q\right),$$

(36)

it suffices to show

$$f_{\infty }\left(q\right)\le 0$$

(37)

instead of (32). We get by (31) that

$$f_{\infty }\left(q\right)=\frac{2{\gamma }^2{L}_0\delta q}{1-q}-q+\eta (1-2{\gamma }^2{L}_0\delta )$$

(38)

so, we must show that

$$\frac{2{\gamma }^2{L}_0\delta q}{1-q}-q+\eta (1-2{\gamma }^2{L}_0\delta )\le 0,$$

(39)

which reduces to showing that

$$\delta \le \frac{\mu }{2{\gamma }^{2}L}\frac{(1+\eta )q-\eta -q^2}{(1+\eta )q-\eta },$$

(40)

which is true by (22). Hence, the induction for (26), (28) and (29) is completed. It follows that sequence $\left\{s_k\right\}$ is nondecreasing, bounded above by $s^{**}$ and as such it converges to its unique least upper bound $s^{*}$ which satisfies (25). □

We need the following result.

Lemma 2

([14]). Suppose that conditions ($\mathcal{A}$) hold. Then, the following assertions also hold:

(i) 

$\parallel F^{\prime }\left(x\right)-F^{\prime }\left(y\right)\parallel \le L\parallel x-y\parallel$

(ii) 

$\parallel F^{\prime }\left(x\right)\parallel \le L\parallel x-y\parallel +2\beta$

(iii) 

If $r<\frac{1}{\gamma L},$ then $F^{\prime }\left(x\right)$ is nonsingular and satisfies

$$\parallel F^{\prime }{\left(x\right)}^{-1}\parallel \le \frac{\gamma }{1-\gamma L\parallel x-x_0\parallel },$$

(41)

where $L=L_h+L_s.$

Next, we show how to improve Lemma 2 and the rest of the results in [3,7]. Notice that it follows from (i) in Lemma 2 that there exists $L_0>0$ such that

$$\parallel F^{\prime }\left(x\right)-F^{\prime }\left(x_0\right)\parallel \le L_0\parallel x-x_0\parallel \mathrm{for}\mathrm{each}x\in \mathsf{\Omega }.$$

(42)

We have that

$$L_0\le L$$

(43)

holds true and $\frac{L}{L_0}$ can be arbitrarily large [2,12]. Then, we have the following improvement of Lemma 2.

Lemma 3.

Suppose that conditions ($\mathcal{A}$) hold. Then, the following assertions also hold:

(i) 

$\parallel F^{\prime }\left(x\right)-F^{\prime }\left(y\right)\parallel \le L\parallel x-y\parallel$

(ii) 

$\parallel F^{\prime }\left(x\right)\parallel \le L_0\parallel x-y\parallel +2\beta$

(iii) 

If $r<\frac{1}{\gamma L_0},$ then $F^{\prime }\left(x\right)$ is nonsingular and satisfies

$$\parallel F^{\prime }{\left(x\right)}^{-1}\parallel \le \frac{\gamma }{1-\gamma L_0\parallel x-x_0\parallel }.$$

(44)

Proof. 

(ii) We have

$$\begin{array}{ccc}\hfill \parallel F^{\prime }\left(x\right)\parallel & =& \parallel F^{\prime }\left(x\right)-F^{\prime }\left(x_0\right)+F^{\prime }\left(x_0\right)\parallel \hfill \\ \hfill & \le & \parallel F^{\prime }\left(x\right)-F^{\prime }\left(x_0\right)\parallel +\parallel F^{\prime }\left(x_0\right)\parallel \hfill \\ \hfill & \le & L_0\parallel x-x_0\parallel +\parallel F^{\prime }\left(x_0\right)\parallel \le L_0\parallel x-x_0\parallel +2\beta .\hfill \end{array}$$

(iii)

$$\gamma \parallel F^{\prime }\left(x\right)-F^{\prime }\left(x_0\right)\parallel \le \gamma L_0\parallel x-x_0\parallel <1.$$

(45)

It follows from the Banach lemma on invertible operators [1] that $F^{\prime }\left(x\right)$ is nonsingular, so that (44) holds. □

Remark 2.

The new estimates (ii) and (iii) are more precise than the corresponding ones in Lemma 2, if $L_0<L.$

Next, we present the semi-local convergence of NHSS using the majorizing sequence $\left\{s_n\right\}$ introduced in Lemma 1.

Theorem 2.

Assume that conditions ($\mathcal{A}$), (22) and (23) hold. Let $\eta =max\left\{{\eta }_k\right\}<1,r=max\{r_1,t^{*}\}$ with

$$\begin{array}{ccc}\hfill r_1& =& \frac{\alpha +\beta }{L}\left(\sqrt{1+\frac{2\alpha \tau \theta }{(2\gamma +\gamma \tau \theta ){(\alpha +\beta )}^2}}-1\right)\hfill \end{array}$$

and $s^{*}$ is as in Lemma 1 and with ${\ell }_{*}=lim{inf}_{k⟶\infty }{\ell }_k$ satisfying ${\ell }_{*}>\lfloor \frac{ln\eta }{ln\left(\right(\tau +1)\theta }\rfloor ,$ (Here $\lfloor .\rfloor$ represents the largest integer less than or equal to the corresponding real number) $\tau \in (0,\frac{1-\theta }{\theta })$ and

$$\theta \equiv \theta (\alpha ,x_0)=\parallel T(\alpha ,x_0)\parallel <1.$$

(46)

Then, the sequence ${\left\{x_k\right\}}_{k=0}^{\infty }$ generated by Algorithm NHSS is well defined and converges to $x_{*},$ so that $F\left(x_{*}\right)=0.$

Proof. 

If we follow the proof of Theorem 3.2 in [3,7] but use (44) instead of (41) for the upper bound on the norms $\parallel F^{\prime }{\left(x_k\right)}^{-1}\parallel$ we arrive at

$$\parallel x_{k+1}-x_k\parallel \le \frac{(1+\eta )\gamma }{1-\gamma L_0{s}_k}\parallel F\left(x_k\right)\parallel ,$$

(47)

where

$$\parallel F\left(x_k\right)\parallel \le \frac{L}{2}{(s_k-s_{k-1})}^2+\eta \frac{1-\gamma L_0{s}_{k-1}}{\gamma (1+\eta )}(s_k-s_{k-1}),$$

(48)

so by (21)

$$\parallel x_{k+1}-x_k\parallel \le (1+\eta )\frac{\gamma }{1-\gamma L_0{s}_k}[\frac{L}{2}(s_k-s_{k-1})+\eta \frac{1-\gamma L_0{s}_{k-1}}{\gamma (1+\eta )}](s_k-s_{k-1})=s_{k+1}-s_k.$$

(49)

We also have that $\parallel x_{k+1}-x_0\parallel \le \parallel x_{k+1}-x_k\parallel +\parallel x_k-x_{k-1}\parallel +\dots +\parallel x_1-x_0\parallel \le s_{k+1}-s_k+s_k-s_{k-1}+\dots +s_1-s_0=s_{k+1}-s_0<s^{*}.$ It follows from Lemma 1 and (49) that sequence $\left\{x_k\right\}$ is complete in a Banach space ${\mathbb{R}}^n$ and as such it converges to some $x_{*}\in \overline{U}(x_0,r)$ (since $\overline{U}(x_0,r)$ is a closed set).

However, $\parallel T(\alpha ;x_{*})\parallel <1$[4] and NHSS, we deduce that $F\left(x_{*}\right)=0.$ □

Remark 3.

(a) 

The point $s^{*}$ can be replaced by $s^{**}$ (given in closed form by (24)) in Theorem 2.

(b) 

Suppose there exist nonnegative constants $L_h^0,L_s^0$ such that for all $x\in U(x_0,r)\subset {\mathsf{\Omega }}_0$

$$\parallel H\left(x\right)-H\left(x_0\right)\parallel \le L_h^0\parallel x-x_0\parallel$$

and

$$\parallel S\left(x\right)-S\left(x_0\right)\parallel \le L_s^0\parallel x-x_0\parallel .$$

Set $L_0=L_h^0+L_s^0.$ Define ${\mathsf{\Omega }}_0^1={\mathsf{\Omega }}_0\cap U(x_0,\frac{1}{\gamma L_0}).$ Replace condition (${\mathcal{A}}_2$) by

(${\mathcal{A}}_2^{\prime }$) There exist nonnegative constants $L_h^{\prime }$ and $L_s^{\prime }$ such that for all $x,y\in U(x_0,r)\subset {\mathsf{\Omega }}_0^1$

$$\parallel H\left(x\right)-H\left(y\right)\parallel \le L_h^{\prime }\parallel x-y\parallel$$

$$\parallel S\left(x\right)-S\left(y\right)\parallel \le L_s^{\prime }\parallel x-y\parallel .$$

Set $L^{\prime }=L_h^{\prime }+L_s^{\prime }.$ Notice that

$$L_h^{\prime }\le L_h,L_s^{\prime }\le Ls\mathrm{and}{L}^{\prime }\le L,$$

(50)

since ${\mathsf{\Omega }}_0^1\subseteq {\mathsf{\Omega }}_0.$ Denote the conditions (${\mathcal{A}}_1$) and (${\mathcal{A}}_2^{\prime }$) by (${\mathcal{A}}^{\prime }$). Then, clearly the results of Theorem 2 hold with conditions (${\mathcal{A}}^{\prime }$), ${\mathsf{\Omega }}_0^1,L^{\prime }$ replacing conditions ($\mathcal{A}$), ${\mathsf{\Omega }}_0$ and $L,$ respectively (since the iterates $\left\{x_k\right\}$ remain in ${\mathsf{\Omega }}_0^1$ which is a more precise location than ${\mathsf{\Omega }}_0$). Moreover, the results can be improved even further, if we use the more accurate set ${\mathsf{\Omega }}_0^2$ containing iterates $\left\{x_k\right\}$ defined by ${\mathsf{\Omega }}_0^2:=\mathsf{\Omega }\cap U(x_1,\frac{1}{\gamma L_0}-\gamma \delta ).$ Denote corresponding to $L^{\prime }$ constant by $L^{\prime \prime }$ and corresponding conditions to (${\mathcal{A}}^{\prime }$) by (${\mathcal{A}}^{\prime \prime }$). Notice that (see also the numerical examples) ${\mathsf{\Omega }}_0^2\subseteq {\mathsf{\Omega }}_0^1\subseteq {\mathsf{\Omega }}_0.$ In view of (50), the results of Theorem 2 are improved and under the same computational cost.

(c) 

The same improvements as in (b) can be made in the case of Theorem 1.

The majorizing sequence $\left\{t_n\right\}$ in [3,7] is defined by

$$\begin{array}{ccc}\hfill t_0& =& 0,t_1=c=2\gamma \delta \hfill \\ \hfill t_{k+1}& =& t_k+\frac{1}{1-\gamma L{t}_k}[p(t_k-t_{k-1})+\eta (1-\gamma L{t}_{k-1})](t_k-t_{k-1}).\hfill \end{array}$$

(51)

Next, we show that our sequence $\left\{s_n\right\}$ is tighter than $\left\{t_n\right\}.$

Proposition 1.

Under the conditions of Theorems 1 and 2, the following items hold

(i) 

$s_n\le t_n$

(ii) 

$s_{n+1}-s_n\le t_{n+1}-t_n$ and

(iii) 

$s^{*}\le t^{*}={lim}_{k⟶\infty }{t}_k\le r_2.$

Proof. 

We use a simple inductive argument, (21), (51) and (43). □

Remark 4.

Majorizing sequences using $L^{\prime }$ or $L^{\prime \prime }$ are even tighter than sequence $\left\{s_n\right\}$.

4. Special Cases and Numerical Examples

Example 1.

The semi-local convergence of inexact Newton methods was presented in [14] under the conditions

$$\begin{array}{ccc}\hfill \parallel F^{\prime }{\left(x_0\right)}^{-1}F\left(x_0\right)\parallel & \le & \beta ,\hfill \\ \hfill \parallel F^{\prime }{\left(x_0\right)}^{-1}(F^{\prime }\left(x\right)-F^{\prime }\left(y\right))\parallel & \le & \gamma \parallel x-y\parallel ,\hfill \\ \hfill \frac{\parallel F^{\prime }{\left(x_0\right)}^{-1}{s}_n\parallel }{\parallel F^{\prime }{\left(x_0\right)}^{-1}F\left(x_n\right)\parallel }& \le & {\eta }_n\hfill \end{array}$$

and

$$\beta \gamma \le g_1\left(\eta \right),$$

where

$$g_1\left(\eta \right)=\frac{\sqrt{{(4\eta +5)}^3}-(2{\eta }^3+14\eta +11)}{(1+\eta ){(1-\eta )}^2}.$$

More recently, Shen and Li [11] substituted $g_1\left(\eta \right)$ with $g_2\left(\eta \right),$ where

$$g_2\left(\eta \right)=\frac{{(1-\eta )}^2}{(1+\eta )(2(1+\eta )-\eta {(1-\eta )}^2)}.$$

Estimate (22) can be replaced by a stronger one but directly comparable to (20). Indeed, let us define a scalar sequence $\left\{u_n\right\}$ (less tight than $\left\{s_n\right\}$) by

$$\begin{array}{ccc}\hfill u_0=0,u_1& =& 2\gamma \delta ,\hfill \\ \hfill u_{k+1}& =& u_k+\frac{(\frac{1}{2}\rho (u_k-u_{k-1})+\eta )}{1-\rho u_k}(u_k-u_{k-1}),\hfill \end{array}$$

(52)

where $\rho =\gamma L_0(1+\eta )\mu .$ Moreover, define recurrent functions $f_k$ on the interval $[0,1)$ by

$$f_k\left(t\right)=\frac{1}{2}\rho c{t}^{k-1}+\rho c(1+t+\dots +t^{k-1})t+\eta -t$$

and function $g\left(t\right)=t^2+\frac{t}{2}-\frac{1}{2}.$ Set $q=\frac{1}{2}.$ Moreover, define function $g_4$ on the interval $[0,\frac{1}{2})$ by

$$g_4\left(\eta \right)=\frac{1-2\eta }{4(1+\eta )}.$$

(53)

Then, following the proof of Lemma 1, we obtain:

Lemma 4.

Let $\beta ,\gamma ,\delta ,L_0,L$ be positive constants and $\eta \in [0,\frac{1}{2}).$ Suppose that

$${\gamma }^{2}L\delta \le g_4\left(\eta \right)$$

(54)

Then, sequence $\left\{u_k\right\}$ defined by (52) is nondecreasing, bounded from above by

$$u^{**}=\frac{c}{1-q}$$

and converges to its unique least upper bound $u^{*}$ which satisfies

$$c\le u^{*}\le u^{**}.$$

Proposition 2.

Suppose that conditions ($\mathcal{A}$) and (54) hold with $r=min\{r_1,u^{*}\}.$ Then, sequence $\left\{x_n\right\}$ generated by algorithm NHSS is well defined and converges to $x_{*}$ which satisfies $F\left(x_{*}\right)=0.$

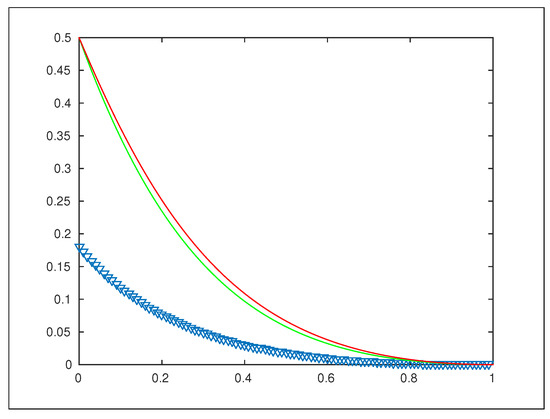
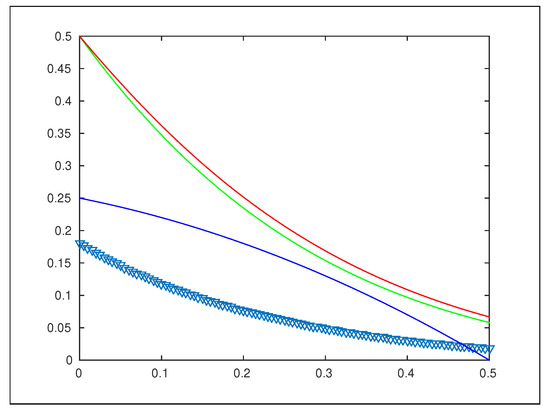
These bound functions are used to obtain semi-local convergence results for the Newton–HSS method as a subclass of these techniques. In Figure 1 and Figure 2, we can see the graphs of the four bound functions $g_1,g_2,{\overline{g}}_3$ and $g_4.$ Clearly our bound function ${\overline{g}}_3$ improves all the earlier results. Moreover, as noted before, function $g_3$ cannot be used, since it is an incorrect bound function.

Figure 1. Graphs of $g_1\left(t\right)$ (Violet), $g_2\left(t\right)$ (Green), ${\overline{g}}_3$ (Red).

Figure 2. Graphs of $g_1\left(t\right)$ (Violet), $g_2\left(t\right)$ (Green), ${\overline{g}}_3$ (Red) and $g_4$ (Blue).

In the second example we compare the convergence criteria (22) and (12).

Example 2.

Let $\eta =1,{\mathsf{\Omega }}_0=\mathsf{\Omega }=U(x_0,1-\lambda ),x_0=1,\lambda \in [0,1).$ Define function F on Ω by

$$F\left(x\right)=x^3-\lambda .$$

(55)

Then, using (55) and the condition ($\mathcal{A}$), we get $\gamma =\frac{1}{3},\delta =1-\lambda ,L=6(2-\lambda ),$$L_0=3(3-\lambda )$ and $\mu =\frac{2(2-\lambda )}{3-\lambda }.$ Choosing $\lambda =0.8.$, we get $L=7.2,L_0=6.6,\delta =0.2,\mu =1.0909091,{\eta }_0=0.594088525,p=1.392,q=0.539681469,$${\gamma }^{2}L\delta =0.16$. Let $\eta =0.16<{\eta }_0,$ then, ${\overline{g}}_3(0.16)=0.159847474,$$\xi =min\{0.176715533,0.20456064\}=0.176715533$. Hence the old condition (12) is not satisfied, since ${\gamma }^{2}L\delta >{\overline{g}}_3(0.16)$. However, the new condition (22) is satisfied, since ${\gamma }^{2}L\delta <\xi .$ Hence, the new results expand the applicability of NHSS method.

The next example is used for the reason already mentioned in (iii) of the introduction.

Example 3.

Consider the two-dimensional nonlinear convection–diffusion equation [7]

$$\begin{array}{ccc}\hfill -(u_{xx}+u_{yy})+q(u_x+u_y)& =& -e^u,(x,y)\in \mathsf{\Omega }\hfill \\ \hfill u(x,y)& =& 0(x,y)\in \partial \mathsf{\Omega }\hfill \end{array}$$

(56)

where $\mathsf{\Omega }=(0,1)\times (0,1)$ and $\partial \mathsf{\Omega }$ is the boundary of $\mathsf{\Omega }.$ Here $q>0$ is a constant to control the magnitude of the convection terms (see [7,15,16]). As in [7], we use classical five-point finite difference scheme with second order central difference for both convection and diffusion terms. If N defines number of interior nodes along one co-ordinate direction, then $h=\frac{1}{N+1}$ and $Re=\frac{qh}{2}$ denotes the equidistant step-size and the mesh Reynolds number, respectively. Applying the above scheme to (56), we obtain the following system of nonlinear equations:

$$\begin{array}{ccc}\hfill \overline{A}u+h^2{e}^u& =& 0\hfill \\ \hfill u& =& {(u_1,u_2,\dots ,u_N)}^T,u_i={(u_{i1},u_{i2},\dots ,u_{iN})}^T,i=1,2,\dots ,N,\hfill \end{array}$$

where the coefficient matrix $\overline{A}$ is given by

$$\overline{A}=T_x\otimes I+I\otimes T_y.$$

Here, ⊗ is the Kronecker product, $T_x$ and $T_y$ are the tridiagonal matrices

$$T_x=tridiag(-1-Re,4,-1+Re),T_y=tridiag(-1-Re,0,-1+Re).$$

In our computations, N is chosen as 99 so that the total number of nodes are $100\times 100$. We use $\alpha =\frac{qh}{2}$ as in [7] and we consider two choices for ${\eta }_k$ i.e., ${\eta }_k=0.1$ and ${\eta }_k=0.01$ for all k.

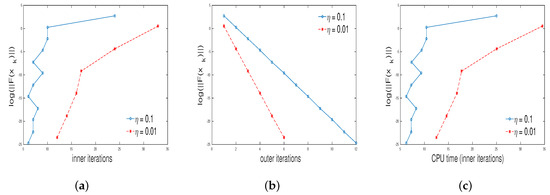
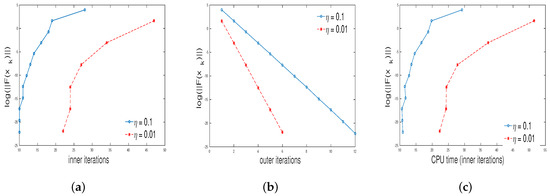
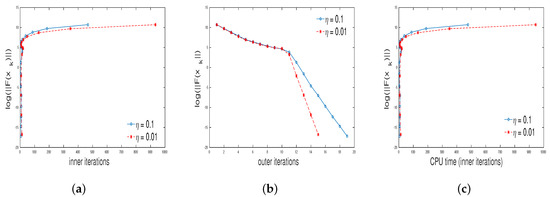
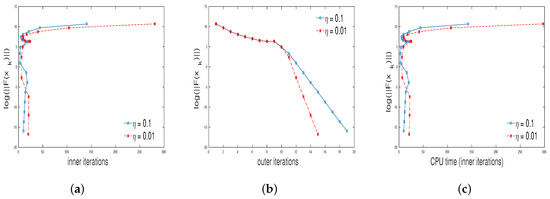
The results obtained in our computation is given in Figure 3, Figure 4, Figure 5 and Figure 6. The total number of inner iterations is denoted by $IT$, the total number of outer iterations is denoted by $OT$ and the total CPU time is denoted by t.

Figure 3. Plots of (a) inner iterations vs. $log(\parallel F\left(x_k\right)\parallel )$, (b) outer iterations vs. $log(\parallel F\left(x_k\right)\parallel )$, (c) CPU time vs. $log(\parallel F\left(x_k\right)\parallel )$ for $q=600$ and $x_0=e$.

Figure 4. Plots of (a) inner iterations vs. $log(\parallel F\left(x_k\right)\parallel )$, (b) outer iterations vs. $log(\parallel F\left(x_k\right)\parallel )$, (c) CPU time vs. $log(\parallel F\left(x_k\right)\parallel )$ for $q=2000$ and $x_0=e$.

Figure 5. Plots of (a) inner iterations vs. $log(\parallel F\left(x_k\right)\parallel )$, (b) outer iterations vs. $log(\parallel F\left(x_k\right)\parallel )$, (c) CPU time vs. $log(\parallel F\left(x_k\right)\parallel )$ for $q=600$ and $x_0=6e$.

Figure 6. Plots of (a) inner iterations vs. $log(\parallel F\left(x_k\right)\parallel )$, (b) outer iterations vs. $log(\parallel F\left(x_k\right)\parallel )$, (c) CPU time vs. $log(\parallel F\left(x_k\right)\parallel )$ for $q=2000$ and $x_0=6e$.

5. Conclusions

A major problem for iterative methods is the fact that the convergence domain is small in general, limiting the applicability of these methods. Therefore, the same is true, in particular for Newton–Hermitian, skew-Hermitian and their variants such as the NHSS and other related methods [4,5,6,11,13,14]. Motivated by the work in [7] (see also [4,5,6,11,13,14]) we:

(a)

Extend the convergence domain of NHSS method without additional hypotheses. This is done in Section 3 using our new idea of recurrent functions. Examples, where the new sufficient convergence criteria hold (but not previous ones), are given in Section 4 (see also the remarks in Section 3).

(b)

The sufficient convergence criterion (16) given in [7] is false. Therefore, the rest of the results based on (16) do not hold. We have revisited the proofs to rectify this problem. Fortunately, the results can hold if (16) is replaced with (12). This can easily be observed in the proof of Theorem 3.2 in [7]. Notice that the issue related to the criteria (16) is not shown in Example 4.5, where convergence is established due to the fact that the validity of (16) is not checked. The convergence criteria obtained here are not necessary too. Along the same lines, our technique in Section 3 can be used to extend the applicability of other iterative methods discussed in [1,2,3,4,5,6,8,9,12,13,14,15,16].