Abstract
An analysis of the invariance properties of self-adjoint extensions of symmetric operators under the action of a group of symmetries is presented. For a given group G, criteria for the existence of G-invariant self-adjoint extensions of the Laplace–Beltrami operator over a Riemannian manifold are illustrated and critically revisited. These criteria are employed for characterising self-adjoint extensions of the Laplace–Beltrami operator on an infinite set of intervals, , constituting a quantum circuit, which are invariant under a given action of the group . A study of the different unitary representations of the group on the space of square integrable functions on is performed and the corresponding -invariant self-adjoint extensions of the Laplace–Beltrami operator are introduced. The study and characterisation of the invariance properties allows for the determination of the spectrum and generalised eigenfunctions in particular examples.
MSC:
Primary 81Q35; Secondary 81Q10, 81R05
1. Introduction
The relation between physics and symmetries has been successful and fruitful up to the point that physical theories, from the most fundamental ones, such as the Standard Model, to the effective ones applied, e.g., in condensed matter physics, are intimately related with the symmetries and transformation properties of their underlying structures, for instance, gauge symmetries in the former case or crystallographic groups in the latter.
One of the aims of this article is to provide a framework for a systematic analysis of the action of symmetry groups on the configuration space of quantum circuits. Even if the configuration space is invariant under the action of a given group, not all the possible self-adjoint extensions need to be compatible with that symmetry group. We use the characterisation introduced in [1] to identify the set of self-adjoint extensions compatible with the action of the symmetry group in the particular case of infinite chains made up by repeating a finite block. This kind of periodic lattices is widely used in solid state physics as approximations for systems such as crystals, when the period is much smaller than the size of the system [2,3]. To have control on the symmetries that the system possess is also important in the determination of the spectrum and the spaces of eigenfunctions, as they will carry the same representation. The importance of this characterisation is that the space of mathematically possible self-adjoint extensions for a given quantum circuit is very large. As is clear in the discussion below and in the subsequent sections, the space of self-adjoint extensions contains all the possible topologies for a given graph and also many other situations that are not compatible with any given topology [4,5].
The study of symmetries in the context of quantum circuits is particularly relevant in relation with the development of new quantum information and processing devices. Superconducting qubits [6,7] are one of the promising technologies that can lead to scalable quantum computation. The framework of quantum circuits provides a natural setting to model and study them. In particular, a superconducting qubit can be seen as a truncation to the lowest energy levels of a corresponding quantum circuit [8]. Quantum circuits are, in general, infinite dimensional quantum systems and this has inherent difficulties in their description. However, one of the sources of decoherence in the description of superconducting qubits arises precisely because of the aforementioned truncation to the lowest orders. Hence, it is worth addressing the system in its full generality and try, for instance, to achieve general controllability results, as was done in [9].
In the most abstract setting, the dynamics of a quantum circuit can be described by the Schrödinger equation, where the Hamiltonian of the system will be given formally by a Laplacian operator defined over a disjoint union of intervals with, possibly, a scalar potential defined over the intervals. The topology of the circuit, which can be described mathematically by a directed graph, will arise from the boundary conditions that one implements at the boundaries of the intervals. These boundary conditions need to be fixed in order to determine a well-defined self-adjoint operator. Otherwise, the dynamics of the system will not satisfy the unitarity of the evolution as characterised by the Stone–von Neumann Theorem.
It was proven by G. Grubb [10] that there is a one-to-one correspondence between self-adjoint extensions of the Laplace–Beltrami operator and boundary conditions defined in terms of pseudo-differential operators. We take here the approach introduced in [11] and further developed in [1], according to which the space of self-adjoint extensions of the Laplace operator is given by a unitary operator acting on the Hilbert space of boundary data. This approach is general enough to accommodate all the physically acceptable self-adjoint extensions. Moreover, the self-adjoint extensions characterised in this way are well suited for the numerical approximation of their spectrum (cf. [12,13]). Another advantage is that the same ideas can be used to analyse other differential operators such as the Dirac operator (cf. [14,15]), which are also important in the context of quantum circuits.
The article is organised as follows. In Section 2, we introduce the definitions of invariance and symmetries that are needed for the rest of the article. In this section, we also carry on with the analysis introduced in [16] to cover other possible situations not covered by the theorems proved in that work. In Section 3, we use the invariance properties to characterise a blockwise structure of the possible self-adjoint extensions that represents a given quantum circuit. Finally, in Section 4, we study the case of an infinite quantum circuit, a quantum chain, that is made of the repetition of elemental finite blocks. Some discussion and outlook are given in Section 5.
2. Self-Adjoint Extensions with Symmetries
In the Schrödinger–Dirac picture of Quantum Mechanics, one associates a Hilbert space with a quantum system, and self-adjoint operators play the role of observables, whereas pure states are elements of the projective Hilbert space . Moreover, dynamics of “closed” quantum systems are described by strongly continuous one-parameter groups of unitary transformations, and according to Stone–von Neumann Theorem the generator of a strongly continuous one-parameter group of unitary transformations is a self-adjoint operator. Therefore, it is evident that self-adjointness plays a fundamental role in any quantum theory and a proper treatment of self-adjoint extensions of symmetric operators is required for a correct description of quantum systems. In particular, in this article, we focus on the definition of self-adjoint extensions of symmetric operators which are compatible with a given group of symmetries, G, of the dynamical system under investigation. This section is devoted to recalling briefly the main results and definitions of the theory of self-adjoint extensions that are needed, as well as to recall the notion of G-invariance.
2.1. G-Invariant Self-Adjoint Extensions
Let be a pair made up of a smooth manifold , with a smooth boundary , and a Riemannian metric . We suppose that the measure is the Riemannian volume form associated with the Riemannian structure . The boundary itself has the structure of a Riemannian smooth manifold without boundary, the metric tensor on the boundary, namely , being the pull-back of via the canonical inclusion . Let be the Hilbert space of square-integrable functions on with respect to the measure , and let be the Laplace–Beltrami operator on acting on a dense domain of the Hilbert space . Due to the presence of the boundary, the operator defined on the subspace of smooth functions with compact support contained in the interior of , is an unbounded densely defined symmetric operator which in general is not self-adjoint: the specification of a proper set of boundary conditions allows to get different self-adjoint extensions . Even if it is not the most general one, the Laplace–Beltrami operator is a paradigmatic example and of fundamental importance in Quantum Mechanics. Indeed, it is the generator of the dynamics of a free particle on . Let us recall that an unbounded linear operator on a complex, separable Hilbert space with dense domain is symmetric if
and it is self-adjoint if, in addition, , where is the adjoint operator whose domain is made up of those vectors such that:
for some . The set of vectors forms the range of the adjoint operator. A self-adjoint extension of a symmetric operator satisfies the conditions
If the operator is symmetric, but not essentially self-adjoint, different self-adjoint extensions determine different quantum systems. On the other hand, symmetries of a certain quantum system are implemented via unitary or anti-unitary linear operators acting on the Hilbert space (cf. [17,18]). Let G be a group of symmetries of the dynamical quantum system described by the operator . This group of symmetries acts on via the strongly continuous unitary representation . Therefore, it is worthwhile asking what self-adjoint extensions are compatible with the group action given by the map V, if we want the quantum system to have the group of symmetries G. Following Ibort et al. [1], we consider the following definition of invariance for a given operator :
Definition 1.
Let be a linear operator with dense domain and consider a unitary representation . The operator is said to be G-invariant if , that is for all and
The issue of the existence and uniqueness of self-adjoint extensions of symmetric operators was addressed by von Neumann [19], who gave a characterisation of self-adjoint extensions in terms of unitary operators, K, between subspaces of , , called deficiency spaces.
However, if we think of self-adjoint extensions of differential operators on manifolds with a boundary (as we consider in this work), the relationship between the unitary operator K defining the self-adjoint extension and the specification of a certain set of boundary conditions is hard to obtain, even if it is possible [10]. Therefore, for the Laplacian operator on a manifold with a boundary , an alternative approach has been proposed in [11,16], according to which self-adjoint extensions of the operator are in correspondence with unitary operators acting on the space of square integrable functions on the boundary of . In the rest of the article, we address the issue of G-invariant self-adjoint extensions of the Laplace–Beltrami operator looking at the boundary data. Therefore, in the remainder of this section, we shortly outline some results concerning a large class of self-adjoint extensions of .
Exploiting the relationship between quadratic forms and self-adjoint operators (cf. [20] (Sec. VI.2) for the details on this relation), it is possible to establish a correspondence between a class of self-adjoint extensions of the Laplace–Beltrami operator on a manifold with a smooth boundary and a class of unitary operators on the space of square-integrable functions on its boundary (see [16] for details). Before introducing this class of unitaries, it is worth providing some additional definitions. The Sobolev Hilbert space of order k on a manifold is denoted by (see, for instance, [21] for a detailed presentation of Sobolev spaces).
Definition 2.
A unitary operator U has spectral gap at if one of the following conditions holds:
- (i)
- is invertible; and
- (ii)
- belongs to the spectrum of the operator U but it is not an accumulation point of .
Let U be a unitary operator having in its spectrum. If P is the projector operator onto the eigenvalue and , the partial Cayley transform of the operator U is defined as follows:
Definition 3.
Let U be a unitary operator having spectral gap at . It is admissible if the partial Cayley transform leaves the subspace invariant and is continuous with respect to the Sobolev norm of order , i.e.,
Then, there is a one-to-one correspondence between a class of self-adjoint extensions of the Laplace–Beltrami operator on a manifold with smooth boundary and the class of unitary operators , which have spectral gap at and are admissible.
Given an admissible unitary with spectral gap at , the associated self-adjoint extension is defined on the subspace whose elements satisfy the following boundary conditions:
where are the boundary data, i.e., is the restriction to the boundary of the function and is the restriction of its normal derivative pointing outwards. These restrictions are obtained via the trace operator , whenever , which is a continuous surjective operator, with kernel defined by the functions in (see, for instance, [21] for more details). Having defined a class of self-adjoint operators in terms of unitary operators at the boundary, one can look for conditions on these unitaries such that the corresponding self-adjoint extensions are G-invariant with respect to some unitary representation of a group of symmetry G. Before introducing the main theorem of this section, let us give some additional definitions.
Definition 4.
A strongly continuous unitary representation has a trace (or it is traceable) along the boundary if there exists another strongly continuous unitary representation such that:
for all and .
We can now state the main theorem characterising G-invariant self-adjoint extensions defined via admissible unitary operators at the boundary with spectral gap at :
Theorem 1
([16] (Thm. 6.10)). Let G be a group and a topological traceable representation of G, with unitary trace along the boundary . Let be an admissible unitary operator with spectral gap at defining a self-adjoint extension of the Laplace–Beltrami operator. Assume that the self-adjoint extension corresponding to Neumann boundary conditions () is G-invariant. Then, we have the following cases:
- (i)
- If for all , then is G-invariant;
- (ii)
- Consider the decomposition of the boundary Hilbert space , where W is the eigenspace relative to the eigenvalue of the operator U, and denote by P the orthogonal projection onto W. If is G-invariant and is continuous, then for all .
In the rest of the article, we make wide use of this result, since we define self-adjoint extensions of the Laplace–Beltrami operator on by specifying a suitable set of boundary conditions. Moreover, we focus on one dimensional manifolds, and, as better clarified in the following sections, many of the technical requirements in the above discussion are automatically satisfied.
2.2. Additional Remarks on Symmetries and Self-Adjoint Extensions
Before moving on, in this subsection, we add some remarks about the previous results. Let us start mentioning a result about G-invariant self-adjoint extensions in the von Neumann approach to the problem. Let be the unitary operator between the two deficiency spaces characterising a given self-adjoint extension of an operator . Then, G-invariant self-adjoint extensions can be built according to the result of the following theorem:
Theorem 2
([16] (Thm. 3.5)). Let be a closed, symmetric and G-invariant operator with equal deficiency indices. Let be the self-adjoint extension defined by the unitary operator . Then, is G-invariant iff .
Therefore, if the symmetric operator is G-invariant, G-invariant self-adjoint extensions are characterised by unitaries K, which commute with all the elements of the representation V of the symmetry group G. However, one possibility not considered in [16] is to study whether it is possible that the symmetric operator is not G-invariant while one (or several) of its self-adjoint extensions are. In particular, one could ask if there exist unitary representations V of a symmetry group G which do not preserve the domain of the operator but preserve the domain of a self-adjoint extension . A simple instance is given by the following example (cf. [22] (Ch. 3)).
Example 1.
Let and let with domain
It is a symmetric operator with deficiency indices , which implies that there are infinitely many self-adjoint extensions characterised by a single real parameter, say α. The domains of these self-adjoint extensions, which we call , can be characterised as:
The unitary representation of the group given by
preserves the domain and commutes with on its domain; therefore, is -invariant. If α is positive the spectrum of is the positive half-line and the generalised eigenfunctions (see, for instance, [23] (Chs. 4 and 9), [24] (Ch. 8) and [25]) can be written in terms of a real parameter k as follows:
Therefore, the action of the unitary operator can be expressed as follows:
where is the Green-kernel associated with the operator .
In this case, however, the symmetric operator is not -invariant since is not invariant with respect to the group action . This is a consequence of the following lemma (see [26] (Lemma 8.4.1)):
Lemma 1.
Let be an unbounded self-adjoint operator on a complex Hilbert space . Let be a dense linear subspace of and suppose leaves invariant. Then, (i.e., restricted to ) is essentially self-adjoint.
Let us recall that essentially self-adjoint means that the operator has a unique self-adjoint extension that coincides with its closure. Indeed, since in the case in question is not essentially self-adjoint, the linear dense subspace cannot be invariant with respect to the action given by . Therefore, is -invariant, whereas is not.
However, we know that it is possible to associate self-adjoint extensions of the Laplace–Beltrami operator on a manifold with boundary with unitaries on the space of boundary data. In this case, Theorem 1 was proven under two assumptions on the unitary representation V, i.e., it has to have a trace and preserve the Neumann self-adjoint extension. Therefore, one could see if there are G-invariant self-adjoint extensions with respect to a representation V of a group G, while either the unitary representation is not traceable or it does not preserve the Neumann self-adjoint extension of the Laplace–Beltrami operator, or both. In fact, the system defined above is an example of this situation, too. Indeed, if a unitary representation is traceable, it has to preserve the kernel of the trace map. Since the kernel of the trace map, which, in the previous example, is given by the subspace , is not preserved the unitary representation V is not traceable. (Indeed, the operator restricted to this domain is symmetric but not essentially self-adjoint. Therefore, according to Lemma 1, this domain is not preserved by the representation V of the group .) Therefore, concerning this situation, the assumption in Theorem 1 on the unitary representation, namely being traceable, is analogous to the assumption in Theorem 2 about the preservation of the domain of the symmetric operator. Since a careful analysis of symmetries which either are not traceable or are not compatible with the symmetric operator or both, is out of the scope of this article, in the following sections, we limit ourselves to representations that respect the hypotheses of the theorems introduced above, and we postpone such an investigation to future works.
After this introduction containing a critical review of previous results, in the following sections, we focus on the issue of self-adjoint extensions of the Laplace–Beltrami operator on quantum circuits, which are compatible with a given group of symmetries.
3. Quantum Circuits: Adjacency and Local Symmetries
The central part of this work focuses on the description of self-adjoint extensions of the Laplace–Beltrami operator for one-dimensional manifolds. As shown below, this discussion can be fruitfully exploited in connection to the theory of quantum circuits. A quantum circuit is nothing but a quantum system consisting of a particle moving in a one-dimensional space. For such a system, the most general setting is that of a particle moving in a collection of intervals, , arranged in such a way that some of them are connected through their endpoints. A good way to depict this arrangement is by associating a directed graph to , with edges representing the intervals and vertices representing their connections (see Figure 1). We use to denote the union of intervals and for the associated directed graph, whose vertex and edge spaces are denoted by and , respectively.

Figure 1.
(a) The intervals for an made out of three intervals; and (b) the associated graph if we connect on one side with , and , and in the other side with . The first of the two connections is represented with the graph vertex labelled by a and the second is represented with the vertex b.
The Hilbert space associated with this quantum system is given by This means, in particular, that the Hilbert space can be characterised as:
Analogously we have the Sobolev spaces with the norm defined as . Note that. since is the disjoint union of intervals, there is no condition on the regularity of functions on at the endpoints: the function at each edge is a priori unrelated to other components of . On the contrary, the Sobolev space would contain different regularity properties due to the topology of the digraph and the vertices connections.
Let and denote the endpoints of the interval . It is clear that the boundary of is the set . Since the boundary consists of a countable set of points, whenever the trace map is well defined, will be a sequence of complex numbers, which, in the most general case, does not need to converge. However, if we consider (and therefore every component is continuous), the fact that both and have to be finite makes
a sequence in , due to the continuity of the trace operator on each interval and provided that the the length of the intervals and their measures are uniformly bounded from above and from below. Moreover, if , the same argument applied to implies that
Therefore, the Hilbert space of boundary data coincides with the induced Hilbert space at the boundary of , .
Instead of the sequential order used above for the boundary data and , we can write them in a way more related to the topology of the underlying graph. We call this arrangement the threaded arrangement, and it consists of placing together the values corresponding to connected endpoints (that is, corresponding to the same vertex on the associated graph). For instance, if we consider the example in Figure 1 using the threaded arrangement we have
where the first four component correspond to the vertex a in Figure 1b and the other two, to the vertex b.
According to Section 2.1, we can describe (a subset of) the self-adjoint extensions of the Laplacian on in terms of admissible unitary operators with gap at through the boundary equation
The end of the previous section anticipates that the technical difficulties do not appear in the one-dimensional case, since we establish above that the space of boundary data is the same as the Hilbert space induced at the boundary. For this reason, every U satisfies the admissibility condition. Hence, we are left only with the spectral gap condition.
According to Equation (14), a general unitary (with gap at ) imposes general conditions involving the boundary data of all the components of functions on the domain of the associated self-adjoint extension. However, to model a quantum circuit its topology should be respected, in the sense that the probability associated with wave functions on the domain of the self-adjoint extension should be continuous throughout the circuit. Since continuity is a local property, it is natural to consider self-adjoint extensions associated to unitaries not relating boundary data from unconnected endpoints. Therefore, we are interested in self-adjoint extensions whose unitary, written according to the threaded arrangement, has a block structure given by the graph vertices:
Further simplification follows when considering circuits whose graphs have finite degree on all its vertices. For such a system, the blocks are matrices, where is the degree of the vertex , and the following property holds.
Proposition 1.
Let be unitary matrices and a unitary operator on . Then, the spectrum of U is given by the closure of the union of the spectra of all . That is, .
Proof.
Since U is unitary, it is a bounded normal operator and thus cannot have residual spectrum (cf. [27], (Thm. 6.10.10)).
Let be the orthogonal projector associated to the ith block of U, that is for every . Since the blocks are finite-dimensional matrices, they have only point spectrum and given any eigenvector it is immediate to promote it to a vector , extending by zero. Therefore, for every i.
Suppose now that . Since is either in the point or in the continuous spectrum, there must exist a sequence such that and . One has that
Since is a unitary matrix, it is unitarily diagonalisable. Let denote the eigenvalues of and the unitary such that . Then,
where denotes the jth component of the vector . Using that , one gets
Therefore, implies that , that is, . □
Remark 1.
This property has two immediate consequences that we use repeatedly in the rest of the work. First, if U is made of a finite number of blocks which are repeated, then it has gap at . Second, if there is an such that for each block the lowest distance between an eigenvalue and is greater than ε, then U has gap at .
Since the probability associated to a wave function is given by its modulus, unitaries enforcing the continuity of such probability need to impose some conditions involving only the function trace, . It is not hard to see that conditions involving only are given by the eigenvalue of U. In fact, acting with the orthogonal projector over , P, on both sides of Equation (14), one gets
Therefore, we look into self-adjoint extensions such that is the space of the traces of functions such that is continuous. It is clear that the projector P must have the same block structure as the unitary U,
Let us denote by the projection of into the block associated with the vertex . It is clear that for to be continuous on the digraph , at every node the entries of can differ only by a relative phase. The selection of the relative phases among the components of the vector , amounts to conditions, in such a way that the space is the following one dimensional space:
and thus has to be the rank-one orthogonal projector onto the linear span of . It immediately follows that the corresponding block of the unitary has the form
where is the only eigenvalue of different from . We call this family of self-adjoint extension the quasi- family, characterised by the parameters . For all the self-adjoint extensions in this family, it is possible to restrict a suitably defined self-adjoint momentum operator. In other words, there exists a self-adjoint extension of the symmetric operator , which can be restricted to the domain of a quasi- self-adjoint extension of the Laplace–Beltrami operator, and is essentially self-adjoint on it.
Now that the unitaries leading to a self-adjoint extension of the Laplacian compatible with a given quantum circuit have been characterised, for the rest of this section, we focus on the study of the symmetries that are compatible with them. When applying Theorem 1 to the one-dimensional case, the fact that the space of traces is also means that the extra condition on Part (ii) of the same theorem is always satisfied, and therefore both parts always hold. The condition for the self-adjoint extension to be invariant under the action of a group is that the trace representation commutes with the unitary operator defining the self-adjoint extension. Therefore, in the remainder of this work, we characterise some unitary representations of a group of symmetries G that commute with a matrix U possessing a blockwise structure as in Equation (17). For that, it is useful to consider each block separately leaving the global aspects for the next section.
Definition 5.
We say that the group G is a local symmetry at the vertex ν of the self-adjoint extension determined by if it admits a faithful representation such that for every .
Remark 2.
It is important to note that it is usually not possible to build an actual symmetry of the associated self-adjoint extension from a collection of local symmetries. In fact, the representation v might not even be the trace of a representation in . Because of this, local symmetries have to be understood only as tools to study global ones.
The following proposition provides a necessary and sufficient condition for G to be a local symmetry of a self-adjoint extension compatible with the quantum circuit.
Proposition 2.
Consider a quasi-δ self-adjoint extension with parameters at the vertex ν. A group G is a local symmetry at ν if and only if it admits a unitary representation such that it leaves invariant the linear space .
Proof.
The proof follows straightforwardly from Equation (17). It is clear that iff . Since is the orthogonal projector onto , the sought result follows. □
Since the only condition to be a local symmetry of this family is to preserve a one-dimensional subspace of , it follows immediately the next corollary:
Corollary 1.
The biggest group which is a local symmetry at the vertex ν of a given quasi-δ family of self-adjoint extensions is the unitary group .
Before ending this section, let us remark that the given characterisation of local symmetry at the vertex is nothing but the preservation of the structure of the eigenspaces of . Consequently, the unitary group not only preserves the family of quasi- self-adjoint extensions but also any other family with the same eigenspaces but different eigenvalues associated to each eigenspace. Each of this families can be seen as different orbits of a subgroup of changing the invariant vector in Proposition 2:
Proposition 3.
Let and denote by the quasi-δ self-adjoint extension parameterised by . Then, every unitary matrix V such that is proportional to transforms into . That is,
Proof.
Denote by the orthogonal projector onto ; since , . Using this and Equation (17), the result follows. □
4. Global Symmetries on the Graph. -invariance
As pointed out in the Introduction, in this section, we consider an example which is useful as an approximation of big, complex quantum circuits consisting of a repeated structure. The simplest example is the case of a graph which is the union of infinitely many intervals arranged in such a way to form a chain with loops at each node (see Figure 2). However, all the discussion can be extended straightforwardly to the general case of an arbitrary quantum circuit provided that the action of the considered group preserves the topology of the underlying graph.
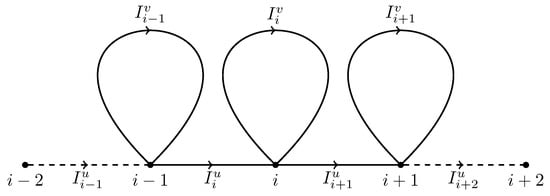
Figure 2.
Representation of the infinite graph associated with .
To properly describe such a structure, let us fix the following nomenclature: any vertex is labelled by an integer . We can distinguish two families of edges in the graph: the edge connecting the vertices and i is denoted by ; the edge forming the loop at vertex i is called . In this way, it is easy to generalise this periodic structure to a graph where the “unit cells” at each node have a more complex structure.
As already explained in the previous section, we consider the manifold
which is a non-connected manifold made up of the disjoint union of all the pairs of intervals . A convenient way to describe this manifold is realised as follows. Assume that there is a reference interval and that there are diffeomorphisms
which play the role of local charts. Then, each point in can be identified by this family of diffeomorphisms , since for any point P we can find a point and a diffeomorphism, say , such that .
Each interval has the structure of a Riemannian manifold with metric . Consequently, the whole manifold possesses a Riemannian metric tensor field
A basis of the tangent space at the point is made up of one vector which is written in the coordinate x. A generic vector field on the manifold is written as
and we have that where we have named both the vector field and its unique component in a given basis.
Therefore, the action of the metric tensor field on a real valued vector field X can be expressed as follows:
The corresponding invariant Riemannian volume form is given by
The previous definitions lead to the following Laplace–Beltrami operator
which acts on a dense subspace of the space of square integrable functions over , denoting the latter by with the induced scalar product defined by
Each of the “local” Laplace–Beltrami operators can be written as follows:
where is the function in , where the measure is the pull-back of the measure via the diffeomorphism . This function represents , and it is supposed regular enough for the previous equation to make sense.
Let us consider the following symmetric domain for the Laplace–Beltrami operator
which is the space of smooth functions with compact support contained in the interior of . This implies that these functions can have support only on a finite number of intervals. Correspondingly, the domain of the adjoint operator is the Sobolev space . As already explained in the previous section, the space of self-adjoint extensions of this operator compatible with the topology of the graph is in correspondence with the space of unitaries U, which have a blockwise structure, i.e.,
each block being a unitary matrix representing the node of the form shown in Figure 3.
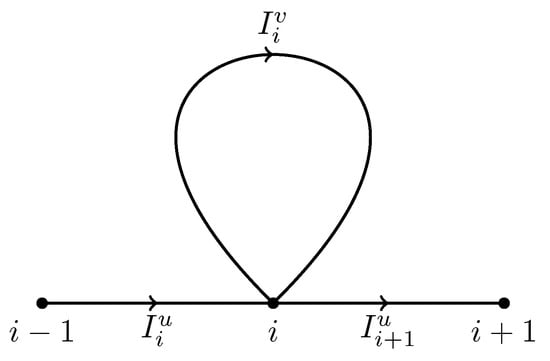
Figure 3.
Elementary cell of the graph .
Any unitary represents the “local” boundary conditions at each vertex of the graph via the formula:
where and denote the boundary data at the node labelled by i:
We now want to study symmetry transformations on our graph, such that we can apply the results of Section 2. In particular, we consider an action of the group , and we start with an action which preserves both the boundary and the adjacency properties of the nodes. We define therefore the following map:
such that, if with , then and
This action, for a fixed , is implemented by a family of diffeomorphisms
which preserve the boundary. It induces an action on the space of smooth functions with compact support on , via the pull-back, i.e.,
In addition, we want this action to define a symmetry of the Laplace–Beltrami operator over with domain , i.e., for all
Clearly, , for all . A sufficient condition for this action to implement a unitary representation of such that is -invariant is that acts as an isometric diffeomorphism, i.e., for all . This requirement imposes a restriction on the class of metric tensors that one can consider; indeed, on the one hand, we have
where are the components of two tangent vectors at the interval , and they remain invariant under the action of the push-forward. On the other hand,
Consequently, if must be invariant, for all . Hence, one has that and are isometric for all . Since we are in one dimension, one can always choose the diffeomorphism such that the metric tensor is constant, and the only remaining freedom in order to choose the Riemannian structure of the manifold amounts to fix the length of the intervals of type u and v for all . We denote these lengths , respectively.
Since the group G acts on via isometric diffeomorphisms, the corresponding action V on the space is a unitary representation of the group which is traceable. Concerning this last point, in fact, it is enough to consider the restriction of the action of G to the boundary :
because, as already mentioned, this action preserves the boundary. Then, the trace representation is obtained from in the same way as V is obtained from , i.e., via the pull-back.
This is not the unique traceable representation that one can obtain from the action . Since is an infinite cyclic group, any unitary representation of the group G can be obtained from a unitary representation of its generator . Therefore, we can consider more generally the unitary representation given by
where can depend both on the interval and the point on the interval. However, for the case under investigation, this action commutes with the Laplace–Beltrami operator on an interval if is constant on each interval. Indeed, we have that
and the multiplication by a constant phase commutes with the Laplace–Beltrami operator.
This representation of the generator induces the following unitary representation of the cyclic group :
and each phase is defined up to the sum of a multiple of .
In particular, if the function is the same for each , we get the following representation
where two different choices for the parameter , satisfying for some , define the same representation of the group .
The representation above induces a trace representation, which acts in the following way:
Before we state the main result of this section, let us recall that the quasi- family of self-adjoint extensions is characterised by the parameters , determining the unitary block associated with the ith vertex.
Theorem 3.
Consider the quantum circuit depicted in Figure 2. The group is a symmetry compatible with every quasi-δ self-adjoint extension such that:
- (i)
- The value of the parameter is the same at each vertex, δ.
- (ii)
- The relative phases between the boundary data associated with the loop is the same in all the vertices, i.e., does not depend on the vertex i.
Proof.
Consider the representation given in Equation (36). Since does not depend on x and is unitary for all k, it follows that this representation preserves the Neumann self-adjoint extension (see [1], (Prop. 6.14)). Then, it follows that the requirements of Theorem 1 are fulfilled, and we only need to proof that there exist such that the trace action defined in Equation (40) satisfies . Since the group is cyclic, it is enough to prove it for its generator, . The matrix representation of U and is the following:
where each element in the matrix is a block. From its definition, it is clear that respects the block structure of U and that the ith block of is equal to , where . Since is unitary, has the same eigenvalues as , and must be equal to . This is satisfied by Hypothesis (i).
The only thing left to show is that . By Proposition 3, this is equivalent to , where . One has that
which shows that can be chosen so that if Condition (ii) holds. □
Before concluding this section, it is important to add a remark. Indeed, the contents of the previous theorem can be analysed also from a different perspective: for any representation of the group , there is a family of quasi- self-adjoint extensions compatible with it. In particular, the action with constantly zero is compatible only with self-adjoint extensions characterised by , which amounts to require that the quasi- condition is the same on every vertex. If is constant and does not depend on the interval i all the relative phases can be incremented by a constant factor from one vertex to another, i.e., must remain constant, and also needs to be independent from i by Hypothesis (ii). However, only if the phase in the representation can vary from an interval to the other, self-adjoint extensions with varying from a vertex to the other are -invariant, once more with the restriction that must be vertex independent. In each of these situations, we can compute the spectrum of the Laplace–Beltrami operator. Indeed, after computing the solutions of the equation in each interval, the generalised eigenfuctions of the Laplace–Beltrami operator can be obtained after imposing the chosen boundary conditions. This procedure results in a set of algebraic linear equations involving the boundary data. For the family of self-adjoint extensions considered in Theorem 3, if k is an eigenvalue and the corresponding solution on the interval , at the i-node, one gets the following system of equations:
where is constant along the graph and as well. As a particular instance of this general form, we can consider the self-adjoint extension for which for all . In this case, the final system of equations simplifies and we get:
If we introduce the new variables
it is immediate to derive the equation and . From these conditions, we derive the following relationships:
After some straightforward computations, one can express the value of the coefficients in terms of as follows:
The same strategy can be used to find the solutions of Equations (41)–(44) for other values of the parameters. Indeed, we can introduce the new variables
which, for , satisfy the relation and . (if , the relation between and is more complicated, but using it we can solve the initial system following the same steps illustrated for the case ) From the definition of the new variables and their relations, we get the following expressions:
and straightforward substitutions lead to the following results:
Eventually, let us also notice that the previous results can be identically extended to the situation in which we consider on each interval the sum of the Laplace–Beltrami operator and a continuous potential bounded from below which has to be periodic, i.e., . Indeed, such a function does not affect the analysis of self-adjoint extensions, which remain those of the Laplace–Beltrami operator.
Before concluding this section, let us remark that the above discussion only shows that the calculated functions are candidates to be generalised eigenfunctions. However, to actually be a generalised eigenfunction, they also need to satisfy an additional property: its inner product with every function in the domain of the Laplacian must be finite. Therefore, even if one can impose the boundary conditions for every k in some interval of the positive line, some of these values might not be in the spectrum of the associated Laplace–Beltrami operator. In Figure 4, Figure 5 and Figure 6, some of the candidates to generalised eigenfunctions are shown for different combinations of k and .
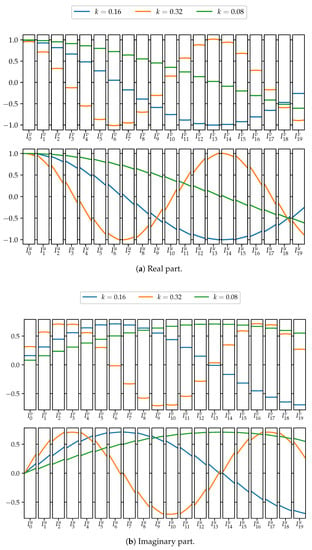
Figure 4.
Real and imaginary parts of a generalised eigenfunction for and several values of k. For each of the images, the upper row shows the value on the loops while the lower row shows the value in the chain.
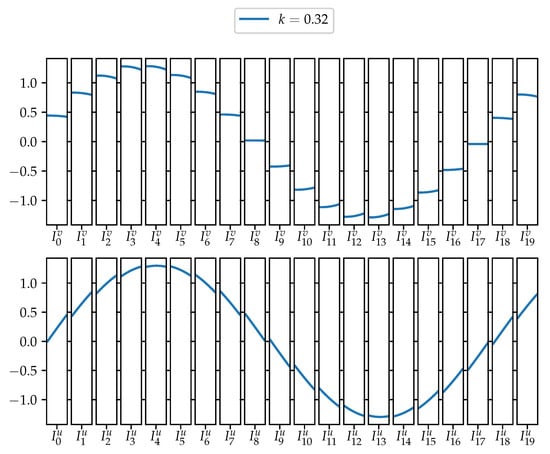
Figure 5.
Value of a generalised eigenfunction for , , and . The upper row shows the value on the loops while the lower row shows the value in the chain.
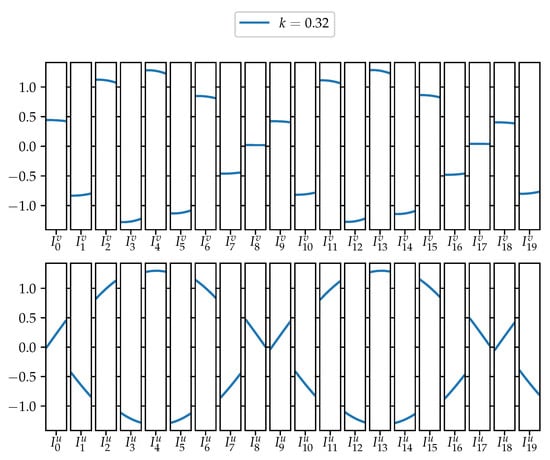
Figure 6.
Value of a generalised eigenfunction for , , , and . The upper row shows the value on the loops while the lower row shows the value in the chain.
5. Conclusions and Discussion
In this paper, we have addressed the issue of the existence of self-adjoint extensions of the Laplace operator on quantum circuits compatible with the action of a group of symmetries. In particular, we have investigated a class of circuits obtained as a chain of small unit cells, each one forming a finite graph. The simple example of unit cells made up of single loops has been fully analysed and different unitary representations of the group of integers on the Hilbert space associated with the quantum system have been provided. Eventually, the features of the -invariant self-adjoint extensions of the Laplace–Beltrami operator with respect to these unitary representations are shown and a way to obtain the generalised eigenfunctions is outlined. The generalisation to more complex unit cells follows straightforwardly. Moreover, the method can be applied without modification to another important situation: the case of closed, compact quantum circuits. For these systems, the same kind of analysis leads to similar conclusions provided that the group under study respects the symmetry of the circuit itself. For instance, one could have considered a chain with a finite number, say m, of repeated cells, with periodic boundary conditions. In this case, the cyclic group of order m, , would act in a similar way as the group on an infinite chain. In this case, the spectrum of the Laplacian operator would be discrete, as the carrier space of the quantum system is compact.
The analysis presented in this work can be considered as a preliminary work towards a complete modelisation of quantum circuits. The attention paid to this topic has recently grown because quantum systems on graphs provide a setting for universal computation [28]. Therefore, coming back to the chain described in this work, any unit cell could be thought of as a gate of a more complex quantum computer, and the family of quasi- self-adjoint extensions provides a set of vertex connections which preserve the underlying topology of the circuit and can be compatible with translational symmetry, too.
As a final remark, let us stress the role played by the group as a symmetry of the quantum system. Indeed, using symmetry considerations, we have been able to identify a wide class of self-adjoint extensions, which preserves the topology of the graph (these self-adjoint extensions are obtained by imposing boundary conditions already known in the literature as quasi- boundary conditions [9]). Notice that the family of self-adjoint extensions obtained is more general than a merely periodic repetition of the parameters defining the self-adjoint extension at each unit cell. Due to the group of symmetries, not all the parameters define -invariant self-adjoint extensions for some representation V of the group . The parameters and introduced in the last section, indeed, have to be constant. Such an action has also allowed us to compute more easily the generalised eigenfunctions only knowing the eigenfunctions on an interval. It would be interesting to see the difference in the spectral properties when a periodic potential is added, and compare these results with those deriving from Bloch theory of periodic quantum systems.
Author Contributions
Conceptualization, Formal Analysis, Writing—Original Draft Preparation, A.B., F.D.C. and J.M.P.-P.
Funding
This research was funded by “Ministerio de Economía, Industria y Competitividad, Gobierno de España” grant number MTM2017-84098-P and QUITEMAD project P2018/TCS-4342 funded by “Comunidad Autónoma de Madrid”. A.B. acknowledges financial support by “Universidad Carlos III de Madrid” through Ph.D. program grant PIPF UC3M 01-1819. F.dC. acknowledges financial support by QUITEMAD project P2018/TCS-4342.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ibort, A.; Lledó, F.; Pérez-Pardo, J. Self-Adjoint Extensions of the Laplace–Beltrami Operator and Unitaries at the Boundary. J. Funct. Anal. 2015, 268, 634–670. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons Inc: Hoboken, NJ, USA, 2004. [Google Scholar]
- Bloch, F. Über die Quantenmechanik der Elektronen in Kristallgittern. Zeitschrift für Physik 1929, 52, 555–600. [Google Scholar] [CrossRef]
- Balachandran, A.P.; Bimonte, G.; Marmo, G.; Simoni, A. Topology Change and Quantum Physics. Nucl. Phys. B 1995, 446, 299–314. [Google Scholar] [CrossRef]
- Pérez-Pardo, J.M.; Barbero-Liñán, M.; Ibort, A. Boundary Dynamics and Topology Change in Quantum Mechanics. Int. J. Geom. Methods Mod. Phys. 2015, 12, 1560011. [Google Scholar] [CrossRef]
- Devoret, M.H.; Schoelkopf, R.J. Superconducting Circuits for Quantum Information: An Outlook. Science 2013, 339, 1169–1174. [Google Scholar] [CrossRef] [PubMed]
- Wendin, G. Quantum Information Processing with Superconducting Circuits: A Review. Rep. Prog. Phys. 2017, 80, 106001. [Google Scholar] [CrossRef] [PubMed]
- Wendin, G.; Shumeiko, V.S. Quantum Bits with Josephson Junctions (Review Article). Low Temp. Phys. 2007, 33, 724–744. [Google Scholar] [CrossRef]
- Balmaseda, A.; Pérez-Pardo, J.M. Quantum Control at the Boundary. In 60 Years Alberto Ibort Fest Classical and Quantum Physics; Marmo, G., de Diego, D.M., Muñoz-Lecanda, M.C., Eds.; Springer Proceedings on Physics: Cham, Switzerland, 2019. [Google Scholar]
- Grubb, G. A Characterization of the Non Local Boundary Value Problems Associated with an Elliptic Operator. Ann. Della Sc. Norm. Super. Pisa-Cl. Sci. 1968, 22, 425–513. [Google Scholar]
- Asorey, M.; Ibort, A.; Marmo, G. Global Theory of Quantum Boundary Conditions and Topology Change. Int. J. Mod. Phys. A 2005, 20, 1001–1025. [Google Scholar] [CrossRef]
- Ibort, A.; Pérez-Pardo, J.M. Numerical Solutions of the Spectral Problem for Arbitrary Self-Adjoint Extensions of the One-Dimensional Schrödinger Equation. SIAM J. Numer. Anal. 2013, 51, 1254–1279. [Google Scholar] [CrossRef]
- López-Yela, A.; Pérez-Pardo, J. Finite Element Method to Solve the Spectral Problem for Arbitrary Self-Adjoint Extensions of the Laplace–Beltrami Operator on Manifolds with a Boundary. J. Comput. Phys. 2017, 347, 235–260. [Google Scholar] [CrossRef]
- Ibort, A.; Perez-Pardo, J.M. On the Theory of Self-Adjoint Extensions of Symmetric Operators and Its Applications to Quantum Physics. arxiv 2015, arXiv:1502.05229. [Google Scholar] [CrossRef]
- Pérez-Pardo, J. Dirac-like Operators on the Hilbert Space of Differential Forms on Manifolds with Boundaries. Int. J. Geom. Methods Mod. Phys. 2017, 14, 1740004. [Google Scholar] [CrossRef]
- Ibort, A.; Lledó, F.; Pérez-Pardo, J.M. On Self-Adjoint Extensions and Symmetries in Quantum Mechanics. Ann. Henri Poincaré 2015, 16, 2367–2397. [Google Scholar] [CrossRef]
- Wigner, E. Gruppentheorie Und Ihre Anwendung Auf Die Quantenmechanik Der Atomspektren; Friedr Vieweg and Sohn: Braunschweig, Germany, 1931. [Google Scholar]
- Weyl, H. The Theory of Groups and Quantum Mechanics; Courier Corporation: Chelmsford, MA, USA, 1950. [Google Scholar]
- v Neumann, J. Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren. Math. Ann. 1930, 102, 49–131. [Google Scholar] [CrossRef]
- Kato, T. Perturbation Theory for Linear Operators; Classics in Mathematics; Springer: Berlin, Germany, 1995. [Google Scholar]
- Adams, R.A.; Fournier, J.J.F. Sobolev Spaces; Pure and Applied Mathematics; Elsevier Science: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Albeverio, S.; Gesztesy, F.; Hoegh-Krohn, R.; Holden, H. Solvable Models in Quantum Mechanics; Springer Science & Business Media: Berlin, Germany, 1988. [Google Scholar]
- Esposito, G.; Marmo, G.; Sudarshan, G. From Classical to Quantum Mechanics: An Introduction to the Formalism, Foundations and Applications; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Reed, M.; Simon, B. Methods of Modern Mathematical Physics I: Functional Analysis, rev and enl ed.; Elsevier: San Diego, CA, USA, 2012. [Google Scholar]
- Gelfand, I.; Shilov, G. Generalised Functions: Theory of Differential Equations; Academic Press: New York, NY, USA, 1967; Volume 3. [Google Scholar]
- Marsden, J.E.; Abraham, R.; Ratiu, T. Manifolds, Tensor Analysis, and Applications, 3rd ed.; Applied Mathematical Sciences; Springer: New York, NY, USA, 1988. [Google Scholar]
- Naylor, A.; Sell, G. Linear Operator Theory in Engineering and Science; Applied Mathematical Sciences; Springer: New York, NY, USA, 1982. [Google Scholar]
- Childs, A. Universal Computation by Quantum Walk. Phys. Rev. Lett. 2009, 102, 180501. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).