Sampling Associated with a Unitary Representation of a Semi-Direct Product of Groups: A Filter Bank Approach

Abstract

An abstract sampling theory associated with a unitary representation of a countable discrete non abelian group G, which is a semi-direct product of groups, on a separable Hilbert space is studied. A suitable expression of the data samples, the use of a filter bank formalism and the corresponding frame analysis allow for fixing the mathematical problem to be solved: the search of appropriate dual frames for ${\ell }^2\left(G\right)$. An example involving crystallographic groups illustrates the obtained results by using either average or pointwise samples.

1. Statement of the Problem

In this paper, an abstract sampling theory associated with non abelian groups is derived for the specific case of a unitary representation of a semi-direct product of groups on a separable Hilbert space. Semi-direct product of groups provide important examples of non abelian groups such as dihedral groups, infinite dihedral group, Euclidean motion groups or crystallographic groups. Concretely, let $(n,h)\mapsto U(n,h)$ be a unitary representation on a separable Hilbert space $\mathcal{H}$ of a semi-direct product $G=N{⋊}_{\varphi }H$, where N is a countable discrete LCA (locally compact abelian) group, H is a finite group, and $\varphi$ denotes the action of the group H on the group N (see Section 2 infra for the details); for a fixed $a\in \mathcal{H}$ we consider the U-invariant subspace in $\mathcal{H}$

$${\mathcal{A}}_a=\left\{\sum _{(n,h)\in G}\alpha (n,h)U(n,h)a:{\left\{\alpha (n,h)\right\}}_{(n,h)\in G}\in {\ell }^2\left(G\right)\right\},$$

where we assume that $\left\{U\right(n,h\left)a\right\}$ is a Riesz sequence for $\mathcal{H}$, i.e., a Riesz basis for ${\mathcal{A}}_a$ (see Ref. [1] for a necessary and sufficient condition). Given K elements $b_k$ in $\mathcal{H}$, which do not belong necessarily to ${\mathcal{A}}_a$, the main goal in this paper is the stable recovery of any $x\in {\mathcal{A}}_a$ from the given data (generalized samples)

$${\mathcal{L}}_{k}x\left(n\right):={〈x,U(n,1_H)b_k〉}_{\mathcal{H}},n\in N\mathrm{and}k=1,2,\dots ,K,$$

where $1_H$ denotes the identity element in H. These samples are nothing but a generalization of average sampling in shift-invariant subspaces of $L^2\left({\mathbb{R}}^d\right)$; see, among others, Refs. [2,3,4,5,6,7,8,9]. The case where G is a discrete LCA group and the samples are taken at a uniform lattice of G has been solved in Ref. [10]; this work relies on the use of the Fourier analysis in the LCA group G (see also Ref. [11]). In the case involved here, a classical Fourier analysis is not available and, consequently, we need to overcome this drawback.

Having in mind the filter bank formalism in discrete LCA groups (see, for instance, Refs. [12,13,14]), the given data ${\left\{{\mathcal{L}}_{k}x\left(n\right)\right\}}_{n\in N;k=1,2,\dots ,K}$ can be expressed as the output of a suitable K-channel analysis filter bank corresponding to the input $\mathit{\alpha }={\left\{\alpha (n,h)\right\}}_{(n,h)\in G}$ in ${\ell }^2\left(G\right)$. As a consequence, the problem consists of finding a synthesis part of the former filter bank allowing perfect reconstruction; in addition, only Fourier analysis on the LCA group N is needed. Then, roughly speaking, substituting the output of the synthesis part in $x={\sum }_{(n,h)\in G}\alpha (n,h)U(n,h)a$, we will obtain the corresponding sampling formula in ${\mathcal{A}}_a$.

This said, as it could be expected, the problem can be mathematically formulated as the search of dual frames for ${\ell }^2\left(G\right)$ having the form

$${\left\{T_n{\mathrm{h}}_k\right\}}_{n\in N;k=1,2,\dots ,K}\mathrm{and}{\left\{T_n{\mathrm{g}}_k\right\}}_{n\in N;k=1,2,\dots ,K}.$$

Here, ${\mathrm{h}}_k,{\mathrm{g}}_k\in {\ell }^2\left(G\right)$, $T_n{\mathrm{h}}_k(m,h)={\mathrm{h}}_k(m-n,h)$ and $T_n{\mathrm{g}}_k(m,h)={\mathrm{g}}_k(m-n,h)$, $(m,h)\in G$, where $n\in N$ and $k=1,2,\dots ,K$. In addition, for any $x\in {\mathcal{A}}_a$, we have the expression for its samples

$${\mathcal{L}}_{k}x\left(n\right)={〈\mathit{\alpha },T_n{\mathrm{h}}_k〉}_{{\ell }^2\left(G\right)},n\in N\mathrm{and}k=1,2,\dots ,K.$$

Needless to say, frame theory plays a central role in what follows; the necessary background on Riesz bases or frame theory in a separable Hilbert space can be found, for instance, in Ref. [15]. Finally, sampling formulas in ${\mathcal{A}}_a$ having the form

$$x=\sum _{k=1}^K\sum _{n\in N}{\mathcal{L}}_{k}x\left(n\right)U(n,1_H)c_k\mathrm{in}\mathcal{H},$$

for some $c_k\in {\mathcal{A}}_a$, $k=1,2,\dots ,K$, will come out by using, for $\mathrm{g}\in {\ell }^2\left(G\right)$ and $n\in N$, the shifting property ${\mathcal{T}}_{U,a}\left(T_n\mathrm{g}\right)=U(n,1_H)\left({\mathcal{T}}_{U,a}\mathrm{g}\right)$ that satisfies the natural isomorphism ${\mathcal{T}}_{U,a}:{\ell }^2\left(G\right)\to {\mathcal{A}}_a$ which maps the usual orthonormal basis ${\left\{{\mathit{\delta }}_{(n,h)}\right\}}_{(n,h)\in G}$ for ${\ell }^2\left(G\right)$ onto the Riesz basis ${\left\{U(n,h)a\right\}}_{(n,h)\in G}$ for ${\mathcal{A}}_a$. All these steps will be carried out throughout the remaining sections. For the sake of completeness, Section 2 includes some basic preliminaries on semi-direct product of groups and Fourier analysis on LCA groups. The paper ends with an illustrative example involving the quasi regular representation of a crystallographic group on $L^2\left({\mathbb{R}}^d\right)$; sampling formulas involving average or pointwise samples are obtained for the corresponding U-invariant subspaces in $L^2\left({\mathbb{R}}^d\right)$.

2. Some Mathematical Preliminaries

In this section, we introduce the basic tools in semi-direct product of groups and in harmonic analysis in a discrete LCA group that will be used in the sequel.

2.1. Preliminaries on Semi-Direct Product of Groups

Given groups $(N,·)$ and $(H,·)$, and a homomorphism $\varphi :H\to Aut\left(N\right),$ their semi-direct product $G:=N{⋊}_{\varphi }H$ is defined as follows: The underlying set of G is the set of pairs $(n,h)$ with $n\in N$ and $h\in H$, along with the multiplication rule

$$(n_1,h_1)·(n_2,h_2):=(n_1{\varphi }_{h_1}\left(n_2\right),h_1{h}_2),(n_1,h_1),(n_2,h_2)\in G,$$

where we denote $\varphi \left(h\right):={\varphi }_h$; usually, the homomorphism $\varphi$ is referred to as the action of the group H on the group N. Thus, we obtain a new group with identity element $(1_N,1_H)$, and inverse ${(n,h)}^{-1}=({\varphi }_{h^{-1}}\left(n^{-1}\right),h^{-1})$.

In addition, we have the isomorphisms $N\simeq N\times \left\{1_H\right\}$ and $H\simeq \left\{1_N\right\}\times H$. Unless ${\varphi }_h$ equals the identity for all $h\in H$, the group $G=N{⋊}_{\varphi }H$ is not abelian, even for abelian N and H groups. The subgroup N is a normal subgroup in G. Some examples of semi-direct product of groups:

• The dihedral group $D_{2N}$ is the group of symmetries of a regular N-sided polygon; it is the semi-direct product $D_{2N}={\mathbb{Z}}_N{⋊}_{\varphi }{\mathbb{Z}}_2$ where ${\varphi }_{\overline{0}}\equiv I{d}_{{\mathbb{Z}}_N}$ and ${\varphi }_{\overline{1}}\left(\overline{n}\right)=-\overline{n}$ for each $\overline{n}\in {\mathbb{Z}}_N$. The infinite dihedral group $D_{\infty }$ defined as $\mathbb{Z}{⋊}_{\varphi }{\mathbb{Z}}_2$ for the similar homomorphism $\varphi$ is the group of isometries of $\mathbb{Z}$.
• The Euclidean motion group $E\left(d\right)$ is the semi-direct product ${\mathbb{R}}^d{⋊}_{\varphi }O\left(d\right)$, where $O\left(d\right)$ is the orthogonal group of order d and ${\varphi }_A\left(x\right)=Ax$ for $A\in O\left(d\right)$ and $x\in {\mathbb{R}}^d$. It contains as a subgroup any crystallographic group $M{\mathbb{Z}}^d{⋊}_{\varphi }\mathsf{\Gamma }$, where $M{\mathbb{Z}}^d$ denotes a full rank lattice of ${\mathbb{R}}^d$ and $\mathsf{\Gamma }$ is any finite subgroup of $O\left(d\right)$ such that ${\varphi }_{\gamma }\left(M{\mathbb{Z}}^d\right)=M{\mathbb{Z}}^d$ for each $\gamma \in \mathsf{\Gamma }$.
• The orthogonal group $O\left(d\right)$ of all orthogonal real $d\times d$ matrices is isomorphic to the semi-direct product $SO\left(d\right){⋊}_{\varphi }{C}_2$, where $SO\left(d\right)$ consists of all orthogonal matrices with determinant 1 and $C_2=\{I,R\}$ a cyclic group of order 2; $\varphi$ is the homomorphism given by ${\varphi }_I\left(A\right)=A$ and ${\varphi }_R\left(A\right)=RA{R}^{-1}$ for $A\in SO\left(d\right)$.

Suppose that N is an LCA group with Haar measure ${\mu }_N$ and H is a locally compact group with Haar measure ${\mu }_H$. Then, the semi-direct product $G=N{⋊}_{\varphi }H$ endowed with the product topology becomes also a topological group. For the left Haar measure on G, see Ref. [1].

2.2. Some Preliminaries on Harmonic Analysis on Discrete LCA Groups

The results about harmonic analysis on locally compact abelian (LCA) groups are borrowed from Ref. [16]. Notice that, in particular, a countable discrete abelian group is a second countable Hausdorff LCA group.

For a countable discrete group $(N,·)$, not necessarily abelian, the convolution of $x,y:N\to \mathbb{C}$ is formally defined as $(x\ast y)\left(m\right):=\sum _{n\in N}x\left(n\right)y\left(n^{-1}m\right)$, $m\in N$. If, in addition, the group is abelian, therefore denoted by $(N,+)$, the convolution reads as

$$(x\ast y)\left(m\right):=\sum _{n\in N}x\left(n\right)y(m-n),m\in N.$$

Let $\mathbb{T}=\{z\in \mathbb{C}:|z|=1\}$ be the unidimensional torus. We said that $\xi :N\mapsto \mathbb{T}$ is a character of N if $\xi (n+m)=\xi \left(n\right)\xi \left(m\right)$ for all $n,m\in N$. We denote $\xi \left(n\right)=\langle n,\xi \rangle$. Defining $(\xi +\gamma )\left(n\right)=\xi \left(n\right)\gamma \left(n\right)$, the set of characters $\widehat{N}$ with the operation + is a group, called the dual group of N; since N is discrete $\widehat{N}$ is compact ([16], Prop. 4.4). For $x\in {\ell }^1\left(N\right),$ we define its Fourier transform as

$$X\left(\xi \right)=\widehat{x}\left(\xi \right):=\sum _{n\in N}x\left(n\right)\overline{\langle n,\xi \rangle }=\sum _{n\in N}x\left(n\right)\langle -n,\xi \rangle ,\xi \in \widehat{N}.$$

It is known ([16], Theorem 4.5) that $\widehat{\mathbb{Z}}\cong \mathbb{T}$, with $\langle n,z\rangle =z^n$, and ${\widehat{\mathbb{Z}}}_s\cong {\mathbb{Z}}_s:=\mathbb{Z}/s\mathbb{Z}$, with $\langle n,m\rangle =W_s^{nm}$, where $W_s=e^{2\pi i/s}$.

There exists a unique measure, the Haar measure $\mu$ on $\widehat{N}$ satisfying $\mu (\xi +E)=\mu \left(E\right)$, for every Borel set $E\subset \widehat{N}$ ([16], Section 2.2), and $\mu \left(\widehat{N}\right)=1$. We denote ${\int }_{\widehat{N}}X\left(\xi \right)d\xi ={\int }_{\widehat{N}}X\left(\xi \right)d\mu \left(\xi \right)$. If $N=\mathbb{Z}$,

$${\int }_{\widehat{N}}X\left(\xi \right)d\xi ={\int }_{\mathbb{T}}X\left(z\right)dz=\frac{1}{2\pi }{\int }_0^{2\pi }X\left(e^{iw}\right)dw,$$

and, if $N={\mathbb{Z}}_s$,

$${\int }_{\widehat{N}}X\left(\xi \right)d\xi ={\int }_{{\mathbb{Z}}_s}X\left(n\right)dn=\frac{1}{s}\sum _{n\in {\mathbb{Z}}_s}X\left(n\right).$$

If $N_1,N_2,\dots N_d$ are abelian discrete groups, then the dual group of the product group is ${\left(N_1\times N_2\times \dots \times N_d\right)}^{\wedge }\cong {\widehat{N}}_1\times {\widehat{N}}_2\times \dots \times {\widehat{N}}_d$ (see ([16], Prop. 4.6)) with

$$〈(n_1,n_2,\dots ,n_d),({\xi }_1,{\xi }_2\dots ,{\xi }_d)〉=\langle n_1,{\xi }_1\rangle \langle n_2,{\xi }_2\rangle \dots \langle n_d,{\xi }_d\rangle .$$

The Fourier transform on ${\ell }^1\left(N\right)\cap {\ell }^2\left(N\right)$ is an isometry on a dense subspace of $L^2\left(\widehat{N}\right)$; Plancherel theorem extends it in a unique manner to a unitary operator of ${\ell }^2\left(N\right)$ onto $L^2\left(\widehat{N}\right)$ ([16], p. 99). The following lemma, giving a relationship between Fourier transform and convolution, will be used later (see Ref. [17]):

Lemma 1.

Assume that $a,b\in {\ell }^2\left(N\right)$ and $\widehat{a}\left(\xi \right)\widehat{b}\left(\xi \right)\in L^2\left(\widehat{N}\right)$. Then, the convolution $a\ast b$ belongs to ${\ell }^2\left(N\right)$ and $\widehat{a\ast b}\left(\xi \right)=\widehat{a}\left(\xi \right)\widehat{b}\left(\xi \right)$, a.e. $\xi \in \widehat{N}$.

3. Filter Bank Formalism on Semi-Direct Product of Groups

In what follows, we will assume that $G=N{⋊}_{\varphi }H$ where $(N,+)$ is a countable discrete abelian group and $(H,·)$ is a finite group. Having in mind the operational calculus $(n,h)·(m,l)=(n+{\varphi }_h\left(m\right),hl)$, ${(n,h)}^{-1}=({\varphi }_{h^{-1}}(-n),h^{-1})$ and ${(n,h)}^{-1}·(m,l)=({\varphi }_{h^{-1}}(m-n),h^{-1}l)$, the convolution $\mathit{\alpha }\ast \mathrm{h}$ of $\mathit{\alpha },\mathrm{h}\in {\ell }^2\left(G\right)$ can be expressed as

$$\begin{array}{cc}\hfill (\mathit{\alpha }\ast \mathrm{h})(m,l)& =\sum _{(n,h)\in G}\alpha (n,h)\mathrm{h}\left[{(n,h)}^{-1}·(m,l)\right]\hfill \\ & =\sum _{(n,h)\in G}\alpha (n,h)\mathrm{h}\left({\varphi }_{h^{-1}}(m-n),h^{-1}l\right),(m,l)\in G.\hfill \end{array}$$

(1)

For a function $\mathit{\alpha }:G\to \mathbb{C}$, its H-decimation ${\downarrow }_H\mathit{\alpha }:N\to \mathbb{C}$ is defined as $\left({\downarrow }_H\mathit{\alpha }\right)\left(n\right):=\alpha (n,1_H)$ for any $n\in N$. Thus, we have

$$\begin{array}{cc}\hfill {\downarrow }_H(\mathit{\alpha }\ast \mathrm{h})\left(m\right)& =(\mathit{\alpha }\ast \mathrm{h})(m,1_H)=\sum _{(n,h)\in G}\alpha (n,h)\mathrm{h}\left({\varphi }_{h^{-1}}(m-n),h^{-1}\right)\hfill \\ & =\sum _{(n,h)\in G}\alpha (n,h)\mathrm{h}\left[{(n-m,h)}^{-1}\right],m\in N.\hfill \end{array}$$

(2)

Defining the polyphase components of $\mathit{\alpha }$ and $\mathrm{h}$ as ${\mathit{\alpha }}_h\left(n\right):=\alpha (n,h)$ and ${\mathrm{h}}_h\left(n\right):=\mathrm{h}\left[{(-n,h)}^{-1}\right]$ respectively, we write

$${\downarrow }_H(\mathit{\alpha }\ast \mathrm{h})\left(m\right)=\sum _{h\in H}\sum _{n\in N}{\mathit{\alpha }}_h\left(n\right){\mathrm{h}}_h(m-n)=\sum _{h\in H}\left({\mathit{\alpha }}_h{\ast }_N{\mathrm{h}}_h\right)\left(m\right),m\in N.$$

For a function $c:N\to \mathbb{C}$, its H-expander ${\uparrow }_{H}c:G\to \mathbb{C}$ is defined as

$$\left({\uparrow }_{H}c\right)(n,h)=\left\{\begin{array}{cc}c\left(n\right)\hfill & \mathrm{if}h=1_H,\hfill \\ 0\hfill & \mathrm{if}h\ne 1_H.\hfill \end{array}\right.$$

In case ${\uparrow }_{H}c$ and $\mathrm{g}$ belong to ${\ell }^2\left(G\right),$ we have

$$\begin{array}{cc}\hfill ({\uparrow }_{H}c\ast \mathrm{g})(m,l)& =\sum _{(n,h)\in G}\left({\uparrow }_{H}c\right)(n,h)\mathrm{g}\left[{(n,h)}^{-1}·(m,l)\right]\hfill \\ & =\sum _{(n,h)\in G}\left({\uparrow }_{H}c\right)(n,h)\mathrm{g}\left({\varphi }_{h^{-1}}(m-n),h^{-1}l\right)\hfill \\ & =\sum _{n\in N}c\left(n\right)\mathrm{g}(m-n,l)=\left(c{\ast }_N{\mathrm{g}}_l\right)\left(m\right),m\in N,l\in H,\hfill \end{array}$$

where ${\mathrm{g}}_l\left(n\right):=\mathrm{g}(n,l)$ is the polyphase component of $\mathrm{g}$.

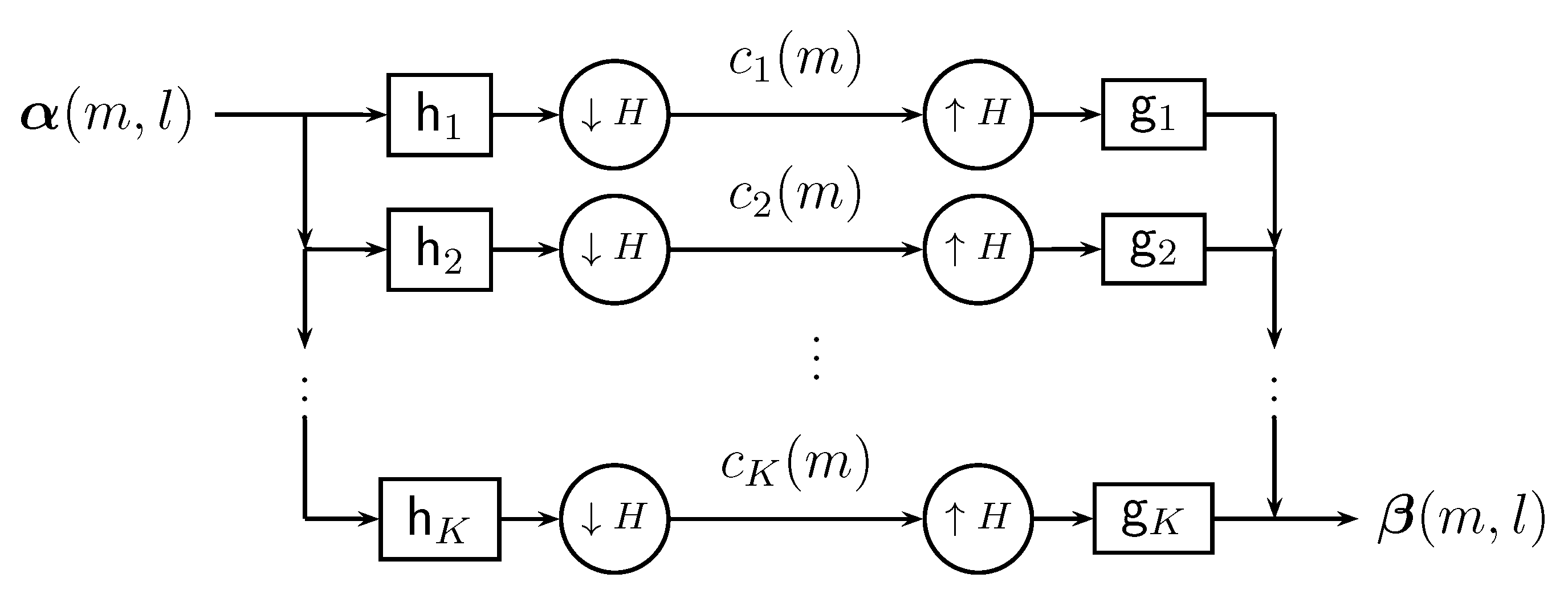
From now on, we will refer to a K-channel filter bank with analysis filters ${\mathrm{h}}_k$ and synthesis filters ${\mathrm{g}}_k$, $k=1,2,\dots ,K$ as the one given by (see Figure 1)

$${\mathbf{c}}_k{:=\downarrow }_H(\mathit{\alpha }\ast {\mathrm{h}}_k),k=1,2,\dots ,K,\mathrm{and}\mathit{\beta }=\sum _{k=1}^K\left({\uparrow }_H{c}_k\right)\ast {\mathrm{g}}_k,$$

(3)

where $\mathit{\alpha }$ and $\mathit{\beta }$ denote, respectively, the input and the output of the filter bank. In polyphase notation,

$$\begin{array}{cc}\hfill {\mathbf{c}}_k\left(m\right)& =\sum _{h\in H}\left({\mathit{\alpha }}_h{\ast }_N{\mathrm{h}}_{k,h}\right)\left(m\right),m\in N,k=1,2,\dots ,K,\hfill \\ \hfill {\mathit{\beta }}_l\left(m\right)& =\sum _{k=1}^K\left({\mathbf{c}}_k{\ast }_N{\mathrm{g}}_{l,k}\right)\left(m\right),m\in N,l\in H,\hfill \end{array}$$

(4)

where ${\mathit{\alpha }}_h\left(n\right):=\alpha (n,h)$, ${\mathit{\beta }}_l\left(n\right):=\beta (n,l)$, ${\mathrm{h}}_{k,h}\left(n\right):={\mathrm{h}}_k\left[{(-n,h)}^{-1}\right]$ and ${\mathrm{g}}_{l,k}\left(n\right):={\mathrm{g}}_k(n,l)$ are the polyphase components of $\mathit{\alpha }$, $\mathit{\beta }$, ${\mathrm{h}}_k$ and ${\mathrm{g}}_k$, $k=1,2,\dots ,K$, respectively. We also assume that ${\mathrm{h}}_k,{\mathrm{g}}_k\in {\ell }^2\left(G\right)$ with ${\widehat{\mathrm{h}}}_{k,h},{\widehat{\mathrm{g}}}_{h,k}\in L^{\infty }\left(\widehat{N}\right)$ for $k=1,2,\dots ,K$ and $h\in H$; from Lemma 1, the filter bank (3) is well defined in ${\ell }^2\left(G\right)$.

The above K-channel filter bank (3) is said to be a perfect reconstruction filter bank if and only if it satisfies $\mathit{\alpha }={\sum }_{k=1}^K\left({\uparrow }_H{c}_k\right)\ast {\mathrm{g}}_k$ for each $\mathit{\alpha }\in {\ell }^2\left(G\right)$, or equivalently, ${\mathit{\alpha }}_h={\sum }_{k=1}^K\left({\mathbf{c}}_k{\ast }_N{\mathrm{g}}_{h,k}\right)$ for each $h\in H$.

Since N is an LCA group where a Fourier transform is available, the polyphase expression (4) of the filter bank (3) allows us to carry out its polyphase analysis.

Polyphase Analysis: Perfect Reconstruction Condition

For notational ease, we denote $L:=\left|H\right|$, the order of the group H, and its elements as $H=\{h_1,h_2,\dots ,h_L\}$. Having in mind Lemma 1, the N-Fourier transform in ${\mathbf{c}}_k\left(m\right)={\sum }_{h\in H}\left({\mathit{\alpha }}_h{\ast }_N{\mathrm{h}}_{k,h}\right)\left(m\right)$ gives ${\widehat{\mathbf{c}}}_k\left(\gamma \right)={\sum }_{h\in H}{\widehat{\mathrm{h}}}_{k,h}\left(\gamma \right){\widehat{\mathit{\alpha }}}_h\left(\gamma \right)$ a.e. $\gamma \in \widehat{N}$ for each $k=1,2,\dots ,K$. In matrix notation,

$$\mathbf{C}(\gamma )=\mathbf{H}(\gamma )\mathbf{A}(\gamma )\mathrm{a}.\mathrm{e}.\gamma \in \widehat{N},$$

where $\mathbf{C}\left(\gamma \right)={\left({\widehat{\mathbf{c}}}_1\left(\gamma \right),{\widehat{\mathbf{c}}}_2\left(\gamma \right),\dots ,{\widehat{\mathbf{c}}}_K\left(\gamma \right)\right)}^{\top }$, $\mathbf{A}\left(\gamma \right)={\left({\widehat{\mathit{\alpha }}}_{h_1}\left(\gamma \right),{\widehat{\mathit{\alpha }}}_{h_2}\left(\gamma \right),\dots ,{\widehat{\mathit{\alpha }}}_{h_L}\left(\gamma \right)\right)}^{\top }$, and $\mathbf{H}\left(\gamma \right)$ is the $K\times L$ matrix

$$\mathbf{H}\left(\gamma \right)=\left(\begin{array}{cccc}{\widehat{\mathrm{h}}}_{1,h_1}\left(\gamma \right)& {\widehat{\mathrm{h}}}_{1,h_2}\left(\gamma \right)& \dots & {\widehat{\mathrm{h}}}_{1,h_L}\left(\gamma \right)\\ {\widehat{\mathrm{h}}}_{2,h_1}\left(\gamma \right)& {\widehat{\mathrm{h}}}_{2,h_2}\left(\gamma \right)& \dots & {\widehat{\mathrm{h}}}_{2,h_L}\left(\gamma \right)\\ \dots & \dots & \dots & \dots \\ {\widehat{\mathrm{h}}}_{K,h_1}\left(\gamma \right)& {\widehat{\mathrm{h}}}_{K,h_2}\left(\gamma \right)& \dots & {\widehat{\mathrm{h}}}_{K,h_L}\left(\gamma \right)\end{array}\right),$$

(5)

where ${\widehat{\mathrm{h}}}_{k,h_i}\in L^2\left(\widehat{N}\right)$ is the Fourier transform of ${\mathrm{h}}_{k,h_i}\left(n\right):={\mathrm{h}}_k\left[{(-n,h_i)}^{-1}\right]\in {\ell }^2\left(N\right)$.

The same procedure for ${\mathit{\beta }}_l\left(m\right)={\sum }_{k=1}^K\left({\mathbf{c}}_k{\ast }_N{\mathrm{g}}_{l,k}\right)\left(m\right)$ gives ${\widehat{\mathit{\beta }}}_l\left(\gamma \right)={\sum }_{k=1}^K{\widehat{\mathrm{g}}}_{l,k}\left(\gamma \right){\widehat{\mathbf{c}}}_k\left(\gamma \right)$ a.e. $\gamma \in \widehat{N}$. In matrix notation,

$$\mathbf{B}(\gamma )=\mathbf{G}(\gamma )\mathbf{C}(\gamma )\mathrm{a}.\mathrm{e}.\gamma \in \widehat{N},$$

where $\mathbf{B}\left(\gamma \right)={\left({\widehat{\mathit{\beta }}}_{h_1}\left(\gamma \right),{\widehat{\mathit{\beta }}}_{h_2}\left(\gamma \right),\dots ,{\widehat{\mathit{\beta }}}_{h_L}\left(\gamma \right)\right)}^{\top }$, $\mathbf{C}\left(\gamma \right)={\left({\widehat{\mathbf{c}}}_1\left(\gamma \right),{\widehat{\mathbf{c}}}_2\left(\gamma \right),\dots ,{\widehat{\mathbf{c}}}_K\left(\gamma \right)\right)}^{\top }$ and $\mathbf{G}\left(\gamma \right)$ is the $L\times K$ matrix

$$\mathbf{G}\left(\gamma \right)=\left(\begin{array}{cccc}{\widehat{\mathrm{g}}}_{h_1,1}\left(\gamma \right)& {\widehat{\mathrm{g}}}_{h_1,2}\left(\gamma \right)& \dots & {\widehat{\mathrm{g}}}_{h_1,K}\left(\gamma \right)\\ {\widehat{\mathrm{g}}}_{h_2,1}\left(\gamma \right)& {\widehat{\mathrm{g}}}_{h_2,2}\left(\gamma \right)& \dots & {\widehat{\mathrm{g}}}_{h_2,K}\left(\gamma \right)\\ \dots & \dots & \dots & \dots \\ {\widehat{\mathrm{g}}}_{h_L,1}\left(\gamma \right)& {\widehat{\mathrm{g}}}_{h_L,2}\left(\gamma \right)& \dots & {\widehat{\mathrm{g}}}_{h_L,K}\left(\gamma \right)\end{array}\right),$$

(6)

where ${\widehat{\mathrm{g}}}_{h_i,k}\in L^2\left(\widehat{N}\right)$ is the Fourier transform of ${\mathrm{g}}_{h_i,k}\left(n\right):={\mathrm{g}}_k(n,h_i)\in {\ell }^2\left(N\right)$.

Thus, in terms of the polyphase matrices $\mathbf{G}\left(\gamma \right)$ and $\mathbf{H}\left(\gamma \right),$ the filter bank (3) can be expressed as

$$\mathbf{B}(\gamma )=\mathbf{G}(\gamma )\mathbf{H}(\gamma )\mathbf{A}(\gamma )\mathrm{a}.\mathrm{e}.\gamma \in \widehat{N}.$$

(7)

As a consequence of Equation (7), we have:

Theorem 1.

The K-channel filter bank given in Equation (3), where ${\mathrm{h}}_k,{\mathrm{g}}_k$ belong to ${\ell }^2\left(G\right)$ and ${\widehat{\mathrm{h}}}_{k,h_i},{\widehat{\mathrm{g}}}_{h_i,k}$ belong to $L^{\infty }\left(\widehat{N}\right)$ for $k=1,2,\dots ,K$ and $i=1,2,\dots ,L$, satisfies the perfect reconstruction property if and only if $\mathbf{G}\left(\gamma \right)\mathbf{H}\left(\gamma \right)={\mathbf{I}}_L$ a.e. $\gamma \in \widehat{N}$, where ${\mathbf{I}}_L$ denotes the identity matrix of order L.

Proof. 

First of all, note that the mapping $\mathit{\alpha }\in {\ell }^2\left(G\right)\mapsto \mathbf{A}\in L_L^2\left(\widehat{N}\right)$ is a unitary operator. Indeed, for each $\mathit{\alpha },\mathit{\beta }\in {\ell }^2\left(G\right),$ we have the isometry property

$$\begin{array}{cc}\hfill {\langle \mathit{\alpha },\mathit{\beta }\rangle }_{{\ell }^2\left(G\right)}& =\sum _{(m,h)\in G}\alpha (m,h)\overline{\beta (m,h)}=\sum _{h\in H}{\langle {\mathit{\alpha }}_h,{\mathit{\beta }}_h\rangle }_{{\ell }^2\left(N\right)}\hfill \\ & =\sum _{h\in H}{\langle {\widehat{\mathit{\alpha }}}_h,{\widehat{\mathit{\beta }}}_h\rangle }_{L^2\left(\widehat{N}\right)}={\langle \mathbf{A},\mathbf{B}\rangle }_{L_L^2\left(\widehat{N}\right)}.\hfill \end{array}$$

It is also surjective since the N-Fourier transform is a surjective isometry between ${\ell }^2\left(N\right)$ and $L^2\left(\widehat{N}\right)$. Having in mind this property, Equation (7) tells us that the filter bank satisfies the perfect reconstruction property if and only if $\mathbf{G}\left(\gamma \right)\mathbf{H}\left(\gamma \right)={\mathbf{I}}_L$ a.e. $\gamma \in \widehat{N}$. □

Notice that, in the perfect reconstruction setting, the number of channels K must be necessarily bigger or equal that the order L of the group H, i.e., $K\ge L$.

4. Frame Analysis

For $m\in N$, the translation operator $T_m:{\ell }^2\left(G\right)\to {\ell }^2\left(G\right)$ is defined as

$$T_m\mathit{\alpha }(n,h):=\alpha \left({(m,1_H)}^{-1}·(n,h)\right)=\alpha (n-m,h),(n,h)\in G.$$

(8)

The involution operator $\mathit{\alpha }\in {\ell }^2\left(G\right)\mapsto \tilde{\mathit{\alpha }}\in {\ell }^2\left(G\right)$ is defined as $\tilde{\alpha }(n,h):=\overline{\alpha \left({(n,h)}^{-1}\right)}$, $(n,h)\in G$. As expected, the classical relationship between convolution and translation operators holds. Thus, for the K-channel filter bank (3), we have (see (2)):

$${\mathbf{c}}_k{\left(m\right)=\downarrow }_H(\mathit{\alpha }\ast {\mathrm{h}}_k)\left(m\right)={〈\mathit{\alpha },T_m{\tilde{\mathrm{h}}}_k〉}_{{\ell }^2\left(G\right)},m\in N,k=1,2,\dots ,K.$$

In addition,

$$({\uparrow }_H{\mathbf{c}}_k\ast {\mathrm{g}}_k)(m,h)=\sum _{n\in N}{\mathbf{c}}_k\left(n\right){\mathrm{g}}_k(m-n,h)=\sum _{n\in N}{\langle \mathit{\alpha },T_n{\tilde{\mathrm{h}}}_k\rangle }_{{\ell }^2\left(G\right)}{T}_n{\mathrm{g}}_k(m,h).$$

In the perfect reconstruction setting, for any $\mathit{\alpha }\in {\ell }^2\left(G\right),$ we have

$$\mathit{\alpha }=\sum _{k=1}^K\sum _{n\in N}{\langle \mathit{\alpha },T_n{\tilde{\mathrm{h}}}_k\rangle }_{{\ell }^2\left(G\right)}{T}_n{\mathrm{g}}_k\mathrm{in}{\ell }^2\left(G\right).$$

(9)

Given K sequences ${\mathrm{f}}_k\in {\ell }^2\left(G\right)$, $k=1,2,\dots ,K$, our main tasks now are: $\left(i\right)$ to characterize the sequence ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ as a frame for ${\ell }^2\left(G\right)$, and $\left(ii\right)$ to find its dual frames having the form ${\left\{T_n{\mathrm{g}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$.

To the first end, we consider a K-channel analysis filter bank with analysis filters ${\mathrm{h}}_k:={\tilde{\mathrm{f}}}_k$, i.e., the involution of ${\mathrm{f}}_k$, $k=1,2,\dots ,K$; let $\mathbf{H}\left(\gamma \right)$ be its associated $K\times L$ polyphase matrix (5). First, we check that Equation (5) is:

$$\mathbf{H}\left(\gamma \right)={\left(\overline{{\widehat{\mathrm{f}}}_{k,h_i}\left(\gamma \right)}\right)}_{\begin{array}{c}k=1,2,\dots ,K\\ i=1,2,\dots ,L\end{array}},$$

(10)

where ${\widehat{\mathrm{f}}}_{k,h_i}\left(\gamma \right)$ denotes the Fourier transform in $L^2\left(\widehat{N}\right)$ of ${\mathrm{f}}_{k,h_i}\left(n\right)={\mathrm{f}}_k(n,h_i)$ in ${\ell }^2\left(N\right)$. Indeed, for $k=1,2,\dots ,K$ and $i=1,2,\dots ,L$, having in mind that ${\mathrm{h}}_{k,h_i}\left(n\right)={\mathrm{h}}_k\left[{(-n,h_i)}^{-1}\right]$ for analysis filters, we have

$$\begin{array}{cc}\hfill {\widehat{\mathrm{h}}}_{k,h_i}\left(\gamma \right)& =\sum _{n\in N}{\mathrm{h}}_{k,h_i}\left(n\right)\langle -n,\gamma \rangle =\sum _{n\in N}{\mathrm{h}}_k\left[{(-n,h_i)}^{-1}\right]\langle -n,\gamma \rangle =\sum _{n\in N}{\tilde{\mathrm{f}}}_k\left[{(-n,h_i)}^{-1}\right]\langle -n,\gamma \rangle \hfill \\ & =\sum _{n\in N}\overline{{\mathrm{f}}_k(-n,h_i)}\langle -n,\gamma \rangle =\overline{\sum _{n\in N}{\mathrm{f}}_k(n,h_i)\langle -n,\gamma \rangle }=\overline{{\widehat{\mathrm{f}}}_{k,h_i}\left(\gamma \right)},\gamma \in \widehat{N}.\hfill \end{array}$$

Next, we consider its associated constants

$$A_{\mathbf{H}}:=\underset{\gamma \in \widehat{N}}{ess\; inf}{\lambda }_{min}\left[{\mathbf{H}}^{\ast }\left(\gamma \right)\mathbf{H}\left(\gamma \right)\right]\mathrm{and}{B}_{\mathbf{H}}:=\underset{\gamma \in \widehat{N}}{ess\; sup}{\lambda }_{max}\left[{\mathbf{H}}^{\ast }\left(\gamma \right)\mathbf{H}\left(\gamma \right)\right].$$

Theorem 2.

For ${\mathrm{f}}_k$ in ${\ell }^2\left(G\right)$, $k=1,2,\dots ,K$, consider the associated matrix $\mathbf{H}\left(\gamma \right)$ given in Equation (10). Then,

1. 

The sequence ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ is a Bessel sequence for ${\ell }^2\left(G\right)$ if and only if $B_{\mathbf{H}}<\infty$.

2. 

The sequence ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ is a frame for ${\ell }^2\left(G\right)$ if and only if the inequalities $0<A_{\mathbf{H}}\le B_{\mathbf{H}}<\infty$ hold.

Proof. 

Using Plancherel theorem ([16], Theorem 4.25), for each $\mathit{\alpha }\in {\ell }^2\left(G\right),$ we get

$$\begin{array}{cc}\hfill {\langle \mathit{\alpha },T_n{\mathrm{f}}_k\rangle }_{{\ell }^2\left(G\right)}& =\sum _{h\in H}{\langle {\mathit{\alpha }}_h,{\mathrm{f}}_{k,h}(·-n)\rangle }_{{\ell }^2\left(N\right)}=\sum _{h\in H}{\int }_{\widehat{N}}{\widehat{\mathit{\alpha }}}_h\left(\gamma \right)\overline{{\widehat{\mathrm{f}}}_{k,h}\left(\gamma \right)\langle -n,\gamma \rangle }d\gamma \hfill \\ & ={\int }_{\widehat{N}}\sum _{h\in H}{\widehat{\mathit{\alpha }}}_h\left(\gamma \right)\overline{{\widehat{\mathrm{f}}}_{k,h}\left(\gamma \right)}\overline{\langle -n,\gamma \rangle }d\gamma ={\int }_{\widehat{N}}{\mathbf{H}}_k\left(\gamma \right)\mathbf{A}\left(\gamma \right)\overline{\langle -n,\gamma \rangle }d\gamma ,\hfill \end{array}$$

where $\mathbf{A}\left(\gamma \right)={\left({\widehat{\mathit{\alpha }}}_{h_1}\left(\gamma \right),{\widehat{\mathit{\alpha }}}_{h_2}\left(\gamma \right),\dots ,{\widehat{\mathit{\alpha }}}_{h_L}\left(\gamma \right)\right)}^{\top }$ and ${\mathbf{H}}_k\left(\gamma \right)$ denotes the k-th row of $\mathbf{H}\left(\gamma \right)$.

Since ${\left\{\langle -n,\gamma \rangle \right\}}_{n\in N}$ is an orthonormal basis for $L^2\left(\widehat{N}\right)$, in case that $\mathbf{H}\left(\gamma \right)\mathbf{A}\left(\gamma \right)\in L_K^2\left(\widehat{N}\right),$ we have

$$\sum _{k=1}^K\sum _{n\in N}{\left|\langle \mathit{\alpha },T_n{\mathrm{f}}_k\rangle \right|}^2=\sum _{k=1}^K{\int }_{\widehat{N}}|{\mathbf{H}}_k\left(\gamma \right)\mathbf{A}\left(\gamma \right){|}^{2}d\gamma ={\int }_{\widehat{N}}\parallel \mathbf{H}\left(\gamma \right)\mathbf{A}\left(\gamma \right){\parallel }^{2}d\gamma .$$

If $B_{\mathbf{H}}<\infty$, having in mind that ${\parallel \mathit{\alpha }\parallel }_{{\ell }^2\left(G\right)}^2={\parallel \mathbf{A}\parallel }_{L_L^2\left(\widehat{N}\right)}^2={\int }_{\widehat{N}}\parallel \mathbf{A}\left(\gamma \right){\parallel }^{2}d\gamma$, the above equality and the Rayleigh–Ritz theorem ([18], Theorem 4.2.2) prove that ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ is a Bessel sequence for ${\ell }^2\left(G\right)$ with Bessel bound less or equal than $B_{\mathbf{H}}$.

On the other hand, if $K<B_{\mathbf{H}},$ then there exists a set $\mathsf{\Omega }\subset \widehat{N}$ having a strictly positive measure such that ${\lambda }_{max}\left[{\mathbf{H}}^{\ast }\left(\gamma \right)\mathbf{H}\left(\gamma \right)\right]>K$ for $\gamma \in \mathsf{\Omega }$. Consider $\mathit{\alpha }$ such that its associated $\mathbf{A}\left(\gamma \right)$ is 0 if $\gamma \notin \mathsf{\Omega }$, and $\mathbf{A}\left(\gamma \right)$ is a unitary eigenvector corresponding to the largest eigenvalue of ${\mathbf{H}}^{\ast }\left(\gamma \right)\mathbf{H}\left(\gamma \right)$ if $\gamma \in \mathsf{\Omega }$. Thus, we have that

$$\sum _{k=1}^K\sum _{n\in N}|\langle \mathit{\alpha },T_n{\mathrm{f}}_k\rangle {|}^2={\int }_{\widehat{N}}\parallel \mathbf{H}\left(\gamma \right)\mathbf{A}\left(\gamma \right){\parallel }^{2}d\gamma >K{\int }_{\widehat{N}}\parallel \mathbf{A}\left(\gamma \right){\parallel }^{2}d\gamma =K{\parallel \mathit{\alpha }\parallel }_{{\ell }^2\left(G\right)}^2.$$

As a consequence, if $B_{\mathbf{H}}=\infty$, the sequence is not Bessel, and, if $B_{\mathbf{H}}<\infty$, the optimal bound is precisely $B_{\mathbf{H}}$.

Similarly, by using inequality $\parallel \mathbf{H}\left(\gamma \right)\mathbf{A}\left(\gamma \right){\parallel }^2\ge {\lambda }_{min}\left[{\mathbf{H}}^{\ast }\left(\gamma \right)\mathbf{H}\left(\gamma \right)\right]\parallel \mathbf{A}\left(\gamma \right){\parallel }^2$, and that equality holds whenever $\mathbf{A}\left(\gamma \right)$ is a unitary eigenvector corresponding to the smallest eigenvalue of ${\mathbf{H}}^{\ast }\left(\gamma \right)\mathbf{H}\left(\gamma \right);$ one proves the other inequality in part 2. □

Corollary 1.

The sequence ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ is a Bessel sequence for ${\ell }^2\left(G\right)$ if and only if for each $k=1,2,\dots ,K$ and $i=1,2,\dots ,L$ the function ${\widehat{\mathrm{f}}}_{k,h_i}$ belongs to $L^{\infty }\left(\widehat{N}\right)$.

Proof. 

It is a direct consequence of the equivalence between the spectral and Frobenius norms for matrices [18]. □

It is worth mentioning that ${\mathrm{f}}_k$ in ${\ell }^1\left(G\right)$, $k=1,2,\dots ,K$, implies that the sequence ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ is always a Bessel sequence for ${\ell }^2\left(G\right)$ since each function ${\widehat{\mathrm{f}}}_{k,h_i}$ is continuous and $\widehat{N}$ is compact. In this case, the frame condition for ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ reduces to $\mathrm{rank}\mathbf{H}\left(\gamma \right)=L$ for all $\gamma \in \widehat{N}$ or, equivalently,

$$\underset{\gamma \in \widehat{N}}{min}\left(det\left[{\mathbf{H}}^{\ast }\left(\gamma \right)\mathbf{H}\left(\gamma \right)\right]\right)>0.$$

To the second end, a K-channel filter bank formalism allows, in a similar manner, to obtain properties in ${\ell }^2\left(G\right)$ of the sequences ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ and ${\left\{T_n{\mathrm{g}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$. In case they are Bessel sequences for ${\ell }^2\left(G\right)$, the idea is to consider a K-channel filter bank (3) where the analysis filters are ${\mathrm{h}}_k:={\tilde{\mathrm{f}}}_k$ and the synthesis filters are ${\mathrm{g}}_k$, $k=1,2,\dots ,K$. As a consequence, the corresponding polyphase matrices $\mathbf{H}\left(\gamma \right)$ and $\mathit{G}\left(\gamma \right)$, given in Equations (5) and (6), are

$$\mathbf{H}\left(\gamma \right)={\left(\overline{{\widehat{\mathrm{f}}}_{k,h_i}\left(\gamma \right)}\right)}_{\begin{array}{c}k=1,2,\dots ,K\\ i=1,2,\dots ,L\end{array}}\mathrm{and}\mathbf{G}\left(\gamma \right)={\left({\widehat{\mathrm{g}}}_{h_i,k}\left(\gamma \right)\right)}_{\begin{array}{c}i=1,2,\dots ,L\\ k=1,2,\dots ,K\end{array}},\gamma \in \widehat{N}.$$

(11)

Theorem 3.

Let ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ and ${\left\{T_n{\mathrm{g}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ be two Bessel sequences for ${\ell }^2\left(G\right)$, and $\mathbf{H}\left(\gamma \right)$ and $\mathbf{G}\left(\gamma \right)$ their associated matrices (11). Under the above circumstances, we have:

(a) 

The sequences ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ and ${\left\{T_n{\mathrm{g}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ are dual frames for ${\ell }^2\left(G\right)$ if and only if condition $\mathbf{G}\left(\gamma \right)\mathbf{H}\left(\gamma \right)={\mathbf{I}}_L$ a.e. $\gamma \in \widehat{N}$ holds.

(b) 

The sequences ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ and ${\left\{T_n{\mathrm{g}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ are biorthogonal sequences in ${\ell }^2\left(G\right)$ if and only if condition $\mathbf{H}\left(\gamma \right)\mathbf{G}\left(\gamma \right)={\mathbf{I}}_K$ a.e. $\gamma \in \widehat{N}$ holds.

(c) 

The sequences ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ and ${\left\{T_n{\mathrm{g}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ are dual Riesz bases for ${\ell }^2\left(G\right)$ if and only if $K=L$ and $\mathbf{G}\left(\gamma \right)=\mathbf{H}{\left(\gamma \right)}^{-1}$ a.e. $\gamma \in \widehat{N}$.

(d) 

The sequence ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ is an A-tight frame for ${\ell }^2\left(G\right)$ if and only if condition ${\mathbf{H}}^{\ast }\left(\gamma \right)\mathbf{H}\left(\gamma \right)=A{\mathbf{I}}_L$ a.e. $\gamma \in \widehat{N}$ holds.

(e) 

The sequence ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ is an orthonormal basis for ${\ell }^2\left(G\right)$ if and only if $K=L$ and ${\mathbf{H}}^{\ast }\left(\gamma \right)=\mathbf{H}{\left(\gamma \right)}^{-1}$ a.e. $\gamma \in \widehat{N}$.

Proof. 

Having in mind Equation (9) and Corollary 1, part $\left(a\right)$ is nothing but Theorem 1.

The output of the analysis filter bank (3) corresponding to the input ${\mathrm{g}}_{k^{\prime }}$ is a K-vector whose k-entry is

$$c_{k,k^{\prime }}{\left(m\right)=\downarrow }_H({\mathrm{g}}_{k^{\prime }}\ast {\mathrm{h}}_k)\left(m\right)={\langle {\mathrm{g}}_{k^{\prime }},T_m{\tilde{\mathrm{h}}}_k\rangle }_{{\ell }^2\left(G\right)}={\langle {\mathrm{g}}_{k^{\prime }},T_m{\mathrm{f}}_k\rangle }_{{\ell }^2\left(G\right)},$$

and whose N-Fourier transform is ${\mathbf{C}}_{k^{\prime }}\left(\gamma \right)=\mathbf{H}\left(\gamma \right){\mathbf{G}}_{k^{\prime }}\left(\gamma \right)$ a.e. $\gamma \in \widehat{N}$, where ${\mathbf{G}}_{k^{\prime }}$ is the $k^{\prime }$-column of the matrix $\mathbf{G}\left(\gamma \right)$. Note that ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ and ${\left\{T_n{\mathrm{g}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ are biorthogonal if and only if ${\langle {\mathrm{g}}_{k^{\prime }},T_m{\mathrm{f}}_k\rangle }_{{\ell }^2\left(G\right)}=\delta (k-k^{\prime })\delta \left(m\right)$. Therefore, the sequences ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ and ${\left\{T_n{\mathrm{g}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ are biorthogonal if and only if $\mathbf{H}\left(\gamma \right)\mathbf{G}\left(\gamma \right)={\mathbf{I}}_K$. Thus, we have proved $\left(b\right)$.

Having in mind ([15], Theorem 7.1.1), from $\left(a\right)$ and $\left(b\right),$ we obtain $\left(c\right)$.

We can read the frame operator corresponding to the sequence ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$, i.e.,

$$\mathcal{S}\left(\mathit{\alpha }\right)=\sum _{k=1}^K\sum _{n\in N}{\langle \mathit{\alpha },T_n{\mathrm{f}}_k\rangle }_{{\ell }^2\left(G\right)}{T}_n{\mathrm{f}}_k,\mathit{\alpha }\in {\ell }^2\left(G\right),$$

as the output of the filter bank (3), whenever ${\mathrm{h}}_k={\tilde{\mathrm{f}}}_k$ and ${\mathrm{g}}_k={\mathrm{f}}_k$, for the input $\mathit{\alpha }$. For this filter bank, the $(k,h_l)$-entry of the analysis polyphase matrix $\mathbf{H}\left(\gamma \right)$ is $\overline{{\widehat{\mathrm{f}}}_{k,h_l}\left(\gamma \right)}$ and the $(h_l,k)$-entry of the synthesis polyphase matrix $\mathbf{G}\left(\gamma \right)$ is ${\widehat{\mathrm{f}}}_{k,h_l}\left(\gamma \right)$; in other words, $\mathbf{G}\left(\gamma \right)={\mathbf{H}}^{\ast }\left(\gamma \right)$. Hence, the sequence ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ is an A-tight frame for ${\ell }^2\left(G\right)$, i.e.,

$$\mathit{\alpha }=\frac{1}{A}\sum _{k=1}^K\sum _{n\in N}{\langle \mathit{\alpha },T_n{\mathrm{f}}_k\rangle }_{{\ell }^2\left(G\right)}{T}_n{\mathrm{f}}_k,\mathit{\alpha }\in {\ell }^2\left(G\right),$$

if and only if ${\mathbf{H}}^{\ast }\left(\gamma \right)\mathbf{H}\left(\gamma \right)=A{\mathbf{I}}_L$ for all $\gamma \in \widehat{N}$. Thus, we have proved $\left(d\right)$.

Finally, from $\left(c\right)$ and $\left(d\right),$ the sequence ${\left\{T_n{\mathrm{f}}_k\right\}}_{n\in N;k=1,2,\dots ,K}$ is an orthonormal system if and only if ${\mathbf{H}}^{\ast }\left(\gamma \right)=\mathbf{H}{\left(\gamma \right)}^{-1}$ a.e. $\gamma \in \widehat{N}$. □

5. Getting on with Sampling

Suppose that ${\left\{U(n,h)\right\}}_{(n,h)\in G}$ is a unitary representation of the group $G=N{⋊}_{\varphi }H$ on a separable Hilbert space $\mathcal{H}$, and assume that for a fixed $a\in \mathcal{H}$ the sequence ${\left\{U(n,h)a\right\}}_{(n,h)\in G}$ is a Riesz sequence for $\mathcal{H}$ (see Ref. ([1], Theorem A)). Thus, we consider the U-invariant subspace in $\mathcal{H}$

$${\mathcal{A}}_a=\left\{\sum _{(n,h)\in G}\alpha (n,h)U(n,h)a:{\left\{\alpha (n,h)\right\}}_{(n,h)\in G}\in {\ell }^2\left(G\right)\right\}.$$

For K fixed elements $b_k\in \mathcal{H}$, $k=1,2,\dots ,K$, not necessarily in ${\mathcal{A}}_a$, we consider for each $x\in {\mathcal{A}}_a$ its generalized samples defined as

$${\mathcal{L}}_{k}x\left(m\right):={〈x,U(m,1_H)b_k〉}_{\mathcal{H}},m\in N\mathrm{and}k=1,2,\dots ,K.$$

(12)

The task is the stable recovery of any $x\in {\mathcal{A}}_a$ from the data ${\left\{{\mathcal{L}}_{k}x\left(m\right)\right\}}_{m\in N;k=1,2,\dots ,K}$.

In what follows, we propose a solution involving a perfect reconstruction K-channel filter bank. First, we express the samples in a more suitable manner. Namely, for each $x={\sum }_{(n,h)\in G}\alpha (n,h)U(n,h)a$ in ${\mathcal{A}}_a$, we have

$$\begin{array}{cc}\hfill {\mathcal{L}}_{k}x\left(m\right)& =\sum _{(n,h)\in G}\alpha (n,h)〈U(n,h)a,U(m,1_H)b_k〉\hfill \\ & =\sum _{(n,h)\in G}\alpha (n,h)〈a,U\left[{(n,h)}^{-1}·(m,1_H)\right]b_k〉{=\downarrow }_H(\mathit{\alpha }\ast {\mathrm{h}}_k)\left(m\right),m\in N,\hfill \end{array}$$

where $\mathit{\alpha }={\left\{\alpha (n,h)\right\}}_{(n,h)\in G}\in {\ell }^2\left(G\right)$, and ${\mathrm{h}}_k(n,h):={〈a,U(n,h)b_k〉}_{\mathcal{H}}$ also belongs to ${\ell }^2\left(G\right)$ for each $k=1,2,\dots ,K$.

Suppose also that there exists a perfect reconstruction K-channel filter-bank with analysis filters the above ${\mathrm{h}}_k$ and synthesis filters ${\mathrm{g}}_k$, $k=1,2,\dots ,K$, such that the sequences ${\left\{T_n{\tilde{\mathrm{h}}}_k\right\}}_{n\in N;k=1,2,\dots K}$ and ${\left\{T_n{\mathrm{g}}_k\right\}}_{n\in N;k=1,2,\dots K}$ are Bessel sequences for ${\ell }^2\left(G\right)$. Having in mind Equation (9), for each $\mathit{\alpha }={\left\{\alpha (n,h)\right\}}_{(n,h)\in G}$ in ${\ell }^2\left(G\right),$ we have

$$\mathit{\alpha }=\sum _{k=1}^K\sum _{n\in N}{\downarrow }_H(\mathit{\alpha }\ast {\mathrm{h}}_k)\left(n\right)T_n{\mathrm{g}}_k=\sum _{k=1}^K\sum _{n\in N}{\mathcal{L}}_{k}x\left(n\right)T_n{\mathrm{g}}_k\mathrm{in}{\ell }^2\left(G\right).$$

(13)

In order to derive a sampling formula in ${\mathcal{A}}_a$, we consider the natural isomorphism ${\mathcal{T}}_{U,a}:{\ell }^2\left(G\right)\to {\mathcal{A}}_a$ which maps the usual orthonormal basis ${\left\{{\mathit{\delta }}_{(n,h)}\right\}}_{(n,h)\in G}$ for ${\ell }^2\left(G\right)$ onto the Riesz basis ${\left\{U(n,h)a\right\}}_{(n,h)\in G}$ for ${\mathcal{A}}_a$, i.e.,

$${\mathcal{T}}_{U,a}:{\mathit{\delta }}_{(n,h)}⟼U(n,h)a\mathrm{for}\mathrm{each}(n,h)\in G.$$

This isomorphism ${\mathcal{T}}_{U,a}$ possesses the following shifting property:

Lemma 2.

For each $m\in N$, consider the translation operator $T_m$ operator defined in Equation (8). For each $m\in N$, the following shifting property holds

$${\mathcal{T}}_{U,a}\left(T_m\mathrm{f}\right)=U(m,1_H)\left({\mathcal{T}}_{U,a}\mathrm{f}\right),\mathrm{f}\in {\ell }^2\left(G\right).$$

(14)

Proof. 

For each ${\mathit{\delta }}_{(n,h)},$ it is easy to check that $T_m{\mathit{\delta }}_{(n,h)}={\mathit{\delta }}_{(m+n,h)}$. Hence,

$${\mathcal{T}}_{U,a}\left(T_m{\mathit{\delta }}_{(n,h)}\right)=U(m+n,h)a=U(m,1_H)U(n,h)a=U(m,1_H)\left({\mathcal{T}}_{U,a}{\mathit{\delta }}_{(n,h)}\right).$$

A continuity argument proves the result for all $\mathrm{f}$ in ${\ell }^2\left(G\right)$. □

Now, for each $x={\mathcal{T}}_{U,a}\mathit{\alpha }\in {\mathcal{A}}_a$, applying the isomorphism ${\mathcal{T}}_{U,a}$ and the shifting property (14) in Equation (13), we get for each $x\in {\mathcal{A}}_a$ the expansion

$$\begin{array}{cc}\hfill x& =\sum _{k=1}^K\sum _{n\in N}{\mathcal{L}}_{k}x\left(n\right){\mathcal{T}}_{U,a}\left(T_n{\mathrm{g}}_k\right)=\sum _{k=1}^K\sum _{n\in N}{\mathcal{L}}_{k}x\left(n\right)U(n,1_H)\left({\mathcal{T}}_{U,a}{\mathrm{g}}_k\right)\hfill \\ & =\sum _{k=1}^K\sum _{n\in N}{\mathcal{L}}_{k}x\left(n\right)U(n,1_H)c_{k,\mathrm{g}}\mathrm{in}\mathcal{H},\hfill \end{array}$$

(15)

where $c_{k,\mathrm{g}}={\mathcal{T}}_{U,a}{\mathrm{g}}_k$, $k=1,2,\dots ,K$. In fact, the following sampling theorem in the subspace ${\mathcal{A}}_a$ holds:

Theorem 4.

For K fixed $b_k\in \mathcal{H}$, let ${\mathcal{L}}_k:{\mathcal{A}}_a\to {\mathbb{C}}^N$ be its associated U-system defined in Equation (12) with corresponding ${\mathrm{h}}_k\in {\ell }^2\left(G\right)$, $k=1,2,\dots ,K$. Assume that its polyphase matrix $\mathbf{H}\left(\gamma \right)$ given in Equation (5) has all its entries in $L^{\infty }\left(\widehat{N}\right)$. The following statements are equivalent:

1. 

The constant ${\displaystyle A_{\mathbf{H}}=\underset{\gamma \in \widehat{N}}{ess\; inf}{\lambda }_{min}\left[{\mathbf{H}}^{\ast }\left(\gamma \right)\mathbf{H}\left(\gamma \right)\right]>0}$.

2. 

There exist ${\mathrm{g}}_k$ in ${\ell }^2\left(G\right)$, $k=1,2,\dots ,K$, such that the associated polyphase matrix $\mathbf{G}\left(\gamma \right)$ given in (6) has all its entries in $L^{\infty }\left(\widehat{N}\right)$, and it satisfies $\mathbf{G}\left(\gamma \right)\mathbf{H}\left(\gamma \right)={\mathbf{I}}_L$ a.e. $\gamma \in \widehat{N}$.

3. 

There exist K elements $c_k\in {\mathcal{A}}_a$ such that the sequence ${\left\{U(n,1_H)c_k\right\}}_{n\in N;k=1,2,\dots ,K}$ is a frame for ${\mathcal{A}}_a$ and, for each $x\in {\mathcal{A}}_a$, the sampling formula

$$x=\sum _{k=1}^K\sum _{n\in N}{\mathcal{L}}_{k}x\left(n\right)U(n,1_H)c_k\mathrm{in}\mathcal{H}$$

(16)

holds.

4. 

There exists a frame ${\left\{C_{k,n}\right\}}_{n\in N;k=1,2,\dots ,K}$ for ${\mathcal{A}}_a$ such that for each $x\in {\mathcal{A}}_a$ the expansion

$$x=\sum _{k=1}^K\sum _{n\in N}{\mathcal{L}}_{k}x\left(n\right)C_{k,n}\mathrm{in}\mathcal{H}$$

holds.

Proof. 

$\left(1\right)$ implies $\left(2\right)$. The $L\times K$ Moore–Penrose pseudo-inverse ${\mathbf{H}}^{†}\left(\gamma \right)$ of $\mathbf{H}\left(\gamma \right)$ is given by ${\mathbf{H}}^{†}\left(\gamma \right)={\left[{\mathbf{H}}^{\ast }\left(\gamma \right)\mathbf{H}\left(\gamma \right)\right]}^{-1}{\mathbf{H}}^{\ast }\left(\gamma \right)$. Its entries are essentially bounded in $\widehat{N}$ since the entries of $\mathbf{H}\left(\gamma \right)$ belong to $L^{\infty }\left(\widehat{N}\right)$ and ${det}^{-1}\left[{\mathbf{H}}^{\ast }\left(\gamma \right)\mathbf{H}\left(\gamma \right)\right]$ is essentially bounded $\widehat{N}$ since $0<A_{\mathbf{H}}$. In addition, ${\mathbf{H}}^{†}\left(\gamma \right)\mathbf{H}\left(\gamma \right)={\mathbf{I}}_L$ a.e. $\gamma \in \widehat{N}$. The inverse N-Fourier transform in $L^2\left(\widehat{N}\right)$ of the k-th column of ${\mathbf{H}}^{†}\left(\gamma \right)$ gives ${\mathrm{g}}_k$, $k=1,2,\dots ,K$.

$\left(2\right)$ implies $\left(3\right)$. According to Theorems 2 and 3, the sequences ${\left\{T_n{\tilde{\mathrm{h}}}_k\right\}}_{n\in N;k=1,2,\dots K}$ and ${\left\{T_n{\mathrm{g}}_k\right\}}_{n\in N;k=1,2,\dots K}$ form a pair of dual frames for ${\ell }^2\left(G\right)$. We deduce the sampling expansion as in Formula (15). In addition, the sequence ${\left\{U(n,1_H)c_{k,\mathrm{g}}\right\}}_{n\in N;k=1,2,\dots ,K}$ is a frame for ${\mathcal{A}}_a$.

Obviously, $\left(3\right)$ implies $\left(4\right)$. Finally, $\left(4\right)$ implies $\left(1\right)$. Applying ${\mathcal{T}}_{U,a}^{-1},$ we get that the sequences ${\left\{T_n{\tilde{\mathrm{h}}}_k\right\}}_{n\in N;k=1,2,\dots K}$ and ${\left\{{\mathcal{T}}_{U,a}^{-1}\left(C_{k,n}\right)\right\}}_{n\in N;k=1,2,\dots ,K}$ form a pair of dual frames for ${\ell }^2\left(G\right)$; in particular, by using Theorem 2, we obtain that $0<A_{\mathbf{H}}$. □

All the possible solutions of $\mathbf{G}\left(\gamma \right)\mathbf{H}\left(\gamma \right)={\mathbf{I}}_L$ a.e. $\gamma \in \widehat{N}$ with entries in $L^{\infty }\left(\widehat{N}\right)$ are given in terms of the Moore–Penrose pseudo inverse by the $L\times K$ matrices $\mathbf{G}\left(\gamma \right):={\mathbf{H}}^{†}\left(\gamma \right)+\mathit{U}\left(\gamma \right)\left[{\mathbf{I}}_K-\mathbf{H}\left(\gamma \right){\mathbf{H}}^{†}\left(\gamma \right)\right]$, where $\mathit{U}\left(\gamma \right)$ denotes any $L\times K$ matrix with entries in $L^{\infty }\left(\widehat{N}\right)$.

Notice that $K\ge L$ where L is the order of the group H. In case $K=L$, we obtain:

Corollary 2.

In the case $K=L$, assume that its polyphase matrix $\mathbf{H}\left(\gamma \right)$ given in Equation (5) has all entries in $L^{\infty }\left(\widehat{N}\right)$. The following statements are equivalent:

1. 

The constant ${\displaystyle A_{\mathbf{H}}=\underset{\gamma \in \widehat{N}}{ess\; inf}{\lambda }_{min}\left[{\mathbf{H}}^{\ast }\left(\gamma \right)\mathbf{H}\left(\gamma \right)\right]>0}$.

2. 

There exist L unique elements $c_k$, $k=1,2,\dots ,L$, in ${\mathcal{A}}_a$ such that the associated sequence ${\left\{U(n,1_H)c_k\right\}}_{n\in N;k=1,2,\dots ,L}$ is a Riesz basis for ${\mathcal{A}}_a$ and the sampling formula

$$x=\sum _{k=1}^L\sum _{n\in N}{\mathcal{L}}_{k}x\left(n\right)U(n,1_H)c_k\mathrm{in}\mathcal{H}$$

holds for each $x\in {\mathcal{A}}_a$.

Moreover, the interpolation property ${\mathcal{L}}_k{c}_{k^{\prime }}\left(n\right)={\mathit{\delta }}_{k,k^{\prime }}{\mathit{\delta }}_{n,0_N}$, where $n\in N$ and $k,k^{\prime }=1,2,\dots ,L$, holds.

Proof. 

In this case, the square matrix $\mathbf{H}\left(\gamma \right)$ is invertible and the result comes out from Theorem 3. From the uniqueness of the coefficients in a Riesz basis expansion, we get the interpolation property. □

Denote $H=\{h_1,h_2,\dots ,h_L\}$; for a fixed $b\in \mathcal{H}$, we consider the samples

$${\mathcal{L}}_{k}x\left(m\right):=〈x,U(m,h_k)b〉,m\in N\mathrm{and}k=1,2,\dots ,L,$$

of any $x\in {\mathcal{A}}_a$. Since $U(m,h_k)b=U(m,1_H)U(0_N,h_k)b=U(m,1_H)b_k$, where $b_k:=U(0_N,h_k)b$, $k=1,2,\dots ,L$, we are in a particular case of Equation (12) with $K=L$.

Notice also that the subspace ${\mathcal{A}}_a$ can be viewed as the multiple generated U-invariant subspace of $\mathcal{H}$

$$\overline{span}\left\{U(n,1_H)a_h:n\in N,h\in H\right\}$$

with L generators $a_h:=U(0_N,h)a\in \mathcal{H}$, $h\in H$, obtained from $a\in \mathcal{H}$ by the action of the group H.

5.1. An Example Involving Crystallographic Groups

The Euclidean motion group $E\left(d\right)$ is the semi-direct product ${\mathbb{R}}^d{⋊}_{\varphi }O\left(d\right)$ corresponding to the homomorphism $\varphi :O\left(d\right)\to Aut\left({\mathbb{R}}^d\right)$ given by ${\varphi }_A\left(x\right)=Ax$, where $A\in O\left(d\right)$ and $x\in {\mathbb{R}}^d$. The composition law on $E\left(d\right)={\mathbb{R}}^d{⋊}_{\varphi }O\left(d\right)$ reads $(x,A)·(x^{\prime },A^{\prime })=(x+A{x}^{\prime },A{A}^{\prime })$.

Let M be a non-singular $d\times d$ matrix and $\mathsf{\Gamma }$ a finite subgroup of $O\left(d\right)$ of order L such that $A\left(M{\mathbb{Z}}^d\right)=M{\mathbb{Z}}^d$ for each $A\in \mathsf{\Gamma }$. We consider the crystallographic group ${\mathcal{C}}_{M,\mathsf{\Gamma }}:=M{\mathbb{Z}}^d{⋊}_{\varphi }\mathsf{\Gamma }$ and its quasi regular representation (see Ref. [1]) on $L^2\left({\mathbb{R}}^d\right)$

$$U(n,A)f\left(t\right)=f\left[A^{\top }(t-n)\right],n\in M{\mathbb{Z}}^d,A\in \mathsf{\Gamma }\mathrm{and}f\in L^2\left({\mathbb{R}}^d\right).$$

For a fixed $\phi \in L^2\left({\mathbb{R}}^d\right)$ such that the sequence ${\left\{U(n,A)\phi \right\}}_{(n,A)\in {\mathcal{C}}_{M,\mathsf{\Gamma }}}$ is a Riesz sequence for $L^2\left({\mathbb{R}}^d\right)$ (see, for instance, Refs. [19,20]) we consider the U-invariant subspace in $L^2\left({\mathbb{R}}^d\right)$

$$\begin{array}{cc}\hfill {\mathcal{A}}_{\phi }& =\left\{\sum _{(n,A)\in {\mathcal{C}}_{M,\mathsf{\Gamma }}}\alpha (n,A)\phi \left[A^{\top }(t-n)\right]:\left\{\alpha (n,A)\right\}\in {\ell }^2\left({\mathcal{C}}_{M,\mathsf{\Gamma }}\right)\right\}\hfill \\ & =\left\{\sum _{(n,A)\in {\mathcal{C}}_{M,\mathsf{\Gamma }}}\alpha (n,A)\phi (At-n):\left\{\alpha (n,A)\right\}\in {\ell }^2\left({\mathcal{C}}_{M,\mathsf{\Gamma }}\right)\right\}.\hfill \end{array}$$

Choosing K functions $b_k\in L^2\left({\mathbb{R}}^d\right)$, $k=1,2,\dots ,K$, we consider the average samples of $f\in {\mathcal{A}}_{\phi }$

$${\mathcal{L}}_{k}f\left(n\right)=\langle f,U(n,I)b_k\rangle =\langle f,b_k(·-n)\rangle ,n\in M{\mathbb{Z}}^d.$$

Under the hypotheses in Theorem 4, there exist $K\ge L$ sampling functions ${\psi }_k\in {\mathcal{A}}_{\phi }$ for $k=1,2,\dots ,K$, such that the sequence ${\left\{{\psi }_k(·-n)\right\}}_{n\in M{\mathbb{Z}}^d;k=1,2,\dots ,K}$ is a frame for ${\mathcal{A}}_{\phi }$, and the sampling expansion

$$f\left(t\right)=\sum _{k=1}^K\sum _{n\in M{\mathbb{Z}}^d}{〈f,b_k(·-n)〉}_{L^2\left({\mathbb{R}}^d\right)}{\psi }_k(t-n)\mathrm{in}{L}^2\left({\mathbb{R}}^d\right)$$

(17)

holds.

If the generator $\phi \in C\left({\mathbb{R}}^d\right)$ and the function $t\mapsto {\sum }_n{\left|\phi (t-n)\right|}^2$ is bounded on ${\mathbb{R}}^d$, a standard argument shows that ${\mathcal{A}}_{\phi }$ is a reproducing kernel Hilbert space (RKHS) of bounded continuous functions in $L^2\left({\mathbb{R}}^d\right)$. As a consequence, convergence in $L^2\left({\mathbb{R}}^d\right)$-norm implies pointwise convergence which is absolute and uniform on ${\mathbb{R}}^d$.

Notice that the infinite dihedral group $D_{\infty }=\mathbb{Z}{⋊}_{\varphi }{\mathbb{Z}}_2$ is a particular crystallographic group with lattice $\mathbb{Z}$ and $\mathsf{\Gamma }={\mathbb{Z}}_2$. Its quasi regular representation on $L^2\left(\mathbb{R}\right)$ reads

$$U(n,0)f\left(t\right)=f(t-n)\mathrm{and}U(n,1)f\left(t\right)=f(-t+n),n\in \mathbb{Z}\mathrm{and}f\in L^2\left(\mathbb{R}\right).$$

Thus, we could obtain sampling formulas as (17) for $K\ge 2$ average functions $b_k$.

The quasi regular unitary representation of a crystallographic group ${\mathcal{C}}_{M,\mathsf{\Gamma }}$ on $L^2\left({\mathbb{R}}^d\right)$ motivates the next section:

5.2. The Case of Pointwise Samples

Let ${\left\{U(n,h)\right\}}_{(n,h)\in G}$ be a unitary representation of the group $G=N{⋊}_{\varphi }H$ on the Hilbert space $\mathcal{H}=L^2\left({\mathbb{R}}^d\right)$. If the generator $\phi \in L^2\left({\mathbb{R}}^d\right)$ satisfies that, for each $(n,h)\in G$, the function $U(n,h)\phi$ is continuous on ${\mathbb{R}}^d$, and the condition

$$\underset{t\in {\mathbb{R}}^d}{sup}\sum _{(n,h)\in G}|\left[U(n,h)\phi \right]\left(t\right){|}^2<\infty ,$$

then the subspace ${\mathcal{A}}_{\phi }$ is an RKHS of bounded continuous functions in $L^2\left({\mathbb{R}}^d\right)$; proceeding as in [21], one can prove that the above conditions are also necessary.

For K fixed points $t_k\in {\mathbb{R}}^d$, $k=1,2,\dots ,K$, we consider for each $f\in {\mathcal{A}}_{\phi }$ the new samples given by

$${\mathcal{L}}_{k}f\left(n\right):=\left[U(-n,1_H)f\right]\left(t_k\right),n\in N\mathrm{and}k=1,2,\dots ,K.$$

(18)

For each $f={\sum }_{(m,h)\in G}\alpha (m,h)U(m,h)\phi$ in ${\mathcal{A}}_{\phi }$ and $k=1,2,\dots ,K$, we have

$$\begin{array}{cc}\hfill {\mathcal{L}}_{k}f\left(n\right)& =\left[\sum _{(m,h)\in G}\alpha (m,h)U[(-n,1_H)·(m,h)]\phi \right]\left(t_k\right)\hfill \\ & =\sum _{(m,h)\in G}\alpha (m,h)\left[U(m-n,h)\phi \right]\left(t_k\right)={〈\mathit{\alpha },T_n{\mathrm{f}}_k〉}_{{\ell }^2\left(G\right)},n\in N,\hfill \end{array}$$

where $\mathit{\alpha }={\left\{\alpha (m,h)\right\}}_{(m,h)\in G}$ and ${\mathrm{f}}_k(m,h):=\overline{\left[U(m,h)\phi \right]\left(t_k\right)}$, $(m,h)\in G$. Notice that ${\mathrm{f}}_k$ belongs to ${\ell }^2\left(G\right)$, $k=1,2,\dots ,K$. As a consequence, under the hypotheses in Theorem 4 (on these new ${\mathrm{h}}_k:={\tilde{\mathrm{f}}}_k$, $k=1,2,\dots ,K$), a sampling formula such as (16) holds for the data sequence ${\left\{{\mathcal{L}}_{k}f\left(n\right)\right\}}_{n\in N;k=1,2,\dots ,K}$ defined in Equation (18).

In the particular case of the quasi regular representation of a crystallographic group ${\mathcal{C}}_{M,\mathsf{\Gamma }}=M{\mathbb{Z}}^d{⋊}_{\varphi }\mathsf{\Gamma }$, for each $f\in {\mathcal{A}}_{\phi }$, the samples (18) read

$${\mathcal{L}}_{k}f\left(n\right)=\left[U(-n,I)f\right]\left(t_k\right)=f(t_k+n),n\in M{\mathbb{Z}}^d\mathrm{and}k=1,2,\dots ,K.$$

Thus (under hypotheses in Theorem 4), there exist K functions ${\psi }_k\in {\mathcal{A}}_{\phi }$, $k=1,2,\dots ,K$, such that for each $f\in {\mathcal{A}}_{\phi }$ the sampling formula

$$f\left(t\right)=\sum _{k=1}^K\sum _{n\in M{\mathbb{Z}}^d}f(t_k+n){\psi }_k(t-n),t\in {\mathbb{R}}^d$$

holds. The convergence of the series in the $L^2\left({\mathbb{R}}^d\right)$-norm sense implies pointwise convergence which is absolute and uniform on ${\mathbb{R}}^d$.

6. Conclusions

In this paper, we have derived an abstract regular sampling theory associated with a unitary representation $(n,h)\mapsto U(n,h)$ of a group G which is a semi-direct product of two groups, N countable discrete abelian group and H finite, on a separable Hilbert space $\mathcal{H}$; here, regular sampling means that we are taken the samples at the group N. Concretely, the sampling theory is obtained in the U-invariant subspace of $\mathcal{H}$ generated by $a\in \mathcal{H}$ that is

$${\mathcal{A}}_a=\left\{\sum _{(n,h)\in G}\alpha (n,h)U(n,h)a:{\left\{\alpha (n,h)\right\}}_{(n,h)\in G}\in {\ell }^2\left(G\right)\right\},$$

and the samples of $x\in {\mathcal{A}}_a$ are given by ${\mathcal{L}}_{k}x\left(n\right):={〈x,U(n,1_H)b_k〉}_{\mathcal{H}}$, $n\in N$, where $b_k$, $k=1,2,\dots ,K$, denote K fixed elements in $\mathcal{H}$ which do not belong necessarily to ${\mathcal{A}}_a$. We look for K elements $c_k\in {\mathcal{A}}_a$ such that the sequence ${\left\{U(n,1_H)c_k\right\}}_{n\in N;k=1,2,\dots ,K}$ is a frame for ${\mathcal{A}}_a$ and, for each $x\in {\mathcal{A}}_a$, the sampling formula $x={\sum }_{k=1}^K{\sum }_{n\in N}{\mathcal{L}}_{k}x\left(n\right)U(n,1_H)c_k$ holds.

A similar problem was solved when the group G is a discrete LCA group and the samples are taken at a uniform lattice of G (see Ref. [10]). In the case of an abelian group, we have the Fourier transform, a basic tool in this previous work. In the present work, a classical Fourier analysis on G is not available, but if G is a semi-direct product of the form $G=N{⋊}_{\varphi }H$, where N is a countable discrete abelian group and H is a finite group, the Fourier transform on the abelian group N allows us to solve the problem by means of a filter bank formalism. Recalling the filter bank formalism in discrete LCA groups, the defined samples are expressed as the output of a suitable K-channel analysis filter bank corresponding to the input $x\in {\mathcal{A}}_a$. The frame analysis of this filter bank along with the synthesis one giving perfect reconstruction allows us to obtain a pair of suitable dual frames for obtaining the desired sampling result, which is written as a list of equivalent statements (see Theorem 4).

Although the semi-direct product of groups represents, so to speak, the simplest case of non-abelian groups, this paper can be a good starting point for finding sampling theorems associated with unitary representations of non abelian groups that are not isomorphic to a semi-direct product of groups.