Abstract
Persisting tensions between high-redshift and low-redshift cosmological observations suggest the dark energy sector of the Universe might be more complex than the positive cosmological constant of the CDM model. Motivated by string theory, wherein symmetry considerations make consistent AdS backgrounds (i.e., maximally-symmetric spacetimes with a negative cosmological constant) ubiquitous, we explore a scenario where the dark energy sector consists of two components: a negative cosmological constant, with a dark energy component with equation of state on top. We test the consistency of the model against low-redshift baryon acoustic oscillation and Type Ia supernovae distance measurements, assessing two alternative choices of distance anchors: the sound horizon at baryon drag determined by the Planck collaboration and the Hubble constant determined by the SH0ES program. We find no evidence for a negative cosmological constant and mild indications for an effective phantom dark energy component on top. A model comparison analysis reveals that the CDM model is favoured over our negative cosmological constant model. While our results are inconclusive, should low-redshift tensions persist with future data, it would be worth reconsidering and further refining our toy negative cosmological constant model by considering realistic string constructions.
1. Introduction
While extremely successful at describing a wide variety of high- and low-redshift observations [1,2,3,4,5], the CDM model has recently begun to display a number of small cracks [6,7]. One of the most tantalizing among these crevices is the so-called “ tension”, referring to the discrepancy between two independent estimates of the Hubble constant . The first is a local estimate from the Hubble Space Telescope (HST), based on a distance ladder approach using Cepheids variables in the hosts of Type Ia Supernovae (SNeIa), yielding [8]. The second is an indirect estimate based on Cosmic Microwave Background (CMB) temperature and polarization anisotropies measurements from the Planck collaboration: assuming an underlying CDM model, a value of [5] is obtained. Besides this cosmological tension, the CDM model also suffers from a number of astrophysical shortcomings at small (galactic or subgalactic) scales, mostly referring to mismatches between simulations of cold dark matter and observations. Such issues include the core-cusp problem [9], the missing satellites problem [10] (although, see for example [11,12]), and the too-big-to-fail problem [13]. See for instance [14,15,16] for recent reviews on the subject. It has been speculated that such issues might signal the need to move away from the collisionless cold dark matter paradigm, and in particular that allowing for interactions between dark matter particles, or between dark matter and baryons, could alleviate these issues (see, e.g., [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31] for an incomplete list of proposed models).
The statistical significance of the tension, currently at a level , has steadily grown over recent years, owing also to improvements in the distance ladder approach [32,33,34,35]. Additional (re)analyses of the local distance ladder [36,37,38,39,40,41,42,43,44,45,46], as well as independent estimates of from strong-lensing time delays [47,48,49] have independently supported the conclusion that local measurements favour a higher value of [8] (see, however, the study in [50]). Given that the Planck estimate of relies on the assumption of an underlying CDM model, it is possible that the tension might be hinting towards new physics, possibly involving non-standard properties of dark matter or dark energy [51,52,53,54]. The task is not easy to accomplish, since the simplest single-field quintessence models cannot solve the tension [55,56], even when a late-time transition from a matter-like Equation of State (EoS) is considered [57]. For an incomplete list of works in this direction, see [55,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141].
Measurements of temperature and polarization anisotropies in the CMB exquisitely constrain , the angular scale of the sound horizon at last-scattering:
where is the redshift of last-scattering, is the redshift of the drag epoch (when baryons are released from the Compton drag of photons), is the comoving sound horizon at redshift , and is the angular diameter distance to redshift . Attempts to address the tension by introducing new physics generally modify either or both and , in such a way that an increase in is required in order to keep fixed. One of the simplest possibilities is to modify the Dark Energy (DE) sector in order to lower the expansion rate at late times, while leaving the early-time expansion rate unaltered. Such a change will keep unchanged, but will raise . In order to keep fixed, a higher value of will be inferred.
One of the simplest modifications to the DE sector that could be considered consists of replacing the positive cosmological constant (whose equation of state is ) with a quintessence field with a time-varying EoS. A single minimally-coupled quintessence field with a standard kinetic term possesses a positive energy density with an equation of state ; it is easy to show that, in this case, the expansion rate actually increases at late times, going in the opposite direction of what is required to address the tension [55]. In fact, insisting on a positive energy density for the DE component brings one to consider phantom DE, i.e., a DE component with equation of state . Phantom DE components, which generically predict the Universe to end in a Big Rip [142] (although this fate can be avoided in certain classes of modified gravity theories [143,144,145,146,147]), are however generically extremely challenging to construct, due to the violation of the strong energy condition. Nonetheless, attempts to realize effectively stable phantom DE components (for instance within modified gravity or brane-world models) exist; see, e.g., [148,149,150,151,152,153,154,155,156,157,158,159,160,161,162].
The situation changes if one chooses not to restrict to the DE energy density being positive. Recent work has in fact shown that a number of persisting low-redshift tensions (including the tension) might be addressed if one allows for an evolving DE component whose energy density can assume negative values (see, e.g., [53,93,163,164,165]). In particular, the work in [165] considered a very interesting case, where the DE sector consists of a slowly-rolling quintessence field (whose energy density is positive) on top of a negative cosmological constant. Such a scenario is extremely interesting from a string theory perspective. In fact, constructing meta-stable de Sitter (dS) vacua (i.e., with a positive cosmological constant) has notoriously been a daunting task in string theory (see, e.g., [166,167,168,169,170,171,172,173,174,175]). These difficulties have led to the suggestion that string theory might not have any dS vacua at all [176,177,178,179,180], an observation that, if correct, would have interesting consequences for cosmology [181,182,183,184,185,186,187,188,189,190] (see, however, also the important work of [191], which appears to provide a possible counterexample to these swampland conjectures). In contrast, a negative cosmological constant (providing an AdS background, i.e., a maximally-symmetric spacetime with a negative cosmological constant) is very natural from symmetry considerations in string theory, as can be argued using the AdS/CFTcorrespondence [192]. Contrary to the case of dS, there does seem to exist a large number of consistent AdS backgrounds that can be obtained from string theory (it has even been suggested that AdS vacua can lead to an accelerating Universe [193]).
Another rather generic prediction of string theory is the plethora of light bosons known as the “axiverse”. These correspond to moduli determining the size and shape of the extra dimensions and could give rise to important observable consequences that might alter the evolution of the Universe between recombination and today [194,195,196,197,198,199,200,201,202,203,204,205,206,207,208]. It is therefore interesting to try matching cosmological data using quintessence (possibly with an effective phantom equation of state, given that one is anyhow not dealing with a single quintessence field) in combination with a negative cosmological constant, both of which are natural from the point of view of string theory. This is an important motivation for our paper.
At any rate, determining the sign of a possible cosmological constant is crucial in order to understand the structure and fabric of space-time itself. In this work, we revisit the possibility that a negative cosmological constant might be allowed by current cosmological data, and more generally explore whether the tension might be relaxed within such a scenario. We first consider the standard CDM model (featuring a positive cosmological constant with equation of state ). We then move on to one of the simplest extension of the CDM model, i.e., the CDM model, wherein the DE EoS is treated as a free parameter. Finally, we consider a scenario in which the present accelerated expansion rate is driven by a combination of a cosmological constant whose density parameter is strictly negative, on top of which we allow for a second DE component with EoS (which can take on values ) and a positive density parameter . While the case for a negative cosmological constant is clearly inspired by a string scenario, the present accelerated expansion rate requires that . We refer to this last model as CDM. Notice that the requirement , necessary in order for the Universe to accelerate, prevents us from considering a model where the dark energy sector consists solely of a negative cosmological constant, without the quintessence field on top.
In this work, we perform a Markov Chain Monte Carlo (MCMC) analysis to compare the three models (in order of increasing complexity CDM, CDM, and CDM) in light of recent low-redshift () distance measurements from a selection of Baryon Acoustic Oscillation (BAO) surveys [3,209,210,211,212,213] and Type Ia Supernovae (SNeIa) from the Pantheon catalogue [214]. The interpretation of BAO measurements requires “anchoring” them to either the cosmic distance ladder through independent measurements of , or to the inverse distance ladder through independent measurements of , the sound horizon at baryon drag [51]. To show the impact of the tension, we choose two different anchors to interpret our BAO data: we first use the local distance ladder measurement of from the “Supernovae and for the Dark Energy Equation of State” (SH0ES) program [8], before comparing our results to those obtained anchoring to the most recent measurement of from the Planck collaboration [5]. More details on the datasets chosen and the choice of anchoring are given in Section 2.
Our treatment of the effective DE component on top of the negative cosmological constant is purely phenomenological, and we remain agnostic as to the underlying Lagrangian for such a component (see, e.g., [215,216] for early works discussing a fundamental origin for this type of composite dark energy). While we envisage such a component being a quintessence field slowly rolling along a potential on top of the negative cosmological constant, we allow the effective equation of state to enter the phantom regime, where . The rationale is that string constructions generically predict a large number of light bosons on top of the stable AdS vacua: therefore, one can in general be faced with a multi-field quintessence scenario, whose effective behaviour might be phantom (see, e.g., [217,218,219,220,221]) (other possibilities for obtaining an effective phantom component from an underlying scalar field model involve considering modifications to gravity [222,223,224,225,226,227,228,229,230,231], couplings between dark energy and dark matter [232,233,234,235,236,237,238,239,240,241,242,243,244,245,246], particle creation mechanisms [247,248,249,250,251,252,253,254,255,256], or invoking scalar fields non-minimally coupled to gravity or with a kinetic term that is non-canonical [257,258,259,260,261]). In the CDM model, the quintessence field (whose effective EoS we allow to be phantom, again from a purely effective perspective) is treated as an additional contribution to the total energy density along with the (possibly negative) cosmological constant and the usual components of matter and radiation. Our results are interesting from a model-building perspective, as we find that from the low-redshift data side, a negative cosmological constant is a valid alternative to a phantom dark energy component.
The rest of the paper is then organized as follows. In Section 2, we describe the datasets we use. In Section 3, we describe in detail the models considered along with their parameter spaces. The MCMC analysis performed in order to constrain the models, as well as the obtained results are described in Section 4. We provide concluding remarks in Section 5.
2. Overview of the Datasets Used
The evolution of the Hubble expansion rate on the redshift , , is usually factored out as , where is the Hubble constant and the normalized expansion rate is a dimensionless function describing the evolution of the expansion rate with the redshift. Let us introduce the angular diameter distance to redshift , , given by the following:
The angular diameter distance in Equation (2) is related to the comoving angular diameter distance to redshift , , by . Let us further define the sound horizon at redshift , , as the distance travelled by an acoustic wave in the baryon-photon plasma from a very early time, given by:
where is the sound speed of the baryon-photon plasma at redshift .
We consider two classes of observational datasets. A first class consists of distance measurements from Baryon Baryon Acoustic Oscillations (BAO) surveys, as well as from Type Ia Supernovae (SNeIa). A second class consists of two different types of anchors used to interpret the BAO measurements. Specifically, we consider two different anchors: direct measurements of the Hubble constant based on the local Cepheids-Supernovae distance ladder and CMB measurements of the comoving sound horizon at baryon drag, further defined in Equation (4) below. We describe these four datasets in more detail below
- BAO: In the early Universe, the interplay between gravity and radiation pressure sets up acoustic oscillations, which produce a sharp feature in the two-point correlation function of luminous matter at a scale equal to the comoving size of the sound horizon at the drag epoch [262,263,264,265,266]:where the drag epoch is the time when the baryons are released from the Compton drag of the photons, and occurs at a redshift . Measurements of the BAO feature, first reported in [265,267], are usually performed at an effective redshift . These measurements can in principle independently constrain the angular diameter distance in units of (for modes in the transverse direction with respect to the line of sight) and (for modes along the line of sight), whereas isotropic BAO measurements constrain a combination of these quantities known as the volume distance . Here, we consider various types of BAO measurements, which constrain the following quantities:See Appendix B of [268] for a more detailed discussion of BAO measurements.In our analysis, we consider anisotropic BAO measurements from the Baryon Oscillation Spectroscopic Survey (BOSS) collaboration [3] Data Release 12 (DR12) at the effective redshifts and from Lyman- forest samples at [211,212]. We also include isotropic BAO measurements from the Six-degree Field Galaxy Survey (6dFGS) at [209], from the Sloan Digital Sky Survey Data (SDSS) Main Galaxy Sample (MGS) release at [210] and from the quasar sample of the extended Baryon Oscillation Spectroscopic Survey (eBOSS) at [213]. For completeness, we collect the BAO measurements used in this work in Table 1. We constructed the likelihood for the BAO data, , using the data described and the correlation matrices provided by the collaborations.
 Table 1. BAO scale measurements used in this work. For BOSS DR12, we set the fiducial scale Mpc [3].
Table 1. BAO scale measurements used in this work. For BOSS DR12, we set the fiducial scale Mpc [3]. - SNeIa: SNeIa catalogues report the corrected apparent magnitude of the supernova, which is given by the following:where is the absolute magnitude of the supernova, which fixes the scale for the global fit. For practical purposes, we rewrite the relation as:where the absolute magnitude has been reabsorbed into a parameter Mpc, which we fit to data. We construct the likelihood:where the vector of apparent magnitude measurements and the corresponding covariance matrix are taken from the Pantheon SNeIA dataset [214]. This catalogue provides luminosity distances for 1048 SNeIa within the range of Type 1a supernovae. Although the Pantheon analysis is marginally model-dependent, as biases in light-curve parameters are corrected assuming a CDM cosmology, independent analyses run using the JLA SN dataset [269] have found that the model-dependence of the light-curve parameters is weak.
- Anchors: The cosmic distance ladder technique relies on measuring distances of extra-galactic objects, at distances beyond 100 Mpc, to map the Hubble flow. The expansion history of the Universe is mapped through Type 1a Supernovae (SNeIa) datasets [214,269,270,271,272,273,274,275] and BAO [265,267]. These distance scales need to be calibrated through anchors either at the high-redshift end (through ) or at the low-redshift end (through ) [276].For instance, BAO measurements constrain the combination . In fact, the tension between measurements at low and high redshifts of can be eased by modifying the value of , which is the standard ruler providing the BAO length scale. The sole measurements of either or are respectively interpreted as anchoring the cosmic distance ladder or the inverse cosmic distance ladder. In any case, in order to interpret the BAO measurements, we have to anchor either or to an independent evaluation [51]. Here, we consider independent approaches, namely calibrating the cosmic distance ladder by means of the recent measurements of in [8] or calibrating the inverse distance ladder by using the CMB measurement of in [5]. It is worth remarking that much (but not all) of the information contained in the CMB temperature and anisotropy spectra resides in the position and height of the first acoustic peak, which accurately constrains given in Equation (1) and provides valuable information about the geometry and the content of the Universe. The position of the first peak is sensitive to early-time modifications through a change in , as well as to late-time modifications through a change in .Here, we consider two scenarios using two different anchors, given by the following:
- Sound horizon at drag epoch (Scenario I): The anchor at the CMB epoch is expressed by the comoving sound horizon at the end of the baryon drag epoch . Measurements of CMB temperature and polarization anisotropies by the Planck collaboration (PlanckTTTEEE + lowP dataset) give Mpc at a 68% Confidence Level (C.L.). When anchoring data to the sound horizon , we construct the likelihood function as a Gaussian in using this measurement.
- Hubble constant (Scenario II): When anchoring data to the present value of the Hubble rate, we use the latest result from the SH0ES program [8], which reports the local measurement . This measurement is used to construct the likelihood function as a Gaussian in .
Since one of our main interests is to compare the results obtained using different anchors, we have not used other available datasets such as direct determinations of the Hubble rate at redshifts [277,278] or “compressed” CMB likelihoods [228,279,280]. For the ease of comparison to related works, we chose to restrict our use of low-redshift data solely to BAO and SNe data, which are the two most robust low-redshift datasets widely used by the community. We did not include other late-time measurements of the expansion history, such as cosmic chronometers or distance measurements from Gamma-ray bursts. However, it would be interesting to further include these datasets, which could perhaps improve our constraints on possible negative cosmological constants, and we leave this exercise for future work.
3. Overview of Models and Model Comparison
As described in the Introduction, we consider three models with increasing level of complexity to fit the data. For each model, represents the energy density in the species , , where is the reduced Planck mass, and we introduce the density parameter . The present energy density in radiation is obtained from the CMB temperature measured from the four-Year COBE-DMR CMB mission [281] as K at 95% C.L. The fractional energy density in neutrinos assumes three active neutrinos of which two are massless and the third has a mass eV, as done in the baseline Planck analyses. The value is the minimal neutrino mass sum allowed within the normal ordering [282], which is mildly favoured by current data [283,284,285,286]. Leaving the neutrino mass as a free parameter would not change our analysis substantially, given the current very tight upper limits on the sum of the neutrino masses [5,283,287,288,289,290,291,292,293]. We refer to the combination of invisible components as . We treat baryons and CDM equivalently, both contributing to a total energy share . The remaining parameters are model-dependent and are discussed in the following.
- CDM model: Here, the normalized expansion rate is modelled as follows:We fix the value of by demanding that , so that the parameter space associated with this model is four-dimensional.
- CDM model: Here, the normalized expansion rate is modelled as follows:where is a constant. We fix the value of by demanding that , so that the parameter space associated with this model is five-dimensional. Note that we allow to enter the phantom regime, where , since we are not restricting our attention to the case where the dark energy component is described by a single minimally-coupled quintessence field with a canonical kinetic term.
- CDM model: Here, the normalized expansion rate is modelled as follows:We fix the value of by demanding that , so that the parameter space associated with this model is six-dimensional. We demand that be strictly negative by exploring the region of the parameter space when fitting the parameters in against the data described in Section 2.
To sample the posterior distribution of the parameters, we perform a Markov Chain Monte Carlo (MCMC) analysis using the open-source Python package emcee [294]. For each model described in Section 3, we explore the associated parameter space by performing the analysis with a Metropolis–Hastings algorithm and assuming flat priors for all variables, except for the anchor for which we assume a Gaussian prior with mean and standard deviation given by the corresponding measurement. In more detail, we assume a flat prior for and Mpc for all models discussed, in addition to the DE EoS for the CDM and CDM models and the cosmological constant for the CDM model. When anchoring the distance ladder to the comoving sound horizon at the drag epoch (Scenario I), we choose the flat prior km/s/Mpc and a Gaussian prior for based on the measurement by the Planck collaboration. When the present Hubble rate is used as the anchor (Scenario II), we choose the flat prior Mpc and a Gaussian prior for given by the SH0eS measurements [8]. We use the expression for the likelihood:
It is worth noting that the CDM and CDM models are nested models, i.e., the former is a particular case of the latter, recovered when setting . As such, we expect that the fit to data (quantified, e.g., through the ) should not worsen when moving from the CDM to the CDM model. However, the same is not true for the CDM model. In fact, within the CDM model, we require , i.e., that the cosmological constant be strictly negative. Therefore, it is not possible to recover either the CDM or the CDM model as a particular limit of CDM. As a result, the fit to data will not necessarily improve when considering a negative cosmological constant.
At any rate, given that the CDM and CDM models possess respectively one and two extra parameters compared to the baseline CDM model, it is important to assess whether the increased model complexity is warranted by a substantially better fit (if any) to the data. We performed a simple model comparison adopting the Akaike Information Criterion (AIC) to compare the competing models. The AIC of a given model is defined as [295]:
where is the number of parameters of the model and is the calculated at the best-fit point of the model. Therefore, for the CDM, CDM, and CDM models, respectively.
Assume we have two competing models and , with AIC values and , respectively, and assume that . Then, model is to be preferred since it has a lower AIC. From Equation (15), we see that one needs an improvement in the fit of at least in order to justify the increased number of parameters (for instance, when moving from CDM to CDM or when moving to CDM). Moreover, the quantity gives the relative likelihood of model with respect to model .
4. Results
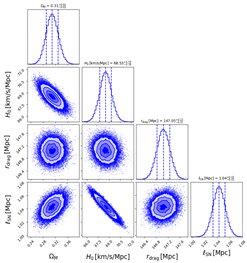
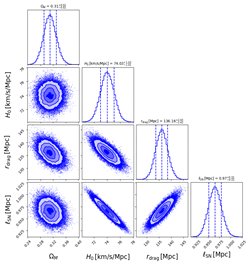
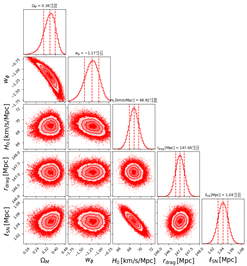
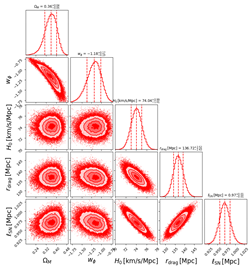
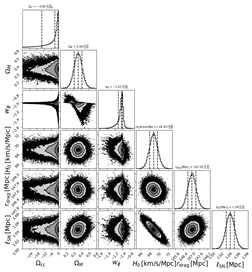
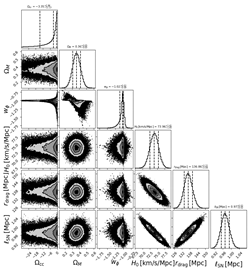
We now discuss the results obtained analysing the datasets described in Section 2 within the context of the three models described in Section 3, which we then compare using the AIC described in the same section. In Table 2, we show corner plots visualizing the 1D marginalized and 2D joint posterior distributions for the parameters of the models considered: CDM model (upper panels), CDM (middle panels), and CDM model (lower panels), anchoring the BAO measurements either to as measured by Planck (left column) or to as measured by SH0ES (right column). Constraints on the parameters of the three models are also presented in Table 3.

Table 2.
Left column: corner plots showing the 1D marginalized and 2D joint posterior distributions for the parameters of the CDM (top panel), CDM (middle panel), and CDM models (bottom panel), when anchoring BAO measurements to as measured Planck [5]. Right column: same as the left column, but anchoring BAO measurements to as measured by the SH0ES program [8].

Table 3.
Constraints on the parameters of the three models considered in this work, obtained using the two different choices of anchor (specified in the first column). We report 68% C.L. intervals on all parameters, except for , for which we do not have a detection, and hence report the 95% C.L. lower bound. The last column reports , defined in Equation (15) and calculated with respect to the CDM model. A positive value of indicates a preference for CDM.
As we see from Table 3, our analysis did not reveal any evidence for a non-zero negative cosmological constant. In fact, when analysing our datasets within the CDM model, we only obtained a lower limit of regardless of whether we used as measured by Planck or as measured by SH0ES as the anchor. Moreover, within both the CDM and CDM models, we saw a preference for a phantom DE component (), indicating that data preferred a late-time expansion rate lower than the one obtained when DE was entirely in the form of a (positive) cosmological constant. We also saw that when moving from the CDM model to the CDM model, the central value of , although still phantom, moved upwards towards . The reason is that, as discussed in Section 1, introducing a negative cosmological constant lowers the expansion rate even more drastically than when considering a phantom DE component, lessening the need for the latter and explaining why moves towards .
It is also worth noting that within the CDM and CDM model, we infer a higher matter density than within CDM (although with uncertainty about twice as large). The reason is again that a phantom dark energy component (with the addition of a negative cosmological constant) lowers the expansion rate at late times, which can be compensated by increasing the matter density. This result is analogous to the one found in [55], where it was shown that in models with , one infers a lower matter density, because the late-time expansion rate in this case is higher, leaving less room for matter components.
We also notice that when anchoring BAO measurements to as measured by Planck, we recovered a value of , which is essentially for all three models, which indicates that the CDM model was not able to alleviate the tension. Finally, we note that anchoring BAO measurements to as measured by SH0ES, we inferred a value for that was about lower than that obtained when anchoring to as measured by Planck, in full agreement with earlier results [51,108,296].
One further interesting point worth noting from Table 3 is that the values we inferred for certain parameters (such as , , , and ) were essentially the same across different models (particularly for the CDM and CDM models) and for different choices of anchors. One particularly striking case, for example, is , for which we basically inferred for both the CDM and CDM models, regardless of the choice of anchor. On the other hand, for the CDM model, we inferred . This is consistent with the fact that we did not have a detection of a non-zero negative cosmological constant, and therefore, from the point of view of the data we used, there was not much difference between the CDM and CDM models. On the other hand, parameters such as were extremely well determined by BAO data, independent of the choice of anchor. Similar considerations hold for the other parameters whose values inferred within the CDM and CDM models were very similar to one another regardless of the choice of anchor.
We now compare the three models using the Akaike information criterion introduced in Section 3, beginning with the case when BAO measurements are anchored to . In this case, we found minimal improvements in the best-fit when moving away from the CDM model. In particular, we found and for the CDM and CDM models, respectively. According to Equation (15), these values correspond to and for the CDM and CDM models, respectively. In both cases , indicating that the tiny improvement in fit did not warrant the addition of extra parameters (one extra parameter and two extra parameters for CDM and CDM, respectively) and, therefore, that the baseline CDM model was preferred from a statistical point of view. In fact, we found that the relative likelihoods of the CDM and CDM models over CDM were 0.38 and 0.16, respectively.
We found completely analogous, if not less optimistic results, when anchoring BAO measurements to . In this case, we found and for the CDM and CDM models, respectively. We saw that within the CDM model, the quality of the fit had actually worsened. According to Equation (15), these values corresponded to and for the CDM and CDM models, respectively. Again, in both cases, , with relative likelihoods for the CDM and CDM models over the CDM model being 0.52 and 0.09, respectively.
5. Conclusions
In this work, we revisited the possibility that the dark energy sector might feature two components: a negative cosmological constant and a component with positive energy density (such as a quintessence field, but with the possibility that is equation of state might be phantom) on top. While such a model (which we referred to as CDM model) is certainly a toy model, it can be seen as a proxy for more realistic string-inspired models [176,177,178,179,180], where it is rather natural to have an AdS background with on top a large number of light bosons corresponding to moduli determining the size and shape of the extra dimensions. We tested our toy CDM model against low-redshift distance measurements from a collection of recent BAO surveys and the Pantheon SNeIa catalogue. To interpret our BAO measurements, we required either an anchor either at high or low redshift. We experimented with two different choices of anchor: a high-redshift anchor based on the sound horizon at the drag epoch as determined by the Planck collaboration [5] or a low-redshift anchor based on the local distance ladder measurement of the Hubble constant measured by the SH0ES program [8].
Our results are summarized in Table 2 and Table 3. We found no evidence for a negative cosmological constant, but only obtained the very loose lower bound . Moreover, we found a mild preference for a phantom equation of state () for the dark energy component on top of the negative cosmological constant, in agreement with recent works.
We also compared the three models considered in this work: the baseline CDM model, the one-parameter CDM extension where we allowed the DE EoS to vary freely, and finally, the CDM model with a negative cosmological constant in addition. We found that for most choices of anchor/model, the increased model complexity only marginally improved the quality of the fit (which actually deteriorated when considering the CDM model and anchoring BAO measurements to ). When accounting for the increased model complexity by comparing the three models using the Akaike information criterion, we found that the baseline CDM model was always statistically favoured over the extensions we considered.
The results of our work were less optimistic than earlier results in, e.g., [93,164,165], which found indications for a negative dark energy density at . There were nonetheless some fundamental differences between the approaches of [93,164,165] and ours. We have not attempted to non-parametrically reconstruct the dark energy density, but rather focused on a string-inspired toy model, which we then fitted to the data. Moreover, on top of the negative cosmological constant, we considered a dark energy component with a constant equation of state, although an obvious extension would be to consider a time-varying equation of state (which is very natural for a quintessence model). In any case, our results suggest that a negative cosmological constant is certainly consistent with data. Should the trend that sees low-redshift data favouring a lower expansion rate continue (for instance in light of the persisting tension), our scenario featuring a negative cosmological constant with a quintessence component on top might be worth reconsidering. It is worth reminding once more that, while being a toy model, our CDM model nonetheless enjoyed a fundamental string-inspired motivation.
Finally, there are several avenues by which we can extend and improve the current work. From the observational side, an analysis performing a full fit to CMB data from the Planck satellite, following the upcoming public release of the 2019 legacy likelihood, would be valuable. It would also be worth allowing for more freedom in the dark energy sector, for instance by considering a time-varying dark energy component on top of the negative cosmological constant (in this work, we restricted ourselves to the case where the equation of state was a constant). Finally, it would also be interesting to consider forecasts for how our constraints could improve when data from future CMB experiments become available (such as Simons Observatory [297,298] or CMB-S4 [299]) or gravitational wave standard sirens will improve constraints on the late-time expansion rate (e.g., along the lines of [300]). On the theory side, it would be worth further refining our toy model by more carefully modelling the negative cosmological constant and quintessence component emerging from realistic string constructions. We plan to report on these and other issues in upcoming work.
Author Contributions
Conceptualization, L.V., S.V., and U.D.; methodology, L.V. and S.V.; software, L.V. and S.V.; formal analysis, L.V.; writing, original draft preparation, L.V.; writing, review and editing, L.V., S.V., and U.D.; supervision, U.D.
Funding
L.V. and S.V. are funded by the Vetenskapsrådet (Swedish Research Council) through Contract No. 638-2013-8993 and the Oskar Klein Centre for Cosmoparticle Physics. S.V. is additionally funded by the Isaac Newton Trust and the Kavli Foundation through a Newton–Kavli fellowship. U.D. is funded by the Vetenskapsrådet (Swedish Research Council) under Contract 2015-04814.
Acknowledgments
We thank Massimiliano Lattanzi for useful suggestions that significantly improved this work. L.V. acknowledges the kind hospitality of the INFN Laboratori Nazionali di Frascati and the Leinweber Center for Theoretical Physics where part of this work was carried out.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; nor in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| AdS | anti-de Sitter |
| AIC | Akaike Information Criterion |
| BAO | Baryon Acoustic Oscillations |
| BOSS | Baryon Oscillation Spectroscopic Survey |
| CMB | Cosmic Microwave Background |
| DE | Dark Energy |
| DR12 | Data Release 12 |
| dS | de Sitter |
| eBOSS | Extended Baryon Oscillation Spectroscopic Survey |
| EoS | Equation of State |
| HST | Hubble Space Telescope |
| MCMC | Markov Chain Monte Carlo |
| MGS | Main Galaxy Sample |
| SDSS | Sloan Digital Sky Survey |
| SH0ES | Supernovae and H0 for the Dark Energy Equation of State |
| SNeIa | Type Ia Supernovae |
| 6dFGS | Six-degree Field Galaxy Survey |
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua1, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2017, 470, 2617–2652. [Google Scholar] [CrossRef]
- Dark Energy Survey Collaboration. Dark Energy Survey Year 1 results: Cosmological constraints from cosmic shear. Phys. Rev. D 2018, 98, 043528. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. arXiv 2018, arXiv:1807.06209. [Google Scholar]
- Freedman, W.L. Cosmology at a Crossroads. Nat. Astron. 2017, 1, 0121. [Google Scholar] [CrossRef]
- Di Valentino, E. Crack in the cosmological paradigm. Nat. Astron. 2017, 1, 569–570. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics Beyond LambdaCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- de Blok, W.J.G. The Core-Cusp Problem. Adv. Astron. 2010, 2010, 789293. [Google Scholar] [CrossRef]
- Klypin, A.A.; Kravtsov, A.V.; Valenzuela, O.; Prada, F. Where are the missing Galactic satellites? Astrophys. J. 1999, 522, 82–92. [Google Scholar] [CrossRef]
- Simon, J.D.; Geha, M. The Kinematics of the Ultra-Faint Milky Way Satellites: Solving the Missing Satellite Problem. Astrophys. J. 2007, 670, 313–331. [Google Scholar] [CrossRef]
- Kim, S.Y.; Peter, A.H.G.; Hargis, J.R. Missing Satellites Problem: Completeness Corrections to the Number of Satellite Galaxies in the Milky Way are Consistent with Cold Dark Matter Predictions. Phys. Rev. Lett. 2018, 121, 211302. [Google Scholar] [CrossRef] [PubMed]
- Boylan-Kolchin, M.; Bullock, J.S.; Kaplinghat, M. Too big to fail? The puzzling darkness of massive Milky Way subhaloes. Mon. Not. R. Astron. Soc. 2011, 415, L40. [Google Scholar] [CrossRef]
- Weinberg, D.H.; Bullock, J.S.; Governato, F.; Kuzio de Naray, R.; Peter, A.H.G. Cold dark matter: Controversies on small scales. Proc. Nat. Acad. Sci. USA 2015, 112, 12249–12255. [Google Scholar] [CrossRef] [PubMed]
- Del Popolo, A.; Le Delliou, M. Small scale problems of the ΛCDM model: A short review. Galaxies 2017, 5, 17. [Google Scholar] [CrossRef]
- Bullock, J.S.; Boylan-Kolchin, M. Small-Scale Challenges to the ΛCDM Paradigm. Ann. Rev. Astron. Astrophys. 2017, 55, 343–387. [Google Scholar] [CrossRef]
- Spergel, D.N.; Steinhardt, P.J. Observational evidence for selfinteracting cold dark matter. Phys. Rev. Lett. 2000, 84, 3760–3763. [Google Scholar] [CrossRef] [PubMed]
- Strigari, L.E.; Bullock, J.S.; Kaplinghat, M.; Diemand, J.; Kuhlen, M.; Madau, P. Redefining the Missing Satellites Problem. Astrophys. J. 2007, 669, 676–683. [Google Scholar] [CrossRef]
- van den Aarssen, L.G.; Bringmann, T.; Pfrommer, C. Is dark matter with long-range interactions a solution to all small-scale problems of Λ CDM cosmology? Phys. Rev. Lett. 2012, 109, 231301. [Google Scholar] [CrossRef]
- Tulin, S.; Yu, H.B.; Zurek, K.M. Beyond Collisionless Dark Matter: Particle Physics Dynamics for Dark Matter Halo Structure. Phys. Rev. D 2013, 87, 115007. [Google Scholar] [CrossRef]
- Foot, R.; Vagnozzi, S. Dissipative hidden sector dark matter. Phys. Rev. D 2015, 91, 023512. [Google Scholar] [CrossRef]
- Foot, R.; Vagnozzi, S. Diurnal modulation signal from dissipative hidden sector dark matter. Phys. Lett. B 2015, 748, 61–66. [Google Scholar] [CrossRef]
- Kaplinghat, M.; Tulin, S.; Yu, H.B. Dark Matter Halos as Particle Colliders: Unified Solution to Small-Scale Structure Puzzles from Dwarfs to Clusters. Phys. Rev. Lett. 2016, 116, 041302. [Google Scholar] [CrossRef] [PubMed]
- Foot, R.; Vagnozzi, S. Solving the small-scale structure puzzles with dissipative dark matter. JCAP 2016, 1607, 013. [Google Scholar] [CrossRef]
- Binder, T.; Covi, L.; Kamada, A.; Murayama, H.; Takahashi, T.; Yoshida, N. Matter Power Spectrum in Hidden Neutrino Interacting Dark Matter Models: A Closer Look at the Collision Term. JCAP 2016, 1611, 043. [Google Scholar] [CrossRef]
- Tang, Y. Interacting Scalar Radiation and Dark Matter in Cosmology. Phys. Lett. B 2016, 757, 387–392. [Google Scholar] [CrossRef]
- Bringmann, T.; Ihle, H.T.; Kersten, J.; Walia, P. Suppressing structure formation at dwarf galaxy scales and below: Late kinetic decoupling as a compelling alternative to warm dark matter. Phys. Rev. D 2016, 94, 103529. [Google Scholar] [CrossRef]
- Du, X.; Behrens, C.; Niemeyer, J.C. Substructure of fuzzy dark matter haloes. Mon. Not. R. Astron. Soc. 2017, 465, 941–951. [Google Scholar] [CrossRef]
- Tulin, S.; Yu, H.B. Dark Matter Self-interactions and Small Scale Structure. Phys. Rep. 2018, 730, 1–57. [Google Scholar] [CrossRef]
- Deng, H.; Hertzberg, M.P.; Namjoo, M.H.; Masoumi, A. Can Light Dark Matter Solve the Core-Cusp Problem? Phys. Rev. D 2018, 98, 023513. [Google Scholar] [CrossRef]
- Robles, V.H.; Bullock, J.S.; Boylan-Kolchin, M. Scalar Field Dark Matter: Helping or Hurting Small-Scale Problems in Cosmology? Mon. Not. R. Astron. Soc. 2019, 483, 289–298. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.; Casertano, S.; Sosey, M.; Lampeitl, H.; Ferguson, H.C.; Filippenko, A.V.; Jha, S.W.; Li, W.; Chornock, R.; et al. A Redetermination of the Hubble Constant with the Hubble Space Telescope from a Differential Distance Ladder. Astrophys. J. 2009, 699, 539–563. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.; Casertano, S.; Lampeitl, H.; Ferguson, H.C.; Filippenko, A.V.; Jha, S.W.; Li, W.; Chornock, R. A 3% Solution: Determination of the Hubble Constant with the Hubble Space Telescope and Wide Field Camera 3. Astrophys. J. 2011, 730, 119. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% Determination of the Local Value of the Hubble Constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.; Anderson, J.; MacKenty, J.W.; Bowers, J.B.; Clubb, K.I.; Filippenko, A.V.; Jones, D.O.; et al. New Parallaxes of Galactic Cepheids from Spatially Scanning the Hubble Space Telescope: Implications for the Hubble Constant. Astrophys. J. 2018, 855, 136. [Google Scholar] [CrossRef]
- Efstathiou, G. H0 Revisited. Mon. Not. R. Astron. Soc. 2014, 440, 1138–1152. [Google Scholar] [CrossRef]
- Cardona, W.; Kunz, M.; Pettorino, V. Determining H0 with Bayesian hyper-parameters. JCAP 2017, 1703, 056. [Google Scholar] [CrossRef]
- Zhang, B.R.; Childress, M.J.; Davis, T.M.; Karpenka, N.V.; Lidman, C.; Schmidt, B.P.; Smith, M. A blinded determination of H0 from low-redshift Type Ia supernovae, calibrated by Cepheid variables. Mon. Not. R. Astron. Soc. 2017, 471, 2254–2285. [Google Scholar] [CrossRef]
- Feeney, S.M.; Mortlock, D.J.; Dalmasso, N. Clarifying the Hubble constant tension with a Bayesian hierarchical model of the local distance ladder. Mon. Not. R. Astron. Soc. 2018, 476, 3861–3882. [Google Scholar] [CrossRef]
- Dhawan, S.; Jha, S.W.; Leibundgut, B. Measuring the Hubble constant with Type Ia supernovae as near-infrared standard candles. Astron. Astrophys. 2018, 609, A72. [Google Scholar] [CrossRef]
- Follin, B.; Knox, L. Insensitivity of the distance ladder Hubble constant determination to Cepheid calibration modelling choices. Mon. Not. R. Astron. Soc. 2018, 477, 4534–4542. [Google Scholar] [CrossRef]
- Gómez-Valent, A.; Amendola, L. H0 from cosmic chronometers and Type Ia supernovae, with Gaussian Processes and the novel Weighted Polynomial Regression method. JCAP 2018, 1804, 051. [Google Scholar] [CrossRef]
- Burns, C.R.; Parent, E.; Phillips, M.M.; Stritzinger, M.; Krisciunas, K.; Suntzeff, N.B.; Hsiao, E.Y.; Contreras, C.; Anais, J.; Boldt, L.; et al. The Carnegie Supernova Project: Absolute Calibration and the Hubble Constant. Astrophys. J. 2018, 869, 56. [Google Scholar] [CrossRef]
- Collett, T.; Montanari, F.; Rasanen, S. Model-independent determination of H0 and ΩK0 from strong lensing and type Ia supernovae. arXiv 2019, arXiv:1905.09781. [Google Scholar]
- Camarena, D.; Marra, V. Cosmology-independent local determination of H0 in strong tension with CMB. arXiv 2019, arXiv:1906.11814. [Google Scholar]
- Freedman, W.L.; Madore, B.F.; Hatt, D.; Hoyt, T.J.; Jang, I.S.; Beaton, R.L.; Burns, C.R.; Lee, M.G.; Monson, A.J.; Neeley, J.R.; et al. The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch. arXiv 2019, arXiv:1907.05922. [Google Scholar]
- Bonvin, V.; Courbin, F.; Suyu, S.H.; Marshall, P.J.; Rusu, C.E.; Sluse, D.; Tewes, M.; Wong, K.C.; Collett, T.; Fassnacht, C.D.; et al. H0LiCOW–V. New COSMOGRAIL time delays of HE 0435-1223: H0 to 3.8 per cent precision from strong lensing in a flat ΛCDM model. Mon. Not. R. Astron. Soc. 2017, 465, 4914–4930. [Google Scholar] [CrossRef]
- Birrer, S.; Treu, T.; Rusu, C.E.; Bonvin, V.; Fassnacht, C.D.; Chan, J.H.H. H0LiCOW–IX. Cosmographic analysis of the doubly imaged quasar SDSS 1206+4332 and a new measurement of the Hubble constant. Mon. Not. R. Astron. Soc. 2019, 484, 4726. [Google Scholar] [CrossRef]
- Wong, K.C.; Suyu, S.H.; Chen, G.C.F.; Rusu, C.E.; Millon, M.; Sluse, D. H0LiCOW XIII. A 2.4% measurement of H0 from lensed quasars: 5.3σ tension between early and late-Universe probes. arXiv 2019, arXiv:1907.04869. [Google Scholar]
- Lombriser, L. Consistency of the local Hubble constant with the cosmic microwave background. arXiv 2019, arXiv:1906.12347. [Google Scholar]
- Bernal, J.L.; Verde, L.; Riess, A.G. The trouble with H0. JCAP 2016, 1610, 019. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Reconciling Planck with the local value of H0 in extended parameter space. Phys. Lett. B 2016, 761, 242–246. [Google Scholar] [CrossRef]
- Mörtsell, E.; Dhawan, S. Does the Hubble constant tension call for new physics? JCAP 2018, 1809, 025. [Google Scholar] [CrossRef]
- Guo, R.Y.; Zhang, J.F.; Zhang, X. Can the H0 tension be resolved in extensions to ΛCDM cosmology? JCAP 2019, 1902, 054. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Dhawan, S.; Gerbino, M.; Freese, K.; Goobar, A.; Mena, O. Constraints on the sum of the neutrino masses in dynamical dark energy models with w(z)≥−1 are tighter than those obtained in ΛCDM. Phys. Rev. D 2018, 98, 083501. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Cosmological constraints in extended parameter space from the Planck 2018 Legacy release. arXiv 2019, arXiv:1908.01391. [Google Scholar]
- Di Valentino, E.; Ferreira, R.Z.; Visinelli, L.; Danielsson, U. Late time transitions in the quintessence field and the H0 tension. arXiv 2019, arXiv:1906.11255. [Google Scholar]
- Barreira, A.; Li, B.; Baugh, C.; Pascoli, S. Modified gravity with massive neutrinos as a testable alternative cosmological model. Phys. Rev. D 2014, 90, 023528. [Google Scholar] [CrossRef]
- Murgia, R.; Gariazzo, S.; Fornengo, N. Constraints on the Coupling between Dark Energy and Dark Matter from CMB data. JCAP 2016, 1604, 014. [Google Scholar] [CrossRef]
- Huang, Q.G.; Wang, K. How the dark energy can reconcile Planck with local determination of the Hubble constant. Eur. Phys. J. C 2016, 76, 506. [Google Scholar] [CrossRef]
- Tram, T.; Vallance, R.; Vennin, V. Inflation Model Selection meets Dark Radiation. JCAP 2017, 1701, 046. [Google Scholar] [CrossRef][Green Version]
- Ko, P.; Tang, Y. Light dark photon and fermionic dark radiation for the Hubble constant and the structure formation. Phys. Lett. B 2016, 762, 462–466. [Google Scholar] [CrossRef]
- Karwal, T.; Kamionkowski, M. Dark energy at early times, the Hubble parameter, and the string axiverse. Phys. Rev. D 2016, 94, 103523. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C. Probing the interaction between dark matter and dark energy in the presence of massive neutrinos. Phys. Rev. D 2016, 94, 123511. [Google Scholar] [CrossRef]
- Xia, D.M.; Wang, S. Constraining interacting dark energy models with latest cosmological observations. Mon. Not. R. Astron. Soc. 2016, 463, 952–956. [Google Scholar] [CrossRef]
- Chacko, Z.; Cui, Y.; Hong, S.; Okui, T.; Tsai, Y. Partially Acoustic Dark Matter, Interacting Dark Radiation, and Large Scale Structure. JHEP 2016, 12, 108. [Google Scholar] [CrossRef]
- Zhao, G.B.; Raveri, M.; Pogosian, L.; Wang, Y.; Crittenden, R.G.; Handley, W.J. Dynamical dark energy in light of the latest observations. Nat. Astron. 2017, 1, 627–632. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C. Echo of interactions in the dark sector. Phys. Rev. D 2017, 96, 103511. [Google Scholar] [CrossRef]
- Agrawal, P.; Cyr-Racine, F.Y.; Randall, L.; Scholtz, J. Dark Catalysis. JCAP 2017, 1708, 021. [Google Scholar] [CrossRef]
- Benetti, M.; Graef, L.L.; Alcaniz, J.S. Do joint CMB and HST data support a scale invariant spectrum? JCAP 2017, 1704, 003. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, J.F.; Zhang, X. A search for sterile neutrinos with the latest cosmological observations. Eur. Phys. J. C 2017, 77, 418. [Google Scholar] [CrossRef]
- Zhao, M.M.; He, D.Z.; Zhang, J.F.; Zhang, X. Search for sterile neutrinos in holographic dark energy cosmology: Reconciling Planck observation with the local measurement of the Hubble constant. Phys. Rev. D 2017, 96, 043520. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Linder, E.V.; Silk, J. Constraining Dark Energy Dynamics in Extended Parameter Space. Phys. Rev. D 2017, 96, 023523. [Google Scholar] [CrossRef]
- Gariazzo, S.; Escudero, M.; Diamanti, R.; Mena, O. Cosmological searches for a noncold dark matter component. Phys. Rev. D 2017, 96, 043501. [Google Scholar] [CrossRef]
- Dirian, Y. Changing the Bayesian prior: Absolute neutrino mass constraints in nonlocal gravity. Phys. Rev. D 2017, 96, 083513. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Mena, O. Can interacting dark energy solve the H0 tension? Phys. Rev. D 2017, 96, 043503. [Google Scholar] [CrossRef]
- Solà, J.; Gómez-Valent, A.; de Cruz Pérez, J. The H0 tension in light of vacuum dynamics in the Universe. Phys. Lett. B 2017, 774, 317–324. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, J.F.; Zhang, X. Searching for sterile neutrinos in dynamical dark energy cosmologies. Sci. China Phys. Mech. Astron. 2018, 61, 050411. [Google Scholar] [CrossRef]
- Renk, J.; Zumalacárregui, M.; Montanari, F.; Barreira, A. Galileon gravity in light of ISW, CMB, BAO and H0 data. JCAP 2017, 1710, 020. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Paliathanasis, A. Latest astronomical constraints on some non-linear parametric dark energy models. Mon. Not. R. Astron. Soc. 2018, 475, 2605–2613. [Google Scholar] [CrossRef]
- Buen-Abad, M.A.; Schmaltz, M.; Lesgourgues, J.; Brinckmann, T. Interacting Dark Sector and Precision Cosmology. JCAP 2018, 1801, 008. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Mota, D.F. Novel approach toward the large-scale stable interacting dark-energy models and their astronomical bounds. Phys. Rev. D 2017, 96, 123508. [Google Scholar] [CrossRef]
- Raveri, M.; Hu, W.; Hoffman, T.; Wang, L.T. Partially Acoustic Dark Matter Cosmology and Cosmological Constraints. Phys. Rev. D 2017, 96, 103501. [Google Scholar] [CrossRef]
- Di Valentino, E.; Linder, E.V.; Melchiorri, A. Vacuum phase transition solves the H0 tension. Phys. Rev. D 2018, 97, 043528. [Google Scholar] [CrossRef]
- Di Valentino, E.; Bøehm, C.; Hivon, E.; Bouchet, F.R. Reducing the H0 and σ8 tensions with Dark Matter-neutrino interactions. Phys. Rev. D 2018, 97, 043513. [Google Scholar] [CrossRef]
- Khosravi, N.; Baghram, S.; Afshordi, N.; Altamirano, N. H0 tension as a hint for a transition in gravitational theory. Phys. Rev. D 2019, 99, 103526. [Google Scholar] [CrossRef]
- Santos, M.A.; Benetti, M.; Alcaniz, J.; Brito, F.A.; Silva, R. CMB constraints on β-exponential inflationary models. JCAP 2018, 1803, 023. [Google Scholar] [CrossRef]
- Peirone, S.; Frusciante, N.; Hu, B.; Raveri, M.; Silvestri, A. Do current cosmological observations rule out all Covariant Galileons? Phys. Rev. D 2018, 97, 063518. [Google Scholar] [CrossRef]
- Benetti, M.; Graef, L.L.; Alcaniz, J.S. The H0 and σ8 tensions and the scale invariant spectrum. JCAP 2018, 1807, 066. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, J.F.; Zhang, X. Search for sterile neutrinos in a universe of vacuum energy interacting with cold dark matter. Phys. Dark Univ. 2019, 23, 100261. [Google Scholar] [CrossRef]
- Belgacem, E.; Dirian, Y.; Foffa, S.; Maggiore, M. Nonlocal gravity. Conceptual aspects and cosmological predictions. JCAP 2018, 1803, 002. [Google Scholar] [CrossRef]
- Nunes, R.C. Structure formation in f(T) gravity and a solution for H0 tension. JCAP 2018, 1805, 052. [Google Scholar] [CrossRef]
- Poulin, V.; Boddy, K.K.; Bird, S.; Kamionkowski, M. Implications of an extended dark energy cosmology with massive neutrinos for cosmological tensions. Phys. Rev. D 2018, 97, 123504. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C.; Yadav, S.K. Cosmological bounds on dark matter-photon coupling. Phys. Rev. D 2018, 98, 043521. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Xu, L.; Mota, D.F. Effects of anisotropic stress in interacting dark matter—Dark energy scenarios. Mon. Not. R. Astron. Soc. 2019, 482, 1858–1871. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Nunes, R.C.; Vagnozzi, S.; Mota, D.F. Tale of stable interacting dark energy, observational signatures, and the H0 tension. JCAP 2018, 1809, 019. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Herrera, R.; Chakraborty, S. Large-scale (in) stability analysis of an exactly solved coupled dark-energy model. Phys. Rev. D 2018, 98, 043517. [Google Scholar] [CrossRef]
- Banihashemi, A.; Khosravi, N.; Shirazi, A.H. Ups and Downs in Dark Energy: Phase transition in dark sector as a proposal to lessen cosmological tensions. arXiv 2018, arXiv:1808.02472. [Google Scholar]
- D’Eramo, F.; Ferreira, R.Z.; Notari, A.; Bernal, J.L. Hot Axions and the H0 tension. JCAP 2018, 1811, 014. [Google Scholar] [CrossRef]
- de Martino, I. Decaying dark energy in light of the latest cosmological dataset. Symmetry 2018, 10, 372. [Google Scholar] [CrossRef]
- Graef, L.L.; Benetti, M.; Alcaniz, J.S. Primordial gravitational waves and the H0-tension problem. Phys. Rev. D 2019, 99, 043519. [Google Scholar] [CrossRef]
- Yang, W.; Mukherjee, A.; Di Valentino, E.; Pan, S. Interacting dark energy with time varying equation of state and the H0 tension. Phys. Rev. D 2018, 98, 123527. [Google Scholar] [CrossRef]
- Benevento, G.; Raveri, M.; Lazanu, A.; Bartolo, N.; Liguori, M.; Brax, P.; Valageas, P. K-mouflage Imprints on Cosmological Observables and Data Constraints. JCAP 2019, 1905, 027. [Google Scholar] [CrossRef]
- Lin, M.X.; Raveri, M.; Hu, W. Phenomenology of Modified Gravity at Recombination. Phys. Rev. D 2019, 99, 043514. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Saridakis, E.N.; Chakraborty, S. Observational constraints on one-parameter dynamical dark-energy parametrizations and the H0 tension. Phys. Rev. D 2019, 99, 043543. [Google Scholar] [CrossRef]
- Yang, W.; Shahalam, M.; Pal, B.; Pan, S.; Wang, A. Cosmological constraints on quintessence scalar field models against the astronomical observations. arXiv 2018, arXiv:1810.08586. [Google Scholar]
- Banihashemi, A.; Khosravi, N.; Shirazi, A.H. Ginzburg-Landau Theory of Dark Energy: A Framework to Study Both Temporal and Spatial Cosmological Tensions Simultaneously. Phys. Rev. D 2019, 99, 083509. [Google Scholar] [CrossRef]
- Aylor, K.; Joy, M.; Knox, L.; Millea, M.; Raghunathan, S.; Wu, W.L.K. Sounds Discordant: Classical Distance Ladder & ΛCDM -based Determinations of the Cosmological Sound Horizon. Astrophys. J. 2019, 874, 4. [Google Scholar] [CrossRef]
- Chiang, C.T.; Slosar, A. Inferences of H0 in presence of a non-standard recombination. arXiv 2018, arXiv:1811.03624. [Google Scholar]
- Poulin, V.; Smith, T.L.; Karwal, T.; Kamionkowski, M. Early Dark Energy Can Resolve The Hubble Tension. arXiv 2018, arXiv:1811.04083. [Google Scholar] [CrossRef]
- Carneiro, S.; de Holanda, P.C.; Pigozzo, C.; Sobreira, F. Is the H0 tension suggesting a 4th neutrino’s generation? Phys. Rev. D 2019, 100, 023505. [Google Scholar] [CrossRef]
- Lazkoz, R.; Ortiz-Baños, M.; Salzano, V. The Umami Chaplygin Model. Phys. Dark Univ. 2019, 24, 100279. [Google Scholar] [CrossRef]
- Kreisch, C.D.; Cyr-Racine, F.Y.; Doré, O. The Neutrino Puzzle: Anomalies, Interactions, and Cosmological Tensions. arXiv 2019, arXiv:1902.00534. [Google Scholar]
- Pandey, K.L.; Karwal, T.; Das, S. Alleviating the H0 and σ8 anomalies with a decaying dark matter model. arXiv 2019, arXiv:1902.10636. [Google Scholar]
- Kumar, S.; Nunes, R.C.; Yadav, S.K. Dark sector interaction: A remedy of the tensions between CMB and LSS data. arXiv 2019, arXiv:1903.04865. [Google Scholar] [CrossRef]
- Vattis, K.; Koushiappas, S.M.; Loeb, A. Late universe decaying dark matter can relieve the H0 tension. arXiv 2019, arXiv:1903.06220. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.; Singha, C.; Saridakis, E.N. Observational constraints on sign-changeable interaction models and alleviation of the H0 tension. arXiv 2019, arXiv:1903.10969. [Google Scholar]
- Colgain, E.O. Recasting H0 tension as Ωm tension at low z. arXiv 2019, arXiv:1903.11743. [Google Scholar]
- Agrawal, P.; Cyr-Racine, F.Y.; Pinner, D.; Randall, L. Rock ’n’ Roll Solutions to the Hubble Tension. arXiv 2019, arXiv:1904.01016. [Google Scholar]
- Alexander, S.; McDonough, E. Axion-Dilaton Destabilization and the Hubble Tension. arXiv 2019, arXiv:1904.08912. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Paliathanasis, A.; Ghosh, S.; Wu, Y. Observational constraints of a new unified dark fluid and the H0 tension. arXiv 2019, arXiv:1904.10436. [Google Scholar]
- Adhikari, S.; Huterer, D. Super-CMB fluctuations can resolve the Hubble tension. arXiv 2019, arXiv:1905.02278. [Google Scholar]
- Keeley, R.E.; Joudaki, S.; Kaplinghat, M.; Kirkby, D. Implications of a transition in the dark energy equation of state for the H0 and σ8 tensions. arXiv 2019, arXiv:1905.10198. [Google Scholar]
- Peirone, S.; Benevento, G.; Frusciante, N.; Tsujikawa, S. First cosmological constraints and phenomenology of a beyond-Horndeski model. arXiv 2019, arXiv:1905.11364. [Google Scholar]
- Lin, M.X.; Benevento, G.; Hu, W.; Raveri, M. Acoustic Dark Energy: Potential Conversion of the Hubble Tension. arXiv 2019, arXiv:1905.12618. [Google Scholar]
- Yang, W.; Pan, S.; Di Valentino, E.; Paliathanasis, A.; Lu, J. Challenging bulk viscous unified scenarios with cosmological observations. arXiv 2019, arXiv:1906.04162. [Google Scholar]
- Cerdonio, M. The H0 tension conundrum: Did a QCD meV axion emerge? arXiv 2019, arXiv:1906.07080. [Google Scholar]
- Agrawal, P.; Obied, G.; Vafa, C. H0 Tension, Swampland Conjectures and the Epoch of Fading Dark Matter. arXiv 2019, arXiv:1906.08261. [Google Scholar]
- Li, X.; Shafieloo, A. Phenomenologically Emergent Dark Energy and Ruling Out Cosmological Constant. arXiv 2019, arXiv:1906.08275. [Google Scholar]
- Gelmini, G.B.; Kusenko, A.; Takhistov, V. Hints of Sterile Neutrinos in Recent Measurements of the Hubble Parameter. arXiv 2019, arXiv:1906.10136. [Google Scholar]
- Yang, W.; Mena, O.; Pan, S.; Di Valentino, E. Dark sectors with dynamical coupling. arXiv 2019, arXiv:1906.11697. [Google Scholar]
- Archidiacono, M.; Hooper, D.C.; Murgia, R.; Bohr, S.; Lesgourgues, J.; Viel, M. Constraining Dark Matter—Dark Radiation interactions with CMB, BAO, and Lyman-α. arXiv 2019, arXiv:1907.01496. [Google Scholar]
- Desmond, H.; Jain, B.; Sakstein, J. A local resolution of the Hubble tension: The impact of screened fifth forces on the cosmic distance ladder. arXiv 2019, arXiv:1907.03778. [Google Scholar]
- Yang, W.; Pan, S.; Vagnozzi, S.; Di Valentino, E.; Mota, D.F.; Capozziello, S. Dawn of the dark: Unified dark sectors and the EDGES Cosmic Dawn 21-cm signal. arXiv 2019, arXiv:1907.05344. [Google Scholar]
- Nesseris, S.; Sapone, D.; Sypsas, S. Evaporating primordial black holes as varying dark energy. arXiv 2019, arXiv:1907.05608. [Google Scholar]
- Baldes, I.; Chowdhury, D.; Tytgat, M.H.G. Forays into the dark side of the swamp. arXiv 2019, arXiv:1907.06663. [Google Scholar]
- Pan, S.; Yang, W.; Di Valentino, E.; Saridakis, E.N.; Chakraborty, S. Interacting scenarios with dynamical dark energy: Observational constraints and alleviation of the H0 tension. arXiv 2019, arXiv:1907.07540. [Google Scholar]
- Vagnozzi, S. New physics in light of the H0 tension: An alternative view. arXiv 2019, arXiv:1907.07569. [Google Scholar]
- Cai, Y.F.; Khurshudyan, M.; Saridakis, E.N. Model-independent reconstruction of f(T) gravity from Gaussian Processes and alleviation of the H0 tension. arXiv 2019, arXiv:1907.10813. [Google Scholar]
- Schoneberg, N.; Lesgourgues, J.; Hooper, D.C. The BAO+BBN take on the Hubble tension. arXiv 2019, arXiv:1907.11594. [Google Scholar]
- Pan, S.; Yang, W.; Di Valentino, E.; Shafieloo, A.; Chakraborty, S. Reconciling H0 tension in a six parameter space? arXiv 2019, arXiv:1907.12551. [Google Scholar]
- Caldwell, R.R.; Kamionkowski, M.; Weinberg, N.N. Phantom energy and cosmic doomsday. Phys. Rev. Lett. 2003, 91, 071301. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Tsujikawa, S. Properties of singularities in (phantom) dark energy universe. Phys. Rev. D 2005, 71, 063004. [Google Scholar] [CrossRef]
- Zhang, X. Heal the world: Avoiding the cosmic doomsday in the holographic dark energy model. Phys. Lett. B 2010, 683, 81–87. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Finite-time future singularities in modified Gauss-Bonnet and F(R,G) gravity and singularity avoidance. Eur. Phys. J. C 2010, 67, 295–310. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Nojiri, S.; Odintsov, S.D.; Yurov, A.V. Phantom Cosmology without Big Rip Singularity. Phys. Lett. B 2012, 709, 396–403. [Google Scholar] [CrossRef]
- Mörtsell, E. Cosmological histories in bimetric gravity: A graphical approach. JCAP 2017, 1702, 051. [Google Scholar] [CrossRef]
- Damour, T.; Gibbons, G.W.; Gundlach, C. Dark Matter, Time Varying G, and a Dilaton Field. Phys. Rev. Lett. 1990, 64, 123–126. [Google Scholar] [CrossRef]
- Sahni, V.; Shtanov, Y. Brane world models of dark energy. JCAP 2003, 311, 014. [Google Scholar] [CrossRef]
- Torres, D.F. Quintessence, superquintessence and observable quantities in Brans-Dicke and nonminimally coupled theories. Phys. Rev. D 2002, 66, 043522. [Google Scholar] [CrossRef]
- Chung, D.J.H.; Everett, L.L.; Riotto, A. Quintessence and the underlying particle physics theory. Phys. Lett. B 2003, 556, 61–70. [Google Scholar] [CrossRef][Green Version]
- Faraoni, V. Possible end of the universe in a finite future from dark energy with w−1. Phys. Rev. D 2003, 68, 063508. [Google Scholar] [CrossRef]
- Carroll, S.M.; De Felice, A.; Trodden, M. Can we be tricked into thinking that w is less than −1? Phys. Rev. D 2005, 71, 023525. [Google Scholar] [CrossRef]
- Das, S.; Corasaniti, P.S.; Khoury, J. Super-acceleration as signature of dark sector interaction. Phys. Rev. D 2006, 73, 083509. [Google Scholar] [CrossRef]
- Jhingan, S.; Nojiri, S.; Odintsov, S.D.; Sami, M.; Thongkool, I.; Zerbini, S. Phantom and non-phantom dark energy: The Cosmological relevance of non-locally corrected gravity. Phys. Lett. B 2008, 663, 424–428. [Google Scholar] [CrossRef]
- Nojiri, S.; Saridakis, E.N. Phantom without ghost. Astrophys. Space Sci. 2013, 347, 221–226. [Google Scholar] [CrossRef]
- Ludwick, K.J. Examining the Viability of Phantom Dark Energy. Phys. Rev. D 2015, 92, 063019. [Google Scholar] [CrossRef]
- Cognola, G.; Myrzakulov, R.; Sebastiani, L.; Vagnozzi, S.; Zerbini, S. Covariant Horava-like and mimetic Horndeski gravity: Cosmological solutions and perturbations. Class. Quant. Grav. 2016, 33, 225014. [Google Scholar] [CrossRef]
- Sebastiani, L.; Vagnozzi, S.; Myrzakulov, R. Mimetic gravity: A review of recent developments and applications to cosmology and astrophysics. Adv. High Energy Phys. 2017, 2017, 3156915. [Google Scholar] [CrossRef]
- Ludwick, K.J. The viability of phantom dark energy: A review. Mod. Phys. Lett. A 2017, 32, 1730025. [Google Scholar] [CrossRef]
- Barenboim, G.; Kinney, W.H.; Morse, M.J.P. Phantom Dirac-Born-Infeld Dark Energy. Phys. Rev. D 2018, 98, 083531. [Google Scholar] [CrossRef]
- Casalino, A.; Rinaldi, M.; Sebastiani, L.; Vagnozzi, S. Mimicking dark matter and dark energy in a mimetic model compatible with GW170817. Phys. Dark Univ. 2018, 22, 108. [Google Scholar] [CrossRef]
- Capozziello, S.; Ruchika; Sen, A.A. Model independent constraints on dark energy evolution from low-redshift observations. Mon. Not. R. Astron. Soc. 2019, 484, 4484. [Google Scholar] [CrossRef]
- Wang, Y.; Pogosian, L.; Zhao, G.B.; Zucca, A. Evolution of dark energy reconstructed from the latest observations. Astrophys. J. 2018, 869, L8. [Google Scholar] [CrossRef]
- Dutta, K.; Ruchika; Roy, A.; Sen, A.A.; Sheikh-Jabbari, M.M. Beyond LCDM with Low and High Redshift Data: Implications for Dark Energy. arXiv 2018, arXiv:1808.06623. [Google Scholar]
- Maldacena, J.M.; Nunez, C. Supergravity description of field theories on curved manifolds and a no go theorem. Int. J. Mod. Phys. A 2001, 16, 822–855. [Google Scholar] [CrossRef]
- Silverstein, E. Simple de Sitter Solutions. Phys. Rev. D 2008, 77, 106006. [Google Scholar] [CrossRef]
- Danielsson, U.H.; Haque, S.S.; Shiu, G.; Van Riet, T. Towards Classical de Sitter Solutions in String Theory. JHEP 2009, 9, 114. [Google Scholar] [CrossRef]
- Wrase, T.; Zagermann, M. On Classical de Sitter Vacua in String Theory. Fortschritte Phys. 2010, 58, 906–910. [Google Scholar] [CrossRef]
- Danielsson, U.H.; Koerber, P.; Van Riet, T. Universal de Sitter solutions at tree-level. JHEP 2010, 5, 090. [Google Scholar] [CrossRef]
- Danielsson, U.H.; Haque, S.S.; Koerber, P.; Shiu, G.; Van Riet, T.; Wrase, T. De Sitter hunting in a classical landscape. Fortschritte Phys. 2011, 59, 897–933. [Google Scholar] [CrossRef]
- Chen, X.; Shiu, G.; Sumitomo, Y.; Tye, S.H.H. A Global View on The Search for de-Sitter Vacua in (type IIA) String Theory. JHEP 2012, 4, 026. [Google Scholar] [CrossRef]
- Danielsson, U.H.; Shiu, G.; Van Riet, T.; Wrase, T. A note on obstinate tachyons in classical dS solutions. JHEP 2013, 3, 138. [Google Scholar] [CrossRef]
- Dasgupta, K.; Gwyn, R.; McDonough, E.; Mia, M.; Tatar, R. de Sitter Vacua in Type IIB String Theory: Classical Solutions and Quantum Corrections. JHEP 2014, 7, 054. [Google Scholar] [CrossRef]
- Cicoli, M.; De Alwis, S.; Maharana, A.; Muia, F.; Quevedo, F. De Sitter vs Quintessence in String Theory. Fortschritte Phys. 2019, 67, 1800079. [Google Scholar] [CrossRef]
- Vafa, C. The String landscape and the swampland. arXiv 2005, arXiv:0509212. [Google Scholar]
- Danielsson, U.H.; Van Riet, T. What if string theory has no de Sitter vacua? Int. J. Mod. Phys. 2018, 27, 1830007. [Google Scholar] [CrossRef]
- Obied, G.; Ooguri, H.; Spodyneiko, L.; Vafa, C. De Sitter Space and the Swampland. arXiv 2018, arXiv:1806.08362. [Google Scholar]
- Ooguri, H.; Palti, E.; Shiu, G.; Vafa, C. Distance and de Sitter Conjectures on the Swampland. Phys. Lett. B 2019, 788, 180–184. [Google Scholar] [CrossRef]
- Palti, E. The Swampland: Introduction and Review. Fortschritte Phys. 2019, 67, 1900037. [Google Scholar] [CrossRef]
- Agrawal, P.; Obied, G.; Steinhardt, P.J.; Vafa, C. On the Cosmological Implications of the String Swampland. Phys. Lett. B 2018, 784, 271–276. [Google Scholar] [CrossRef]
- Andriot, D. On the de Sitter swampland criterion. Phys. Lett. B 2018, 785, 570–573. [Google Scholar] [CrossRef]
- Achúcarro, A.; Palma, G.A. The string swampland constraints require multi-field inflation. JCAP 2019, 1902, 041. [Google Scholar] [CrossRef]
- Garg, S.K.; Krishnan, C. Bounds on Slow Roll and the de Sitter Swampland. arXiv 2018, arXiv:1807.05193. [Google Scholar]
- Kehagias, A.; Riotto, A. A note on Inflation and the Swampland. Fortschritte Phys. 2018, 66, 1800052. [Google Scholar] [CrossRef]
- Heisenberg, L.; Bartelmann, M.; Brandenberger, R.; Refregier, A. Dark Energy in the Swampland. Phys. Rev. D 2018, 98, 123502. [Google Scholar] [CrossRef]
- Kinney, W.H.; Vagnozzi, S.; Visinelli, L. The zoo plot meets the swampland: Mutual (in)consistency of single-field inflation, string conjectures, and cosmological data. Class. Quant. Grav. 2019, 36, 117001. [Google Scholar] [CrossRef]
- Akrami, Y.; Kallosh, R.; Linde, A.; Vardanyan, V. The Landscape, the Swampland and the Era of Precision Cosmology. Fortschritte Phys. 2019, 67, 1800075. [Google Scholar] [CrossRef]
- Murayama, H.; Yamazaki, M.; Yanagida, T.T. Do We Live in the Swampland? JHEP 2018, 12, 032. [Google Scholar] [CrossRef]
- Kinney, W.H. Eternal Inflation and the Refined Swampland Conjecture. Phys. Rev. Lett. 2019, 122, 081302. [Google Scholar] [CrossRef]
- Kachru, S.; Kallosh, R.; Linde, A.D.; Trivedi, S.P. De Sitter vacua in string theory. Phys. Rev. D 2003, 68, 046005. [Google Scholar] [CrossRef]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar] [CrossRef]
- Hartle, J.B.; Hawking, S.W.; Hertog, T. Accelerated Expansion from Negative Λ. arXiv 2012, arXiv:1205.3807. [Google Scholar]
- Svrcek, P.; Witten, E. Axions In String Theory. JHEP 2006, 6, 051. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Dimopoulos, S.; Dubovsky, S.; Kaloper, N.; March-Russell, J. String Axiverse. Phys. Rev. D 2010, 81, 123530. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Dubovsky, S. Exploring the String Axiverse with Precision Black Hole Physics. Phys. Rev. D 2011, 83, 044026. [Google Scholar] [CrossRef]
- Cicoli, M.; Goodsell, M.; Ringwald, A. The type IIB string axiverse and its low-energy phenomenology. JHEP 2012, 10, 146. [Google Scholar] [CrossRef]
- Conlon, J.P.; Marsh, M.C.D. The Cosmophenomenology of Axionic Dark Radiation. JHEP 2013, 10, 214. [Google Scholar] [CrossRef]
- Cicoli, M.; Conlon, J.P.; Marsh, M.C.D.; Rummel, M. 3.55 keV photon line and its morphology from a 3.55 keV axionlike particle line. Phys. Rev. D 2014, 90, 023540. [Google Scholar] [CrossRef]
- Marsh, D.J.E. Axion Cosmology. Phys. Rept. 2016, 643, 1–79. [Google Scholar] [CrossRef]
- Visinelli, L. Light axion-like dark matter must be present during inflation. Phys. Rev. D 2017, 96, 023013. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Grin, D.; Karwal, T.; Kamionkowski, M. Cosmological implications of ultralight axionlike fields. Phys. Rev. D 2018, 98, 083525. [Google Scholar] [CrossRef]
- Kitajima, N.; Soda, J.; Urakawa, Y. Gravitational wave forest from string axiverse. JCAP 2018, 1810, 008. [Google Scholar] [CrossRef]
- Visinelli, L.; Vagnozzi, S. Cosmological window onto the string axiverse and the supersymmetry breaking scale. Phys. Rev. D 2019, 99, 063517. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. f(R) Gravity Inflation with String-Corrected Axion Dark Matter. Phys. Rev. D 2019, 99, 064049. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Unification of Inflation with Dark Energy in f(R) Gravity and Axion Dark Matter. Phys. Rev. D 2019, 99, 104070. [Google Scholar] [CrossRef]
- Ramberg, N.; Visinelli, L. Probing the Early Universe with Axion Physics and Gravitational Waves. Phys. Rev. D 2019, 99, 123513. [Google Scholar] [CrossRef]
- Reynolds, C.S.; Marsh, M.C.D.; Russell, H.R.; Fabian, A.C.; Smith, R.N.; Tombesi, F. Astrophysical limits on very light axion-like particles from Chandra grating spectroscopy of NGC 1275. arXiv 2019, arXiv:1907.05475. [Google Scholar]
- Beutler, F.; Blake, C.; Colless, M.; Jones, D.H.; Staveley-Smith, L.; Campbell, L.; Parker, Q.; Saunders, W.; Watson, F. The 6dF Galaxy Survey: Baryon Acoustic Oscillations and the Local Hubble Constant. Mon. Not. R. Astron. Soc. 2011, 416, 3017–3032. [Google Scholar] [CrossRef]
- Ross, A.J.; Samushia, L.; Howlett, C.; Percival, W.J.; Burden, A.; Manera, M. The clustering of the SDSS DR7 main Galaxy sample–I. A 4 per cent distance measure at z = 0.15. Mon. Not. R. Astron. Soc. 2015, 449, 835–847. [Google Scholar] [CrossRef]
- Des Bourboux, H.D.M.; Le Goff, J.M.; Blomqvist, M.; Guy, J.; Rich, J.; Yèche, C. Baryon acoustic oscillations from the complete SDSS-III Lyα-quasar cross-correlation function at z = 2.4. Astron. Astrophys. 2017, 608, A130. [Google Scholar] [CrossRef]
- Bautista, J.E.; Guy, J.; Rich, J.; Blomqvist, M.; Des Bourboux, H.D.M.; Pieri, M.M. Measurement of baryon acoustic oscillation correlations at z = 2.3 with SDSS DR12 Lyα-Forests. Astron. Astrophys. 2017, 603, A12. [Google Scholar] [CrossRef]
- Ata, M.; Baumgarten, F.; Bautista, J.; Beutler, F.; Bizyaev, D.; Blanton, M.R. The clustering of the SDSS-IV extended Baryon Oscillation Spectroscopic Survey DR14 quasar sample: First measurement of baryon acoustic oscillations between redshift 0.8 and 2.2. Mon. Not. R. Astron. Soc. 2018, 473, 4773–4794. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Grande, J.; Sola, J.; Stefancic, H. LXCDM: A Cosmon model solution to the cosmological coincidence problem? JCAP 2006, 608, 011. [Google Scholar] [CrossRef]
- Grande, J.; Sola, J.; Stefancic, H. Composite dark energy: Cosmon models with running cosmological term and gravitational coupling. Phys. Lett. B 2007, 645, 236–244. [Google Scholar] [CrossRef]
- Guo, Z.K.; Piao, Y.S.; Zhang, X.M.; Zhang, Y.Z. Cosmological evolution of a quintom model of dark energy. Phys. Lett. B 2005, 608, 177–182. [Google Scholar] [CrossRef]
- Hu, W. Crossing the phantom divide: Dark energy internal degrees of freedom. Phys. Rev. D 2005, 71, 047301. [Google Scholar] [CrossRef]
- Cai, Y.F.; Saridakis, E.N.; Setare, M.R.; Xia, J.Q. Quintom Cosmology: Theoretical implications and observations. Phys. Rept. 2010, 493, 1–60. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Weller, J.M. A Quintom scenario with mixed kinetic terms. Phys. Rev. D 2010, 81, 123523. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Tsoukalas, M. Cosmology in new gravitational scalar-tensor theories. Phys. Rev. D 2016, 93, 124032. [Google Scholar] [CrossRef]
- Amendola, L.; Tsujikawa, S. Phantom crossing, equation-of-state singularities, and local gravity constraints in f(R) models. Phys. Lett. B 2008, 660, 125–132. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Ward, J. Quintessence and phantom dark energy from ghost D-branes. Phys. Rev. D 2009, 80, 083003. [Google Scholar] [CrossRef]
- Wu, P.; Yu, H.W. f(T) models with phantom divide line crossing. Eur. Phys. J. C 2011, 71, 1552. [Google Scholar] [CrossRef]
- Elizalde, E.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Oscillations of the F(R) dark energy in the accelerating universe. Eur. Phys. J. C 2012, 72, 1843. [Google Scholar] [CrossRef]
- Saridakis, E.N. Phantom crossing and quintessence limit in extended nonlinear massive gravity. Class. Quant. Grav. 2013, 30, 075003. [Google Scholar] [CrossRef]
- Pan, S.; Chakraborty, S. A Cosmological Study in Massive Gravity theory. Ann. Phys. 2015, 360, 180–193. [Google Scholar] [CrossRef][Green Version]
- Dhawan, S.; Goobar, A.; Mörtsell, E.; Amanullah, R.; Feindt, U. Narrowing down the possible explanations of cosmic acceleration with geometric probes. JCAP 2017, 1707, 040. [Google Scholar] [CrossRef]
- Elizalde, E.; Odintsov, S.D.; Sebastiani, L.; Myrzakulov, R. Beyond-one-loop quantum gravity action yielding both inflation and late-time acceleration. Nucl. Phys. B 2017, 921, 411–435. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K.; Sebastiani, L. Unification of Constant-roll Inflation and Dark Energy with Logarithmic R2-corrected and Exponential F(R) Gravity. Nucl. Phys. B 2017, 923, 608–632. [Google Scholar] [CrossRef]
- Dutta, J.; Khyllep, W.; Saridakis, E.N.; Tamanini, N.; Vagnozzi, S. Cosmological dynamics of mimetic gravity. JCAP 2018, 1802, 041. [Google Scholar] [CrossRef]
- Amendola, L. Coupled quintessence. Phys. Rev. D 2000, 62, 043511. [Google Scholar] [CrossRef]
- Barrow, J.D.; Clifton, T. Cosmologies with energy exchange. Phys. Rev. D 2006, 73, 103520. [Google Scholar] [CrossRef]
- He, J.H.; Wang, B. Effects of the interaction between dark energy and dark matter on cosmological parameters. JCAP 2008, 806, 010. [Google Scholar] [CrossRef]
- Valiviita, J.; Majerotto, E.; Maartens, R. Instability in interacting dark energy and dark matter fluids. JCAP 2008, 807, 020. [Google Scholar] [CrossRef]
- Gavela, M.B.; Hernandez, D.; Lopez Honorez, L.; Mena, O.; Rigolin, S. Dark coupling. JCAP 2009, 907, 034. [Google Scholar] [CrossRef]
- Martinelli, M.; Lopez Honorez, L.; Melchiorri, A.; Mena, O. Future CMB cosmological constraints in a dark coupled universe. Phys. Rev. D 2010, 81, 103534. [Google Scholar] [CrossRef]
- Pan, S.; Bhattacharya, S.; Chakraborty, S. An analytic model for interacting dark energy and its observational constraints. Mon. Not. R. Astron. Soc. 2015, 452, 3038–3046. [Google Scholar] [CrossRef]
- Tamanini, N. Phenomenological models of dark energy interacting with dark matter. Phys. Rev. D 2015, 92, 043524. [Google Scholar] [CrossRef]
- Nunes, R.C.; Pan, S.; Saridakis, E.N. New constraints on interacting dark energy from cosmic chronometers. Phys. Rev. D 2016, 94, 023508. [Google Scholar] [CrossRef]
- Pan, S.; Sharov, G.S. A model with interaction of dark components and recent observational data. Mon. Not. R. Astron. Soc. 2017, 472, 4736–4749. [Google Scholar] [CrossRef]
- Sharov, G.S.; Bhattacharya, S.; Pan, S.; Nunes, R.C.; Chakraborty, S. A new interacting two fluid model and its consequences. Mon. Not. R. Astron. Soc. 2017, 466, 3497–3506. [Google Scholar] [CrossRef]
- Pan, S.; Mukherjee, A.; Banerjee, N. Astronomical bounds on a cosmological model allowing a general interaction in the dark sector. Mon. Not. R. Astron. Soc. 2018, 477, 1189–1205. [Google Scholar] [CrossRef]
- Yang, W.; Banerjee, N.; Paliathanasis, A.; Pan, S. Reconstructing the dark matter and dark energy interaction scenarios from observations. arXiv 2018, arXiv:1812.06854. [Google Scholar]
- Paliathanasis, A.; Pan, S.; Yang, W. Dynamics of nonlinear interacting dark energy models. arXiv 2019, arXiv:1903.02370. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Wang, B.; Wang, A. Forecasting Interacting Vacuum-Energy Models using Gravitational Waves. arXiv 2019, arXiv:1904.11980. [Google Scholar]
- Lima, J.A.S.; Silva, F.E.; Santos, R.C. Accelerating Cold Dark Matter Cosmology (ΩΛ≡0). Class. Quant. Grav. 2008, 25, 205006. [Google Scholar] [CrossRef]
- Lima, J.A.S.; Jesus, J.F.; Oliveira, F.A. CDM Accelerating Cosmology as an Alternative to LCDM model. JCAP 2010, 1011, 027. [Google Scholar] [CrossRef]
- Pan, S.; Chakraborty, S. Will There Be Future Deceleration? A Study of Particle Creation Mechanism in Nonequilibrium Thermodynamics. Adv. High Energy Phys. 2015, 2015, 654025. [Google Scholar] [CrossRef]
- Nunes, R.C.; Pavón, D. Phantom behavior via cosmological creation of particles. Phys. Rev. D 2015, 91, 063526. [Google Scholar] [CrossRef]
- de Haro, J.; Pan, S. Gravitationally induced adiabatic particle production: From Big Bang to de Sitter. Class. Quant. Gravity 2016, 33, 165007. [Google Scholar] [CrossRef]
- Pan, S.; de Haro, J.; Paliathanasis, A.; Slagter, R.J. Evolution and Dynamics of a Matter creation model. Mon. Not. R. Astron. Soc. 2016, 460, 1445–1456. [Google Scholar] [CrossRef]
- Nunes, R.C.; Pan, S. Cosmological consequences of an adiabatic matter creation process. Mon. Not. R. Astron. Soc. 2016, 459, 673–682. [Google Scholar] [CrossRef]
- Pan, S.; Kumar Pal, B.; Pramanik, S. Gravitationally influenced particle creation models and late-time cosmic acceleration. Int. J. Geom. Meth. Mod. Phys. 2017, 15, 1850042. [Google Scholar] [CrossRef]
- Paliathanasis, A.; Barrow, J.D.; Pan, S. Cosmological solutions with gravitational particle production and nonzero curvature. Phys. Rev. D 2017, 95, 103516. [Google Scholar] [CrossRef]
- Pan, S.; Barrow, J.D.; Paliathanasis, A. Two-fluid solutions of particle-creation cosmologies. Eur. Phys. J. C 2019, 79, 115. [Google Scholar] [CrossRef]
- Vikman, A. Can dark energy evolve to the phantom? Phys. Rev. D 2005, 71, 023515. [Google Scholar] [CrossRef]
- Creminelli, P.; D’Amico, G.; Norena, J.; Vernizzi, F. The Effective Theory of Quintessence: The w<−1 Side Unveiled. JCAP 2009, 902, 018. [Google Scholar] [CrossRef]
- Deffayet, C.; Pujolas, O.; Sawicki, I.; Vikman, A. Imperfect Dark Energy from Kinetic Gravity Braiding. JCAP 2010, 1010, 026. [Google Scholar] [CrossRef]
- Akrami, Y.; Kallosh, R.; Linde, A.; Vardanyan, V. Dark energy, α-attractors, and large-scale structure surveys. JCAP 2018, 1806, 041. [Google Scholar] [CrossRef]
- Paliathanasis, A.; Leon, G.; Pan, S. Exact Solutions in Multi-Scalar Field Cosmology. arXiv 2018, arXiv:1811.10038. [Google Scholar]
- Peebles, P.J.E.; Yu, J.T. Primeval adiabatic perturbation in an expanding universe. Astrophys. J. 1970, 162, 815–836. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Zeldovich, Y.B. Small scale fluctuations of relic radiation. Astrophys. Space Sci. 1970, 7, 3–19. [Google Scholar]
- Sunyaev, R.A.; Zeldovich, Y.B. The Interaction of matter and radiation in the hot model of the universe. Astrophys. Space Sci. 1970, 7, 20–30. [Google Scholar]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Aubourg, É.; Bailey, S.; Bautista, J.E.; Beutler, F.; Bhardwaj, V.; Bizyaev, D. Cosmological implications of baryon acoustic oscillation measurements. Phys. Rev. D 2015, 92, 123516. [Google Scholar] [CrossRef]
- Cole, S.; Percival, W.J.; Peacock, J.A.; Norberg, P.; Baugh, C.M.; Frenk, C.S. The 2dF Galaxy Redshift Survey: Power-spectrum analysis of the final dataset and cosmological implications. Mon. Not. R. Astron. Soc. 2005, 362, 505–534. [Google Scholar] [CrossRef]
- Yang, W.; Vagnozzi, S.; Di Valentino, E.; Nunes, R.C.; Pan, S.; Mota, D.F. Listening to the sound of dark sector interactions with gravitational wave standard sirens. arXiv 2019, arXiv:1905.08286. [Google Scholar] [CrossRef]
- Betoule, M.; Kessler, R.; Guy, J.; Mosher, J.; Hardin, D.; Biswas, R. Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. Astron. Astrophys. 2014, 568, A22. [Google Scholar] [CrossRef]
- Riess, A.G.; Strolger, L.G.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Gold, B. New Hubble Space Telescope Discoveries of Type Ia Supernovae at z>=1: Narrowing Constraints on the Early Behavior of Dark Energy. Astrophys. J. 2007, 659, 98–121. [Google Scholar] [CrossRef]
- Hicken, M.; Challis, P.; Jha, S.; Kirshner, R.P.; Matheson, T.; Modjaz, M.; Rest, A.; Wood-Vasey, W.M.; Bakos, G.; Barton, E.J. CfA3: 185 Type Ia Supernova Light Curves from the CfA. Astrophys. J. 2009, 700, 331–357. [Google Scholar] [CrossRef]
- Conley, A.; Guy, J.; Sullivan, M.; Regnault, N.; Astier, P.; Balland, C.; Basa, S.; Carlberg, R.G.; Fouchez, D.; Hardin, D. Supernova Constraints and Systematic Uncertainties from the First Three Years of the Supernova Legacy Survey. Astrophys. J. Suppl. 2011, 192, 1. [Google Scholar] [CrossRef]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N. The Hubble Space Telescope Cluster Supernova Survey. V. Improving the Dark-energy Constraints above z > 1 and Building an Early-type-hosted Supernova Sample. Astrophys. J. 2012, 746, 85. [Google Scholar] [CrossRef]
- Sako, M.; Bassett, B.; Becker, A.C.; Brown, P.J.; Campbell, H.; Wolf, R. The Data Release of the Sloan Digital Sky Survey-II Supernova Survey. Publ. Astron. Soc. Pac. 2018, 130, 064002. [Google Scholar] [CrossRef]
- Jones, D.O.; Scolnic, D.M.; Riess, A.G.; Rest, A.; Kirshner, R.P.; Berger, E. Measuring Dark Energy Properties with Photometrically Classified Pan-STARRS Supernovae. II. Cosmological Parameters. Astrophys. J. 2018, 857, 51. [Google Scholar] [CrossRef]
- Cuesta, A.J.; Verde, L.; Riess, A.; Jimenez, R. Calibrating the cosmic distance scale ladder: The role of the sound horizon scale and the local expansion rate as distance anchors. Mon. Not. R. Astron. Soc. 2015, 448, 3463–3471. [Google Scholar] [CrossRef]
- Meng, X.L.; Wang, X.; Li, S.Y.; Zhang, T.J. Utility of observational Hubble parameter data on dark energy evolution. arXiv 2015, arXiv:1507.02517. [Google Scholar]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6% measurement of the Hubble parameter at z∼0.45: Direct evidence of the epoch of cosmic re-acceleration. JCAP 2016, 1605, 014. [Google Scholar] [CrossRef]
- Kosowsky, A.; Milosavljevic, M.; Jimenez, R. Efficient cosmological parameter estimation from microwave background anisotropies. Phys. Rev. D 2002, 66, 063007. [Google Scholar] [CrossRef]
- Wang, Y.; Mukherjee, P. Observational Constraints on Dark Energy and Cosmic Curvature. Phys. Rev. D 2007, 76, 103533. [Google Scholar] [CrossRef]
- Fixsen, D.J.; Cheng, E.S.; Gales, J.M.; Mather, J.C.; Shafer, R.A.; Wright, E.L. The Cosmic Microwave Background spectrum from the full COBE FIRAS data set. Astrophys. J. 1996, 473, 576. [Google Scholar] [CrossRef]
- de Salas, P.F.; Forero, D.V.; Ternes, C.A.; Tortola, M.; Valle, J.W.F. Status of neutrino oscillations 2018: 3σ hint for normal mass ordering and improved CP sensitivity. Phys. Lett. B 2018, 782, 633–640. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Giusarma, E.; Mena, O.; Freese, K.; Gerbino, M.; Ho, S.; Lattanzi, M. Unveiling ν secrets with cosmological data: Neutrino masses and mass hierarchy. Phys. Rev. D 2017, 96, 123503. [Google Scholar] [CrossRef]
- Simpson, F.; Jimenez, R.; Pena-Garay, C.; Verde, L. Strong Bayesian Evidence for the Normal Neutrino Hierarchy. JCAP 2017, 1706, 029. [Google Scholar] [CrossRef]
- Schwetz, T.; Freese, K.; Gerbino, M.; Giusarma, E.; Hannestad, S.; Lattanzi, M.; Mena, O.; Vagnozzi, S. Comment on “Strong Evidence for the Normal Neutrino Hierarchy”. arXiv 2017, arXiv:1703.04585. [Google Scholar]
- De Salas, P.F.; Gariazzo, S.; Mena, O.; Ternes, C.A.; Tórtola, M. Neutrino Mass Ordering from Oscillations and Beyond: 2018 Status and Future Prospects. Front. Astron. Space Sci. 2018, 5, 36. [Google Scholar] [CrossRef]
- Palanque-Delabrouille, N.; Yèche, C.; Baur, J.; Magneville, C.; Rossi, G.; Lesgourgues, J. Neutrino masses and cosmology with Lyman-alpha forest power spectrum. JCAP 2015, 1511, 011. [Google Scholar] [CrossRef]
- Visinelli, L. Neutrino flavor oscillations in a curved space-time. Gen. Relat. Gravit. 2015, 47, 62. [Google Scholar] [CrossRef]
- Cuesta, A.J.; Niro, V.; Verde, L. Neutrino mass limits: Robust information from the power spectrum of galaxy surveys. Phys. Dark Univ. 2016, 13, 77–86. [Google Scholar] [CrossRef]
- Huang, Q.G.; Wang, K.; Wang, S. Constraints on the neutrino mass and mass hierarchy from cosmological observations. Eur. Phys. J. C 2016, 76, 489. [Google Scholar] [CrossRef]
- Giusarma, E.; Gerbino, M.; Mena, O.; Vagnozzi, S.; Ho, S.; Freese, K. Improvement of cosmological neutrino mass bounds. Phys. Rev. D 2016, 94, 083522. [Google Scholar] [CrossRef]
- Giusarma, E.; Vagnozzi, S.; Ho, S.; Ferraro, S.; Freese, K.; Kamen-Rubio, R.; Luk, K.B. Scale-dependent galaxy bias, CMB lensing-galaxy cross-correlation, and neutrino masses. Phys. Rev. D 2018, 98, 123526. [Google Scholar] [CrossRef]
- Vagnozzi, S. Cosmological searches for the neutrino mass scale and mass ordering. arXiv 2019, arXiv:1907.08010. [Google Scholar]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306–312. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Lemos, P.; Lee, E.; Efstathiou, G.; Gratton, S. Model independent H(z) reconstruction using the cosmic inverse distance ladder. Mon. Not. R. Astron. Soc. 2019, 483, 4803–4810. [Google Scholar] [CrossRef]
- Ade, P.; Aguirre, J.; Ahmed, Z.; Aiola, S.; Ali, A.; Alonso, D. The Simons Observatory: Science goals and forecasts. JCAP 2019, 1902, 056. [Google Scholar] [CrossRef]
- Abitbol, M.H.; Adachi, S.; Ade, P.; Aguirre, J.; Ahmed, Z.; Aiola, S. The Simons Observatory: Astro2020 Decadal Project Whitepaper. arXiv 2019, arXiv:1907.08284. [Google Scholar]
- Abazajian, K.N.; Adshead, P.; Ahmed, Z.; Allen, S.W.; Alonso, D.; Arnold, K.S. CMB-S4 science book. arXiv 2016, arXiv:1610.02743. [Google Scholar]
- Du, M.; Yang, W.; Xu, L.; Pan, S.; Mota, D.F. Future Constraints on Dynamical Dark-Energy using Gravitational-Wave Standard Sirens. arXiv 2018, arXiv:1812.01440. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).