The Maximum Hosoya Index of Unicyclic Graphs with Diameter at Most Four

Abstract

The Hosoya index of a graph is defined by the total number of the matchings of the graph. In this paper, we determine the maximum Hosoya index of unicyclic graphs with n vertices and diameter 3 or 4. Our results somewhat answer a question proposed by Wagner and Gutman in 2010 for unicyclic graphs with small diameter.

1. Introduction

Numerous topological and chemical indices/measures have been used for analyzing molecular graphs [1,2,3,4]. A prominent example is the Hosoya index introduced by Hosoya [5] in 1971 as a molecular-graph based structure descriptor. Hosoya discovered that certain physico-chemical properties of alkanes (= saturated hydrocarbons)—in particular, their boiling points—are well correlated with this index. Gutman et al. further considered it in the chemical view [6]. As is known, structural graph descriptors have been investigated extensively in chemistry, drug design and related disciplines [1,2,3,4].

The Hosoya index got much attention by many researchers in the past decades. They have been interested in identifying the maximum or minimum value of Hosoya index for various classes of graphs (with certain restrictions), such as trees [7,8,9], unicyclic graphs [10,11,12,13,14], bicyclic graphs [15] and so on. For an exhaustive survey for this topic, we refer to [16].

Even though there is a considerable amount of literature on the topic of maximizing or minimizing the Hosoya index, there are still many interesting open questions left. In [16], it is mentioned that:

-

It seems to be difficult to obtain results of the maximum Hosoya index among trees with a given number of leaves or given diameter. However, partial results are available, so the problem might not be totally intractable, and results in this direction would definitely be interesting.

-

If the aforementioned questions can be answered for trees, then it is also natural to consider the analogous questions for treelike graphs (such as unicyclic graphs).

For two vertices $u,v$ in a graph G, the distance $d(u,v)$ between u and v is the length of a shortest path connecting them. The diameter of G is $max\left\{d\right(u,v)\mid u,v\in V(G\left)\right\}$. Confirming a conjecture proposed by Ou [12], Liu [8] considered the maximum Hosoya index of trees with diameter 4. Motivated by this line of research, we here consider the maximal Hosoya index of unicyclic graphs with small diameter. It seems that unicyclic graphs are only one more edge than trees, however, some of their properties change drastically such as the girth.

At the end of this section, we define some notation as well as some preliminary results that we frequently use in the sequel.

Let G be a simple connected graph with vertex set $V\left(G\right)$. For $u\in V\left(G\right)$, we denote its neighborhood by $N_G\left(u\right)$, and denote $d_G\left(u\right):=N_G\left(u\right)$. A pendent vertex is a vertex of degree 1. For two vertices $u_1$ and $u_2$, the distance between $u_1$ and $u_2$ is the number of edges in a shortest path joining $u_1$ and $u_2$. We use $G-u$ to denote the graph that arises from G by deleting the vertex $u\in V\left(G\right)$. For other undefined notations, we refer to [17].

Given a molecular graph G, let $m(G,k)$ be the number of k matchings of G. It would be convenient to define $m(G,0)=1,$ $m(G,1)=e\left(G\right).$ The Hosoya index $z=z\left(G\right)$ is defined as the number of subsets of $E\left(G\right)$ in which no edges are incident, in other words, the total number of the matchings of the graph G. Then,

$$z\left(G\right)=\sum _{k\ge 0}m(G,k).$$

For the star $K_{1,p}$ of order $p+1$, when $k\ge 2$, we have $m(G,k)=0$. Then, $z\left(K_{1,p}\right)={\sum }_{k\ge 0}m(G,k)=m(G,0)+m(G,1)=1+p$.

The double star $S_{p,q}$ is a tree of order n obtained from $K_{1,p}$ and $K_{1,q-1}$, by identifying a pendent vertex of $K_{1,p}$ with the center of $K_{1,q-1}$, where $p+q=n$. For $S_{p,q}$, when $k\ge 3$, we have $m(G,k)=0$, therefore

$$\begin{array}{cc}\hfill z\left(S_{p,q}\right)& =\sum _{k\ge 0}m(G,k)=m(G,0)+m(G,1)+m(G,2)\hfill \\ & =1+(p+q-1)+(p-1)(q-1)=pq+1.\hfill \end{array}$$

The following two lemmas are needed in this paper, which can be found on page 337 of [16].

Lemma 1.

Let G be a graph and v be a vertex of G. Then,

$$\begin{array}{cc}\hfill z\left(G\right)& =z(G-v)+\sum _{u\in N_G\left(v\right)}z(G-\{u,v\}).\hfill \end{array}$$

Lemma 2.

If $G_1,G_2,\cdots ,G_t$ are the components of a graph G, then

$$\begin{array}{cc}\hfill z\left(G\right)& ={\Pi }_{i=1}^{t}z\left(G_i\right).\hfill \end{array}$$

For $n\ge 6$, the unique unicyclic graph with diameter two is obtained from the star $K_{1,n-1}$ by adding an edge. For unicyclic graphs with diameter at least 5, things become more complicated, and we believe more techniques are needed. Thus, we only consider the cases for diameter 3 and 4. In Section 2, we determine the maximal Hosoya index of unicyclic graphs with n vertices and diameter 3 (see Theorem 5). In Section 3, we determine the maximal Hosoya index of unicyclic graphs with n vertices and diameter 4 (see Theorem 15).

2. The Unicyclic Graphs with Diameter 3

In this section, we study the maximal Hosoya index of unicyclic graphs with n vertices and diameter 3.

Let ${\mathcal{U}}_n^3$ be the set of all unicyclic graphs with n vertices and diameter 3. According to the length of the unique cycle and the distribution of other vertices, we may classify all the members in ${\mathcal{U}}_n^3$. Let ${\mathcal{U}}_i$ be the set of unicyclic graph of the form $G_i$, $i=1,2,3,4$. It is easy to see that the graphs from ${\mathcal{U}}_1$, ${\mathcal{U}}_2$, ${\mathcal{U}}_3$, and ${\mathcal{U}}_4$, and $C_5$, $C_6$, and $C_7$ are all unicyclic graphs with diameter 3.

Let ${\mathcal{U}}_1$ be the set of unicyclic graphs of the form $G_1$ (as depicted in Figure 1), where $a+b+c=n$, $a,b,c\ge 1$ and at least two of $a,b,c$ are greater than 2. Let $G_1^{*}$ be the graph of the form $G_1$ satisfying $a,b,c$ almost equal (hereafter “almost equal” means the difference of any two numbers is at most one).

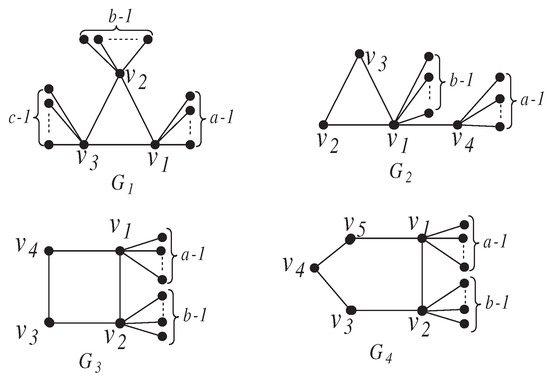
Figure 1. Four unicyclic graphs with diameter 3.

Theorem 1.

The graph $G_1^{*}$ has the maximum Hosoya index among all graphs in ${\mathcal{U}}_1$.

Proof. 

Assume $G_1\in {\mathcal{U}}_1$ with $1\le a\le b\le c$. By Lemmas 1 and 2, we obtain

$$\begin{array}{cc}\hfill z\left(G_1\right)& =z(G_1-v_1)+\sum _{w\in N_{G_1}\left(v_1\right)}z(G_1-\{v_1,w\})\hfill \\ & =z(G_1-v_1)+z(G_1-\{v_1,v_2\})+z(G_1-\{v_1,v_3\})\hfill \\ & +(a-1)z(G_1-\{v_1,y\})\hfill \\ & =(bc+1)+c+b+(a-1)(bc+1)\hfill \\ & =abc+a+b+c:=f_1(a,b,c),\hfill \end{array}$$

where y is one of pendent vertex adjacent to $v_1$ in $G_1$.

If $b-a\ge 2$, then we get

$$\begin{array}{cc}\hfill f_1(a+1,b-1,c)-f_1(a,b,c)& =(b-a-1)c>0.\hfill \end{array}$$

As $a,b,c$ have the same status as shown in the graph, we conclude that, when $a,b,c$ are almost equal, $G_1$ has the maximal Hosoya index. □

Let ${\mathcal{U}}_2$ be the set of unicyclic graphs of the form $G_2$ (as depicted in Figure 1), where $a+b=n-2$, $a\ge 2,b\ge 1$. Let $G_2^{*}$ be the graph of the form $G_2$ satisfying $0\le a-b\le 2$.

Theorem 2.

The graph $G_2^{*}$ has the maximum Hosoya index among all graphs in ${\mathcal{U}}_2$.

Proof. 

Assume $G_2\in {\mathcal{U}}_2$. By Lemmas 1 and 2, we obtain

$$\begin{array}{cc}\hfill z\left(G_2\right)& =z(G_2-v_1)+\sum _{v^{\prime }\in N_{G_2}\left(v_1\right)}z(G_2-\{v_1,v^{\prime }\})\hfill \\ & =z(G_2-v_1)+z(G_2-\{v_1,v_2\})+z(G_2-\{v_1,v_3\})\hfill \\ & +z(G_2-\{v_1,v_4\})+(b-1)z(G_2-\{v_1,y\})\hfill \\ & =2a+a+a+2+2a(b-1)\hfill \\ & =2ab+2a+2:=f_2(a,b),\hfill \end{array}$$

where y is one of pendent vertexs adjacent to $v_1$ in $G_2$.

If $b-a\ge 1$, then we get

$$f_2(a+1,b-1)-f_2(a,b)=2(b-a)>0.$$

If $a-b\ge 3$, then we get

$$f_2(a-1,b+1)-f_2(a,b)=2(a-b-2)>0.$$

Thus, we obtain the result. □

Let ${\mathcal{U}}_3$ be the set of unicyclic graph of the form $G_3$ (as depicted in Figure 1), where $v_1$ and $v_2$ are two vertices with $a-1$, $b-1$ pendent vertices satisfying $a+b=n-2,a,b\ge 1$, one of a and b is at least 2. Let $G_3^{*}$ be the graph of the form $G_3$ satisfying $a,b$ almost equal.

Theorem 3.

The graph $G_3^{*}$ has the maximum Hosoya index among all graphs in ${\mathcal{U}}_3$.

Proof. 

For $G_3\in {\mathcal{U}}_3$ with $a\ge b\ge 1$, by Lemmas 1 and 2, we obtain

$$\begin{array}{cc}\hfill z\left(G_3\right)& =z(G_3-v_1)+\sum _{v^{\prime }\in N_{G_3}\left(v_1\right)}z(G_3-\{v_1,v^{\prime }\})\hfill \\ & =z(G_3-v_1)+z(G_3-\{v_1,v_2\})+z(G_3-\{v_1,v_4\})\hfill \\ & +(a-1)z(G_3-\{v_1,y\})\hfill \\ & =(2b+1)+2+(b+1)+(a-1)(2b+1)\hfill \\ & =2ab+a+b+3:=f_3(a,b),\hfill \end{array}$$

where y is one of pendent vertex adjacent to $v_1$ in $G_3$.

If $a-b\ge 2$, then we get

$$\begin{array}{cc}\hfill f_3(a-1,b+1)-f_3(a,b)& =2(a-b-1)>0.\hfill \end{array}$$

Therefore, when a and b are almost equal, $G_2$ has the maximal Hosoya index. □

Let ${\mathcal{U}}_4$ be the set of unicyclic graphs of the form $G_4$ (as depicted in Figure 1), where $v_1$ and $v_2$ are two vertices with $a-1$, $b-1$ pendent vertices, respectively, $a+b=n-3$, $a,b\ge 1$. Let $G_4^{*}$ be the graph of the form $G_4$ satisfying $|a-b|\le 1$.

Theorem 4.

The graph $G_4^{*}$ has the maximum Hosoya index among all graphs in ${\mathcal{U}}_4$.

Proof. 

Assume $G_4\in {\mathcal{U}}_4$ with $a\ge 2,b\ge 1$. By Lemmas 1 and 2, we obtain

$$\begin{array}{cc}\hfill z\left(G_4\right)& =z(G_4-v_1)+\sum _{v^{\prime }\in N_{G_4}\left(v_1\right)}z(G_4-\{v_1,v^{\prime }\})\hfill \\ & =z(G_4-v_1-v_2)+\sum _{y\in N_{G_4-v_1}\left(v_2\right)}z(G_4-v_1-\{v_2,y\})\hfill \\ & +\sum _{v^{\prime }\in N_{G_4}\left(v_1\right)}z(G_4-\{v_1,v^{\prime }\})\hfill \\ & =z(G_4-v_1-v_2)+[z(G_4-v_1-\{v_2,v_3\})\hfill \\ & +(b-1)z(G_4-v_1-\{v_2,y\})]\hfill \\ & +[z(G_4-\{v_1,v_2\})+z(G_4-\{v_1,v_5\})\hfill \\ & +(a-1)z(G_4-\{v_1,v^{\prime }\})]\hfill \\ & =[3+2+3(b-1\left)\right]+[3+2b+1+(a-1\left)\right(3b+2\left)\right]\hfill \\ & =3ab+2a+2b+4:=f_4(a,b),\hfill \end{array}$$

where $v^{\prime }$ is a pendent vertex adjacent to $v_1$, y is a pendent vertex adjacent to $v_2$.

If $a-b\ge 2$, then we get

$$\begin{array}{cc}\hfill f_4(a-1,b+1)-f_4(a,b)& =3(a-b-1)>0.\hfill \end{array}$$

This implies the result. □

Theorem 5.

The graph $G_1^{*}$ has the maximum Hosoya index among all graphs in ${\mathcal{U}}_n^3$ if $n\ge 17$.

Proof. 

We only need to compare the Hosoya indices of $G_i^{*}$ for $i=1,2,3,4$.

For $G_1^{*}$, we assume that $a\le b\le c$. As $a,b,c$ are almost equal and $a+b+c=n$, then we have $a\ge \frac{n-2}{3}$. Thus,

$$\begin{array}{ccc}\hfill z\left(G_1^{*}\right)& =& abc+a+b+c\hfill \\ & \ge & \frac{{(n-2)}^3}{27}+n:=g_1\left(n\right).\hfill \end{array}$$

For $G_2^{*}$, as $0\le a-b\le 2$ and $a+b=n-2$, we have $a-2\le b\le a$ and thus $a\le \frac{n}{2}$. Thus

$$\begin{array}{ccc}\hfill z\left(G_2^{*}\right)& =& 2ab+2a+2\hfill \\ & \le & 2a^2+2a+2\hfill \\ & \le & \frac{n^2}{2}+n+2:=g_2\left(n\right).\hfill \end{array}$$

The last inequality holds for a function $f\left(a\right)=2a^2+2a+2$ that is strictly increasing for $1\le a\le \frac{n}{2}$.

For $G_3^{*}$, as $a,b$ are almost equal and $a+b=n-2$, then we have

$$\begin{array}{ccc}\hfill z\left(G_3^{*}\right)& =& 2ab+a+b+3\hfill \\ & \le & \frac{{(a+b)}^2}{2}+a+b+3\hfill \\ & =& \frac{{(n-2)}^2}{2}+n+1:=g_3\left(n\right).\hfill \end{array}$$

For $G_4^{*}$, as $a,b$ are almost equal and $a+b=n-3$, then we have

$$\begin{array}{ccc}\hfill z\left(G_4^{*}\right)& =& 3ab+2a+2b+4\hfill \\ & \le & \frac{3{(a+b)}^2}{4}+2(a+b)+4\hfill \\ & =& \frac{3{(n-3)}^2}{4}+2n-2:=g_4\left(n\right).\hfill \end{array}$$

By using the software “Mathematica”, we see $g_4\left(n\right)>g_2\left(n\right)>g_3\left(n\right)$ for $n\ge 14$, $g_1\left(n\right)>g_4\left(n\right)$ for $n\ge 17.$ A direct computation yields to $z\left(C_5\right)=11,z\left(C_6\right)=18,z\left(C_7\right)=29$.

From above, we obtain the result. □

3. The Unicyclic Graphs with Diameter 4

In this section, we aim to determine the maximal Hosoya index of unicyclic graphs with n vertices and diameter 4.

Let ${\mathcal{V}}_n^4$ be the set of all unicyclic graphs with n vertices and diameter 4. According to the length of the unique cycle and the distribution of other vertices, we may classify all the members in ${\mathcal{V}}_n^4$. Let ${\mathcal{V}}_i$ be the set of unicyclic graphs of the form $H_i$, $i=1,2,3,4,5,6,7,8$. It is easy to see that the graphs from ${\mathcal{V}}_1$, ${\mathcal{V}}_2$, ${\mathcal{V}}_3$, ${\mathcal{V}}_4$, ${\mathcal{V}}_5$, ${\mathcal{V}}_6$, ${\mathcal{V}}_7$, ${\mathcal{V}}_8$, and ${\mathcal{V}}_9$ and two cycles $C_8$ and $C_9$ are all members of the unicyclic graphs with diameter 4.

Let ${\mathcal{V}}_1$ be the set of unicyclic graphs of the form $H_1$ (as depicted in Figure 2), where $v_1$, $v_4$, and $v_5$ are three vertices with $c-1$, $b-1$, and $a-1$ pendent vertices, $a+b+c=n-2$, $a\ge 2,b\ge 1,c\ge 1$. Let $H_1^{*}$ be the graph of the form $H_1$ satisfying $0\le a-b\le 1,0\le a-c\le 2,0\le b-c\le 1$.

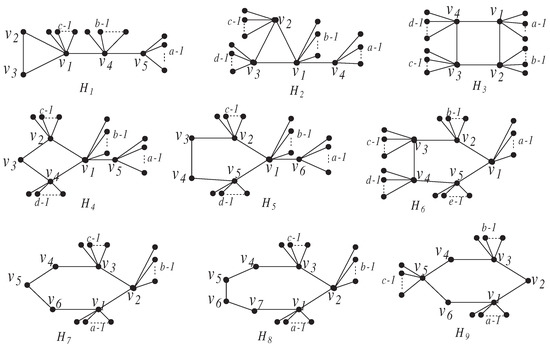
Figure 2. Eight unicyclic graphs with diameter 4.

Theorem 6.

The graph $H_1^{*}$ has the maximum Hosoya index among all graphs in ${\mathcal{V}}_1$.

Proof. 

For $H_1\in {\mathcal{V}}_1$, by Lemmas 1 and 2, we have

$$\begin{array}{cc}\hfill z\left(H_1\right)& =z(H_1-v_1)+\sum _{v^{\prime }\in N_{H_1}\left(v_1\right)}z(H_1-\{v_1,v^{\prime }\})\hfill \\ & =z(H_1-v_1)+z(H_1-\{v_1,v_2\})+z(H_1-\{v_1,v_3\})\hfill \\ & +z(H_1-\{v_1,v_4\})+(c-1)z(H_1-\{v_1,y\})\hfill \\ & =2(ab+1)+(ab+1)+(ab+1)+2a+2(c-1)(ab+1)\hfill \\ & =2abc+2ab+2a+2c+2:=g_1(a,b,c),\hfill \end{array}$$

where y is one pendent vertex adjacent to $v_1$ in $H_1$.

Case 1. If $b-a\ge 1$, then

$$\begin{array}{cc}\hfill g_1(a+1,b-1,c)-g_1(a,b,c)& =(b-a-1)(2c+2)+2>0.\hfill \end{array}$$

Case 2. If $a-b\ge 2$, then

$$\begin{array}{cc}\hfill g_1(a-1,b+1,c)-g_1(a,b,c)& =(a-b-1)(2c+2)-2\ge 2c>0.\hfill \end{array}$$

Cases 1 and 2 imply that, if $H_1$ has maximum Hosoya index, then we infer $0\le a-b\le 1$.

Case 3. If $c-a\ge 1$, then

$$\begin{array}{cc}\hfill g_1(a+1,b,c-1)-g_1(a,b,c)& =2b(c-a-1)+2b>0.\hfill \end{array}$$

Case 4. If $a-c\ge 3$, then

$$\begin{array}{cc}\hfill g_1(a-1,b,c+1)-g_1(a,b,c)& =2b(a-c-2)\ge 2b>0.\hfill \end{array}$$

Cases 3 and 4 imply that, if $H_1$ has maximum Hosoya index, then we infer $0\le a-c\le 2$.

Case 5. If $c-b\ge 1$, then

$$\begin{array}{cc}\hfill g_1(a,b+1,c-1)-g_1(a,b,c)& =2a(c-b)-2>0.\hfill \end{array}$$

Case 6. If $b-c\ge 2$, then

$$\begin{array}{cc}\hfill g_1(a,b-1,c+1)-g_1(a,b,c)& =2a(b-c-2)+2>0.\hfill \end{array}$$

Cases 5 and 6 imply that if $H_1$ has maximum Hosoya index, then we infer $0\le b-c\le 1$ are almost equal.

From the above, we get the result. □

Let ${\mathcal{V}}_2$ be the set of unicyclic graphs of the form $H_2$ (as depicted in Figure 2), where $v_4$, $v_1$, $v_2$, and $v_3$ are four vertices with $a-1$, $b-1$, $c-1$, and $d-1$ pendent vertices, respectively, $a+b+c+d=n$. As the diameter is 4, we infer $a\ge 2$ and one value of c and d is at least 2. Let $H_2^{*}$ be the graph of the form $H_2$ satisfying $0\le a-b\le 2$, $0\le a-c\le 1$, $|c-d|\le 1$.

Theorem 7.

The graph $H_2^{*}$ has the maximum Hosoya index among all graphs in ${\mathcal{V}}_2$.

Proof. 

For $H_2\in {\mathcal{V}}_2$, by Lemmas 1 and 2, we have

$$\begin{array}{cc}\hfill z\left(H_2\right)& =z(H_2-v_1)+\sum _{v^{\prime }\in N_{H_2}\left(v_1\right)}z(H_2-\{v_1,v^{\prime }\})\hfill \\ & =z(H_2-v_1)+z(H_2-\{v_1,v_2\})+z(H_2-\{v_1,v_3\})\hfill \\ & +z(H_2-\{v_1,v_4\})+(b-1)z(H_2-\{v_1,y\})\hfill \\ & =a(cd+1)+ad+ac+(cd+1)+a(b-1)(cd+1)\hfill \\ & =abcd+ab+ac+ad+cd+1:=g_2(a,b,c,d),\hfill \end{array}$$

where y is one of pendent vertex adjacent to $v_1$ in $H_2$.

Case 1. If $c-d\ge 2$, then

$$\begin{array}{cc}\hfill g_2(a,b,c-1,d+1)-g_2(a,b,c,d)& =(ab+1)(c-d-1)>0.\hfill \end{array}$$

Case 2. If $d-c\ge 2$, we infer

$$\begin{array}{cc}\hfill g_2(a,b,c+1,d-1)-g_2(a,b,c,d)& =(ab+1)(d-c-1)>0.\hfill \end{array}$$

Cases 1 and 2 imply that, if $H_2$ has maximum Hosoya index, then we infer $|c-d|\le 1$.

Case 3. If $a-b\ge 3$, then

$$\begin{array}{cc}\hfill g_2(a-1,b+1,c,d)-g_2(a,b,c,d)& =(a-b-1)cd\hfill \\ & +(a-b-1)-c-d\hfill \\ & \ge 2cd+2-c-d\hfill \\ & =cd+1+(c-1)(d-1)>0.\hfill \end{array}$$

Case 4. If $b-a\ge 1$, then

$$\begin{array}{cc}\hfill g_2(a+1,b-1,c,d)-g_2(a,b,c,d)& =(b-a-1)cd\hfill \\ & +(b-a-1)+c+d\hfill \\ & \ge c+d>0.\hfill \end{array}$$

Cases 3 and 4 imply that, if $H_2$ has maximum Hosoya index, then infer $0\le a-b\le 2$.

Case 5. If $a-c\ge 2$, then

$$\begin{array}{cc}\hfill g_2(a-1,b,c+1,d)-g_2(a,b,c,d)& =(a-c-1)bd\hfill \\ & -b+(a-c-1)\hfill \\ & \ge bd-b+1>0.\hfill \end{array}$$

Case 6. If $c-a\ge 1$, then

$$\begin{array}{cc}\hfill g_2(a+1,b,c-1,d)-g_2(a,b,c,d)& =(c-a-1)bd\hfill \\ & +b+(c-a-1)\hfill \\ & \ge b>0.\hfill \end{array}$$

Cases 5 and 6 imply that, if $H_2$ has maximum Hosoya index, then we infer $0\le a-c\le 1$.

From the above cases, we get the result. □

Let ${\mathcal{V}}_3$ be the set of unicyclic graphs of the form $H_3$ (as depicted in Figure 2), where $v_1$, $v_2$, $v_3$, and $v_4$ are four vertices with $a-1$, $b-1$, $c-1$, and $d-1$ pendent vertices, $a+b+c+d=n$, $a,b,c,d\ge 1$. As the diameter is 4, a and c, or b and d, are at least 2. Let $H_3^{*}$ be the graph of the form $H_3$ satisfying $a,b,c,d$ almost equal.

Theorem 8.

The graph $H_3^{*}$ has the maximum Hosoya index among all graphs in ${\mathcal{V}}_3$.

Proof. 

For $H_3\in {\mathcal{V}}_3$, by Lemmas 1 and 2, we have

$$\begin{array}{cc}\hfill z\left(H_3\right)& =z(H_3-v_1)+\sum _{v^{\prime }\in N_{H_3}\left(v_1\right)}z(H_3-\{v_1,v^{\prime }\}).\hfill \end{array}$$

For $z(H_3-v_1)$, by Lemma 1, we have

$$\begin{array}{cc}\hfill z(H_3-v_1)& =z(H_3-v_1-v_2)+\sum _{v^{\prime }\in N_{H_3-v_1}\left(v_2\right)}z(H_3-v_1-\{v_2,v^{\prime }\})\hfill \\ & =z(H_3-v_1-v_2)\hfill \\ & +z(H_3-v_1-\{v_2,v_3\})\hfill \\ & +(b-1)z(H_3-v_1-\{v_2,y\})\hfill \\ & =(cd+1)+d+(b-1)(cd+1)\hfill \\ & =bcd+b+d,\hfill \end{array}$$

where y is one pendent vertex adjacent to $v_2$ in $H_3$.

For ${\sum }_{v^{\prime }\in N_{H_3}\left(v_1\right)}z(H_3-\{v_1,v^{\prime }\})$, by Lemmas 1 and 2, we have

$$\begin{array}{c}\sum _{v^{\prime }\in N_{H_3}\left(v_1\right)}z(H_3-\{v_1,v^{\prime }\})\hfill \\ =z(H_3-\{v_1,v_2\})+z(H_3-\{v_1,v_4\})+(a-1)z(H_3-\{v_1,w\})\hfill \\ =(cd+1)+(bc+1)+(a-1)(bcd+b+d),\hfill \end{array}$$

where w is one of pendent vertex adjacent to $v_1$ in $H_3$. Therefore,

$$\begin{array}{cc}\hfill z\left(H_3\right)& =z(H_3-v_1)+\sum _{v^{\prime }\in N_{H_3}\left(v_1\right)}z(H_3-\{v_1,v^{\prime }\})\hfill \\ & =(bcd+b+d)+\left[\right(cd+1)+(bc+1)+(a-1\left)\right(bcd+b+d\left)\right]\hfill \\ & =abcd+ab+ad+bc+cd+2:=g_3(a,b,c,d).\hfill \end{array}$$

Case 1. If $a-c\ge 2$, then

$$\begin{array}{cc}\hfill g_3(a-1,b,c+1,d)-g_3(a,b,c,d)& =bd(a-c-1)>0.\hfill \end{array}$$

From Case 1, we have, when a and c are almost equal, $H_3$ has larger Hosoya index. Similarly, as $b,d$ have the same status as shown in the graph, we conclude that, when b and d are almost equal, $H_3$ has larger Hosoya index.

Case 2. If $a-b\ge 2$, then

$$\begin{array}{cc}\hfill g_3(a-1,b+1,c,d)-g_3(a,b,c,d)& =(a-b-1)cd\hfill \\ & +(a-b-1)-d+c\hfill \\ & \ge cd+1-d+c\hfill \\ & =(c-1)(d+1)+2>0.\hfill \end{array}$$

Therefore, from Case 2, when $H_3$ has maximum Hosoya index, we infer that a and b are almost equal, and, similarly, a and d are almost equal.

From Case 1, b and d are almost equal, so a, b and d are almost equal. Similarly, a, b and c are almost equal. Hence, we get $a,b,c,d$ are almost equal. □

Let ${\mathcal{V}}_4$ be the set of unicyclic graphs of the form $H_4$ (as depicted in Figure 2), where $v_5$, $v_1$, $v_2$, and $v_4$ are four vertices with $a-1$, $b-1$, $c-1$, and $d-1$ pendent vertices with $a+b+c+d=n$, $a\ge 2,b,c,d\ge 1$. Let $H_4^{*}$ be the graph of the form $H_4$ satisfying $0\le a-b\le 2,|c-d|\le 1,0\le a-c\le 1$.

Theorem 9.

The graph $H_4^{*}$ has the maximum Hosoya index among all graphs in ${\mathcal{V}}_4$.

Proof. 

For $H_4\in {\mathcal{V}}_4$, by Lemmas 1 and 2, we have

$$\begin{array}{cc}\hfill z\left(H_4\right)& =z(H_4-v_1)+\sum _{v^{\prime }\in N_{H_4}\left(v_1\right)}z(H_4-\{v_1,v^{\prime }\}).\hfill \end{array}$$

For $z(H_4-v_1)$, by Lemma 1, we get

$$\begin{array}{cc}\hfill z(H_4-v_1)& =z(H_4-v_1-v_2)+\sum _{v^{\prime }\in N_{H_4-v_1}\left(v_2\right)}z(H_4-v_1-\{v_2,v^{\prime }\})\hfill \\ & =z(H_4-v_1-v_2)+z(H_4-v_1-\{v_2,v_3\})\hfill \\ & +(c-1)z(H_4-v_1-\{v_2,y\})\hfill \\ & =a(d+1)+ad+(c-1)a(d+1)\hfill \\ & =acd+ac+ad,\hfill \end{array}$$

where y is one pendent vertex adjacent to $v_2$ in $H_4$. For ${\sum }_{v^{\prime }\in N_{H_4}\left(v_1\right)}z(H_4-\{v_1,v^{\prime }\})$, by Lemmas 1 and 2,

$$\begin{array}{cc}\hfill \sum _{v^{\prime }\in N_{H_4}\left(v_1\right)}z(H_4-\{v_1,v^{\prime }\})& =z(H_4-\{v_1,v_2\})+z(H_4-\{v_1,v_4\})\hfill \\ & +z(H_4-\{v_1,v_5\})\hfill \\ & +(b-1)z(H_4-\{v_1,v_{b-1}\})\hfill \\ & =z(H_4-\{v_1,v_2\})\hfill \\ & +z(H_4-\{v_1,v_4\})\hfill \\ & +[z(H_4-\{v_1,v_5\}-v_2)\hfill \\ & +z(H_4-\{v_1,v_5\}-\{v_2,v_3\})\hfill \\ & +(c-1)z(H_4-\{v_1,v_5\}-\{v_2,y\})]\hfill \\ & +(b-1)z(H_4-\{v_1,w\})\hfill \\ & =a(d+1)+a(c+1)\hfill \\ & +(cd+c+d)\hfill \\ & +(b-1)(acd+ac+ad),\hfill \end{array}$$

where w is one pendent vertex adjacent to $v_1$ in $H_4$. Hence, it follows that

$$\begin{array}{cc}\hfill z\left(H_4\right)& =z(H_4-v_1)+\sum _{v^{\prime }\in N_{H_4}\left(v_1\right)}z(H_4-\{v_1,v^{\prime }\})\hfill \\ & =(acd+ac+ad)\hfill \\ & +\left[a\right(d+1)+a(c+1)\hfill \\ & +(cd+c+d)+(b-1)(acd+ac+ad)]\hfill \\ & =abcd+abc+abd+ac+ad+cd+2a+c+d\hfill \\ & :=g_4(a,b,c,d).\hfill \end{array}$$

Case 1. If $c-d\ge 2$, then

$$\begin{array}{cc}\hfill g_4(a,b,c-1,d+1)-g_4(a,b,c,d)& -(abcd+abc\hfill \\ & +abd+ac+ad\hfill \\ & +cd+2a+c+d)\hfill \\ & =(ab+1)(c-d-1)>0.\hfill \end{array}$$

Similarly, if $d-c\ge 2$, then we have

$$\begin{array}{cc}\hfill g_4(a,b,c+1,d-1)-g_4(a,b,c,d)& =(ab+1)(d-c-1)>0.\hfill \end{array}$$

Cases 1 implies that, if $H_4$ has the maximum Hosoya index, we conclude $|d-c|\le 1$.

Case 2. If $a-b\ge 3$, then

$$\begin{array}{cc}\hfill g_4(a-1,b+1,c,d)-g_4(a,b,c,d)& =(a-b-1)cd\hfill \\ & +(a-b-1)(c+d)\hfill \\ & -c-d-2\hfill \\ & \ge 2cd+c+d-2>0.\hfill \end{array}$$

Case 3. If $b-a\ge 1$, then

$$\begin{array}{c}{g}_4(a+1,b-1,c,d)-g_4(a,b,c,d)\hfill \\ =(b-a-1)cd+(b-a-1)(c+d)+c+d+2\hfill \\ \ge c+d+2>0.\hfill \end{array}$$

Cases 2 and 3 imply that, if $H_4$ has the maximum Hosoya index, we conclude $0\le a-b\le 2$.

Case 4. If $a-c\ge 2$, then

$$\begin{array}{cc}\hfill g_4(a-1,b,c+1,d)-g_4(a,b,c,d)& =(a-c-1)bd\hfill \\ & +(a-c-1)b\hfill \\ & -bd+(a-c-1)-1>0.\hfill \end{array}$$

Case 5. If $c-a\ge 1$, then

$$\begin{array}{cc}\hfill g_4(a+1,b,c-1,d)-g_4(a,b,c,d)& =(c-a-1)bd\hfill \\ & +(c-a-1)b+bd\hfill \\ & +(c-a-1)+1>0.\hfill \end{array}$$

Thus, we have $z\left(H_{46}\right)>z\left(H_4\right)$.

Cases 4 and 5 imply that, if $H_4$ has the maximum Hosoya index, we conclude $0\le a-c\le 1$.

All the above cases imply the desired result. □

Let ${\mathcal{V}}_5$ be the set of unicyclic graphs of the form $H_5$ (as depicted in Figure 2), where $v_6$, $v_1$, $v_2$, and $v_5$ are four vertices with $a-1$, $b-1$, $c-1$, and $d-1$ pendent vertices, $a+b+c+d=n-2$, and $a\ge 2,b,c,d\ge 1$. Let $H_5^{*}$ be the graph of the form $H_5$ satisfying $0\le a-b\le 2,|c-d|\le 1,0\le a-c\le 1$.

Theorem 10.

The graph $H_5^{*}$ has the maximum Hosoya index among all graphs in ${\mathcal{V}}_5$.

Proof. 

For $H_5\in {\mathcal{V}}_5$, by Lemmas 1 and 2,

$$\begin{array}{cc}\hfill z\left(H_5\right)& =z(H_5-v_1)+\sum _{v^{\prime }\in N_{H_5}\left(v_1\right)}z(H_5-\{v_1,v^{\prime }\})\hfill \\ & =z(H_5-v_1)+z(H_5-\{v_1,v_2\})+z(H_5-\{v_1,v_5\})\hfill \\ & +z(H_5-\{v_1,v_6\})+(b-1)z(H_5-\{v_1,y\}),\hfill \end{array}$$

where y is one pendent vertex adjacent to $v_1$ in $H_5$.

For $z(H_5-v_1)$, By Lemma 1, we have

$$\begin{array}{cc}\hfill z(H_5-v_1)& =z(H_5-v_1-v_2)+\sum _{v^{\prime }\in N_{H_5-v_1}\left(v_2\right)}z(H_5-v_1-\{v_2,v^{\prime }\})\hfill \\ & =z(H_5-v_1-v_2)+z(H_5-v_1-\{v_2,v_3\})\hfill \\ & +(c-1)z(H_5-v_1-\{v_2,w\})\hfill \\ & =a(2d+1)+a(d+1)+(c-1)a(2d+1)\hfill \\ & =2acd+ac+ad+a,\hfill \end{array}$$

where w is one pendent vertex adjacent to $v_2$ in $H_5$, $z(H_5-\{v_1,v_2\})=a(2d+1)$, and $z(H_5-\{v_1,v_3\})=a(2c+1)$. Therefore,

$$\begin{array}{cc}\hfill z\left(H_5\right)& =(2acd+ac+ad+a)+a(2d+1)+a(2c+1)\hfill \\ & +(2cd+c+d+1)+(b-1)(2acd+ac+ad+a)\hfill \\ & =2abcd+abc+abd+ab+2ac\hfill \\ & +2ad+2cd+2a+c+d+1:=g_5(a,b,c,d).\hfill \end{array}$$

Case 1. If $c-d\ge 2$, then

$$\begin{array}{cc}\hfill g_5(a,b,c-1,d+1)-g_5(a,b,c,d)& =(2ab+2)(c-d-1)>0.\hfill \end{array}$$

Case 2. If $d-c\ge 2$, this yields to

$$g_5(a,b,c+1,d-1)-g_5(a,b,c,d)=(2ab+2)(d-c-1)>0.$$

Cases 1 and 2 imply that, if $H_5$ has the maximum Hosoya index, we infer $|d-c|\le 1$.

Case 3. If $a-b\ge 3$, then

$$\begin{array}{cc}\hfill g_5(a-1,b+1,c,d)-g_5(a,b,c,d)& =(2cd+c+d+1)(a-b-1)\hfill \\ & -2c-2d-2\hfill \\ & \ge 4cd>0.\hfill \end{array}$$

Case 4. If $b-a\ge 1$, then

$$\begin{array}{cc}\hfill g_5(a+1,b-1,c,d)-g_5(a,b,c,d)& =(2cd+c+d+1)(b-a-1)\hfill \\ & +2c+2d+2>0.\hfill \end{array}$$

Cases 3 and 4 imply that, if $H_5$ has the maximum Hosoya index, we conclude $0\le a-b\le 2$.

Case 5. If $a-c\ge 2$, then

$$\begin{array}{cc}\hfill g_5(a-1,b,c+1,d)-g_5(a,b,c,d)& =(2bd+b+2)(a-c-1)\hfill \\ & -bd-b-1\ge bd+1>0.\hfill \end{array}$$

Case 6. If $c-a\ge 1$, then

$$\begin{array}{cc}\hfill g_5(a+1,b,c-1,d)-g_5(a,b,c,d)& =(2bd+b+2)(c-a-1)\hfill \\ & +bd+b+1>0.\hfill \end{array}$$

Cases 5 and 6 imply that, if $H_5$ has the maximum Hosoya index, we conclude $0\le a-c\le 1$.

From all above, we get the result. □

Let ${\mathcal{V}}_6$ be the set of unicyclic graphs of the form $H_6$ (as depicted in Figure 2), where $v_1$, $v_2$, $v_3$, $v_4$, and $v_5$ are five vertices with $a-1$, $b-1$, $c-1$, $d-1$, and $e-1$ pendent vertices, $a+b+c+d+e=n$, and $a,b,c,d,e\ge 1$. As the diameter is 4, from symmetry, we may assume a and c, or a and d, are at least 2. Let $H_6^{*}$ be the graph of the form $H_6$ satisfying $a,b,c,d,e$ almost equal.

Theorem 11.

The graph $H_6^{*}$ has the maximum Hosoya index among all graphs in ${\mathcal{V}}_6$.

Proof. 

For $H_6\in {\mathcal{V}}_6$, by Lemmas 1 and 2, we have

$$\begin{array}{cc}\hfill z\left(H_6\right)& =z(H_6-v_1)+\sum _{v^{\prime }\in N_{H_6}\left(v_1\right)}z(H_6-\{v_1,v^{\prime }\})\hfill \\ & =z(H_6-v_1)+z(H_6-\{v_1,v_2\})+z(H_6-\{v_1,v_5\})\hfill \\ & +(a-1)z(H_6-\{v_1,y\}),\hfill \end{array}$$

where y is one pendent vertex adjacent to $v_1$ in $H_6$.

For $z(H_6-v_1)$, by Lemma 1, we have

$$\begin{array}{cc}\hfill z(H_6-v_1)& =z(H_6-v_1-v_2)+\sum _{v^{\prime }\in N_{H_6-v_1}\left(v_2\right)}z(H_6-v_1-\{v_2,v^{\prime }\})\hfill \\ & =z(H_6-v_1-v_2)+z(H_6-v_1-\{v_2,v_3\})\hfill \\ & +(b-1)z(H_6-v_1-\{v_2,v_{b-1}\})\hfill \\ & =[z(H_6-v_1-v_2-v_3)+z(H_6-v_1-v_2-\{v_3,v_4\})\hfill \\ & +(c-1)z(H_6-v_1-v_2-\{v_3,v_{c-1}\})]\hfill \\ & +z(H_6-v_1-\{v_2,v_3\})\hfill \\ & +(b-1)z(H_6-v_1-\{v_2,v_{b-1}\})\hfill \\ & =\left[\right(de+1)+e+(c-1\left)\right(de+1\left)\right]\hfill \\ & +(de+1)+(b-1)(cde+c+e)\hfill \\ & =bcde+bc+be+de+1,\hfill \end{array}$$

where $v_{b-1}$ is one pendent vertex adjacent to $v_2$ in $H_6$, $v_{c-1}$ is one pendent vertex adjacent to $v_3$, $z(H_6-\{v_1,v_2\})=cde+c+e$, and

$$\begin{array}{cc}\hfill z(H_6-\{v_1,v_5\})& =z(H_6-\{v_1,v_5\}-v_4)+z(H_6-\{v_1,v_5\}\hfill \\ & -\{v_4,v_3\})+(d-1)z(H_6-\{v_1,v_5\}\hfill \\ & -\{v_4,v_{d-1}\})\hfill \\ & =(bc+1)+b+(d-1)(bc+1)\hfill \\ & =bcd+b+d.\hfill \end{array}$$

Therefore, we obtain

$$\begin{array}{cc}\hfill z\left(H_6\right)& =(bcde+bc+be+de+1)\hfill \\ & +(cde+c+e)+(bcd+b+d)\hfill \\ & +(a-1)(bcde+bc+be+de+1)\hfill \\ & =abcde+abc+abe+ade\hfill \\ & +bcd+cde+a+b+c+d+e.\hfill \end{array}$$

If $a-b\ge 2$, let $H_6^{\prime }$ be the graph obtained from $H_6$ by removing a pendent edge at $v_1$ to $v_2$. Then, we get

$$\begin{array}{cc}\hfill z\left(H_6^{\prime }\right)-z\left(H_6\right)& =(a-b-1)cde+(a-b-1)(c+e)-de+cd\hfill \\ & \ge cde+c+e-de+cd\hfill \\ & =(c-1)de+cd+c+e>0.\hfill \end{array}$$

As $a,b,c,d,e$ have the same status as depicted in Figure 2, we obtain that, when $a,b,c,d,e$ are almost equal, $H_6$ has the maximal Hosoya index. □

Let ${\mathcal{V}}_7$ be the set of unicyclic graphs of the form $H_7$ (as depicted in Figure 2), where $v_1$, $v_2$, and $v_3$ are three vertices with $a-1$, $b-1$, and $c-1$ pendent vertices, $a+b+c=n-3$, $a,b,c\ge 1$, and one of $a,b,c$ is at least 2. Let $H_7^{*}$ be the graph of the form $H_7$ satisfying $a,b,c$ almost equal.

Theorem 12.

The graph $H_7^{*}$ has the maximum Hosoya index among all graphs in ${\mathcal{V}}_7$.

Proof. 

For $H_7\in {\mathcal{V}}_7$, by Lemmas 1 and 2, we have

$$\begin{array}{cc}\hfill z\left(H_7\right)& =z(H_7-v_1)+\sum _{v^{\prime }\in N_{H_7}\left(v_1\right)}z(H_7-\{v_1,v^{\prime }\})\hfill \\ & =z(H_7-v_1)+z(H_7-\{v_1,v_2\})\hfill \\ & +z(H_7-\{v_1,v_6\})+(a-1)z(H_7-\{v_1,v_{a-1}\}),\hfill \end{array}$$

where $v_{a-1}$ is one pendent vertex adjacent to $v_1$ in $H_7$.

For $z(H_7-v_1)$, by Lemma 1, we have

$$\begin{array}{cc}\hfill z(H_7-v_1)& =z(H_7-v_1-v_2)+\sum _{v^{\prime }\in N_{H_7-v_1}\left(v_2\right)}z(H_7-v_1-\{v_2,v^{\prime }\})\hfill \\ & =[3+2+3(c-1\left)\right]+3+(b-1)(3c+2)\hfill \\ & =3bc+2b+3,\hfill \end{array}$$

where $v_{c-1}$ is one pendent vertex adjacent to $v_3$, $v_{b-1}$ is one pendent vertex adjacent to $v_2$ in $H_7$, $z(H_7-\{v_1,v_2\})=3c+2$, and

$$\begin{array}{cc}\hfill z(H_7-\{v_1,v_6\})& =\left[b\right(c+1)+1]+b(c+1)\hfill \\ & =2bc+b+2.\hfill \end{array}$$

Therefore, we obtain

$$\begin{array}{cc}\hfill z\left(H_7\right)& =(3bc+2b+3)+(3c+2)\hfill \\ & +(2bc+b+2)+(a-1)(3bc+2b+3)\hfill \\ & =3abc+2ab+2bc+3a+b+3c+4:=g_7(a,b,c).\hfill \end{array}$$

Case 1. If $a-b\ge 2$, then

$$\begin{array}{cc}\hfill g_7(a-1,b+1,c)-g_7(a,b,c)& =(3c+2)(a-b-1)\hfill \\ & +2c-2\ge 5c>0.\hfill \end{array}$$

Case 2. If $b-a\ge 2$, then we conclude

$$\begin{array}{cc}\hfill g_7(a+1,b-1,c)-g_7(a,b,c)& =(3c+2)(b-a-1)\hfill \\ & -2c+2>0.\hfill \end{array}$$

Cases 1 and 2 imply that, if $H_7$ has the maximum Hosoya index, we conclude $|a-b|\le 1$. Similarly, by using symmetry, we may obtain $|c-b|\le 1$.

Case 3. If $a-c\ge 2$, then

$$\begin{array}{cc}\hfill g_7(a-1,b,c+1)-g_7(a,b,c)& =3b(a-c-1)>0.\hfill \end{array}$$

Case 4. If $c-a\ge 2$, then get

$$g_7(a+1,b,c-1)-g_7(a,b,c)=3b(c-a-1)>0.$$

Cases 3 and 4 imply that, if $H_7$ has the maximum Hosoya index, we conclude $|a-c|\le 1$.

In conclusion, when $a,b,c$ are almost equal, $H_7$ has the maximal Hosoya index. □

Let ${\mathcal{V}}_8$ be the set of unicyclic graphs of the form $H_8$ (as depicted in Figure 2), where $v_1$, $v_2$, and $v_3$ are three vertices with $a-1$, $b-1$, and $c-1$ pendent vertices, $a+b+c=n-4$, $a,b,c\ge 1$, NS one of $a,b,c$ is at least 2. Let $H_8^{*}$ be the graph of the form $H_8$ satisfying $a,b,c$ almost equal.

Theorem 13.

The graph $H_8^{*}$ has the maximum Hosoya index among all graphs in ${\mathcal{V}}_8$.

Proof. 

For $H_8\in {\mathcal{V}}_8$, by Lemmas 1 and 2, we have

$$\begin{array}{cc}\hfill z\left(H_8\right)& =z(H_8-v_1)+\sum _{v^{\prime }\in N_{H_8}\left(v_1\right)}z(H_8-\{v_1,v^{\prime }\})\hfill \\ & =z(H_8-v_1)+z(H_8-\{v_1,v_2\})\hfill \\ & +z(H_8-\{v_1,v_7\})+(a-1)z(H_8-\{v_1,v_{1,a-1}\}),\hfill \end{array}$$

where $v_{a-1}$ is one pendent vertex adjacent to $v_1$ in $H_8$.

For $z(H_8-v_1)$, by Lemma 1, we have

$$\begin{array}{cc}\hfill z(H_8-v_1)& =z(H_8-v_1-v_2)\hfill \\ & +\sum _{v^{\prime }\in N_{H_8-v_1}\left(v_2\right)}z(H_8-v_1-\{v_2,v^{\prime }\})\hfill \\ & =z(H_8-v_1-v_2)+z(H_8-v_1-\{v_2,v_3\})\hfill \\ & +(b-1)z(H_8-v_1-\{v_2,v_{b-1}\})\hfill \\ & =[z(H_8-v_1-v_2-v_3)\hfill \\ & +z(H_8-v_1-v_2-\{v_3,v_4\})\hfill \\ & +(c-1)z(H_8-v_1-v_2-\{v_3,v_{c-1}\})]\hfill \\ & +z(H_8-v_1-\{v_2,v_3\})\hfill \\ & +(b-1)z(H_8-v_1-\{v_2,v_{b-1}\})\hfill \\ & =[5+3+5(c-1\left)\right]+5+(b-1)(5c+3)\hfill \\ & =5bc+3b+5,\hfill \end{array}$$

where $v_{c-1}$ is one pendent vertex adjacent to $v_3$ in $H_8$, $v_{b-1}$ is one pendent vertex adjacent to $v_2$ in $H_8$, $z(H_8-\{v_1,v_2\})=5c+3$, and

$$\begin{array}{cc}\hfill z(H_8-\{v_1,v_7\})& =z(H_8-\{v_1,v_7\}-v_6)\hfill \\ & +z(H_8-\{v_1,v_7\}-\{v_6,v_5\})\hfill \\ & =z(H_8-\{v_1,v_7\}-v_6-v_5)\hfill \\ & +z(H_8-\{v_1,v_7\}-v_6-\{v_5,v_4\})]\hfill \\ & +z(H_8-\{v_1,v_7\}-\{v_6,v_5\})\hfill \\ & =2\left[b\right(c+1)+1]+bc+1\hfill \\ & =3bc+2b+3.\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill z\left(H_8\right)& =(5bc+3b+5)+(5c+3)\hfill \\ & +(3bc+2b+3)+(a-1)(5bc+3b+5)\hfill \\ & =5abc+3ab+3bc+5a+2b+5c+6:=g_8(a,b,c).\hfill \end{array}$$

Case 1. If $a-b\ge 2$, then

$$\begin{array}{cc}\hfill g_8(a-1,b+1,c)-g_8(a,b,c)& =(5c+3)(a-b-1)\hfill \\ & +3c-3\ge 8c>0.\hfill \end{array}$$

Case 2. If $b-a\ge 2$, then

$$\begin{array}{cc}\hfill g_8(a+1,b-1,c)-g_8(a,b,c)& =(5c+3)(b-a-1)\hfill \\ & -3c+3\ge 2c+6>0.\hfill \end{array}$$

Cases 1 and 2 imply that, if $H_8$ has the maximum Hosoya index, we conclude $|a-b|\le 1$. Similarly, we obtain $|c-b|\le 1$.

Case 3. If $a-c\ge 2$, then

$$\begin{array}{cc}\hfill g_8(a-1,b,c+1)-g_8(a,b,c)& =5b(a-c-1)>0.\hfill \end{array}$$

Case 4. If $c-a\ge 2$, then we have

$$g_8(a+1,b,c-1)-g_8(a,b,c)=5b(c-a-1)>0.$$

Cases 3 and 4 imply that, if $H_8$ has the maximum Hosoya index, we conclude $|a-c|\le 1$.

In conclusion, when $a,b,c$ are almost equal, $H_8$ has the maximal Hosoya index. □

Let ${\mathcal{V}}_9$ be the set of unicyclic graphs of the form $H_9$ (as depicted in Figure 2), where $v_1$, $v_3$, and $v_5$ are three vertices with $a-1$, $b-1$, and $c-1$ pendent vertices, $a+b+c=n-3$, $a,b,c\ge 1$, and one of $a,b,c$ is at least 2. Let $H_9^{*}$ be the graph of the form $H_9$ satisfying $a,b,c$ almost equal.

Theorem 14.

The graph $H_9^{*}$ has the maximum Hosoya index among all graphs in ${\mathcal{V}}_9$.

Proof. 

For $H_9\in {\mathcal{V}}_9$, from Lemmas 1 and 2, we have

$$\begin{array}{cc}\hfill z\left(H_9\right)& =z(H_9-v_1)+\sum _{v^{\prime }\in N_{H_9}\left(v_1\right)}z(H_9-\{v_1,v^{\prime }\})\hfill \\ & =z(H_9-v_1)+z(H_9-\{v_1,v_2\})\hfill \\ & +z(H_9-\{v_1,v_6\})+(a-1)z(H_9-\{v_1,v_{1,a-1}\}).\hfill \end{array}$$

For $z(H_9-v_1)$, by Lemmas 1 and 2, we have

$$\begin{array}{cc}\hfill z(H_9-v_1)& =z(H_9-v_1-v_2)\hfill \\ & +\sum _{v^{\prime }\in N_{H_9-v_1}\left(v_2\right)}z(H_9-v_1-\{v_2,v^{\prime }\})\hfill \\ & =z(H_9-v_1-v_2)+z(H_9-v_1-\{v_2,v_3\})\hfill \\ & =[z(H_9-v_1-v_2-v_3)+z(H_9-v_1-v_2-\{v_3,v_4\})\hfill \\ & +(b-1)z(H_9-v_1-v_2-\{v_3,x\})]\hfill \\ & +z(H_9-v_1-\{v_2,v_3\})\hfill \\ & =\left[\right(c+2)+(c+1)+(b-1\left)\right(c+2\left)\right]+(c+2)\hfill \\ & =bc+2b+2c+3.\hfill \end{array}$$

Here, x is a pendent vertex attached at $v_3$.

Observe that $z(H_9-\{v_1,v_2\})=bc+2b+c+1$,

$$\begin{array}{cc}\hfill z(H_9-\{v_1,v_6\})& =z(H_9-\{v_1,v_6\}-v_5)\hfill \\ & +z(H_9-\{v_1,v_6\}-\{v_5,v_4\})\hfill \\ & +(c-1)z(H_9-\{v_1,v_6\}-\{v_5,y\})\hfill \\ & =(b+2)+(b+1)+(c-1)(b+2)\hfill \\ & =bc+b+2c+1,\hfill \end{array}$$

where y is one pendent vertex attached at $v_5$.

Thus, we obtain

$$\begin{array}{cc}\hfill z\left(H_9\right)& =z(H_9-v_1)+z(H_9-\{v_1,v_2\})\hfill \\ & +z(H_9-\{v_1,v_6\})+(a-1)z(H_9-\{v_1,v_{1,a-1}\})\hfill \\ & =(bc+2b+2c+3)+(bc+2b+c+1)\hfill \\ & +(bc+b+2c+1)+(a-1)(bc+2b+2c+3)\hfill \\ & =abc+2ab+2ac+2bc+3a+3b+3c+2:=g_9(a,b,c).\hfill \end{array}$$

If $a-b\ge 2$, then we have

$$\begin{array}{c}{g}_9(a-1,b+1,c)-g_9(a,b,c)\hfill \\ =\left[\right(a-1\left)\right(b+1)c+2(a-1\left)\right(b+1)\hfill \\ +2(a-1)c+2(b+1)c+3(a-1)\hfill \\ +3(b+1)+3c+2]\hfill \\ -(abc+2ab+2ac+2bc+3a+3b+3c+2)\hfill \\ =(c+2)(a-b-1)\hfill \\ \ge 0.\hfill \end{array}$$

Thus, we have $z\left(H_{91}\right)>z\left(H_9\right)$.

This implies that, if $H_9$ has the maximum Hosoya index, we conclude $|a-c|\le 1$.

As $b,c$ (resp. a, c) have the same status as shown in Figure 2, we also have $|b-c|\le 1$. $|a-c|\le 1$. This is the desired result. □

Theorem 15.

The graph $H_6^{*}$ has the maximum Hosoya index among all graphs in ${\mathcal{V}}_n^4$ for $n\ge 50$.

Proof. 

We need only compare $z\left(H_i^{*}\right)$ for $1\le i\le 8$.

For $H_1^{*}$, as $0\le a-b\le 1,0\le a-c\le 2,0\le b-c\le 1$, we have $b\le a,c\le a,c\le b\le a$, and $b\ge a-1,c\ge a-2$. Since $a+b+c=n-2$, we get $n-2=a+b+c\ge a+a-1+a-2=3a-3$, this leads to $a\le \frac{n+1}{3}$. Therefore,

$$\begin{array}{ccc}\hfill z\left(H_1^{*}\right)& =& 2abc+2ab+2a+2c+2\hfill \\ & \le & 2a^3+2a^2+4a+2\hfill \\ & \le & \frac{2{(n+1)}^3}{27}+\frac{2{(n+1)}^2}{9}+\frac{4(n+1)}{3}+2:=h_1\left(n\right)\hfill \end{array}$$

The last inequality holds for a function $f_1\left(a\right)=2a^3+2a^2+4a+2$ that is strictly increasing for $2\le a\le \frac{n+1}{3}$.

For $H_2^{*}$, we have $0\le a-b\le 2$, $0\le a-c\le 1$, $|c-d|\le 1$. We may assume $0\le c-d\le 1$ without loss of generality. Then, $b\le a,c\le a,d\le c\le a$, and $b\ge a-2,c\ge a-1,d\ge c-1\ge a-2$. Thus, $n=a+b+c+d\ge a+a-2+a-1+a-2=4a-5$, and hence $a\le \frac{n+5}{4}$. Therefore,

$$\begin{array}{ccc}\hfill z\left(H_2^{*}\right)& =& abcd+ab+ac+ad+cd+1\hfill \\ & \le & a^4+4a^2+1\hfill \\ & \le & \frac{{(n+5)}^4}{256}+\frac{{(n+5)}^2}{4}+1:=h_2\left(n\right).\hfill \end{array}$$

The last inequality holds for a function $f_2\left(a\right)=a^4+4a^2+1$ that is strictly increasing for $2\le a\le \frac{n+5}{4}$.

For $H_3^{*}$, as $a,b,c,d$ are almost equal and $a+b+c+d=n$, we have $a,b,c,d\le \frac{n+3}{4}$

$$\begin{array}{ccc}\hfill z\left(H_3^{*}\right)& =& abcd+ab+ad+bc+cd+2\hfill \\ & \le & \frac{{(n+3)}^4}{256}+\frac{{(n+3)}^2}{4}+2:=h_3\left(n\right).\hfill \end{array}$$

For $H_4^{*}$, $0\le a-b\le 2,|c-d|\le 1,0\le a-c\le 1$. We may assume $0\le c-d\le 1$ without loss of generality. Then, $b\le a,c\le a,d\le c\le a$, and $b\ge a-2,c\ge a-1,d\ge c-1\ge a-2$. Thus, $n-1=a+b+c+d\ge a+a-2+a-1+a-2=4a-5$, and hence $a\le \frac{n+4}{4}$. Therefore,

$$\begin{array}{ccc}\hfill z\left(H_4^{*}\right)& =& abcd+abc+abd+ac+ad+cd+2a+c+d\hfill \\ & \le & a^4+2a^3+3a^2+4a\hfill \\ & \le & {\left(\frac{n+4}{4}\right)}^4+2{\left(\frac{n+4}{4}\right)}^3+3{\left(\frac{n+4}{4}\right)}^2+4\frac{n+4}{4}\hfill \\ & =& \frac{{(n+4)}^4}{256}+\frac{{(n+4)}^3}{32}+\frac{3{(n+4)}^2}{16}+n+4:=h_4\left(n\right).\hfill \end{array}$$

The last inequality holds for a function $f_3\left(a\right)=a^4+2a^3+3a^2+4a$ that is strictly increasing for $2\le a\le \frac{n+4}{4}$.

For $H_5^{*}$, $0\le a-b\le 2,|c-d|\le 1,0\le a-c\le 1$. We may assume $0\le c-d\le 1$ without loss of generality. Then, $b\le a,c\le a,d\le c\le a$, and $b\ge a-2,c\ge a-1,d\ge c-1\ge a-2$. Thus, $n-2=a+b+c+d\ge a+a-2+a-1+a-2=4a-5$, and hence $a\le \frac{n+3}{4}$. Therefore,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill z\left(H_5^{*}\right)& =2abcd+abc+abd+ab\hfill \\ & +2ac+2ad+2cd+2a+c+d+1\hfill \\ & \le 2a^4+2a^3+7a^2+4a+1\hfill \\ & \le 2{\left(\frac{n+3}{4}\right)}^4+2{\left(\frac{n+3}{4}\right)}^3\hfill \\ & +7{\left(\frac{n+3}{4}\right)}^2+4\left(\frac{n+3}{4}\right)+1:=h_5\left(n\right).\hfill \end{array}\end{array}$$

The last inequality holds for a function $f_4\left(a\right)=2a^4+2a^3+7a^2+4a+1$ that is strictly increasing for $2\le a\le \frac{n+3}{4}$.

For $H_6^{*}$, $a,b,c,d,e$ are almost equal. Then, $a,b,c,d,e\ge \frac{n-4}{5}$ as $a+b+c+d+e=n$. Therefore,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill z\left(H_6^{*}\right)& =abcde+abc+abe+ade+bcd+cde\hfill \\ & +a+b+c+d+e\hfill \\ & \ge {\left(\frac{n-4}{5}\right)}^5+5{\left(\frac{n-4}{5}\right)}^3+5\frac{n-4}{5}:=h_6\left(n\right).\hfill \end{array}\end{array}$$

For $H_7^{*}$, $a,b,c$ are almost equal. We may assume $a-1\le b\le a+1,0\le a-c\le 1$. Then, we have $b\le a+1,c\le a$, and $b\ge a-1,c\ge a-1$. Thus, $n-3=a+b+c\ge a+a-1+a-1=3a-2$, and hence $a\le \frac{n-1}{3}$. Therefore,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill z\left(H_7^{*}\right)& =3abc+2ab+2bc+3a+b+3c+4\hfill \\ & \le 3a^2(a+1)+2a(a+1)+2a(a+1)\hfill \\ & +3a+a+1+3a+4\hfill \\ & =3a^3+7a^2+11a+5\hfill \\ & \le 3{\left(\frac{n-1}{3}\right)}^3+7{\left(\frac{n-1}{3}\right)}^2+11\frac{n-1}{3}+5:=h_7\left(n\right).\hfill \end{array}\end{array}$$

The last inequality holds for a function $f_5\left(a\right)=3a^3+7a^2+11a+5$ which is strictly increasing for $1\le a\le \frac{n-1}{3}$.

Let $H_8^{*}$, $a,b,c$ are almost equal. We may assume $a-1\le b\le a+1,0\le a-c\le 1$. Then, we have $b\le a+1,c\le a$, and $b\ge a-1,c\ge a-1$. Thus, $n-4=a+b+c\ge a+a-1+a-1=3a-2$, and hence $a\le \frac{n-2}{3}$. Therefore,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill z\left(H_8^{*}\right)& =5abc+3ab+3bc+5a+2b+5c+6\hfill \\ & \le 5a^2(a+1)+3a(a+1)+3a(a+1)\hfill \\ & +5a+2(a+1)+5a+6\hfill \\ & =5a^3+11a^2+18a+8\hfill \\ & \le 5{\left(\frac{n-2}{3}\right)}^3+11{\left(\frac{n-2}{3}\right)}^2+18\frac{n-2}{3}+8:=h_8\left(n\right).\hfill \end{array}\end{array}$$

The last inequality holds for a function $f_6\left(a\right)=5a^3+11a^2+18a+8$ is strictly increasing for $1\le a\le \frac{n-2}{3}$.

For $H_9^{*}$, since $a,b,c$ are almost equal, We may assume $a-1\le b\le a+1,0\le a-c\le 1$. Then $b\le a+1,c\le a$, $b\ge a-1,c\ge a-1$. As $n-3=a+b+c\ge a+a-1+a-1=3a-2$, therefore $a\le \frac{n-1}{3}$. Thus, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill z\left(H_9^{*}\right)=& abc+2ab+2ac+2bc+3a+3b+3c+2\hfill \\ & \le a^2(a+1)+2a(a+1)+2a^2+2a(a+1)\hfill \\ & +3a+3(a+1)+3a+2\hfill \\ & =a^3+7a^2+13a+5\hfill \\ & \le {\left(\frac{n-1}{3}\right)}^3+7{\left(\frac{n-1}{3}\right)}^2+13\frac{n-1}{3}+5:=h_9\left(n\right).\hfill \end{array}\end{array}$$

The last inequality holds as $f_7\left(a\right)=a^3+7a^2+13a+5$ is strictly increasing for $1\le a\le \frac{n-1}{3}$.

By using the software “Mathematica”, we obtain the following comparison.

$h_2\left(n\right)-h_1\left(n\right)=\frac{1}{6912}(\mathrm{41,889}+\mathrm{16,956}n+2706n^2+28n^3+27n^4)>0.$

$h_2\left(n\right)-h_3\left(n\right)=\frac{1}{32}(164+81n+12n^2+n^3)>0.$

$h_4\left(n\right)-h_2\left(n\right)=\frac{1}{256}(79+140n+26n^2+4n^3)>0.$

$h_6\left(n\right)-h_4\left(n\right)=\frac{1}{\mathrm{800,000}}(-\mathrm{13,510,144}-\mathrm{1,336,320}n-\mathrm{1,297,840}{n}^2-2040n^3-8245n^4+256n^5)>0$ for $n\ge 37$.

$h_8\left(n\right)-h_7\left(n\right)=\frac{1}{27}(-70+24n-9n^2+2n^3)>0$ for $n\ge 4$.

$h_7\left(n\right)-h_9\left(n\right)=\frac{1}{27}(16-12n-6n^2+2n^3)\ge 0$ for $n\ge 4$.

$h_6\left(n\right)-h_8\left(n\right)=\frac{1}{\mathrm{84,375}}(-\mathrm{531,148}-315n-\mathrm{67,155}{n}^2-7390n^3-540n^4+27n^5)>0$ for $n\ge 32$.

$h_6\left(n\right)-h_5\left(n\right)=\frac{1}{\mathrm{400,000}}(-\mathrm{6,520,697}-\mathrm{793,160}n-\mathrm{730,170}{n}^2-\mathrm{13,520}{n}^3-5685n^4+128n^5)>0$ for $n\ge 50$.

The direct computation yields to $z\left(C_8\right)=47,z\left(C_9\right)=76$.

From the above discussion, we get the result. □

4. Summary and Conclusions

In this paper, we investigate extremal properties of the famous Hosoya index for unicyclic graphs with diameter at most four. There is no doubt that topological indices have been proven useful for analyzing molecules by means of their graph structure. Especially the Hosoya index is demanding to calculate for general graphs. Thus, special analytical results for the Hosoya index contribute to a better understanding of molecular topology when using this measure. Because of the problem of calculating the Hosoya index efficiently, we also believe that our results can be used for QSAR/QSPR problems. Moreover, the Hosoya index could be calculated on existing drugbanks to determine the value distributions and using them within QSAR/QSPR. Note that this index has a meaningful structural interpretation. As future work, we would like to continue to prove analytical results when establishing interrelations between the Hosoya index and known graph measures which have been proven useful for drug design and QSAR/QSPR.