Abstract
This work presents a comprehensive performance evaluation and optimum design of a novel symmetrical 4-PPR (P indicates the prismatic joint, R denotes the revolute joint, and the letter with underline represents an active joint) redundant planar parallel manipulator. The kinematic model is established, upon which the inverse position and singularity are analyzed. Based on the evaluation of dexterity, velocity, and stiffness performance, the optimum region is achieved. With the optical design parameters, a case study for the analysis of dynamic behavior is conducted. Performance comparison between the redundant manipulator and another two non-redundant 3-PPR planar parallel manipulators, one with a Δ-shape symmetrical structure and the other with U-shape symmetrical structure, is presented. Simulation results reveal that the U-shape manipulator has the greatest velocity performance. Moreover, the redundant manipulator possesses the best dexterity, stiffness, and dynamic performance.
1. Introduction
Parallel manipulators (PMs) are closed-loop mechanisms modeled as a set of serial kinematic chains connected in parallel to two rigid bodies—the mobile platform (MP) and the base platform. In comparison to serial ones, PMs possess the advantages of greater load bearing capacity, higher precision, reduced effective inertia, better mechanical rigidity, and suitable positional actuators arrangement. However, PMs suffer from some drawbacks, such as complicated singularities, low accuracy, coupled dynamics, and limited workspace [1,2,3].
Planar parallel manipulators (PPMs), performing a rotation angle around the z-axis and two translations along the x- and y-axes, are a special type of PM which can provide planar motion [4]. Angeles et al. [5] reported the optimum kinematic design for a 3-RRR PPM. Nonsingular assembly mode change of PPMs has been discussed in [6]. With the application of the screw theory, a singularity analysis of some PPMs with identical serial chains was presented in [7]. The performances of types of PPMs were compared in [8]. The kinematics and dynamics of the known 3-PRR were analyzed in [9]. A geometrical approach for workspace analysis of PPMs was presented in [10]. Kinematics analysis of a proposed 3-PRP PPM was developed in [11]. Geometric analysis of the kinematic sensitivity of PPMs is available in [12].
For the 3-PPR PPMs, extensive research has been reported in [13,14,15,16,17]. Kinematic analysis and optimal design of a 3-PPR PPM with a Δ-shape (equilateral triangle) base platform were presented in [13]. In order to maximize the manipulator’s workspace, a 3-PPR PPM with a U-shape (square) base platform was introduced in [14]. The dynamics and controller performance of the U-shape 3-PPR PPM was investigated in [15]. 3-PPR PPMs with Δ- and U-shape base platforms were compared with respect to kinematic sensitivity to joint clearances and workspace in [16]. Aiming at the optimum shape design of the MP and the base platform, a parametric model of general 3-PPR PPMs is available in [17].
As mentioned above, only the first prismatic joint in each limb is actuated, which means the manipulator is a 3-PPR PPM. Note that the structural arrangement will bring some technical problems, such as cantilever effect and misalignment, which affect the manipulator’s overall performance. In order to tackle these issues, an additional passive PPR limb is added to the proposed 3-PPR PPM, as considered in [18]. The added limb will not increase the manipulator’s degree of freedom, so the proposed manipulator is still a PPM, which is addressed as 3PPR + PPR PPM, and this manipulator is expected to serve reliably and effectively in the bio-medical and industrial fields. Moreover, a manipulator with three active PPR limbs and a passive PPR limb is adopted as an experimental setup of a visual alignment system, where all four limbs support the MP to determine the position and to stand the payload, as presented in [19].
In fact, three active limbs are enough to implement the planar motion. However, the manipulator will carry a greater payload as the display panel size becomes larger. Usually, this problem can be resolved by extending the number of driving limbs, namely redundant actuation. As it is well known, redundant actuation is an effective method to optimize the kinematic and dynamic performance of PMs [20,21,22]. In order to improve the dexterity, stiffness, and dynamic performance of the 3-PPR PPM, another identical PPR limb is added to the manipulator, namely, a 4-PPR PPM is obtained. Although the two non-redundant PPMs (Δ- and U-shape 3-PPR PPMs) have been studied, there is no comparative study on the non-redundant PPMs and the redundant counterpart. So, a performance comparison between this redundant 4-PPR PPM and the other two non-redundant PPMs are conducted in this work, upon which the optimum regions are obtained.
One of the objectives of this work is to explore the influence of the platform shape on the manipulator’s performance. Since most 3-PPR PPMs studied are assumed to have a fixed symmetrical platform of a Δ- or U-shape, their comprehensive performance is rarely considered. Thus, it is desirable to study what will happen with a different platform shape. Another objective of this work is the performance analysis of the proposed 4-PPR redundant PPM with a symmetrical structure. Both the 3PPR and 3PPR + PPR PPM are non-redundant manipulators, which have been analyzed in some research, and it will be interesting to have an analysis of redundant actuation. The added PPR limb will cause the manipulator to be a redundant PPM with an enhanced comprehensive performance, while its degree of freedom remains unchanged. The last objective is the optimum design of the non-redundant and redundant actuation manipulators. It would be of great significance if new mechanisms can be inspired by the optimum design parameters.
The rest of this paper is organized as follows. A kinematics analysis of the considered redundant PPM is presented in Section 2. Performance indices in dexterity, velocity, and stiffness are illustrated in Section 3. Section 4 contains the analysis of performance evaluation and optimum design. A dynamic analysis is provided in Section 5. A performance comparison between this redundant PPM and the other two non-redundant PPMs is conducted in Section 6. Finally, conclusions are described.
2. Kinematics Analysis
The proposed redundant 4-PPR PPM, aiming at providing planar motion with great dexterity, stiffness, and dynamic performance for an assembly platform, is depicted in Figure 1. In this application, the first prismatic joint in each PPR leg was chosen as the active joint, which transmitted actuator movements to the MP through ball screw transmission, cross-roller guide (two prismatic joints for translation), and bearing (a revolute joint for rotation). As depicted in Figure 2, the base platform and the MP were both modeled as squares, and their side lengths were b and a, respectively. The global coordinate system {O0} was fixed on the square base [23], with the origin coinciding with a vertex of the base. On the other hand, the local coordinate system {O} was attached to the center of the MP. The vector p = [x, y]T provided the position of the MP with respect to the global coordinate system, and θ is the corresponding rotation angle. Moreover, θ = 0° was defined as the initial assembly mode.

Figure 1.
3D model of the 4-PPR redundant PPM.
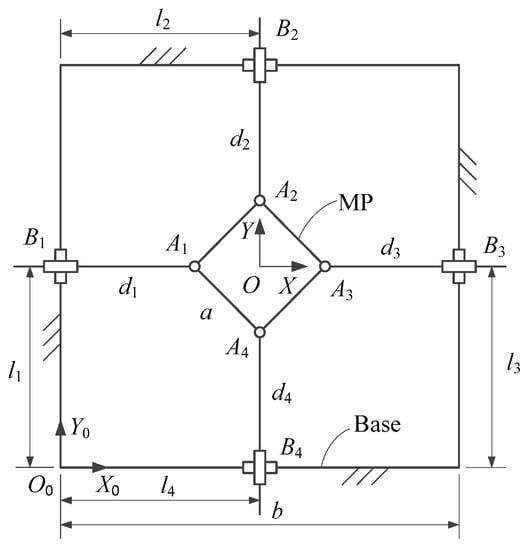
Figure 2.
Kinematic description of the 4-PPR redundant PPM.
2.1. Inverse Kinematics
The inverse kinematic problem is to determine the input of each active joint with the given posture of the MP. Here, the posture of the MP is defined as (x, y, θ), the position vector of point Ai in the global coordinate system can be denoted by:
where R represents the rotation matrix of the MP, p is the position vector, and denotes the position vector of point Ai in the local coordinate system, which can be expressed as:
The position vector of point Ai can also be expressed in a form as follows:
with
where di represents the displacement of each passive prismatic joint, li denotes the input of each active prismatic joint. Moreover, i and j represent the unit vectors of X0- and Y0-axes.
Combining Equations (1) and (3) yields solutions for the inverse kinematics problem:
2.2. Singularity Analysis
For general PMs, the relationship between the velocity of the active joints and the velocity of the MP can be expressed as:
where J represents the Jacobian matrix.
Differentiating both sides of Equation (6) with respect to time, we obtain,
where represents the velocity vector of the MP, denotes the velocity vector of the active joints. J1 is the Jacobian matrix, which can be obtained as:
For redundant PMs, singularity will occur when the rank of the Jacobian matrix J is lower than its number of rows, namely, the determinant of JTJ is equal to zero [24]. For the considered 4-PPR PPM, we have:
Obviously, singularity occurs when θ = ±90°, and the corresponding singular configurations are depicted in Figure 3. In order to get free from singularity, the feasible range of the workspace of the considered redundant PPM is defined as −90° < θ < 90°.

Figure 3.
Singular configurations of the 4-PPR PPM.
3. Performance Indices
In the design process, singularity is not the only important issue that should be considered. Some criteria, such as isotropy, dexterity, velocity, stiffness, and payload capability, could be involved. For practical application, dexterity, velocity, and stiffness capability are usually used to evaluate the manipulators’ performance [4]. Then, these three main performances are investigated for the considered PPMs.
3.1. Dexterity Index
Dexterity index is an important performance index for mechanism design. The dexterity of a PM is defined as the ability to change its position and orientation arbitrarily, which can be measured in terms of condition number. With regard to condition number, it is regarded as the local performance index for evaluating the velocity, accuracy, and rigidity mapping characteristics between the joint variables and the MP [25]. For a Jacobian matrix of full rank, the corresponding condition number can be expressed as:
where is the Frobenius norm of the matrix, J−1 represents the inverse matrix.
Note that the first two columns of the Jacobian matrix, as mentioned in Equation (9), are without units, while the third has units of length. A simple method for rendering these units homogeneous is to divide the elements of the third column by a characteristic length [4]. With regard to the considered manipulator, side length (a + b)/2 is chosen as the characteristic length. Moreover, for the 4-PPR PPM, the Jacobian matrix is not invertible. Since the columns are linearly independent, is invertible, so there is a left-inverse matrix , which can be taken into consideration for the calculation of condition number.
As well known, the value of condition number will range from one to infinity, without an upper bound. So, the reciprocal of the condition number, called the local conditioning index (LCI), is used more commonly:
LCI is a local performance metric bounded between 0 and 1, and singular poses are characterized by LCI = 0, whereas the optimal (isotropic) configurations are denoted by LCI = 1. Obviously, the manipulator has a great dexterity performance when its LCI is large.
3.2. Velocity Index
As is well known, PMs are suitable for high-speed application, for which the velocity index will be another important performance index for PMs. For the velocity index, it indicates the extreme velocity the mechanism can obtain. Referring to Equation (7), the relationship between the velocity of the active joints and the velocity of the MP can be expressed in another form, as follows:
Then, we have:
Let the velocity vector of the active joints be a unit vector (), the norm of velocity vector of the MP can be expressed as:
where λvi is an eigenvalue of the matrix .
Therefore, the extremum of the output velocity of the MP can be expressed as:
In practical applications, both Vmax and Vmin can be chosen as the velocity indices, but for the 4-PPR PPM, the matrix , while its rank is less than 4, this means there is always a zero eigenvalue, which leads to Vmin = 0, so we choose Vmax as the velocity index. The larger the Vmax is, the better the velocity performance of the manipulator is.
3.3. Stiffness Index
If an external force acts on the end-effector, there will be deformation on the mechanism. The deformation is determined by the external force and mechanism stiffness. Moreover, the mechanism’s stiffness will affect its dynamics and the position accuracy, for which stiffness is an important performance index. As reported in [26], the stiffness matrix of PPMs can be written as:
where is a matrix describing the stiffness of the platform mounted with elastic elements. For simplicity, . The deflection of the MP is thus,
where denotes the vector of moment and forces applied to the MP, represents the corresponding deflections.
It can be found that the maximum or minimum eigenvalue λsi of is the limit value of ||ΔX||2. Let k1 = k2 = k3 = 1 and ||f|| = 1, the minimum and maximum deformations can be expressed as:
In fact, both minimum and maximum deformations can be chosen as the stiffness indices. To keep consistent with the velocity index, the maximum deformation Smax is chosen as the stiffness index. The larger the deformation is, the worse the stiffness performance of the PPMs is.
4. Performance Evaluation and Optimum Design of the 4-PPR PPM
With the three performance indices introduced above, performance evaluation and optimum design will be conducted. As analyzed in Section 2.2, only θ and a have influence on the Jacobian matrix, so these two parameters are taken into consideration for performance evaluation. Note that the 4-PPR PPM will be singular when θ = ±90°, for this reason the feasible range of the workspace is defined as −90° < θ < 90°. Moreover, the feasible range of the side length of the MP is defined as 0 mm < a < 1000 mm.
We look first at the dexterity performance. As shown in Figure 4, the distribution of dexterity of the redundant PPM is symmetrical at about θ = 0°, and the dexterity is good near θ = 0°. On the other hand, the dexterity is poor when the PPM approaches singular configurations. Moreover, the bigger the side length a is, the better the dexterity performance is.
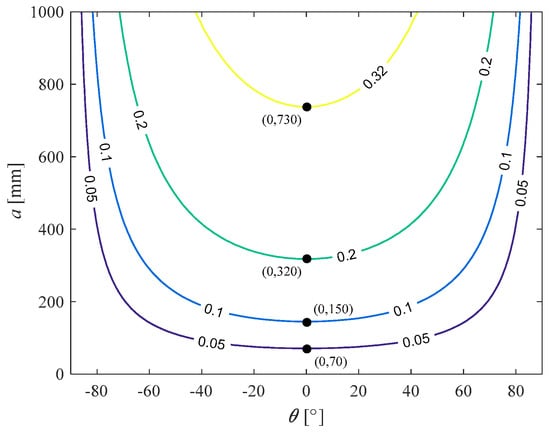
Figure 4.
Dexterity performance of the 4-PPR PPM.
For the velocity index, the simulation result is depicted in Figure 5. The distribution of the velocity performance of the 4-PPR PPM is also symmetrical at about θ = 0°. The velocity performance is great when the PPM approaches singular configurations, but it is not so good near θ = 0°. It is also found that the smaller the side length a is, the better the velocity performance is.

Figure 5.
Velocity performance of the 4-PPR PPM.
At last, the stiffness index is considered, the result is shown in Figure 6. It is also found that the distribution of stiffness performance is symmetrical at about θ = 0°. The stiffness performance will become poor when the PPM approaches singular configurations and the zone near θ = 0° possesses good stiffness performance. Note that the larger the side length a is, the better the stiffness performance is.

Figure 6.
Stiffness performance of the 4-PPR PPM.
In practical applications, dexterity performance, velocity performance, and stiffness performance are all important. Hence, three indices LCI, Vmax, and Smax are all taken into consideration for optimum design. Based on the analysis above, the region with LCI > 0.1, Vmax > 2, and Smax < 80 is defined as the optimum region. As depicted in Figure 7, it is found that the considered redundant PPM has a U-shape optimum region, which is symmetrical at about θ = 0°. Within the U-shape optimum region, the manipulator will obtain a relatively great comprehensive performance, which should be taken into consideration for mechanism design.
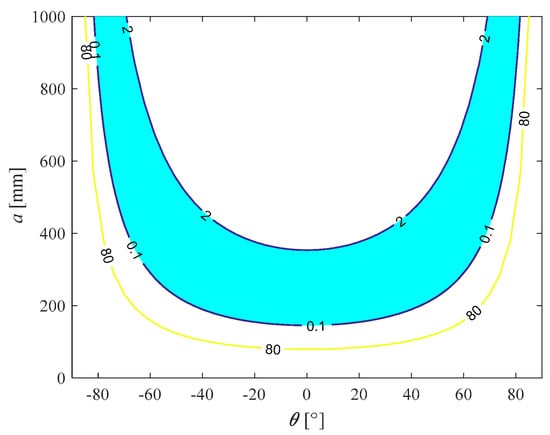
Figure 7.
Optimum region of the 4-PPR PPM.
5. Dynamic Analysis
In this section, a dynamics analysis of the considered 4-PPR PPM is conducted. With an explicit formulation and simple expression, the Lagrange formulation method [27] is adopted for dynamic modeling. The dynamic model with independent coordinates can be expressed as:
where L = T − V is the Lagrangian function, T and V are the kinetic energy and the potential energy of the system, respectively, and τ is the vector of generalized forces.
Then, under the static environment, the expression of the corresponding driving forces can be obtained as:
Since the Jacobian matrix J1 of the 4-PPR PPM is non-square, driving forces have infinite solutions. To get a unique solution, the left-inverse matrix , as discussed in Section 3.1, is adopted to minimize the two-norm of driving forces.
For the considered redundant PPM, the masses are taken as m1 = 1.7574 kg, m2 = 0.8313 kg, m3 = 48.4972 kg, where m1, m2 are the masses of the active and passive components, and m3 represents the mass of the MP. The moments of inertia of corresponding components are taken as I1 = 0.0043 kg·m2, I2 = 0.0039 kg·m2, and I3 = 2.9431 kg·m2.
As mentioned in [17], the proposed 3-PPR PPM under study obtained a good comprehensive performance when the side length of the MP was half of the base. Moreover, the 4-PPR PPM will obtain a relatively great comprehensive performance at about a = 350 mm, which can be learnt from Figure 7, so the dimensional parameters are taken as a = 350 mm, b = 700 mm.
A predefined motion trajectory of the MP for dynamic simulation is given by:
The driving forces Fi of the ith limb within the given motion can be readily obtained, as shown in Figure 8. The distribution of the four driving forces is relatively uniform, and the maximum driving forces for this PPM with the given motion trajectory is 1.12 N.
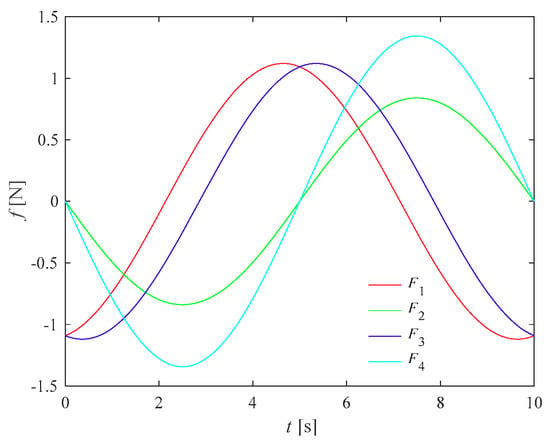
Figure 8.
Driving forces of the 4-PPR PPM.
6. Performance Evaluation of the Non-Redundant PPMs
The considered Δ- and U-shape 3-PPR PPMs are depicted in Figure 9a,b. With regard to the Δ-shape 3-PPR PPM [13], it is designed to be a nano order precision assembly platform. To make it easy to control, the connection between the active and passive prismatic joint is considered to be a right angle. Analysis results reveal that this manipulator has the advantages of a void-free workspace with a convex type of borderline and a closed type of direct kinematics. For the U-shape 3-PPR PPM [15], the motion control with disturbance observer is proposed and validated. Here, the manipulator can perform as a motion table in the range of meso (between micro- and milli-metre levels), and it can be used for applications, providing accurate positioning and trajectory capabilities to the end-effector, especially for milling and other machining processes.

Figure 9.
The considered non-redundant PPMs: (a) the Δ-shape PPM and (b) the U-shape PPM.
Both of the Δ- and U-shape 3-PPR PPMs consist of three PPR kinematic chains with identical topology, and they have a same equilateral triangle MP with side length a, as shown in Figure 10a,b. For the Δ-shape PPM, the base platform is modeled as an equilateral triangle with side length b, while the U-shape PPM has a square base platform with the same length.
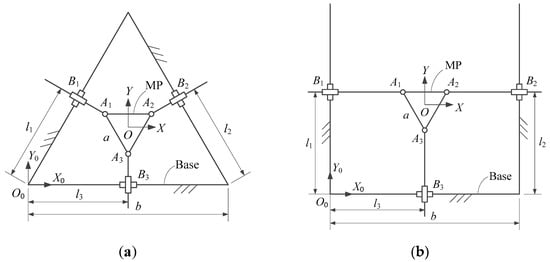
Figure 10.
Kinematic description of: (a) the Δ-shape PPM and (b) the U-shape PPM.
6.1. Kinematics Analysis
By a similar method to that discussed in Section 2, or referring to [17], the inverse position of the Δ-shape 3-PPR PPM can be obtained as:
Similarly, the inverse position of the U-shape PPM can be expressed as:
Differentiating both sides of Equations (25) and (26) with respect to time, the Jacobian matrices can be written as:
Singularity occurs when the Jacobian matrix is singular, namely, the determinant of the Jacobian matrix is equal to 0. For the considered PPMs, we have:
The Jacobian matrices are equal to 0 when θ = ±90° for the two considered PPMs, the corresponding singular configurations are depicted in Figure 11. To obtain a workspace free from singularity, the feasible range of the workspace of the considered PPMs is also defined as −90° < θ < 90°.
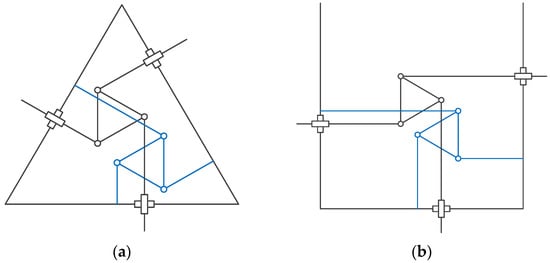
Figure 11.
Singular configurations of (a) the Δ-shape and (b) the U-shape 3-PPR PPMs.
6.2. Performance Evaluation
Distributions of the three considered performances of these two PPMs are depicted in Figure 12, Figure 13 and Figure 14, respectively. Since the distribution law is very similar to the redundant PPM, we will not discuss it in detail in this section.
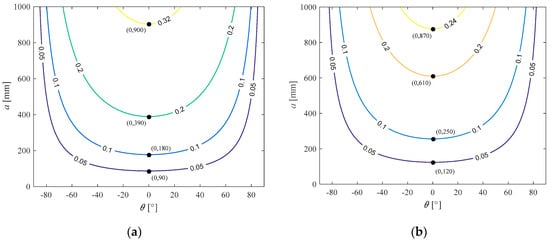
Figure 12.
Dexterity performance of (a) the Δ-shape and (b) the U-shape 3-PPR PPMs.
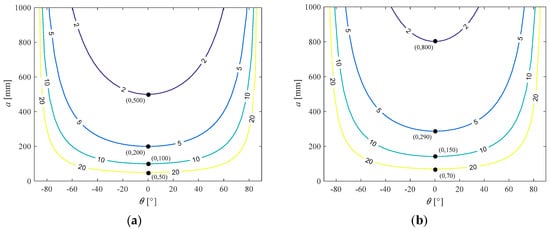
Figure 13.
Velocity performance (a) the Δ-shape and (b) the U-shape 3-PPR PPMs.
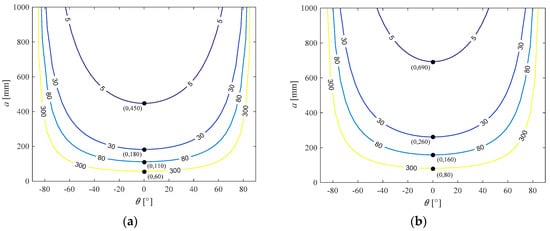
Figure 14.
Stiffness performance of (a) the Δ-shape and (b) the U-shape 3-PPR PPMs.
Here, under the same situation (the same a), a performance comparison between the three considered PPMs is conducted. It was found that the U-shape 3-PPR PPM possesses the best velocity performance of the three PPMs, but both dexterity and stiffness performances of the U-shape PPM are the worst. On the contrary, the 4-PPR redundant PPM has the worst velocity performance, but its dexterity and stiffness performances are the best. On the other hand, all three performances of the Δ-shape 3-PPR PPM are at the mid-level.
Optimum regions of the Δ- and U-shape PPMs are depicted in Figure 15a,b, it is also found that both of them have a U-shape optimum region, which is symmetrical at about θ = 0°. Compared with the redundant PPM, the area of the optimum region of the U-shape PPM is the largest, and that of the redundant PPM is the smallest. From the aspect of optimum region area, the performance of the U-shape PPM is the best among the three PPMs.

Figure 15.
Optimum regions of (a) the Δ-shape and (b) the U-shape 3-PPR PPMs.
6.3. Dynamic Analysis
In this section, the same mass parameters and given motion are taken into consideration for a dynamic analysis of the two non-redundant PPMs, and their driving forces are depicted in Figure 16a,b. The maximum driving forces for these two non-redundant PPMs with the given motion trajectory are 1.77 N and 2.11 N, while that of the redundant PPM is 1.12 N. Here, we assume that the smaller the magnitude of the driving force is, the better the dynamic performance of the manipulator is. Then, it can be found that the 4-PPR redundant PPM possesses the best dynamic performance of the three PPMs. Moreover, the Δ-shape PPM has a better dynamic performance than the U-shape PPM.
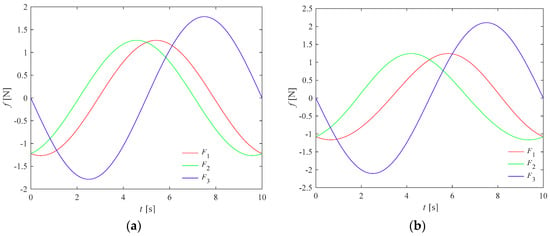
Figure 16.
Simulation of driving forces of (a) the Δ-shape and (b) the U-shape 3-PPR PPMs.
7. Conclusions
In this work, a novel 4-PPR redundant PPM with a symmetrical structure was proposed for precision assembly. The performance of the redundant manipulator and another two non-redundant PPMs with symmetrical structure were compared, where the evaluation was mainly based on their dexterity, velocity, and stiffness performance. For the three considered PPMs, the distributions of all the three performances were symmetrical. Under the same situation, the velocity performance of the U-shape PPM was the best, and that of the redundant PPM was the worst. Moreover, the dexterity and stiffness performance of the redundant PPM were the best, while these performances of the U-shape PPM were the worst. In addition, all three performances of the Δ-shape PPM are at the mid-level.
Based on the performance evaluation, the U-shape optimum regions are obtained for the three PPMs. The area of the optimum region of the U-shape PPM is the largest and that of the redundant PPM is the smallest. From the aspect of optimum region area, the performance of the U-shape PPM is the best. Note that the obtained U-shape optimum regions are useful, which should be taken into consideration for mechanism design. With the optical design parameters, the dynamic performance is investigated, and the simulation results reveal that the redundant PPM also possesses the best dynamic performance.
To sum up, the velocity performance of the U-shape PPM is the best. Moreover, the redundant PPM shows advantages on dexterity, stiffness, and dynamic performance. From these results, it can be concluded that the comprehensive performance of the redundant PPM is the best—the performance is improved by redundant actuation.
In this work, only two typical non-redundant 3-PPR PPMs were considered, other 3-PPR PPMs with different shapes or actuation modes should be analyzed. On the other hand, the performance of the 3PPR + PPR PPM should be evaluated. Needless to say, new PPMs with optical design parameters and their applications will be topics of future research.
Funding
This work is financially supported by the National Natural Science Foundation of China (U51605059 & No.51805060), the Scientific Research Foundation of Chongqing University of Technology.
Acknowledgments
The author acknowledge Shaoping Bai, Aalborg University, Denmark, for the discussion and comments.
Conflicts of Interest
The author declare no conflict of interest.
References
- Wu, X.; Xie, Z. Forward kinematics analysis of a novel 3-DOF parallel manipulator. Sci. Iran. Trans. B Mech. Eng. 2019, 26, 346–357. [Google Scholar] [CrossRef]
- Corves, B.; Brinker, J.; Lorenz, M.; Wahle, M. Design methodology for translational parallel manipulators exhibiting actuation redundancy. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 425–436. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, J.; Cao, Y.; Liang, B.; Zhao, T. Constant motion/force transmission analysis and synthesis of a class of translational parallel mechanisms. Mech. Mach. Theory 2017, 108, 57–74. [Google Scholar] [CrossRef]
- Wu, J.; Wang, J.; You, Z. A comparison study on the dynamics of planar 3-DOF 4-RRR, 3-RRR and 2-RRR parallel manipulators. Robot. Comput. Manuf. 2011, 27, 150–156. [Google Scholar] [CrossRef]
- Gosselin, C.; Angeles, J. The Optimum Kinematic Design of a Planar Three-Degree-of-Freedom Parallel Manipulator. J. Mech. Transm. Autom. Des. 1988, 110, 35–41. [Google Scholar] [CrossRef]
- Husty, M.L. Non-singular assembly mode change in 3-RPR-parallel manipulators. In Computational Kinematics: Proceedings of the 5th International Workshop on Computational Kinematics; Kecskeméthy, A., Müller, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 51–60. [Google Scholar]
- Bonev, I.A.; Gosselin, C.M.; Zlatanov, D. Singularity Analysis of 3-DOF Planar Parallel Mechanisms via Screw Theory. J. Mech. Des. 2003, 125, 573–581. [Google Scholar] [CrossRef]
- Zhu, Z.; Dou, R. Optimum design of 2-DOF parallel manipulators with actuation redundancy. Mechatronics 2009, 19, 761–766. [Google Scholar] [CrossRef]
- Staicu, S. Inverse dynamics of the 3-PRR planar parallel robot. Robot. Auton. Syst. 2009, 57, 556–563. [Google Scholar] [CrossRef]
- Merlet, J.-P.; Gosselin, C.M.; Mouly, N. Workspaces of planar parallel manipulators. Mech. Mach. Theory 1998, 33, 7–20. [Google Scholar] [CrossRef]
- Zarkandi, S. Kinematics of a star-triangle planar parallel manipulator. J. Mech. Sci. Technol. 2011, 25, 3223–3230. [Google Scholar] [CrossRef]
- Saadatzi, M.H.; Masouleh, M.T.; Taghirad, H.D.; Gosselin, C.; Cardou, P. Geometric analysis of the kinematic sensitivity of planarparallel mechanisms. Trans. Can. Soc. Mech. Eng. 2011, 35, 477–490. [Google Scholar] [CrossRef]
- Choi, K.-B. Kinematic analysis and optimal design of 3-PPR planar parallel manipulator. KSME Int. J. 2003, 17, 528–537. [Google Scholar] [CrossRef]
- Bai, S.; Caro, S. Design and analysis of a 3-PPR planar robot with U-shape base. In Proceedings of the International Conference on Advanced Robotics, Munich, Germany, 22–26 June 2009; pp. 1–6. [Google Scholar]
- Singh, Y.; Vinoth, V.; Kiran, Y.R.; Mohanta, J.K.; Mohan, S. Inverse dynamics and control of a 3-DOF planar parallel (U-shaped 3-PPR) manipulator. Robot. Comput. Manuf. 2015, 34, 164–179. [Google Scholar] [CrossRef]
- Binaud, N.; Caro, S.; Bai, S.; Wenger, P. Comparison of 3-PPR parallel planar manipulators based on their sensitivity to joint clearances. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 2778–2783. [Google Scholar]
- Wu, X.; Xie, Z.; Kepler, J.A.; Bai, S. A parametric model of 3-PPR planar parallel manipulators for optimum shape design of platforms. Mech. Mach. Theory 2017, 118, 139–153. [Google Scholar] [CrossRef]
- Singh, Y.; Shah, S.P.; Gandhi, P.S. High resolution flexible 4-PPR U-base planar parallel microstage robotic manipulator. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; p. 012034. [Google Scholar]
- Kwon, S.; Hwang, J. Kinematics, pattern recognition, and motion control of mask–panel alignment system. Control. Eng. Pr. 2011, 19, 883–892. [Google Scholar] [CrossRef]
- Qu, H.; Guo, S.; Zhang, Y. Kinematics analysis of a redundantly actuated 4-RUU translational parallel manipulator and its nonredundant 3-RUU counterpart. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 231, 3238–3249. [Google Scholar] [CrossRef]
- Luces, M.; Mills, J.K.; Benhabib, B. A Review of Redundant Parallel Kinematic Mechanisms. J. Intell. Robot. Syst. 2017, 86, 175–198. [Google Scholar] [CrossRef]
- Yao, J.; Gu, W.; Feng, Z.; Chen, L.; Xu, Y.; Zhao, Y. Dynamic analysis and driving force optimization of a 5-DOF parallel manipulator with redundant actuation. Robot. Comput. Manuf. 2017, 48, 51–58. [Google Scholar] [CrossRef]
- Jiang, Q.; Gosselin, C.M. Geometric Synthesis of Planar 3-Rpr Parallel Mechanisms for Singularity-Free Workspace. Trans. Can. Soc. Mech. Eng. 2009, 33, 667–678. [Google Scholar] [CrossRef]
- Ebrahimi, I.; Carretero, J.A.; Boudreau, R. 3-PRRR redundant planar parallel manipulator: Inverse displacement, workspace and singularity analyses. Mech. Mach. Theory 2007, 42, 1007–1016. [Google Scholar] [CrossRef]
- Patel, S.; Sobh, T. Manipulator performance measures-a comprehensive literature survey. J. Intell. Robot. Syst. 2015, 77, 547–570. [Google Scholar] [CrossRef]
- Klimchik, A.; Chablat, D.; Pashkevich, A. Stiffness modeling for perfect and non-perfect parallel manipulators under internal and external loadings. Mech. Mach. Theory 2014, 79, 1–28. [Google Scholar] [CrossRef]
- Bai, S.; Zhou, L.; Wu, G. Manipulator Dynamics. In Handbook of Manufacturing Engineering and Technology; Nee, A., Ed.; Springer: London, UK, 2013; pp. 1–17. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).