1. Introduction
Symmetry breaking is a universal singularity which happens suddenly once a system of particles is exposed to size variation or non-homogenous thermo-physical properties. As a random procedure, even minor variations applied on a system of particles can randomly drive it to a bifurcation branch. In addition, control of heat and fluid flow has an important role in modern industry. High heat motions are normal in the present age of exploratory combination reactors and future combination control plants [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30]. Huge warmth loads must be carried far from the reactor and towards the power age framework in a quick, proficient and dependable way, to guarantee the safe and economic activity of the combination control plant. High warmth motion parts [
3,
4,
5,
6,
7,
8,
9,
10], for example the diverter, are required to produce very high warmth loads. Consequently, propelled cooling strategies must be utilized to guarantee operational unwavering quality and life span [
4]. Subcooled water cooling at transitional weights is the chosen technique for warming the executives for the design of the International Thermonuclear Experimental Reactor (ITER) since subcooled bubbling warmth exchange can cause high warmth motions [
5,
6,
7,
8]. However, water has two points of interest and inconveniences as a coolant in applied structures of future combination control plants [
9,
10,
11,
12,
13]. Its fundamental downside emerges from stage change restrictions [
9]. A review on multiphase flow shows the application of that type of flow in industry [
19].
Nanofluids are set up by scattering nano-particles (usually metal particles) into base liquids. They have demonstrated promising highlights from the movement of warmth to thermo-physical properties, for example, warm conductivity and warmth limit [
4,
10,
11,
12,
13]. For the most part, the warm conductivity of utilized nano-particles is more advanced than that of pure fluids; for example, ethanol, water, and motor oil, methanol, and basic instruments for upgrade in heat conductivity of nanofluids may be ascribed to covering at the strong/fluid boundary, surface phonon, movement of the nano-particles with Brownian form at the sub-atomic and micro-scale [
14,
15]. Numerical simulation of compressible flows by lattice Boltzmann method [
20] and Smoothed Particle Hydrodynamics (SPH) approach were performed on this topic [
21,
22,
23,
24]. The effect of turbulence [
25,
26,
27] and adding of nano-particles were discussed in the literature [
28,
29,
30]. The symmetry of a physical system is a constant feature of a system that is constant through transformation. In the MHD system, the magnetic charge is conserved. By the use of magnetohydrodynamic (MHD) forces and broken symmetry caused by the nano size particles a more controllable fluid and thermal system is formed. Although the applied magnetic field could be symmetric, the stochastic nature of nano-fluid and the occurrence of two-phase phenomena causes unsymmetrical effects.
Recently, Jamalabadi [
16,
17,
18] worked on the EMHD effects on a straight up flow in annular pipe in a two-phase flow regime. However, the effect of MHD and nanoparticles on subcooled vertical pipe flow has not been calculated yet. Motivated by the above-stated summary of the current research, in this research, the impression of Lorentz forces on heat transfer mode in boiling at the subcooled regime and its impression on the framework is calculated. The current document deals with nanoparticle addition to the two-phase flow and sees their effect as well as the effects of MHD forces.
2. Geometry and Physical Condition
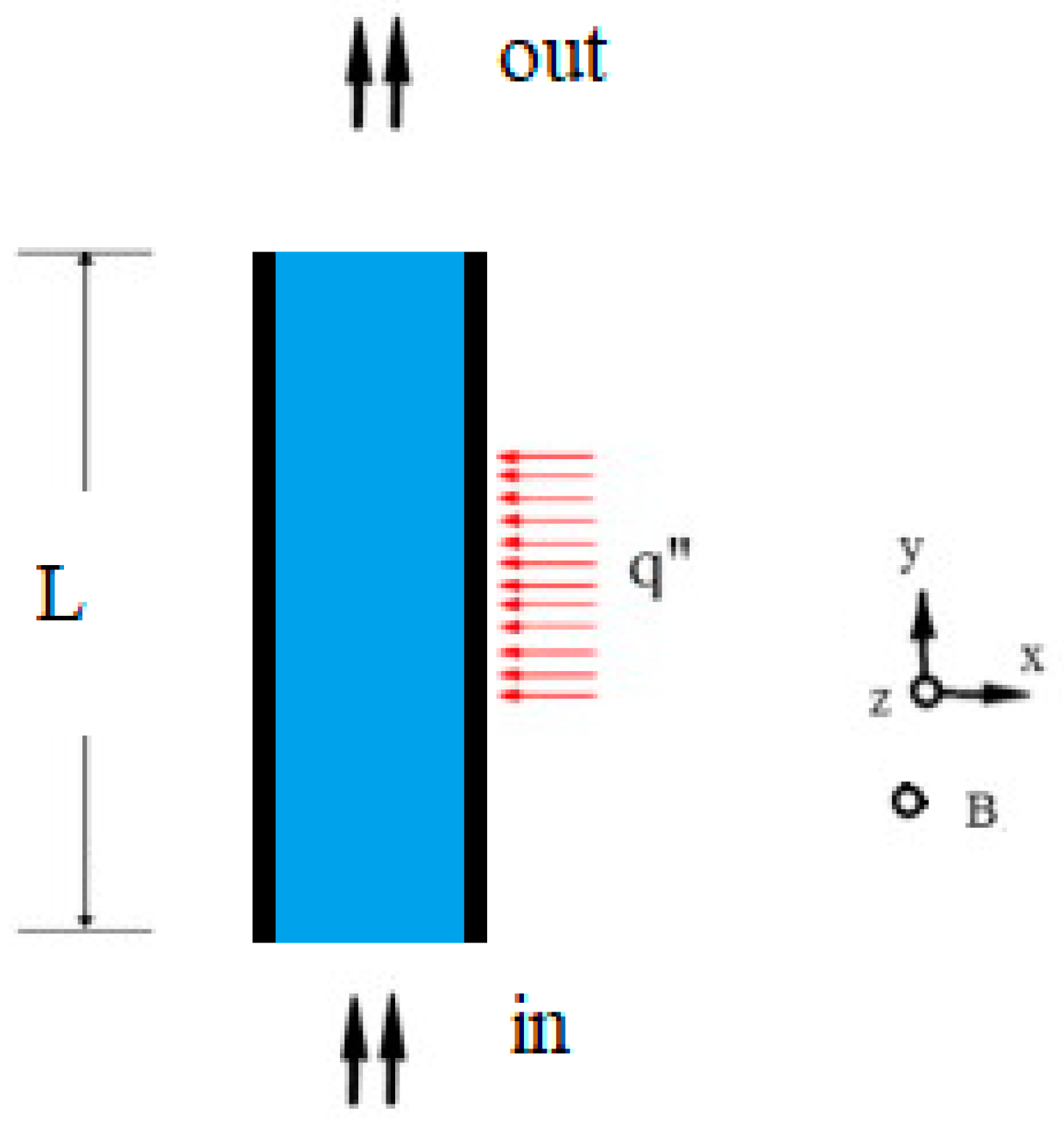
Figure 1 demonstrates the schematic of the problem where a vertical tube which partially warmed the inlet, outlet, and the direction of the magnetic force. The experimental rig consists of a holding tank, in which the thermal condition of the degassed and distilled water is monitored and checked by a cooling coil, a submerged electric heater, a circulating pump, and a preheater. As is evident, the unadulterated fluid water comes into the channel (gulf circumstance is at
y = 0) with inlet T
in (beneath the immersion saturation) and constant inlet normal speed (283.1 kg/m
2s) and there is an overlap of 3.64 cm
2 despite the fact that its weight at the exit pressure is fixed as given in
Table 1. The annular entry of liquid stream (inward cylinder breadth 12.7 mm, external cylinder width, 25.4 mm, and 114.6 cm length is somewhat homogeneously warmed between the height of 34 cm and 64.6 cm. The magnetic conditions presented in
Table 2 are utilized to calculate the force liquid stream in opposition to the vertical motion. To simplify the calculations the issue is broken up in the current examination by the 1D perspective and the pressure-driven measurement (0.123 cm) is not exactly longitudinal size (1.146 cm). No channel surfaces have warmth scattering properties (adiabatic). In CFD, the usual delta speed is recommended and the exit pressure is zero. To force the fluid in a vertical direction, the liquids are guided either through a weight slope (Pin and Pout required) or through a gulf speed with a surge circumstance, or, intermittently, in an elective region. This is common standard where weight angles are concerned.
3. Governing Equations
The overlap which occurs at the midpoint of the (one-dimensional) two-stage issue under the nearby harmony supposition and indiscretion of spreading between stages, vapor buildup at divider, interfacial energy reservation, and surface strain powers, is considered to generate the various factors at each stage (temperature, speed, weight, void portion), the interfacial and divider warmth and mass transmit factors.
The one-dimensional mass balance conditions of the two-liquid for any stage (i.e., fluid, vapor) in
Table 3 are acquired from Collier and Thome in [
3]. The
is a mass transmitting period between stages (due to buildup or dissipation). The force balance conditions of the two-liquid model for any stage (
i refers to fluid or vapor) in
Table 3 can be found in Collier and Thome [
3]. Here, the inertial force term in the interfacial momentum exchange model has been combined into single expressions to avoid the use of regime maps [
16,
17,
18]. The Lorentz term considers powers other than weight and trituration powers, for example, magneto-hydrodynamic power. The bubbly stream is rearranged with respect to each stage. Physical occurrences in the two-stage stream are depicted by a solid impression of surface strain and a thermally initiated surface pressure incline.
4. Result and Discussion
A code with FORTRAN software is extended to solve the governing equations. The governing equations of the system are presented in
Table 3 with material properties given in
Table 4. As shown in
Table 5, the matrix reliance is similar to that depicted in
Table 1. The most reduced framework is viewed as the definitive arrangement and the relative blunder percent is calculated versus average error for each particular case. As shown, by reducing the framework it is possible to estimate the difference in the decline. For the present research, the lattice dx = 0.01 is utilized for the following examples. The correlation among simulation and exact result is delineated in
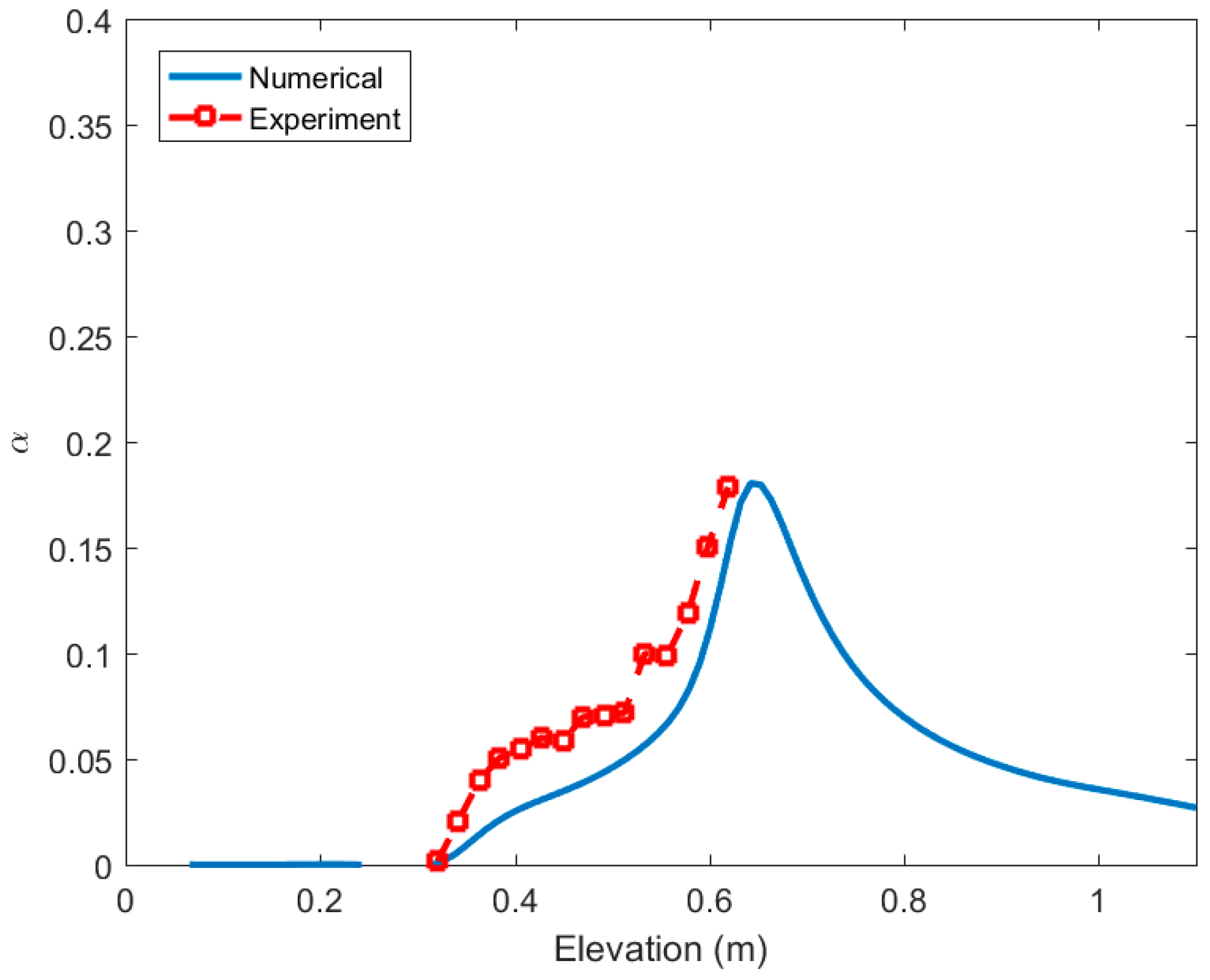
Figure 2. As stated in [
6] the statistical error was reduced to less than 1–2% by counting for a long enough time. In addition, the maximum absolute error was estimated to be 0.015, which is lower than the error bars we would have shown in
Figure 2. However, the error bars were not shown in
Figure 2. Customarily, when static and uniform attractive fields are respected, the Lorentz external body force equates to breaking powers which are inclined to slightly decelerate the stream. The correlation that we used, which is delineated in
Figure 2, just shelters the warmed piece of the congruity area and adequately fulfils its task.
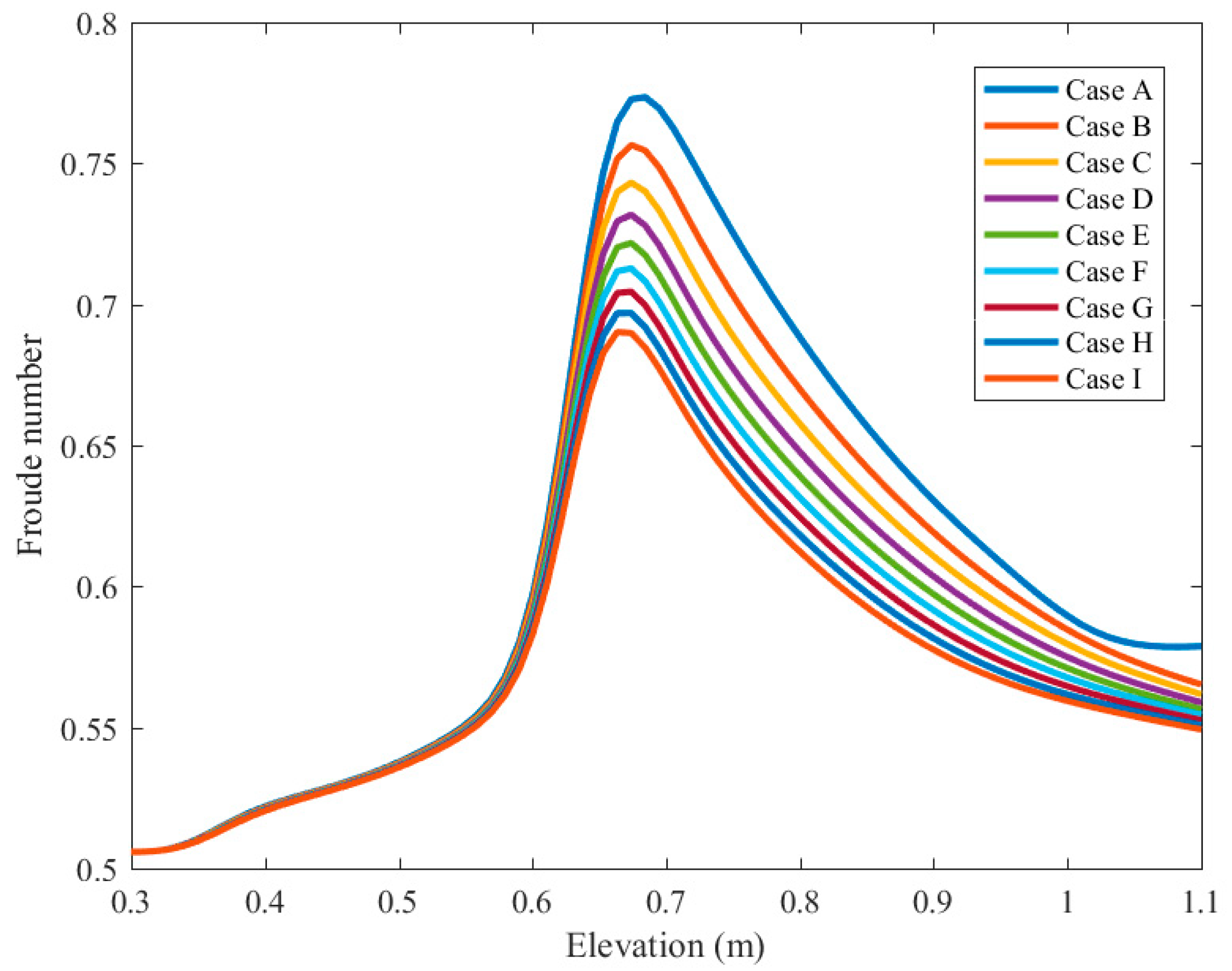
Figure 3 demonstrates the epitome of the Froude number against the distance from the inlet for numerous occurrences of Magnetic conditions. Considering the Froude value argumentation (this is generally portrayed as being regularly stirred up with Fraud number in the substance). As shown by the increase of elevation, the Froude number is increased up to the heated point where the value dramatically increases to the maximum value at the end of the heated region. By the use of Lorentz forces, the ratio of inertial forces to gravity load could be controlled.
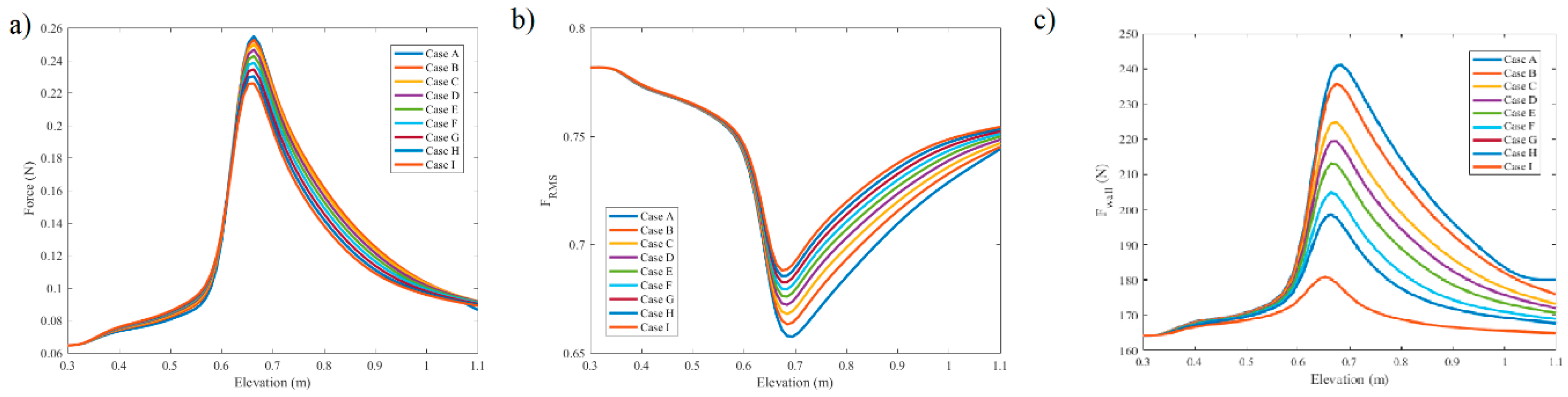
Figure 4a exposes the numerous attractive considerations on liquid cross-sectional power through the height of the cylinder. As portrayed, the beginning of the swaying process is improved as the stream undergoes modification from the liquid stage to liquid-vapor. As portrayed by the improvement of interim from the start of the pipe, the liquid force impression will upgrade on multiple occasions until it reaches the center of the warmed part. The structured power is obtained from the Bernoulli weight (an assignment of blend thickness and speed) and the cross-sectional surface of the cylinder. On account of the structural arrangement in the cylinder, a piece of this power could become (as indicated by cross-sectional of development) an energizing power for the 1-D or 2-D rhythmical oscillator. As it has been seen for various cases, the liquid power crest causes constant shrinkage. In this manner, the Lorentz force controls the liquid impression power.
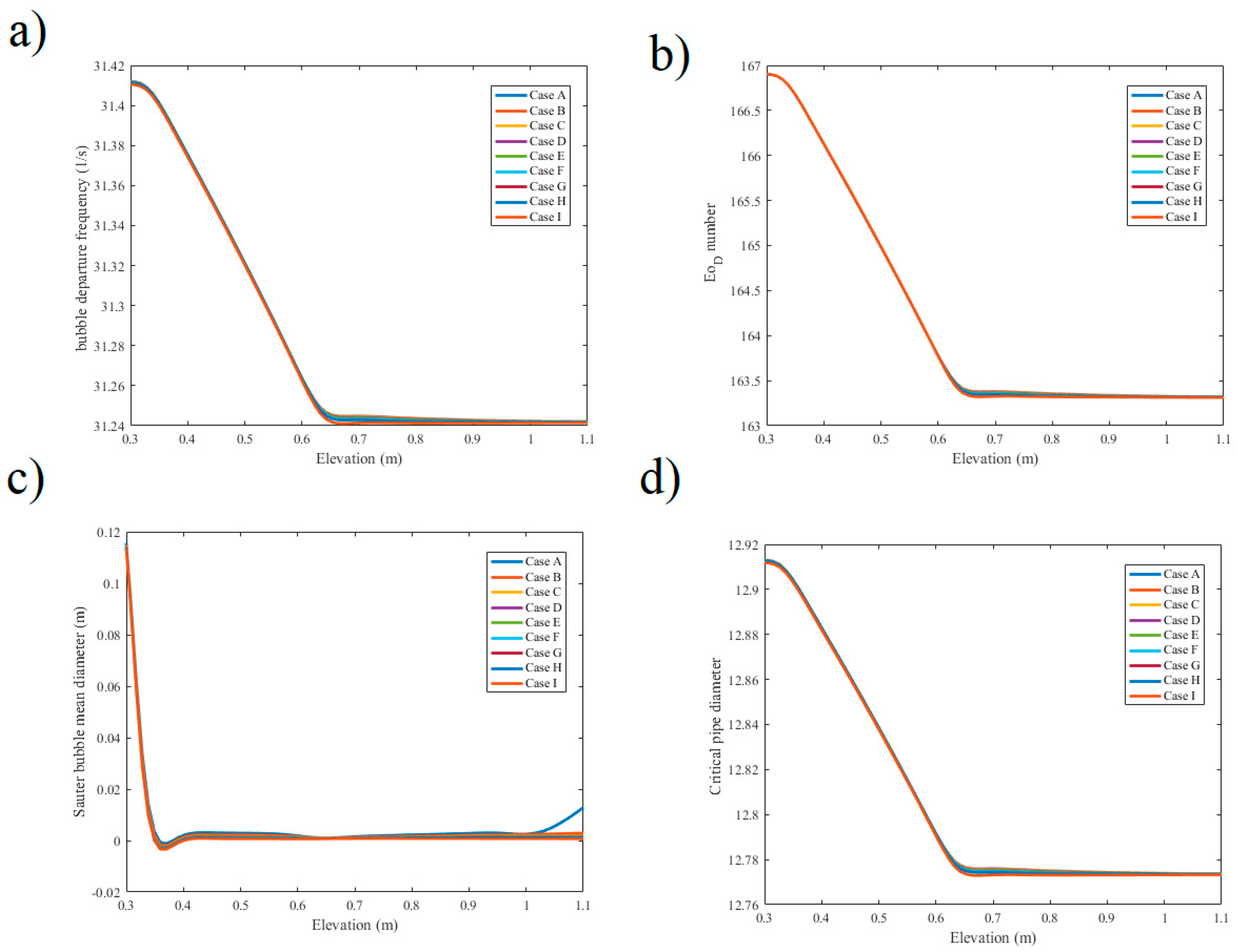
Figure 5a shows the air pocket takeoff recurrence against the height for numerous circumstances involving magnetic conditions. This is equivalent to the rate of gas phase creation because of nucleation bubbling from the fluid to the vapor stage. As demonstrated, the air pocket takeoff recurrence is lessened under warm conditioned and the use of Lorentz force does not have a precise impact on it.
Figure 5d delineates the basic pipe width against the height of the tube for numerous incidents of Magnetic conditions. As documented, the basic pipe breadth is decreased after the warmed piece of the cylinder and the use of Lorentz force is not critical.
Figure 5d delineates that the basic pipe measurement is not exactly the basic estimation of 40. Subsequently, the disengaged stream routine is not solid and the bubbly routine must be enlisted.
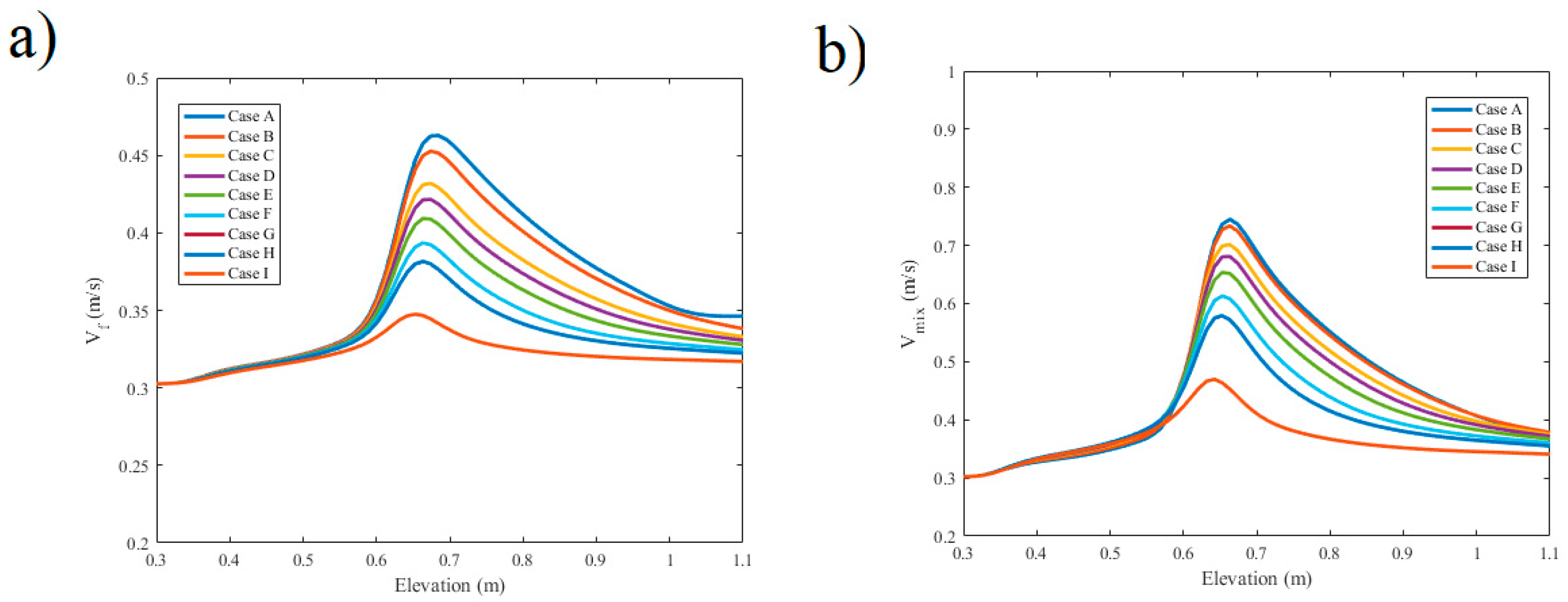
Liquid speed and mixed speed versus vertical direction of the cylinder for numerous circumstances of Magnetic conditions are given away in
Figure 6a,b. Thus, as recognized, the two speeds improve at the warmed part. This impact is more significant for varied speed in light of the water vapor speed impression. By the using of Lorentz forces, the pinnacle speeds are reduced and an increasingly smoothed plan will be picked up. The end point of all through-constrained convective bubbling semi-empirical equations for the inward stream is archived from exploratory information for coolers, cryogens and water.
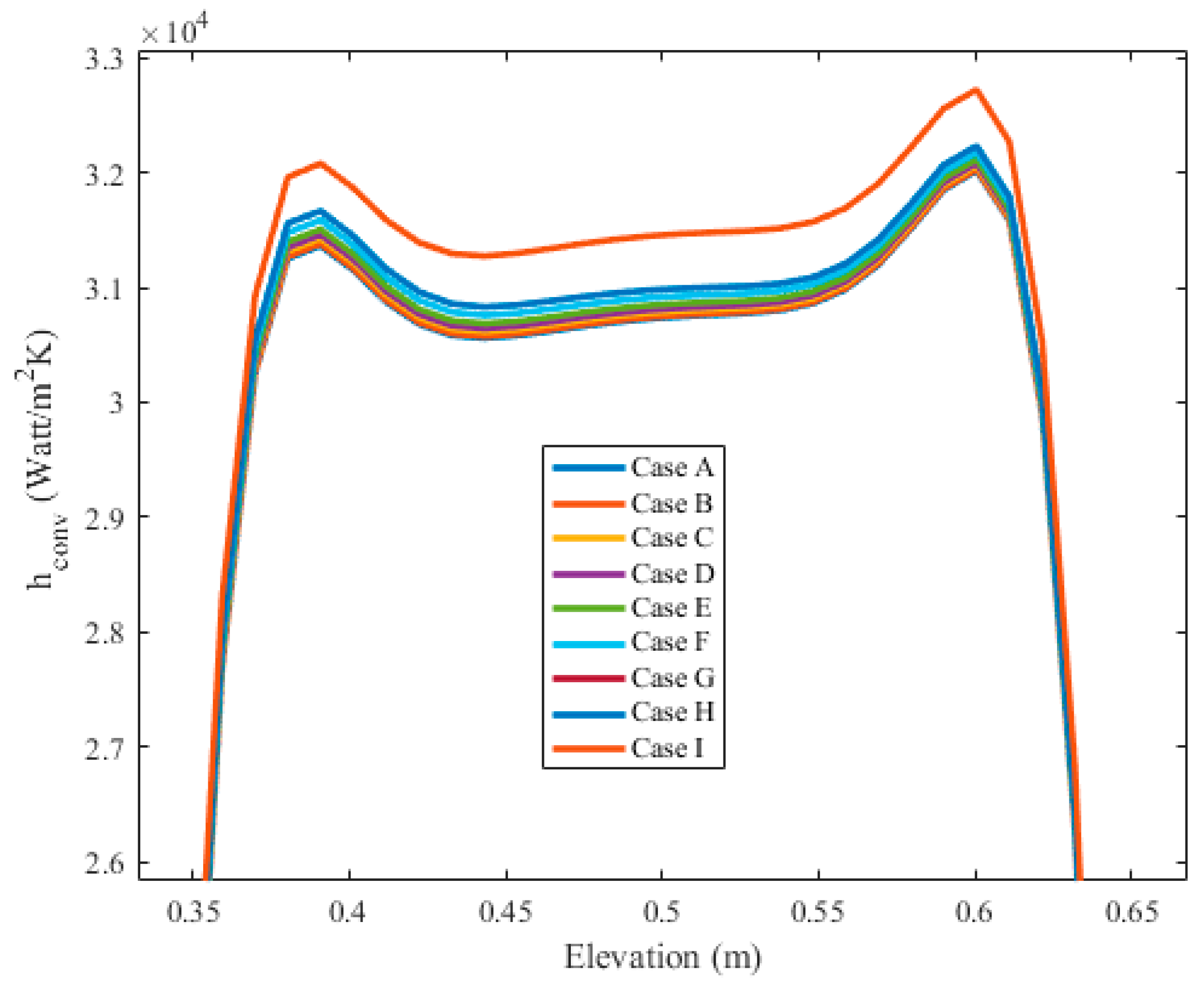
Convective warmth switches over on the solid body against the vertical direction for certain occasions of Magnetic conditions, as delineated in
Figure 7. As is self-evident, except for the binary zones toward the start and the closure of the cylinder, the convective warmth switchover coefficient is comparable. The vast majority of convective warmth switchover is added to the nucleate bubbling territory of single-stage fluid (Dictus-Boelter) coefficient of heat over length. By using the Lorentz phenomena, the convection heat transfer coefficient was marginally improved.
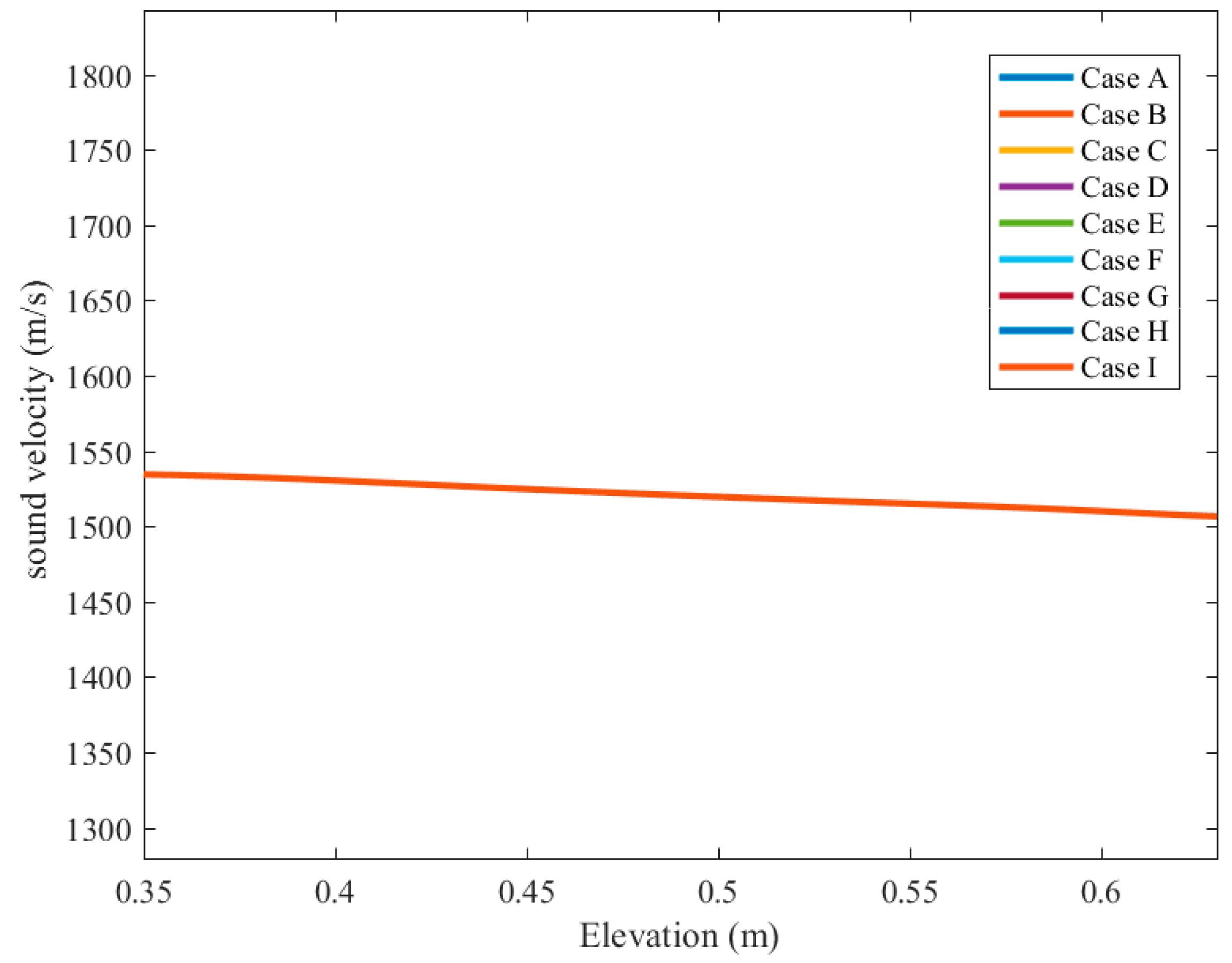
The most critical segment of the water hammer effect is as indicated by sound speed.
Figure 8 demonstrates the sound speed against the perpendicular distance for numerous occurrences of Magnetic conditions. As shown, the speed of the sound is marginally reduced as the distance from the beginning point is increased. By using Lorentz phenomena, the estimation of the speed of sound is not modified.
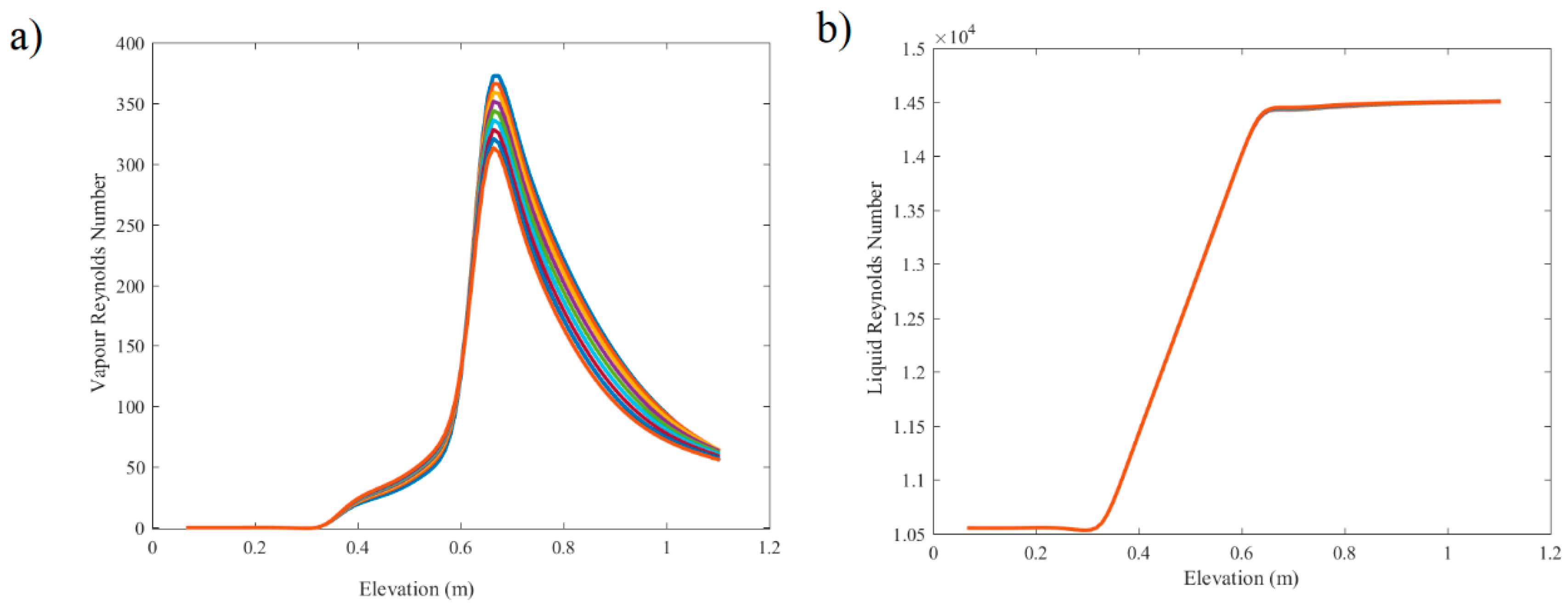
Gas Reynolds number and fluid Reynolds number against the distance of a point from the inlet for various occasions of Magnetic conditions are envisioned in
Figure 9a,b. Both gas Reynolds number and fluid Reynolds number improve by upgrading the space from the earliest starting point of the cylinder. The ascent of vapor is higher than fluid, on account of a greater improvement in vapor speed because of the bubbling void that has been created. By using Lorentz phenomena, the estimation of both gas and fluid characteristic value is decreased.
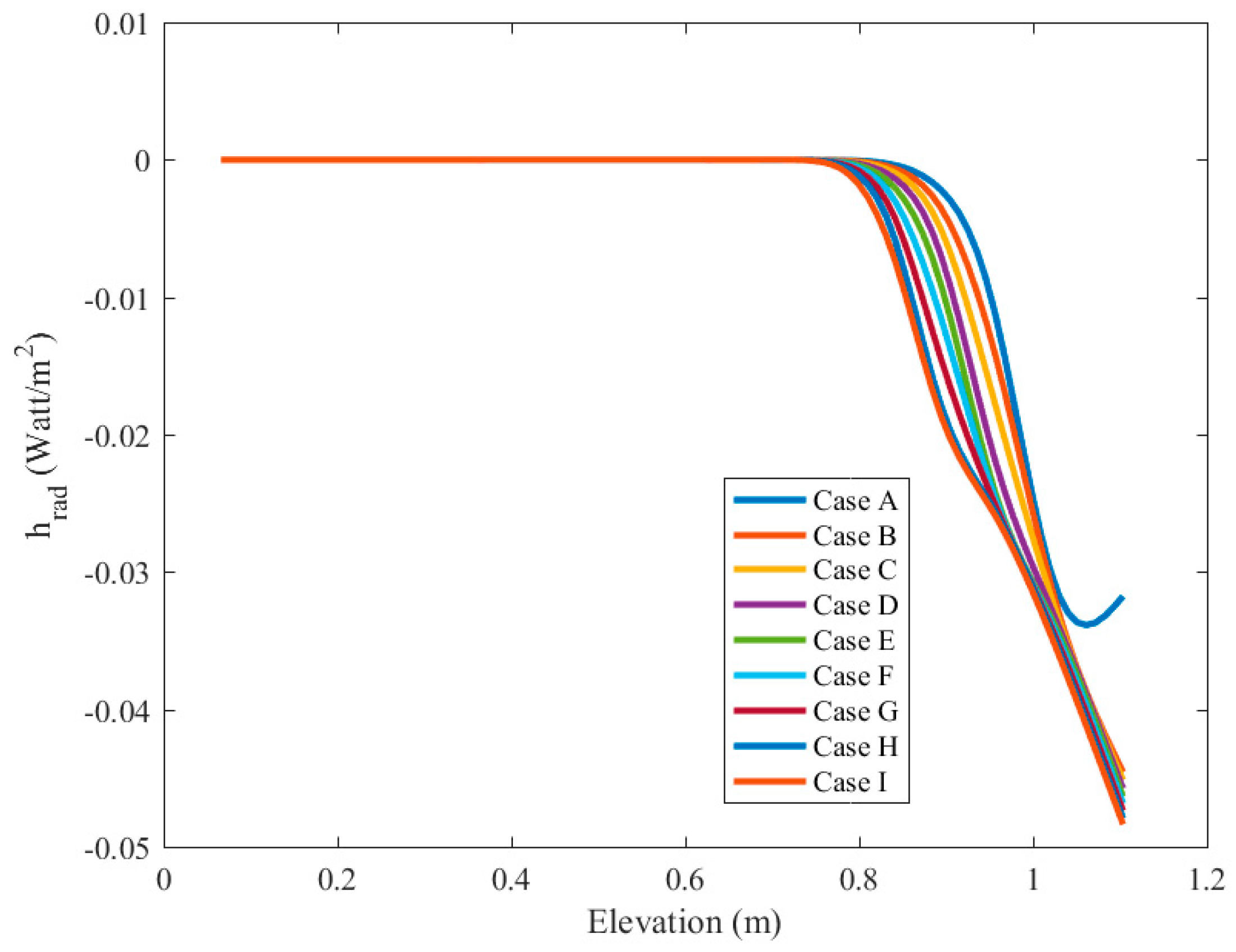
Figure 10 exposes the radiation heat transfer coefficient against the vertical coordinate of the cylinder for various cases of Magnetic conditions. As portrayed in
Figure 10, the radiative heat transition is critical. Later, at the start of warmed part and by utilizing Lorentz forces, the estimation of warm radiation motion is improved.
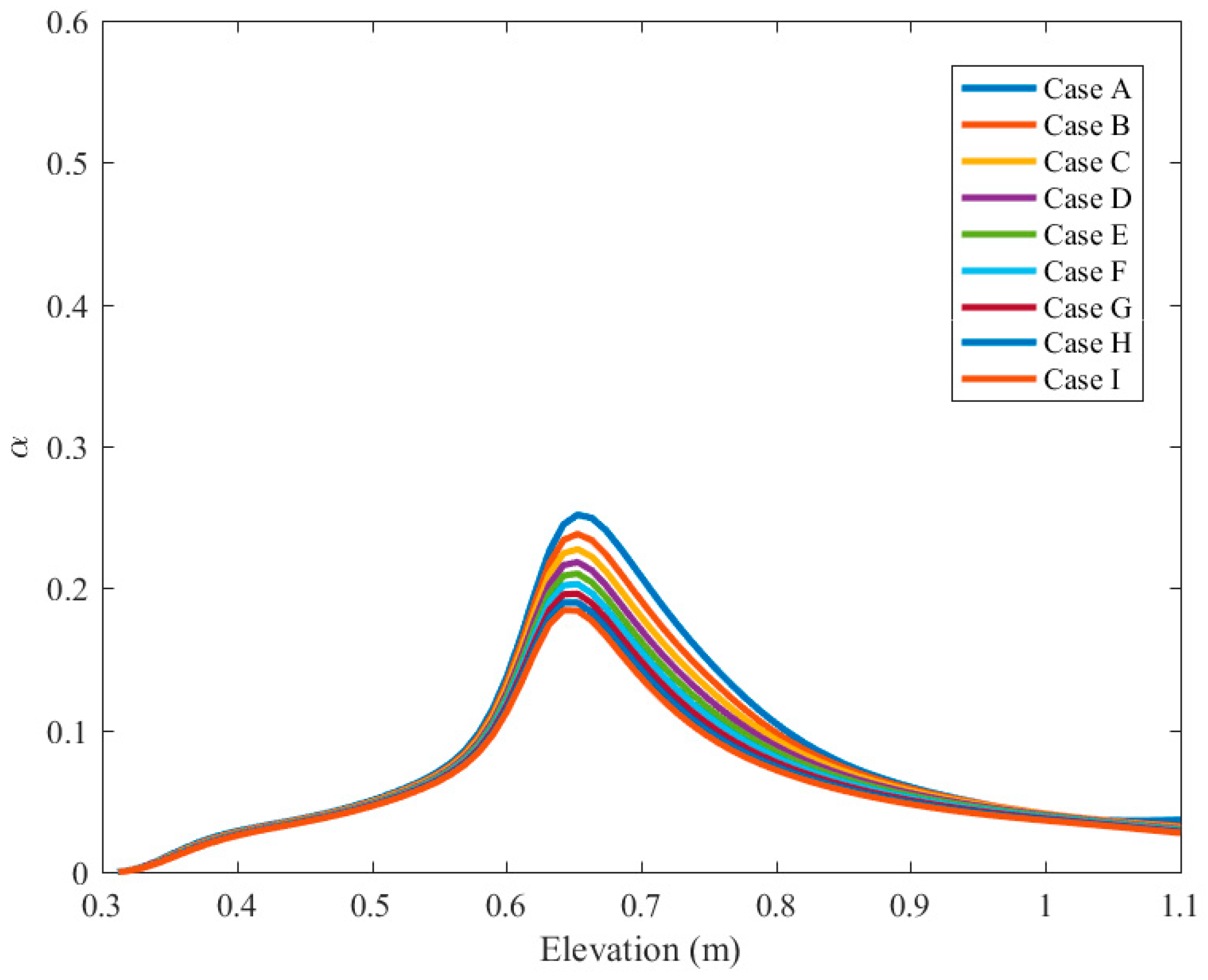
Figure 11 shows the void portion against the distance from the inlet for different occasions of magnetic conditions. By improving the Lorentz forces, the sum or vapor stage is decreased. Subcooled stream bubbling restricts the development of the air pocket from the cylinder divider. A theoretical arrangement of air pocket elements is found from the balance and equilibrium between surface waves and lightness weight of the outside and inside air pocket pressure.
Figure 12 displays the impact of various Lorentz forces connected to the air pocket development width against the length of the cylinder. As shown, upgrading the hub separates the air pocket development. The width improves until its optimum and remains at this level until the end of the cylinder. Throughout warmth trading frameworks, the working condition or weight flux is less than the outlined circumstance. This is conducive to nucleation of the bubble in a sub-cooled regime that could likely be the cause of the slug happening or beat stream routine. This is associated with the recurrence of weight or energy motion variances with the Taylor bubbles recurrence and the regular recurrence of the tube. Points were found where the void has the impact of separating the huge irritations into little ones, thus diminishing the general vacillation vitality. As the measurement of funnels is bigger than the Taylor bubble distance across the annular section, it has little consequence regarding the overwhelming recurrence. The utilization of Lorentz force does not have a noteworthy effect on the air pocket development width plot. Moreover, the bubbling surface and divider object have, to a certain extent, been envisioned to have a noteworthy effect upon warmth division amid the bubbling warmth transmission and to have an impact on the occurrence of the basic warmth motion phenomenon. As often as possible, the fluid stream over the vapor bubble additionally prompts the magnetic forces that work in opposition to the relative development. Here, the impact of the condensation, vaporization, and buildup in the assessment of the air pocket development breadth is negligible.
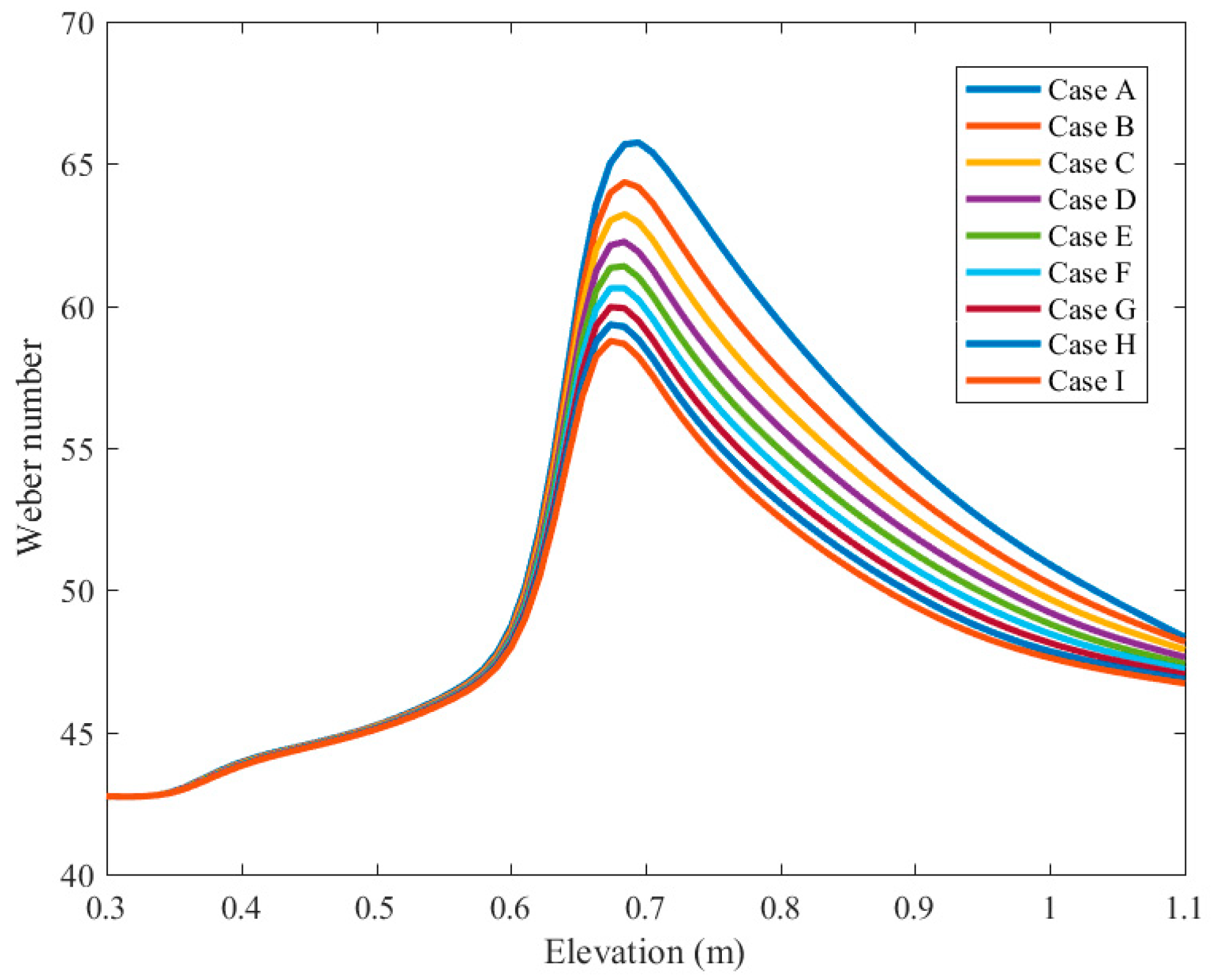
Figure 13 plots the change of Weber number throughout the vertical direction. The Weber number, which is the ratio of inertial force to surface forces, increases in the heated region while this increase can be controlled by applying magnetic force. Taylor bubbles and film thickness over the wall are also controlled when the Weber number decreases. As shown, the effect of the magnetic forces on Weber number before and after the heated region is negligible.
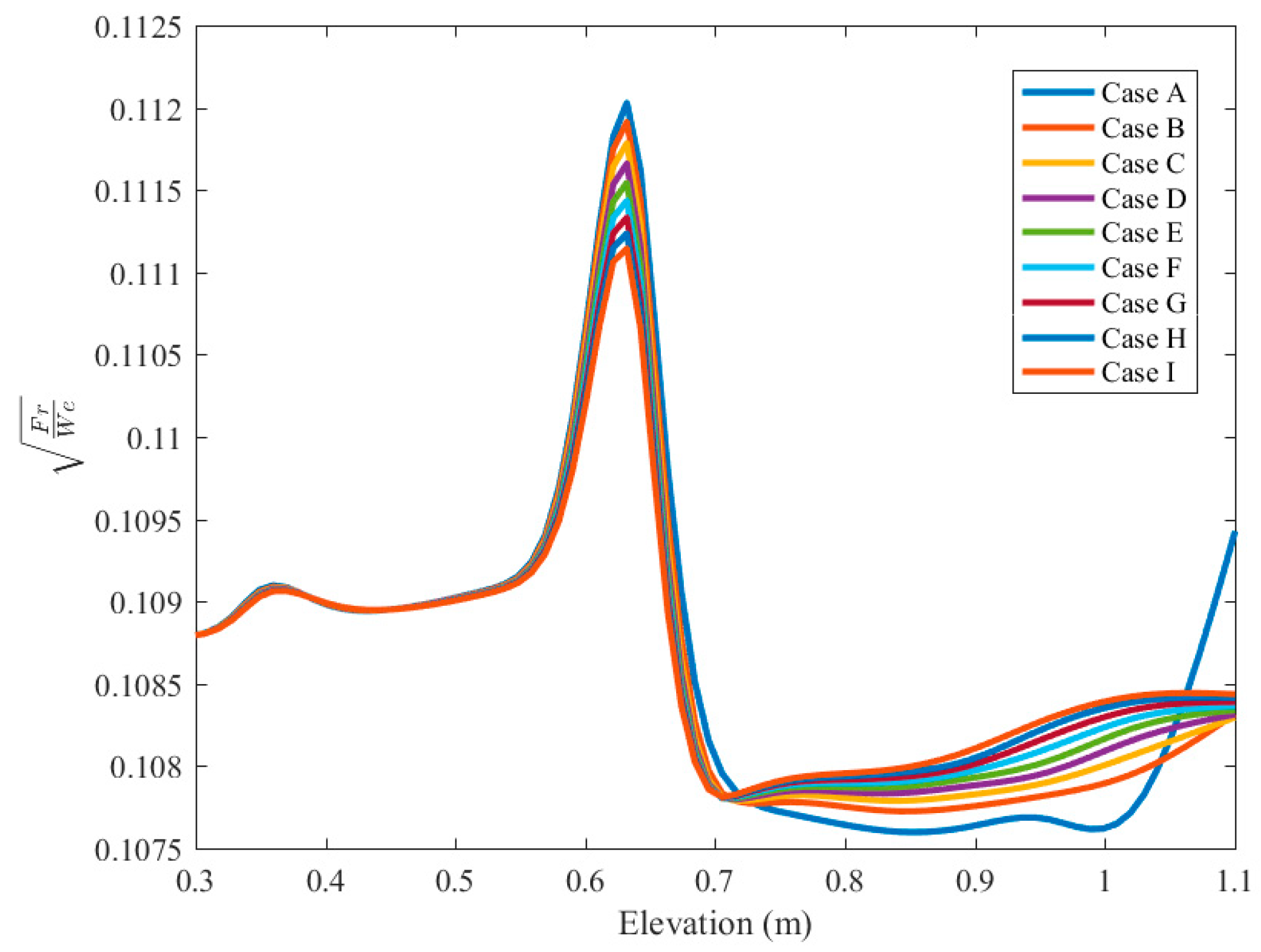
The impacts of the wave between gas and liquid phases on the recurrence of energy motions against the part of the cylinder for numerous Magnetic conditions are portrayed in
Figure 14. The parameter of the square of Fraud to Weber number here is used as a measure of the frequency of two-phase fluctuations. As portrayed, the extent of this parameter improves before the warmed part and overshoots after the warmed part. The application of magnetic force reduces the adequacy of the measure of the frequency of two-phase fluctuations.
Figure 15,
Figure 16,
Figure 17,
Figure 18 and
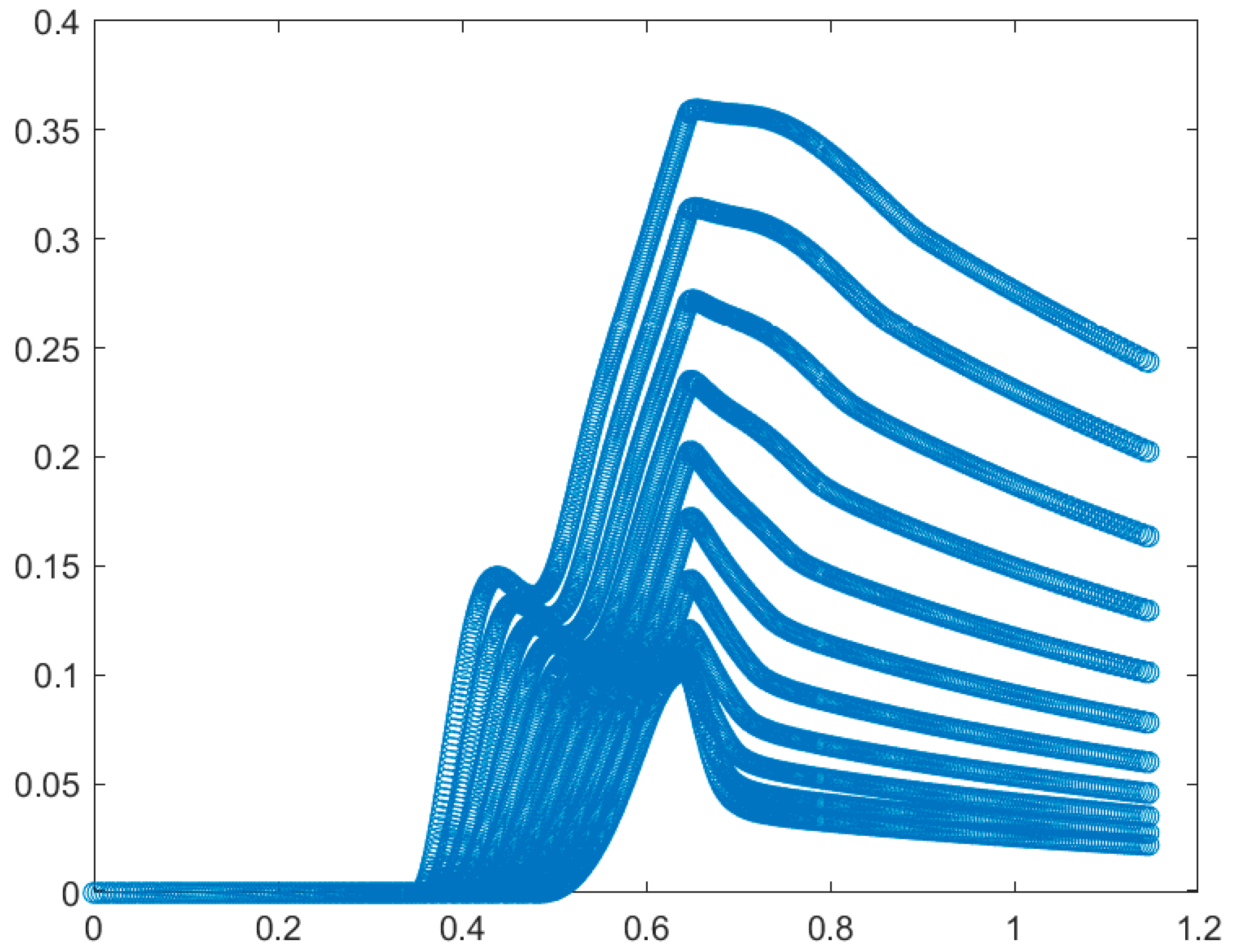
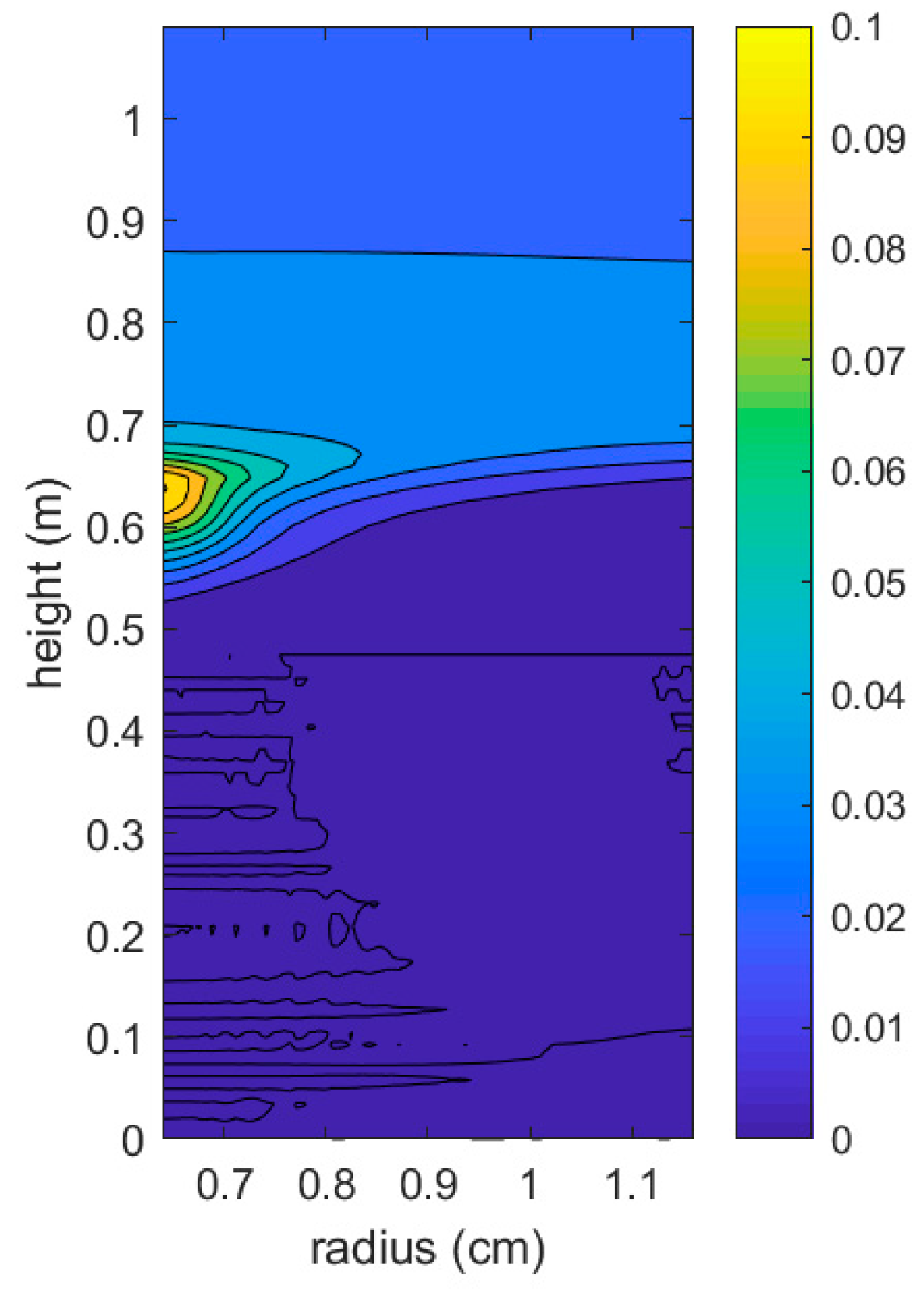
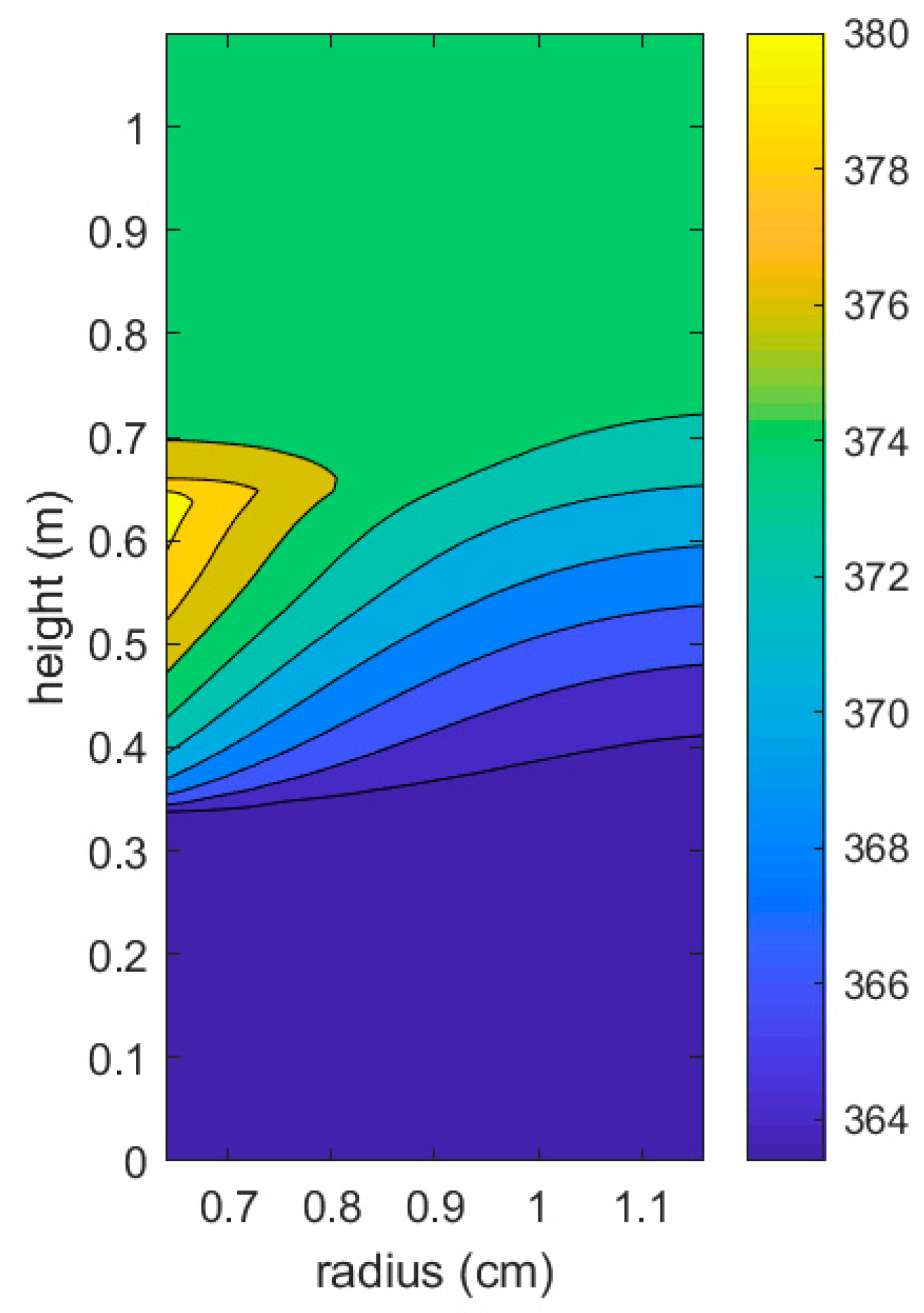
Figure 19 presents the effect of a concentration of nano-particles on vapor phase and thermal conditions. As shown by the increase of particle fraction from 0 to 10%, the vapor fraction decreases. As shown by the increase of nanoparticle concentration, the maximum temperatures decrease.
5. Conclusions and Recommendation
Simulation of two-phase flow is advanced to mimic the water-vapor stream in an upright warmed tube. The correlation between the experimental and numerical results demonstrates the suitable course of action between them. The parameter contemplates the Lorentz force sway on two-stage stream incited vibration. In this study, by using the Froude number as a measure of the linearized motion of surface wave between the phases, the stability phenomena are discussed. In addition, the magnetic asset of vacillation is upgraded as the liquid phase started to change into the gas phase. By improving evaporation, the liquid force significance will unmistakably upgrade. By improving magnetic control over fluid, the consistent shrinkage of the liquid power crest and liquid awe power are checked. The impact of liquid momentum is improved at the warmed territory but, by upgrading the Lorentz force, the pinnacle of the divider powers diminishes. The bubble generation, on the other hand, is reduced at the warmed length and the use of Lorentz force is not practical. When using Lorentz force, the pinnacle speeds are diminished and an increasingly level plan will emerge. The warmth convection coefficient was marginally upgraded by using Lorentz force. The use of Lorentz force enabled the estimation of both fluid and gas Reynolds number and the measure of the gas stage, and reduced the liquid mass effects. By improving the Lorentz force, the liquid mass is reduced for superficial pressure powers. As shown by the increase of particle fraction from 0 to 10 percent, the vapor fraction decreases. As shown by the increase of nanoparticle concentration, the maximum temperatures decrease. In further study, we recommend performing an experiment based on the framework of the current research.