1. Introduction
Manufacturing is a critical part of a national economy. With economic globalization and the emergence of Industry 4.0, it has become increasingly important to enhance efficiency and promote business transformation of enterprises. Research in the area of prognostics and health management (PHM) plays a pivotal role in promoting the transformation of the production industry [
1]. Current topics of interest in the PHM focus on identifying potential relationships within the data by searching and analyzing massive amounts of industrial data with the aid of artificial intelligence algorithms. The goal of such research is to further optimize production processes; recent results have allowed the maintenance of industrial equipment to evolve from expert, experience based methods to automated adaptive learning methods. Ultimately, these intelligent detection methods can help to improve the efficiency of manufacturing processes from a number of perspectives.
Tool wear monitoring is an important aspect in the PHM area. During the machining process, the tool wear occurs, which affects the quality of the machined surface and may lead to the risk of the machine tool damage [
2]. Tool wear measuring methods can be categorized into direct and indirect methods. For the direct methods, the tool wear value can be obtained directly by a machine vision, surface measurement, or laser technique. However, it is often necessary to interrupt the manufacturing process due to the influences of interference sources such as coolant. This results in a detrimental impact on productivity in real-time environments, which limits their practicability [
3]. For the indirect methods, sensing equipment is used to collect the signals and acquire the signal features related to the wear value. Since the sensor does not have direct contact with the tool and does not affect the machining process, this class of methods is well-suited for practical working conditions in production workshops. At present, sensor-based tool data acquisition mainly includes the following signals; cutting force, vibration, acoustic emission, current, and torque [
4,
5,
6]. In traditional tool wear detection methods, the acquired data is preprocessed with normalizing and denoising methods. Then, design features are manually extracted from the time domain, the frequency domain, the time-frequency domain, respectively, to reduce the dimensionality. Finally, a hidden Markov model (HMM), neural networks, or support vector machine (SVM) is used for the classification or regression purposes [
7,
8,
9,
10,
11,
12].
Most of the current tool wear detection algorithms collect signals with the indirect methods, which is implemented using machine learning algorithms. For example, Liao et al. propose a tool wear condition monitoring system based on the acoustic emission technology [
7]. By analyzing representative acoustic signals, the energy ratios from six different frequency bands are selected from the time-frequency domain. These are used as a classification feature to determine the amount of tool wear. In this method, the SVM is used as the classification method, which can ultimately achieve the accuracy ratio of 93.3%. In [
10], the cutting force signal and the multiscale hybrid HMM are combined to monitor the wear state of the tool. From the perspectives of local and global analyses, this method can deeply capture the tool wear state information; accurate performance monitoring of the tool wear value is achieved. The experimental results indicate the hybrid approach achieves better performance in comparison to that obtained by the use of the HMM alone. Zhang et al. apply the multifractal theory to calculate the generalized fractal dimensionality of the acoustic emission signal during the cutting process [
12]. Here, the generalized dimensional spectrum of the acoustic emission signal is obtained under different tool conditions. The generalized fractal dimensionality and cutting process parameters are used as the input feature vector of a backpropagation neural network (BPNN), where the initial weight value of the network is optimized with a genetic algorithm. The experimental results show that this method is able to predict the tool wear effectively, where the tool machining efficiency can be further improved. The above methods are often constrained by the quality of the extracted features; manually refining the features requires researchers to master specific experience and skills related to the production environment. Therefore, the enhancement of the machine learning models remains rather limited.
In recent years, rapid developments have seen for deep learning methods based on artificial neural networks. These methods can extract different features by building a deep neural network structure. In contrast, the traditional methods are only able to extract specific features. Multifeature learning can describe the research problem more comprehensively and improve the accuracy and robustness of the algorithm. Therefore, deep learning methods have demonstrated superior performance in various classification and regression tasks; in particular, they have received attention in the fields of image and speech processing [
13,
14,
15]. Remarkably, the deep neural network can replace the feature extractor and classifier (regressor) in conventional feature learning theory. It can be considered as an end-to-end model, which does not depend on the complicated preprocessing of original data. As a result, these networks are more concise and fast. The deep learning method has shown promising results in related areas of the PHM, and has been applied to fault diagnosis, equipment life prediction, and tool wear detection [
16,
17,
18,
19]. In [
16] a bearing fault diagnosis method is proposed based on a fully connected competitive self-encoder. This model can explicitly activate certain neurons from all of the samples of a minibatch, where the life cycle sparsity can be encoded into the features. A soft voting method is further used to make predictions on the signal segments generated from the sliding window. The experimental results show that the methods using a two-layer network can obtain higher diagnostic accuracy under normal conditions and can also demonstrate better robustness than methods with deeper and more complicated network models. Zhang et al. propose a transferring learning and Long Short-Term Memory (LSTM) based model for predicting the remaining life of equipment [
18]. This research addresses the problem of a small sample size, due to the difficulty in acquiring the faulty data. In particular, this model can be pretrained on different, but related, datasets. Subsequently, the network structure and the training parameters are finely tuned for the target dataset. The experimental results demonstrate that the transfer learning method is capable of improving the model’s prediction accuracy using a small number of samples. Zhang et al. apply the wavelet packet transform method to transform the acquired tool vibration signal to the energy spectrum, which is further used as input into the convolutional neural network (CNN) [
19]. Therefore, features can be automatically learnt and accurately classified with the powerful image feature extraction capability of the CNN. It is indicated in [
19] that a deep learning based CNN can achieve superior accuracy in comparison to other classical tool wear prediction models for the milling cutter wear classification problem.
In summary, significant progress on deep learning methods has been reported in a variety of areas. However, research on their use in tool wear monitoring is just beginning to emerge. The end-to-end processing the deep learning methods provide has the potential for significant impact in manufacturing industries. A crucial, open research area is the development of algorithms that are capable of adaptively extracting features from time-domain signals and can also strike a balance between accuracy and speed by adjusting the training methodology and model structure.
3. Experimental Results and Analysis
The intelligent manufacturing laboratory of Guizhou University, Guizhou Province, China, is selected as the validation platform. The experimental equipment is as follows; one computer numerical control (CNC) milling machine for machining workpieces; one die steel (S163H) as the workpiece to be machined—the machining tool has a cemented carbide 4-edge milling cutter (diameter of 6 mm) and its surface is covered with layers of titanium aluminium nitride coating; and a signal processing unit. The cutting parameters are set as shown in
Table 2.
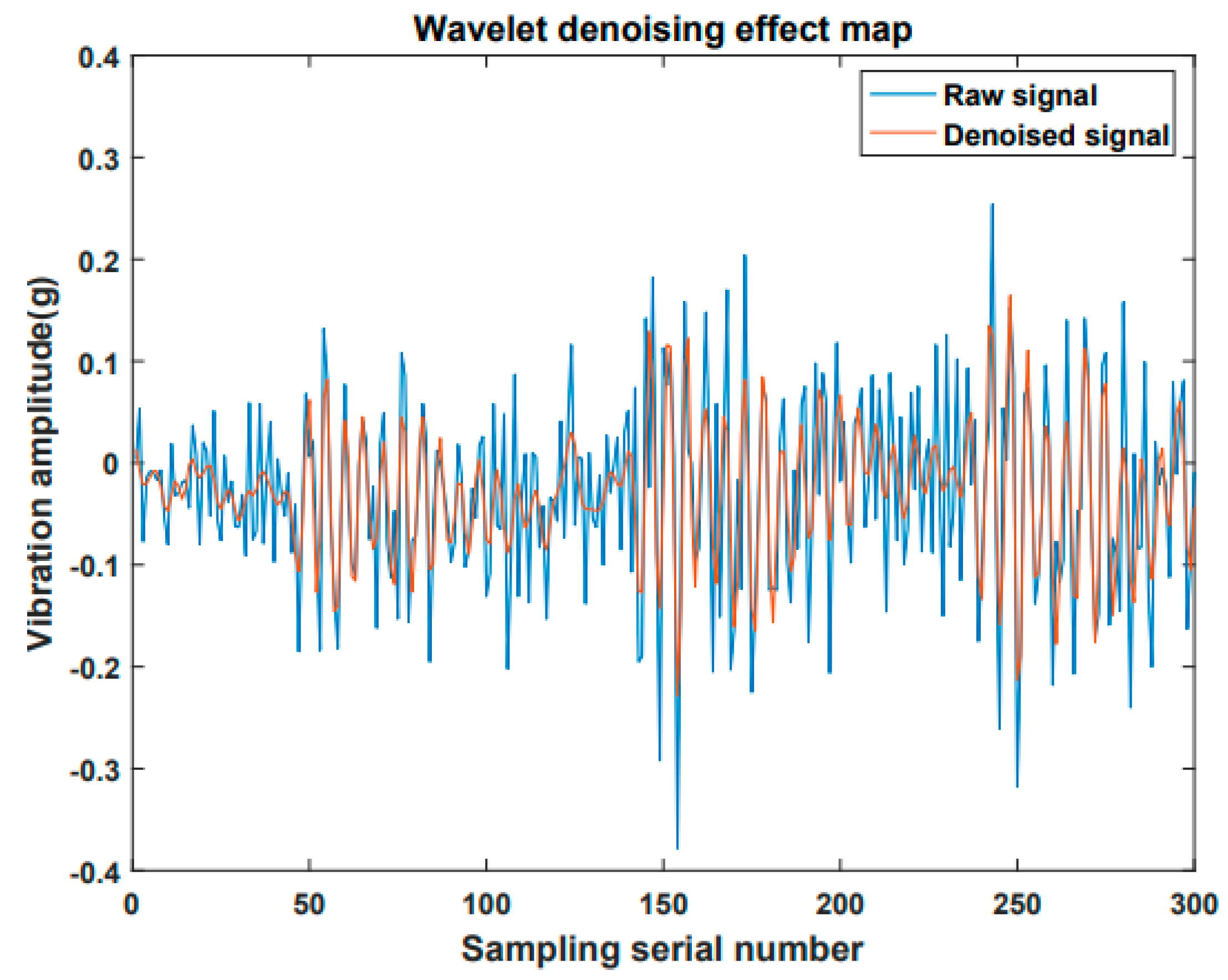
The signal preprocessing mainly transmits the three-axis vibration signal from the tool processing to the upper computer through the acquisition unit. The upper computer performs the wavelet threshold noise reduction. In traditional machine learning methods, the corresponding features are first extracted from the time domain, the frequency domain, and the time-frequency domain. Then, these methods are used to reduce the dimensions of the features and input them into the neural network (or SVR regression) in order to obtain the wear detection value. In this paper, the deep RDN model is used to adaptively extract features from the time-domain signal after the noise reduction, and the wear detection value is obtained. The network training parameters are as follows; the learning rate is initialized to 0.001 and set to exponential decay, the batch size is 32, the epoch is 100, the optimizer uses Adam, the weights and bias are randomly initialized.
3.1. Signal Processing Unit
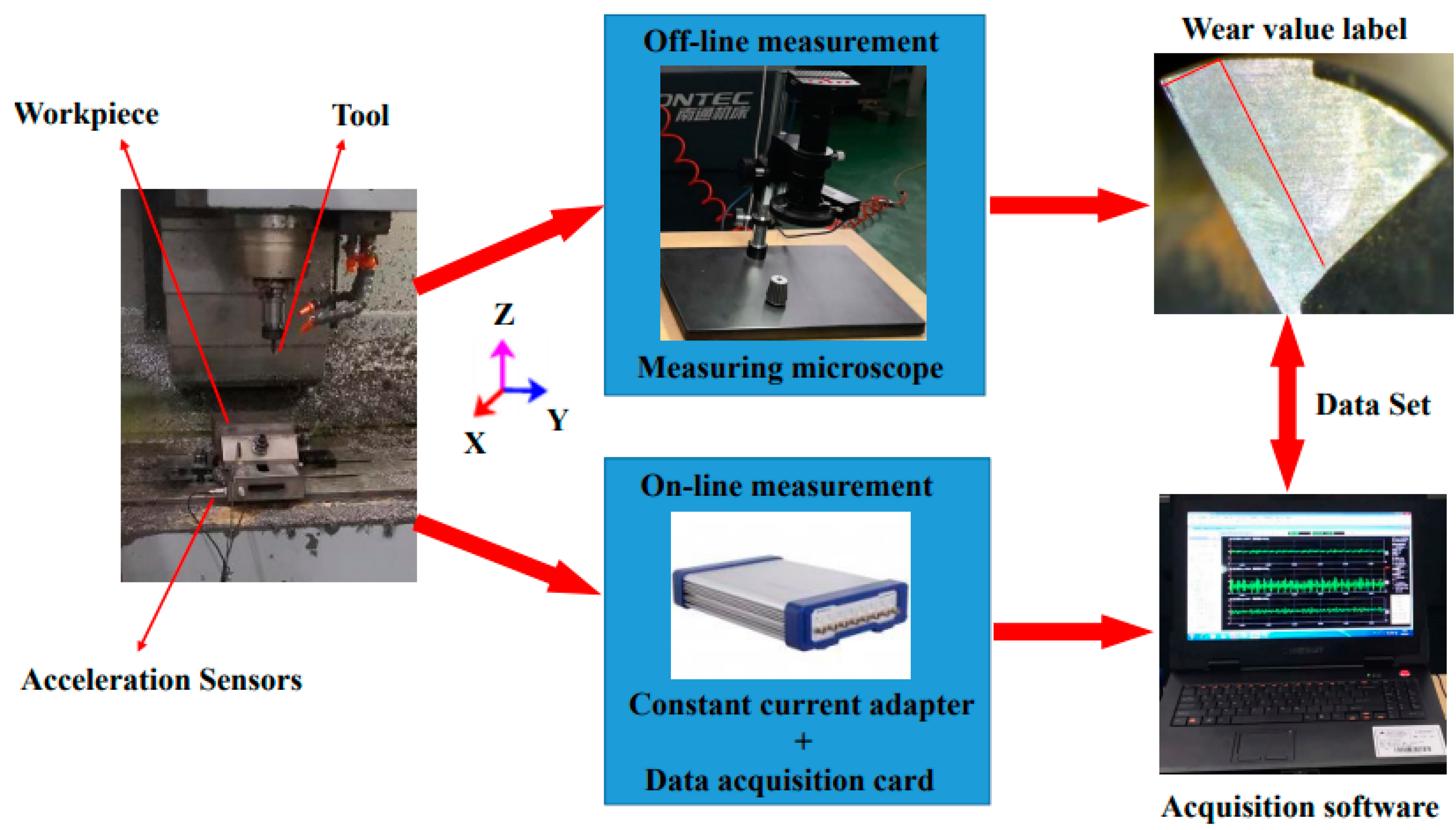
The signal processing unit can be divided into a data acquisition unit and an upper computer analysis unit. The data acquisition unit consists of an acceleration sensor, a constant current adapter, a digital acquisition card, an acquisition software program, and a microscope (workflow as shown in
Figure 8). Before the start of the data acquisition, three accelerometers are installed in the X, Y, and Z directions of the workbench. Then the magnification of the microscope is adjusted and the measurement calibration of the microscope is completed. The sampling frequency of the digital acquisition card is set to 20 KHz. Each tool performs 330 feeds in the X-axis direction, with a feed of 200 mm each time. When the machining completes, the cutter is removed from the machine and a picture is taken. The measurement process selects the position of the rear edge as the measurement position. This position is the most prone to wear. The same datum line is used to ensure the position remains unchanged during the measurement. The wear value is calculated by subtracting the length of the current rear edge from the last rear edge length.
The hardware configuration of the upper computer analysis unit is as follows; Intel Core i7 7700 K processor, clocked at 4.2 GHz; 32 GB memory; and two linked GeForce 1080 Ti graphics cards. The software uses the Ubuntu 16.04 as the operating system; the deep learning framework uses Keras as the front-end and TensorFlow as the back-end. Before the model is trained, the vibration signal generated by each tool feed is segmented into 10 time-domain signal samples of length 5000. After that, the samples from three tools are scrambled as the training set; the samples from the remaining tool are used as the validation set.
3.2. Evaluation Indicators
In this paper, the root mean square error (RMSE), the coefficient of determination R-square, and the mean absolute percentage error (MAPE) are used as the evaluation indicators of the prediction accuracy. Specifically, the RMSE indicates the degree to which the predicted value deviates from the true label. The closer the value is to zero, the better the performance is. The RMSE calculation is as follows
where
is the true label value of the
ith sample wear value, here it represents the tool wear value measured by the microscope;
is the predicted value of the
ith sample wear value, here it represents the predicted value of designed model; and
is the total sample number of the test set, here it represents the number of vibration samples for prediction.
The coefficient of determination R-square represents the degree of fit between the predicted value of the tool wear value and the real label. The closer the value is to one, the better the fit is. The R-square calculation is as follows
where,
represents the mean value of all the true label values in the test set
.
The MAPE represents the mean value of the absolute value of the relative error. The closer the value is to zero, the better the prediction performance is. The MAPE calculation is as follows
3.3. Experimental Results of Network Structure Comparison
3.3.1. Impact of BN and Dropout Strategies on Model Performance
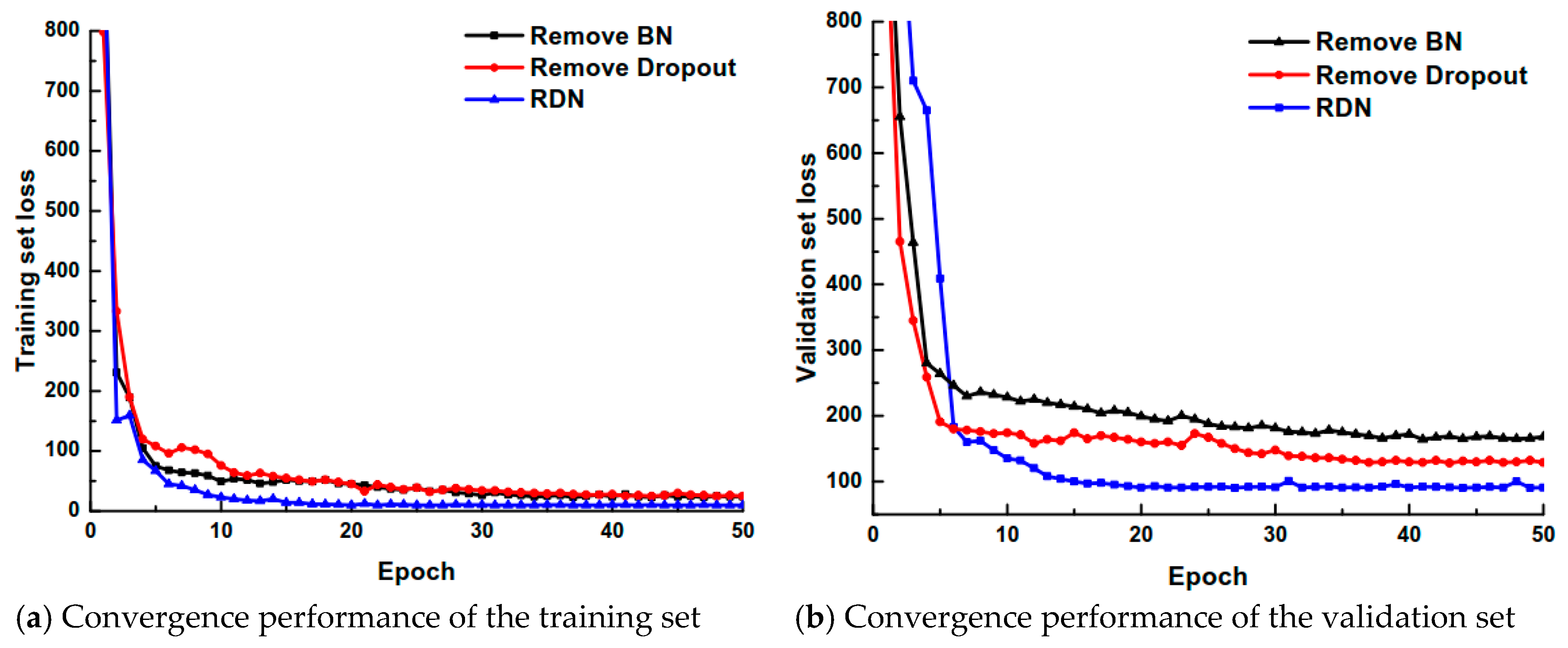
In the experiment, we mainly focus on the impact of the BN batch normalization and the Dropout regularization strategy on the network convergence performance in RDN. The network convergence performance is compared on the training set and the validation set as the basis for judging the results. The comparisons are performed by (1) removing the BN layer of the RDN network and (2) removing the Dropout layer of the RDN network. The comparison results are shown in
Figure 9.
According to the results in the figure, there is no gradient explosion or dispersion in the three network structures, and the network convergence speed is fast without overfitting. It indicates that the RDN convergence performance is superior and the generalization ability is strong. The RDN network with the BN and Dropout layers converges faster than the RDN network with the BN layer removed or the Dropout layer removed. After 15 iterations, the loss function value is close to its lowest value. In the subsequent iterative process, changes of the loss function values are small and the convergence performance is good. However, the performance of the RDN network with the BN layer removed or the dropout layer removed is impeded. The model needs to iterate 35 times in the training set to converge to the minimum value, the convergence speed is slower on the verification set, and the obtained loss function is also higher. The above experiments demonstrate the effectiveness of the RDN model proposed in this paper, which adopts the BN block and the Dropout layer.
3.3.2. Impact of Network Layer Number on Model Performance
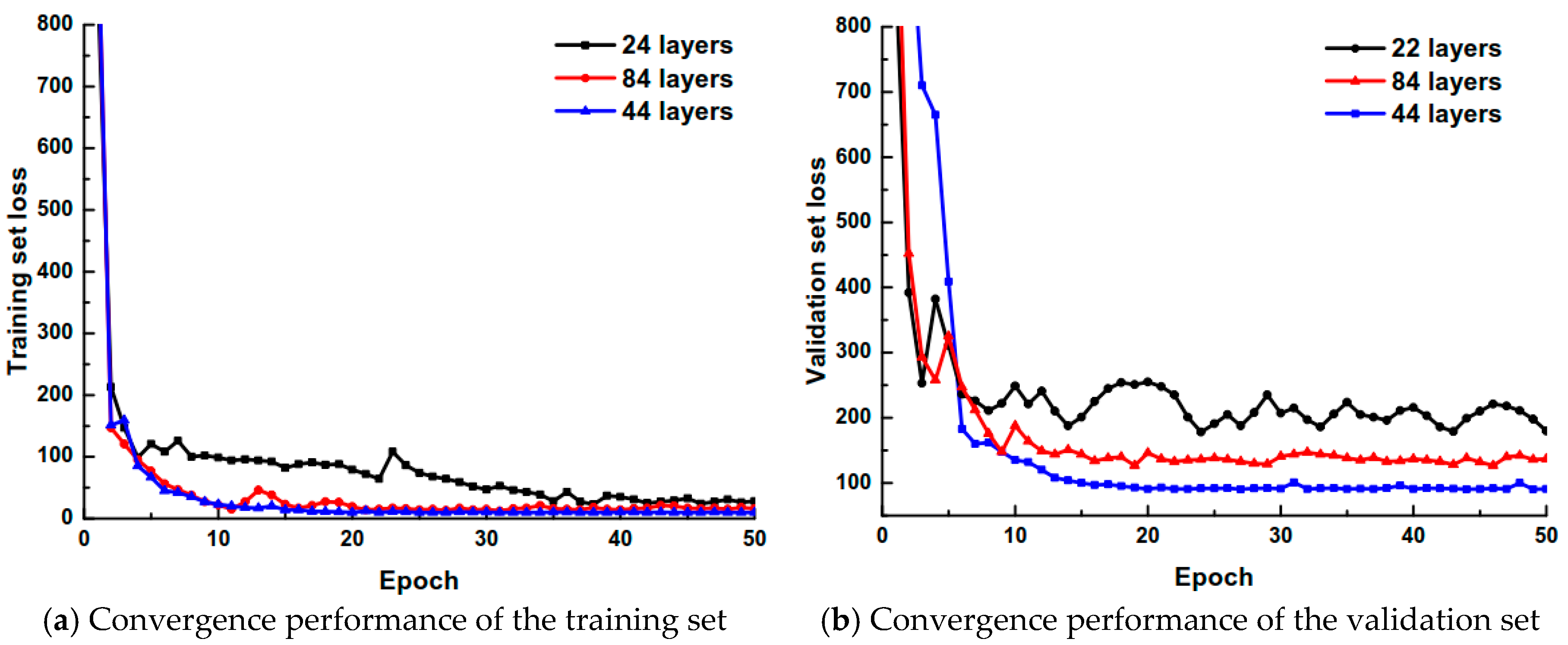
In order to verify the impact of different network depths on the performance of the model, 24-, 44-(the network used in this paper), and 84-layer networks have been selected for analysis. All of the networks use the same dense block and transition block. The difference is in the inconsistent number of dense blocks. The comparison of the convergence performance on the training set and the validation set for the varying depths is shown in
Figure 10.
It can be shown that a certain depth of the network can better extract the effective features and reduce the RMSE between the predicted value and the true value. However, when the network structure is continuously deepened to a certain extent, gradient dispersion occurs in the model. This causes the loss function to remain at a certain large value; it cannot be decreased. During the training progression, the network model with a depth of 44 layers has the best convergence performance. The mean value of the loss function dropped to 3.82 in the last five iterations on the training set, and reached 94.67 on the validation set. Therefore, a more appropriate network depth can improve the feature extraction quality and cause the loss function value to continually decrease. At the same time, the choice of depth balances the network complexity and prediction accuracy, reduces the hardware requirements of the network, and makes it more portable and scalable.
3.4. Comparison Results of Deep Learning Models
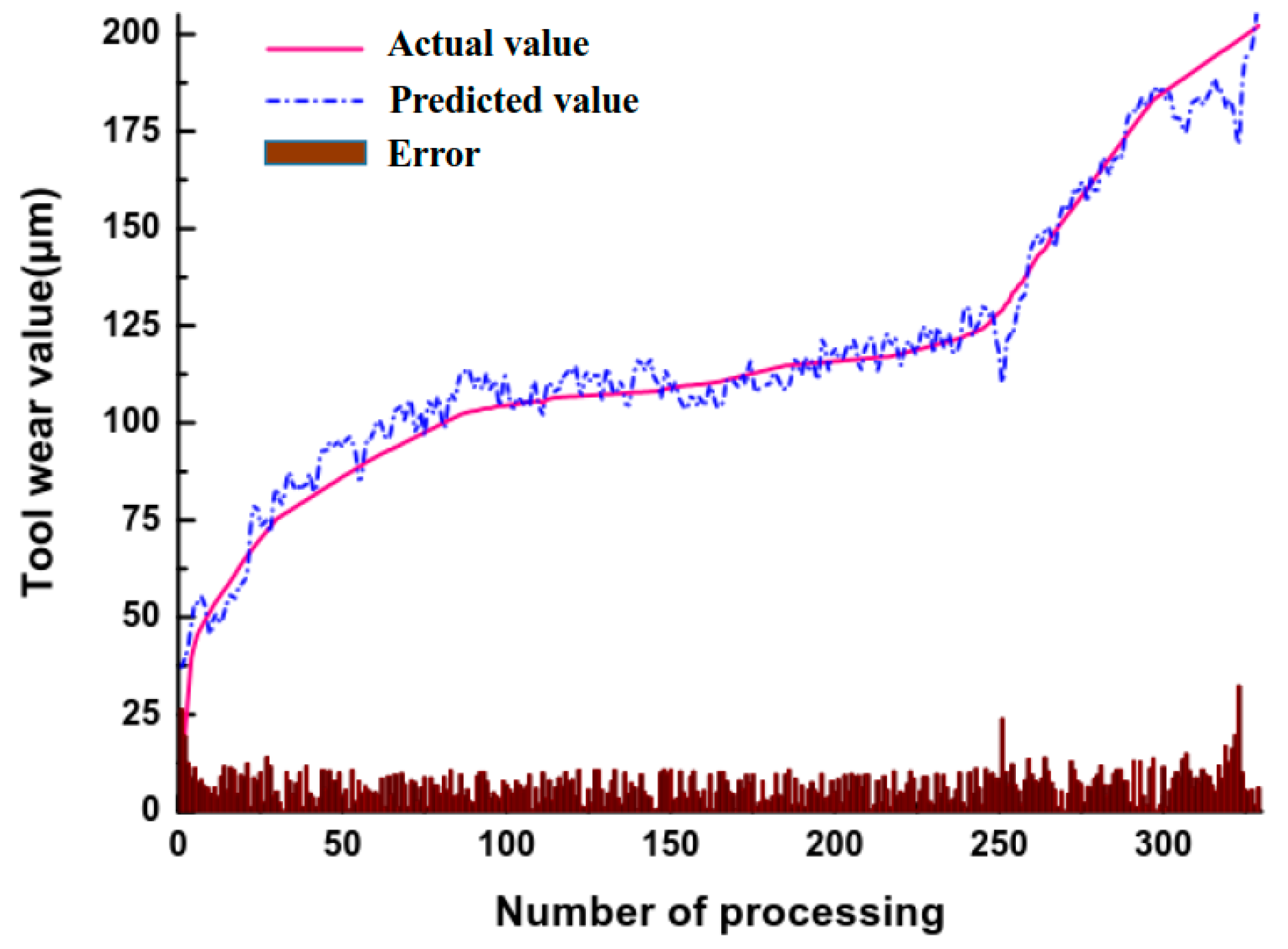
The regression performance of the RDN method proposed in this paper is shown in
Figure 11. The true wear value in the figure is measured by microscope after each feed. In the figure, the RDN has a large prediction error value at the initial wear stage and at the severe wear stage; the predicted value is relatively stable in the moderate wear stage. This aligns with the actual need for tool wear detection. The results also show the RDN learns the data features adaptively to achieve better prediction results, i.e., separate steps to extract and refine features are not needed.
In the deep learning model, CNNs and cyclic neural networks are commonly used to deal with sequence problems, such as speech recognition and natural language processing. VGGNet-16 [
24] and ResNet-50 are used in the experiment, which have achieved excellent results in the ImageNet competition. In addition, the convolution method is replaced with a one-dimensional convolution. At the same time, the RNN [
25] and LSTM [
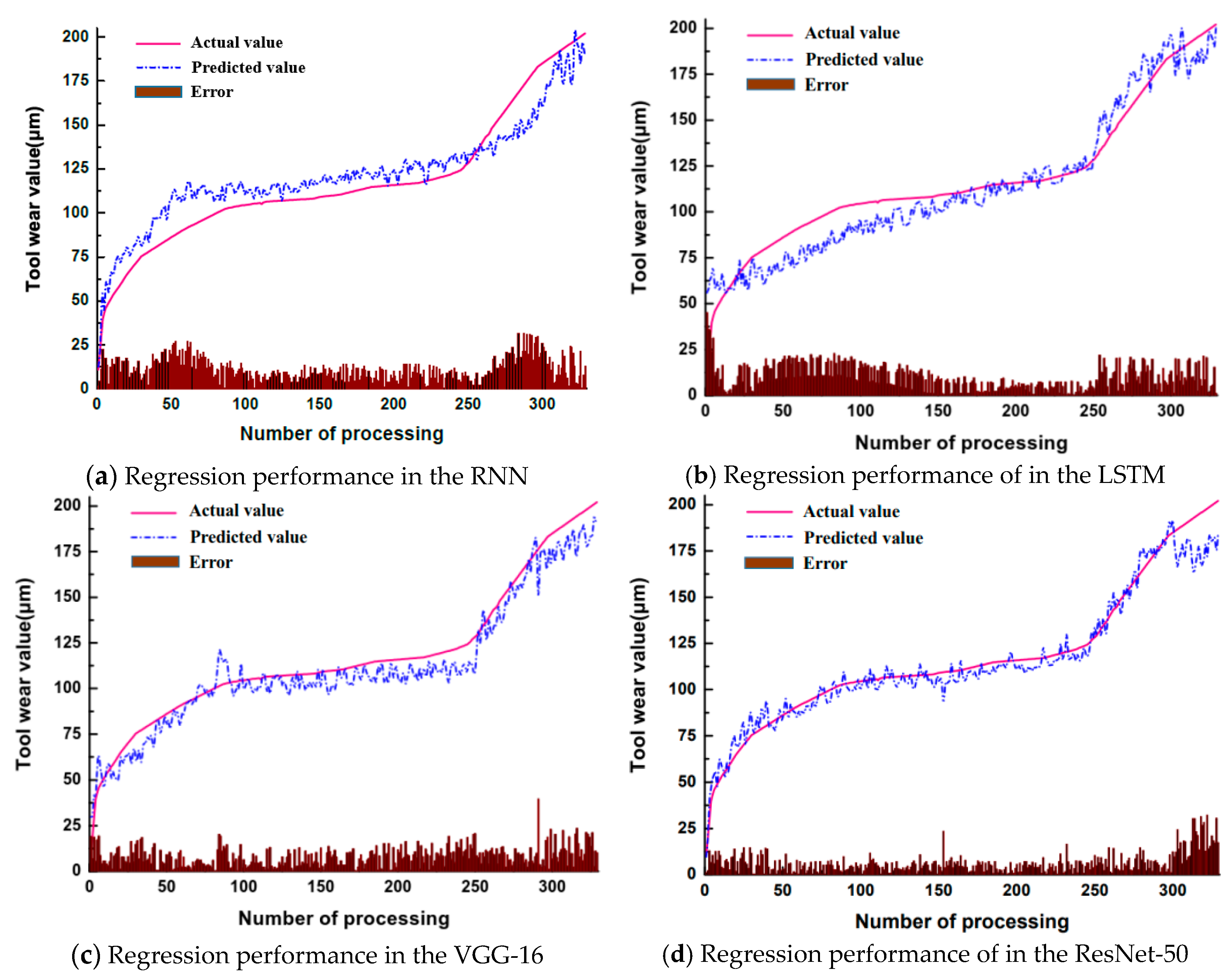
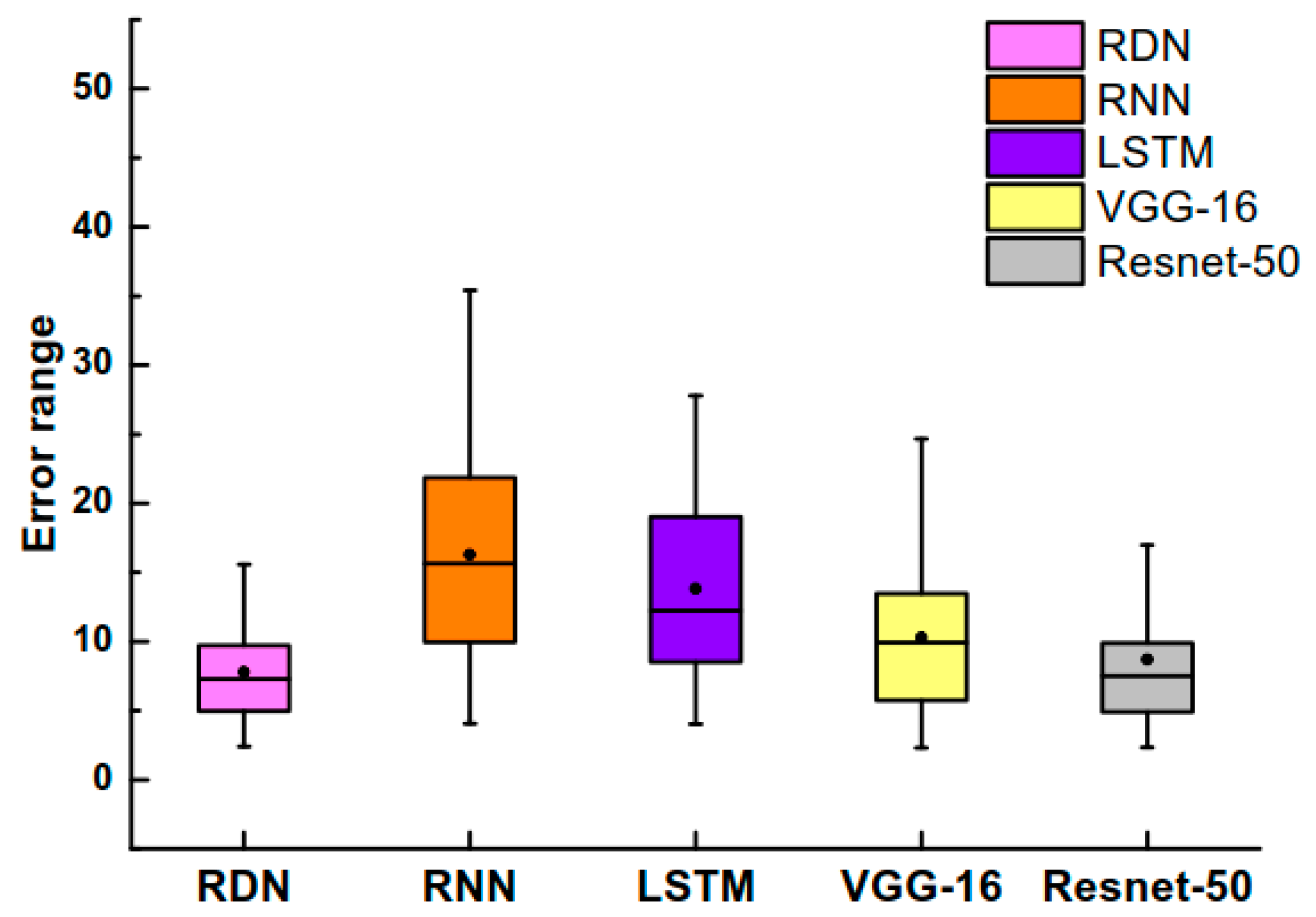
26] models are also selected. The network structure is set to a two-layer structure with neurons of 120 and 50, and then regression is performed after the fully connected layers. The above four models are compared with the RDN proposed in this paper. The results are shown in
Figure 12,
Figure 13 and
Table 3.
The results are the performance of the models on the validation set. It can be seen from the analysis that when the RNN and LSTM models (with certain advantages in processing time series data) are directly used to predict the wear value, their performance is not satisfactory. One reason may be that the above models did not extract the characteristics of the vibration signals well. In addition, the performance may also be due to the model structure and preprocessing method selected in the experiment. For CNNs, VGG-16 has the worst performance among three convolutional structures because the number of convolutional layers is not large; high-dimensional signal features are not extracted. However, the performance results of VGG-16 are better than the designed cyclic neural network. Both ResNet-50 and RDN have achieved satisfactory results. The results show that it is feasible to use CNNs for tool wear value regression.
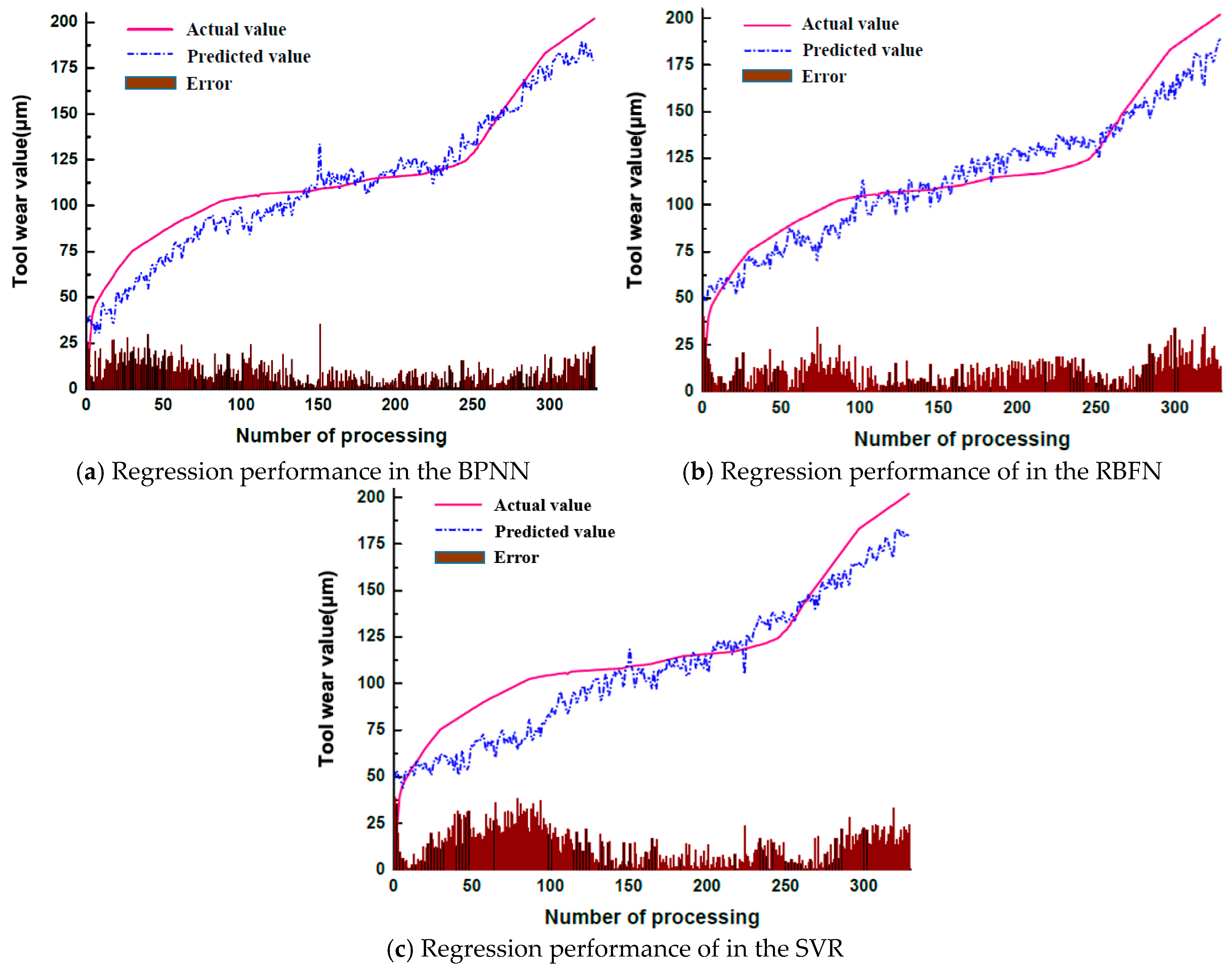
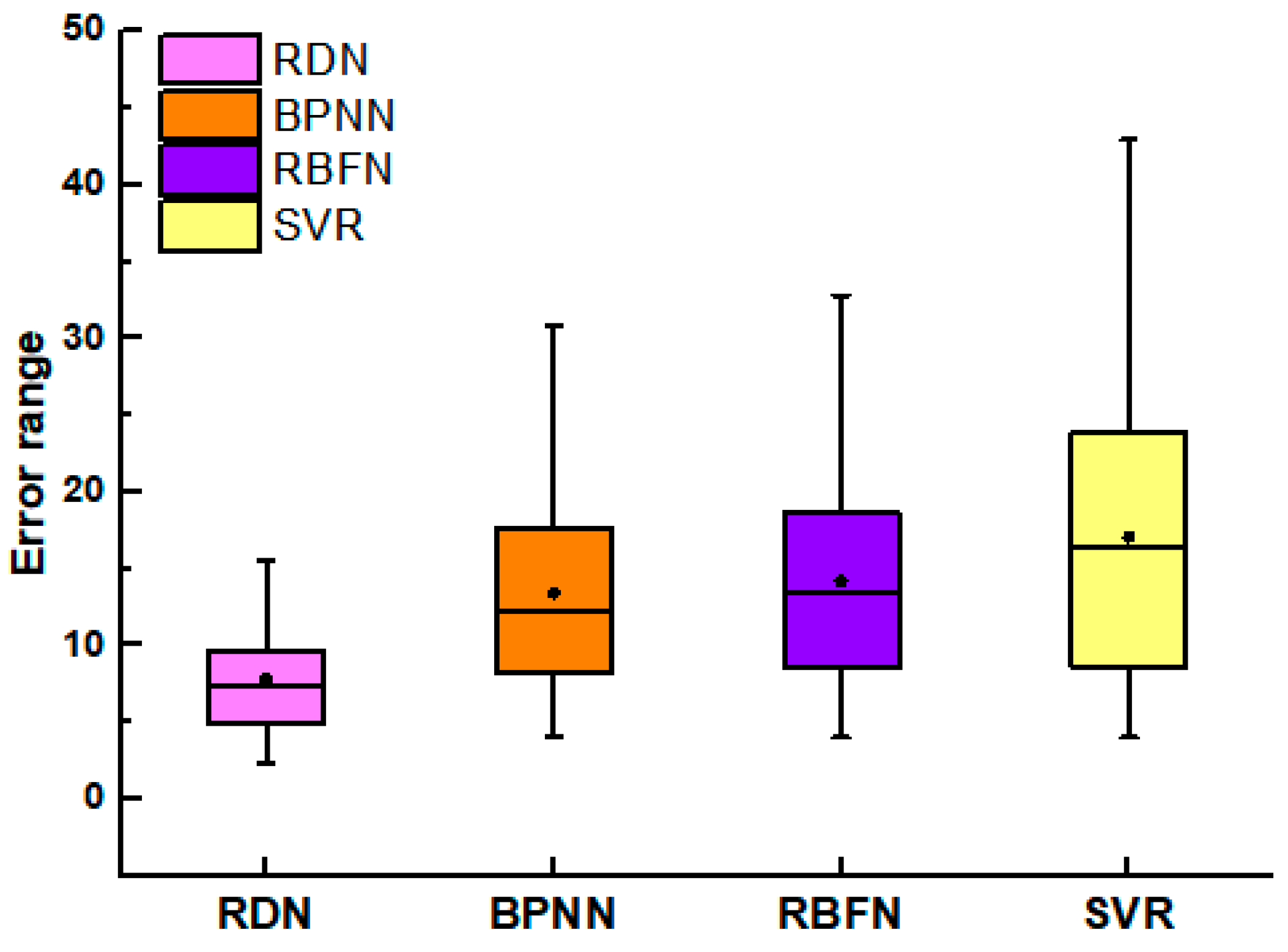
3.5. Comparison Results of Machine Learning Models
In order to further validate the feasibility of the proposed RDN model, a comparative experiment is designed with alternative machine learning models. More specifically, the commonly used models in the traditional tool wear value detection approaches including the BP neural network (BPNN), the radial basis functions neural network (RBFN), and the support vector regression model (SVR) are compared with the RDN network proposed in this paper. The data preprocessing and feature extraction methods are as follows.
- (1)
The wavelet threshold denoising method is employed to perform the noise reduction processing on the acquired three-axis acceleration signal.
- (2)
The data features of time domain, frequency domain, and time-frequency domain are extracted, and the specific extraction methods are shown in
Table 4.
- (3)
Pearson’s Correlation Coefficient (PCC) is used to reflect the correlation between the feature and the wear value, and the feature with a correlation coefficient greater than 0.9 is selected as the extraction object to reduce the feature dimension.
- (4)
The extracted features are used as the inputs of the machine learning model.
According to the results, it can be seen that the results obtained from the machine learning models are not stable. Compared to the deep learning model, only the BPNN can achieve better results than the RNN model. This is due to the fact that the accuracy of the network prediction is largely influenced by the data preprocessing, feature extraction, and model structure selection. Deep learning can achieve very strong results with an adaptive feature learning process and a reasonable network depth design. These results can be achieved under the premise of little or no data preprocessing. Compared with the other algorithm models, RDN achieves a significant performance improvement. The time for the forward operation of the RDN is approximately 112 ms. Although this result is not as good as the partial comparison model, the RDN model provides a better balance between time and accuracy. Therefore, it can be adopted to meet the real-time and accuracy requirements in industrial production.
4. Conclusions
In this paper, we propose to innovatively apply the idea of the DRRN, originally used for super-resolution image reconstruction, to the tool wear value detection problem. To be more suitable for this application, the network parameters and the structure are optimized based on the characteristics of the vibration signal, and the loss function is redesigned. In the preprocessing stage, a wavelet denoising procedure is used on the time domain signal of the acceleration sensor, and the redundant signals generated by each tool are segmented into multiple training samples to filter out noise and improve the robustness of the algorithm. Moreover, the DRRN is further improved. Specifically, the global residual, local residual, and dense network ideas are integrated together. A meta-structure, called the RDN, is proposed. To further alleviate the problem of gradient dispersion, BN layers and Dropout layers are added to the network; these have effectively improved the convergence of the network. The feasibility of this method is validated with the milling cutter wear value detection platform. In this experiment, the signal acquisition unit and the upper computer analysis unit are built; the proposed deep learning framework is used to predict the tool wear value. The experimental results demonstrate that the proposed tool wear value detection method is both efficient and accurate, has a clear workflow, and can adapt to the hardware system of most production environments. These results are promising, and indicate the RDN has the potential to meet the stringent requirements of real-time production environments.
In practical production, the working procedures and site conditions are often complicated and variable. The proposed signal acquisition method and prediction model are restricted by the training data volume and processing method, which may not be applicable to arbitrary working conditions. In the future research, the following two directions are worthy of further investigation. First, from the signal acquisition perspective, the generalization capability of the prediction model can be improved by using multiple sensors to monitor the processing. The RDN approach can be extended to combine multisource data fusion technology with deep learning theory. Second, from the perspective of network design, the network prediction performance can be further improved by combining CNNs with other intelligent models.