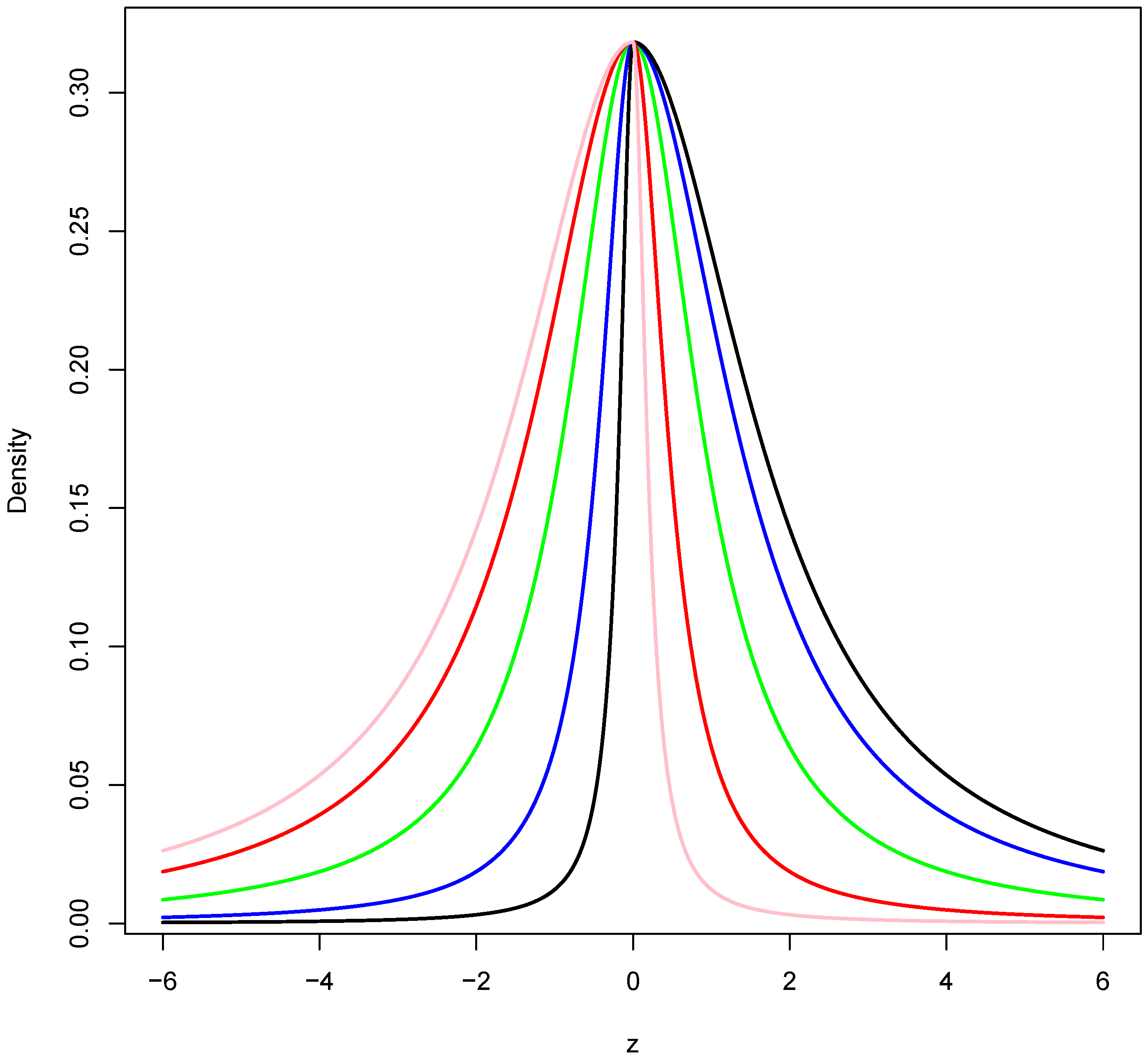
1. Introduction
Mudholkar and Hutson (2000) [
1] studied an asymmetric normal distribution that they called the epsilon–skew–normal
, with asymmetry or skewness parameter
When the parameter
assumes the value 0, the distribution simplifies to become a standard normal distribution. The family thus consists of a parameterized set of usually asymmetric distributions that includes the symmetric standard normal density as a special case. Specifically, we say that
if its density is of the form:
where
,
is the standard normal density and
is the sign function.
Arellano-Valle et al. (2005) [
2] discuss extension of this model, together with associated inference procedures. They consider a class of Epsilon-skew-symmetric distributions associated with a particular symmetric density
that is indexed by an asymmetry parameter
with densities given by
where
and
.
If
X has density of the form (
1), then we say that
X is an epsilon-skew-symmetric random variable and we write
. Arellano-Valle et al. (2005) [
2] extend this family to the model epsilon-skew-exponential-power, a model that has major and minor asymmetry and kurtosis that the ESN model. On the other hand Gómez et al. (2007) [
3] study the Fisher information matrix for epsilon-skew-t model, which was used before in the study a financial series by Hansen (1994) [
4]; see also Gómez et al. (2008) [
5]. Note that if in (
1) we set
, we obtain the epsilon–skew–Cauchy model.
We will write to indicate that X has a standard normal distribution, and we will write to indicate that Y has a standard half-normal distribution, i.e., that where
The distribution of the ratio
of two random variables is of interest in problems in biological and physical sciences, econometrics, and ranking and selection. It is well known that if
,
and
are independent, then the random variables
and
both have Cauchy distributions; see Johnson et al. (1994, [
6] Chapter 16). Behboodian, et al. (2006) [
7] and Huang and Chen (2007) [
8] study the distribution of such quotients when the component random variables are skew-normal (of the form studied in Azzalini (1985) [
9]). The principle objective of the present paper is to study the behavior of such quotients when the component random variables have epsilon-skew-normal distributions.
The paper is organized in the following manner. In
Section 2, we describe a representation of the epsilon–skew–Cauchy model. In
Section 3, we consider the distribution of the ratio of two independent random variables, one of which has an
distribution and the other a standard normal distribution. In addition, an extension of the epsilon–skew–Cauchy (ESC) distribution is introduced. Bivariate versions of these distributions are discussed in
Section 4. Extensions to higher dimensions can be readily envisioned, but are not discussed here. In
Section 5, some of the bivariate distributions introduced in this paper are considered as possible models for a particular real-world data set.
4. General Bivariate Mudholkar-Hutson Distribution
Define
to be i.i.d. standard normal random variables. For
define
where
,
,
,
,
,
are positive numbers and
. So, the parameters
and
indicate the propensity in which the discrete random variable takes negative and positive values, respectively. The parameters
control how often negative and positive values are taken by
.
In addition assume that all six random variables
and
are independent, and define
The model (
2) is highly flexible since it allows for different behavior in each of the four quadrants of the plane. From (
2) it may be recognized that only fractional moments of
X and
Y exist.
Note that if we define
, it is readily verified that
in which case we say that
has a standard bivariate half-Cauchy distribution.
Using (
3) and conditioning on
and
we obtain the density of
in the albeit complicated form:
Some special cases which might be considered include the following:
Mudholkar and Hutson type. For this we set: , and for .
In this case the density (
4) simplifies somewhat to become:
A further specialization of the density (
5) can be considered, as follows.
Homogenous Mudholkar and Hutson type. For this we set: , and for .
This homogeneity results in a little simplification of (
4), thus:
It is easy to see that the parameter
is not identifiable in (
6) because
. An adjustment to ensure identifiability involves introducing the constraint
.
Equal weights. In this case we assume that
are positive numbers and
for
.
The pdf (
7) is not identifiable because the values of
can be interchanged with those of
and
does not change. Moreover, multiplying all of the
’s and
’s by a constant does not change
. So, one way to get identifiability in the model (
7) is to set
and
equal to 1. In that case, Equation (
7) takes the form
However, this is then recognizable as being simply a scaled version of the standard bivariate Cauchy density (compare with Equation (
3)).
We now consider the marginal densities for the random variable
defined by (
2). From (
2) we have
and
and the density of
is a standard half-Cauchy density, i.e.,
.
Consequently, the density of
X is of the form
which is a mixture of half-Cauchy densities. The density of
Y is then of the same form with
replaced by
.
To get a more direct bivariate version of the original Mudholkar-Hutson density in which the
’s,
’s and
’s were related to each other, we go back to the original representation, i.e., Equation (
2), but now we set
,
,
,
,
,
and
. So the density is of the form
with marginal density
A more general version of the density with
is of the form: (without loss of generality set
)
with corresponding marginal
Needless to say we can consider analogous models in which, instead of assuming that
has a density of the form (
3) we assume that it has another bivariate density with support
, e.g., bivariate normal restricted to
, or bivariate Pareto, etc.
Another general bivariate MH model which includes the bivariate skew-Cauchy distribution given by (
2) is the bivariate skew
t model. This model can be obtained replacing
by
in Equation (
2). Thus, if we assume that all six random variables
,
;
and
are independent, and define
then, because
has density
the density of
is
The pair of variables in (8) allows one to model a wider variety of paired data sets than that given in (
2) because it also can model light and heavy “tails” in a different way for each quadrant of the coordinate axis. Additionally, it is possible to compute the
order moments.
Proposition 3. The expected value of in (8) is given byprovided that . Proof. For it is immediate that and .
On the other hand, since
then
Therefore, from (8) we have
and the result is obtained straightforward. ☐
Following the proof of the previous proposition it is possible to obtain the order moments provided that .
In applications, it will usually be appropriate to augment these models by the introduction of location, scale and rotation parameters, i.e., to consider
where
and
is positive definite.
5. Application
The data that we will use were collected by the Australian Institute of Sport and reported by Cook and Weisberg (1994) [
10]. The data set consists of values of several variables measured on
Australian athletes. Specifically, we shall consider the pair of variables (Ht,Wt) which are the height (cm) and the weight (Kg) measured for each athlete.
We fitted the bivariate Mudholkar-Hutson distributions for five different cases. In addition to the general case which is given by the pdf
, based on (9), where
, and
is the location parameter and
is the symmetric positive definite scale matrix, we also consider four special cases:
When the pdf is given by Equation (
4). That is taking
in the bivariate skew
t MH model.
When the pdf is given by
which is the bivariate MH distribution specified using the special case (1.), where
for all
.
When the pdf is given by
which is the bivariate MH distribution specified using the special case (2.), where
.
When the pdf is given by
which is the bivariate Cauchy distribution (as in (
3)).
All fits were done by maximizing the likelihood through numerical methods which combine algorithms based on the Hessian matrix and the Simulated Annealing algorithm. Standard errors of the estimations were computed based on 1000 bootstrap data samples.
To compare model fits, we used the Akaike criterion (see Akaike, 1974 [
11]), namely
where
k is the dimension of
which is the vector of parameters of the model being considered.
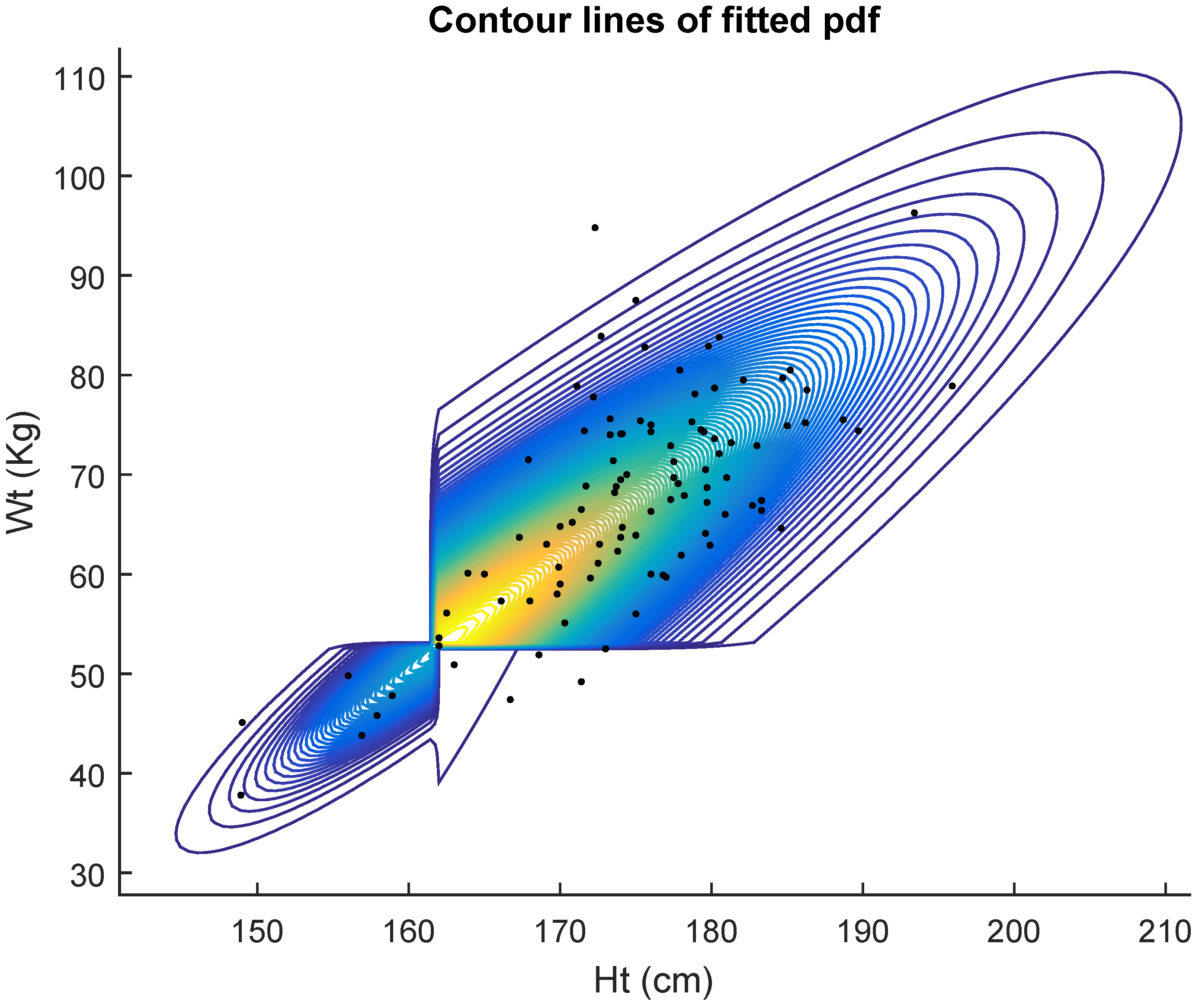
Table 1 displays the results of the fits for 100 women. In
Table 1, we see the results of fitting the five competing models. They are the general bivariate skew
MH model with pdf given in Equation (9), General bivariate MH with pdf given in Equation (
4), Bivariate MH (1.) with pdf given in Equation (
5), Bivariate MH (2.) with pdf given in Equation (
6) and Bivariate Cauchy. It shows the maximum likelihood estimates (mle’s) of the five models. The last column shows the estimated standard errors (se) of the estimates. Non identifiability of the bivariate skew
MH model is evidenced by the huge value of the estimated standard error of the estimate of
. However, the AIC criterion indicates that data are better fitted by the general bivariate skew
MH (9) model.
Figure 2 shows the contour lines of the fitted pdf.
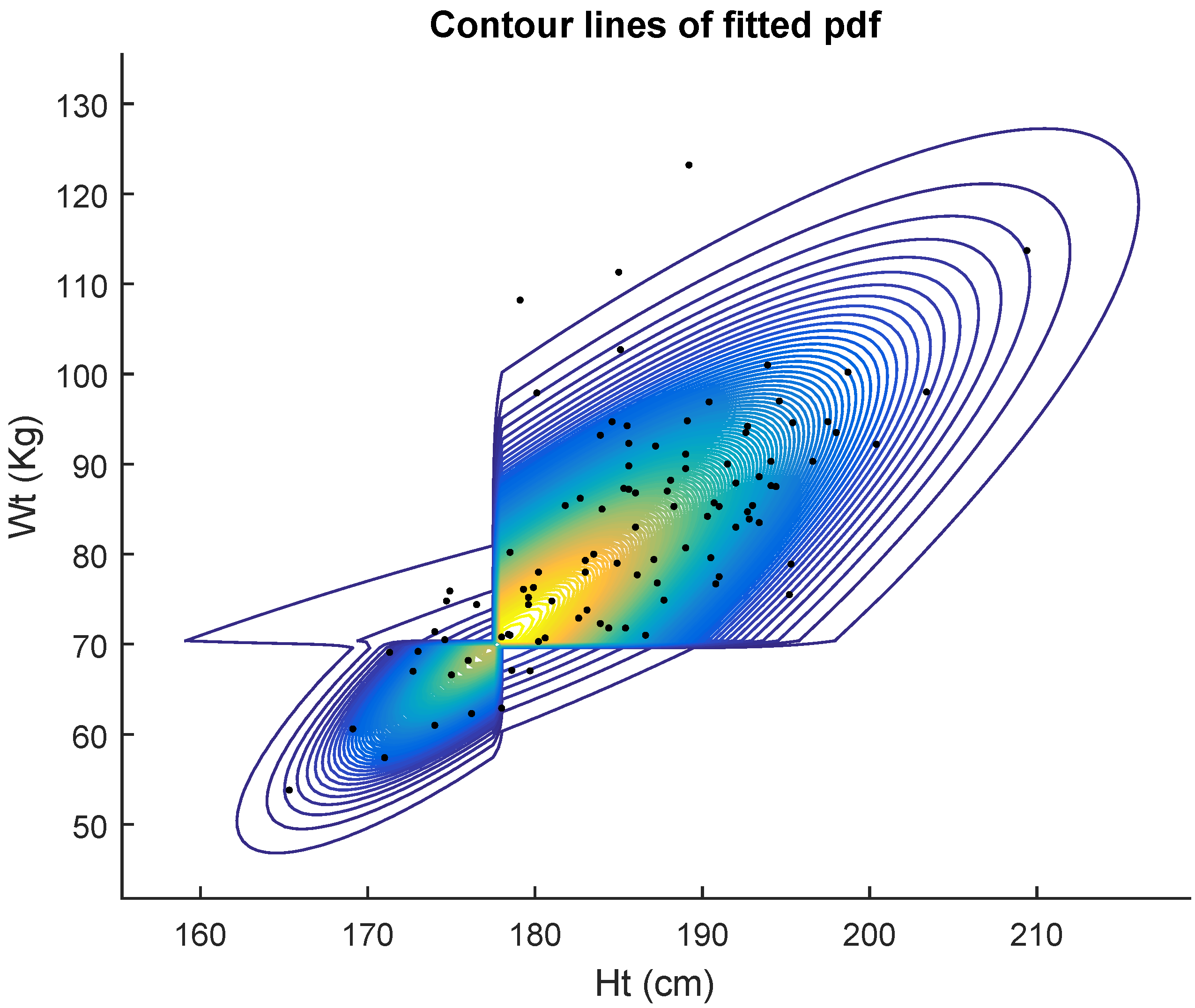
Table 2 displays the results of the fits for 102 men. In
Table 2 we again compare five competing models. The maximum likelihood estimates (mle’s) of the five models, the corresponding Akaike criterion values and estimated standard errors of the estimates are displayed in the table. Again, the AIC indicates that the data are better fitted by the general bivariate skew
MH (9) model.
Figure 3 shows the contour lines of the fitted pdf. Non identifiability of the general bivariate skew
MH (9) and General bivariate MH (
4) models is shown by the large values of the estimated standard errors for some estimates.
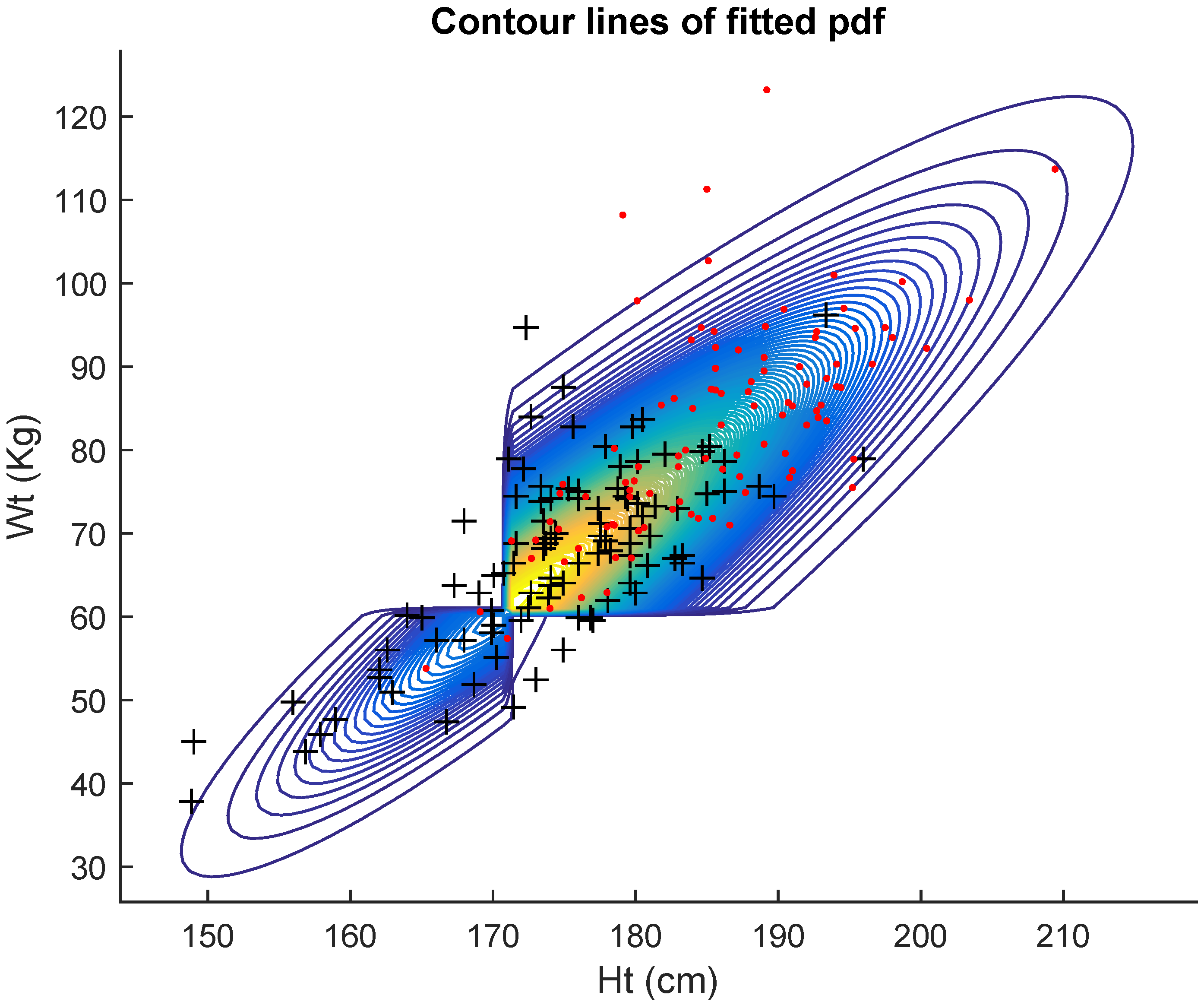
Table 3 displays the results of the fits for the full set of
Australian athletes, regardless of gender.
Table 3 shows the maximum likelihood estimates (mle’s) of the five models together with the corresponding Akaike criterion values and estimated standard errors of the estimates. The AIC here also indicates that the data are better fitted by the general bivariate skew
MH model (9).
Figure 4 shows the contour lines of the fitted pdf. Thus, in all three cases, males, females and combined, the best fitting model was the general bivariate skew
MH.
For the three real cases analyzed the general bivariate skew-t MH model (9) was indicated as the best fitted. That means that it seems worth considering the more general model to explain the variability of these data sets.
6. Concluding Remarks
The Mudholkar–Hutson skewing mechanism admits flexible extensions in both the univariate and multivariate cases. Stochastic representations of such extended models typically have corresponding likelihood functions that are somewhat complicated (for example Equations (
4) and (9)). This is partly compensated for by the ease of simulation for such models using the representation in terms of latent variables ( the
’s and
’s in (
2) or (8)). The data set analyzed in
Section 5 illustrates the potential advantage of considering the extended bivariate Mudholkar-Hutson model, since the basic bivariate M-H model does not provide an acceptable fit to the “athletes” data. Needless to say, applying Occam’s razor, it would always be desirable to consider the hierarchy of the five nested bivariate models that were considered in
Section 5, in order to determine whether one of the simpler models might be adequate to describe a particular data set. Indeed there may be other special cases of the model (
4), intermediate between (
4) and (
5) say, that might profitably be considered for some data sets. However, it should be remarked that selection of such sub-models for consideration should be done prior to inspecting the data. The addition of the GBMH model to the data analysts tool-kit should provide desirable flexibility for modeling data sets which exhibit behavior somewhat akin to, but not perfectly adapted to, more standard bivariate Cauchy models.