Dual Hesitant q-Rung Orthopair Fuzzy Hamacher Aggregation Operators and their Applications in Scheme Selection of Construction Project

Abstract

The q-rung orthopair fuzzy set (q-ROFS), which is the extension of intuitionistic fuzzy set (IFS) and Pythagorean fuzzy set (PFS), satisfies the sum of q-th power of membership degree and nonmembership degree is limited 1. Evidently, the q-ROFS can depict more fuzzy assessment information and consider decision-maker’s (DM’s) hesitance. Thus, the concept of a dual hesitant q-rung orthopair fuzzy set (DHq-ROFS) is developed in this paper. Then, based on Hamacher operation laws, weighting average (WA) operator and weighting geometric (WG) operator, some dual hesitant q-rung orthopair fuzzy Hamacher aggregation operators are developed, such as the dual hesitant q-rung orthopair fuzzy Hamacher weighting average (DHq-ROFHWA) operator, the dual hesitant q-rung orthopair fuzzy Hamacher weighting geometric (DHq-ROFHWG) operator, the dual hesitant q-rung orthopair fuzzy Hamacher ordered weighted average (DHq-ROFHOWA) operator, the dual hesitant q-rung orthopair fuzzy Hamacher ordered weighting geometric (DHq-ROFHOWG) operator, the dual hesitant q-rung orthopair fuzzy Hamacher hybrid average (DHq-ROFHHA) operator, and the dual hesitant q-rung orthopair fuzzy Hamacher hybrid geometric (DHq-ROFHHG) operator. The precious merits and some particular cases of above mentioned aggregation operators are briefly introduced. In the end, an actual application for scheme selection of construction project is provided to testify the proposed operators and deliver a comparative analysis.

1. Introduction

In real-life decision-making problems, how to select the most desirable alternative from a given alternative set is very important. The most common method is fusing the evaluation information given by experts, and ranking all alternatives according to fused results to select best one(s). Thus, how to derive reasonable evaluation information is worth studying. To do this, Atanassov [1] firstly extended the fuzzy set (FS) [2] and introduced intuitionistic fuzzy set (IFS). The intuitionistic fuzzy set (IFS) is mainly characterized by the function of membership degree $\mu$ and nonmembership degree $v$, which satisfies $\mu +v\le 1$. The intuitionistic fuzzy set (IFS) and its extensions have attracted a large amount of scholars’ attention since its emergence [3,4,5,6,7,8,9,10,11,12,13,14,15,16]. More recently, the Pythagorean fuzzy set (PFS) [17] has been proposed to depict more fuzzy assessment information. The PFS is also consisted of the membership degree $\mu$ and nonmembership degree $v$, which satisfies ${\mu }^2+v^2\le 1$, so, it is obvious that the PFS can express more assessment information than the IFS. However, the scope of assessment information is still limited under Pythagorean fuzzy environment. For instance, given the evaluation value (0.7,0.9), we can easily find that ${0.7}^2+{0.9}^2\cancel{\le }1,$ which indicates that PFS cannot deal with such MADM problems. Then, to describe more evaluation information, Yager [18] further defined the q-rung orthopair fuzzy set (q-ROFS), q-ROFS is also consisted of the membership degree $\mu$ and nonmembership degree $v$ which satisfies ${\mu }^q+v^q\le 1.$ Obviously, q-ROFS can be regarded as the extension of the IFS and PFS, when $q=1$, the q-ROFS reduces to IFS, when $q=2$, the q-ROFS reduces to PFS (see Figure 1). Afterwards, more and more works about q-ROFS have been studied by numerous scholars [19,20,21,22,23,24,25].

However, the above-mentioned methods do not consider the human’s hesitance. In order to overcome this limitation, the hesitant fuzzy sets (HFSs) [26] and dual hesitant fuzzy sets (DHFSs) [27,28] have been proposed to deal with MADM issues effectively. Combining the advantages of the two fuzzy sets, Xu et al. [29] gave the concept of the dual hesitant q-rung orthopair fuzzy set (DHq-ROFS) and presented some Heronian mean operators for MADM. Obviously, the dual hesitant q-rung orthopair fuzzy numbers (DHq-ROFNs) can express evaluation information more convenience in actual MADM applications.

In the decision-making process, the way to express evaluation information is only one aspect; another vital aspect is fusing this information. Hamacher operations [30], which include Hamacher product and Hamacher sum, can replace the traditional algebraic product and algebraic sum, respectively. In past few years, numerous investigators studied the Hamacher aggregation operators and their applications [31,32,33,34,35,36,37,38,39,40,41]. In this paper, based on Hamacher operations, we shall develop some new operation laws of DHq-ROFNs, then, by utilizing the new operation laws, we can aggregate dual hesitant q-rung orthopair fuzzy information by Hamacher WA and Hamacher WG operator. The Hamacher operations have the advantage of considering the relationship between the values being fused, thus the fused results are more reasonable and accuracy. Clearly, DHq-ROFN is a meaningful tool to express evaluation information; Hamacher operations are good to fuse evaluation information, so it’s worth to develop some Hamacher operators under dual hesitant q-rung orthopair fuzzy environments.

The mainly novelty and contribution of our manuscript is developing some new Hamacher operators to aggregate the dual hesitant q-rung orthopair fuzzy information. Evidently, these operators have the following advantages. (1) The DHq-ROFS can not only extend the scope of the assessment information to depict more fuzzy information, but also consider the human’s hesitance, thus it is more useful and reasonable to derive decision-making results. (2) The Hamacher operations can consider the relationship between fused arguments, obviously, Hamacher operations are more suitable for handling practical MADM problems. Thus, it is of great significance to propose some new operators based on the dual hesitant q-rung orthopair fuzzy information and Hamacher operations.

To achieve this goal, the rest of our article is constructed as follows. Section 2 introduces some works on Pythagorean fuzzy set and q-rung orthopair fuzzy set. Section 3 briefly reviews some fundamental theories of q-ROFSs and DHq-ROFSs. Section 4 introduces some HWA and HWG operators under DHq-ROFS environment, such as the DHq-ROFHWA operator, the DHq-ROFHWG operator, the DHq-ROFHOWA operator, the DHq-ROFHOWG operator, the DHq-ROFHHA operator, and the (DHq-ROFHHG operator. Section 5 proposes an actual application for scheme selection of construction project with DHq-ROFNs and compares our developed operators with other existing methods in this filed. Section 6 concludes the paper with some remarks.

2. Literature Review

In previous literature, research on the Pythagorean fuzzy set (PFS) has been conducted by many scholars. Zhang and Xu [42] defined the Pythagorean fuzzy TOPSIS model to solve the MADM problems. Peng and Yang [43] primarily proposed two Pythagorean fuzzy operations, including the division and subtraction operations, to better understand PFS. Reformat and Yager [44] handled the collaborative-based recommender system with Pythagorean fuzzy information. Combined the Maclaurin Symmetric Mean (MSM) [45] operators and Pythagorean fuzzy information, Yang and Pang [46] developed some new Pythagorean fuzzy interaction MSM operators to handle MADM problems. Gou et al. [47] studied some precious properties of continuous Pythagorean fuzzy assessment information. Yang et al. [48] studied the partitioned Bonferroni mean (PBM) operators under Pythagorean fuzzy environment and defined some Pythagorean fuzzy interaction PBM operators to solve MADM. Based on Hamacher operation laws and Pythagorean fuzzy information, Wu and Wei [49] proposed some new aggregation operators to fuse Pythagorean fuzzy information and applied them to MADM problems. Liang et al. [50] studied the Pythagorean fuzzy set (PFS) based on the GA operations and Bonferroni mean (BM) operators. Ren et al. [51] developed the Pythagorean fuzzy TODIM model. Wei and Lu [52] developed Pythagorean fuzzy MSM (PFMSM) operator and Pythagorean fuzzy weighted MSM (PFWMSM) operator for MADM. Liang et al. [53] defined some novel Bonferroni mean operators under PFS environment. Consider the interrelationship between being fused arguments, Li et al. [11] gave some new Pythagorean fuzzy aggregation operators for selection of green supplier based on traditional Hamy mean (HM) operators. Peng et al. [54] presented some novel Pythagorean fuzzy information measures for MADM problems. On account of the PFSs [17,55] and DHFSs [27,28], Xu and Wei [56] further defined the dual hesitant Pythagorean fuzzy sets (DHPFSs), then, based on Hamacher operation laws weighting average (WA) operator and weighting geometric (WG) operator, some new aggregation operators under dual hesitant Pythagorean fuzzy environment were developed for MADM problems.

In terms of the q-ROFS, according to the traditional WA and WG operators, Liu and Wang [57] introduced two q-rung orthopair fuzzy aggregation operators to fuse q-rung orthopair fuzzy numbers (q-ROFNs). Combined q-rung orthopair fuzzy information and MSM operators, Wei et al. [58] proposed some new q-rung orthopair fuzzy aggregation operators. Bai et al. [59] defined some q-rung orthopair fuzzy Partitioned Maclaurin Symmetric Mean (q-ROFPMSM) operators for MADM. Liu et al. [60] developed some q-rung orthopair fuzzy Power MSM operators. Liu et al. [61] developed some extended Bonferroni mean operators under q-rung orthopair fuzzy environment. Liu and Liu [62] presented some Bonferroni mean operators to fuse q-rung orthopair fuzzy information; Liu and Liu [63] proposed the concept of linguistic q-rung orthopair fuzzy set (Lq-ROFS) and introduced some PBM operators to fuse linguistic q-rung orthopair fuzzy information. Yang and Pang [64] studied Partitioned Bonferroni mean operators under q-rung orthopair fuzzy environment. The contribution of different authors under q-ROFNs is listed in

Table 1. The contribution of different authors under q-ROFNs.

Authors	Production	Consider the Interrelationship	Consider the Parameter Vector	Consider the Human’s Hesitancy	Consider the Order Position Weights and Itself Weights
Liu and Wang [57]	q-ROFWA operator	No	No	No	No
Liu and Wang [57]	q-ROFWG operator	No	No	No	No
Wei, et al. [58]	q-ROFMSM operators	Yes	Yes	No	No
Bai, et al. [59]	q-ROF-Partitioned-MSM operators	Yes	Yes	No	No
Liu, et al. [60]	q-ROF-Power-MSM operators	Yes	Yes	No	No
Liu, et al. [61]	q-ROFEBM operators	Yes	Yes	No	No
Liu and Liu [62]	q-ROFBM operators	Yes	Yes	No	No
Liu and Liu [63]	Lq-ROF-Power-BM operators	Yes	Yes	No	No
Yang and Pang [64]	q-ROF-Partitioned-BM operators	Yes	Yes	No	No
Wei, et al. [65]	q-R2TLOFHM operators	Yes	Yes	No	No
Liu, et al. [66]	q-ROFHM operators	Yes	Yes	No	No
Xu, et al. [29]	q-RDHOFHM operators	Yes	Yes	Yes	No
Proposed model	DHq-ROFHHA and DHq-ROFHHG operators	Yes	Yes	Yes	Yes

.

Wei et al. [65] defined some q-rung orthopair fuzzy Heronian mean (q-ROFHM) operator. Liu et al. [66] provided some Heronian mean operator to aggregate q-ROFNs. In this paper, according to the dual hesitant q-rung orthopair set defined by Xu et al. [29], we shall propose some q-rung orthopair fuzzy Hamacher operation laws to fuse the q-rung orthopair fuzzy information. The goal of our paper is to develop some operators that can consider human’s hesitance and the interrelationship between being fused arguments.

3. Preliminaries

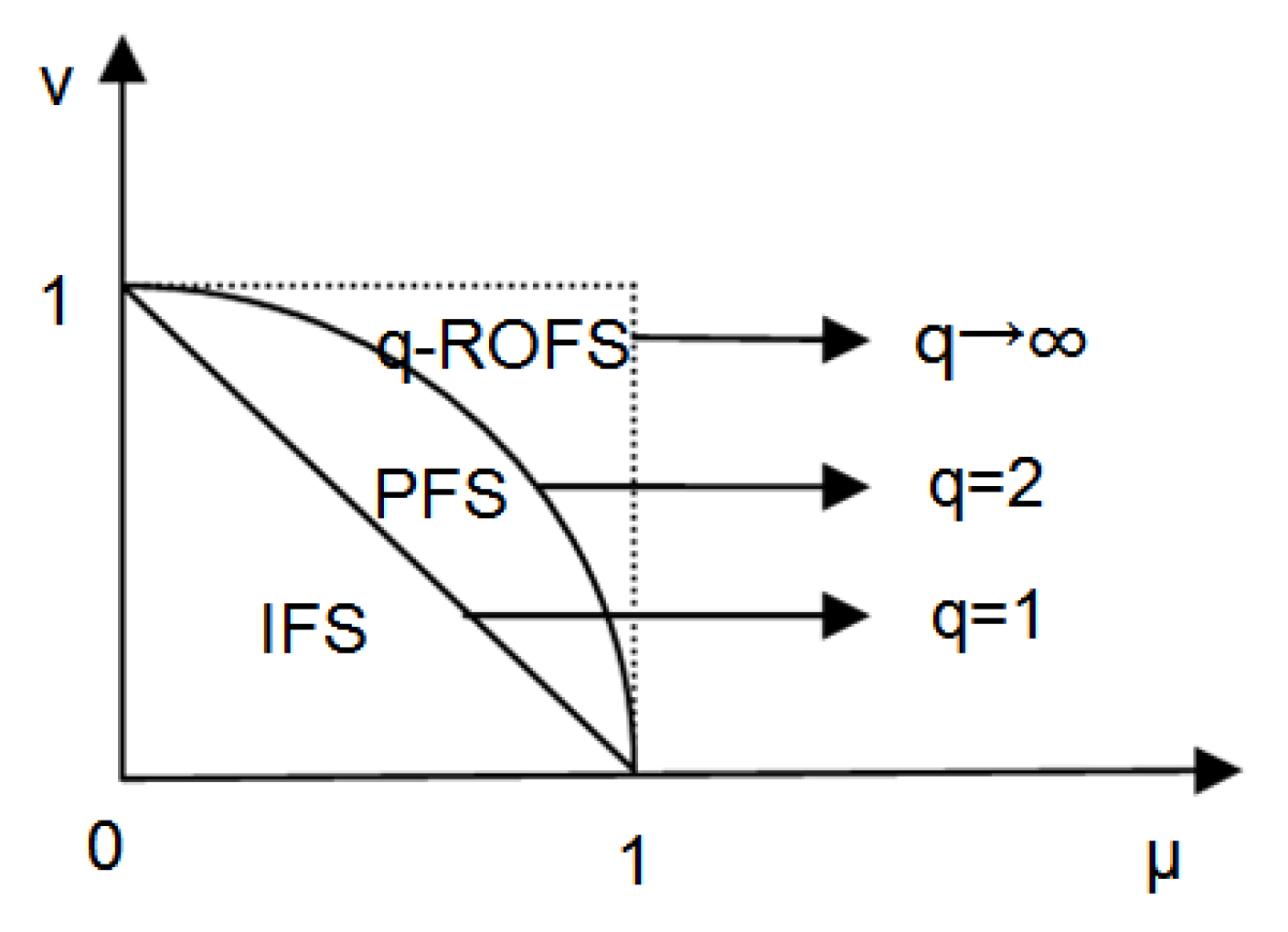
3.1. The q-Rung Orthopair Fuzzy Set

As the generalization of IFS and PFS, the basic definition, score function, accuracy function, and operation laws of the q-rung orthopair fuzzy sets (q-ROFSs) [18] can be listed as below.

Definition 1

[18]. Let $X$ be a fix set. A q-rung orthopair fuzzy set can be denoted as

$$P=\left\{\langle x,\left({\mu }_P\left(x\right),{\nu }_P\left(x\right)\right)\rangle |x\in X\right\}$$

(1)

where ${\mu }_P:X\to \left[0,1\right]$ indicates the function of membership degree and ${\nu }_P:X\to \left[0,1\right]$ indicates the function of nonmembership degree, which satisfies

$${\left({\mu }_p\left(x\right)\right)}^q+{\left({\nu }_p\left(x\right)\right)}^q\le 1,q\ge 1$$

(2)

Based on membership degree and nonmembership degree, the indeterminacy degree can be calculated as

$${\pi }_p\left(x\right)=\sqrt[q]{{\left({\mu }_p\left(x\right)\right)}^q+{\left({\nu }_p\left(x\right)\right)}^q-{\left({\mu }_p\left(x\right)\right)}^q{\left({\nu }_p\left(x\right)\right)}^q}$$

(3)

For convenience, we named $p=\left(\mu ,\nu \right)$ a q-rung orthopair fuzzy number (q-ROFN).

Definition 2

[57]. Suppose that $p_1=\left({\mu }_1,{\nu }_1\right)$ and $p_2=\left({\mu }_2,{\nu }_2\right)$ be two q-ROFNs, let $s\left(p_1\right)=\frac{1}{2}\left(1+{\left({\mu }_1\right)}^q-{\left({\nu }_1\right)}^q\right)$ and $s\left(p_2\right)=\frac{1}{2}\left(1+{\left({\mu }_2\right)}^q-{\left({\nu }_2\right)}^q\right)$ be the score results of $p_1$ and $p_2$, let $H\left(p_1\right)={\left({\mu }_1\right)}^q+{\left({\nu }_1\right)}^q$ and $H\left(p_2\right)={\left({\mu }_2\right)}^q+{\left({\nu }_2\right)}^q$ be the accuracy results of $p_1$ and $p_2$, then we can give the comparative laws between any two q-ROFNs: if $s\left(p_1\right)<s\left(p_2\right)$, then $p_1<p_2$; if $s\left(p_1\right)=s\left(p_2\right)$, then (1) if $H\left(p_1\right)=H\left(p_2\right)$, then $p_1=p_2$; (2) if $H\left(p_1\right)<H\left(p_2\right)$, $p_1<p_2$.

Definition 3

[57]. Assume that $p_1=\left({\mu }_1,{\nu }_1\right)$, $p_2=\left({\mu }_2,{\nu }_2\right)$, and $p=\left(\mu ,\nu \right)$ be three q-ROFNs, then

$$\begin{array}{l}(1)p_1\oplus p_2=\left(\sqrt[q]{{\left({\mu }_1\right)}^q+{\left({\mu }_2\right)}^q-{\left({\mu }_1\right)}^q{\left({\mu }_2\right)}^q},{\nu }_1{\nu }_2\right);\\ (2)p_1\otimes p_2=\left({\mu }_1{\mu }_2,\sqrt[q]{{\left({\nu }_1\right)}^q+{\left({\nu }_2\right)}^q-{\left({\nu }_1\right)}^q{\left({\nu }_2\right)}^q}\right);\\ (3)\lambda p=\left(\sqrt[q]{1-{\left(1-{\mu }^q\right)}^{\lambda }},{\nu }^{\lambda }\right),\lambda >0;\\ (4){\left(p\right)}^{\lambda }=\left({\mu }^{\lambda },\sqrt[q]{1-{\left(1-{\nu }^q\right)}^{\lambda }}\right),\lambda >0;\\ (5)p^c=\left(\nu ,\mu \right).\end{array}$$

3.2. Dual Hesitant q-Rung Orthopair Fuzzy Set

In accordance of the q-ROFSs and DHFSs [27,28], we further introduce the dual hesitant q-rung orthopair fuzzy sets (DHq-ROFSs) [29] as follows.

Definition 4

[29]. Let $X$ be a fix set, then a DHq-ROFS on $X$ can be denoted as

$$d=\left(\langle x,h_P\left(x\right),g_P\left(x\right)\rangle |x\in X\right)$$

(4)

where $h_P\left(x\right)$ indicates membership hesitancy set with several values in [0,1], $g_P\left(x\right)$ indicates nonmembership hesitancy set with values in $\left[0,1\right]$, which satisfies

$${\cup }_{\alpha \in h}{\left(\max \left(\alpha \right)\right)}^q+{\cup }_{\beta \in g}{\left(\max \left(\beta \right)\right)}^q\le 1$$

(5)

where $\alpha \in h_P\left(x\right),\beta \in g_P\left(x\right)$. Then we named $d\left(x\right)=\left(h_P\left(x\right),g_P\left(x\right)\right)$ a dual hesitant q-rung orthopair fuzzy number (DHq-ROFN) described by $d=\left(h,g\right)$, which satisfies $\alpha \in h,\beta \in g,$ $0\le \alpha ,\beta \le 1$ and ${\cup }_{\alpha \in h}{\left(\max \left(\alpha \right)\right)}^q+{\cup }_{\beta \in g}{\left(\max \left(\beta \right)\right)}^q\le 1.$

Definition 5

[29]. Assume that $d=\left(h,g\right)$ is a DHq-ROFN, let $s\left(d\right)=\frac{1}{2}\left(1+\frac{1}{\#h}{\displaystyle {\sum }_{\alpha \in h}{\alpha }^q}-\frac{1}{\#g}{\displaystyle {\sum }_{\beta \in g}{\beta }^q}\right)$ be the score results of $d=\left(h,g\right)$ and $E\left(d\right)=\frac{1}{\#h}{\displaystyle {\sum }_{\alpha \in h}{\alpha }^q}+\frac{1}{\#g}{\displaystyle {\sum }_{\beta \in g}{\beta }^q}$ be the accuracy results of $d=\left(h,g\right)$, where $\#h$ indicates the number of elements in set $h$ and $\#g$ indicates the number of elements in set $g$, respectively, assume that $d_i=\left(h_i,g_i\right)\left(i=1,2\right)$ be any two DHq-ROFNs, then if $s\left(d_1\right)>s\left(d_2\right)$, then $d_1\succ d_2$; if $s\left(d_1\right)=s\left(d_2\right)$, then: (1) If $E\left(d_1\right)=E\left(d_2\right)$, then $d_1=d_2$; (2) If $E\left(d_1\right)>E\left(d_2\right)$, then $d_1\succ d_2$.

Definition 6

[29]. Let $d_1=\left(h_1,g_1\right)$, $d_2=\left(h_2,g_2\right)$, and $d=\left(h,g\right)$ be three DHq-ROFNs, then, some new operations on the DHq-ROFNs are defined as

(1)

$d^{\lambda }={\cup }_{\alpha \in h,\beta \in g}\left\{\left\{{\alpha }^{\lambda }\right\},\left\{\sqrt[q]{1-{\left(1-{\beta }^q\right)}^{\lambda }}\right\}\right\},\lambda >0$;

(2)

$\lambda d={\cup }_{\alpha \in h,\beta \in g}\left\{\left\{\sqrt[q]{1-{\left(1-{\alpha }^q\right)}^{\lambda }}\right\},\left\{{\beta }^{\lambda }\right\}\right\},\lambda >0$;

(3)

$d_1\oplus d_2={\cup }_{{\alpha }_1\in h_1,{\alpha }_2\in h_2,{\beta }_1\in g_1,{\beta }_2\in g_2}\left\{\left\{\sqrt[q]{{\left({\alpha }_1\right)}^q+{\left({\alpha }_2\right)}^q-{\left({\alpha }_1\right)}^q{\left({\alpha }_2\right)}^q}\right\},\left\{{\beta }_1{\beta }_2\right\}\right\};$

(4)

$d_1\otimes d_2={\cup }_{{\alpha }_1\in h_1,{\alpha }_2\in h_2,{\beta }_1\in g_1,{\beta }_2\in g_2}\left\{\left\{{\alpha }_1{\alpha }_2\right\},\left\{\sqrt[q]{{\left({\beta }_1\right)}^q+{\left({\beta }_2\right)}^q-{\left({\beta }_1\right)}^q{\left({\beta }_2\right)}^q}\right\}\right\}.$

3.3. Hamacher Operations of Dual Hesitant q-rung Orthopair Fuzzy Set

Definition 7.

Let $d_1=\left(h_1,g_1\right)$, $d_2=\left(h_2,g_2\right)$, and $d=\left(h,g\right)$ be three DHq-ROFNs, $\gamma >0$, and based on the traditional Hamacher operations [30], some basic Hamacher operations of DHq-ROFNS are defined as follows

$$\begin{array}{r}{d}_1\oplus d_2={\cup }_{{\alpha }_1\in h_1,{\alpha }_2\in h_2,{\beta }_1\in g_1,{\beta }_2\in g_2}(\left\{\sqrt[q]{\frac{{\left({\alpha }_1\right)}^q+{\left({\alpha }_2\right)}^q-{\left({\alpha }_1\right)}^q{\left({\alpha }_2\right)}^q-(1-\gamma ){\left({\alpha }_1\right)}^q{\left({\alpha }_2\right)}^q}{1-(1-\gamma ){\left({\alpha }_1\right)}^q{\left({\alpha }_2\right)}^q}}\right\},\\ \left\{\frac{{\beta }_1{\beta }_2}{\sqrt[q]{\gamma +(1-\gamma )\left({\left({\beta }_1\right)}^q+{\left({\beta }_2\right)}^q-{\left({\beta }_1\right)}^q{\left({\beta }_2\right)}^q\right)}}\right\});\end{array}$$

(6)

$$\begin{array}{ll}{d}_1\otimes d_2={\cup }_{{\alpha }_1\in h_1,{\alpha }_2\in h_2,{\beta }_1\in g_1,{\beta }_2\in g_2}& (\left\{\frac{{\alpha }_1{\alpha }_2}{\sqrt[q]{\gamma +(1-\gamma )\left({\left({\alpha }_1\right)}^q+{\left({\alpha }_2\right)}^q-{\left({\alpha }_1\right)}^q{\left({\alpha }_2\right)}^q\right)}}\right\},\\ & \left\{\sqrt[q]{\frac{{\left({\beta }_1\right)}^q+{\left({\beta }_2\right)}^q-{\left({\beta }_1\right)}^q{\left({\beta }_2\right)}^q-(1-\gamma ){\left({\beta }_1\right)}^q{\left({\beta }_2\right)}^q}{1-(1-\gamma ){\left({\beta }_1\right)}^q{\left({\beta }_2\right)}^q}}\right\});\end{array}$$

(7)

$$\begin{array}{ll}\lambda d={\cup }_{\alpha \in h,\beta \in g}& (\left\{\sqrt[q]{\frac{{\left(1+\left(\gamma -1\right){\left(\alpha \right)}^q\right)}^{\lambda }-{\left(1-{\left(\alpha \right)}^q\right)}^{\lambda }}{{\left(1+\left(\gamma -1\right){\left(\alpha \right)}^q\right)}^{\lambda }+\left(\gamma -1\right){\left(1-{\left(\alpha \right)}^q\right)}^{\lambda }}}\right\}\\ & \left\{\frac{\sqrt[q]{\gamma }{\left(\beta \right)}^{\lambda }}{\sqrt[q]{{\left(1+\left(\gamma -1\right)\left(1-{\left(\beta \right)}^q\right)\right)}^{\lambda }+\left(\gamma -1\right){\left(\beta \right)}^{q\lambda }}}\right\});\end{array}$$

(8)

$$\begin{array}{ll}{d}^{\lambda }={\cup }_{\alpha \in h,\beta \in g}& (\left\{\sqrt[q]{\frac{{\left(1+\left(\gamma -1\right){\left(\beta \right)}^q\right)}^{\lambda }-{\left(1-{\left(\beta \right)}^q\right)}^{\lambda }}{{\left(1+\left(\gamma -1\right){\left(\beta \right)}^q\right)}^{\lambda }+\left(\gamma -1\right){\left(1-{\left(\beta \right)}^q\right)}^{\lambda }}}\right\}\\ & \left\{\frac{\sqrt[q]{\gamma }{\left(\alpha \right)}^{\lambda }}{\sqrt[q]{{\left(1+\left(\gamma -1\right)\left(1-{\left(\alpha \right)}^q\right)\right)}^{\lambda }+\left(\gamma -1\right){\left(\alpha \right)}^{q\lambda }}}\right\}).\end{array}$$

(9)

4. Dual Hesitant q-Rung Orthopair Fuzzy Hamacher Operators

4.1. Dual Hesitant q-Rung Orthopair Fuzzy Hamacher Averaging Operators

In this section, based on the Hamacher operations of dual hesitant q-rung orthopair fuzzy numbers (DHq-ROFNs), we shall present some dual hesitant q-rung orthopair fuzzy Hamacher weighting average (DHq-ROFHWA) operators.

Definition 8.

Assume that $d_j=\left(h_j,g_j\right)\left(j=1,2,\dots ,n\right)$ is a list of DHq-ROFNs with weighting vector be $w_i={(w_1,w_2,\dots ,w_n)}^T$, which satisfies $w_i\in \left[0,1\right]$ and ${\displaystyle {\sum }_{i=1}^n{w}_i}=1$. Then the DHq-ROFHWA aggregation operator can be denoted as

$$\text{DHq-ROFHWA}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{d}_j$$

(10)

According to the operation laws of DHq-ROFNs, we can obtain the computed result:

Theorem 1.

The computing results by utilizing DHq-ROFHWA operator is

$$\begin{array}{c}\text{DHq-ROFHWA}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{d}_j\\ ={\cup }_{{\alpha }_j\in h_j,{\beta }_j\in g_j}(\left\{\sqrt[q]{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\alpha }_j\right)}^q\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\alpha }_j\right)}^q\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\alpha }_j\right)}^q\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-{\left({\alpha }_j\right)}^q\right)}^{w_j}}}}}\right\},\\ \left\{\frac{\sqrt[q]{\gamma }{\displaystyle \prod _{j=1}^n{\left({\beta }_j\right)}^{w_j}}}{\sqrt[q]{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-{\left({\beta }_j\right)}^q\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\beta }_j\right)}^{q{w}_j}}}}\right\})\end{array}$$

(11)

Example 1.

Given four dual hesitant q-rung orthopair fuzzy numbers: $d_1=\left\{\left\{0.7,0.8\right\},\left\{0.5\right\}\right\},d_2=\left\{\left\{0.4\right\},\left\{0.6\right\}\right\},d_3=\left\{\left\{0.6\right\},\left\{0.7,0.9\right\}\right\},d_4=\left\{\left\{0.3\right\},\left\{0.2\right\}\right\}$ with weighting vector be $w_j=\left(0.4,0.1,0.3,0.2\right)$, suppose that $q=3,\gamma =3$, then for membership degree $\alpha$, we can derive

$$\begin{array}{l}{\alpha }_1=\text{DHq-ROFHWA}\left(0.7,0.4,0.6,0.3\right)\\ =\sqrt[3]{\frac{\left(\begin{array}{l}\left({\left(1+2\times {0.7}^3\right)}^{0.4}\times {\left(1+2\times {0.4}^3\right)}^{0.1}\times {\left(1+2\times {0.6}^3\right)}^{0.3}\times {\left(1+2\times {0.3}^3\right)}^{0.2}\right)\\ -\left({\left(1-{0.7}^3\right)}^{0.4}\times {\left(1-{0.4}^3\right)}^{0.1}\times {\left(1-{0.6}^3\right)}^{0.3}\times {\left(1-{0.3}^3\right)}^{0.2}\right)\end{array}\right)}{\left(\begin{array}{l}\left({\left(1+2\times {0.7}^3\right)}^{0.4}\times {\left(1+2\times {0.4}^3\right)}^{0.1}\times {\left(1+2\times {0.6}^3\right)}^{0.3}\times {\left(1+2\times {0.3}^3\right)}^{0.2}\right)\\ +2\times \left({\left(1-{0.7}^3\right)}^{0.4}\times {\left(1-{0.4}^3\right)}^{0.1}\times {\left(1-{0.6}^3\right)}^{0.3}\times {\left(1-{0.3}^3\right)}^{0.2}\right)\end{array}\right)}}\\ =0.5284\end{array}$$

In the same way, we have ${\alpha }_2=\text{DHq-ROFHWA}\left(0.8,0.4,0.6,0.3\right)=0.5787$, thus $\alpha =\left\{0.5284,0.5787\right\}$. For nonmembership $\beta$, we can derive

$$\begin{array}{l}{\beta }_1=\text{DHq-ROFHWA}\left(0.5,0.6,0.7,0.2\right)\\ =\left(\frac{\sqrt[3]{3}\times {0.5}^{0.4}\times {0.6}^{0.1}\times {0.7}^{0.3}\times {0.2}^{0.2}}{\sqrt[q]{\begin{array}{l}{\left(1+2\times \left(1-{0.5}^3\right)\right)}^{0.4}\times {\left(1+2\times \left(1-{0.6}^3\right)\right)}^{0.1}\times {\left(1+2\times \left(1-{0.7}^3\right)\right)}^{0.3}\\ \times {\left(1+2\times \left(1-{0.2}^3\right)\right)}^{0.2}+2\times {0.5}^{1.2}\times {0.6}^{0.3}\times {0.7}^{0.9}\times {0.2}^{0.6}\end{array}}}\right)\\ =0.2498\end{array}$$

In the same way, we have ${\beta }_2=\text{DHq-ROFHWA}\left(0.5,0.6,0.9,0.2\right)=0.2668$, thus $\beta =\left\{0.2498,0.2668\right\}$. So $\text{DHq-ROFHWA}\left(d_1,d_2,d_3,d_4\right)=\{\left\{0.5284,0.5787\right\},$ $\left\{0.2498,0.2668\right\}\}.$

It’s clear that the DHq-ROFHWA operator satisfies some properties including Idempotency, Monotonicity and Boundedness.

Property 1.

(Idempotency) Assume that $d_j=\left(h_j,g_j\right)\left(j=1,2,\dots ,n\right)$ are equal, we can obtain

$$\text{DHq-ROFHWA}(d_1,d_2,\dots ,d_n)=d$$

(12)

Property 2.

(Monotonicity) Let $d_j=\left(h_j,g_j\right)$ and ${d^{\prime }}_j=\left(h_j^{\prime },g_j^{\prime }\right),j=1,2,\dots ,n$ be two sets of DHq-ROFNs. If $h_j\le h_j^{\prime }$ and $g_j\ge g_j^{\prime }$ hold for all $j$, then

$$\text{DHq-ROFHWA}(d_1,d_2,\dots ,d_n)\le \text{DHq-ROFHWA}(d_1^{\prime },d_2^{\prime },\dots ,d_n^{\prime })$$

(13)

Property 3.

(Boundedness) Assume that $d_j=\left(h_j,g_j\right)\left(j=1,2,\dots ,n\right)$ be a set of DHq-ROFNs. If $d^{+}={\cup }_{{\alpha }_j\in h_j,{\beta }_j\in g_j}\left\{\left\{{\max }_i\left({\alpha }_i\right)\right\},\left\{{\min }_i\left({\beta }_i\right)\right\}\right\},d^{-}={\cup }_{{\alpha }_j\in h_j,{\beta }_j\in g_j}\left\{\left\{{\min }_i\left({\alpha }_i\right)\right\},\left\{{\max }_i\left({\beta }_i\right)\right\}\right\}$, then

$$d^{-}\le \text{DHq-ROFHWA}(d_1,d_2,\dots ,d_n)\le d^{+}$$

(14)

Next, by changing $\gamma$ and $q$ we shall derive some special results.

Case 1.

When $\gamma =1$, the DHq-ROFHWA operator is going to degrade into the dual hesitant q-rung orthopair fuzzy weighting average (DHq-ROFWA) aggregation operator presented as

$$\begin{array}{l}\text{DHq-ROFWA}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{d}_j\\ ={\cup }_{{\alpha }_j\in h_j,{\beta }_j\in g_j}\left(\left\{\sqrt[q]{1-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\alpha }_j\right)}^q\right)}^{w_j}}}\right\},\left\{{\displaystyle \prod _{j=1}^n{\left({\beta }_j\right)}^{w_j}}\right\}\right)\end{array}$$

(15)

Case 2.

When $\gamma =2$, the DHq-ROFHWA operator is going to degrade into the dual hesitant q-rung orthopair fuzzy Einstein weighting average (DHq-ROEWA) operator, presented as

$$\begin{array}{c}\text{DHq-ROFEWA}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{d}_j\\ ={\cup }_{{\alpha }_j\in h_j,{\beta }_j\in g_j}(\left\{\sqrt[q]{\frac{{\displaystyle \prod _{j=1}^n{\left(1+{\left({\alpha }_j\right)}^q\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\alpha }_j\right)}^q\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+{\left({\alpha }_j\right)}^q\right)}^{w_j}+{\displaystyle \prod _{j=1}^n{\left(1-{\left({\alpha }_j\right)}^q\right)}^{w_j}}}}}\right\},\\ \left\{\frac{\sqrt[q]{2}{\displaystyle \prod _{j=1}^n{\left({\beta }_j\right)}^{w_j}}}{\sqrt[q]{{\displaystyle \prod _{j=1}^n{\left(2-{\left({\beta }_j\right)}^q\right)}^{w_j}}+{\displaystyle \prod _{j=1}^n{\left({\beta }_j\right)}^{q{w}_j}}}}\right\})\end{array}$$

(16)

Case 3.

When $q=1$, the DHq-ROFHWA operator is going to degrade into the dual hesitant intuitionistic fuzzy Hamacher weighting average (DHIFHWA) operator, presented as

$$\begin{array}{c}\mathrm{DHIFHWA}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{d}_j\\ ={\cup }_{{\alpha }_j\in h_j,{\beta }_j\in g_j}(\left\{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left({\alpha }_j\right)\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-\left({\alpha }_j\right)\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left({\alpha }_j\right)\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-\left({\alpha }_j\right)\right)}^{w_j}}}}\right\},\\ \left\{\frac{\gamma {\displaystyle \prod _{j=1}^n{\left({\beta }_j\right)}^{w_j}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-\left({\beta }_j\right)\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\beta }_j\right)}^{w_j}}}\right\})\end{array}$$

(17)

Case 4.

When $q=2$, the DHq-ROFHWA operator is going to degrade into the dual hesitant Pythagorean fuzzy Hamacher weighting average (DHPFHWA) operator [56], presented as

$$\begin{array}{c}\mathrm{DHPFHWA}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{d}_j\\ ={\cup }_{{\alpha }_j\in h_j,{\beta }_j\in g_j}(\left\{\sqrt{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\alpha }_j\right)}^2\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\alpha }_j\right)}^2\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\alpha }_j\right)}^2\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-{\left({\alpha }_j\right)}^2\right)}^{w_j}}}}}\right\},\\ \left\{\frac{\sqrt{\gamma }{\displaystyle \prod _{j=1}^n{\left({\beta }_j\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-{\left({\beta }_j\right)}^2\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\beta }_j\right)}^{2w_j}}}}\right\})\end{array}$$

(18)

Furthermore, to consider the order positions of being fused arguments, we develop the dual hesitant q-rung orthopair fuzzy Hamacher ordered weighting average (DHq-ROFHOWA) operator as follows.

Definition 9.

Assume that $d_j=\left(h_j,g_j\right)\left(j=1,2,\dots ,n\right)$ is a group of DHq-ROFNs, the dual hesitant q-rung orthopair fuzzy Hamacher ordered weighting average (DHq-ROFHOWA) operator with associated weighting vector be $w={\left(w_1,w_2,\cdots ,w_n\right)}^T$, which satisfies the conditions of $w_j>0$ and ${\displaystyle \sum _{j=1}^n{w}_j}=1$, then

$$\begin{array}{c}\text{DHq-ROFHOWA}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{d}_{\sigma \left(j\right)}\\ ={\cup }_{{\alpha }_{\sigma \left(j\right)}\in h_j,{\beta }_{\sigma \left(j\right)}\in g_j}(\left\{\sqrt[q]{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\alpha }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\alpha }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\alpha }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-{\left({\alpha }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}}}\right\},\\ \left\{\frac{\sqrt[q]{\gamma }{\displaystyle \prod _{j=1}^n{\left({\beta }_{\sigma \left(j\right)}\right)}^{w_j}}}{\sqrt[q]{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-{\left({\beta }_{\sigma \left(j\right)}\right)}^q\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\beta }_{\sigma \left(j\right)}\right)}^{q{w}_j}}}}\right\})\end{array}$$

(19)

where $\left(\sigma \left(1\right),\sigma \left(2\right),\cdots ,\sigma \left(n\right)\right)$ is a permutation of $\left(1,2,\cdots ,n\right)$, and $d_{\sigma \left(j-1\right)}\ge d_{\sigma \left(j\right)}$ for all $j=2,\cdots ,n$.

It is clear that the DHq-ROFHOWA operator satisfies some properties including idempotency, monotonicity, and boundedness.

Property 4.

(Idempotency) Assume that $d_j=\left(h_j,g_j\right)\left(j=1,2,\dots ,n\right)$ are equal, we can obtain

$$\text{DHq-ROFHOWA}(d_1,d_2,\dots ,d_n)=d$$

(20)

Property 5.

(Monotonicity) Assume that $d_j=\left(h_j,g_j\right)$ and $d_j^{\prime }=\left(h_j^{\prime },g_j^{\prime }\right),j=1,2,\dots ,n$ are two groups of DHq-ROFNs. If $h_j\le h_j^{\prime }$ and $g_j\ge g_j^{\prime }$ hold for all $j$, then

$$\text{DHq-ROFHOWA}(d_1,d_2,\dots ,d_n)\le \text{DHq-ROFHOWA}(d_1^{\prime },d_3^{\prime },\dots ,d_n^{\prime })$$

(21)

Property 6.

(Boundedness) Assume that $d_j=\left(h_j,g_j\right)\left(j=1,2,\dots ,n\right)$ is a set of DHq-ROFNs. If $d^{+}={\cup }_{{\alpha }_{\sigma \left(j\right)}\in h_j,{\beta }_{\sigma \left(j\right)}\in g_j}\left\{\left\{{\max }_i\left({\alpha }_i\right)\right\},\left\{{\min }_i\left({\beta }_i\right)\right\}\right\},d^{-}={\cup }_{{\alpha }_{\sigma \left(j\right)}\in h_j,{\beta }_{\sigma \left(j\right)}\in g_j}\left\{\left\{{\min }_i\left({\alpha }_i\right)\right\},\left\{{\max }_i\left({\beta }_i\right)\right\}\right\}$, then

$$d^{-}\le \text{DHq-ROFHOWA}(d_1,d_2,\dots ,d_n)\le d^{+}$$

(22)

Next, by changing $\gamma$ and $q$ we shall derive some special results.

Case 1.

When $\gamma =1$, the DHq-ROFHOWA operator is going to degrade into the dual hesitant q-rung orthopair fuzzy ordered weighting average (DHq-ROFOWA) operator, presented as

$$\begin{array}{l}\text{DHq-ROFOWA}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{d}_{\sigma \left(j\right)}\\ ={\cup }_{{\alpha }_{\sigma \left(j\right)}\in h_j,{\beta }_{\sigma \left(j\right)}\in g_j}\left(\left\{\sqrt[q]{1-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\alpha }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}\right\},\left\{{\displaystyle \prod _{j=1}^n{\left({\beta }_{\sigma \left(j\right)}\right)}^{w_j}}\right\}\right)\end{array}$$

(23)

Case 2.

When $\gamma =2$, the DHq-ROFHOWA operator is going to degrade into the dual hesitant q-rung orthopair fuzzy Einstein ordered weighting average (DHq-ROEOWA) operator, presented as

$$\begin{array}{c}\text{DHq-ROFEOWA}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{d}_{\sigma \left(j\right)}\\ ={\cup }_{{\alpha }_{\sigma \left(j\right)}\in h_j,{\beta }_j\in g_{\sigma \left(j\right)}}(\left\{\sqrt[q]{\frac{{\displaystyle \prod _{j=1}^n{\left(1+{\left({\alpha }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\alpha }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+{\left({\alpha }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}+{\displaystyle \prod _{j=1}^n{\left(1-{\left({\alpha }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}}}\right\},\\ \left\{\frac{\sqrt[q]{2}{\displaystyle \prod _{j=1}^n{\left({\beta }_{\sigma \left(j\right)}\right)}^{w_j}}}{\sqrt[q]{{\displaystyle \prod _{j=1}^n{\left(2-{\left({\beta }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}+{\displaystyle \prod _{j=1}^n{\left({\beta }_{\sigma \left(j\right)}\right)}^{q{w}_j}}}}\right\})\end{array}$$

(24)

Case 3.

When $q=1$, the DHq-ROFHOWA operator is going to degrade into the dual hesitant intuitionistic fuzzy Hamacher ordered weighting average (DHIFHOWA) operator, presented as

$$\begin{array}{c}\mathrm{DHIFHOWA}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{d}_{\sigma \left(j\right)}\\ ={\cup }_{{\alpha }_j\in h_{\sigma \left(j\right)},{\beta }_j\in g_{\sigma \left(j\right)}}(\left\{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left({\alpha }_{\sigma \left(j\right)}\right)\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-\left({\alpha }_{\sigma \left(j\right)}\right)\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left({\alpha }_{\sigma \left(j\right)}\right)\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-\left({\alpha }_{\sigma \left(j\right)}\right)\right)}^{w_j}}}}\right\},\\ \left\{\frac{\gamma {\displaystyle \prod _{j=1}^n{\left({\beta }_{\sigma \left(j\right)}\right)}^{w_j}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-\left({\beta }_{\sigma \left(j\right)}\right)\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\beta }_{\sigma \left(j\right)}\right)}^{w_j}}}\right\})\end{array}$$

(25)

Case 4.

When $q=2$, the DHq-ROFHOWA operator is going to degrade into the dual hesitant Pythagorean fuzzy Hamacher ordered weighting average (DHPFHOWA) operator [56], presented as

$$\begin{array}{c}\mathrm{DHPFHOWA}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{d}_{\sigma \left(j\right)}\\ ={\cup }_{{\alpha }_{\sigma \left(j\right)}\in h_j,{\beta }_{\sigma \left(j\right)}\in g_j}(\left\{\sqrt{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\alpha }_{\sigma \left(j\right)}\right)}^2\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\alpha }_{\sigma \left(j\right)}\right)}^2\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\alpha }_{\sigma \left(j\right)}\right)}^2\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-{\left({\alpha }_{\sigma \left(j\right)}\right)}^2\right)}^{w_j}}}}}\right\},\\ \left\{\frac{\sqrt{\gamma }{\displaystyle \prod _{j=1}^n{\left({\beta }_{\sigma \left(j\right)}\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-{\left({\beta }_{\sigma \left(j\right)}\right)}^2\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\beta }_{\sigma \left(j\right)}\right)}^{2w_j}}}}\right\})\end{array}$$

(26)

According to Definitions 8–9, we can obtain that the DHq-ROFHWA operators can only weigh the DHq-ROFN itself, while the DHq-ROFHOWA operators can only weigh the ordered positions of the DHq-ROFN. To consider both two weights, we will develop the dual hesitant q-rung orthopair fuzzy Hamacher hybrid averaging (DHq-ROFHHA) operator as follows.

Definition 10.

Let $d_j=\left(h_j,g_j\right)\left(j=1,2,\dots ,n\right)$ be a group of DHq-ROFNs. A dual hesitant q-rung orthopair fuzzy Hamacher hybrid average (DHq-ROFHHA) operator mapping DHq-ROFHHA: $P^n\to P,$ such that

$$\begin{array}{c}\text{DHq-ROFHHA}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{\dot{d}}_{\sigma \left(j\right)}\\ ={\cup }_{{\dot{\alpha }}_{\sigma \left(j\right)}\in h_j,{\dot{\beta }}_{\sigma \left(j\right)}\in g_j}(\left\{\sqrt[q]{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}}}\right\},\\ \left\{\frac{\sqrt[q]{\gamma }{\displaystyle \prod _{j=1}^n{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^{w_j}}}{\sqrt[q]{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^q\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^{q{w}_j}}}}\right\})\end{array}$$

(27)

where $w=\left(w_1,w_2,\cdots ,w_n\right)$ means the associated weights, which satisfies $w_j\in \left[0,1\right]$, ${\displaystyle \sum _{j=1}^n{w}_j}=1$, and ${\dot{d}}_{\sigma \left(j\right)}$ denotes the j-th largest number of DHq-ROFNs ${\dot{d}}_j\left({\dot{d}}_j=\left(n{\omega }_j\right)d_j,j=1,2,\cdots ,n\right)$, $\omega =\left({\omega }_1,{\omega }_2,\cdots ,{\omega }_n\right)$ represents the weights of the DHq-ROFNs $d_j(j=1,2,\cdots ,n)$, which satisfies ${\omega }_j\in \left[0,1\right]$, ${\displaystyle \sum _{j=1}^n{\omega }_j}=1$, and $n$ indicates the balance coefficient.

When $w={\left(1/n,1/n,\cdots ,1/n\right)}^T$, the DHq-ROFHHA operator is going to degrade into the DHq-ROFHWA operator; when $\omega =\left(1/n,1/n,\cdots ,1/n\right)$, the DHq-ROFHHA operator is going to degrade into the dual (DHq-ROFHOWA operator.

Next, by changing $\gamma$ and $q$, we shall derive some special results.

Case 1.

When $\gamma =1$, theDHq-ROFHHA operator is going to degrade into the dual hesitant q-rung orthopair fuzzy hybrid averaging (DHq-ROFHA) operator, presented as

$$\begin{array}{l}\text{DHq-ROFHA}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{\dot{d}}_{\sigma \left(j\right)}\\ ={\cup }_{{\dot{\alpha }}_{\sigma \left(j\right)}\in h_j,{\dot{\beta }}_{\sigma \left(j\right)}\in g_j}\left(\left\{\sqrt[q]{1-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}\right\},\left\{{\displaystyle \prod _{j=1}^n{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^{w_j}}\right\}\right)\end{array}$$

(28)

Case 2.

When $\gamma =2$, the DHq-ROFHHA operator is going to degrade into the dual hesitant q-rung orthopair fuzzy Einstein hybrid averaging (DHq-ROFEHA) operator, presented as

$$\begin{array}{c}\text{DHq-ROFEHA}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{\dot{d}}_{\sigma \left(j\right)}\\ ={\cup }_{{\dot{\alpha }}_{\sigma \left(j\right)}\in h_j,{\dot{\beta }}_j\in g_{\sigma \left(j\right)}}(\left\{\sqrt[q]{\frac{{\displaystyle \prod _{j=1}^n{\left(1+{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}+{\displaystyle \prod _{j=1}^n{\left(1-{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}}}\right\},\\ \left\{\frac{\sqrt[q]{2}{\displaystyle \prod _{j=1}^n{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^{w_j}}}{\sqrt[q]{{\displaystyle \prod _{j=1}^n{\left(2-{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}+{\displaystyle \prod _{j=1}^n{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^{q{w}_j}}}}\right\})\end{array}$$

(29)

Case 3.

When $q=1$, the DHq-ROFHHA operator is going to degrade into the dual hesitant intuitionistic fuzzy Hamacher hybrid averaging (DHIFHHA) operator, presented as

$$\begin{array}{c}\mathrm{DHIFHHA}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{\dot{d}}_{\sigma \left(j\right)}\\ ={\cup }_{{\dot{\alpha }}_j\in h_{\sigma \left(j\right)},{\dot{\beta }}_j\in g_{\sigma \left(j\right)}}(\left\{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)\right)}^{w_j}}}}\right\},\\ \left\{\frac{\gamma {\displaystyle \prod _{j=1}^n{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^{w_j}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-\left({\dot{\beta }}_{\sigma \left(j\right)}\right)\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^{w_j}}}\right\})\end{array}$$

(30)

Case 4.

When $q=2$, the DHq-ROFHHA operator is going to degrade into the dual hesitant Pythagorean fuzzy Hamacher hybrid averaging (DHPFHHA) operator [56]:

$$\begin{array}{c}\mathrm{DHPFHHA}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\oplus }}{w}_j{\dot{d}}_{\sigma \left(j\right)}\\ ={\cup }_{{\dot{\alpha }}_{\sigma \left(j\right)}\in h_j,{\dot{\beta }}_{\sigma \left(j\right)}\in g_j}(\left\{\sqrt{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^2\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^2\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^2\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^2\right)}^{w_j}}}}}\right\},\\ \left\{\frac{\sqrt{\gamma }{\displaystyle \prod _{j=1}^n{\left({\dot{\beta }}_j\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^2\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^{2w_j}}}}\right\})\end{array}$$

(31)

4.2. Dual Hesitant q-Rung Orthopair Fuzzy Hamacher Geometric Operators

In accordance with the DHq-ROFHWA aggregation operators and the geometric operations, we will define some dual hesitant q-rung orthopair fuzzy Hamacher weighting geometric (DHq-ROFHWG) aggregation operators as follows.

Definition 11.

Let $d_j=\left(h_j,g_j\right)\left(j=1,2,\dots ,n\right)$ be a collection of DHq-ROFNs. The dual hesitant q-rung orthopair fuzzy Hamacher weighting geometric (DHq-ROFHWG) aggregation operator can be depicted as

$$\text{DHq-ROFHWG}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left(d_j\right)}^{w_j}$$

(32)

According to Hamacher operations of DHq-ROFNs, we can obtain the computed result as follows:

Theorem 2.

The fused results by utilizing DHq-ROFHWA operator can be shown as

$$\begin{array}{c}\text{DHq-ROFHWG}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left(d_j\right)}^{w_j}\\ ={\cup }_{{\alpha }_j\in h_j,{\beta }_j\in g_j}(\left\{\frac{\sqrt[q]{\gamma }{\displaystyle \prod _{j=1}^n{\left({\alpha }_j\right)}^{w_j}}}{\sqrt[q]{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-{\left({\alpha }_j\right)}^q\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\alpha }_j\right)}^{q{w}_j}}}}\right\},\\ \left\{\sqrt[q]{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\beta }_j\right)}^q\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\beta }_j\right)}^q\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\beta }_j\right)}^q\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-{\left({\beta }_j\right)}^q\right)}^{w_j}}}}}\right\})\end{array}$$

(33)

Example 2.

Given four dual hesitant q-rung orthopair fuzzy numbers—$d_1=\left\{\left\{0.7,0.8\right\},\left\{0.5\right\}\right\},d_2=\left\{\left\{0.4\right\},\left\{0.6\right\}\right\},d_3=\left\{\left\{0.6\right\},\left\{0.7,0.9\right\}\right\},d_4=\left\{\left\{0.3\right\},\left\{0.2\right\}\right\}$—with weighting vector will be $w_j=\left(0.4,0.1,0.3,0.2\right)$, suppose that $q=3,\gamma =3$, then for membership degree $\alpha$, we can derive

$$\begin{array}{l}{\alpha }_1=\text{DHq-ROFHWG}\left(0.7,0.4,0.6,0.3\right)\\ =\left(\frac{\sqrt[3]{3}\times {0.7}^{0.4}\times {0.4}^{0.1}\times {0.6}^{0.3}\times {0.3}^{0.2}}{\sqrt[q]{\begin{array}{l}{\left(1+2\times \left(1-{0.7}^3\right)\right)}^{0.4}\times {\left(1+2\times \left(1-{0.4}^3\right)\right)}^{0.1}\times {\left(1+2\times \left(1-{0.6}^3\right)\right)}^{0.3}\\ \times {\left(1+2\times \left(1-{0.3}^3\right)\right)}^{0.2}+2\times {0.7}^{1.2}\times {0.4}^{0.3}\times {0.6}^{0.9}\times {0.3}^{0.6}\end{array}}}\right)\\ =0.1040\end{array}$$

In the same way, we have ${\alpha }_2=\text{DHq-ROFHWG}\left(0.8,0.4,0.6,0.3\right)=0.1104$, thus, $\alpha =\left\{0.1040,0.1104\right\}$. For nonmembership $\beta$, we can derive

$$\begin{array}{l}{\beta }_1=\text{DHq-ROFHWG}\left(0.5,0.6,0.7,0.2\right)\\ =\sqrt[3]{\frac{\left(\begin{array}{l}\left({\left(1+2\times {0.5}^3\right)}^{0.4}\times {\left(1+2\times {0.6}^3\right)}^{0.1}\times {\left(1+2\times {0.7}^3\right)}^{0.3}\times {\left(1+2\times {0.2}^3\right)}^{0.2}\right)\\ -\left({\left(1-{0.5}^3\right)}^{0.4}\times {\left(1-{0.6}^3\right)}^{0.1}\times {\left(1-{0.7}^3\right)}^{0.3}\times {\left(1-{0.2}^3\right)}^{0.2}\right)\end{array}\right)}{\left(\begin{array}{l}\left({\left(1+2\times {0.5}^3\right)}^{0.4}\times {\left(1+2\times {0.6}^3\right)}^{0.1}\times {\left(1+2\times {0.7}^3\right)}^{0.3}\times {\left(1+2\times {0.2}^3\right)}^{0.2}\right)\\ +2\times \left({\left(1-{0.5}^3\right)}^{0.4}\times {\left(1-{0.6}^3\right)}^{0.1}\times {\left(1-{0.7}^3\right)}^{0.3}\times {\left(1-{0.2}^3\right)}^{0.2}\right)\end{array}\right)}}\\ =0.5553\end{array}$$

In the same way, we have ${\beta }_2=\text{DHq-ROFHWG}\left(0.5,0.6,0.9,0.2\right)=0.6003$, thus, $\beta =\left\{0.5553,0.6003\right\}$. So $\text{DHq-ROFHWG}\left(d_1,d_2,d_3,d_4\right)=\{\left\{0.1040,0.1104\right\},$ $\left\{0.5553,0.6003\right\}\}$.

It is clear that the DHq-ROFHWG operator satisfies some properties including idempotency, monotonicity, and boundedness.

Property 7.

(Idempotency) Assume that $d_j=\left(h_j,g_j\right)\left(j=1,2,\dots ,n\right)$ are equal, we can obtain

$$\text{DHq-ROFHWG}(d_1,d_2,\dots ,d_n)=d$$

(34)

Property 8.

(Monotonicity) Assume that $d_j=\left(h_j,g_j\right)$ and $d_j^{\prime }=\left(h_j^{\prime },g_j^{\prime }\right),j=1,2,\dots ,n$ be two sets of DHq-ROFNs. If $h_j\le h_j^{\prime }$ and $g_j\ge g_j^{\prime }$ hold for all $j$, then

$$\text{DHq-ROFHWG}(d_1,d_2,\dots ,d_n)\le \text{DHq-ROFHWG}(d_1^{\prime },d_1^{\prime },\dots ,d_n^{\prime })$$

(35)

Property 9.

(Boundedness) Assume that $d_j=\left(h_j,g_j\right)\left(j=1,2,\dots ,n\right)$ be a set of DHq-ROFNs. If $d^{+}={\cup }_{{\alpha }_j\in h_j,{\beta }_j\in g_j}\left\{\left\{{\max }_i\left({\alpha }_i\right)\right\},\left\{{\min }_i\left({\beta }_i\right)\right\}\right\},d^{-}={\cup }_{{\alpha }_j\in h_j,{\beta }_j\in g_j}\left\{\left\{{\min }_i\left({\alpha }_i\right)\right\},\left\{{\max }_i\left({\beta }_i\right)\right\}\right\}$, then

$$d^{-}\le \text{DHq-ROFHWG}(d_1,d_2,\dots ,d_n)\le d^{+}$$

(36)

Next, by changing $\gamma$ and $q$, we shall derive some special results.

Case 1.

When $\gamma =1$, the DHq-ROFHWG operator is going to degrade into the dual hesitant q-rung orthopair fuzzy weighting geometric (DHq-ROFWG) operator, presented as

$$\begin{array}{l}\text{DHq-ROFWG}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left(d_j\right)}^{w_j}\\ ={\cup }_{{\alpha }_j\in h_j,{\beta }_j\in g_j}\left(\left\{{\displaystyle \prod _{j=1}^n{\left({\alpha }_j\right)}^{w_j}}\right\},\left\{\sqrt[q]{1-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\beta }_j\right)}^q\right)}^{w_j}}}\right\}\right)\end{array}$$

(37)

Case 2.

When $\gamma =2$, the DHq-ROFHWG operator is going to degrade into the dual hesitant q-rung orthopair fuzzy Einstein weighting geometric (DHq-ROFEWG) operator, presented as

$$\begin{array}{c}\text{DHq-ROFEWG}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left(d_j\right)}^{w_j}\\ ={\cup }_{{\alpha }_j\in h_j,{\beta }_j\in g_j}(\left\{\frac{\sqrt[q]{2}{\displaystyle \prod _{j=1}^n{\left({\alpha }_j\right)}^{w_j}}}{\sqrt[q]{{\displaystyle \prod _{j=1}^n{\left(2-{\left({\alpha }_j\right)}^q\right)}^{w_j}}+{\displaystyle \prod _{j=1}^n{\left({\alpha }_j\right)}^{q{w}_j}}}}\right\},\\ \left\{\sqrt[q]{\frac{{\displaystyle \prod _{j=1}^n{\left(1+{\left({\beta }_j\right)}^q\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\beta }_j\right)}^q\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+{\left({\beta }_j\right)}^q\right)}^{w_j}+{\displaystyle \prod _{j=1}^n{\left(1-{\left({\beta }_j\right)}^q\right)}^{w_j}}}}}\right\})\end{array}$$

(38)

Case 3.

When $q=1$, the DHq-ROFHWG operator is going to degrade into the dual hesitant intuitionistic fuzzy Hamacher weighting geometric (DHIFHWG) operator, presented as

$$\begin{array}{c}\mathrm{DHIFHWG}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left(d_j\right)}^{w_j}\\ ={\cup }_{{\alpha }_j\in h_j,{\beta }_j\in g_j}(\left\{\frac{\gamma {\displaystyle \prod _{j=1}^n{\left({\alpha }_j\right)}^{w_j}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-\left({\alpha }_j\right)\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\alpha }_j\right)}^{w_j}}}\right\},\\ \left\{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left({\beta }_j\right)\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-\left({\beta }_j\right)\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left({\beta }_j\right)\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-\left({\beta }_j\right)\right)}^{w_j}}}}\right\})\end{array}$$

(39)

Case 4.

When $q=2$, the DHq-ROFHWG operator is going to degrade into the dual hesitant Pythagorean fuzzy Hamacher weighting geometric (DHPFHWG) operator [56], presented as

$$\begin{array}{c}\mathrm{DHPFHWG}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left(d_j\right)}^{w_j}\\ ={\cup }_{{\alpha }_j\in h_j,{\beta }_j\in g_j}(\left\{\frac{\sqrt{\gamma }{\displaystyle \prod _{j=1}^n{\left({\alpha }_j\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-{\left({\alpha }_j\right)}^2\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\alpha }_j\right)}^{2w_j}}}}\right\},\\ \left\{\sqrt{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\beta }_j\right)}^2\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\beta }_j\right)}^2\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\beta }_j\right)}^2\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-{\left({\beta }_j\right)}^2\right)}^{w_j}}}}}\right\})\end{array}$$

(40)

Furthermore, to consider the order positions of being fused arguments, we proposed the dual hesitant q-rung orthopair fuzzy Hamacher ordered weighted geometric (DHq-ROFHOWG) operator as follows.

Definition 12.

Let $d_j=\left(h_j,g_j\right)\left(j=1,2,\dots ,n\right)$ be a group of DHq-ROFNs, the DHq-ROFHOWG operator with associated weights $w={\left(w_1,w_2,\cdots ,w_n\right)}^T$, which satisfies the condition of $w_j>0$ and ${\displaystyle \sum _{j=1}^n{w}_j}=1$, then

$$\begin{array}{c}\text{DHq-ROFHOWG}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left(d_{\sigma \left(j\right)}\right)}^{w_j}\\ ={\cup }_{{\alpha }_{\sigma \left(j\right)}\in h_j,{\beta }_{\sigma \left(j\right)}\in g_j}(\left\{\frac{\sqrt[q]{\gamma }{\displaystyle \prod _{j=1}^n{\left({\alpha }_{\sigma \left(j\right)}\right)}^{w_j}}}{\sqrt[q]{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-{\left({\alpha }_{\sigma \left(j\right)}\right)}^q\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\alpha }_{\sigma \left(j\right)}\right)}^{q{w}_j}}}}\right\},\\ \left\{\sqrt[q]{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\beta }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\beta }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\beta }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-{\left({\beta }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}}}\right\})\end{array}$$

(41)

where $\left(\sigma \left(1\right),\sigma \left(2\right),\cdots ,\sigma \left(n\right)\right)$ is a permutation of $\left(1,2,\cdots ,n\right)$, such that $d_{\sigma \left(j-1\right)}\ge d_{\sigma \left(j\right)}$ for all $j=2,\cdots ,n$.

We can easily obtain that the DHq-ROFHOWG operator satisfies the following properties.

Property 10.

(Idempotency) Assume that $d_j=\left(h_j,g_j\right)\left(j=1,2,\dots ,n\right)$ are equal, we can obtain

$$\text{DHq-ROFHOWG}(d_1,d_2,\dots ,d_n)=d$$

(42)

Property 11.

(Monotonicity) Assume that $d_j=\left(h_j,g_j\right)$ and $d_j^{\prime }=\left(h_j^{\prime },g_j^{\prime }\right),j=1,2,\dots ,n$ be two sets of DHq-ROFNs. If $h_j\le h_j^{\prime }$ and $g_j\ge g_j^{\prime }$ hold for all $j$, then

$$\text{DHq-ROFHOWG}(d_1,d_2,\dots ,d_n)\le \text{DHq-ROFHOWG}(d_1^{\prime },d_2^{\prime },\dots ,d_n^{\prime })$$

(43)

Property 12.

(Boundedness) Assume that $d_j=\left(h_j,g_j\right)\left(j=1,2,\dots ,n\right)$ is a set of DHq-ROFNs. If $d^{+}={\cup }_{{\alpha }_{\sigma \left(j\right)}\in h_j,{\beta }_{\sigma \left(j\right)}\in g_j}\left\{\left\{{\max }_i\left({\alpha }_i\right)\right\},\left\{{\min }_i\left({\beta }_i\right)\right\}\right\},d^{-}={\cup }_{{\alpha }_{\sigma \left(j\right)}\in h_j,{\beta }_{\sigma \left(j\right)}\in g_j}\left\{\left\{{\min }_i\left({\alpha }_i\right)\right\},\left\{{\max }_i\left({\beta }_i\right)\right\}\right\}$, then

$$d^{-}\le \text{DHq-ROFHOWG}(d_1,d_2,\dots ,d_n)\le d^{+}$$

(44)

Next, by changing $\gamma$ and $q$, we shall derive some special results.

Case 1.

When $\gamma =1$, the DHq-ROFHOWG operator is going to degrade into the dual hesitant q-rung orthopair fuzzy ordered weighting geometric (DHq-ROFOWG) operator, presented as

$$\begin{array}{l}\text{DHq-ROFOWG}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left(d_{\sigma \left(j\right)}\right)}^{w_j}\\ ={\cup }_{{\alpha }_{\sigma \left(j\right)}\in h_j,{\beta }_{\sigma \left(j\right)}\in g_j}\left(\left\{{\displaystyle \prod _{j=1}^n{\left({\alpha }_{\sigma \left(j\right)}\right)}^{w_j}}\right\},\left\{\sqrt[q]{1-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\beta }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}\right\}\right)\end{array}$$

(45)

Case 2.

When $\gamma =2$, the DHq-ROFHOWG operator is going to degrade into the dual hesitant q-rung orthopair fuzzy Einstein ordered weighting geometric (DHq-ROEOWG) operator, presented as

$$\begin{array}{c}\text{DHq-ROFEOWG}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left(d_{\sigma \left(j\right)}\right)}^{w_j}\\ ={\cup }_{{\alpha }_{\sigma \left(j\right)}\in h_j,{\beta }_j\in g_{\sigma \left(j\right)}}(\left\{\frac{\sqrt[q]{2}{\displaystyle \prod _{j=1}^n{\left({\alpha }_{\sigma \left(j\right)}\right)}^{w_j}}}{\sqrt[q]{{\displaystyle \prod _{j=1}^n{\left(2-{\left({\alpha }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}+{\displaystyle \prod _{j=1}^n{\left({\alpha }_{\sigma \left(j\right)}\right)}^{q{w}_j}}}}\right\},\\ \left\{\sqrt[q]{\frac{{\displaystyle \prod _{j=1}^n{\left(1+{\left({\beta }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\beta }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+{\left({\beta }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}+{\displaystyle \prod _{j=1}^n{\left(1-{\left({\beta }_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}}}\right\})\end{array}$$

(46)

Case 3.

When $q=1$, the DHq-ROFHOWG operator is going to degrade into the dual hesitant intuitionistic fuzzy Hamacher ordered weighting geometric (DHIFHOWG) operator, presented as

$$\begin{array}{c}\mathrm{DHIFHOWG}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left(d_{\sigma \left(j\right)}\right)}^{w_j}\\ ={\cup }_{{\alpha }_j\in h_{\sigma \left(j\right)},{\beta }_j\in g_{\sigma \left(j\right)}}(\left\{\frac{\gamma {\displaystyle \prod _{j=1}^n{\left({\alpha }_{\sigma \left(j\right)}\right)}^{w_j}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-\left({\alpha }_{\sigma \left(j\right)}\right)\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\alpha }_{\sigma \left(j\right)}\right)}^{w_j}}}\right\},\\ \left\{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left({\beta }_{\sigma \left(j\right)}\right)\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-\left({\beta }_{\sigma \left(j\right)}\right)\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left({\beta }_{\sigma \left(j\right)}\right)\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-\left({\beta }_{\sigma \left(j\right)}\right)\right)}^{w_j}}}}\right\})\end{array}$$

(47)

Case 4.

When $q=2$, the DHq-ROFHOWG operator is going to degrade into the dual hesitant Pythagorean fuzzy Hamacher ordered weighting geometric (DHPFHOWG) operator [56], presented as

$$\begin{array}{c}\mathrm{DHPFHOWG}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left(d_{\sigma \left(j\right)}\right)}^{w_j}\\ ={\cup }_{{\alpha }_{\sigma \left(j\right)}\in h_j,{\beta }_{\sigma \left(j\right)}\in g_j}(\left\{\frac{\sqrt{\gamma }{\displaystyle \prod _{j=1}^n{\left({\alpha }_{\sigma \left(j\right)}\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-{\left({\alpha }_{\sigma \left(j\right)}\right)}^2\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\alpha }_{\sigma \left(j\right)}\right)}^{2w_j}}}}\right\},\\ \left\{\sqrt{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\beta }_{\sigma \left(j\right)}\right)}^2\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\beta }_{\sigma \left(j\right)}\right)}^2\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\beta }_{\sigma \left(j\right)}\right)}^2\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-{\left({\beta }_{\sigma \left(j\right)}\right)}^2\right)}^{w_j}}}}}\right\})\end{array}$$

(48)

According to Definitions 11 and 12, we can deduce that the DHq-ROFHWG operators can only weigh the DHq-ROFN itself, and the DHq-ROFHOWG operators can only weigh the ordered positions of the DHq-ROFN. In order to consider both two weights, we will develop the dual hesitant q-rung orthopair fuzzy Hamacher hybrid geometric (DHq-ROFHHG) operator as follows.

Definition 13.

Let $d_j=\left(h_j,g_j\right)\left(j=1,2,\dots ,n\right)$ be a group of DHq-ROFNs. A dual hesitant q-rung orthopair fuzzy Hamacher hybrid geometric (DHq-ROFHHG) operator a mapping DHq-ROFHHG: $P^n\to P,$ such that

$$\begin{array}{c}\text{DHq-ROFHHG}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left({\dot{d}}_{\sigma \left(j\right)}\right)}^{w_j}\\ ={\cup }_{{\dot{\alpha }}_{\sigma \left(j\right)}\in h_j,{\dot{\beta }}_{\sigma \left(j\right)}\in g_j}(\left\{\frac{\sqrt[q]{\gamma }{\displaystyle \prod _{j=1}^n{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^{w_j}}}{\sqrt[q]{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^q\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^{q{w}_j}}}}\right\},\\ \left\{\sqrt[q]{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}}}\right\})\end{array}$$

(49)

where $w=\left(w_1,w_2,\cdots ,w_n\right)$ means the associated weights, which satisfies $w_j\in \left[0,1\right]$, ${\displaystyle \sum _{j=1}^n{w}_j}=1$, and ${\dot{d}}_{\sigma \left(j\right)}$ is the j-th largest number of DHq-ROFNs ${\dot{d}}_j\left({\dot{d}}_j={\left(d_j\right)}^{n{\omega }_j},j=1,2,\cdots ,n\right)$, $\omega =\left({\omega }_1,{\omega }_2,\cdots ,{\omega }_n\right)$ means the weights of DHq-ROFNs $d_j\left(j=1,2,\cdots ,n\right)$ itself, which satisfies ${\omega }_j\in \left[0,1\right]$, ${\displaystyle \sum _{j=1}^n{\omega }_j}=1$, and $n$ indicates the balance coefficient.

When $w={\left(1/n,1/n,\cdots ,1/n\right)}^T$, the DHq-ROFHHG operator is going to degrade into the DHq-ROFHWG operator; when $\omega =\left(1/n,1/n,\cdots ,1/n\right)$, the DHq-ROFHHG operator is going to degrade into the dual (DHq-ROFHOWG operator.

Next, by changing $\gamma$ and $q$, we shall derive some special results.

Case 1.

When $\gamma =1$, the DHq-ROFHHG operator is going to degrade into the dual hesitant q-rung orthopair fuzzy hybrid geometric (DHq-ROFHG) operator, presented as

$$\begin{array}{l}\text{DHq-ROFHG}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left({\dot{d}}_{\sigma \left(j\right)}\right)}^{w_j}\\ ={\cup }_{{\dot{\alpha }}_{\sigma \left(j\right)}\in h_j,{\dot{\beta }}_{\sigma \left(j\right)}\in g_j}\left(\left\{{\displaystyle \prod _{j=1}^n{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^{w_j}}\right\}\left\{\sqrt[q]{1-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}\right\}\right)\end{array}$$

(50)

Case 2.

When $\gamma =2$, the DHq-ROFHHG operator is going to degrade into the dual hesitant q-rung orthopair fuzzy Einstein hybrid geometric (DHq-ROFEHG) operator, presented as

$$\begin{array}{c}\text{DHq-ROFEHG}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left({\dot{d}}_{\sigma \left(j\right)}\right)}^{w_j}\\ ={\cup }_{{\dot{\alpha }}_{\sigma \left(j\right)}\in h_j,{\dot{\beta }}_j\in g_{\sigma \left(j\right)}}(\left\{\frac{\sqrt[q]{2}{\displaystyle \prod _{j=1}^n{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^{w_j}}}{\sqrt[q]{{\displaystyle \prod _{j=1}^n{\left(2-{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}+{\displaystyle \prod _{j=1}^n{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^{q{w}_j}}}}\right\},\\ \left\{\sqrt[q]{\frac{{\displaystyle \prod _{j=1}^n{\left(1+{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}+{\displaystyle \prod _{j=1}^n{\left(1-{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^q\right)}^{w_j}}}}}\right\})\end{array}$$

(51)

Case 3.

When $q=1$, the DHq-ROFHHG operator is going to degrade into the dual hesitant intuitionistic fuzzy Hamacher hybrid geometric (DHIFHHG) operator, presented as

$$\begin{array}{c}\mathrm{DHIFHHG}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left({\dot{d}}_{\sigma \left(j\right)}\right)}^{w_j}\\ ={\cup }_{{\dot{\alpha }}_j\in h_{\sigma \left(j\right)},{\dot{\beta }}_j\in g_{\sigma \left(j\right)}}(\left\{\frac{\gamma {\displaystyle \prod _{j=1}^n{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^{w_j}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^{w_j}}}\right\},\\ \left\{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left({\dot{\beta }}_{\sigma \left(j\right)}\right)\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-\left({\dot{\beta }}_{\sigma \left(j\right)}\right)\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left({\dot{\beta }}_{\sigma \left(j\right)}\right)\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-\left({\dot{\beta }}_{\sigma \left(j\right)}\right)\right)}^{w_j}}}}\right\})\end{array}$$

(52)

Case 4.

When $q=2$, the DHq-ROFHHG operator is going to degrade into the dual hesitant Pythagorean fuzzy Hamacher hybrid geometric (DHPFHHG) operator [56], presented as

$$\begin{array}{c}\mathrm{DHPFHHG}\left(d_1,d_2,\cdots ,d_n\right)=\underset{j=1}{\overset{n}{\otimes }}{\left({\dot{d}}_{\sigma \left(j\right)}\right)}^{w_j}\\ ={\cup }_{{\dot{\alpha }}_{\sigma \left(j\right)}\in h_j,{\dot{\beta }}_{\sigma \left(j\right)}\in g_j}(\left\{\frac{\sqrt{\gamma }{\displaystyle \prod _{j=1}^n{\left({\dot{\alpha }}_j\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right)\left(1-{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^2\right)\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left({\dot{\alpha }}_{\sigma \left(j\right)}\right)}^{2w_j}}}}\right\},\\ \left\{\sqrt{\frac{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^2\right)}^{w_j}-{\displaystyle \prod _{j=1}^n{\left(1-{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^2\right)}^{w_j}}}}{{\displaystyle \prod _{j=1}^n{\left(1+\left(\gamma -1\right){\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^2\right)}^{w_j}+\left(\gamma -1\right){\displaystyle \prod _{j=1}^n{\left(1-{\left({\dot{\beta }}_{\sigma \left(j\right)}\right)}^2\right)}^{w_j}}}}}\right\})\end{array}$$

(53)

Given an numerical example with DHq-ROFNs information to briefly depict the decision steps, suppose there are $m$ alternatives $A_i$ denoted by $n$ attributes $G_j$, let $w_j$ be attribute weights with $0\le w_j\le 1,{\displaystyle {\sum }_{j=1}^n{w}_j}=1$, then the decision-making steps are listed as follows.

• Step 1. Collect the dual hesitant q-rung orthopair fuzzy decision-making information given by experts and construct the evaluation matrix $R_{ij}^{}={\left(r_{ij}\right)}_{m\times n}$;
• Step 2. According to the attribute weights, we can fuse the dual hesitant q-rung orthopair fuzzy information by utilizing the equation (11) or (33);
• Step 3. Compute the score and accuracy results to determine the rank of all the alternatives.

5. Numerical Example and Comparative Analysis

5.1. Numerical Example

Since the prefabricated building has obvious advantages such as high construction quality, environmental protection, and labor-saving compared with the traditional cast-in-place construction method, this construction method has been gradually promoted in the construction field. However, this immature construction method often overlaps with construction safety risks such as on-site assembly and parallel construction. In addition, the quality of on-site construction personnel is generally low, and it is difficult to adapt to the needs of new construction techniques, which is very likely to cause construction safety accidents. In order to control the incidence of construction-type construction safety accidents with a gradual upward trend, only correct and scientific decision-making of a construction safety program can be of great significance for the control of PC construction safety. Thus, how to select the scheme of construction project is an interesting topic. To select the scheme of construction project is a classical MADM problem [67,68]. In this part, we shall give an actual application about scheme selection of construction project with dual hesitant q-rung orthopair fuzzy information in order to demonstrate the aggregation operators developed in our manuscript. There are five possible construction projects $A_i\left(i=1,2,3,4,5\right)$ to be selected. The experts selects four attribute to estimate the five possible construction projects: ①G₁ is the Human and management factors; ②G₂ is the Hoisting construction operation factors; ③G₃ is the PC component installation factor; and ④G₄ is the environmental factor. The five possible construction projects $A_i\left(i=1,2,3,4,5\right)$ are to be evaluated using the dual hesitant q-rung orthopair fuzzy information which is shown in

Table 2. DHq-ROFN decision matrix ($R$).

Alternatives	G1	G2	G3	G4
A1	{{0.3,0.4},{0.6}}	{{0.4,0.5},{0.2,0.3)}}	{{0.5,0.6},{0.8}}	{{0.1,0.5},{0.7}}
A2	{{0.2},{0.4}}	{{0.1,0.2,0.3},{0.2}}	{{0.5},{0.2,0.3,0.6}}	{{0.8},{0.1,0.2}}
A3	{{0.7,0.9},{0.1}}	{{0.6},{0.3,0.5}}	{{0.4,0.5,0.6},{0.1}}	{{0.5,0.6,0.7},{0.2}}
A4	{{0.4},{0.2})}	{{0.3,0.4,0.5},{0.4}}	{{0.3,0.5},{0.4}}	{{0.4},{0.4,0.5,0.6}}
A5	{{0.3,0.4},{0.2}}	{{0.4,0.5,0.6},{0.4}}	{{0.5,0.6},{0.7}}	{{0.2,0.4,0.5},{0.5}}

. (The attribute’s weights are $\omega ={\left(0.26,0.42,0.18,0.14\right)}^T$).

In the following, we utilize the DHq-ROFHWA operator and the DHq-ROFHWG operator to study scheme selection of construction project from five possible construction projects.

• Step 1. Based on the decision-making information given in the Table 2, We shall utilize the DHq-ROFHWA operator to derive the overall preference values $r_i$ of the construction projects $A_i\left(i=1,2,3,4,5\right)$ (let $\gamma =3,q=3$):

  $$\begin{array}{ll}{r}_1& =\text{DHq-ROFHWA}\left(r_{11},r_{12},r_{13},r_{14}\right)=\underset{j=1}{\overset{4}{\oplus }}{w}_j{r}_{1j}\\ & =\left\{\left\{\begin{array}{l}0.3743,0.4118,0.3974,0.4314,0.4331,0.4625,0.4510,0.4785,\\ 0.3961,0.4303,0.4171,0.4484,0.4500,0.4776,0.4668,0.4927\end{array}\right\},\left\{\begin{array}{l}0.1971,\\ 0.2337\end{array}\right\}\right\}\\ r_2& =\text{DHq-ROFHWA}\left(r_{21},r_{22},r_{23},r_{24}\right)=\underset{j=1}{\overset{4}{\oplus }}{w}_j{r}_{2j}\\ & =\left\{\left\{0.4420,0.4480,0.4635\right\},\left\{0.1053,0.1158,0.1106,0.1216,0.1219,0.1339\right\}\right\}\\ r_3& =\text{DHq-ROFHWA}\left(r_{31},r_{32},r_{33},r_{34}\right)=\underset{j=1}{\overset{4}{\oplus }}{w}_j{r}_{3j}\\ & =\left\{\begin{array}{l}\left\{\begin{array}{l}0.6014,0.6131,0.6285,0.6084,0.6198,0.6349,0.6182,0.6292,0.6439,\\ 0.6981,0.7066,0.7181,0.7032,0.7116,0.7229,0.7104,0.7187,0.7297\end{array}\right\},\\ \left\{0.1102,0.1443\right\}\end{array}\right\}\\ r_4& =\text{DHq-ROFHWA}\left(r_{41},r_{42},r_{43},r_{44}\right)=\underset{j=1}{\overset{4}{\oplus }}{w}_j{r}_{4j}\\ & =\left\{\left\{0.3467,0.3761,0.3904,0.4145,0.4455,0.4647\right\},\left\{0.1619,0.1676,0.1732\right\}\right\}\\ r_5& =\text{DHq-ROFHWA}\left(r_{51},r_{52},r_{53},r_{54}\right)=\underset{j=1}{\overset{4}{\oplus }}{w}_j{r}_{5j}\\ & =\left\{\begin{array}{l}\left\{\begin{array}{l}0.3767,0.3946,0.4118,0.3996,0.4157,0.4314,0.4349,0.4488,0.4625,\\ 0.4527,0.4657,0.4785,0.4997,0.5106,0.5215,0.5137,0.5241,0.5345,\\ 0.3983,0.4145,0.4303,0.4190,0.4339,0.4484,0.4517,0.4647,0.4776,\\ 0.4684,0.4806,0.4927,0.5129,0.5233,0.5337,0.5263,0.5362,0.5462\end{array}\right\},\\ \left\{0.1827\right\}\end{array}\right\}\end{array}$$
• Step 2. Compute the score values $S\left(r_i\right)\left(i=1,2,\cdots ,5\right)$ of the overall DHq-ROFNs $r_i\left(i=1,2,\cdots ,5\right)$

  $$\begin{array}{l}S\left(r_1\right)=0.5378,S\left(r_2\right)=0.5451,S\left(r_3\right)=0.6499,\\ S\left(r_4\right)=0.5322,S\left(r_5\right)=0.5497\end{array}$$
• Step 3. Determine the ordering of all the construction projects $A_i\left(i=1,2,3,4,5\right)$ with respect to the score values $S\left(r_i\right)\left(i=1,2,\cdots ,5\right)$, then we can derive: $A_3\succ A_5\succ A_2\succ A_1\succ A_4,$ and the best construction project is $A_3$.

Based on the DHq-ROFHWG operator, the decision-making steps can be depicted as.

• Step 1. Based on the decision-making information given in the Table 2, We shall utilize the DHq-ROFHWG operator to derive the overall preference values $r_i$ of the construction projects $A_i\left(i=1,2,3,4,5\right)$ (let $\gamma =3,q=3$):

  $$\begin{array}{ll}{r}_1& =\text{DHq-ROFHWG}\left(r_{11},r_{12},r_{13},r_{14}\right)=\underset{j=1}{\overset{4}{\otimes }}{\left(r_{1j}\right)}^{w_j}\\ & =\left\{\left\{\begin{array}{l}0.1532,0.1903,0.1577,0.1956,0.1727,0.2128,0.1776,0.2183,\\ 0.1653,0.2043,0.1700,0.2097,0.1859,0.2275,0.1911,0.2332\end{array}\right\},\left\{\begin{array}{l}0.5506,\\ 0.5614\end{array}\right\}\right\}\\ r_2& =\text{DHq-ROFHWG}\left(r_{21},r_{22},r_{23},r_{24}\right)=\underset{j=1}{\overset{4}{\otimes }}{\left(r_{2j}\right)}^{w_j}\\ & =\left\{\left\{0.0997,0.1382,0.1670\right\},\left\{0.2772,0.2815,0.2868,0.2908,0.3561,0.3588\right\}\right\}\\ r_3& =\text{DHq-ROFHWG}\left(r_{31},r_{32},r_{33},r_{34}\right)=\underset{j=1}{\overset{4}{\otimes }}{\left(r_{3j}\right)}^{w_j}\\ & =\left\{\begin{array}{l}\left\{\begin{array}{l}0.2837,0.2904,0.2976,0.2895,0.2961,0.3032,0.2952,0.3016,0.3085,\\ 0.3216,0.3281,0.3351,0.3271,0.3333,0.3400,0.3324,0.3384,0.3449\end{array}\right\},\\ \left\{0.2432,0.3919\right\}\end{array}\right\}\\ r_4& =\text{DHq-ROFHWG}\left(r_{41},r_{42},r_{43},r_{44}\right)=\underset{j=1}{\overset{4}{\otimes }}{\left(r_{4j}\right)}^{w_j}\\ & =\left\{\left\{0.1622,0.1730,0.1860,0.1978,0.2081,0.2206\right\},\left\{0.3664,0.3860,0.4114\right\}\right\}\\ r_5& =\text{DHq-ROFHWG}\left(r_{51},r_{52},r_{53},r_{54}\right)=\underset{j=1}{\overset{4}{\otimes }}{\left(r_{5j}\right)}^{w_j}\\ & =\left\{\begin{array}{l}\left\{\begin{array}{l}0.1678,0.1841,0.1903,0.1725,0.1892,0.1956,0.1885,0.2061,0.2128,\\ 0.1937,0.2116,0.2183,0.2098,0.2284,0.2354,0.2154,0.2342,0.2412,\\ 0.1807,0.1978,0.2043,0.1857,0.2031,0.2097,0.2025,0.2206,0.2275,\\ 0.2079,0.2263,0.2332,0.2246,0.2435,0.2505,0.2304,0.2493,0.2564\end{array}\right\},\\ \left\{0.4475\right\}\end{array}\right\}\end{array}$$
• Step 2. Compute the score values $S\left(r_i\right)\left(i=1,2,\cdots ,5\right)$ of the overall DHq-ROFNs $r_i\left(i=1,2,\cdots ,5\right)$:

  $$\begin{array}{l}S\left(r_1\right)=0.4177,S\left(r_2\right)=0.4861,S\left(r_3\right)=0.4971,\\ S\left(r_4\right)=0.4742,S\left(r_5\right)=0.4601\end{array}$$
• Step 3. Determine the ordering of all the construction projects $A_i\left(i=1,2,3,4,5\right)$ with respect to the score values $S\left(r_i\right)\left(i=1,2,\cdots ,5\right)$, then we can derive: $A_3\succ A_2\succ A_4\succ A_5\succ A_1,$ and the best construction project is $A_3$.

5.2. Influence of the Parameter on the Final Result

In order to depict the effects on the ordering results by altering parameters of $\gamma$ and $q$ in the DHq-ROFHWA (DHq-ROFHWG) operators, all the results are list in

Table 3. Ordering results by altering $\gamma$ in the DHq-ROFHWA operator.

Alternatives	s(A1)	s(A2)	s(A3)	s(A4)	s(A5)	Ordering
$\gamma =1$	0.5072	0.5512	0.6523	0.5144	0.5291	$A_3\succ A_2\succ A_5\succ A_4\succ A_1$
$\gamma =2$	0.5271	0.5481	0.6512	0.5271	0.5438	$A_3\succ A_2\succ A_5\succ A_4\succ A_1$
$\gamma =3$	0.5378	0.5451	0.6499	0.5322	0.5497	$A_3\succ A_5\succ A_2\succ A_1\succ A_4$
$\gamma =4$	0.5405	0.5422	0.6482	0.5335	0.5509	$A_3\succ A_5\succ A_2\succ A_1\succ A_4$
$\gamma =6$	0.5414	0.5376	0.6456	0.5340	0.5509	$A_3\succ A_5\succ A_1\succ A_2\succ A_4$
$\gamma =10$	0.5408	0.5321	0.6428	0.5339	0.5500	$A_3\succ A_5\succ A_1\succ A_4\succ A_2$

and

Table 4. Ordering results by altering $\gamma$ in the DHq-ROFHWG operator.

Alternatives	s(A1)	s(A2)	s(A3)	s(A4)	s(A5)	Ordering
$\gamma =1$	0.4344	0.4944	0.6062	0.5019	0.4936	$A_3\succ A_4\succ A_2\succ A_5\succ A_1$
$\gamma =2$	0.4213	0.4886	0.5318	0.4821	0.4695	$A_3\succ A_2\succ A_4\succ A_5\succ A_1$
$\gamma =3$	0.4177	0.4861	0.4971	0.4742	0.4601	$A_3\succ A_2\succ A_4\succ A_5\succ A_1$
$\gamma =4$	0.4191	0.4856	0.4878	0.4724	0.4585	$A_3\succ A_2\succ A_4\succ A_5\succ A_1$
$\gamma =6$	0.4212	0.4856	0.4848	0.4719	0.4585	$A_2\succ A_3\succ A_4\succ A_5\succ A_1$
$\gamma =10$	0.4232	0.4858	0.4838	0.4719	0.4590	$A_2\succ A_3\succ A_4\succ A_5\succ A_1$

.

Based on the calculated results listed in Table 3 and Table 4, the rank of all alternatives is slightly different with different parameters $\gamma$ in DHq-ROFHWA and DHq-ROFHWG operators. According to the comparative analysis, when the parameter $\gamma$ becomes larger, the fused results by DHq-ROFHWA and DHq-ROFHWG operators become smaller, at the same time, the fused results become more and more steady.

In order to depict the effects on the ordering results by altering parameters of $q$ in the DHq-ROFHWA (DHq-ROFHWG) operators, all the results are list in

Table 5. Ordering results by altering $q$ in the DHq-ROFHWA operator.

Alternatives	s(A1)	s(A2)	s(A3)	s(A4)	s(A5)	Ordering
$q=1$	0.6104	0.6145	0.7666	0.6187	0.6374	$A_3\succ A_5\succ A_4\succ A_2\succ A_1$
$q=2$	0.5702	0.5705	0.7123	0.5680	0.5898	$A_3\succ A_5\succ A_2\succ A_1\succ A_4$
$q=3$	0.5378	0.5451	0.6499	0.5322	0.5497	$A_3\succ A_5\succ A_2\succ A_1\succ A_4$
$q=4$	0.5194	0.5317	0.6063	0.5145	0.5267	$A_3\succ A_2\succ A_5\succ A_1\succ A_4$
$q=6$	0.5050	0.5182	0.5588	0.5029	0.5079	$A_3\succ A_2\succ A_5\succ A_1\succ A_4$
$q=10$	0.5004	0.5073	0.5259	0.5001	0.5008	$A_3\succ A_2\succ A_5\succ A_1\succ A_4$

and

Table 6. Ordering results by altering $q$ in the DHq-ROFHWG operator.

Alternatives	s(A1)	s(A2)	s(A3)	s(A4)	s(A5)	Ordering
$q=1$	0.3438	0.4319	0.5166	0.4087	0.3982	$A_3\succ A_2\succ A_4\succ A_5\succ A_1$
$q=2$	0.3810	0.4682	0.5018	0.4472	0.4320	$A_3\succ A_2\succ A_4\succ A_5\succ A_1$
$q=3$	0.4177	0.4861	0.4971	0.4742	0.4601	$A_3\succ A_2\succ A_4\succ A_5\succ A_1$
$q=4$	0.4428	0.4938	0.4971	0.4879	0.4767	$A_3\succ A_2\succ A_4\succ A_5\succ A_1$
$q=6$	0.4709	0.4985	0.4988	0.4973	0.4912	$A_3\succ A_2\succ A_4\succ A_5\succ A_1$
$q=10$	0.4910	0.4999	0.4999	0.4998	0.4982	$A_3\succ A_2\succ A_4\succ A_5\succ A_1$

.

Based on the calculated results listed in Table 5 and Table 6, the rank of all alternatives is slightly different with different parameters $q$ in DHq-ROFHWA and DHq-ROFHWG operators. According to the comparative analysis for DHq-ROFHWA operator, when the parameter $q$ becomes larger, the fused results by DHq-ROFHWA operator become smaller, at the same time, the fused results become more and more steady. For DHq-ROFHWG operator, except for s(A₂), when the parameter $q$ becomes larger, the fused results by DHq-ROFHWG operator become larger, at the same time, the fused results become more and more steady.

5.3. Comparative Analysis

In this part, we shall compare our defined dual hesitant q-rung orthopair fuzzy Hamacher aggregation operators with other existing information fusion methods such as the q-ROFWA operator and the q-ROFWG operator developed by Liu and Wang [57] and the dual hesitant Pythagorean fuzzy Hamacher aggregation operators proposed by Xu and Wei [56]. From the below analysis, we can easily obtain that our proposed methods are more flexible and reasonable in the applications of MADM problems.

(1)

Compared our proposed methods with the information fusion operators presented by Liu and Wang [57], our defined operators are mainly characteristic of the advantages that can take the interrelationship between the being fused arguments into consideration and scientifically consider the human’s hesitance in practical MADM problems, whereas the q-ROFWA and q-ROFWG operators developed by Liu and Wang [57] have the limitation of considering the interrelationship between being fused arguments and cannot think about the hesitance of decision-maker. Thus, it is obvious that our methods are more general to express fuzzy information. Our method can conquer the disadvantages of two aggregation operators developed by Liu and Wang [57], because the DHq-ROFHWA and DHq-ROFHWG operators can provides more effective and flexible information fusion and make it more adequate to deal with MADM problems in which the attributes are dependent. Based on the above mentioned comparisons and analysis, the DHq-ROFHWA and DHq-ROFHWG operators we developed are better than the two aggregation operators developed by Liu and Wang [57] for fusing the dual hesitant q-rung orthopair fuzzy information. Therefore, the DHq-ROFHWA and DHq-ROFHWG operators are more valid to handle multiple attribute decision-making under dual hesitant q-rung orthopair fuzzy environment.

(2)

Compared our proposed methods with the dual hesitant Pythagorean fuzzy Hamacher operators presented by Xu and Wei [56], if we let the parameter $q=2$, it is clear that dual hesitant Pythagorean fuzzy Hamacher operators presented by Xu and Wei [56] are special cases of our methods. Evidently, our methods can express more fuzzy information and apply broadly situations in real MADM problems. Furthermore, in complicated decision-making environment, the decision-maker’s risk attitude is an important factor to think about, our methods can make this come true by altering the parameter’s $q$, whereas dual hesitant Pythagorean fuzzy Hamacher operators presented by Xu and Wei [56] do not have the ability that dynamic adjust to the parameter based on the decision-maker’s risk attitude, thus, it is difficult to deal with the risk multiple attribute decision-making (MADM) in real practice.

6. Conclusions

Based on the Hamacher operation laws, we utilize the Hamacher weighting average (HWA) operator and Hamacher weighting geometric (HWG) operator to develop some DHq-ROFHWA and DHq-ROFHWG aggregation operators with DHq-ROFNs: the dual hesitant q-rung orthopair fuzzy Hamacher weighting average (DHq-ROFHWA) operator, the dual hesitant q-rung orthopair fuzzy Hamacher weighting geometric (DHq-ROFHWG) operator, the dual hesitant q-rung orthopair fuzzy Hamacher ordered weighted average (DHq-ROFHOWA) operator, the dual hesitant q-rung orthopair fuzzy Hamacher ordered weighting geometric (DHq-ROFHOWG) operator, the dual hesitant q-rung orthopair fuzzy Hamacher hybrid average (DHq-ROFHHA) operator, and the dual hesitant q-rung orthopair fuzzy Hamacher hybrid geometric (DHq-ROFHHG) operator. Of course, the precious merits and some special cases of these defined operators are investigated. In the end, we take a concrete example for appraising the construction scheme selection to demonstrate our defined model and to testify its accuracy and scientific. It is clear that our defined operators can consider human’s hesitance and the interrelationship between being fused arguments, in addition, the newly developed methods also can dynamic adjust to the parameter based on the decision-maker’s risk attitude. However, the limitation of our approach is that the calculation formula is too complicated, thus, in future we will continue to study MADM problems and propose some simplified operators to other decision-making fields [69,70,71,72,73,74]. Furthermore, the application of the proposed methods in addressing practical MADM problems in other manufacturing environment, such as selection of an automated inspection system, selection of an industrial robot, selection of an additive manufacturing process and selection of a machine tool and will also be studied in our future work.