Abstract
The fuzzy linguistic approach provides favorable outputs in several areas, whose description is relatively qualitative. The encouragement for the utilization of sentences or words instead of numbers is that linguistic characterizations or classifications are usually less absolute than algebraic or arithmetical ones. In this research article, we animate the m-polar fuzzy (mF) linguistic approach and elaborate it with real life examples and tabular representation to develop the affluence of linguistic variables based on mF approach. As an extension of the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method, we develop an m-polar fuzzy linguistic TOPSIS approach for multi-criteria group decision-making (MCGDM). It is used to evaluate the best alternative, to get more authentic and comparable results and to handle the real life problems of having multi-polar information in terms of linguistic variables and values. In this approach decision-makers contribute their estimations in the form of linguistic term sets. To show the efficiency and compatibility of the proposed approach, we compare it with the m-polar fuzzy linguistic ELECTRE-I (Elimination and Choice Translating Reality) approach. Finally, we draw a flow chart of our proposed approach as an algorithm and generate a computer programming code.
1. Introduction
Problems that are related to uncertain conditions usually exist in decision-making, but are demanding because of the challenging situation of modeling and handling that comes with such uncertainties. A number of theories and mechanisms have been used to overcome these problems, such as probability, however, in several ways uncertainty is not probabilistic in description but rather relatively vague. Thus, other theories, such as the fuzzy set theory and fuzzy logic [1,2] have been applied to deal with immature, imprecise and vague information. Nonetheless, to hold such a vagueness and imprecision, where two or more roots of imprecision occur together, the modeling mechanisms of traditional fuzzy sets are finite. Due to it, several extensions and generalizations of fuzzy sets have been proposed, including intuitionistic fuzzy sets (IFSs) [3], hesitant fuzzy sets (HFSs) [4,5], bipolar fuzzy sets (BFSs) [6] and m-polar fuzzy sets (mF sets) [7].
In typical decision-making problems, such as selecting a place to visit, deciding which candidate is suitable for election or choosing the best car to buy, Chen et al. [7] introduced the approach of mF sets, which is the generalization of BFSs, in which they state that BFSs or 2-polar fuzzy sets are cryptomorphic mathematical approaches. The basic concept regarding this approach is that multipolar knowledge (not only bipolar knowledge, which coincides with two-valued logic) occurs because facts and knowledge for real world problems are sometimes from n agents . This new idea motivated researchers to introduce several novel concepts related to mF sets and its hybrid models, such as Akram et al. [8], who proposed a new multi-criteria decision-making MCDM method based on mF soft rough sets by combining the mF soft sets with rough sets. Akram and Adeel [9] introduced novel hybrid decision-making methods based on mF rough information. Further, Akram et al. [10] worked on decision-making methods based on hybrid mF models. Furthermore, Akram [11] introduced many new concepts including mF graphs, mF line graphs, mF labeling graphs and certain metrics in mF graphs.
The foregoing fuzzy mechanisms are favorable for the problems discussed in quantitative directions, but these mechanisms are not favorable for the problems having relatively qualitative description, in which ambiguity is due to the uncertain conditions approved by decision-makers. For such a situation, Zadeh [12,13,14] introduced the fuzzy linguistic approach which provided favorable outputs in several areas and applications [15]. In group decision analysis a number of researchers motivated by the concept of linguistic variables, such as Herrera et al. [16] introduced a fusion approach for managing multi-granularity linguistic term sets in decision-making. Meng et al. [17] proposed the multi-attribute decision analysis under a linguistic hesitant fuzzy environment. By group decision-making, Wang et al. [18] evaluated the flexibility in a manufacturing system by using a fuzzy linguistic approach. Liu and Su [19] extended the TOPSIS method based on trapezoid fuzzy linguistic variables. Selvachandran and Salleh [20] proposed the concept of intuitionistic fuzzy hedges and intuitionistic fuzzy linguistic variables. Liao et al. [21] discussed the distance and similarity measures for hesitant fuzzy linguistic term sets and their application in MCDM. Later, Riera et al. [22] introduced some interesting properties of the fuzzy linguistic model based on discrete fuzzy numbers to manage hesitant fuzzy linguistic information. Rodriguez [23] worked with a view to overcome such limitations, taking into account the idea under the concept of HFSs, to deal with several values in a membership function having quantitative setting.
In real-world systems, sometimes we obverse the activities and tasks, in which it is compulsory to adopt decision-making mechanisms. Usually, decision-making is a intellectual measure that depends on distinct reasoning and spiritual processes that leads one to choose the suitable alternative from a set of feasible alternatives in the resolution condition. Nowadays, in linguistic decision-making (LDM), the hesitant fuzzy linguistic term sets (HFLTSs) are considered as a focal point in decision-making methods. In several subjective decision environments, decision-makers assume certain feasible criteria’s or linguistic values more than an individual term for an alternative or variable. In actual decision-making methods, rather than the existing ones constituted to distinct aspects, the TOPSIS method proposed in [24] is an effective, favorable and widely used multi-criteria group decision-making (MCGDM) method. Precisely the method of TOPSIS derives from the perception that the selected alternative should have the precised distance from the positive ideal solution and the extreme distance from the negative ideal solution. Since then, several extended TOPSIS methods have been applied to different MCDM problems including [25,26,27]. Further, Alghamdi et al. [28] introduced the multi-criteria decision-making methods in the bipolar fuzzy environment. Chu and Lin [29] used the fuzzy TOPSIS method for the selection of robots. Nadaban et al. [30] discussed a general view on fuzzy TOPSIS. Yue [31] proposed a method for group decision-making based on determining weights of decision-makers using TOPSIS. By considering the triangular fuzzy numbers and defining the crisp Euclidean distance between two fuzzy numbers, Chen [32] introduced an extended TOPSIS method for MCDM. Roszkowska [33] proposed the MCDM models by applying the TOPSIS method to crisp and interval data. Further, Roszkowska and Wachowicz [34] applied the fuzzy TOPSIS method to score the negotiation offers in ill-structured negotiation problems. Ren et al. [35] developed a new hesitant fuzzy (HF) linguistic TOPSIS method for group multi-criteria linguistic decision-making. Ashtiani et al. [36] extended the fuzzy TOPSIS method based on interval-valued fuzzy sets. Beg and Rashid [37] introduced TOPSIS for hesitant fuzzy linguistic term sets. Boran et al. [38] proposed the multi-criteria intuitionistic fuzzy group decision-making for supplier selection with the TOPSIS method. Chu [39] discussed the selection of facility location using fuzzy TOPSIS under group decisions. Wang [40] extended the hesitant fuzzy linguistic term sets and their aggregation in group decision-making.
The field of linguistic multi-criteria decision-analysis is a significant and fascinating scientific area. Therefore, it is interesting to know about fuzzy multi-criteria decision methods other than TOPSIS. Currently the existing MCDM methods yield results that may be questionable and unreliable. These methods very often ignore the issue of rank reversal paradox, which is a fundamental and essential challenge of MCDM methods. In response to this challenge, the Characteristic Objects Method (COMET) was developed. The classical COMET is entirely free of the rank reversal paradox. Several researchers explored and discussed MCDM methods based on COMET including [41,42,43]. For other concepts, terminologies, applications and MCDM methods, the readers are referred to [44,45,46,47,48,49,50,51,52,53,54,55].
The methods proposed in the above cited articles are unable to provide any information, when the given data is in the form of sentences and words with m different numeric and fuzzy values within its crisp domain. Traditional methods are ineffective to study this type of imprecise behavior of linguistic computations and assessments. To deal with such a complexity, Akram et al. [56] proposed the concept of the m-polar fuzzy linguistic variable (mFLV) and to apply it on the mF linguistic ELECTRE-I approach. In this research article, we elaborate the concept of mFLV with graphical representation for an easy understanding and propose the novel approach of mF linguistic TOPSIS to solve the MCGDM problems. We define such a decision-making technique to increase the affluence of linguistic variables based on the mF approach and to choose the best alternative without ranking the relation of the remaining alternatives. The novelty of the proposed approach is proven as it is used to get more authentic and comparable results when we have to evaluate the alternatives being having multi-polar information in terms of linguistic variables and its values. In other words, we can say it is used to deal with the problems and systems with more than one argument. The proposed approach is more compatible as compared to various extensions of TOPSIS and several other MCGDM methods, because in this method a variable and its linguistic values are considered as a fixed criteria for the ranking and evaluation of alternatives. All the linguistic values are further classified by m different numeric and fuzzy values, which provide more accurate and compatible results as compared to other MCGDM methods. For its justification and authentication, we compare our proposed method with an other MCGDM techniques. This approach is valid to resolve the MCGDM problems in every day decision science.
The organization of this research article is as follows: In Section 2, we review some basic concepts and elaborate our novel concept with real life examples. In Section 3, we describe an mF linguistic TOPSIS approach for MCGDM. We also present our proposed method in a flow chart and generate its computer programming code. In Section 3.1 and Section 3.2, we apply our proposed approach to real life examples. In Section 4, we study comparison analysis of the proposed approach. In Section 5, we present the conclusion.
2. -Polar Fuzzy Linguistic Variable
In this section, we review some basic concepts and elaborate the concept of an mFLV with practical examples and graphical representation. In terms of this variable, a linguistic value such as ‘extremely young’ is characterized by m different characterizations and classifications, which shows the mF restrictions on the values of the base variable. These mF restrictions clearly explain the meaning of term ‘extremely young’.
Definition 1
([7]). An mF set on a universe X is a function where the projection mapping is defined as is the smallest element in and is the largest element in
Definition 2
([12]). A linguistic variable is a variable, whose values are sentences or words in an artificial or natural language. If these words are expressed by fuzzy sets defined over a universal set, then the variable is called a fuzzy linguistic variable.
Definition 3
([56]). An mFLV is characterized by a tuple such that
- a.
- is the name of an mFLV,
- b.
- V is the set of linguistic values of ,
- c.
- is the physical domain in which an mFLV takes its crisp values,
- d.
- M is the semantic rule that relates every linguistic value in V with mF set.
Remark 1.
- 1.
- The linguistic variable () is called an mFLV since its linguistic values are further classified by m different characteristics.
- 2.
- mFLV takes its crisp values from the physical domain () and can be arranged in parts for linguistic values according to the given requirements.
- 3.
- M is called semantic rule, that differs the mFLV from previously defined linguistic variables. The rule relates the linguistic values of mFLV within the mF set, which shows that each linguistic value is further classified by m different characteristics, and the degree of linguistic values is defined byIt clearly shows m different characterizations of each linguistic value. For more details and clarifications about an mF set and its degree of memberships the readers are referred to [7].
We discuss the contribution of mFLV in real life as follows:
Example 1.

Consider a linguistic variable “age" that describes its different stages by a set , which is the set of linguistic values of “age", where
- “EY" stands for extremely young,
- “Y" stands for young,
- “O" stands for old,
- “EO" stands for extremely old.
The physical domain for the linguistic variable is , which is the set of real non-negative numbers, and each linguistic value has a different range of physical domain given as follows
- For extremely young age, the physical domain is 1–20,
- For young age, the physical domain is 20–50,
- For old age, the physical domain is 50–80,
- For extremely old age, the physical domain is 80–100.
We call this linguistic variable a 4-polar fuzzy linguistic variable (4FLV), because we describe a semantic rule M which describes each linguistic value in set V with a 4-polar fuzzy set (4F set). According to the 4F set, each linguistic value is characterized as
- serves as “Physically energetic", it describes someone who has lots of get-up-and-go depending upon his physical health and requires that the person is active enough with enthusiasm and excitement to do a task.
- serves as “Mental health", it means being generally able to think, feel and react in the ways that someone needs and wants to live his life.
- serves as “Ability", it is an acquired or natural capacity or talent that enables an individual to perform a particular job or task successfully.
- serves as “Effort", it is an earnest or strenuous attempt to achieve a specified purpose.
where Thus, we have
In terms of the linguistic variable (age), the linguistic value such as extremely young is characterized by four different specifications including physically energetic, mental difficulty, ability and effort which show the 4F restrictions on the linguistic values of base variable. These 4F restrictions show the different states considered for linguistic values to evaluate the base variable in terms of the 4F set, which clearly describe the meaning of linguistic value “extremely young age" and remaining linguistic values. Thus, age is called a 4F linguistic variable by Definition 3. The tabular representation of 4FLV “age" is described by Table 1, which shows the range of each linguistic value in terms of the 4F set.

Table 1.
Tabular representation of 4FLV (age).
The tabular representation clearly shows the range of each linguistic value in terms of the 4F set and shows how each 4F set is related with the physical domain . It simply defines the meaning of a 4F linguistic variable, which shows that the 4F linguistic variable (age) has four linguistic values, which have specified physical domains according to their limits. Each linguistic value is further classified by four different specifications according to the states of the linguistic values.
From Table 1, in extremely young age the range of the physical domain is from 1 to 20 and each physical domain is associated with specific values of a 4F set. For example, the physical domain value “10” is associated with the tuple which describes that a person who compared to others is considered extremely young at the age of 10 may have the following specifications:
- The membership value 0.39 shows that an extremely young person at the age of 10 is physically energetic.
- The membership value 0.60 shows that the mental health of an extremely young person at the age of 10 is .
- The membership value 0.56 shows that the ability of an extremely young person to do a task successfully at the age of 10 is .
- The membership value 0.60 shows that the effort of an extremely young person to achieve a specified purpose at the age of 10 is .
Now, we analyze and describe the MCGDM phenomenon which is concerned on the theory that we already have expressed. MCGDM is a measure in which a number of decision-makers have to choose the best alternative from a set of possible alternatives which are described in terms of the criteria’s situation, and MCDM is a specific case of MCGDM in which a single decision-maker is responsible to choose the best alternative. Therefore, we define the respective algorithm and generate a computer programming code for required problems which are described by mFLV. To prove their significance and efficiency, we apply the TOPSIS method to situations which are fully developed. TOPSIS is a technique to select the alternative that should have the shortest distance from the positive ideal solution (PIS) and the largest distance from the negative ideal solution (NIS). This technique is actually used for ranking the objects and to achieve the best performance in MCGDM. We expand this method to take the information relating to mFLV. An mF linguistic TOPSIS approach deals with MCGDM problems based on mFLV.
3. F Linguistic TOPSIS Approach for MCGDM
Our proposed TOPSIS approach based on mFLV deals with MCGDM problems, in which we choose an mFLV and , the set of mFLV of different alternatives. According to an mFLV, we take the set of linguistic values of , where these linguistic values are classified by m different characteristics. In such a case, a group of r decision-makers () is responsible for evaluating mFLV of p different alternatives under q linguistic values and the suitable ratings of alternatives are according to all decision-makers, assessed in terms of m different characteristics under the physical domain . The degree of each alternative () over all linguistic values are given by the mF set where and classify the different characteristics of each criteria by decision-makers. is the actual physical domain in which the mFLV takes its quantitative (crisp) values, i.e., In this case, we take the most suitable m values from the physical domain of each linguistic value. Tabular representation of mF linguistic decision matrix under each group of decision-makers is given by Table 2, which describes the ratings given by each decision-maker.

Table 2.
Tabular representation of the mF linguistic decision matrix under group decision-making.
Table 2 shows the different ratings of linguistic values assigned by a group of r decision-makers, in which each decision-maker assigns ratings according to his choice. The final mF linguistic decision matrix under each group of decision-makers is the aggregated mF linguistic decision matrix, that is, the average ratings of all decision-makers. Aggregated ratings are calculated as follows:
For final decision and ratings, the aggregated mF linguistic decision matrix is calculated in Table 3 by using above average ratings.

Table 3.
Tabular representation of aggregated mF linguistic decision matrix.
Decision-makers have an authority to assign weights to each linguistic value of alternatives according to their choice and the importance of each linguistic value, but we are discussing the case of mFLV, so decision-makers have to assign the weights in terms of the linguistic term set . We suppose that the weights assigned by the decision-makers are
Weights assigned by the decision-makers satisfy the normalized condition, i.e.,
Aggregated weights according to decision-makers are where,
The weighted aggregated mF linguistic decision matrix under group decision-making is calculated as
The mF linguistic positive ideal solution and the mF linguistic negative ideal solution of alternatives under mF environment can be calculated as given in Equations (1) and (2).
where,
We define an mF linguistic Euclidean distance of each alternative from and by Equations (3) and (4).
The relative mF linguistic closeness coefficient of each alternative can be computed by using the following formula as described in Equation (5).
The alternative with the highest mF linguistic closeness coefficient is the best one and we can determine the ranking order of each alternative.
We present the flow chart of our proposed method of decision-making in Figure 1 as an algorithm.
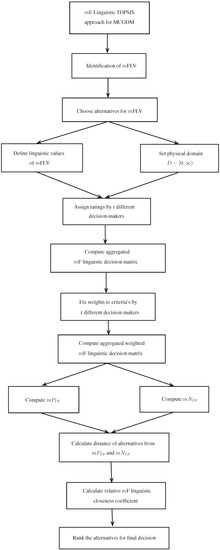
Figure 1.
Flow chart of mF linguistic Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) for multi-criteria group decision-making (MCGDM).
3.1. Models Ranking According to Their Appearance
Finally, in Appendix A we show the computer programming code of proposed approach in Table A1 by using MATLAB (Version: R2014a, Manufacturer: Cleve Moler, Developer: MathWorks, Country: United States of America, Platform: IA-32, x86-64). Evaluating different personalities based on their physical appearance is a challenging task for decision-makers, especially when a group of decision-makers have to evaluate them. We propose the method of mF linguistic TOPSIS for MCGDM, in which is the linguistic variable, i.e., appearance and is the set of appearance of five different models, whereas is the set of linguistic values of appearance. Decision-makers have to evaluate the models on the basis of the linguistic values of their appearance and they have to design a physical domain in which appearance takes its quantitative values, i.e., The physical domain for linguistic values of appearance is given as follows:
- For Less attractive appearance, thephysical domain is 10–40/100,
- For Fairly cute appearance, the physical domain is 40–70/100,
- For Quite pretty appearance, the physical domain is 70–90/100,
- For Very beautiful appearance, the physical domain is 90–100/100.
The physical domain of each linguistic value shows the range of marks given by a group of decision-makers out of The degree of appearance of each model, over all the linguistic values are given by 3F set where
- serves for “face features”, the distinguishing elements of a face having attraction, such as beautiful eyes, sharp nose and shaped lips.
- serves for “postures”, a way according to which someone arranges his limbs and positions his body.
- serves for “body figure”, it is the cumulative product of someone’s skeletal structure, the distribution and quantity of muscle and fat on his body.
Where , and A tabular representation of the 3F linguistic group decision matrix is given by Table 4. It shows the different ratings of linguistic values assigned by a group of four decision-makers, in which each decision-maker assigns ratings according to his choice.

Table 4.
Tabular representation of the 3F linguistic group decision matrix.
For final decision and ratings, an aggregated 3F linguistic decision matrix is calculated in Table 5.

Table 5.
Tabular representation of the aggregated 3F linguistic decision matrix.
The weights of linguistic values completely depend upon the decision-makers and the weights of each decision-maker has its own importance. Weights assigned by decision-makers are given in terms of the linguistic term set as , whereas the numerical values assigned to this linguistic term set by each decision-maker is given in Table 6 and these values that satisfy the normalized condition. In same Table, aggregated weights are also calculated.

Table 6.
Tabular representation of weights assigned by decision-makers.
The weighted aggregated 3F linguistic decision matrix is calculated in Table 7.

Table 7.
Tabular representation of weighted aggregated 3F linguistic decision matrix.
Use Equations (3) and (4) to calculate the 3F linguistic Euclidean distance of appearance of each model from its and , that are calculated as follows:
Use Equation (5) to calculate the relative 3F linguistic closeness coefficients of appearance of each model.
We show the comparison of appearance of models and summarize the whole procedure in Table 8.

Table 8.
Tabular representation comparison of appearance of models.
For the comparison, we arrange the 3F linguistic closeness coefficients of appearance of models { as shown in Table 8. Hence, model has the highest ranking according to her appearance and the ranking of appearance of models is as follows:
3.2. Ranking of High Speed Racing Cars
In this subsection, we discuss the specific case of MCGDM in which only one decision-maker is responsible for choosing the ratings of alternatives according to linguistic values. Choosing and comparing high speed racing cars for different racing competitions is a difficult task for experts. So, in this case we choose “speed” as a linguistic variable and is the set of six different high speed racing cars, whereas is the set of linguistic values of speed. is the actual physical domain in which speed takes its quantitative values, i.e., The physical domain for linguistic values of speed is given as follows:
- For slightly fast speed, the physical domain is 40–60 km/h,
- For very fast speed, the physical domain is 60–80 km/h,
- For completely fast speed, the physical domain is 80–100 km/h.
The degree of speed of each car over all the linguistic values is given by 4F set where
- serves for “power of engine”, it is the producer of the power to move the vehicle. Basically it is the rate at which work is done and the car moves.
- serves for “quality of tire”, it totally depends upon the speed ratings, tread wear warranty and typical wheel size.
- serves for “condition of car”, it describes the model specifications, history and outside look of a car.
- serves for “shape of car”, it describes the cars having straight line speed including the front splitter, rear wing, diffuser and underbody of the car.
Where , and . The tabular representation of 4F linguistic decision matrix is given by Table 9.

Table 9.
Tabular representation of the 4F linguistic decision matrix.
The weights of linguistic values completely depend upon the decision-maker. Weights assigned by the decision-maker are given in terms of linguistic term set as , whereas the numerical values assigned to this linguistic term set is given in Equation (6), and these values satisfy the normalized condition.
The weighted 4F linguistic decision matrix is calculated in Table 10.

Table 10.
Tabular representation of the weighted 4F linguistic decision matrix.
We use Equations (3) and (4) to calculate the 4F linguistic Euclidean distance of speed of each car from its and , which are calculated as follows:
We use Equation (5) to calculate the relative 4F linguistic closeness coefficients of speed of each car.
We show the comparison of cars according to their speed and summarize the whole procedure in Table 11.

Table 11.
Tabular representation comparison of cars according to their speed.
For comparison, we arrange the speed of cars { according to their values obtained from relative closeness coefficients as shown in Table 11. Hence, car has the highest ranking according to its speed and the ranking of cars according to their speed is as follows:
Note the followings points:
- The only condition for weights assigned by decision-makers is that the weights should be normalized. It is not compulsory to take four digits after the decimal point. Readers are free to take the weights according to their choice. We take four values after the decimal point for our convenience.
- Linguistic variables (appearance and speed) considered in this article can depend on other characteristics also according to the criterias or conditions set by readers.
4. Comparison Analysis of Proposed Approach
In this section, we discuss the comparison analysis of our purposed decision-making method by the mF linguistic ELECTRE-I method defined in [56].
- All the TOPSIS methods for decision-making are not suitable for such situations, where the alternatives are assessed by the decision-makers depending on the linguistic values of variables, which are further classified by m different characteristics. To handle such a complex situations we extend the TOPSIS approach to the mF linguistic TOPSIS approach, which provides more flexible and precise results for choosing the best alternative under complex fuzzy data. The proposed mF linguistic TOPSIS approach is constructed according to observation and recognition of the expertise idea about the linguistic variable and values of alternatives in form of words and sentences having multi-polar information. Its calculations are very simple, and it is also independent of the number of criterias associated in the problem. It provides us with the best alternative as well as the final ranking of alternatives.
- An mF linguistic ELECTRE-I method is also considered as a flexible approach as compared to various other extensions of ELECTRE-I, because in this method a variable and its linguistic values are considered as a fixed criteria for the ranking and evaluation of alternatives. This method only provides us with the best alternative of having a maximum ranking value, but it does not provide us with any authentic knowledge about the ranking of the alternative. This approach is difficult to understand and has large, difficult calculations compared to the mF linguistic TOPSIS approach. This approach does not point out the one alternative appearing amongst others, rather it points out the small subset of preferable alternatives, and due to this decision-makers face difficulties in choosing the best one and ranking the alternatives.
For comparison, we consider an example of the mF linguistic ELECTRE-I method (Subsection 4.1, [56]) where we consider C as the set of seven countries and V the set of its linguistic values. After large, difficult calculations as described in Table 12, we end up with the most corrupted country as compared to others.

Table 12.
Tabular representation of comparison of countries by using the mF linguistic ELECTRE-I method.
We show the comparison of countries and summarize the whole procedure of the mF linguistic ELECTRE-I method in Table 12.
From Table 12, we get the final result in the form of the most corrupted country, but we do not get the final ranking of all the required countries.
Now we calculate the same Example by using mF linguistic TOPSIS method as described in Section 3. We show the comparison of countries and summarize the whole procedure of the mF linguistic TOPSIS method in Table 13.

Table 13.
Tabular representation of comparison of countries by using the mF linguistic TOPSIS method.
From Table 13, we recognize the most corrupted country as well as the final ranking of all the required countries. There is no difference between the final results of both techniques in choosing the most corrupted country, but the mF linguistic TOPSIS method is more preferable compared to mF linguistic ELECTRE-I method due to its outranking relation of countries with simple and easy calculations.
5. Conclusions
It has always been a very challenging task for decision-makers to evaluate alternatives on the basis of numeric values. Traditional methods are determined ineffective in studying the imprecise behavior of linguistic computations and assessments, because it has become difficult to collect data regarding linguistic assessments in terms of numeric and fuzzy values. To deal with such complexities, we have elaborated the concept of mFLV defined in [56], which can deal with thiz situation when we have data in terms of linguistic assessments and m different numeric or fuzzy values as well. We have illustrated our novel concept with real life examples. In this contribution, we also have developed an mF linguistic TOPSIS approach for MCGDM problems as an extension of the TOPSIS method. Finally, we have applied our technique on real life problems and developed a computer programming code for ease of calculations. Our future work will aim to explore the real life applications related to concepts based on the neutrosophic linguistic variable, the fuzzy rough linguistic variable, and the rough fuzzy linguistic variable. Our proposed model may be extended in new directions including generalized fuzzy Euler graphs, generalized fuzzy Hamiltonian graphs and competitions by generalized fuzzy graphs based on [52,53].
Author Contributions
A.A., M.A. and A.N.A.K. conceived of the presented concept. A.A. and M.A. developed the theory and performed the computations. A.N.A.K. verified the analytical methods.
Funding
This research received no external funding.
Acknowledgments
The authors are grateful to the Editor of the Journal and anonymous referees for their valuable comments.
Conflicts of Interest
The authors declare that they have no conflict of interest regarding the publication of the research article.
Appendix A
We show the computer programming code of proposed approach in Table A1 by using MATLAB R2014a.

Table A1.
Computer programming code of proposed approach for MCGDM.
Table A1.
Computer programming code of proposed approach for MCGDM.
| MATLAB Computer Programming Code |
|---|
| 1. clc |
| 2. p=input(‘no. of alternatives against linguistic variable’); |
| 3. q=input(‘no.of linguistic values’); |
| 4. m=input(‘no. of membership values’); |
| 5. r=input(‘no. of decision maker’); |
| 6. Rr=(1:p);Cr=1:m*q;Cw=1:q;A_g=zeros(p,m*q);w_g=zeros(1,q); |
| 7. W=zeros(p,m*q);mP_IS=zeros(1,m*q);mN_IS=ones(1,m*q); |
| 8. Y1=zeros(p,m*q);Y2=zeros(p,m*q);Z1=zeros(p,q);Z2=zeros(p,q); |
| 9. for i=1:r |
| 10. D= input(‘enter the m-polar fuzzy linguistic decision matrix pxqxm’); |
| 11. A_g(Rr,Cr)=A_g(Rr,Cr)+D;w=input(‘enter the weights’);w_g(1,Cw)=w_g(1,Cw)+w; |
| 12. end |
| 13. A_g=A_g/r |
| 14. w=w_g/r |
| 15. for j=1:p |
| 16. k=1; |
| 17. for s=1:m*q |
| 18. W(j,s)=A_g(j,s).*w(1,k); |
| 19. if mod(s,m)==0 |
| 20. k=k+1; |
| 21. end |
| 22. end |
| 23. end |
| 24. W |
| 25. for j=1:p |
| 26. for s=1:(m*q) |
| 27. mP_IS(1,s)=max(mP_IS(1,s),W(j,s)); mN_IS(1,s)=min(mN_IS(1,s),W(j,s)); |
| 28. end |
| 29. end |
| 30. mP_IS |
| 31. mN_IS |
| 32. for j=1:p |
| 33. k=0; |
| 34. for s=1:m*q |
| 35. Y1(j,s)=(W(j,s)-mP_IS(1,s)). 2; Y2(j,s)=(W(j,s)-mN_IS(1,s)). 2; |
| 36. if mod(s,m)==1 |
| 37. k=k+1; |
| 38. end |
| 39. Z1(j,k)=Z1(j,k)+Y1(j,s);Z2(j,k)=Z2(j,k)+Y2(j,s); |
| 40. end |
| 41. end |
| 42. D_P=sqrt(sum(Z1,2)./m) |
| 43. D_N=sqrt(sum(Z2,2)./m) |
| 44. E=D_N./(D_P+D_N) |
References
- Dubois, D.; Prade, H. Fuzzy Sets and Systems: Theory and Applications; Kluwer: New York, NY, USA, 1980. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Torra, V.; Narukawa, Y. On hesitant fuzzy sets and decisions. In Proceedings of the IEEE International Conference on Fuzzy Systems, Jeju Island, Korea, 20–24 August 2009; pp. 1378–1382. [Google Scholar]
- Zhang, W.-R. Bipolar fuzzy sets and relations: A computational framework forcognitive modeling and multiagent decision analysis. In Proceedings of the First International Joint Conference of the North American Fuzzy Information Processing Society Biannual Conference, the Industrial Fuzzy Control and Intellige, San Antonio, TX, USA, 18–21 December 1994; pp. 305–309. [Google Scholar]
- Chen, J.; Li, S.; Ma, S.; Wang, X. m-polar fuzzy sets: An extension of bipolar fuzzy sets. Sci. World J. 2014, 2014, 416530. [Google Scholar] [CrossRef]
- Akram, M.; Ali, G.; Alshehri, N.O. A new multi-attribute decision-making method based on m-polar fuzzy soft rough sets. Symmetry 2017, 9, 271. [Google Scholar] [CrossRef]
- Akram, M.; Adeel, A. Novel hybrid decision-making methods based on mF rough information. Granul. Comput. 2018, 1–17. [Google Scholar] [CrossRef]
- Akram, M.; Ali, G.; Waseem, N.; Davvaz, B. Decision-making methods based on hybrid mF models. J. Intell. Fuzzy Syst. 2018. [Google Scholar] [CrossRef]
- Akram, M. m-Polar fuzzy graphs-theory, methods & applications. In Studies in Fuzziness and Soft Computing; Springer: Basel, Switzerland, 2019; Volume 371, pp. 1–284. ISBN 978-3-030-03750-5. [Google Scholar]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—II. Inf. Sci. 1975, 8, 301–357. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—III. Inf. Sci. 1975, 8, 43–80. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L.; Herrera, F. A group decision making model dealing with comparative linguistic expressions based on hesitant fuzzy linguistic term sets. Inf. Sci. 2013, 241, 28–42. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Martinez, L. A fusion approach for managing multi-granularity linguistic term sets in decision making. Fuzzy Sets Syst. 2000, 114, 43–58. [Google Scholar] [CrossRef]
- Meng, F.; Chen, X.; Zhang, Q. Multi-attribute decision analysis under a linguistic hesitant fuzzy environment. Inf. Sci. 2014, 267, 287–305. [Google Scholar] [CrossRef]
- Wang, R.C.; Chuu, S.J. Group decision-making using a fuzzy linguistic approach for evaluating the flexibility in a manufacturing system. Eur. J. Oper. Res. 2004, 154, 563–572. [Google Scholar] [CrossRef]
- Liu, P.D.; Su, Y. The extended TOPSIS based on trapezoid fuzzy linguistic variables. J. Converg. Inf. Technol. 2010, 5, 38–53. [Google Scholar]
- Selvachandran, G.; Salleh, A.R. Intuitionistic fuzzy linguistic variables and intuitionistic fuzzy hedges. Far East J. Math. Sci. 2014, 95, 221. [Google Scholar]
- Liao, H.C.; Xu, Z.S.; Zeng, X.J. Distance and similarity measures for hesitant fuzzy linguistic term sets and their application in multi-criteria decision-making. Inf. Sci. 2014, 271, 125–142. [Google Scholar] [CrossRef]
- Riera, J.V.; Massanet, S.; Herrera-Viedma, E.; Torrens, J. Some interesting properties of the fuzzy linguistic model based on discrete fuzzy numbers to manage hesitant fuzzy linguistic information. Appl. Soft Comput. 2015, 36, 383–391. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision-making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attributes Decision Making Methods and Applications; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Akram, M.; Shumaiza; Smarandache, F. Decision-making with bipolar neutrosophic topsis and bipolar neutrosophic ELECTRE-I. Axioms 2018, 7, 33. [Google Scholar] [CrossRef]
- Shih, H.; Shyur, H.; Lee, E. An extension of TOPSIS for group decision-making. Math. Comput. Model. 2007, 45, 801–813. [Google Scholar] [CrossRef]
- Wang, Y.J.; Lee, H.S. Generalizing TOPSIS for fuzzy multiple-criteria group decision-making. Comput. Math. Appl. 2007, 53, 1762–1772. [Google Scholar] [CrossRef]
- Alghamdi, M.A.; Alshehria, N.O.; Akram, M. Multi-criteria decision-making methods in bipolar fuzzy environment. Int. J. Fuzzy Syst. 2018, 20, 2057–2064. [Google Scholar] [CrossRef]
- Chu, T.-C.; Lin, Y.-C. A fuzzy TOPSIS method for robot selection. Int. J. Advanced Manuf. Technol. 2003, 21, 284–290. [Google Scholar] [CrossRef]
- Nadaban, S.; Simona, D.; Ioan, D. Fuzzy topsis: A general view. Procedia Comput. Sci. 2017, 9, 823–831. [Google Scholar]
- Yue, Z. A method for group decision-making based on determining weights of decision-makers using TOPSIS. Appl. Math. Model. 2001, 35, 1926–1936. [Google Scholar] [CrossRef]
- Chen, C.-T. Extension of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Roszkowska, E. Multi-criteria decision-making models by applying the TOPSIS method to crisp and interval data. Mult. Criteria Decis. Mak./Univ. Econ. Katow. 2011, 6, 200–230. [Google Scholar]
- Roszkowska, E.; Wachowicz, T. Application of fuzzy TOPSIS to scoring the negotiation offers in ill-structured negotiation problems. Eur. J. Oper. Res. 2015, 242, 920–932. [Google Scholar] [CrossRef]
- Ren, F.; Kong, M.; Pei, Z. A new hesitant fuzzy linguistic TOPSIS method for group multi-criteria linguistic decision-making. Symmetry 2017, 9, 289. [Google Scholar] [CrossRef]
- Ashtiani, B.; Haghighirad, F.; Makui, A.; Montazer, G. Extension of fuzzy TOPSIS method based on interval-valued fuzzy sets. Appl. Soft Comput. 2009, 9, 457–461. [Google Scholar] [CrossRef]
- Beg, I.; Rashid, T. TOPSIS for hesitant fuzzy linguistic term sets. Int. J. Intell. Syst. 2013, 28, 1162–1171. [Google Scholar] [CrossRef]
- Boran, F.E.; Gen, S.; Kurt, M.; Akay, D. A multi-criteria intuitionistic fuzzy group decision-making for supplier selection with TOPSIS method. Expert Syst. Appl. 2009, 36, 11363–11368. [Google Scholar] [CrossRef]
- Chu, T.C. Facility location selection using fuzzy TOPSIS under group decisions. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2002, 10, 687–701. [Google Scholar] [CrossRef]
- Wang, H. Extended hesitant fuzzy linguistic term sets and their aggregation in group decision-making. Int. J. Comput. Intell. Syst. 2015, 8, 14–33. [Google Scholar] [CrossRef]
- Faizi, S.; Salabun, W.; Rashid, T.; Watrobski, J.; Zafar, S. Group decision-making for hesitant fuzzy sets based on characteristic objects method. Symmetry 2017, 9, 136. [Google Scholar] [CrossRef]
- Piegat, A.; Salabun, W. Identification of a multi-criteria decision-making model using the characteristic objects method. Appl. Comput. Intell. Soft Comput. 2014, 2014, 536492. [Google Scholar] [CrossRef]
- Salabun, W. The characteristic objects method: A new distance-based approach to multi-criteria decision-making problems. J. Multi-Criteria Decis. Anal. 2015, 22, 37–50. [Google Scholar] [CrossRef]
- Adeel, A.; Akram, M.; Koam, A.N. Multi-criteria decision-making under mHF ELECTRE-I and HmF ELECTRE-I. Energies 2019, 12, 1661. [Google Scholar] [CrossRef]
- Akram, M.; Adeel, A. TOPSIS approach for MAGDM based on interval-valued hesitant fuzzy N-soft environment. Int. J. Fuzzy Syst. 2018, 1–17. [Google Scholar] [CrossRef]
- Akram, M.; Adeel, A.; Alcantud, J.C.R. Group decision-making methods based on hesitant N-soft sets. Expert Syst. Appl. 2019, 115, 95–105. [Google Scholar] [CrossRef]
- Akram, M.; Waseem, N.; Liu, P. Novel approach in decision-making with m-polar fuzzy ELECTRE-I. Int. J. Fuzzy Syst. 2018, 21, 1117–1129. [Google Scholar] [CrossRef]
- Akram, M.; Adeel, A.; Alcantud, J.C.R. Fuzzy N-soft sets: A novel model with applications. J. Intell. Fuzzy Syst. 2018, 35, 4757–4771. [Google Scholar] [CrossRef]
- Bollinger, D.; Pictet, J. Multiple criteria decision analysis of treatment and land-filling technologies for waste incineration residues. Omega 2008, 36, 418–428. [Google Scholar] [CrossRef]
- Chen, S.J.; Hwang, C.L. Fuzzy Multiple Attribute Decision-Making; Springer: Berlin, Germany, 1992. [Google Scholar]
- Roszkowska, E.; Wachowicz, T. Negotiation support with fuzzy topsis. In Proceedings of the Group Decision and Negotiations, Recife, Brazil, 20–24 May 2012; pp. 161–174. [Google Scholar]
- Samanta, S.; Sarkar, B. Generalized fuzzy Euler graphs and generalized fuzzy Hamiltonian graphs. J. Intell. Fuzzy Syst. 2018, 35, 3413–3419. [Google Scholar] [CrossRef]
- Samanta, S.; Sarkar, B. Representation of competitions by generalized fuzzy graphs. Int. J. Comput. Intell. Syst. 2018, 11, 1005–1015. [Google Scholar] [CrossRef]
- Wiecek, M.M.; Ehrgott, M.; Fadel, G.; Figueira, J.R. Multiple criteria decision-making for engineering. Omega 2008, 36, 337–339. [Google Scholar] [CrossRef]
- Zhang, N. Hesitant fuzzy linguistic information aggregation in decision-making. Int. J. Oper. Res. 2014, 21, 489–507. [Google Scholar] [CrossRef]
- Adeel, A.; Akram, M.; Ahmad, I.; Nazar, K. Novel m-polar fuzzy linguistic ELECTRE-I method for group decision-making. Symmetry 2019, 11, 471. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).