Abstract
The purpose of this paper is to introduce a new algorithm to approximate a common solution for a system of generalized mixed equilibrium problems, split variational inclusion problems of a countable family of multivalued maximal monotone operators, and fixed-point problems of a countable family of left Bregman, strongly asymptotically non-expansive mappings in uniformly convex and uniformly smooth Banach spaces. A strong convergence theorem for the above problems are established. As an application, we solve a generalized mixed equilibrium problem, split Hammerstein integral equations, and a fixed-point problem, and provide a numerical example to support better findings of our result.
1. Introduction and Preliminaries
Let E be a real normed space with dual . A map is called:
- (i)
- monotone if, for each , , ∀, , where denotes duality pairing,
- (ii)
- -inverse strongly monotone if there exists , such that ,
- (iii)
- maximal monotone if B is monotone and the graph of B is not properly contained in the graph of any other monotone operator. We note that B is maximal monotone if, and only if it is monotone, and for all , J is the normalized duality map on E and is the range of (cf. [1]).
Let and be Hilbert spaces. For the maximal monotone operators and , Moudafi [2] introduced the following split monotone variational inclusion:
where is a bounded linear operator, and are given operators. In 2000, Moudafi [3] proposed the viscosity approximation method, which is formulated by considering the approximate well-posed problem and combining the non-expansive mapping S with a contraction mapping f on a non-empty, closed, and convex subset C of . That is, given an arbitrary in C, a sequence defined by
converges strongly to a point of , the set of fixed point of S, whenever such that as .
In [4,5], the viscosity approximation method for split variational inclusion and the fixed point problem in a Hilbert space was presented as follows:
where and are maximal monotone operators, and are resolvent mappings of and , respectively, f is the Meir Keeler function, T a non-expansive mapping, and is the adjoint of A, and .
The algorithm introduced by Schopfer et al. [6] involves computations in terms of Bregman distance in the setting of p-uniformly convex and uniformly smooth real Banach spaces. Their iterative algorithm given below converges weakly under some suitable conditions:
where denotes the Bregman projection and denotes metric projection onto C. However, strong convergence is more useful than the weak convergence in some applications. Recently, strong convergence theorems for the split feasibility problem (SFP) have been established in the setting of p-uniformly convex and uniformly smooth real Banach spaces [7,8,9,10].
Suppose that
where are bifunctions on a closed and convex subset C of a Banach space, which satisfy the following special properties and :
The well-known, generalized mixed equilibrium problem (GMEP) is to find an , such that
where B is nonlinear mapping.
In 2016, Payvand and Jahedi [11] introduced a new iterative algorithm for finding a common element of the set of solutions of a system of generalized mixed equilibrium problems, the set of common fixed points of a finite family of pseudo contraction mappings, and the set of solutions of the variational inequality for inverse strongly monotone mapping in a real Hilbert space. Their sequence is defined as follows:
where are bifunctions, are inverse strongly monotone mappings, are monotone and Lipschtz continuous mappings, are convex and lower semicontinuous functions, A is a inverse strongly monotone mapping, and f is an contraction mapping and .
In this paper, inspired by the above cited works, we use a modified version of (1), (2) and (4) to approximate a solution of the problem proposed here. Both the iterative methods and the underlying space used here are improvements and extensions of those employed in [2,6,7,9,10,11] and the references therein.
Let be conjugate exponents, that is, . For each , let be a gauge function where with and We define the generalized duality map by
In the sequel, denotes .
Lemma 1
([12]). In a smooth Banach space E, the Bregman distance of x to y, with respect to the convex continuous function , such that , is defined by
for all and .
A Banach space E is said to be uniformly convex if, for , , where where .
Definition 1.
A Banach space E is said to be uniformly smooth, if for , where and .
It is shown in [12] that:
- 1.
- is continuous, convex, and nondecreasing with and
- 2.
- The function is nondecreasing and fulfils for all .
Definition 2
([13]). Let E be a smooth Banach space. Let be the Bregman distance. A mapping is said to be a strongly non-expansive left Bregman with respect to the non-empty fixed point set of T, , if
Furthermore, if is bounded and , then it follows that .
Definition 3.
Let E be a smooth Banach space. Let be the Bregman distance. A mapping is said to be a strongly asymptotically non-expansive left Bregman with if there exists non-negative real sequences with , such that , .
Lemma 2
([14]). Let E be a real uniformly convex Banach space, K a non-empty closed subset of E, and an asymptotically non-expansive mapping. Then, is demi-closed at zero, if converges weakly to a point and , then .
Lemma 3
([12]). In a smooth Banach space E, let . Consider the following assertions:
- 1.
- 2.
- and
- 3.
- .
The implication (1) ⟹ (2) ⟹ (3) are valid. If E is also uniformly convex, then the assertions are equivalent.
Lemma 4.
Let E be a smooth Banach space. Let and be the mappings defined by for all and for all . Then, for all .
Lemma 5
([12]). Let E be a reflexive, strictly convex, and smooth Banach space, and be a duality mapping of E. Then, for every closed and convex subset and , there exists a unique element , such that ; here, denotes the Bregman projection of x onto C, with respect to the function . Moreover, is the Bregman projection of x onto C if
or equivalently
Lemma 6
([15]). In the case of a uniformly convex space, E, with the duality map of , we have
Lemma 7
([12]). Let E be a reflexive, strictly convex, and smooth Banach space. If we write for all for the Bregman distance on the dual space with respect to the function , then we have .
Lemma 8
([16]). Let be a sequence of non-negative real numbers, such that , where is a sequence in and is a sequence in R, such that
- 1.
- 2.
- .
Then,
Lemma 9.
Let E be reflexive, smooth, and strictly convex Banach space. Then, for all and the following facts hold:
- 1.
- and iff ;
- 2.
- .
Lemma 10
([17]). Let E be a real uniformly convex Banach space. For arbitrary , let . Then, there exists a continuous strictly increasing convex function
such that for every and , the following inequalities hold:
and
Lemma 11
([18]). Suppose that . Then, for each , converges strongly to some point of C. Moreover, let T be a mapping of C onto itself, defined by for all . Then, . Consequently, by Lemma 3, .
Lemma 12
([19]). Let E be a reflexive, strictly convex, and smooth Banach space, and C be a non-empty, closed convex subset of E. If be two bifunctions which satisfy the conditions , in (3), then for every and , there exists a unique point such that ∀
For , Reich and Sabach [20] obtained the following technical result:
Lemma 13.
Let E be a reflexive, strictly convex, and smooth Banach space, and C be a non-empty, closed, and convex subset of E. Let be two bifunctions which satisfy the conditions , in (3). Then, for every and , we define a mapping as follows;
Then, the following conditions hold:
- 1.
- is single-valued;
- 2.
- is a Bregman firmly non-expansive-type mapping, that is,or equivalently;
- 3.
- here MEP stands for mixed equilibrium problem;
- 4.
- is closed and convex;
- 5.
- for all and for all , .
2. Main Results
Let and be uniformly convex and uniformly smooth Banach spaces and and be their duals, respectively. For , let and , be multi-valued maximal monotone operators. For , , and closed and convex, let , , be bifunctions satisfying in (3), let be resolvent operators defined by and be resolvent operators defined by . Let be a bounded and linear operator, denotes the adjoint of A and be closed and convex. For each , let be a uniformly continuous Bregman asymptotically non-expansive operator with the sequences satisfying . Denote by a firmly non-expansive mapping. Suppose that, for , are convex and lower semicontinuous functions, are inverse strongly monotone mappings and , are monotone and Lipschitz continuous mappings. Let be a contraction mapping, where . Suppose that is a generalized Bregman projection onto . Let be the set of solution of the split variational inclusion problem, be the solution set of a system of generalized mixed equilibrium problems, and be the common fixed-point set of for each . Let the sequence be defined as follows:
where .
We shall strictly employ the above terminology in the sequel.
Lemma 14.
Suppose that is the function (5) in Lemma 6 for the characteristic inequality of the uniformly smooth dual . For the sequence defined by (7), let , , and , . Let, for be defined by
Then for
where is the constant defined in Lemma 6 and is the modulus of smoothness of .
Proof.
However, by (9) and Definition 1(2), we have
In addition, by Lemma 6, we have
However, by (8) and Definition 1(2), we have
Lemma 15.
For the sequence , defined by (7), , let , , and , be defined by
and
where and are chosen such that
and
Then, for all , we get
and
Proof.
By Lemmas 13, 4 and 6, for each , we get that , and hence it follows that
By Lemmas 6 and 14, we have
Thus, (22) holds.
Now, for each , let and . By Lemma 4, we have
where,
As is closed and convex, by Lemma 5 and the variational inequality for the Bregman projection of zero onto , we arrive at
and therefore,
By Lemma 6, 14 and (27), we get
Thus, (21) holds as desired.□
We now prove our main result.
Theorem 1.
Let , , be bifunctions satisfying in (3). For and , let , , be demi-closed at zero. Let be chosen arbitrarily and the sequence be defined as follows;
where , and such that ,
and are chosen such that
with, , , for , , and . If , then converges strongly to , where , for each .
Proof.
For and , let . Since are bi-functions satisfying in (3) and are monotone and Lipschitz continuous mappings, and are convex and lower semicontinuous functions, therefore satisfy the conditions in (3), and hence the algorithm (29) can be written as follows:
We will divide the proof into four steps.
Step One: We show that is a bounded sequence.
Assume that and Then, by (32), we have
By (33) and Lemma 13, for each , we have that . By Lemma 4 and for and , we have
In addition, for each , let . By Lemma 4 and for , we have
Now assume that and Then by (32), we have that
In addition, for each , , (21) in Lemma 15 gives
This implies that
In addition, it follows from the assumption , (43), Definition 3, Lemmas 9 and 4
By (44), we conclude that is bounded, and hence, from (42), (34), (35), (44), (38), and (37), and are also bounded.
Step Two: We show that . By Lemmas 1, 4, 10, and 7, we have, by the convexity of in the first argument and for ,
where
In view of the assumption and (45), Lemmas 11 and 8 imply
Step Three: We show that .
For each , we have
Then,
By (47) and Definition 2, we get
By uniform continuity of S, we have
Step Four: We show that .
Note that,
Therefore, by (51) and the boundedness of , and since by (46), is Cauchy, we can assume without loss of generality that for some . It follows from Lemmas 2, 3, and (48) that , for each . This means that
In addition, by (31) and the fact that , we arrive at
From (53), (54), and (52), by passing n to infinity in (52), we have that . This implies that In addition, by (48), we have . Thus, by (53), (54) and an application of the demi-closeness of at zero, we have that Therefore, as . This means that
Now, we show that . By (32), we have
Since , for each , are monotone, that is, for all ,
therefore,
By the lower semicontinuity of , for each , the weak upper semicontinuity of G, and the facts that, for each , as and is uniformly continuous on a bounded subset of , we have
Now, we set . From (55), we get
From (56), and by the convexity of , for each , in the second variable, we arrive at
which implies that
From (57), by the lower semicontinuity of , for each , we have for as
Therefore, by (58) we can conclude that . This means that . Hence, .
Finally, we show that , as . By Definition 3, we have
By (59) and Lemma 8, we have that
The proof is completed.□
In Theorem 1, leads to the following new result.
Corollary 1.
Let be bifunctions satisfying in (3). Let be demiclosed at zero. Suppose that is chosen arbitrarily and the sequence is defined as follows:
where , and such that , and
and and are chosen such that
and , for , , and . If , then converges strongly to , where .
3. Application to Generalized Mixed Equilibrium Problem, Split Hammerstein Integral Equations and Fixed Point Problem
Definition 4.
Let be bounded. Let and be measurable real-valued functions. An integral equation of Hammerstien-type has the form
where the unknown function u and non-homogeneous function w lies in a Banach space E of measurable real-valued functions. By transforming the above equation, we have that
and therefore, without loss of generality, we have
The split Hammerstein integral equations problem is formulated as finding such that
and such that
where , and , are maximal monotone mappings.
Lemma 16
([21]). Let E be a Banach space. Let , be bounded and maximal monotone operators. Let be defined by for all . Then, the mapping D is maximal monotone.
By Lemma 16, if K, , and F, are multi-valued maximal monotone operators then, we have two resolvent mappings,
where , are multi-valued and maximal monotone operators, is defined by for all , and , are multi-valued and maximal monotone operators, is defined by for all . Then D and are maximal monotone by Lemma 16.
When and in Corollary 1, the algorithm (60) becomes
and its strong convergence is guaranteed, which solves the problem of a common solution of a system of generalized mixed equilibrium problems, split Hammerstein integral equations, and fixed-point problems for the mappings involved in this algorithm.
4. A Numerical Example
Let , , and , for . The generalized mixed equilibrium problem is formulated as finding a point such that,
Let and define , and .
Clearly, satisfies the conditions and is a Bregman asymptotically non-expansive mapping, as well as a inverse strongly monotone mapping. Since is single-valued, therefore for , we have that
As (65) is a nonnegative quadratic function with respect to y variable, so it implies that the coefficient of is positive and the discriminant , and therefore Hence,
By Lemma 13 and (66), and . Define
It is clear that and are multi-valued maximal monotone mappings, such that and . We define the contraction mapping by , , and . Hence, for
we get,
In particular,
By Theorem 1, the sequence converges strongly to . The Figure 1 and Figure 2 below obtained by software indicate convergence of given by (32) with and , respectively.
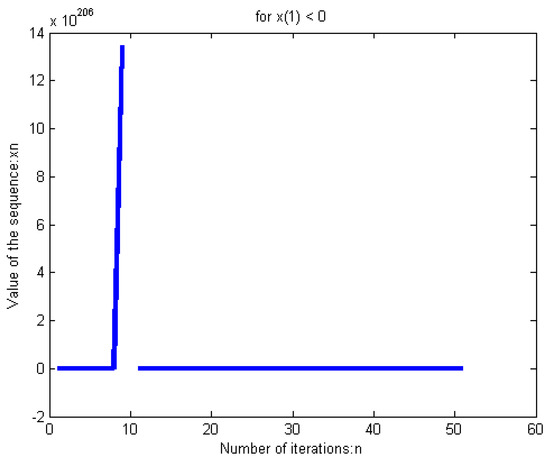
Figure 1.
Sequence convergence with initial condition .
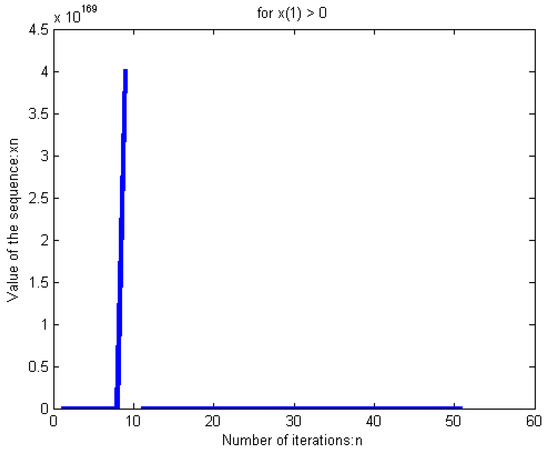
Figure 2.
Sequence convergence with initial condition 10.0.
Remark 1.
Our results generalize and complement the corresponding ones in [2,7,9,10,22,23].
Author Contributions
all the authors contribute equally to all the parts of the manuscript.
Funding
This work has been co-funded by the Deanship of Scientific Research (DSR) at University of Petroleum and Minerals (King Fahd University of Petroleum and Minerals KFUPM, Saudi Arabia) through Project No. IN141047 and by the Spanish Government and European Commission through Grant RTI2018-094336-B-I00 (MINECO/FEDER, UE).
Acknowledgments
The author A.R. Khan would like to acknowledge the support provided by the Deanship of Scientific Research (DSR) at University of Petroleum and Minerals (KFUPM)for funding this work through project No. IN141047.
Conflicts of Interest
The authors declare no confilct of interest.
References
- Barbu, V. Maximal Monotone Operators in Banach Spaces, Nonlinear Differential Equations of Monotone Types in Banach Spaces; Springer Monographs in Mathematics; Springer: New York, NY, USA, 2011. [Google Scholar]
- Moudafi, A. Split monotone variational inclusions. J. Optim. Theory Appl. 2011, 150, 275–283. [Google Scholar] [CrossRef]
- Moudafi, A. Viscosity approximation methods for fixed points problems. J. Math. Anal. Appl. 2000, 241, 46–55. [Google Scholar] [CrossRef]
- Kazmi, K.R.; Rizvi, S.H. An iterative method for split variational inclusion problem and fixed point problem for a nonexpansive mapping. Optim. Lett. 2014, 8, 1113–1124. [Google Scholar] [CrossRef]
- Nimit, N.; Narin, P. Viscosity Approximation Methods for Split Variational Inclusion and Fixed Point Problems in Hilbert Spaces. In Proceedings of the International Multi-Conference of Engineers and Computer Scientists (IMECS 2014), Hong Kong, China, 12–14 March 2014; Volume II. [Google Scholar]
- Schopfer, F.; Schopfer, T.; Louis, A.K. An iterative regularization method for the solution of the split feasibility problem in Banach spaces. Inverse Probl. 2008, 24, 055008. [Google Scholar] [CrossRef]
- Chen, J.Z.; Hu, H.Y.; Ceng, L.C. Strong convergence of hybrid Bregman projection algorithm for split feasibility and fixed point problems in Banach spaces. J. Nonlinear Sci. Appl. 2017, 10, 192–204. [Google Scholar] [CrossRef]
- Nakajo, K.; Takahashi, W. Strong convergence theorem for nonexpansive mappings and nonexpansive semigroups. J. Math. Anal. Appl. 2003, 279, 372–379. [Google Scholar] [CrossRef]
- Takahashi, W. Split feasibility problem in Banach spaces. J. Nonlinear Convex Anal. 2014, 15, 1349–1355. [Google Scholar]
- Wang, F.H. A new algorithm for solving multiple-sets split feasibility problem in Banach spaces. Numer. Funct. Anal. Optim. 2014, 35, 99–110. [Google Scholar] [CrossRef]
- Payvand, M.A.; Jahedi, S. System of generalized mixed equilibrium problems, variational inequality, and fixed point problems. Fixed Point Theory Appl. 2016, 2016, 93. [Google Scholar] [CrossRef][Green Version]
- Schopfer, F. Iterative Methods for the Solution of the Split Feasibility Problem in Banach Spaces; der Naturwissenschaftlich-Technischen Fakultaten, Universitat des Saarlandes: Saarbrücken, Germany, 2007. [Google Scholar]
- Martin, M.V.; Reich, S.; Sabach, S. Right Bregman nonexpansive operators in Banach spaces. Nonlinear Anal. 2012, 75, 5448–5465. [Google Scholar] [CrossRef]
- Xu, H.K. Existence and convergence for fixed points of mappings of asymptotically nonexpansive type. Nonlinear Anal. 1991, 16, 1139–1146. [Google Scholar] [CrossRef]
- Xu, H.K. Inequalities in Banach spaces with applications. Nonlinear Anal. 1991, 16, 1127–1138. [Google Scholar] [CrossRef]
- Liu, L.S. Ishikawa and Mann iterative process with errors for nonlinear strongly accretive mappings in Banach spaces. J. Math. Anal. Appl. 1995, 194, 114–125. [Google Scholar] [CrossRef]
- Xu, H.K.; Xu, Z.B. An Lp inequality and its applications to fixed point theory and approximation theory. Proc. R. Soc. Edinb. 1989, 112A, 343–351. [Google Scholar] [CrossRef]
- Aoyamaa, K.; Yasunori, K.; Takahashi, W.; Toyoda, M. Mann Approximation of common fixed points of a countable family of nonexpansive mappings in a Banach space. Nonlinear Anal. 2007, 67, 2350–2360. [Google Scholar] [CrossRef]
- Deng, B.C.; Chen, T.; Yin, Y.L. Srong convergence theorems for mixed equilibrium problem and asymptotically I-nonexpansive mapping in Banach spaces. Abstr. Appl. Anal. 2014, 2014, 965737. [Google Scholar]
- Reich, S.; Sabach, S. Two strong convergence theorems for Bregman strongly nonexpansive operators in reflexive Banach spaces. Nonlinear Anal. 2010, 73, 122–135. [Google Scholar] [CrossRef]
- Chidume, C.E.; Idu, K.O. Approximation of zeros bounded maximal monotone mappings, solutions of Hammertein integral equations and convex minimization problems. Fixed Point Theory Appl. 2016, 2016, 97. [Google Scholar] [CrossRef]
- Khan, A.R.; Abbas, M.; Shehu, Y. A general convergence theorem for multiple-set split feasibilty problem in Hilbert spaces. Carpathian J. Math. 2015, 31, 349–357. [Google Scholar]
- Ogbuisi, F.U.; Mewomo, O.T. On split generalized mixed equilibrium problem and fixed point problems with no prioir knowledge of operator norm. J. Fixed Point Theory Appl. 2017, 19, 2109–2128. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).