Abstract
A number of higher order iterative methods with derivative evaluations are developed in literature for computing multiple zeros. However, higher order methods without derivative for multiple zeros are difficult to obtain and hence such methods are rare in literature. Motivated by this fact, we present a family of eighth order derivative-free methods for computing multiple zeros. Per iteration the methods require only four function evaluations, therefore, these are optimal in the sense of Kung-Traub conjecture. Stability of the proposed class is demonstrated by means of using a graphical tool, namely, basins of attraction. Boundaries of the basins are fractal like shapes through which basins are symmetric. Applicability of the methods is demonstrated on different nonlinear functions which illustrates the efficient convergence behavior. Comparison of the numerical results shows that the new derivative-free methods are good competitors to the existing optimal eighth-order techniques which require derivative evaluations.
MSC:
65H05; 41A25; 49M15
1. Introduction
Approximating a root (say, ) of a function is a very challenging task. It is also very important in many diverse areas such as Mathematical Biology, Physics, Chemistry, Economics and also Engineering to mention a few [1,2,3,4]. This is the case since problems from these areas are reduced to finding . Researchers are utilizing iterative methods for approximating since closed form solutions can not be obtained in general. In particular, we consider derivative-free methods to compute a multiple root (say, ) with multiplicity m, i.e., and , of the equation .
A number of higher order methods, either independent or based on the Newton’s method ([5])
have been proposed and analyzed in literature, see [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Such methods require the evaluation of derivative. However, higher order derivative-free methods to handle the case of multiple roots are yet to be investigated. Main reason of the non-availability of such methods is due to the difficulty in obtaining their order of convergence. The derivative-free methods are important in the situations where derivative of the function f is complicated to evaluate or is expensive to obtain. One such derivative-free method is the classical Traub-Steffensen method [1] which actually replaces the derivative in the classical Newton’s method by a suitable approximation based on finite difference quotient,
where and . In this way the modified Newton’s method (1) becomes the modified Traub-Steffensen method
The modified Traub-Steffensen method (2) is a noticeable improvement of Newton’s iteration, since it preserves the order of convergence without using any derivative.
Very recently, Sharma et al. in [25] have developed a family of three-point derivative free methods with seventh order convergence to compute the multiple zeros. The techniques of [25] require four function evaluations per iteration and, therefore, according to Kung-Traub hypothesis these do not possess optimal convergence [26]. According to this hypothesis multipoint methods without memory based on n function evaluations have optimal order . In this work, we introduce a family of eighth order derivative-free methods for computing multiple zeros that require the evaluations of four functions per iteration, and hence the family has optimal convergence of eighth order in the sense of Kung-Traub hypothesis. Such methods are usually known as optimal methods. The iterative scheme uses the modified Traub-Steffensen iteration (2) in the first step and Traub-Steffensen-like iterations in the second and third steps.
Rest of the paper is summarized as follows. In Section 2, optimal family of eighth order is developed and its local convergence is studied. In Section 3, the basins of attractors are analyzed to check the convergence region of new methods. In order to check the performance and to verify the theoretical results some numerical tests are performed in Section 4. A comparison with the existing methods of same order requiring derivatives is also shown in this section. Section 5 contains the concluding remarks.
2. Development of Method
Given a known multiplicity , we consider the following three-step scheme for multiple roots:
where , , and is analytic in a neighborhood of . Note that this is a three-step scheme with first step as the Traub-Steffensen iteration (2) and next two steps are Traub-Steffensen-like iterations. Notice also that third step is weighted by the factor , so this factor is called weight factor or weight function.
We shall find conditions under which the scheme (3) achieves eighth order convergence. In order to do this, let us prove the following theorem:
Theorem 1.
Let be an analytic function in a domain enclosing a multiple zero (say, α) with multiplicity m. Suppose that initial guess is sufficiently close to α, then the local order of convergence of scheme (3) is at least 8, provided that , , , , , , , , and , where ,
Proof.
Let be the error in the k-th iteration. Taking into account that and the Taylor’s expansion of about yields
where for .
Using (4) in , we obtain that
Expanding about
where
Expanding about , we have that
Also,
and
By inserting (4)–(10) in the second step of (3), we have
where , Here, expressions of are not being produced explicitly since they are very lengthy.
In order to obtain fourth-order convergence, the coefficients of and should be equal to zero. This is possible only for the following values of and , which can be calculated from the expression (11):
Then, the error Equation (11) is given by
where ,
Expansion of about leads us to the expression
and so yields
Expanding in neighborhood of origin by Taylor’s series, it follows that
where ,
It is clear from the Equation (15) that we will obtain at least eighth order convergence if we choose , , and . We choose in Then, we get
By using and (16) in , we will obtain
Thus, the eighth order convergence is established. □
Remark 1.
It is important to note that the weight function plays a significant role in the attainment of desired convergence order of the proposed family of methods. However, only and are involved in the error Equation (19). On the other hand, , , , , , and do not affect the error Equation (19). So, we can assume them as dummy parameters.
Remark 2.
Remark 3.
Notice that the parameter β, which is used in the iteration , does not appear in the expression (7) of and also in later expressions. We have observed that this parameter has the appearance in the terms and higher order. However, these terms are difficult to compute in general. Moreover, we do not need these in order to show the eighth convergence.
Some Particular Forms of Proposed Family
- (1)
- Let us consider the following function which satisfies the conditions of Theorem 1Then, the corresponding eighth-order iterative scheme is given by
- (2)
- Next, consider the rational functionSatisfying the conditions of Theorem 1. Then, corresponding eighth-order iterative scheme is given by
- (3)
- Consider another rational function satisfying the conditions of Theorem 1, which is given byThen, corresponding eighth-order iterative scheme is given by
- (4)
- Next, we suggest another rational function satisfying the conditions of Theorem 1, which is given byThen, corresponding eighth-order iterative scheme is given by
- (5)
- Lastly, we consider yet another function satisfying the conditions of Theorem 1Then, the corresponding eighth-order method is given as
3. Complex Dynamics of Methods
Our aim here is to analyze the complex dynamics of new methods based on graphical tool the basins of attraction of the zeros of a polynomial in complex plane. Analysis of the basins of attraction gives an important information about the stability and convergence of iterative methods. This idea was floated initially by Vrscay and Gilbert [27]. In recent times, many researchers used this concept in their work, see, for example [28,29,30] and references therein. To start with, let us recall some basic dynamical concepts of rational function associated to an iterative method. Let be a rational function, the orbit of a point is defined as the set
of successive images of by the rational function.
The dynamical behavior of the orbit of a point of can be classified depending on its asymptotic behavior. In this way, a point is a fixed point of if it satisfies . Moreover, is called a periodic point of period if it is a point such that but , for each . Also, a point is called pre-periodic if it is not periodic but there exists a such that is periodic. There exist different type of fixed points depending on the associated multiplier . Taking the associated multiplier into account, a fixed point is called: (a) attractor if , (b) superattractor if , (c) repulsor if and (d) parabolic if .
If is an attracting fixed point of the rational function , its basin of attraction is defined as the set of pre-images of any order such that
The set of points whose orbits tend to an attracting fixed point is defined as the Fatou set. Its complementary set, called Julia set, is the closure of the set consisting of repelling fixed points, and establishes the borders between the basins of attraction. That means the basin of attraction of any fixed point belongs to the Fatou set and the boundaries of these basins of attraction belong to the Julia set.
The initial point is taken in a rectangular region that contains all the zeros of a polynomial The iterative method when starts from point in a rectangle either converges to the zero or eventually diverges. The stopping criterion for convergence is considered as up to a maximum of 25 iterations. If the required tolerance is not achieved in 25 iterations, we conclude that the method starting at point does not converge to any root. The strategy adopted is as follows: A color is allocated to each initial point in the basin of attraction of a zero. If the iteration initiating at converges, then it represents the attraction basin with that particular assigned color to it, otherwise if it fails to converge in 25 iterations, then it shows the black color.
To view complex geometry, we analyze the basins of attraction of the proposed methods M-I (I ) on following polynomials:
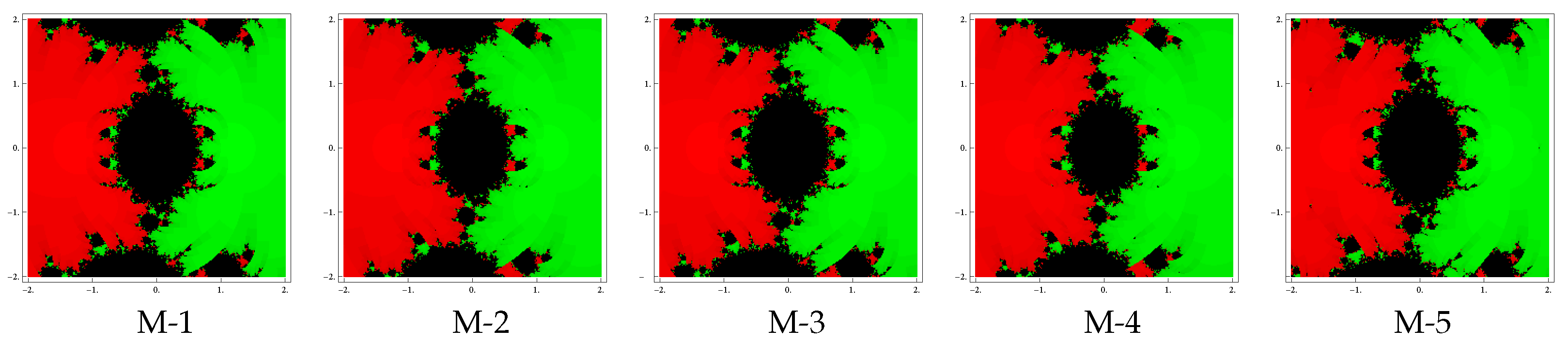
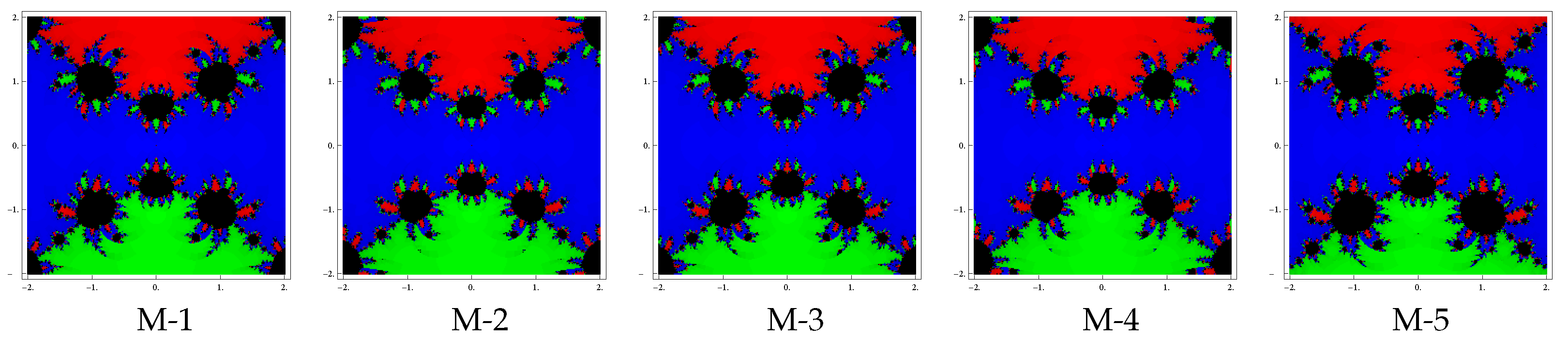
Test problem 1. Consider the polynomial having two zeros with multiplicities . The basin of attractors for this polynomial are shown in Figure 1, Figure 2 and Figure 3, for different choices of A color is assigned to each basin of attraction of a zero. In particular, to obtain the basin of attraction, the red and green colors have been assigned for the zeros and 1, respectively. Looking at the behavior of the methods, we see that the method M-2 and M-4 possess less number of divergent points and therefore have better convergence than rest of the methods. Observe that there is a small difference among the basins for the remaining methods with the same value of . Note also that the basins are becoming larger as the parameter assumes smaller values.
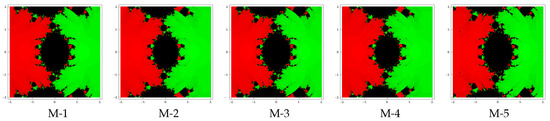
Figure 1.
Basins of attraction for methods M-1 to M-5 in polynomial .
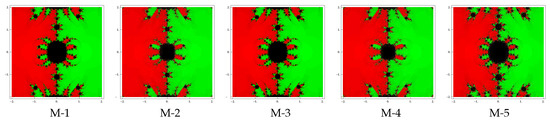
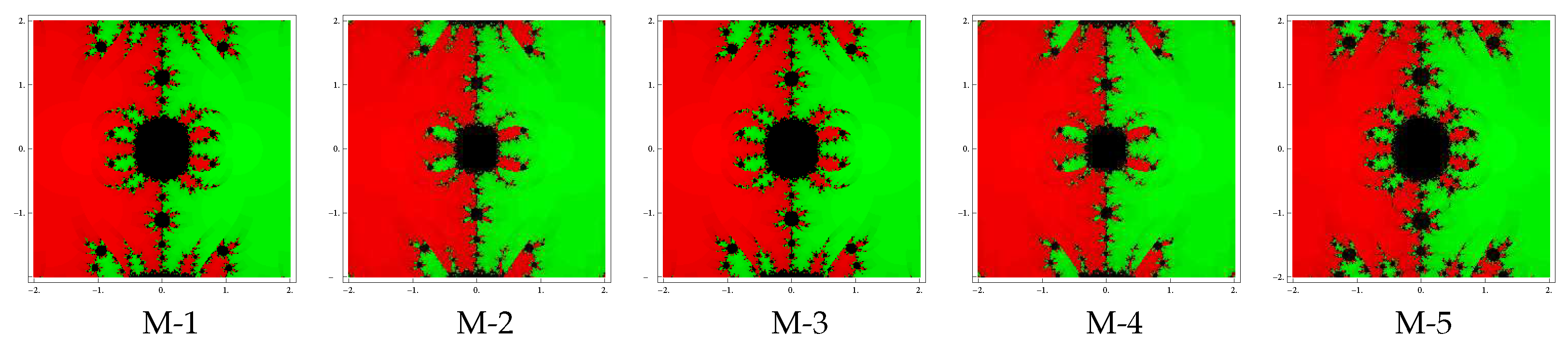
Figure 2.
Basins of attraction for methods M-1 to M-5 in polynomial .
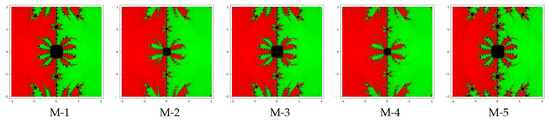
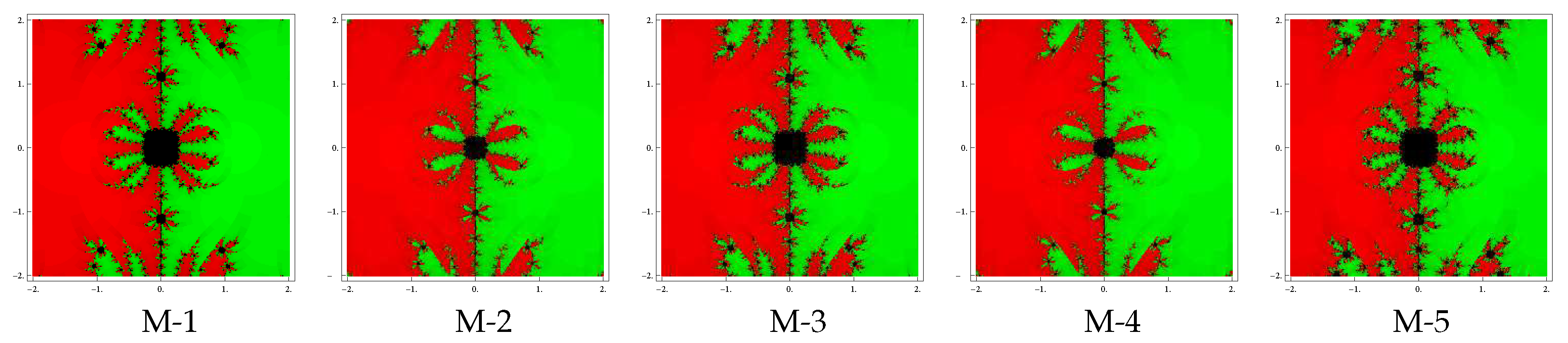
Figure 3.
Basins of attraction for methods M-1 to M-5 in polynomial .
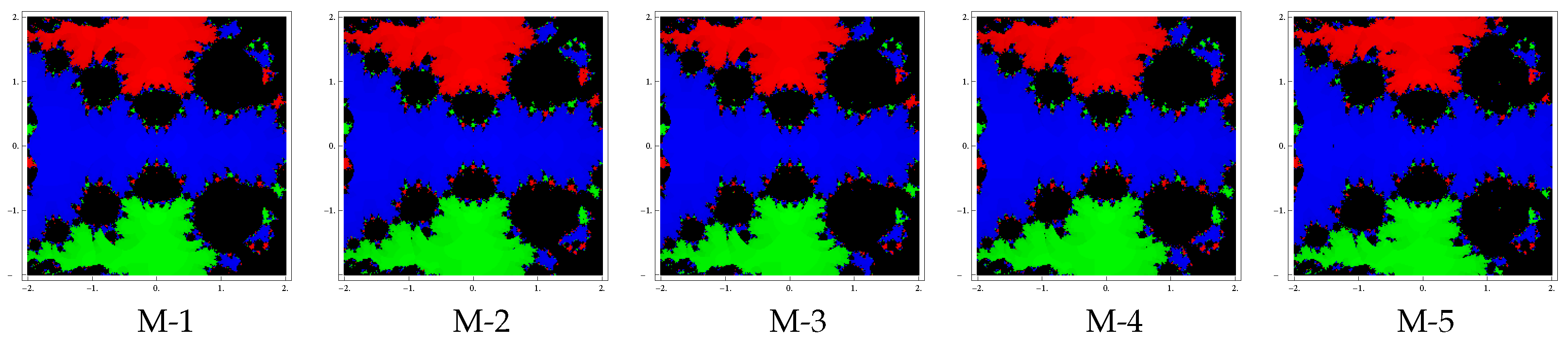
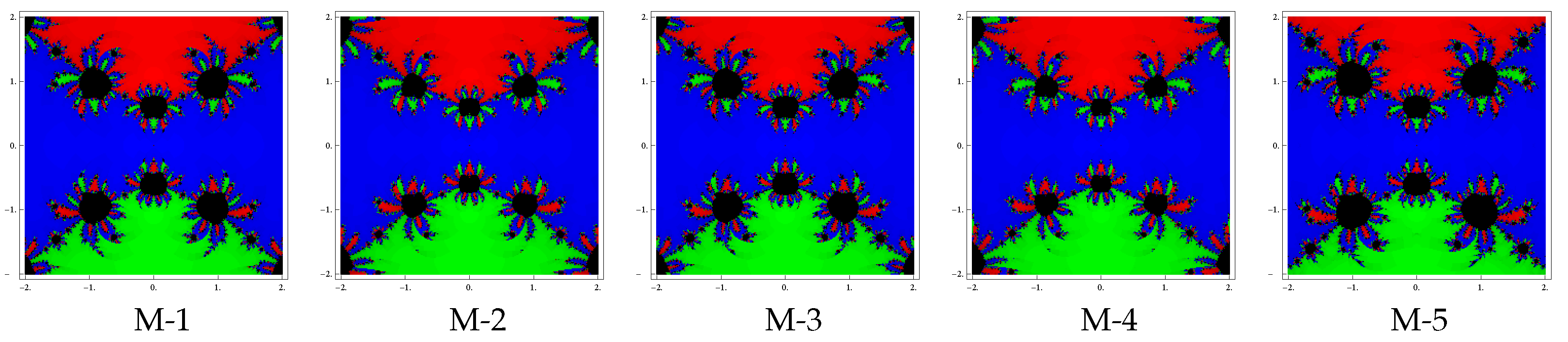
Test problem 2. Let having three zeros with multiplicities . The basin of attractors for this polynomial are shown in Figure 4, Figure 5 and Figure 6, for different choices of A color is allocated to each basin of attraction of a zero. For example, we have assigned the colors: green, red and blue corresponding to the basins of the zeros , i and 0, From graphics, we see that the methods M-2 and M-4 have better convergence due to a lesser number of divergent points. Also observe that in each case, the basins are getting broader with the smaller values of . The basins in methods M-1, M-3 are almost the same and method M-5 has more divergent points.
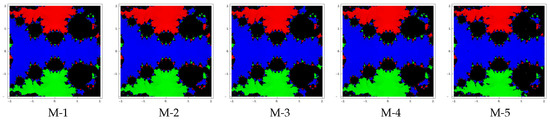
Figure 4.
Basins of attraction for methods M-1 to M-5 in polynomial .
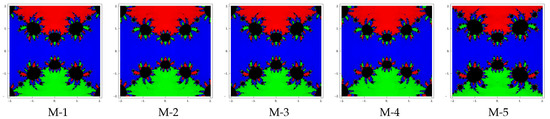
Figure 5.
Basins of attraction for methods M-1 to M-5 in polynomial .
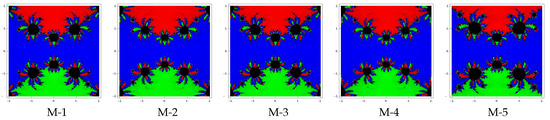
Figure 6.
Basins of attraction for methods M-1 to M-5 in polynomial .
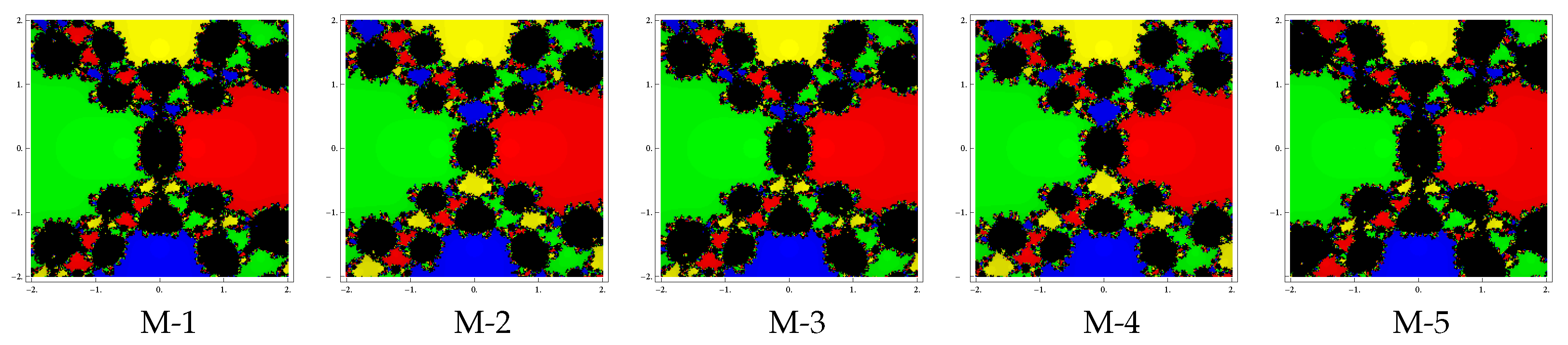
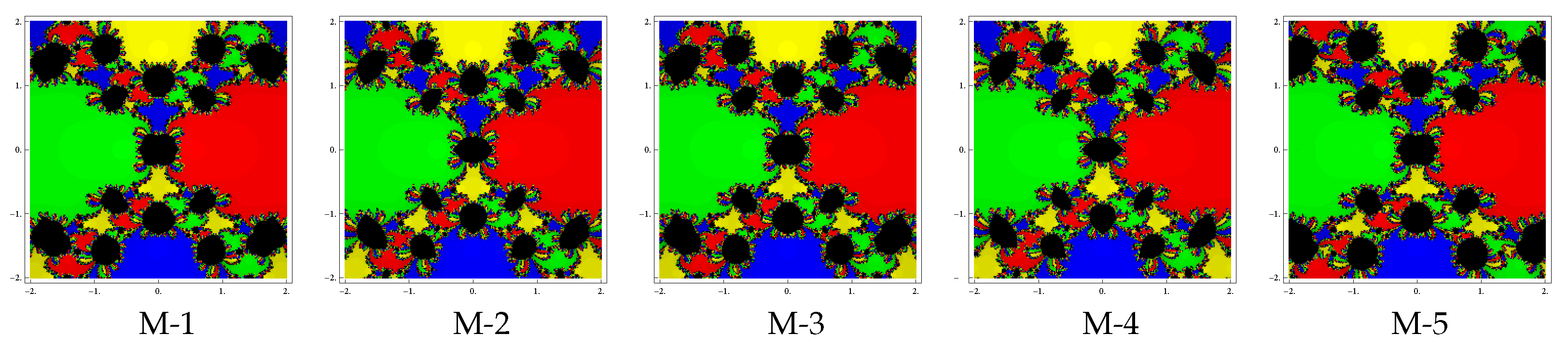
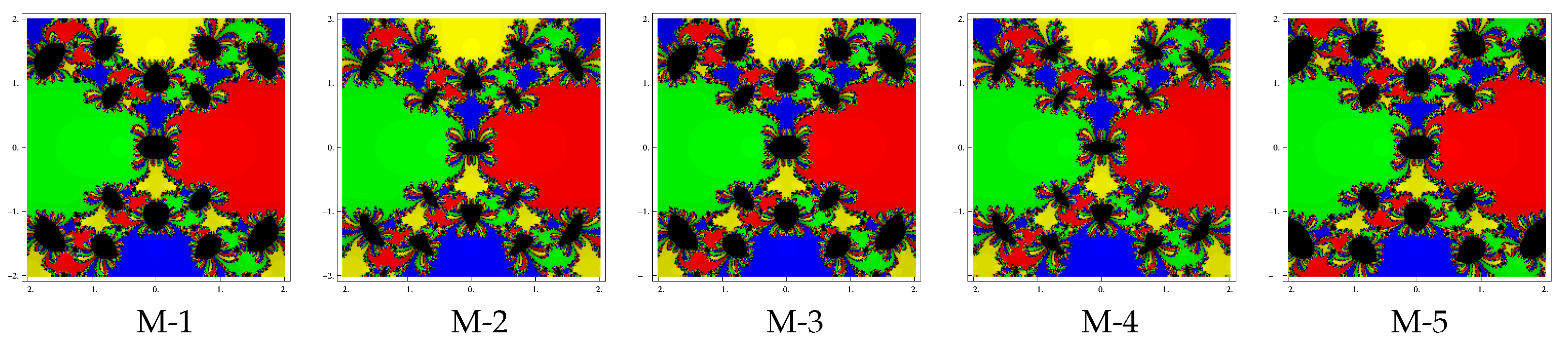
Test problem 3. Let having four simple zeros . To see the dynamical view, we allocate the colors green, red, blue and yellow corresponding to basins of the zeros , , and . The basin of attractors for this polynomial are shown in Figure 7, Figure 8 and Figure 9, for different choices of Looking at the graphics, we conclude that the methods M-2 and M-4 have better convergence behavior since they have lesser number of divergent points. The remaining methods have almost similar basins with the same value of . Notice also that the basins are becoming larger with the smaller values of .
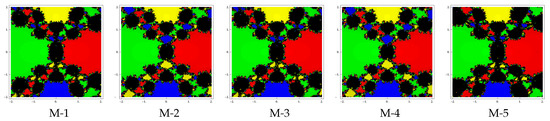
Figure 7.
Basins of attraction for methods M-1 to M-5 in polynomial .
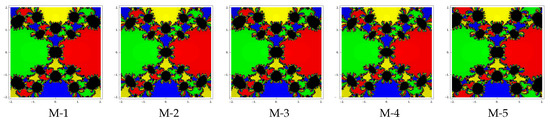
Figure 8.
Basins of attraction for methods M-1 to M-5 in polynomial .
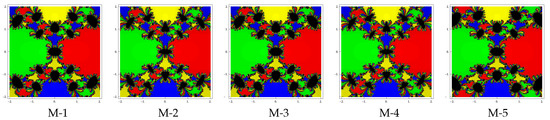
Figure 9.
Basins of attraction for methods M-1 to M-5 in polynomial .
From these graphics one can easily evaluate the behavior and stability of any method. If we choose an initial point in a zone where distinct basins of attraction touch each other, it is impractical to predict which root is going to be attained by the iterative method that starts in . Hence, the choice of in such a zone is not a good one. Both the black zones and the regions with different colors are not suitable to take the initial guess when we want to acquire a unique root. The most adorable pictures appear when we have very tricky frontiers between basins of attraction and they correspond to the cases where the method is more demanding with respect to the initial point and its dynamic behavior is more unpredictable. We conclude this section with a remark that the convergence nature of proposed methods depends upon the value of parameter . The smaller is the value of , the better is the convergence of the method.
4. Numerical Results
In this section, we apply the methods M1–M5 of family (3) to solve few nonlinear equations, which not only depict the methods practically but also serve to verify the validity of theoretical results that we have derived. The theoretical order of convergence is verified by calculating the computational order of convergence (COC) using the formula (see [31])
Performance is compared with some existing eighth-order methods requiring derivative evaluations in their formulae. For example, we choose the methods by Zafar et al. [19] and Behl et al. [23,24]. These methods are expressed as follows:
Zafar et al. method (ZM-1):
Zafar et al. method (ZM-2):
where , and
Behl et al. method (BM-1):
Behl et al. method (BM-2):
where , , .
Behl et al. method (BM-3):
where , and
All computations are performed in the programming package Mathematica [32] in PC with Intel(R) Pentium(R) CPU B960 @ 2.20 GHz, 2.20 GHz (32-bit Operating System) Microsoft Windows 7 Professional and 4 GB RAM using multiple-precision arithmetic. Performance of the new methods is tested by choosing value of the parameter . Choice of the initial approximation in the examples is obtained by using the procedure proposed in [33]. For example, the procedure when applied to the function of Example 2 in the interval [2, 3.5] using the statements
in programming package Mathematica yields a close initial approximation to the root .
f[x_ ]=x9-29x8+349x7-2261x6+8455x5-17663x4+15927x3+6993x2-24732x+12960;
a=2; b=3.5; k=1; x0=0.5*(a+b+Sign[f[a]]*NIntegrate[Tanh[k *f[x]],{x,a,b}])
a=2; b=3.5; k=1; x0=0.5*(a+b+Sign[f[a]]*NIntegrate[Tanh[k *f[x]],{x,a,b}])
Numerical results displayed in Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 contain: (i) values of first three consecutive errors , (ii) number of iterations needed to converge to the required solution with the stopping criterion , (iii) computational order of convergence (COC) using (25) and (iv) the elapsed CPU-time (CPU-time) in seconds computed by the Mathematica command “TimeUsed[ ]”. Further, the meaning of is in Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6.

Table 1.
Performance of methods for example 1.

Table 2.
Performance of methods for example 2.

Table 3.
Performance of methods for example 3.

Table 4.
Performance of methods for example 4.

Table 5.
Performance of methods for example 5.

Table 6.
Performance of methods for example 6.
The following examples are chosen for numerical tests:
Example 1.
We consider the Planck’s radiation law problem [34]:
which determines the energy density with in an isothermal black body. Here, c is the speed of light, λ is the wavelength of the radiation, k is Boltzmann’s constant, T is the absolute temperature of the black body and h is the Planck’s constant. Suppose, we would like to calculate wavelength λ which corresponds to maximum energy density . From (26), we get
It can be seen that a maximum value for φ occurs when , that is, when
Then, setting , the above equation becomes
We consider this case for four times and obtained the required nonlinear function
The aim is to find a multiple root of the equation . Obviously, one of the multiple root is not taken into account. As argued in [34], the left-hand side of (27) is zero for and right-hand side is 6.74 × 10. Hence, it is expected that another multiple root of the equation might exist near to . The calculated value of this multiple root is given by with . As a result, the wavelength (λ) corresponding to which the energy density is maximum is approximately given as
Numerical results are shown in Table 1.
Example 2.
Finding eigen values of a large sparse matrix is a challenging task in applied mathematics and engineering. Calculating even the roots of a characteristic equation of square matrix greater than 4 is another big challenge. So, we consider the following 9× 9 matrix (see [23])
The characteristic polynomial of the matrix (M) is given as
This function has one multiple zero at of multiplicity 4. We find this zero with initial approximation . Numerical results are shown in Table 2.
Example 3.
Consider an isentropic supersonic flow along a sharp expansion corner (see [2]). Then relationship between the Mach number before the corner (i.e., ) and after the corner (i.e., ) is given by
where , γ is the specific heat ratio of the gas.
For a special case study, we solve the equation for given that , and . In this case, we have
where .
We consider this case for ten times and obtained the required nonlinear function
The above function has zero at with multiplicity 10. This zero is calculated using initial approximation . Numerical results are shown in Table 3.
Example 4.
The van der Waals equation-of-state
explains the behavior of a real gas by introducing in the ideal gas equations two parameters, and , specific for each gas. Determination of the volume V of the gas in terms of the remaining parameters requires the solution of a nonlinear equation in V.
Given the parameters and of a particular gas, one can obtain values for n, P and T, such that this equation has three real zeros. By using the particular values (see [23]), we obtain the nonlinear equation
where . This equation has a multiple root with multiplicity 2. We further increase the multiplicity of this root to 8 by considering this case for four times and so obtain the nonlinear function
The initial guess chosen to obtain the solution 1.75 is . Numerical results are shown in Table 4.
Example 5.
Next, we assume a standard nonlinear test function from Behl et al. [17] which is defined by
The function has multiple zero at of multiplicity 6. We select initial approximation to obtain zero of this function. Numerical results are exhibited in Table 5.
Example 6.
Lastly, we consider another standard test function which is defined as
This function has multiple zero of multiplicity 4. Let us choose the initial approximation to compute this zero. The computed results are displayed in Table 6.
From the numerical values of errors we examine that the accuracy in the values of successive approximations increases as the iteration proceed. This explains the stable nature of methods. Also, like the existing methods the new methods show consistent convergence nature. At the stage when stopping criterion has been satisfied we display the value ‘0’ of . From the calculation of computational order of convergence shown in the penultimate column in each table, we verify the theoretical eighth order of convergence. However, this is not true for the existing eighth-order methods BM−1 and BM−2, since the eighth order convergence is not maintained. The efficient nature of proposed methods can be observed by the fact that the amount of CPU time consumed by the methods is less than that of the time taken by existing methods. In addition, the new methods are more accurate because error becomes much smaller with increasing n as compare to the error of existing techniques. The main purpose of implementing the new derivative-free methods for solving different type of nonlinear equations is purely to illustrate the exactness of the approximate solution and the stability of the convergence to the required solution. Similar numerical experiments, performed for many other different problems, have confirmed this conclusion to a good extent.
5. Conclusions
In the foregoing study, we have proposed the first ever, as far as we know, class of optimal eighth order derivative-free iterative methods for solving nonlinear equations with multiple roots. Analysis of the local convergence has been carried out, which proves the order eight under standard assumptions of the function whose zeros we are looking for. Some special cases of the class are presented. These are implemented to solve nonlinear equations including those arising in practical problems. The methods are compared with existing techniques of same order. Testing of the numerical results shows that the presented derivative-free methods are good competitors to the existing optimal eighth-order techniques that require derivative evaluations in their algorithm. We conclude the work with a remark that derivative-free techniques are good options to Newton-type iterations in the cases when derivatives are expensive to compute or difficult to evaluate.
Author Contributions
Methodology, J.R.S.; Writing—review & editing, J.R.S.; Investigation, S.K.; Data Curation, S.K.; Conceptualization, I.K.A.; Formal analysis, I.K.A.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Traub, J.F. Iterative Methods for the Solution of Equations; Chelsea Publishing Company: New York, NY, USA, 1982. [Google Scholar]
- Hoffman, J.D. Numerical Methods for Engineers and Scientists; McGraw-Hill Book Company: New York, NY, USA, 1992. [Google Scholar]
- Argyros, I.K. Convergence and Applications of Newton-Type Iterations; Springer-Verlag: New York, NY, USA, 2008. [Google Scholar]
- Argyros, I.K.; Magreñán, Á.A. Iterative Methods and Their Dynamics with Applications; CRC Press: New York, NY, USA, 2017. [Google Scholar]
- Schröder, E. Über unendlich viele Algorithmen zur Auflösung der Gleichungen. Math. Ann. 1870, 2, 317–365. [Google Scholar] [CrossRef]
- Hansen, E.; Patrick, M. A family of root finding methods. Numer. Math. 1977, 27, 257–269. [Google Scholar] [CrossRef]
- Victory, H.D.; Neta, B. A higher order method for multiple zeros of nonlinear functions. Int. J. Comput. Math. 1983, 12, 329–335. [Google Scholar] [CrossRef]
- Dong, C. A family of multipoint iterative functions for finding multiple roots of equations. Int. J. Comput. Math. 1987, 21, 363–367. [Google Scholar] [CrossRef]
- Osada, N. An optimal multiple root-finding method of order three. J. Comput. Appl. Math. 1994, 51, 131–133. [Google Scholar] [CrossRef]
- Neta, B. New third order nonlinear solvers for multiple roots. Appl. Math. Comput. 2008, 202, 162–170. [Google Scholar] [CrossRef]
- Li, S.; Liao, X.; Cheng, L. A new fourth-order iterative method for finding multiple roots of nonlinear equations. Appl. Math. Comput. 2009, 215, 1288–1292. [Google Scholar]
- Li, S.G.; Cheng, L.Z.; Neta, B. Some fourth-order nonlinear solvers with closed formulae for multiple roots. Comput. Math. Appl. 2010, 59, 126–135. [Google Scholar] [CrossRef]
- Sharma, J.R.; Sharma, R. Modified Jarratt method for computing multiple roots. Appl. Math. Comput. 2010, 217, 878–881. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, X.; Song, Y. Constructing higher-order methods for obtaining the multiple roots of nonlinear equations. J. Comput. Math. Appl. 2011, 235, 4199–4206. [Google Scholar] [CrossRef]
- Kansal, M.; Kanwar, V.; Bhatia, S. On some optimal multiple root-finding methods and their dynamics. Appl. Appl. Math. 2015, 10, 349–367. [Google Scholar]
- Geum, Y.H.; Kim, Y.I.; Neta, B. A class of two-point sixth-order multiplezero finders of modified double-Newton type and their dynamics. Appl. Math. Comput. 2015, 270, 387–400. [Google Scholar]
- Behl, R.; Cordero, A.; Motsa, S.S.; Torregrosa, J.R.; Kanwar, V. An optimal fourth-order family of methods for multiple roots and its dynamics. Numer. Algor. 2016, 71, 775–796. [Google Scholar] [CrossRef]
- Geum, Y.H.; Kim, Y.I.; Neta, B. Constructing a family of optimal eighth-order modified Newton-type multiple-zero finders along with the dynamics behind their purely imaginary extraneous fixed points. J. Comp. Appl. Math. 2017. [Google Scholar] [CrossRef]
- Zafar, F.; Cordero, A.; Quratulain, R.; Torregrosa, J.R. Optimal iterative methods for finding multiple roots of nonlinear equations using free parameters. J. Math. Chem. 2017. [Google Scholar] [CrossRef]
- Zafar, F.; Cordero, A.; Sultana, S.; Torregrosa, J.R. Optimal iterative methods for finding multiple roots of nonlinear equations using weight functions and dynamics. J. Comp. Appl. Math. 2018, 342, 352–374. [Google Scholar] [CrossRef]
- Zafar, F.; Cordero, A.; Torregrosa, J.R. An efficient family of optimal eighth-order multiple root finders. Mathematics 2018, 6, 310. [Google Scholar] [CrossRef]
- Behl, R.; Cordero, A.; Motsa, S.S.; Torregrosa, J.R. An eighth-order family of optimal multiple root finders and its dynamics. Numer. Algor. 2018, 77, 1249–1272. [Google Scholar] [CrossRef]
- Behl, R.; Zafar, F.; Alshormani, A.S.; Junjua, M.U.D.; Yasmin, N. An optimal eighth-order scheme for multiple zeros of unvariate functions. Int. J. Comput. Meth. 2018. [Google Scholar] [CrossRef]
- Behl, R.; Alshomrani, A.S.; Motsa, S.S. An optimal scheme for multiple roots of nonlinear equations with eighth-order convergence. J. Math. Chem. 2018. [Google Scholar] [CrossRef]
- Sharma, J.R.; Kumar, D.; Argyros, I.K. An efficient class of Traub-Steffensen-like seventh order multiple-root solvers with applications. Symmetry 2019, 11, 518. [Google Scholar] [CrossRef]
- Kung, H.T.; Traub, J.F. Optimal order of one-point and multipoint iteration. J. Assoc. Comput. Mach. 1974, 21, 643–651. [Google Scholar] [CrossRef]
- Vrscay, E.R.; Gilbert, W.J. Extraneous fixed points, basin boundaries and chaotic dynamics for Schröder and König rational iteration functions. Numer. Math. 1988, 52, 1–16. [Google Scholar] [CrossRef]
- Varona, J.L. Graphic and numerical comparison between iterative methods. Math. Intell. 2002, 24, 37–46. [Google Scholar] [CrossRef]
- Scott, M.; Neta, B.; Chun, C. Basin attractors for various methods. Appl. Math. Comput. 2011, 218, 2584–2599. [Google Scholar] [CrossRef]
- Lotfi, T.; Sharifi, S.; Salimi, M.; Siegmund, S. A new class of three-point methods with optimal convergence order eight and its dynamics. Numer. Algorithms 2015, 68, 261–288. [Google Scholar] [CrossRef]
- Weerakoon, S.; Fernando, T.G.I. A variant of Newton’s method with accelerated third-order convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar] [CrossRef]
- Wolfram, S. The Mathematica Book, 5th ed.; Wolfram Media: Champaign, IL, USA, 2003. [Google Scholar]
- Yun, B.I. A non-iterative method for solving non-linear equations. Appl. Math. Comput. 2008, 198, 691–699. [Google Scholar] [CrossRef]
- Bradie, B. A Friendly Introduction to Numerical Analysis; Pearson Education Inc.: New Delhi, India, 2006. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).