Abstract
A novel method based on multiscale and multidirectional feature fusion in the shearlet transform domain and kurtosis maximization for detecting the dim target in infrared images with a low signal-to-noise ratio (SNR) and serious interference caused by a cluttered and non-uniform background is presented in this paper. First, an original image is decomposed using the shearlet transform with translation invariance. Second, various directions of high-frequency subbands are fused and the corresponding kurtosis of fused image is computed. The targets can be enhanced by strengthening the column with maximum kurtosis. Then, processed high-frequency subbands on different scales of images are merged. Finally, the dim targets are detected by an adaptive threshold with a maximum contrast criterion (MCC). The experimental results show that the proposed method has good performance for infrared target detection in comparison with the nonsubsampled contourlet transform (NSCT) method.
1. Introduction
Infrared dim target detection plays an important role in remote surveillance, infrared warnings, infrared target recognition, tracking systems, and so on. The thermal sensors are far away from the imagery sensors in respect of target size and features. The size of dim targets is commonly less than 80 pixels in the imaging plane. Also, there are no fixed shapes and textures [1] for the infrared dim targets. Moreover, the infrared dim targets are often interfered with by non-uniform backgrounds, such as houses, trees, and clouds [2,3]. It has been shown that the infrared dim target might be completely submerged in the complicated cluttered background and is imaged with low signal-to-clutter ratio (SCR < 0.3) and low signal-to-noise ratio (SNR < 2 dB). Thus, it is difficult to detect dim targets in infrared images for their complex imaging characteristics.
Over the last decade, in order to improve efficiency and accuracy, a wide range of theories and methods [4,5] of infrared dim target detection have been presented by many scientists and hundreds of papers published in related journals covering the scientific and engineering fields. In general, the method of target detection in the single-frame infrared image can be divided into two categories, which are global feature-based or local feature-based. The detection approaches based on the global features of the image include maximum entropy estimation [6], spatial filtering [7], modification of partial differential equations [8], non-convex rank approximation minimization [9], non-convex optimization with Lp-norm [10], partial sum of tensor nuclear norm [11], etc. However, its global features corresponding to the infrared dim target are not obvious, and its performance of target detection may be degraded due to the dim feature with local maximums in the region. Recently, the target detection based on local features was developed as well such as facet-based [12], filter-based [13], cellular automata [14], and contrast-based features [15], and so on. In addition, the artificial neural networks (ANNs) [16] and the wavelet transform [17] were also used for the target detection of single-frame infrared images. However, it is difficult for them to distinguish the dim target from the cluttered background in infrared images with low SNR and SCR.
Compared with the traditional wavelets, the multiscale geometric analysis (MGA), also called “the beyond wavelets”, contains novel harmonic analysis and sparse representation ideas for a signal or an image. It is very efficient to deal with sharp transitions, such as edges in high dimension functions or signal space, and can overcome the limitation of the traditional wavelet transform that handles pointwise singularities only. It has been proved that MGA is good at dealing with directional information and anisotropic features to capture singularities accurately and efficiently in infrared images. Furthermore, MGA can enhance targets by eliminating the background and noise in the image, which improves the performance of dim target detection. Thus far, curvelets, nonsubsampled contourlets, and shearlets are presented as MGA methods, which make lots of achievements and are applied in the field of infrared dim target detection [18,19,20]. As a new MGA approach, the shearlet transform is derived from the curvelet [21], and nonsubsampled contourlet transforms (NSCT) [22]. The shearlet is much related to them in idealized frequency decompositions for the image, only differing in their construction and implementation model.
In addition to suppressing the background, it is also necessary to enhance the targets. Kurtosis is a statistical measure that is used to describe the shape of distribution tails and the degree of steepness. It represents the characteristics of peakedness of a probability distribution curve at the average value. Any distribution that is leptokurtic corresponds to a greater kurtosis than a mesokurtic distribution. Furthermore, the leptokurtic distribution is characterized with long tails. By comparison, the platykurtic distribution has shorter tails and is flatter than normal distribution. Due to the presence of the target, the distribution of the target is similar to that of the leptokurtosis. Moreover, the kurtosis measure is sensitive to the target and thus can be used to measure the deviation of background distribution to detect the target. Small targets correspond to large and positive coefficients of kurtosis. However, for large targets, the corresponding coefficients of kurtosis are smaller, and can even be negative.
A novel method for detecting dim targets in infrared images using maximum kurtosis in the shearlet domain is proposed in this paper. Firstly, the image is decomposed by the shearlet transform and is fused with various directions of high frequency on each scale. Then, the maximum kurtosis coefficient is found to enhance the target. Finally, high frequency images of all scales are merged, and the dim targets are detected by an adaptive threshold with a maximum contrast criterion (MCC). The experimental results show that the proposed method has better performance on infrared dim target detection compared to the nonsubsampled contourlet transform (NSCT) method.
This paper is organized as follows. Section 2 briefly introduces the shearlet transform and multiscale and multidirectional representation for the infrared image. Section 3 describes the principle of multiscale feature fusion and the process of dim target detection in the shearlet transform domain by the maximum kurtosis and adaptive threshold. The experimental results of the proposed method and its performance evaluation for the dim target detection is shown in Section 4. We conclude this paper with a summary in Section 5.
2. Multiscale Directional Representation of Image Using Shearlet Transform
Guo and Labate, and Easley et al. [23,24] recently constructed a geometric representation method of multidimensional function in the special form of affine systems with composite dilations, called shearlet transform, which can yield the optimal approximation properties. The shearlet transform is similar to curvelet transform with a nonlinearity approximation order in multiresolution analysis, but supports feature subdivision of multidimensional function in the frequency-spatial domain, which is suitable for optimal sparse representation to dim targets in infrared images.
The decomposition of shearlets in the time domain consist of the multiscale partition and directional localization [24,25,26,27]. Given an image , the discrete analog of is , the discrete nonsubsampled shearlet transform (DNSST) can be described as follows:
(1) The multiscale partition. Scale is the level of the shearlet decomposition, which indicates the resolution of the shearlet coefficients. A previous image can be decomposed into a low-pass subband image and a high-pass subband at scale using the nonsubsampled Laplacian pyramid (NLP), and the subbands and have the same size of the previous subband . In this paper, we used the à trous algorithm [28] to implement DNSST, which has less computation complexity compared with other nonsubsampled operators but can meet the requirements of translation invariance for detecting targets in an original image. The algorithm is defined as:
where denotes circular convolution, and are a low-pass filter and a high-pass filter, respectively. The filters and denote that zeros will be inserted between each sample of the filters and . Thus, the high-pass image at scale can be obtained by computing iteratively by Equation (1).
(2) The directional localization. We constructed the filters using a Meyer wavelet [24] as the window function , and the shearing filters were obtained by converting the filters from the pseudo-polar back into the Cartesian coordinate system.
The Meyer wavelet is a band-limited spectrum function, whose Fourier transform is smooth. We constructed the window function by the Fourier transform of . The different directional components were obtained by simply translating the window function . The Meyer wavelet is shown in Figure 1a.
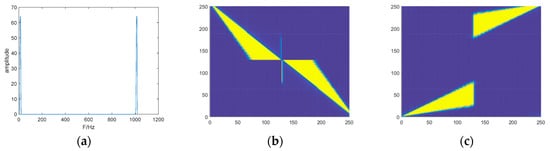
Figure 1.
The shearing filters constructed using a Meyer wavelet as the window function; (a) the window function , (b,c) are the shearing filters in two directions.
The pseudo-polar coordinates [21] are defined as follows. The pseudo-polar grid in the frequency domain is divided into two parts, which include the basic vertical lines and basic horizontal lines. This grid has often been called the concentric squares grid in signal processing, and the pseudo-radial variable has level sets which are squares rather than circles. The polar grid is the intersection between the set of radial lines and that of Cartesian lines parallel to the axes, where denotes a given radial line and is the position of the point on that line. To be more specific, the sample points along a radial line whose angle with the vertical axis is less or equal to are obtained by intersecting with the set of horizontal lines. Similarly, the intersection with the vertical lines defines our sample points whenever the angle between and the horizontal axis is less or equal to . The converted equation is defined as
where denotes the horizontal cone, denotes the vertical cone, and are the Cartesian coordinates. The shearing filters (see Figure 1b,c) were obtained after converting these filters into a Cartesian coordinate system that can be defined as
Finally, we applied the shearing filters and the discrete Fourier transform (DFT) of the high-pass image by a simple pointwise multiplication in the frequency domain, and then the shearlet coefficients can be computed by
where denotes the 2D inverse Fourier transform (IFT).
Figure 2 illustrates the shearlet transform with translation invariance at a fixed resolution level 2.
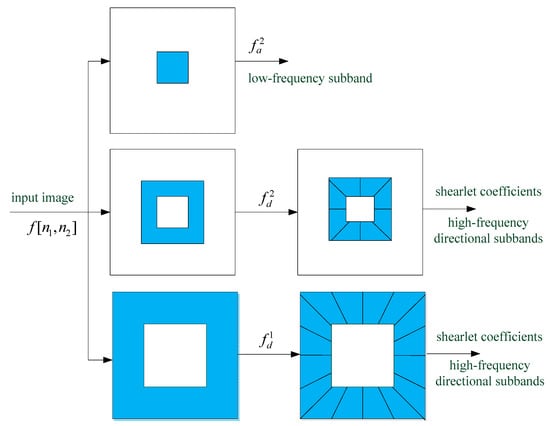
Figure 2.
The block diagram of the nonsubsampled shearlet transform (NSST) for an infrared image.
3. Dim Target Detection Using Multiple Feature Fusion and Maximum Kurtosis
It is very efficient for the shearlet transform to treat all kinds of singularities of infrared images, which can not only exactly describe its singularities with different scales, but also trace the singular curvilinear direction adaptively. In this paper, the dim target detection is implemented using multiscale feature fusion in the shearlet transform domain and searching maximum kurtosis to enhance the target. The procedure is divided into three parts: high-frequency subband fusion, maximization of kurtosis, and an adaptive threshold strategy for detecting targets.
3.1. Shearlet Decomposition and Subband Fusion
A significant advantage of the shearlet transform over the NSCT is that it is not limited to the direction numbers of shearing filters. That is, the high-frequency components at each decomposition level could be sheared in any direction at a fixed resolution level . The block diagram of NSST for an image with two-level decomposition, which is similar to the NSCT method, is shown in Figure 2. In order to eliminate the spectrum aliasing phenomenon and enhance its directional sensitivity, the particular form of the shearlet transform in our method is to use NLP with a combination of the shearing filters. For example, a low-frequency subband and some high-frequency subbands () can be obtained while we implement the NSST at scales for an original image. It was observed that the images and have the same size as the original image, where denotes the shearlet coefficients of the high-frequency subband at scale and shearing direction . The low-frequency subband is an approximate representation of the original image and preserves its cluttered background. High-frequency subbands (detail coefficients) represent some distinctive features in an infrared image, such as target, lines, and region boundaries, so that we locate and detect the dim target using the details of the shearlet transform.
The principle of multiscale feature fusion is to integrate different characteristics of modulus maximums of the shearlet coefficients at various scales and directions, which is suitable to strengthen the dim feature of targets and preserve the useful information. For subbands at various directions of each scale, local maximums appear in target regions, but it is difficult to appear at each direction simultaneously for these maximums in its cluttered background. Moreover, for subbands at various scales, local maximums of target regions increase at a larger scale. On the contrary, these large values decrease with the scale increasing for background and noise. An illustration of the characteristics using 3D graphs of the shearlet coefficients’ modulus is shown in Figure 3. The first and the second level decomposition all generate four directional subbands for the infrared image shown in Figure 3a. Figure 3b,c show that large absolute values of detail coefficients correspond to sharp intensity changes, such as the target and cloudy boundaries, that exhibit different characteristics at various directions, and these local maximums change differently at the second level. According to these characteristics, the background and noise of the infrared image are suppressed and targets can be enhanced by fusing the multiscale and multidirectional shearlet coefficients.
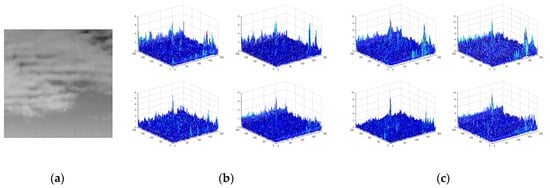
Figure 3.
3D display of the shearlet coefficients’ modulus; (a) the original infrared image; (b,c) the shearlet coefficients’ modulus of four directional subbands at the first and second level decomposition, respectively.
At the first level decomposition, the modulus maximums of shearlet coefficients appear at the target position accurately, but these coefficients are affected by a cluttered background that will generate lots of pseudo extremes at a small scale, as shown in Figure 3b. However, at the second level decomposition, the number of maximums is relatively stable because of the noise-smoothing effect at a large scale, which results in a deviation of the local maximums’ position. Therefore, in order to detect the dim target, we need to fuse the shearlet coefficients at various scales. In general, after the two-level decomposition of the image, the target can be enhanced by eliminating the background and noise, but the detection results could produce pseudo targets when the image is affected seriously by strong noise. Thus, we need to increase the number of decomposition layers. Considering the computational efficiency, we used three-level decomposition for infrared images in this paper.
Furthermore, for its sensitivity to the target, kurtosis can be used to measure the deviation of background distribution and thus detect the target. A small target corresponds to great and positive coefficients of kurtosis. However, for a large target, the corresponding coefficients of kurtosis are smaller, and can even be negative. Therefore, we found the maximum kurtosis and enhanced the corresponding locations to make the target stand out. In summary, multiscale and multidirectional feature fusion and kurtosis maximization for target detection using shearlet transform can be divided into four steps as follows.
First, a simple superposition method to fuse the shearlet coefficients at various directions of each scale was utilized. We obtained a superposed subband expression on a fixed scale:
where denotes a high-frequency subband after fusing directional shearlet coefficients’ modulus at scale , is the number of shearing directions, and denotes detail coefficients at scale and shearing direction .
Secondly, calculating the coefficients of kurtosis of the fused subband, the expression is shown as
where is a transversal vector. Each value in corresponds to a column of fused high-frequency subband. Then, we detected the highest coefficient of kurtosis as follows:
where denotes the highest coefficient of kurtosis. Then, a constructed mapping function was built to enhance the corresponding column of which included dim and small target pixels. The calculation is as follows:
where denotes an expanding gain coefficient and its value can be 5–12 generally. y represents the column with maximum kurtosis and c is a varied range of the target. According to experimental data and the general size of a dim target, we set .
Third, a normalization of subband , and the normalized image is written as
Then, a multiplication method was utilized to fuse the superposed high-frequency subbands of various sales which can realize target enhancement and cluttered background and noise suppression:
where , , and denote normalized images at scale , , and , respectively, is a spatial location, and is the image after fusing the multiscale and multidirectional shearlet coefficients.
Finally, we made the gray levels of the normalized image enlarged to the scope of gray levels . The converted image can be computed by
3.2. Adaptive Threshold with Maximum Contrast Criterion
In order to detect the dim target, we needed to choose a proper threshold to segment image . The threshold is directly related to the false alarm rate (FAR) and the missing alarm rate (MAR). The target intensity was much greater than that of clutter background intensity after using multiscale feature fusion in the shearlet transform domain, and the contrast between targets and their background had obviously changed. Therefore, we used an adaptive threshold strategy with a maximum contrast criterion (MCC) to classify the dim target and its background.
Contrast is the difference in visual properties that makes an object distinguishable from other objects and its background. In an infrared image, contrast is determined by the difference in the brightness of the target and its background. We calculate the absolute contrast as
where () denotes the average gray level, which is higher (lower) than a threshold .
The optimal segmenting threshold is the threshold that makes the maximum of and can be written as
where denotes the change interval of . Then a binary image can be obtained by segmenting image with the threshold .
The flow chart of the abovementioned algorithm for detecting a dim target in an infrared image is shown in Algorithm 1. The details of the procedure have been given in Section 3.1 and Section 3.2.
| Algorithm 1 Process of the Proposed Method for Detecting Infrared Targets |
| Input: An original infrared image. Output: Detection result. 1: Set the number of scales and directions for the shearlet transform; 2: Use a trous algorithm to implement the nonsubsampled Laplacian pyramid transform; 3: High-frequency subbands ; 4: 2D Fast Fourier transform (FFT) ; 5: Use Meyer wavelets as the window function ; 6: Translate to obtain the different directional components; 7: Convert to the Cartesian coordinate system to obtain shearing filters ; 8: ; 9: 2D inverse FFT to obtain the shearlet coefficients ; 10: High-frequency subbands at n directions of each scale; 11: Fuse the subbands by superposition; 12: Searching the maximum kurtosis and enhance the corresponding columns; 13: Normalization; 14: Fuse the high-frequency subbands at various scales by multiplication; 15: Maximum contrast threshold segmentation; 16: Output results. |
4. Experimental Results
To verify the effectiveness of the proposed method, some experiments were performed on a Celeron 2.40-GHz PC with Windows XP and the algorithm was implemented using a MATLAB 2015b development tool. Real-time infrared image sequences acquired from real scenes were characterized by small size, low contrast, and noise disturbed imaging under a complicated sky background. The tested image size was pixels, and the target SNR over the entire image was less than 2 dB. In addition, we implemented the shearing on three scales of the NLP decomposition, and the shearing filters from finer to coarser with the number of shearing directions was chosen to be 8, 8, and 8. Similarly, the NSCT detecting method of using 8, 8, and 8 directions from finer to coarser scales was chosen. Figures 5 and 6 show the experimental results.
4.1. Example of Detection Results
The selected IR images are those that include dim targets with low SNR and contrast under the cluttered and non-uniform background, which come from our field experiments. Two initial images of two sequential scenes are shown in Figures 5 and 6. The bright spot in the image plane is an interesting target (see Figures 5a and 6a, target in a white box), which only takes a few pixels, and its background includes varying clutter and clouds.
Figure 4 and Figure 6 illustrate the clutter suppression results for the infrared image using the shearlet transform and NSCT method, respectively. In Figure 4b, it can be observed that the NSCT method removes large areas of clouds and clutter due to good directional selectivity, but there are still quite a few noises adulterated in the image, which have almost the same intensity as that of the real target. By comparing and analyzing it, we know the shearlet transform can provide a much better background suppression effect than that of NSCT due to supporting the shearing filter with a small scale, which greatly improves the contrast between the target and its background and makes it easy to segment targets from the background, as shown in Figure 5c.

Figure 4.
Clutter suppression performance of the nonsubsampled contourlet transform (NSCT) and shearlet transform method; (a) the original infrared image; (b) the NSCT method; (c) the proposed method.

Figure 5.
Clutter suppression performance of the NSCT and shearlet transform method; (a) the original infrared image; (b) the NSCT method; (c) the proposed method.
The normalized 3D gray profiles of the infrared image after background and noise suppression using multiscale feature fusion in NSST and NSCT domains are shown in Figure 6, respectively. The dim target in the infrared image is represented as a pulse on its background, which is much flatter comparatively and is much easier to recognize, and both methods are of good performance. However, compared with the NSCT method, one or more steeples that strong noises take on are diminished using NSST, as shown in Figure 7b,d.
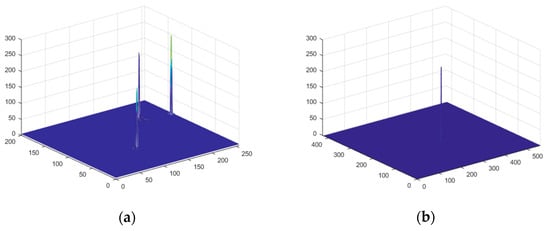
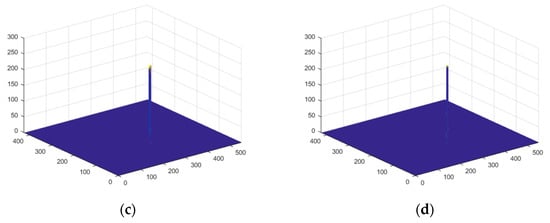

Through the background suppression, the contrast of local areas was obviously enhanced, as shown as in Figure 5b,c and Figure 6b,c. Then the adaptive threshold with MCC was applied to extract the dim target from the enhanced image. Figure 7 shows that the two methods possess an extremely high detection probability despite the low SNR images. However, as can be seen in Figure 7a, there was a false target appearing in the resulting image. This can be supposed to be a strong interference noise or clutter. Hence, with respect to this visual comparison, the shearlet transform method outperforms the NSCT method as illustrated in Figure 8a,b.
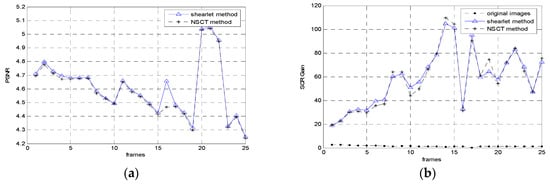
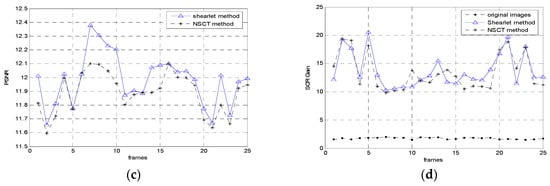
Figure 8.
Experimental comparative analysis of image sequences; (a,c) PSNR, (b,d) SCR gain.
4.2. Performance Evaluation
Other criteria is introduced to analyze how efficient our scheme is to preserve the target sinal and remove the background. These criteria include peak signal-to-noise ratio (PSNR), signal-to-clutter ratio (SCR), and the gain of signal-to-clutter ratio (GSCR), which defined as follows:
(1) PSNR (dB)
(2) SCR
(3) GSCR
where MSE denotes the mean squared error between the original image and the image processed. is the average gray level of the target areas, is the average gray level of the whole image, and is the standard variance of the background plus noise. and are the SCR of the original image and the image after clutter removal, respectively. In addition, the computation complexity (elapsed time, EST) is also used.
Table 1 gives the values of and PSNR of typical infrared images shown in Figure 5a and Figure 6a that were processed by the two methods earlier. The larger values of and PSNR mean better performance of dim target enhancement. In Table 1, the NSCT and shearlet transform approaches all have the capability in improving the value of and PSNR, which have subtle differences in different cluttered backgrounds. As for the dark target in the background with strong noise disturbance shown in Figure 5a, the shearlet transform algorithm maintains better performance illustrated by the larger values of and PSNR. In particular, the shearlet transform method consumes less time (1.4 s), and the EST reduces evidently.

Table 1.
Performance comparison of different methods. SCR: signal-to-clutter ratio; PSNR: peak signal-to-noise ratio; EST: elapsed time.
In order to give a comprehensive evaluation of the proposed algorithm, we plotted the performance comparison curves of the evaluation criteria with PSNR and SCR gain for each frame in the image sequences. The analysis results of the two methods are shown in Figure 8, which include 25 frames randomly selected from two infrared image sequences under a complicated cloudy background. It was obviously seen that the shearlet transform method had a slight improvement in terms of PSNR over the NSCT algorithm. Moreover, the shearlet transform method exhibits larger values of SCR gain in most of the frames. Evidently, we can see from the curves in Figure 8a–d that the proposed method has good performance and stability for dim detection under various situations.
In addition, the detection rate (PR) and the false alarm rate (FAR) were also used as criteria to evaluate the performance competitively. The PR denotes the ratio of the number of detected targets to the number of true targets, and the FAR is the ratio of the number of pseudo targets to the number of true targets. Statistically, Table 2 shows the PR and FAR of 100 frames of infrared images with low SNR and SCR using different methods. We can see from it that the performance of our algorithm is better than the NSCT with low FAR.

Table 2.
Comparison of the detection rate (PR) and false alarm rate (FAR) using different methods.
5. Conclusions
In this paper, we presented a novel and efficient strategy for detecting dim targets in infrared images with low SNR and SCR, which utilizes the high-frequency shearlet coefficients at various scales and directions and maximum kurtosis to realize target enhancement and cluttered background suppression. The experimental results show that the proposed algorithm has better performance than the NSCT method at detecting infrared dim targets in real image sequences. However, the single frame-based detection method may fail with pseudo targets due to the poor suppression of the strong noise and edges in infrared images. To apply it to the complicated cluttered backgrounds more effectively, we need to study the correlation or similarity between neighboring frames of infrared image sequences in the future work.
Author Contributions
L.P. proposed the original idea, performed the experiments, and wrote the manuscript. T.Z., Y.L., and M.L. reviewed and edited the manuscript. Z.P. contributed to the direction, content, and revised the manuscript.
Funding
This work is supported by National Natural Science Foundation of China (61571096, 61775030), the Key Laboratory Fund of Beam Control, Chinese Academy of Sciences (2017LBC003) and Sichuan Science and Technology Program (2019YJ0167).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, X.; Chen, Y.; Peng, Z.; Wu, J.; Wang, Z. Infrared image super-resolution reconstruction based on quaternion fractional order total variation with Lp quasinorm. Appl. Sci. 2018, 8, 1864. [Google Scholar] [CrossRef]
- Lai, R.; Yue, G.; Zhang, G. Total Variation Based Neural Network Regression for Nonuniformity Correction of Infrared Images. Symmetry 2018, 10, 157. [Google Scholar] [CrossRef]
- Jian, X.; Lv, C.; Wang, R. Nonuniformity Correction of Single Infrared Images Based on Deep Filter Neural Network. Symmetry 2018, 10, 612. [Google Scholar] [CrossRef]
- Peng, Z.; Zhang, Q.; Wang, J.; Zhang, Q.P. Dim target detection based on nonlinear multi-feature fusion by Karhunen-Loeve transform. Opt. Eng. 2004, 43, 2954–2958. [Google Scholar]
- Peng, Z.; Zhang, Q.; Guan, A. Extended target tracking using projection curves and matching pel count. Opt. Eng. 2007, 46, 066401. [Google Scholar]
- Beghdadi, A.; Negrate, A.L.; Lesegno, P.V. Entropic Thresholding Using a Block Soure Model. Comput. Model Image Process 1995, 57, 197–205. [Google Scholar] [CrossRef]
- Chan, D.S.K.; Langan, D.A.; Stayer, D.A. Spatial processing techniques for the detection of small targets in IR clutter. Proc. SPIE 1990, 1305, 53–62. [Google Scholar]
- Zhang, B.; Zhang, T.; Cao, Z.; Zhang, K. Fast new small target detection algorithm based on a modified partial differential equation in infrared clutter. SPIE Opt. Eng. 1990, 46, 106401–106406. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, L.; Zhang, T.; Cao, S.; Peng, Z. Infrared small target detection via non-convex rank approximation minimization joint l2, 1 norm. Remote Sens. 2018, 10, 1821. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, H.; Liu, Y.; Peng, L. Infrared Small Target Detection Based on Non-Convex Optimization with Lp-Norm Constraint. Remote Sens. 2019, 11, 559. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, Z. Infrared Small Target Detection Based on Partial Sum of the Tensor Nuclear Norm. Remote Sens. 2019, 11, 382. [Google Scholar] [CrossRef]
- Wang, G.D.; Chen, C.Y.; Shen, X.B. Facet-Based Infrared Small Target Detection Method. Electron. Lett. 2005, 41, 1244–1246. [Google Scholar] [CrossRef]
- Bosch, I.; Gomez, S.; Vergara, L.; Moragues, J. Infrared image processing and its application to forest fire surveillance. In Proceedings of the IEEE Conference on Advanced Video and Signal Based Surveillance, London, UK, 5–7 September 2007; pp. 283–288. [Google Scholar]
- Rosin, P.L. Training cellular automata for image processing. IEEE Trans. Image Process. 2006, 15, 2076–2087. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Yu, J.G.; Tan, Y.; Tian, J.; Ma, J. A novel spatio-temporal saliency approach for robust dim moving target detection from airborne infrared image sequences. Inf. Sci. 2016, 369, 548–563. [Google Scholar] [CrossRef]
- Leung, H.; Dubash, N.; Xie, N. Detection of Small Objects in Clutter Using a GA-RBF Neural Network. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 98–118. [Google Scholar] [CrossRef]
- DelMarco, S.; Agaian, S. The design of wavelets for image enhancement and target detection. Proc. SPIE 2009, 7351. [Google Scholar] [CrossRef]
- Tian, L.; Peng, Z. Determining the optimal order of fractional Gabor transform based on kurtosis maximization and its application. J. Appl. Geophys. 2014, 108, 152–158. [Google Scholar] [CrossRef]
- Kong, D.; Peng, Z.; Fan, H.; He, Y. Seismic random noise attenuation using directional total variation in shearlet domain. J. Seism. Explor. 2016, 25, 321–338. [Google Scholar]
- Kong, D.; Peng, Z. Seismic random noise attenuation using shearlet and total generalized variation. J. Geophys. Eng. 2015, 12, 1024–1035. [Google Scholar] [CrossRef]
- Emmanuel, J.S.; Cands, J.; Donoho, D.L. The Curvelet Transform for Image Denoising. IEEE Trans. Image Process. 2002, 6, 670–684. [Google Scholar]
- Arthur, L.; Zhou, J.; Do, M.N. The Nonsubsampled Contourlet Transform: Theory, Design and Applications. IEEE Trans. Image Process. 2006, 15, 3089–3101. [Google Scholar]
- Guo, K.; Labate, D. Optimally Sparse Multidimensional Representation using Shearlets. SIAM J. Math. Anal. 2007, 39, 298–318. [Google Scholar] [CrossRef]
- Easley, G.; Labate, D.; Lim, W. Sparse Directional Image Representation using the Discrete Shearlet Transform. Appl. Comput. Harmon. Anal. 2008, 25, 25–46. [Google Scholar] [CrossRef]
- Kutyniok, G.; Shahram, M.; Donoho, D.L. Development of a Digital Shearlet Transform Based on Pseudo-Polar FFT. Proc. SPIE 2009, 7446. [Google Scholar] [CrossRef]
- Kutyniok, G.; Sauer, T. Adaptive Directional Subdivision Schemes and Shearlet Multiresolution Analysis. SIAM J. Math. Anal. 2009, 41, 1436–1471. [Google Scholar] [CrossRef]
- Lim, W.-Q. The Discrete Shearlet Transform: A New Directional Transform and Compactly Supported Shearlet Frames. IEEE Tran. Image Process. 2010, 19, 1166–1180. [Google Scholar]
- Shensa, M.J. The discrete wavelet transform: Wedding the àtrous and mallat algorithms. IEEE Trans. Signal Process. 1992, 40, 2464–2482. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).