Abstract
Let R be a Krasner hyperring. In this paper, we prove a factorization theorem in the category of Krasner R-hypermodules with inclusion single-valued R-homomorphisms as its morphisms. Then, we prove various isomorphism theorems for a smaller category, i.e., the category of Krasner R-hypermodules with strong single-valued R-homomorphisms as its morphisms. In addition, we show that the latter category is balanced. Finally, we prove that for every strong single-valued R-homomorphism and , we have .
1. Introduction
Algebraic hyperstructure theory addresses the study of algebraic objects endowed with multivalued operations, which are intended to generalize classical algebraic structures as groups, rings, or modules [1,2,3,4,5]. In the framework of that theory, hypergroups play a major role. A hypergroup is basically a set endowed by an associative multivalued binary operation, which fulfills an additional condition called reproducibility. Their inspection may reveal complex relationships among algebra, combinatorics, graphs, and numeric sequences [6,7]. Indeed, hyperstructures are inherently more complicated and bizarre than their classical counterparts. Hence, one of the main research directions in hyperstructure theory consists of identifying a subclass of a rather generic hyperstructure on the basis of a reasonable set of axioms, symmetries, or properties and proceeding with their analysis, in order to construct a theory that is at the same time general, profound, and beautiful.
Here, we consider one of the most important classes of hypergroups, that is the class of canonical hypergroups introduced by Mittas in [8]. This class constitutes the additive hyperstructure of many other hyperstructures, for example some types of hyperrings, hyperfields, and hypermodules. Notably, hyperrings and hyperfields, whose additive hyperstructure is a canonical hypergroup, were firstly introduced by Krasner [9]. Later, various authors defined and studied many other kinds of hyperrings and hypermodules; see, e.g., [5,10,11,12]. In the context of canonical hypergroups, Madanshekaf [11] and Massouros [12] studied hypermodules whose additive structure is a canonical hypergroup equipped with a single-valued external multiplication. We call Krasner hypermodule a hypermodule equipped with a canonical hypergroup as its additive hyperstructure and an external single-valued multiplication, in order to distinguish it from other types of hypermodules. In fact, the name “Krasner” has been given to this kind of hypermodule in [13], inspired by the structure of the Krasner hyperring [9], even though such a hyperstructure has been previously considered by other authors in [11,12]. In fact, Krasner hypermodules are meant to generalize the concept of the Krasner hyperring.
In this work, our aim is to take a detailed look at isomorphism theorems for Krasner hypermodules. The relevance of isomorphism theorems is undoubtable, in all algebraic studies. In fact, in every category of algebraic structures, homomorphisms describe the relationship between objects. However, due to the multivalued nature of hyperstructure algebra, the analysis of isomorphisms on hypermodules is very involved. In fact, one encounters various kinds of homomorphisms when studying Krasner hypermodules. In [14,15,16], both single-valued and multi-valued homomorphisms were introduced; and in both classes, at least three different kinds of homomorphisms can be considered, that is the so-called inclusion homomorphisms, strong homomorphisms, and weak homomorphisms, depending on their behavior with respect to the multivalued addition. We mention that Davvaz proved in [17] that for a strong hyperring homomorphism, a first isomorphism theoremholds provided that its kernel is normal. Furthermore, Verlajan and Asokkumar proved in [18] similar results without the latter condition for a strong hyperring homomorphism in a different and more general class of hyperrings.
Here, by fixing a Krasner hyperring R, we consider the class of Krasner hypermodules over R together with inclusion, strong and weak single-valued R-homomorphisms among them (with the usual composition of mappings), and the so-called primary categories of Krasner R-hypermodules [19], which are denoted by , , and , respectively. When dealing with multivalued R-homomorphisms, the composition of morphisms is defined in a more general way, and we obtain different categories whose morphisms are multivalued R-homomorphisms. The corresponding categories, which are called secondary categories, fall outside the scope of the present work. We note in passing that in [12], Massouros worked with multivalued R-homomorphisms, while Madanshekaf in [11] considered only strong single-valued R-homomorphisms.
This paper is organized as follows. In Section 2, we state some basic concepts, definitions, and basic results needed to develop our work. Krasner hypermodules are presented in Section 3 together with their main properties. Section 4 contains the main results of this paper. In particular, by considering a generic Krasner hyperring R, Theorem 1 provides a factorization theorem in the category . Subsequently, we prove various isomorphism theorems in . The last section contains concluding remarks and a suggestion for possible further research.
2. Preliminaries
Throughout this paper, we use a few basic concepts and definitions that belong to standard terminology in hyperstructure theory. For more details about hyperstructures, the interested reader can refer to the classical references [1,2,3,4,5].
Let H be a non-empty set; let denote the set of all subsets of H; and let . Then, H together with a map:
is called a hypergroupoid and is denoted by . The operation + is called the hyperoperation on H. Let . The hyperoperation is defined as:
If there is no confusion, for simplicity , , and are denoted by a, , and , respectively.
Definition 1.
A non-empty set S together with the hyperoperation +, denoted by , is called a semihypergroup if for all , , that is, the hyperoperation is associative.
Definition 2.
A semihypergroup satisfying the reproducibility condition for every is called a hypergroup.
Let e be an element of a semihypergroup such that for all . Then, e is called a left scalar identity. A right scalar identity is defined analogously. Moreover, an element x of a semihypergroup is called a scalar identity if it is both a left and right scalar identity. A scalar identity in a semihypergroup H is unique, if it exists. In that case, we denote the scalar identity of H by . Let be the scalar identity of hypergroup and . An element is called an inverse of x in if .
Definition 3.
A non-empty set M together with the hyperoperation + is called a canonical hypergroup if the following axioms hold:
- 1.
- is a semihypergroup (associativity);
- 2.
- is commutative (commutativity);
- 3.
- there is a scalar identity (existence of scalar identity);
- 4.
- for every , there is a unique element denoted by called the inverse of x such that , which for simplicity, we write as (existence of inverse);
- 5.
- for all , it holds that (reversibility).
In the sequel, denotes the inverse of x in the hypergroup , and we write instead of . If there is no confusion, sometimes we omit the indication of the hyperoperation in a hypergroup, and for simplicity, we write M instead of .
Definition 4.
Let M be a hypergroup. A non-empty subset N of M is called a canonical subhypergroup of M, denoted by , if it is a canonical hypergroup itself.
It is easy to verify that if and only if and for all . Clearly, it follows that . Hereafter, we recall some results discussed in [20] concerning the structure of the quotient of a canonical hypergroup with respect to a canonical subhypergroup.
Let be a canonical hypergroup; let N be an arbitrary canonical subhypergroup of M; and set . Consider the hyperoperation on defined as:
For notational convenience, we may write instead of .
Lemma 1.
([20], Lemma 3.1) implies .
Proposition 1.
([20], Proposition 3.2) For every canonical hypergroup M, if , then is a canonical hypergroup.
Proposition 2.
([20], Proposition 3.3) The hyperoperation on is the same as defined by:
Finally, we recall some concepts from category theory; see, e.g., [21].
Definition 5.
In every category ,
- 1.
- a morphism is said to be a mono if for every the following implication holds:
- 2.
- a morphism is said to be an epi if for every the following implication holds:
- 3.
- A morphism of a category is called an iso in if there exists some (in ) such that and . In that case, g is denoted by .
3. Krasner Hypermodules
We start this section with a notable generalization of classical rings introduced by Krasner in [9] and called “Krasner hyperrings” by many authors; see [4,13,14,15,16,19].
Definition 6.
A non-empty set R together with the hyperoperation + and the operation · is called a Krasner hyperring if the following axioms hold:
- 1.
- is a canonical hypergroup;
- 2.
- is a semigroup including as a bilaterally-absorbing element, that is for all ;
- 3.
- and for all .
Definition 7.
Let be a hyperring, and let S be a non-empty subset of R that is closed under the maps + and · in R. If S is itself a hyperring under these maps, then S is called a subhyperring of R. A subhyperring I of R is called a left (resp., right) hyperideal if and implies (resp., ). A left and right hyperideal I is simply called a hyperideal of R.
We use the notation when the set I is a hyperideal of R. Moreover, we write if and , that is I is a proper hyperideal.
From now on, we overlook the name “Krasner” and simply use “hyperring”. Furthermore, by R, we mean a (Krasner) hyperring. Usually, R is said to have a unit element if there exists such that for every . If the element y exists, then it is unique, and we use the notation to denote it. In that case, we say that R is unitary.
Definition 8.
Let X and Y be two non-empty sets. A map sending to is called a left external multiplication on Y. That operation is naturally extended to any and by and .
Analogously to the previous definition, a right external multiplication on Y is defined by sending to .
Definition 9.
Let be a hyperring. A canonical hypergroup together with the left external multiplication is called a left Krasner hypermodule over R if for all and for all , the following axioms hold:
- 1.
- ;
- 2.
- ;
- 3.
- ;
- 4.
- .
Remark 1.
- (i)
- If A is a left Krasner hypermodule over a Krasner hyperring R, then we say that A is a left Krasner R-hypermodule. Similarly, the right Krasner R-hypermodule is defined by the map satisfying the similar properties mentioned in Definition 9 with affection on the right.
- (ii)
- If R is a hyperring with the unit element and A is a Krasner R-hypermodule satisfying (resp. ) for all , then A is said to be a unitary left (resp. right) Krasner R-hypermodule.
- (iii)
- From now on, for convenience, every hyperring R is assumed to have the unit element and by “an R-hypermodule A”, we mean a unitary left Krasner R-hypermodule, unless otherwise stated.
Definition 10.
A non-empty subset B of an R-hypermodule A is said to be an R-subhypermodule of A, denoted by , if B is an R-hypermodule itself, that is for all and all , and .
Remark 2.
We list here below some examples and properties related to R-subhypermodules, whose simple proofs are omitted for brevity:
- 1.
- Every hyperring R is an R-hypermodule, and every is an R-subhypermodule of R.
- 2.
- Let R be a hyperring. Every canonical hypergroup A can be considered as an R-hypermodule with the trivial external multiplication for every and .
- 3.
- Let A be an R-hypermodule and . For every ,is an R-subhypermodule of A.
- 4.
- Let be a family of R-subhypermodules of A. Then, .
Definition 11.
Let A and B be R-hypermodules. A function that satisfies the conditions:
- 1.
- ;
- 2.
for all and all , is said to be an (inclusion) R-homomorphism from A into B. Moreover, if the equality holds in Point 1, then f is called a strong (or good) R-homomorphism; and if holds instead of 1, then f is called a weak R-homomorphism.
The category whose objects are all R-hypermodules and whose morphisms are all R-homomorphisms is denoted by . The class of all R-homomorphisms from A into B is denoted by . Moreover, we denote by (resp., ) the category of all R-hypermodules whose morphisms are strong (resp., weak) R-homomorphisms. The class of all strong (resp., weak) R-homomorphisms from A into B is denoted by (resp., ). It is easy to see that is a subcategory of , and is a subcategory of . Using standard notations, we express this as:
The categories are usually called the primary categories of R-hypermodules; see, e.g., [19].
Now, let , and define:
For further reference, we gather hereafter some information about and from [13]:
- is an R-subhypermodule of A.
- Clearly, may not be an R-subhypermodule of B.
- For every morphism f in , is always an R-subhypermodule of the codomain of f.
Recall that if A is an R-hypermodule and B is a non-empty subset of A such that B is itself a hypermodule over R, then B is said to be an R-subhypermodule of B denoted by . Clearly, for every R-hypermodule A, and A are two R-subhypermodules of A. In the following, we construct another R-hypermodule from A and called the quotient R-hypermodule.
Proposition 3.
Let be an R-hypermodule. Then, the canonical hypergroup with the hyperoperation defined as in (1) is an R-hypermodule with the external multiplication ⊙ defined by:
for and .
Proof.
As mentioned in Proposition 1, is a canonical hypergroup. First, we show that ⊙ is well defined. Hence, let and . We prove that . In fact, since for , we have , so . Consequently . Analogously, . Thus, and ⊙ is well defined.
Next, we check the axioms mentioned in Definition 9. Let and . Clearly, , in A. Moreover, the zero element of is (or B). Therefore, and imply that Axiom 4 of Definition 9 holds true. In order to prove the first axiom of Definition 9, note that:
Furthermore, the second axiom of Definition 9 holds. Indeed,
By Proposition 2,
Thus:
Finally, as concerns the third axiom of Definition 9, we have:
and the proof is complete. □
4. Main Results
Factorization theorems are keystone results in abstract algebra. Indeed, these kinds of theorems relate the structure of two objects between which a homomorphism is given, in terms of the kernel and the image of the homomorphism. Moreover, they are preliminary steps toward more stringent results, where homomorphisms are replaced by isomorphisms. We start this section with a factorization theorem for an R-homomorphism between R-hypermodules.
Theorem 1.
(Factorization theorem) Let . If C is any R-subhypermodule included in , then there exists a unique R-homomorphism such that , where is the canonical quotient map. Hence, the diagram:
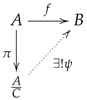 commutes.
commutes.

Proof.
By assumption, . Define by . Clearly, makes the diagram commute. Now, we need to check that it is a unique well-defined R-homomorphism.
Suppose that . Then, . Clearly, implies . Then, there is with . Thus, . Therefore, . Consequently, . Therefore, , and is well defined.
Moreover,
Now, assume . Then:
Suppose there is another map satisfying the conditions. Then, for all , but for all . This means and . Thus, , so that it is unique. □
A mono in the category (resp., ) is called an R-monomorphism (resp., strong R-monomorphism). An epi in the category (resp., ) is called an R-epimorphism (resp., strong R-epimorphism). An iso in the category (resp., ) is called an R-isomorphism (resp., strong R-isomorphism). When we say is an R-isomorphism in , automatically, f is a strong R-homomorphism.
Remark 3.
We point out some properties of R-isomorphisms in and .
- (i)
- An iso in the category (or an R-isomorphism) is surjective and injective, i.e., bijective. For this, let be an iso in . Therefore, and . Clearly, implies f is surjective. Furthermore, if , then implies that .
- (ii)
- is an R-isomorphism in if and only if it is bijective. To show this fact, suppose is bijective. Then, is also an R-homomorphism. Indeed, for every , there are (unique) such that for , and since , we obtain . Finally, implies , and so, is an R-homomorphism. Therefore, and , and f is an R-isomorphism. The converse fact follows from (i) since every R-isomorphism in is an R-isomorphism in .
Notation 1.
If there exists an iso between R-hypermodules A and B in (resp., ), we use the notation (resp., ). Moreover, if and , for convenience, we use instead of .
Theorem 2.
(First strong isomorphism theorem) If , then:
as R-hypermodules.
Proof.
First note that is an R-subhypermodule of B. Let . Define a map by for all . Suppose that , where . Then, and for some . Hence,
Therefore, . Thus, , and the map f is well defined.
If , then:
On the other hand,
Hence, . Moreover,
Thus, f is an R-homomorphism. Let be such that . Then, . This means that , that is for some . Therefore, . Now,
Since and is a partition for A, we have , i.e., , and hence, f is injective. Clearly, f is surjective. Thus, according to the part (ii) of Remark 3, we have , and the proof is complete. □
Theorem 3.
(Second strong isomorphism theorem) If A and B are R-subhypermodules of an R-hypermodule H, then in .
Proof.
It is clear that we can consider the R-subhypermodule of the R-hypermodule H as an R-hypermodule for which A is an R-subhypermodule. Similarly, the R-subhypermodule B of the R-hypermodule H as an R-hypermodule B for which is an R-subhypermodule. Hence, define by for every . For all ,
Furthermore,
Thus, g is a strong R-homomorphism. Now, implies that for some . That is, for some , . Since , we get by Lemma 1. Thus, , and g is surjective.
Finally, let . Then,
Thus, if and only if . Hence, by the first strong isomorphism theorem, and the theorem is proved. □
Theorem 4.
(Third strong isomorphism theorem) If A and B are R-subhypermodules of an R-hypermodule H such that , then .
Proof.
Define a map by . Then, h is a strong and surjective R-homomorphism with . Therefore, by the first strong isomorphism theorem, , and we have the claim. □
Proposition 4.
(i) Let or . Then, f is an R-monomorphism if and only if it is injective. (ii) is injective if and only if .
Proof.
- (i)
- (⇐) It is clear.(⇒) Let (resp., ) be an R-monomorphism and . Then, for an arbitrary . Now, define with and for each . Clearly, . Since f is monic, we have . Therefore, implies .
- (ii)
- (⇐) Let and . Therefore, . Thus, there is such that . By assumption, . Now, implies .(⇒) Let and f is injective. Therefore, . On the other hand . Thus, by injectivity. □
Corollary 1.
In the category , is an R-monomorphism if and only if .
Proposition 5.
(i) In the category , every surjective R-homomorphism is an R-epimorphism. (ii) In the category , an R-homomorphism is an R-epimorphism if and only if it is surjective.
Proof.
- (i)
- Let be surjective, and let . If , then for all , we have . Now, let . Clearly, there is such that . Thus, . Hence, f is an R-epimorphism.
- (ii)
- (⇐) It is clear from (i).(⇒) Let be an R-epimorphism and . Suppose f is not surjective. Then, . Define with and . Then, clearly, , but . This contradiction shows that f is surjective. □
A morphism is said to be a bimorphism if it is a mono, as well as an epi. A category is said to be balanced when a morphism is a bimorphism if and only if it is an iso.
Proposition 6.
The category is balanced. □
Proof.
is a bimorphism if and only if f is bijective by Propositions 4(i) and 5(ii) if and only if f is an R-isomorphism by Remark 3(ii). □
We conclude this section with a result concerning .
Proposition 7.
Let and . Let
Then, .
Proof.
Setting , we have:
and the proof is complete. □
5. Conclusions
Krasner hypermodules have been already considered from the standpoint of category theory by various authors in, e.g., [11,12,13,15], focusing on the properties of different types of homomorphisms, notably the so-called inclusion homomorphisms, strong homomorphisms, and weak homomorphisms, according to their behavior with respect to the multivalued addition. Since morphisms play an important role in every category, one needs a clear understanding of fundamental theorems concerning homomorphisms, such as factorization and isomorphism theorems, in order to pursue fundamental studies in category theory. In this paper, we first studied the primary categories of Krasner hypermodules over a Krasner hyperring, introduced in [19]. In particular, we proved factorization and isomorphism theorems regarding both inclusion and strong single-valued homomorphisms as their morphisms. Moreover, we focused on strong isomorphism theorems between quotient hypermodules, and we showed that the category of Krasner R-hypermodules with strong single-valued homomorphisms is balanced. Arguably, analogous results may have a different and more complex form in other categories of (general) Krasner hypermodules, depending on multivalued homomorphisms. On the basis of preliminary results presented in [13,15,19], we believe that the exploration of factorization and isomorphism theorems for multivalued homomorphisms between hypermodules is a possible direction for further research.
Author Contributions
Writing, original draft preparation, H.S.; writing, review and editing, D.F.
Funding
The work of D.F. was partially supported by the department research project ICON, DMIF-PRID 2017, University of Udine, Italy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Corsini, P. Prolegomena of Hypergroup Theory, 2nd ed.; Aviani editore: Tricesimo, Italy, 1993. [Google Scholar]
- Corsini, P.; Leoreanu-Fotea, V. Applications of Hyperstructures Theory; Kluwer Academic Publisher: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Davvaz, B. Polygroup Theory and Related Systems; World Scientific: Hackensack, NJ, USA, 2013. [Google Scholar]
- Davvaz, B.; Leoreanu-Fotea, V. Hyperring Theory and Applications; International Academic Press: Palm Harbor, FL, USA, 2007. [Google Scholar]
- Vougiouklis, T. Hyperstructures and Their Representations; Hadronic Press Inc.: Palm Harber, FL, USA, 1994. [Google Scholar]
- De Salvo, M.; Fasino, D.; Freni, D.; Lo Faro, G. Fully simple semihypergroups, transitive digraphs, and sequence A000712. J. Algebra 2014, 415, 65–87. [Google Scholar] [CrossRef]
- Fasino, D.; Freni, D. Minimal order semihypergroups of type U on the right. Mediterranean J. Math. 2008, 5, 295–314. [Google Scholar] [CrossRef]
- Mittas, M. Hypergroupes canoniques. Math. Balkanica 1972, 2, 165–179. [Google Scholar]
- Krasner, M. A class of hyperrings and hyperfelds. Internat. J. Math. Math. Sci. 1983, 6, 307–311. [Google Scholar] [CrossRef]
- Ameri, R. On categories of hypergroups and hypermodules. J. Discrete Math. Sci. Cryptogr. 2003, 6, 121–132. [Google Scholar] [CrossRef]
- Madanshekaf, A. Exact category of hypermodules. Internat. J. Math. Math. Sci. 2006. [Google Scholar] [CrossRef]
- Massouros, C.G. Free and cyclic hypermodules. Ann. Mat. Pura Appl. 1988, 150, 153–166. [Google Scholar] [CrossRef]
- Shojaei, H.; Ameri, R. Some results on categories of Krasner hypermodules. J. Fundam. Appl. Sci. 2016, 8, 2298–2306. [Google Scholar]
- Shojaei, H.; Ameri, R. Some unavoidable questions about Krasner hypermodules. Int. J. Open Probl. Compt. Math. 2018, 11, 38–46. [Google Scholar]
- Shojaei, H.; Ameri, R.; Hoskova-Mayerova, S. On properties of various morphisms in the categories of general Krasner hypermodules. Ital. J. Pure Appl. Math. 2017, 39, 475–484. [Google Scholar]
- Shojaei, H.; Ameri, R.; Hoskova-Mayerova, S. Pre-semihyperadditive categories. An. Sti. U. Ovid. Co-Mat. 2019, 27, 269–288. [Google Scholar]
- Davvaz, B. Isomorphism theorems of hyperrings. Indian J. Pure Appl. Math. 2004, 35, 321–331. [Google Scholar]
- Velrajan, M.; Asokkumar, A. Note on isomorphism theorems of hyperrings. Internat. J. Math. Math. Sci. 2010. [Google Scholar] [CrossRef]
- Shojaei, H.; Ameri, R. Various kinds of freeness in the categories of Krasner hypermodules. Int. J. Anal. Appl. 2018, 16, 793–808. [Google Scholar]
- Shojaei, H.; Ameri, R. Various Kinds of Quotient of a Canonical Hypergroup. Sigma J. Eng. Nat. Sci. 2018, 9, 133–141. [Google Scholar]
- Awody, S. Category Theory; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).