Non-Coercive Radially Symmetric Variational Problems: Existence, Symmetry and Convexity of Minimizers

Abstract

We prove the existence of radially symmetric solutions and the validity of Euler–Lagrange necessary conditions for a class of variational problems with slow growth. The results are obtained through the construction of suitable superlinear perturbations of the functional having the same minimizers of the original one.

1. Introduction

This paper is concerned with the variational problem

$$\underset{u\in W_0^{1,1}\left(B_R\right)}{min}{\int }_{B_R}\left[g\left(\right|x|,|\nabla u\left|\right)+h\left(\right|x|,u)\right]dx,$$

where $B_R\subseteq {\mathbb{R}}^N$ is the open ball centered at the origin and with radius $R>0$.

Under the sole assumptions of increasing monotonicity of the Lagrangian with respect to the gradient variable, one can prove, by means of a symmetrization procedure proposed in Reference [1], that the problem admits a one–dimensional reduction, obtained by evaluating the functional only on the set of radially symmetric functions (see Section 3).

This reduction step leads to consideration of the minimum problem

$$\underset{u\in {\mathcal{W}}_{\mathrm{rad}}^1}{min}{\int }_0^R{r}^{N-1}\left[g\right(r,|u^{\prime }\left(r\right)\left|\right)+h(r,u\left(r\right))]dr$$

on the space

$${\mathcal{W}}_{\mathrm{rad}}^1:=\left\{u\in A{C}_{\mathrm{loc}}\left(\right]0,R\left]\right):u\left(R\right)=0,r^{N-1}\left|u^{\prime }\left(r\right)\right|\in L^1\left(\right]0,R\left[\right)\right\}.$$

The qualitative features of the Lagrangian are that $g(r,·)$ is convex (in fact this assumption can be dropped in the autonomous case, see Corollary 2) and with, at least, linear growth, while $h(r,t)$ is Lipschitz continuous in the t variable. These assumptions do not assure that every minimizing sequence of the functional is precompact in $L^1$, and hence the direct methods of Calculus of Variations fail.

For this reason, indirect methods, based on the solvability of the associated Euler–Lagrange equations, have often been adopted in the literature (see References [2,3,4,5,6,7,8,9,10,11,12,13]). Specifically, if the Lagrangian is convex with respect to both variables u and $|u^{\prime }|$, then any solution of the Euler–Lagrange conditions provides a minimizer, and vice-versa.

The main feature of the present work is that we do not require convexity of the Lagrangian in the u variable, so that the above mentioned indirect methods cannot be implemented, and a brand-new approach is needed.

Our starting points are an existence result and the validity of the Euler–Lagrange necessary conditions under the additional requirement that $g(r,·)$ has superlinear growth. These properties can be easily obtained by applying well-known results (see Step 1 of the proof of Theorem 2). Exploiting the necessary conditions, we obtain explicit a-priori estimates on the derivative of minimizers of superlinear functionals, that depend on the Lipschitz constant of $h(r,·)$.

When $g(r,·)$ satisfies only a linear growth condition, say $g(r,s)\ge Ms-C$ for some positive constants M and C, and the Lipschitz constant of $h(r,·)$ is not too large compared with M (see the compatibility relation (hgr) between g and h in the statement of Theorem 2), then we proceed as follows. As a first step, we construct an ad-hoc superlinear perturbation of the slow growth functional, for which we have a Lipschitz minimizer satisfying some a-priori estimates. Then, relying on these estimates, we show that this function is in fact a minimizer of the original slow-growth problem.

In some sense, our technique is reminiscent of the semiclassical approach, based on the construction of barrier functions, for the minimization of functionals of the type ${\int }_{\mathsf{\Omega }}L(\nabla u)dx$ on functions $u\in W^{1,1}\left(\mathsf{\Omega }\right)$ satisfying some prescribed boundary condition (see, e.g., Reference [14], Chapter 1).

As an application of our results, in Section 5 we prove existence of convex Lipschitz continuous minimizers for variational problems with a constraint on the gradient. For related convexity results, obtained by means of convex rearrangements, see Reference [15,16].

Finally, we believe that our techniques can also be successfully implemented for minimization problems related to slow-growth integral functionals ${\int }_{\mathsf{\Omega }}\left[g\right(|\nabla u|)+h\left(u\right)]dx$ in a space of functions depending only on the distance from the boundary of $\mathsf{\Omega }$ (see, e.g., References [17,18,19,20,21,22,23,24,25,26,27,28]).

2. Notation and Preliminaries

In what follows $|·|$ will denote the Euclidean norm in ${\mathbb{R}}^N$, $N\ge 1$, and $B_R\subset {\mathbb{R}}^N$ is the open ball centered at the origin and with radius $R>0$.

We shall denote by $\overline{A}$ and $intA$ respectively the closure and the interior of a set A, and by $Dom\phi$ the essential domain of an extended real–valued function $\phi :A\to ]-\infty ,+\infty ]$, that is, $Dom\phi =\{x\in A:\phi (x)<+\infty \}$. We shall always consider proper functions, that is $Dom\phi \ne \varnothing$.

Given a locally Lipschitz function $\phi :A\subset \mathbb{R}\to \mathbb{R}$, for every $x\in A$ we denote by $\partial \phi \left(x\right)$ its generalized gradient at x in the sense of Clarke (see Reference [29], Chapter 2). We recall that, if x is an interior point of A, then $\partial \phi \left(x\right)$ is a non-empty, convex, compact set (see Reference [29], Proposition 2.1.2(a)). Moreover, if $D\subset A$ denotes the set of points where $\phi$ is differentiable, then

$$\partial \phi \left(x\right)=conv\left\{\underset{j}{lim}{\phi }^{\prime }\left(x_j\right):\left(x_j\right)\subset D,x_j\to x\right\}$$

(see Reference [29], Theorem 2.5.1). Hence, if $\phi :\mathbb{R}\to \mathbb{R}$ is a monotone non-decreasing K-Lipschitz function, then $\varnothing \ne \partial \phi \left(x\right)\subseteq [0,K]$ for every $x\in \mathbb{R}$.

For notational convenience, if $\phi$ also depends on an additional variable $r\in \mathbb{R}$, we denote by $\partial \phi (r,x)$ the generalized gradient of the function $x\mapsto \phi (r,x)$.

If $\phi :\mathbb{R}\to ]-\infty ,+\infty ]$ is a lower semicontinuous convex function, the generalized gradient $\partial \phi \left(x\right)$ coincides with the subgradient (in the sense of convex analysis) at every point $x\in intDom\phi$, and hence $\partial \phi \left(x\right)=[{\phi }_{-}^{\prime }\left(x\right),{\phi }_{+}^{\prime }\left(x\right)]$, where ${\phi }_{-}^{\prime }\left(x\right)$ and ${\phi }_{+}^{\prime }\left(x\right)$ are the left and right derivative of $\phi$ at x (see Reference [29], Proposition 2.2.7). We shall often use the following implication, due to the monotonicity of the subgradient:

$$p\in \partial \phi \left(x\right),q\in \partial \phi \left(y\right),\mathrm{and}p<q⟹x\le y.$$

If $\phi :\mathbb{R}\to ]-\infty ,+\infty ]$, we denote by ${\phi }^{*}$ its Fenchel–Legendre transform, or conjugate function (see Reference [30], Section I.4). With some abuse of notation, if $\phi :[0,+\infty [\to ]-\infty ,+\infty ]$, we use ${\phi }^{*}$ to denote the Fenchel–Legendre transform of the even function $\mathbb{R}\ni z\mapsto \phi \left(\right|z\left|\right)$, so that

$${\phi }^{*}\left(p\right)=\underset{x\in \mathbb{R}}{sup}\{px-\phi (\left|x\right|\left)\right\}.$$

We remark that, in this case, ${\phi }^{*}$ is a lower semicontinuous convex even function.

If $\phi$ is a lower semicontinuous convex function, its subgradient and the subgradient of the conjugate function are related in the following way:

$$p\in \partial \phi \left(x\right)⟺x\in \partial {\phi }^{*}\left(p\right)$$

(see Reference [30], Corollary I.5.2).

We say that $f:[0,R]\times \mathbb{R}\times [0,+\infty [\to ]-\infty ,+\infty ]$ is a normal integrand if $f(r,·,·)$ is lower semicontinuous for almost every (a.e.) $r\in [0,R]$, and there exists a Borel function $\widehat{f}:[0,R]\times [0,+\infty [\to ]-\infty ,+\infty ]$ such that $\widehat{f}(r,·,·)=f(r,·,·)$ for a.e. $r\in [0,R]$ (see Reference [30], Definition VIII.1.1).

3. Symmetry of Minimizers

In this section we deal with the symmetry properties of minimizers in $W_0^{1,1}\left(B_R\right)$ of functionals of the form

$$F\left(u\right):={\int }_{B_R}f\left(\right|x|,u,|\nabla u\left|\right)dx$$

under very mild assumptions on the Lagrangian f.

Our aim is to prove that the minimization problem for F in $W_0^{1,1}\left(B_R\right)$ is, in fact, equivalent to the minimization problem for the one–dimensional functional

$$F_{\mathrm{rad}}\left(u\right):={\int }_0^R{r}^{N-1}f(r,u\left(r\right),|u^{\prime }\left(r\right)\left|\right)dr,$$

(1)

in the functional space

$${\mathcal{W}}_{\mathrm{rad}}^1:=\left\{u\in A{C}_{\mathrm{loc}}\left(\right]0,R\left]\right):u\left(R\right)=0,r^{N-1}\left|u^{\prime }\left(r\right)\right|\in L^1\left(\right]0,R\left[\right)\right\}.$$

(2)

Remark 1.

Notice that the functional $F_{\mathrm{rad}}$ is, up to a constant factor, the functional F evaluated on the radially symmetric functions belonging to $W_0^{1,1}\left(B_R\right)$. In particular, we underline that every function $u\in {\mathcal{W}}_{\mathrm{rad}}^1$ satisfies

$$r^{N-1}\left|u\left(r\right)\right|\le {\int }_r^R{\rho }^{N-1}|u^{\prime }\left(\rho \right)|d\rho \le \parallel {\rho }^{N-1}{u}^{\prime }{\left(\rho \right)\parallel }_{L^1}\forall r\in ]0,R],$$

so that $r^{N-1}\left|u\left(r\right)\right|\in L^{\infty }\left([0,R]\right)$.

We adopt a symmetrization procedure introduced in Reference [1]. Given a representative of $u\in W_0^{1,1}\left(B_R\right)$, and $\theta \in \partial B_1$, let

$$u_{\theta }\left(x\right):=u\left(\theta \right|x\left|\right),x\in B_R,$$

(3)

be the radial symmetric function obtained from the profile of u along the straight line through 0 and with direction $\theta$.

In Reference [1], Lemma 3.1, it is proved that $u_{\theta }\in W_0^{1,1}\left(B_R\right)$ for a.e. $\theta \in \partial B_1$, and

$$|\nabla u_{\theta }\left(x\right)|=\left|\theta ·\nabla u\left(\theta \right|x\left|\right)\frac{x}{\left|x\right|}\right|\le |\nabla u(\theta \left|x\right|\left)\right|.$$

(4)

Following the lines of the proof of Reference [1], Theorem 3.4, we show that, for some $\theta$, $u_{\theta }$ is a better competitor than u in the minimization problem for F.

Theorem 1.

Let $f:[0,R]\times \mathbb{R}\times [0,+\infty [\to ]-\infty ,+\infty ]$ be a normal integrand such that for almost every $(r,t)\in [0,R]\times \mathbb{R}$, the map $s\mapsto f(r,t,s)$ is monotone non-decreasing. Then for every $u\in W_0^{1,1}\left(B_R\right)$ there exists a radially symmetric function $v\in W_0^{1,1}\left(B_R\right)$ such that $F\left(v\right)\le F\left(u\right)$. In particular, if F admits minimizers in $W_0^{1,1}\left(B_R\right)$, then it admits a radially symmetric minimizer.

If, in addition, for almost every $(r,t)\in [0,R]\times \mathbb{R}$, the map $s\mapsto f(r,t,s)$ is strictly monotone increasing, then every minimizer of F in $W_0^{1,1}\left(B_R\right)$ is a radially symmetric function.

Proof. 

Let u be a function in $W_0^{1,1}\left(B_R\right)$ such that $F\left(u\right)<+\infty$, and let $u_{\theta }$ be the radially symmetric function defined in (3). We claim that,

$$\frac{1}{{\mathcal{H}}^{N-1}(\partial B_1)}{\int }_{\partial B_1}F\left(u_{\theta }\right)d\theta \le F\left(u\right),$$

(5)

where ${\mathcal{H}}^{N-1}$ is the $(N-1)$-dimensional Hausdorff measure. Namely, observing that

$$u_{\theta }\left(r\omega \right)=u_{\theta }\left(r\theta \right)=u\left(r\theta \right),\forall \omega ,\theta \in \partial B_1,$$

using (4) and the monotonicity property of the Lagrangian f, we obtain that

$$\begin{array}{cc}\hfill \frac{1}{{\mathcal{H}}^{N-1}(\partial B_1)}{\int }_{\partial B_1}F\left(u_{\theta }\right)d\theta & ={\int }_{\partial B_1}{\int }_{\partial B_1}{\int }_0^{R}f(r,u_{\theta }\left(r\omega \right),|\nabla u_{\theta }\left(r\omega \right)\left|\right)r^{N-1}drd\omega d\theta \hfill \\ & ={\int }_{\partial B_1}{\int }_{\partial B_1}{\int }_0^{R}f(r,u_{\theta }\left(r\theta \right),|\nabla u_{\theta }\left(r\theta \right)\left|\right)r^{N-1}drd\omega d\theta \hfill \\ & \le {\int }_{\partial B_1}{\int }_{\partial B_1}{\int }_0^{R}f(r,u\left(r\theta \right),|\nabla u\left(r\theta \right)\left|\right)r^{N-1}drd\omega d\theta =F\left(u\right).\hfill \end{array}$$

From (5) follows that there exists a set $\mathsf{\Theta }\subseteq \partial B_1$, with ${\mathcal{H}}^{N-1}\left(\mathsf{\Theta }\right)>0$, such that $F\left(u_{\theta }\right)\le F\left(u\right)$ for every $\theta \in \mathsf{\Theta }$. Moreover, if u is a minimizer for F, then $F\left(u_{\theta }\right)\ge F\left(u\right)$ for a.e. $\theta \in \partial B_1$, and (5) implies that

$$F\left(u_{\theta }\right)=F\left(u\right)\mathrm{for}{\mathcal{H}}^{N-1}–\mathrm{a}.\mathrm{e}.\theta \in \partial B_1,$$

(6)

hence almost every $u_{\theta }$ is a (radially symmetric) minimizer of F.

Assume now that for almost every $(r,t)\in [0,R]\times \mathbb{R}$, the map $s\mapsto f(r,t,s)$ is strictly monotone increasing, and let u be a minimizer for F. From the computation above, we deduce that (6) holds if and only if

$$f(r,u_{\theta }\left(r\theta \right),|\nabla u_{\theta }\left(r\theta \right)\left|\right)=f(r,u\left(r\theta \right),|\nabla u\left(r\theta \right)\left|\right)\mathrm{for}\mathcal{L}\times {\mathcal{H}}^{N-1}–\mathrm{a}.\mathrm{e}.(r,\theta )\in [0,R]\times \partial B_1.$$

Since $u_{\theta }\left(r\theta \right)=u\left(r\theta \right)$ for a.e. $(r,\theta )$, from the strict monotonicity assumption on f we deduce that $|\nabla u_{\theta }\left(r\theta \right)|=|\nabla u\left(r\theta \right)|$ for $\mathcal{L}\times {\mathcal{H}}^{N-1}$–a.e. $(r,\theta )$, hence, from (4), we obtain that $\nabla u\left(r\theta \right)$ is parallel to $\theta$ and then u is radially symmetric (see Reference [1], Lemma 3.3). □

As a consequence of Theorem 1, we obtain the following 1–dimensional reduction of the minimum problem.

Corollary 1.

Let f be as in Theorem 1. Then the minimization problem

$$min\{F\left(u\right):u\in W_0^{1,1}\left(B_R\right)\}$$

(7)

admits a solution if and only if the one-dimensional minimization problem

$$min\{F_{\mathrm{rad}}\left(u\right):u\in {\mathcal{W}}_{\mathrm{rad}}^1\}$$

(8)

admits a solution, where $F_{\mathrm{rad}}$ and ${\mathcal{W}}_{\mathrm{rad}}^1$ are defined in (1) and (2) respectively.

Proof. 

If problem (7) admits a solution $u\in W_0^{1,1}\left(B_R\right)$, then by Theorem 1 there exists a radially symmetric function $v\in W_0^{1,1}\left(B_R\right)$ such that $F\left(v\right)\le F\left(u\right)$, hence $\overline{v}\left(r\right):=v\left(\right|x\left|\right)$ is a solution to problem (8).

Assume now that problem (8) admits a solution $\overline{u}\in {\mathcal{W}}_{\mathrm{rad}}^p$, and let us prove that $u\left(x\right):=\overline{u}\left(\right|x\left|\right)$ is a solution to (7). Namely, if we assume by contradiction that there exists a function $v\in W_0^{1,1}\left(B_R\right)$ such that $F\left(v\right)<F\left(u\right)$, then by Theorem 1 there exists a radially symmetric function $w\in W_0^{1,1}\left(B_R\right)$ such that $F\left(w\right)\le F\left(v\right)$, so that the function $\overline{w}\left(r\right):=w\left(\right|x\left|\right)$ satisfies $F_{\mathrm{rad}}\left(\overline{w}\right)<F_{\mathrm{rad}}\left(\overline{u}\right)$, a contradiction. □

4. Existence of Minimizers and Euler–Lagrange Inclusions

In this section, we focus our attention on functionals of the form

$$F\left(u\right):={\int }_{B_R}\left[g\left(\right|x|,|\nabla u\left|\right)+h\left(\right|x|,u)\right]dx,u\in W_0^{1,1}\left(B_R\right),$$

whose corresponding one-dimensional functional is

$$F_{\mathrm{rad}}\left(u\right):={\int }_0^R{r}^{N-1}\left[g\right(r,|u^{\prime }\left(r\right)\left|\right)+h(r,u\left(r\right))]dr,u\in {\mathcal{W}}_{\mathrm{rad}}^1.$$

We prove the existence of radially symmetric Lipschitz continuous minimizers, and the validity of necessary optimality conditions of Euler–Lagrange type, when g is a convex function with possibly linear growth in the gradient variable, and h is a Lipschitz continuous function with respect to u.

As usual, the Euler–Lagrange conditions involve a pair $(\overline{u},p)$, where $\overline{u}$ is a minimizer in ${\mathcal{W}}_{\mathrm{rad}}^1$, while the function p belongs to the space

$${\mathcal{W}}_{\mathrm{rad}}^{1,*}:=\left\{p\in AC\left([0,R]\right):p\left(0\right)=0,r^{1-N}{p}^{\prime }\left(r\right)\in L^1\left(\right]0,R\left[\right)\right\}.$$

We call p a momentum associated with $\overline{u}$.

Theorem 2.

Let $g:[0,R]\times [0,+\infty [\to [0,+\infty ]$, and $h:[0,R]\times \mathbb{R}\to \mathbb{R}$ satisfy:

(g1r) 

g is a normal integrand, the function $z\mapsto g(r,|z\left|\right)$ is convex for a.e. $r\in [0,R]$, and $r^{N-1}g(r,0)\in L^1\left(\right]0,R\left[\right)$.

(g2r) 

There exists a function $\psi :[0,+\infty [\to [0,+\infty [$ such that

$$fora.e.r\in [0,R]:g(r,s)-g(r,0)\ge \psi \left(s\right)\forall s\ge 0,$$

and $M:={lim\; inf}_{s\to +\infty }\psi \left(s\right)/s>0$.

(h1r) 

h is a Borel function, $r^{N-1}h(r,0)\in L^1\left(\right]0,R\left[\right)$, and there exists $H_0\in L^1\left(\right]0,R\left[\right)$ such that

$$fora.e.r\in [0,R]:|h(r,t)-h(r,\tau )|\le H_0\left(r\right)|t-\tau |\forall t,\tau \in \mathbb{R}.$$

(hgr) 

The functions g and h are related by the condition

$$M_0:=\underset{r\in ]0,R]}{sup}{r}^{1-N}{\int }_0^r{\rho }^{N-1}{H}_0\left(\rho \right)d\rho <M.$$

Then the following holds true.

(i) 

F admits a radially symmetric minimizer in $W_0^{1,1}\left(B_R\right)$, and $F_{\mathrm{rad}}$ admits a minimizer in ${\mathcal{W}}_{\mathrm{rad}}^1$.

(ii) 

Every minimizer of $F_{\mathrm{rad}}$ is Lipschitz continuous.

(iii) 

For every minimizer $\overline{u}\in {\mathcal{W}}_{\mathrm{rad}}^1$ of $F_{\mathrm{rad}}$ there exists $p\in {\mathcal{W}}_{\mathrm{rad}}^{1,*}$ such that the following Euler–Lagrange inclusions hold:

$$\begin{array}{c}{p}^{\prime }\left(r\right)\in r^{N-1}\partial h(r,\overline{u}\left(r\right)),fora.e.r\in [0,R],\end{array}$$

(9)

$$\begin{array}{c}p\left(r\right)\in r^{N-1}\partial g(r,|{\overline{u}}^{\prime }\left(r\right)\left|\right),fora.e.r\in [0,R].\end{array}$$

(10)

Remark 2.

In (g2r) it is not restrictive to assume that ψ is a non-decreasing function, with $\psi \left(0\right)=0$, and that $\mathbb{R}\ni z\mapsto \psi \left(\right|z\left|\right)$ is convex and smooth (possibly replacing ψ with a suitable regularization of its convex envelope). As a consequence of these assumptions, the function $s\mapsto \psi \left(s\right)/s$ turns out to be strictly increasing in $]s_0,+\infty [$, where $s_0:=max\{\psi =0\}$, and hence, for every $m\in ]0,M[$, there exists (a unique) $\sigma >s_0$ such that $\psi \left(\sigma \right)/\sigma =m$. In the following we shall always assume that the function ψ in (g2r) satisfies these additional properties. We recall that, if $M=+\infty$, such a function is called a Nagumo function (see, e.g., Reference [31], Section 10.3).

Remark 3.

If g satisfies (g1r) and (g2r), then

$$\begin{array}{c}]-M,M[\subset Dom{g}^{*}(r,·),fora.e.r\in [0,R],\end{array}$$

(11)

$$\begin{array}{c}{r}^{N-1}{g}^{*}(r,m)\in L^1\left(\right]0,R\left[\right),\forall m\in ]-M,M[.\end{array}$$

(12)

Specifically, by symmetry it is enough to show that, for every $m\in ]0,M[$, $m\in Dom{g}^{*}(r,·)$ for a.e. $r\in [0,R]$ and (12) holds. Let $m\in ]0,M[$ and let $\sigma >0$ satisfy $\psi \left(\sigma \right)/\sigma =m$. Then

$$\frac{g(r,s)-g(r,0)}{s}\ge \frac{\psi \left(s\right)}{s}\ge \frac{\psi \left(\sigma \right)}{\sigma }=m,\forall s\ge \sigma ,$$

so that $-g(r,0)\le g^{*}(r,m)={sup}_{s\ge 0}[ms-g(r,s)]\le m\sigma -g(r,0)$. Hence, (11) and (12) follow from the assumption $r^{N-1}g(r,0)\in L^1\left(\right]0,R\left[\right)$.

Remark 4.

If h satisfies (h1r), then the quantity $M_0$ defined in (hgr) is always finite, since

$$r^{1-N}{\int }_0^r{\rho }^{N-1}{H}_0\left(\rho \right)d\rho \le {\int }_0^r{H}_0\left(\rho \right)d\rho \le \parallel H_0{\parallel }_{L^1},\forall r\in ]0,R].$$

We start by proving some a-priori estimates for the solutions of the Euler–Lagrange inclusions.

Lemma 1.

Let $(\overline{u},p)\in {\mathcal{W}}_{\mathrm{rad}}^1\times {\mathcal{W}}_{\mathrm{rad}}^{1,*}$. Then the following hold:

(i) 

If h satisfies (h1r) and $(\overline{u},p)$ satisfies (9), then $r^{1-N}\left|p\left(r\right)\right|\le M_0$ for every $r\in ]0,R]$, where $M_0$ is the (finite) quantity defined in (hgr).

(ii) 

If g and h satisfy (g1r)-(g2r)-(h1r)-(hgr), and the pair $(\overline{u},p)$ satisfies the Euler–Lagrange inclusions (9) and (10), then

$$|{\overline{u}}^{\prime }\left(r\right)|\le \sigma \left(r\right):={\left(g^{*}\right)}_{+}^{\prime }(r,M_0),fora.e.r\in [0,R].$$

(13)

Moreover, if ${\sigma }_0>0$ is defined by

$$\frac{\psi \left({\sigma }_0\right)}{{\sigma }_0}=M_0,$$

(14)

then $\sigma \left(r\right)\le {\sigma }_0$ for a.e. $r\in [0,R]$, i.e., $\overline{u}$ is Lipschitz continuous and

$$|{\overline{u}}^{\prime }\left(r\right)|\le {\sigma }_0,fora.e.r\in [0,R].$$

(15)

Proof. 

(i) From Remark 4, the quantity $M_0$ defined in (hgr) is finite. By (h1r) we have that $\partial h(r,t)\subseteq [-H_0\left(r\right),H_0\left(r\right)]$ for a.e. $r\in [0,R]$, so that (9) gives the estimate

$$|p^{\prime }\left(r\right)|\le r^{N-1}{H}_0\left(r\right)\mathrm{for}\mathrm{a}.\mathrm{e}.r\in [0,R],$$

and hence

$$\underset{r\in ]0,R]}{sup}{r}^{1-N}\left|p\left(r\right)\right|\le \underset{r\in ]0,R]}{sup}{r}^{1-N}{\int }_0^r{\rho }^{N-1}{H}_0\left(\rho \right)d\rho =M_0.$$

(16)

(ii) From (10) we have that $|u^{\prime }\left(r\right)|\in \partial g^{*}(r,r^{1-N}p\left(r\right))$, and, from (16), we deduce that

$$|{\overline{u}}^{\prime }\left(r\right)|\le {\left(g^{*}\right)}_{+}^{\prime }(r,r^{1-N}p\left(r\right))\le {\left(g^{*}\right)}_{+}^{\prime }(r,M_0)\mathrm{for}\mathrm{a}.\mathrm{e}.r\in [0,R],$$

so that (13) holds. Moreover, if ${\sigma }_0$ is defined by (14), then, by the convexity assumption on $g(r,·)$, we obtain the estimate

$$g_{-}^{\prime }(r,{\sigma }_0)\ge M_0\mathrm{for}\mathrm{a}.\mathrm{e}.r\in [0,R]$$

(with the convention $g_{-}^{\prime }(r,{\sigma }_0)=+\infty$ if ${\sigma }_0\notin Domg(r,·)$). On the other hand, by the very definition of $\sigma \left(r\right)$, we have that $M_0\in \partial g(r,\sigma \left(r\right))$, hence

$$g_{-}^{\prime }(r,{\sigma }_0)\ge M_0\ge g_{-}^{\prime }(r,\sigma \left(r\right))\mathrm{for}\mathrm{a}.\mathrm{e}.r\in [0,R],$$

which in turn implies that $\sigma \left(r\right)\le {\sigma }_0$ for a.e. $r\in [0,R]$, and (15) follows. □

The proof of Theorem 2 is divided into two steps: first we show that the result is valid in the superlinear case, that is, when $M=+\infty$, and then we obtain the result when $M<+\infty$ by constructing, with the help of the a-priori estimates obtained by the Euler–Lagrange conditions, a family of superlinear functionals whose radially symmetric minimizers also minimize the functional F.

Proof of Theorem 2.

Step 1: superlinear Lagrangians.

(i) In order to use a standard existence result for coercive functionals (see, e.g., Reference [30], Theorem 2.2), we need to rewrite the functional F in a suitable form.

Let us define

$$\begin{array}{c}P\left(r\right):={\int }_0^r{\rho }^{N-1}{H}_0\left(\rho \right)d\rho ,G(r,s):=g(r,s)+r^{1-N}P\left(r\right)s,\\ H(r,t):=h(r,t)-h(r,0)+H_0\left(r\right)\left|t\right|=h(r,t)-h(r,0)+r^{1-N}{P}^{\prime }\left(r\right)\left|t\right|.\end{array}$$

Since, by (h1r), it holds that

$$h(r,t)\ge h(r,0)-H_0\left(r\right)\left|t\right|,\forall r\in [0,R],t\in \mathbb{R},$$

then $H(r,t)\ge 0$ for all $r\in [0,R]$ and $t\in \mathbb{R}$. Moreover, we have that

$$\begin{array}{cc}\hfill F_{\mathrm{rad}}\left(u\right)=& {\int }_0^R{r}^{N-1}\left[g(r,|u^{\prime }\left|\right)+h(r,u)-h(r,0)+H_0\left(r\right)\left|u\right|\right]dr\hfill \\ & -{\int }_0^R{P}^{\prime }\left(r\right)\left|u\right|dr+{\int }_0^R{r}^{N-1}h(r,0)dr.\hfill \end{array}$$

Since $\left(\right|u|,P)\in {\mathcal{W}}_{\mathrm{rad}}^1\times {\mathcal{W}}_{\mathrm{rad}}^{1,*}$, it holds that

$${\int }_0^R{P}^{\prime }\left(r\right)\left|u\right|dr=-{\int }_0^R{P\left(r\right)\left|u\right|}^{\prime }dr=-{\int }_0^{R}P\left(r\right)\left|u^{\prime }\right|dr$$

(see, e.g., the derivation of formula (13) in Reference [9]). Setting $C:={\int }_0^R{r}^{N-1}h(r,0)dr$, we get

$$F_{\mathrm{rad}}\left(u\right)={\int }_0^R{r}^{N-1}\left[G(r,|u^{\prime }\left|\right)+H(r,u)\right]dr+C.$$

Observe that, by (g2r), it holds

$$G(r,s)+H(r,t)\ge G(r,s)\ge \psi \left(s\right)-M_{0}s+g(r,0).$$

Since $\psi$ is a Nagumo function, then by Theorem 2.2 in Reference [30] the functional

$$\widehat{F}\left(u\right):={\int }_{B_R}\left[G\right(\left|x\right|,|\nabla u|)+H\left(\right|x|,u)]dx$$

admits a minimizer in $W_0^{1,1}\left(B_R\right)$. Hence, by Corollary 1, the functional $F_{\mathrm{rad}}$ admits a minimizer in ${\mathcal{W}}_{\mathrm{rad}}^1$.

(ii)–(iii) Let us prove that, for every minimizer $\overline{u}$ of F in ${\mathcal{W}}_{\mathrm{rad}}^1$, there exists a momemtum $p\in {\mathcal{W}}_{\mathrm{rad}}^{1,*}$ associated with $\overline{u}$. (Hence, the Lipschitz continuity of $\overline{u}$ will follow from Lemma 1). Specifically, the conclusion follows from Reference [29], Theorem 4.2.2, once we show that all the assumptions are satisfied. The Lagrangian $L(r,t,s):=r^{N-1}\left[g\right(r,\left|s\right|)+h(r,t)]$ is convex with respect to s, and satisfies the Basic Hypotheses 4.1.2 in Reference [29]. Moreover, the Hamiltonian of the problem, that is, the Fenchel–Legendre transform of L with respect to the last variable:

$$H(r,t,p):=\underset{s\in \mathbb{R}}{sup}[ps-L(r,t,s)]=r^{N-1}[g^{*}(r,r^{1-N}p)-h(r,t)],\forall (r,t,p)\in ]0,R]\times \mathbb{R}\times \mathbb{R},$$

satisfies the strong Lipschitz condition near every arc, since, by (h1r),

$$|H(r,t,p)-H(r,\tau ,p)|=r^{N-1}|h(r,t)-h(r,\tau )|\le r^{N-1}{H}_0\left(r\right)|t-\tau |.$$

Finally, the minimization problem is calm, since it is a free-endpoint problem, hence all assumptions of Theorem 4.2.2 in Reference [29] are satisfied.

Step 2: slow growth Lagrangians.

(i) Let ${\sigma }_0>0$ be defined by (14), and, for $a>{\sigma }_0$ given, let ${\mathsf{\Phi }}_a$ be the class of all convex superlinear non-decreasing functions $\phi :[0,+\infty [\to [0,+\infty [$, such that $\phi \left(s\right)=0$ for every $s\in [0,a]$.

Given $\lambda >0$ and $\phi \in {\mathsf{\Phi }}_a$, let us define the superlinear Lagrangian

$$g_{\phi ,\lambda }(r,s):=g(r,|s\left|\right)+\lambda \phi \left(\right|s\left|\right)$$

and the corresponding functional

$$\begin{array}{cc}\hfill F_{\phi ,\lambda }\left(u\right):=& {\int }_0^R{r}^{N-1}[g_{\phi ,\lambda }(r,|u^{\prime }\left|\right)+h(r,u)]dr\hfill \\ \hfill =& F_{\mathrm{rad}}\left(u\right)+\lambda {\int }_0^R{r}^{N-1}\phi \left(\right|u^{\prime }\left(r\right)\left|\right)dr,u\in {\mathcal{W}}_{\mathrm{rad}}^1.\hfill \end{array}$$

(17)

For every $\lambda >0$ and $\phi \in {\mathsf{\Phi }}_a$ the functional $F_{\phi ,\lambda }$ satisfies the assumptions of Step 1, hence there exist a minimizer ${\overline{u}}_{\phi ,\lambda }$ of $F_{\phi ,\lambda }$ in ${\mathcal{W}}_{\mathrm{rad}}^1$ and an associated momentum $p_{\phi ,\lambda }\in {\mathcal{W}}_{\mathrm{rad}}^{1,*}$, such that

$$\begin{array}{cc}\hfill p_{\phi ,\lambda }^{\prime }\left(r\right)& \in r^{N-1}\partial h(r,{\overline{u}}_{\phi ,\lambda }\left(r\right)),\mathrm{for}\mathrm{a}.\mathrm{e}.r\in [0,R],\hfill \\ \hfill p_{\phi ,\lambda }\left(r\right)& \in r^{N-1}\partial g_{\phi ,\lambda }(r,|{\overline{u}}_{\phi ,\lambda }^{\prime }\left(r\right)\left|\right),\mathrm{for}\mathrm{a}.\mathrm{e}.r\in [0,R].\hfill \end{array}$$

By Lemma 1(i), we obtain that $r^{1-N}\left|p_{\phi ,\lambda }\left(r\right)\right|\le M_0$ for every $r\in ]0,R]$. On the other hand, since

$$r^{1-N}{p}_{\phi ,\lambda }\left(r\right)\in \left[{\left(g_{\phi ,\lambda }\right)}_{-}^{\prime }(r,|{\overline{u}}_{\phi ,\lambda }^{\prime }\left(r\right)\left|\right),{\left(g_{\phi ,\lambda }\right)}_{+}^{\prime }(r,|{\overline{u}}_{\phi ,\lambda }^{\prime }\left(r\right)\left|\right)\right]$$

and, by Lemma 1(ii), $M_0\in \partial g(r,\sigma \left(r\right))$ with $\sigma \left(r\right)\le {\sigma }_0<a$, we obtain that

$$g_{-}^{\prime }(r,|{\overline{u}}_{\phi ,\lambda }^{\prime }\left(r\right)\left|\right)\le {\left(g_{\phi ,\lambda }\right)}_{-}^{\prime }(r,|{\overline{u}}_{\phi ,\lambda }^{\prime }\left(r\right)\left|\right)\le M_0\le g_{+}^{\prime }(r,\sigma \left(r\right))\le g_{-}^{\prime }(r,a).$$

Hence, $|{\overline{u}}_{\phi ,\lambda }^{\prime }|\le a$ a.e. in $[0,R]$, so that $\phi (|{\overline{u}}_{\phi ,\lambda }^{\prime }|)=0$, and $F_{\phi ,\lambda }\left({\overline{u}}_{\phi ,\lambda }\right)=F_{\mathrm{rad}}\left({\overline{u}}_{\phi ,\lambda }\right)$.

By the discussion above, for every $\phi \in {\mathsf{\Phi }}_a$ and every $\mu \ge \lambda >0$, we have that

$$F_{\phi ,\lambda }\left({\overline{u}}_{\phi ,\mu }\right)\ge F_{\phi ,\lambda }\left({\overline{u}}_{\phi ,\lambda }\right)=F_{\phi ,\mu }\left({\overline{u}}_{\phi ,\lambda }\right)\ge F_{\phi ,\mu }\left({\overline{u}}_{\phi ,\mu }\right)\ge F_{\phi ,\lambda }\left({\overline{u}}_{\phi ,\mu }\right),$$

hence we conclude that $m:=F_{\mathrm{rad}}\left({\overline{u}}_{\phi ,\lambda }\right)$ is independent of $\lambda >0$ and $\phi \in {\mathsf{\Phi }}_a$.

We claim that $m={min}_{{\mathcal{W}}_{\mathrm{rad}}^1}{F}_{\mathrm{rad}}$. Specifically, assume by contradiction that there exists $v\in {\mathcal{W}}_{\mathrm{rad}}^1$ such that $F_{\mathrm{rad}}\left(v\right)<m$. Since $|\nabla v(\left|x\right|\left)\right|\in L^1\left(B_R\right)$, by the de La Vallée Poussin criterion (see, e.g., Reference [31], Theorem 10.3.i), there exists a function $\phi \in {\mathsf{\Phi }}_a$ such that ${\int }_{B_R}\phi \left(\right|\nabla v\left(\right|x\left|\right)\left|\right)dx<+\infty$, i.e.,

$${\int }_0^R{r}^{N-1}\phi \left(\right|v^{\prime }\left(r\right)\left|\right)dr<+\infty .$$

By (17), for $\lambda >0$ small enough we have that $F_{\phi ,\lambda }\left(v\right)<m=min{F}_{\phi ,\lambda }$, a contradiction.

(ii) Let $\overline{u}$ be a minimizer of F in ${\mathcal{W}}_{\mathrm{rad}}^1$, and let us prove that $\overline{u}$ is Lipschitz continuous.

Assume by contradiction that $\overline{u}$ is not Lipschitz continuous, that is, $\mathcal{L}\left(\right\{|{\overline{u}}^{\prime }|>a\})>0$ for every $a>0$ (here $\mathcal{L}$ denotes the Lebesgue measure on $\mathbb{R}$).

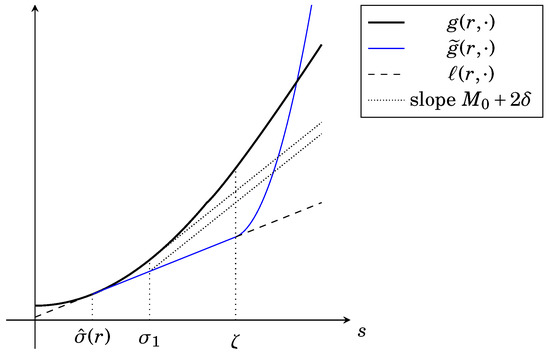
Let us define $\delta$, $\widehat{\sigma }$ and ${\sigma }_1$ by:

$$\delta :=\frac{M-M_0}{3},\widehat{\sigma }\left(r\right):={\left(g^{*}\right)}_{-}^{\prime }(r,M_0+\delta ),\frac{\psi \left({\sigma }_1\right)}{{\sigma }_1}=M_0+2\delta .$$

Observe that, by (g2r),

$$g_{-}^{\prime }(r,{\sigma }_1)\ge \frac{\psi \left({\sigma }_1\right)}{{\sigma }_1}=M_0+2\delta >M_0+\delta \ge g_{-}^{\prime }(r,\widehat{\sigma }\left(r\right)),$$

so that ${\sigma }_1\ge \widehat{\sigma }\left(r\right)$ for every $r\in [0,R]$. (The inequality is trivially satisfied for those values of r such that ${\sigma }_1\notin Domg(r,·)$.) Let us define the function

$$\ell (r,s):=g(r,\widehat{\sigma }\left(r\right))+(M_0+\delta )(s-\widehat{\sigma }\left(r\right)),r\in [0,R],s\ge 0.$$

Since $M_0+\delta \in \partial g(r,\widehat{\sigma }\left(r\right))$, we have that $g(r,s)\ge l(r,s)$ for every $r\in [0,R]$ and $s\ge 0$.

Let $\phi$ be a Nagumo function such that ${\int }_0^R{r}^{N-1}\phi \left(\right|{\overline{u}}^{\prime }\left|\right)dr<+\infty$. Given $a>0$, let us define ${\phi }_a:=[(\phi -\phi \left(a\right))\vee 0]\in {\mathsf{\Phi }}_a$. Since $0\le {\phi }_a\le \phi$, we have that

$$0\le \underset{a\to +\infty }{lim}{\int }_{\left\{\right|{\overline{u}}^{\prime }|>a\}}{r}^{N-1}{\phi }_a\left(\right|{\overline{u}}^{\prime }\left|\right)dr\le \underset{a\to +\infty }{lim}{\int }_{\left\{\right|{\overline{u}}^{\prime }|>a\}}{r}^{N-1}\phi \left(\right|{\overline{u}}^{\prime }\left|\right)dr=0,$$

whereas

$$\underset{a\to +\infty }{lim}{\int }_{\{{\sigma }_1\le |{\overline{u}}^{\prime }|\le a\}}{r}^{N-1}\left(\right|{\overline{u}}^{\prime }|-{\sigma }_1)dr={\int }_{\{{\sigma }_1\le |{\overline{u}}^{\prime }\left|\right\}}{r}^{N-1}\left(\right|{\overline{u}}^{\prime }|-{\sigma }_1)dr>0,$$

hence there exists $\zeta >{\sigma }_1$ such that

$$\delta {\int }_{\{{\sigma }_1\le |{\overline{u}}^{\prime }|\le \zeta \}}{r}^{N-1}\left(\right|{\overline{u}}^{\prime }|-{\sigma }_1)dr>{\int }_{\left\{\right|{\overline{u}}^{\prime }|>\zeta \}}{r}^{N-1}{\phi }_{\zeta }\left(\right|{\overline{u}}^{\prime }\left|\right)dr.$$

(18)

For every $r\in [0,R]$, let us define the function (see Figure 1)

$$\tilde{g}(r,s):=\left\{\begin{array}{cc}g(r,s),\hfill & \mathrm{if}0\le s\le \widehat{\sigma }\left(r\right),\hfill \\ \ell (r,s)+{\phi }_{\zeta }\left(s\right),\hfill & \mathrm{if}s\ge \widehat{\sigma }\left(r\right),\hfill \end{array}\right.$$

and let

$$\tilde{F}\left(v\right):={\int }_0^R{r}^{N-1}[\tilde{g}(r,|v^{\prime }\left|\right)+h(r,v)]dr,v\in {\mathcal{W}}_{\mathrm{rad}}^1.$$

Figure 1. Construction of $\tilde{g}$.

Since $g_{-}^{\prime }(r,{\sigma }_1)\ge M_0+2\delta$, for every $s\in [{\sigma }_1,\zeta ]$ we have that

$$\begin{array}{cc}\hfill g(r,s)& \ge g(r,{\sigma }_1)+(M_0+2\delta )(s-{\sigma }_1)\hfill \\ & \ge \tilde{g}(r,{\sigma }_1)+(M_0+\delta )(s-{\sigma }_1)+\delta (s-{\sigma }_1)\hfill \\ & =\tilde{g}(r,s)+\delta (s-{\sigma }_1).\hfill \end{array}$$

(19)

Observe that, by the definition of $\tilde{g}$ and (19),

$$\begin{array}{cc}\tilde{g}(r,|{\overline{u}}^{\prime }\left|\right)\le g(r,|{\overline{u}}^{\prime }\left|\right),\hfill & \mathrm{a}.\mathrm{e}.\mathrm{in}\left\{\right|{\overline{u}}^{\prime }|<{\sigma }_1\},\hfill \\ \tilde{g}(r,|{\overline{u}}^{\prime }\left|\right)\le g(r,|{\overline{u}}^{\prime }\left|\right)-\delta \left(\right|{\overline{u}}^{\prime }|-{\sigma }_1),\hfill & \mathrm{a}.\mathrm{e}.\mathrm{in}\{{\sigma }_1\le |{\overline{u}}^{\prime }|\le \zeta \},\hfill \\ \tilde{g}(r,|{\overline{u}}^{\prime }\left|\right)\le g(r,|{\overline{u}}^{\prime }\left|\right)+{\phi }_{\zeta }\left(\right|{\overline{u}}^{\prime }\left|\right),\hfill & \mathrm{a}.\mathrm{e}.\mathrm{in}\left\{\right|{\overline{u}}^{\prime }|>\zeta \},\hfill \end{array}$$

hence, by (18),

$$\tilde{F}\left(\overline{u}\right)\le F_{\mathrm{rad}}\left(\overline{u}\right)-\delta {\int }_{\{{\sigma }_1\le |{\overline{u}}^{\prime }|\le \zeta \}}{r}^{N-1}\left(\right|{\overline{u}}^{\prime }|-{\sigma }_1)dr+{\int }_{\left\{\right|{\overline{u}}^{\prime }|>\zeta \}}{r}^{N-1}{\phi }_{\zeta }\left(\right|{\overline{u}}^{\prime }\left|\right)dr<F_{\mathrm{rad}}\left(\overline{u}\right).$$

On the other hand, if $\tilde{u}$ is a minimizer of $\tilde{F}$, then by Step 1 there exists $p\in {\mathcal{W}}_{\mathrm{rad}}^{1,*}$ such that $(\tilde{u},p)$ satisfies the Euler–Lagrange inclusions (9) and (10) with g replaced by $\tilde{g}$. From Lemma 1(i) we deduce that

$$|{\tilde{u}}^{\prime }\left(r\right)|\le {\left({\tilde{g}}^{*}\right)}_{+}^{\prime }(r,r^{1-N}p\left(r\right))\le {\left({\tilde{g}}^{*}\right)}_{-}^{\prime }(r,M_0+\delta )\le \widehat{\sigma }\left(r\right),\mathrm{for}\mathrm{a}.\mathrm{e}.r\in [0,R],$$

(where the last inequality follows from ${\tilde{g}}^{\prime }(r,\widehat{\sigma }\left(r\right))=M_0+\delta$), hence

$$\tilde{g}(r,|{\tilde{u}}^{\prime }\left|\right)=g(r,|{\tilde{u}}^{\prime }\left|\right),\mathrm{for}\mathrm{a}.\mathrm{e}.r\in [0,R],$$

and, in conclusion,

$$F_{\mathrm{rad}}\left(\tilde{u}\right)=\tilde{F}\left(\tilde{u}\right)\le \tilde{F}\left(\overline{u}\right)<F_{\mathrm{rad}}\left(\overline{u}\right),$$

in contradiction with the assumption that $\overline{u}$ is a minimizer of F.

(iii) Finally, let us prove that $\overline{u}$ satisfies the Euler–Lagrange inclusions. Let $\sigma >0$ be such that $|{\overline{u}}^{\prime }|\le \sigma$ a.e. in $[0,R]$. Reasoning as in the existence proof, $\overline{u}$ is a minimizer of $F_{\phi ,\lambda }$ for every $\lambda >0$ and $\phi \in {\mathsf{\Phi }}_a$, with $a>\sigma \vee {\sigma }_0$. Hence, $\overline{u}$ satisfies the Euler–Lagrange inclusions with $g_{\phi ,\lambda }$ instead of g. Since $\partial g_{\phi ,\lambda }(r,|{\overline{u}}^{\prime }\left|\right)=\partial g(r,|{\overline{u}}^{\prime }\left|\right)$ for a.e. $r\in [0,R]$, the conclusion follows. □

5. Convex Solutions of Variational Problems with Gradient Constraints

As an application of the previous results, we obtain the existence of convex radially symmetric minimizers for autonomous functionals of the form

$$F\left(u\right):={\int }_{B_R}\left[g\left(\right|\nabla u\left|\right)+h\left(u\right)\right]dx,$$

(20)

in the space

$${\mathcal{W}}_{\mu }^1:=\left\{u\in W_0^{1,1}\left(\mathsf{\Omega }\right):|\nabla u\left(x\right)|\le \mu \left(\right|x\left|\right)\mathrm{for}\mathrm{a}.\mathrm{e}.x\in B_R\right\}$$

of Sobolev functions with gradient constraint given by a monotone non-decreasing function $\mu :[0,R]\to ]0,+\infty ]$.

Theorem 3.

Let us consider the integral functional (20), where $g:[0,+\infty [\to \mathbb{R}$ and $h:\mathbb{R}\to \mathbb{R}$ satisfy the following assumptions:

(g1) 

$\mathbb{R}\ni z\mapsto g\left(\right|z\left|\right)$ is a convex function;

(g2) 

$M:={lim}_{s\to +\infty }g\left(s\right)/s>0$;

(h1) 

h is a convex function;

(hg) 

$min\left\{\right|h_{-}^{\prime }\left(0\right)|,|h_{+}^{\prime }\left(0\right)\left|\right\}<\frac{NM}{R}$.

Then the following hold.

(i) 

F admits a radially symmetric minimizer $u\left(x\right)=\overline{u}\left(\right|x\left|\right)$ in ${\mathcal{W}}_{\mu }^1$.

(ii) 

There exists a momentum $p\in {\mathcal{W}}_{\mathrm{rad}}^{1,*}$ such that the following Euler–Lagrange inclusions hold:

$$\begin{array}{c}{p}^{\prime }\left(r\right)\in r^{N-1}\partial h\left(\overline{u}\left(r\right)\right),fora.e.r\in [0,R],\end{array}$$

(21)

$$\begin{array}{c}p\left(r\right)\in r^{N-1}\mathsf{\Gamma }(r,|{\overline{u}}^{\prime }\left(r\right)\left|\right)fora.e.r\in [0,R],\end{array}$$

(22)

where

$$\mathsf{\Gamma }(r,s):=\left\{\begin{array}{cc}\partial g\left(s\right),\hfill & if0\le s<\mu \left(r\right),\hfill \\ \mu \left(r\right),+\infty [,\hfill & ifs=\mu \left(r\right),\hfill \\ \varnothing ,\hfill & ifs>\mu \left(r\right).\hfill \end{array}\right.$$

(iii) 

If $h_{+}^{\prime }\left(0\right)\ge 0$ [resp. $h_{-}^{\prime }\left(0\right)\le 0$], then u is a convex [resp. concave] function.

(iv) 

If, in addition, g has a strict minimum point at 0, or h is a strictly monotone function, then every minimizer of F in ${\mathcal{W}}_{\mu }^1$ is radially symmetric.

Proof. 

The constraint $|\nabla u(x\left)\right|\le \mu \left(\right|x\left|\right)$ in the definition of the functional space ${\mathcal{W}}_{\mu }^1$ can be incorporated into the Lagrangian. Specifically, let us define

$$\tilde{g}(r,s):=g\left(s\right)+{\mathbb{I}}_{[0,\mu (r\left)\right]}\left(s\right),\tilde{F}\left(u\right):={\int }_{B_R}[\tilde{g}\left(\right|x|,|\nabla u\left(x\right)\left|\right)+h\left(u\left(x\right)\right)]dx,$$

where ${\mathbb{I}}_B$ is the indicator function of a set B, defined by ${\mathbb{I}}_B\left(s\right)=0$ if $s\in B$ and $+\infty$ otherwise. Then minimizing F in ${\mathcal{W}}_{\mu }^1$ is equivalent to minimizing $\tilde{F}$ in $W_0^{1,1}\left(B_R\right)$.

We remark that, if g satisfies (g1)–(g2), then $\tilde{g}$ satisfies (g1r)–(g2r) and

$$\partial \tilde{g}(r,s)=\mathsf{\Gamma }(r,|s\left|\right),\forall (r,s)\in [0,R]\times \mathbb{R}.$$

(23)

We shall prove the theorem only in the case $h_{+}^{\prime }\left(0\right)\ge 0$ (since the case $h_{-}^{\prime }\left(0\right)\le 0$ can be handled similarly).

If 0 is a minimum point of h, then clearly parts (i)–(ii)–(iii) are satisfied choosing $u\equiv 0$ and $p\equiv 0$. Hence, it is not restrictive to prove (i)–(ii)–(iii) under the additional assumption that 0 is not a minimum point of h. Since $h_{+}^{\prime }\left(0\right)\ge 0$, and h is a convex function, we have that $h_{+}^{\prime }\left(0\right)\ge h_{-}^{\prime }\left(0\right)>0$.

Since $h_{-}^{\prime }\left(0\right)>0$, the (possibly empty) convex and closed set $argminh$ is contained in the open half-line $]-\infty ,0[$. If $argminh\ne \varnothing$, let $m:=maxargminh$, otherwise let $m=-\infty$. Let us define

$$\tilde{h}\left(t\right):=\left\{\begin{array}{cc}h\left(m\right),\hfill & \mathrm{if}t\le m,\hfill \\ h\left(t\right),\hfill & \mathrm{if}m<t\le 0,\hfill \\ h\left(0\right)+h_{-}^{\prime }\left(0\right)t,\hfill & \mathrm{if}t>0,\hfill \end{array}\right.$$

(the first condition is empty if $m=-\infty$) and

$$\widehat{F}\left(u\right):={\int }_{B_R}[\tilde{g}\left(\right|x|,|\nabla u\left|\right)+\tilde{h}\left(u\right)]dx,u\in W_0^{1,1}\left(B_R\right).$$

Given $v\in W_0^{1,1}\left(B_R\right)$, let $v_m:=(v\wedge 0)\vee m$, and observe that $\widehat{F}\left(v_m\right)\le \widehat{F}\left(v\right)$. If u is a minimizer of $\widehat{F}$, then also $u_m$ is a minimizer of $\widehat{F}$; moreover, we have that

$$\tilde{F}\left(u_m\right)=\widehat{F}\left(u_m\right)\le \widehat{F}\left(v_m\right)=\tilde{F}\left(v_m\right)\le \tilde{F}\left(v\right),\forall v\in W_0^{1,1}\left(B_R\right),$$

so that $u_m$ is a minimizer of $\tilde{F}$.

Hence, we have proved the following

Claim 1: If u is a minimizer of $\widehat{F}$, then $u_m$ is a minimizer of both $\widehat{F}$ and $\tilde{F}$.

After this preliminary reduction, let us prove (i)–(iv).

(i) Thanks to Claim 1 and Theorem 1, assertion (i) is a consequence of the following

Claim 2: There exists a Lipschitz continuous, monotone non-decreasing minimizer $\overline{u}$ of ${\widehat{F}}_{\mathrm{rad}}$ in ${\mathcal{W}}_{\mathrm{rad}}^1$ satisfying $m\le \overline{u}\le 0$.

Specifically, from (hg) we have that

$$0\le {\tilde{h}}_{-}^{\prime }\left(t\right)\le {\tilde{h}}_{+}^{\prime }\left(t\right)\le {\tilde{h}}_{-}^{\prime }\left(0\right)=:K<\frac{NM}{R},\forall t\in \mathbb{R}.$$

Hence, from Theorem 2 the functional ${\widehat{F}}_{\mathrm{rad}}$ admits a Lipschitz continuous minimizer $\widehat{u}\in {\mathcal{W}}_{\mathrm{rad}}^1$.

Let us define

$$S:=\left\{r\in ]0,R[:{\widehat{u}}_m\left(r\right)>\underset{[r,R]}{inf}{\widehat{u}}_m\right\}.$$

By Riesz’s Rising Sun Lemma, we have that S is the union of a finite or countable family $]a_k,b_k[$, $k\in J$, of pairwise disjoint open intervals, with ${\widehat{u}}_m\left(a_k\right)={\widehat{u}}_m\left(b_k\right)$ for every k (unless $a_k=0$, in which case ${\widehat{u}}_m\left(0\right)\le {\widehat{u}}_m\left(b_k\right)$). Hence, the function

$$\overline{u}\left(r\right):=\left\{\begin{array}{cc}{\widehat{u}}_m\left(b_k\right),\hfill & \mathrm{if}r\in ]a_k,b_k[\mathrm{for}\mathrm{some}k\in J,\hfill \\ {\widehat{u}}_m\left(r\right),\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

is a Lipschitz continuous, monotone non-decreasing function and ${\widehat{F}}_{\mathrm{rad}}\left(\overline{u}\right)\le {\widehat{F}}_{\mathrm{rad}}\left(\widehat{u}\right)$, i.e., $\overline{u}$ is a minimizer of ${\widehat{F}}_{\mathrm{rad}}$ with the required properties, and Claim 2 is proved.

(ii) Here and in the following, $\overline{u}$ will denote the minimizer of ${\widehat{F}}_{\mathrm{rad}}$ constructed in Claim 2. By Theorem 2, there exists a momentum $p\in {\mathcal{W}}_{\mathrm{rad}}^{1,*}$ such that the Euler–Lagrange inclusions (21) and (22) are satisfied with h replaced by $\tilde{h}$. Observing that $m\le \overline{u}\le 0$, and that

$$\partial \tilde{h}\left(0\right)=\left\{h_{-}^{\prime }\left(0\right)\right\}\subseteq \partial h\left(0\right),\partial \tilde{h}\left(m\right)\subseteq \partial h\left(m\right),\partial \tilde{h}\left(t\right)=\partial h\left(t\right),\forall t\in ]m,0[,$$

we conclude that the same pair satisfies also the Euler–Lagrange inclusions (21) and (22) (with the original h).

(iii) Let us first prove the claim under the additional assumption that $\tilde{h}\in C^2$. In this case, the inclusion (21) is, in fact, the equation

$$p^{\prime }\left(r\right)=r^{N-1}{h}^{\prime }\left(\overline{u}\left(r\right)\right),\mathrm{for}\mathrm{a}.\mathrm{e}.r\in [0,R],$$

p is monotone non-decreasing, and $p^{\prime }$ is Lipschitz continuous.

Since $\overline{u}$ is monotone non-decreasing, there exists $r_0\in [0,R[$ such that $\overline{u}\left(r\right)=m$ for every $r\in [0,r_0[$, and $\overline{u}\left(r\right)>m$ for every $r\in ]r_0,R]$. Hence, to prove that $x\mapsto \overline{u}\left(\right|x\left|\right)$ is convex in $B_R$, it is enough to prove that ${\overline{u}}^{\prime }$ is (equivalent to) a non-decreasing function in $[r_0,R]$.

Moreover, by (22), the explicit form (23) of $\partial \tilde{g}$, and the monotonicity of $\mu$, this property will follow once we prove that $r^{1-N}p\left(r\right)$ is strictly increasing in $]r_0,R]$.

For $r\in ]r_0,R]$, we have that $h_{-}^{\prime }\left(\overline{u}\left(r\right)\right)>0$, hence $p^{\prime }\left(r\right)>0$. As a consequence, p is strictly positive and strictly monotone increasing in $]r_0,R]$.

Let us fix $\delta \in ]0,1]$. We have that

$${\left[r^{1-N-\delta }p\left(r\right)\right]}^{\prime }=r^{-N-\delta }[r{p}^{\prime }\left(r\right)-(N-1+\delta )p\left(r\right)]=:r^{-N-\delta }\lambda \left(r\right).$$

(24)

Since $0\le p^{\prime }\left(r\right)\le K{r}^{N-1}$, the function $\lambda \left(r\right):=r{p}^{\prime }\left(r\right)-(N-1+\delta )p\left(r\right)$ is absolutely continuous in $[0,R]$ and $\lambda \left(0\right)=0$. Moreover, since the function $r\mapsto h^{\prime }\left(\overline{u}\left(r\right)\right)$ is monotone non-decreasing,

$$\begin{array}{cc}\hfill {\lambda }^{\prime }\left(r\right)& ={[r^N{h}^{\prime }\left(\overline{u}\left(r\right)\right)-(N-1+\delta )p\left(r\right)]}^{\prime }\hfill \\ & =N{r}^{N-1}{h}^{\prime }\left(\overline{u}\left(r\right)\right)+r^N{\left[h^{\prime }\left(\overline{u}\left(r\right)\right)\right]}^{\prime }-(N-1+\delta )p^{\prime }\left(r\right)\ge (1-\delta )p^{\prime }\left(r\right)\ge 0.\hfill \end{array}$$

Hence, $\lambda \left(r\right)\ge 0$ for every r, so that from (24) we deduce that the function $r^{1-N-\delta }p\left(r\right)$ is monotone non-decreasing. As a consequence, the function $r^{1-N}p\left(r\right)=r^{\delta }\left[r^{1-N-\delta }p\left(r\right)\right]$ is strictly increasing in $[r_0,R]$.

Finally, the assumption $h\in C^2$ can be dropped as in Reference [8] (§4, Step 3) (see also References [11,12]).

(iv) If 0 is a strict minimum point of g, then g is strictly monotone increasing in $[0,+\infty [$, and the result follows from Theorem 1. If h is a strictly monotone function, the proof can be found in Reference [32] (step (c) in the proof of Theorem 1). □

Example 1

(The case N = 1). Let $N=1$, let $\mu :[0,R]\to ]0,+\infty ]$ be a non-decreasing function, let g satisfy (g1)–(g2), and let $h:\mathbb{R}\to \mathbb{R}$ be a $C^1$ function satisfying $0<h^{\prime }\left(t\right)\le K<M/R$ for every $t\in \mathbb{R}$. Then every minimizer u of F in ${\mathcal{W}}_{\mu }^1$ is convex. Specifically, let $\overline{u}\left(x\right)=u\left(\right|x\left|\right)$ and let $p\in {\mathcal{W}}_{\mathrm{rad}}^{1,*}$ be an associated momentum. From (9) we deduce that $p^{\prime }\left(r\right)=h^{\prime }\left(\overline{u}\left(r\right)\right)>0$ for every $r\in ]0,R]$, hence p is a strictly increasing function. Since ${\overline{u}}^{\prime }\ge 0$ and $p\left(r\right)\in \partial \tilde{g}(r,{\overline{u}}^{\prime }\left(r\right))$, we conclude that ${\overline{u}}^{\prime }$ is non-decreasing, hence $\overline{u}$ is a convex function.

Example 2.

We show that, if $N>1$ and h is not convex, then a minimizer of F need not be convex. Let $N=2$, $R=2$, $g\left(s\right)=s^2/2$, $\mu \equiv +\infty$, $\epsilon \in ]0,\sqrt{log2}]$, and consider the function

$$h\left(u\right):=\left\{\begin{array}{cc}4(u+\epsilon ),\hfill & ifu\le -\epsilon ,\hfill \\ 0,\hfill & ifu>\epsilon .\hfill \end{array}\right.$$

We claim that the non-convex function

$$\overline{u}\left(r\right):=\left\{\begin{array}{cc}{r}^2-1-\epsilon ,\hfill & ifr\in [0,1],\hfill \\ \epsilon \frac{log(r/2)}{log2},\hfill & ifr\in [1,2],\hfill \end{array}\right.$$

is a minimizer of $F_{\mathrm{rad}}$. Specifically, the family of all solution of the Euler–Lagrange inclusions (9) and (10) is given by the trivial pair $(0,0)$ and by the pairs of the form $({\overline{u}}_k,p_k)$, with $k\in \mathbb{R}$, $p_k\left(r\right)=r{\overline{u}}_k^{\prime }\left(r\right)$, and

$${\overline{u}}_k\left(r\right):=\left\{\begin{array}{cc}{r}^2-1-\epsilon +klogr,\hfill & ifr\in ]0,1],\hfill \\ \epsilon \frac{log(r/2)}{log2},\hfill & ifr\in [1,2],\hfill \end{array}\right.$$

so that $\overline{u}={\overline{u}}_0$. A direct computation shows that $F_{\mathrm{rad}}\left(0\right)=0$, $F_{\mathrm{rad}}\left({\overline{u}}_k\right)=+\infty$ for every $k\ne 0$, and $F_{\mathrm{rad}}\left(\overline{u}\right)=({\epsilon }^2-log2)/(2log2)<0$, hence the claim follows.

From the analysis above we can prove the following result without requiring the convexity of g. In the following, $g^{**}$ denotes the bi-conjugate function of $z\mapsto g\left(\right|z\left|\right)$.

Corollary 2.

Let us consider the integral functional (20), where $g:[0,+\infty [\to [0,+\infty [$ satisfies the following assumptions:

(g0) 

g is a lower semicontinuous proper function, such that $g\left(0\right)=g^{**}\left(0\right)$;

(g2) 

$M:={lim\; inf}_{s\to +\infty }g\left(s\right)/s>0$.

Moreover, assume that $h:\mathbb{R}\to \mathbb{R}$ satisfies (h1) and (hg). Then F admits a radially symmetric minimizer in ${\mathcal{W}}_{\mu }^1$.

Proof. 

The relaxed functional

$$\overline{F}\left(u\right):={\int }_{B_R}\left[g^{**}\left(\right|\nabla u\left|\right)+h\left(u\right)\right]dx,u\in W_0^{1,1}\left(B_R\right),$$

satisfies all the assumptions of Theorem 3, hence there exist a radial minimizer $u\left(x\right)=\overline{u}\left(\right|x\left|\right)$ of $\overline{F}$ in ${\mathcal{W}}_{\mu }^1$ and a momentum $p\in {\mathcal{W}}_{\mathrm{rad}}^{1,*}$ such that (21) and (22) hold.

As in the proof of Theorem 3(iii), considering without loss of generality $h\in C^2$ and $h_{-}^{\prime }\left(0\right)>0$, we have already proved that u is convex and there exists $r_0\in [0,R[$ such that $\overline{u}\left(r\right)=m$ for every $r\in [0,r_0[$, and $\overline{u}\left(r\right)>m$ for every $r\in ]r_0,R]$. Moreover, the function $r^{1-N}p\left(r\right)$ is strictly increasing in $]r_0,R]$.

Let P be the set of all $z\in \mathbb{R}$ such that $(z,g^{**}\left(z\right))$ belongs to the set of the extremal points of the epigraph of $g^{**}$. We recall that $g\left(z\right)=g^{**}\left(x\right)$ for every $z\in P$ (see Reference [9], Remark 5.3). Reasoning as in Reference [32] (see the proof of Theorem 2), from the strict monotonicity of $r^{1-N}p\left(r\right)$ in $]r_0,R]$ follows that $|{\overline{u}}^{\prime }\left(r\right)|\in P$ for a.e. $r\in [r_0,R]$. Since ${\overline{u}}^{\prime }\left(r\right)=0$ for every $r\in [0,r_0[$, we conclude that ${\overline{F}}_{\mathrm{rad}}\left(\overline{u}\right)=F_{\mathrm{rad}}\left(\overline{u}\right)$, hence $\overline{u}$ is a minimizer of $F_{\mathrm{rad}}$. □