1. Introduction
Let
n be a positive integer,
,
,
N be the set of all positive integers,
be the set of all complex numbers,
be the set of all
complex matrices and
I be the identity matrix. Let
and
be the set of all eigenvalues of
A. For
, denote
and
. A matrix
A is called a strictly diagonally dominant (
) matrix if, for each
,
In addition,
A is doubly strictly diagonally dominant (
) if, for any
,
Locating eigenvalue and bounding infinity norm of the inverse for nonsingular matrices are two major problems in applied linear algebra [
1,
2,
3,
4,
5,
6,
7]. The first problem is to find a set in the complex plane to include all eigenvalues of matrices, as if the obtained set is on the right-hand side of the complex plane. Then, one can conclude the positive definiteness of the corresponding matrix. Moreover, the “eigenvalue localization” is very important for the convergence speed of algorithms on which web searching engines are based. For the case of PageRank, see [
4] and references therein. Another problem is to bound the infinity norm for the inverse of nonsingular matrices, as it can be used to estimate the condition number for the linear systems of equations [
5], as well as linear complementarity problems [
6]. In general, it is not easy to discuss these two problems for an arbitrary given nonsingular matrix. One traditional way for solving the two problems is to locate all eigenvalues or to bound the infinity norm for some subclasses of nonsingular matrices.
In 2015, Cvetković [
7] et al. extended the class of
matrices to the class of eventually
(
) matrices, and proved that
matrices are nonsingular.
Definition 1 ([
7], Definition 1)
. Let , where . A is called an matrix if is for a positive integer k. To bound the infinity norm for the inverse of
matrices, Cvetković et al. [
7] gave the following results.
Theorem 1 ([
7], Theorem 2)
. Let . Then, for two certain numbers s and k, It is worth noting in Theorem 1 that, from Examples 3 and 4 in [
7] and the structure of
, which includes two parameters
s and
k, one can conclude that, if there exists two groups of different numbers
s and
k, both such that
A is an
matrix, then the different selection of
s and
k will affect the infinity norm bounds for the inverse of
A.
According to the non-singularity of
matrices, Liu et al. [
8] obtained the following eigenvalue inclusion set of matrices, which corrects Theorem 1 of [
7].
Theorem 2 ([
8], Theorem 2)
. Let . For any given positive integer k, In 2016, Liu [
9] introduced the class of eventually
(
) matrices, and located all its eigenvalues.
Definition 2 ([
9], Definition 3.2.1)
. Let , where . A is called an matrix if is for a positive integer k. Remark 1. From Definition 2, a meaningful discussion is concerned: Unfortunately, the answer is negative. Let It is easy to validate that, if , then is , and that is not .
Theorem 3 ([
9], Theorem 3.3.1)
. Let . For any given positive integer k,and Note here that, when
, the sets
in Theorem 3 are ovals, while the sets
with
are lemniscates; see [
10] (pp. 35–52), for details.
As everyone knows that
matrices are
matrices and
matrices are nonsingular, hence,
By Label (
1), and Definitions 1 and 2, the following two relations hold clearly:
and
Besides
matrices,
matrices,
matrices and
matrices, there are many other subclasses of nonsingular matrices; see [
11] for details.
The outline of the rest of this paper is as follows. In
Section 2, by some existing criteria for non-singularity of matrices, a new eigenvalue localization set of matrices is derived. That is, a tighter eigenvalue localization set is obtained by excluding some proper subsets from
in Theorem 3, which is proved to not include any eigenvalues of matrices. In
Section 3, the infinity norm for the inverse of
matrices is given. Finally, some concluding remarks are given in
Section 4 to summarize this paper.
2. Eigenvalue Localization of Matrices
Firstly, a lemma in [
12] is listed, which is very useful for deriving a new eigenvalue inclusion set.
Lemma 1 ([
12, Corollary 1]).
Let . If for each , , eitherorfor some and , then A is nonsingular. Lemma 2. Let . For any given positive integer k,whereand Proof. Let
. Given
k, suppose that
, i.e., for any
,
, which is equivalent to that
or
, then
or for some
,
Then, by Lemma 1, we have is nonsingular, i.e., is not an eigenvalue of . On the other hand, because , there is a vector x, , such that . Furthermore, we have , which implies that is an eigenvalue of . This is a contradiction. Hence, . The conclusion holds. ☐
By the arbitrariness of and in Lemma 2, the following eigenvalue localization theorem is obtained easily.
Theorem 4. Let . Then, For all
, the relationship
holds, hence the following comparison theorem for Theorem 3, Lemma 2 and Theorem 4 is given easily.
Theorem 5. Let . Given an arbitrary positive integer k, then Note here that, from the proof of Lemma 2, it can be seen that does not contain any eigenvalues of A, and that is derived by excluding some proper subsets from . Hence, is called an exclusion set of . By Theorem 5, one can exclude some regions that do not include any eigenvalues of matrices to locate them more precisely.
Taking
in Theorem 4, the following result, which is also Theorem 4 in [
12], is deduced immediately.
Corollary 1. Let . Then,whereand Next, based on Lemma 2 and the fact that if and only if for a matrix A, the following condition such that is given easily.
Corollary 2. Let . If there is a positive integer k such that for any , eitheror for some and ,then A is nonsingular. Note here that, if taking and , then Corollary 2 is reduced to Lemma 1. That is to say, Corollary 2 is a generalization of Lemma 1.
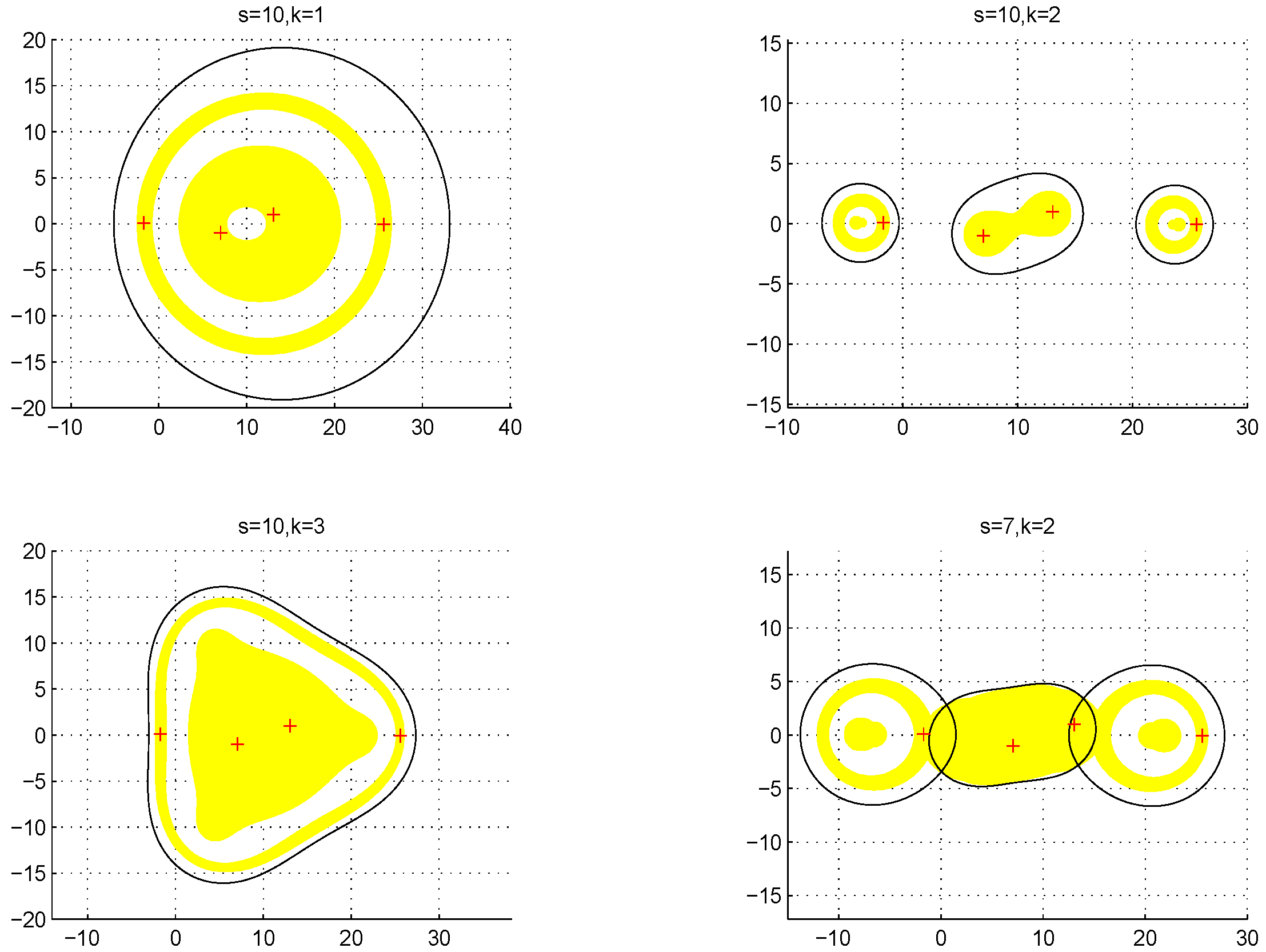
Finally, an example is given to validate Theorem 5, and show that the different selection of s and k will affect the eigenvalue location and the determination of non-singularity of .
Example 1. Consider the matrix provided in [12]: By computation, the spectrum of
A is
The eigenvalue inclusion set
,
and
with different
s and
k, and all eigenvalues are drawn in
Figure 1, where
,
and
, respectively, are showed by black boundary, yellow zone and its interior, and yellow zone. All eigenvalues are plotted by ‘+’.
- (1)
Whether
or
, it can be seen that
obtained by Theorem 1 for the same
k and
s.
- (2)
When , if taking , and , then differences of the three eigenvalue inclusion sets , , are clear. This implies that, if s is the same, but k is different, then these eigenvalue inclusion sets are different in general.
- (3)
When , if taking and , then the two eigenvalue inclusion sets and are also different, which implies that, if k is the same, but s is different, then these eigenvalue inclusion sets are also different in general.
- (4)
When and , we can see that . When and , we can see that , and . That is to say, we cannot determine the non-singularity of A when and , but we can do it when and , respectively. When k is the same one, the upper bounds and , respectively, are less than or equal to the upper bounds and , and and . In addition, if taking and , the upper bound , which reaches the true value of .
Then, an interesting problem is considered naturally: how to choose s and k to minimize the eigenvalue inclusion set and determine the non-singularity of ? Hence, it is essential to study this question in the future.
3. Infinity Norm Bounds for the Inverse of Matrices
Firstly, a lemma is listed, which is used to obtain the infinity norm bounds for the inverse of matrices.
Lemma 3 ([
13])
. If , then Theorem 6. Let . Then, for two certain numbers s and k, Proof. Since
, there exists
such that
. Obviously,
A and
are both nonsingular. By
we have
Since
, by Lemma 3, we have
This implies that Label (
2) holds. The proof is completed. ☐
Proof. Since
A is
, i.e.,
hence
. In order to obtain Label (
3), it is sufficient to show that for all
, the following inequality holds:
Indeed, if
then multiplying this inequality with
gives
i.e.,
This can be rewritten as
i.e.,
On the contrary, if
multiplying this inequality with
, we get
i.e.,
which can be rewritten as
i.e.,
The proof is completed. ☐
Next, a comparison for the bounds in Theorems 1 and 6 is given.
Theorem 7. If , then, for two certain numbers s and k, Proof. Since
, i.e., for some
and some
,
is
, then by Lemma 4, we have
Furthermore, by
, Label (
4) holds clearly. ☐
Finally, an example is given to validate Theorem 7, and show that the different selection of s and k will affect the infinity norm bounds for the inverse of .
Example 2. Consider the matrix provided in [7]: By computations,
Taking
, 5 and 10 for
, respectively, we can validate that
are all
matrices. Obviously, they are all
matrices too. Thus, we can use Theorems 1 and 6 to estimate
. The numerical results are listed in
Table 1.
Numerical results in
Table 1 show that:
- (1)
The upper bound obtained by Theorem 6 is less than or equal to the bound obtained by Theorem 1 for the same k and s.
- (2)
When s is the same, the upper bounds and do not increase with the increase of k. When k is the same one, the upper bounds and , respectively, are less than or equal to the upper bounds and , and and . In addition, if taking and , the upper bound , which reaches the true value of .
Then, another interesting problem arises naturally: How to choose s and k to minimize the upper bound ? Hence, it is essential to study this question in the future.
4. Conclusions
In this paper, by excluding some proper subsets of that do not contain any eigenvalues of A, we obtain a tighter eigenvalue localization set than those in Theorems 2 and 3. Then, the bound for the infinity norm of the inverse of matrices is given. Numerical examples show the effectiveness of the obtained results. However, there is a problem that has not been solved: how can s and k be picked to minimize the eigenvalue localization set and the infinity norm bounds ? This is a question worthy of further study.
Finally, the relationship between
matrices and
matrices is discussed. Consider again the matrix
A in Example 2. It is not difficult to validate that
A is an
matrix, but not a
matrix, which implies that an
matrix is not necessarily a
matrix, that is,
Then, another meaningful discussion is concerned: whether
matrices are
matrices or not. That is, whether the relationship
holds or not. This question is also interesting and worthy of further study.