Free Vibration Analysis of Functionally Graded Shells Using an Edge-Based Smoothed Finite Element Method
Abstract
:1. Introduction
2. Theoretical Formulation
2.1. Functionally Grade Material
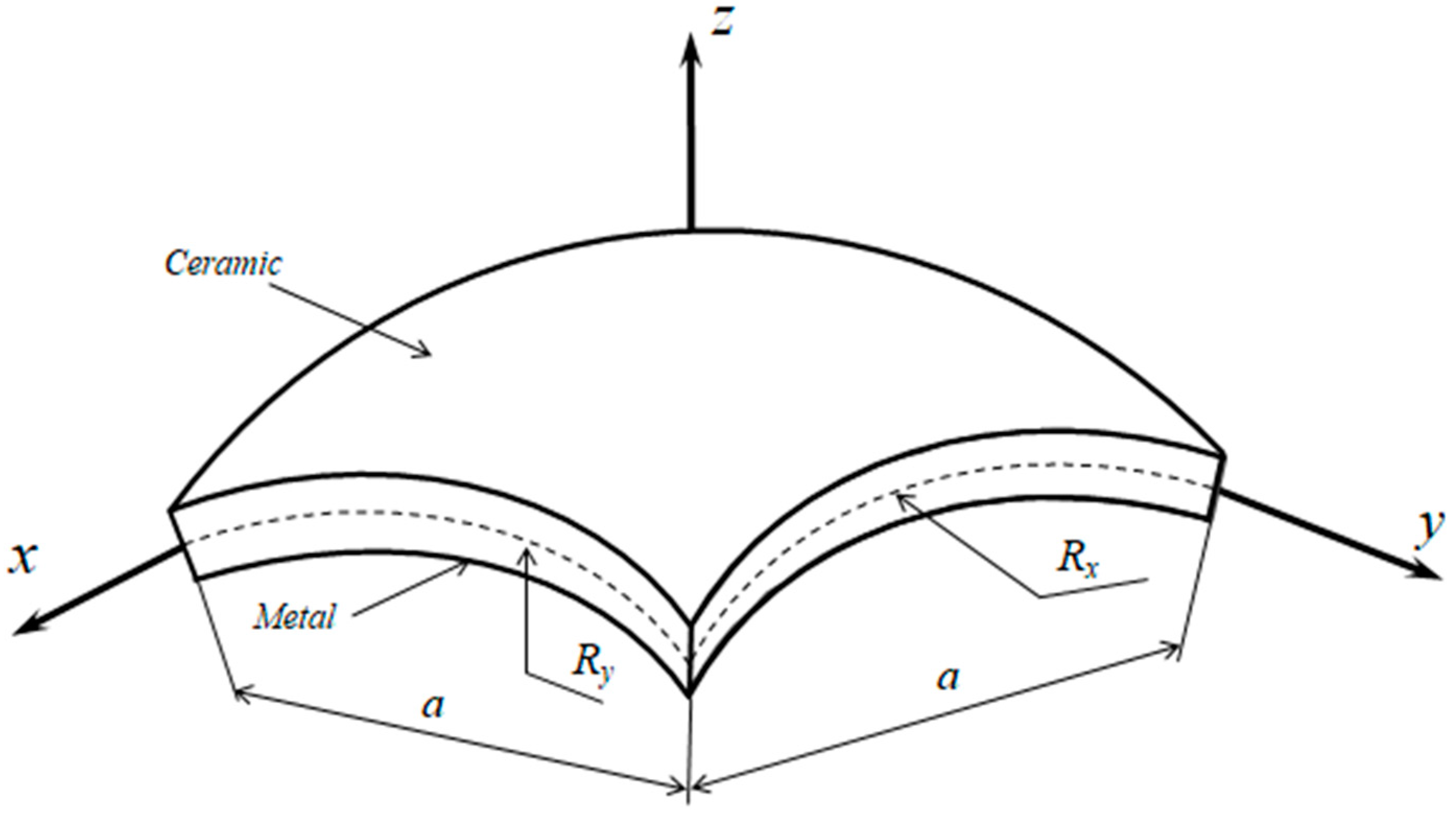
2.2. The FGM Shell Model
2.3. Finite Element Formulation for Shell Analysis
3. Formulation of ES-MITC3 Finite Element Method for FGM Shells
3.1. Brief on the MITC3 Formulation
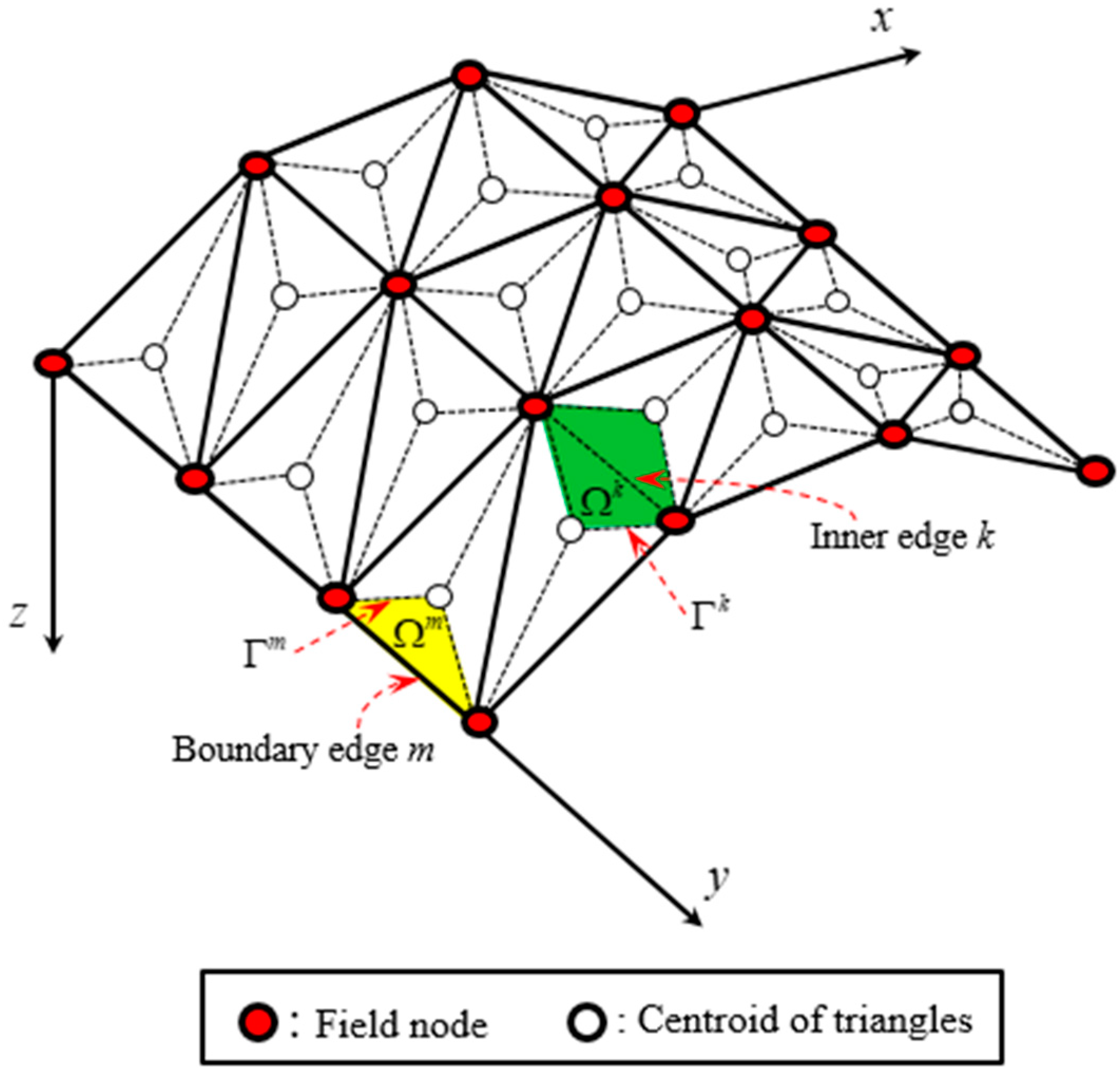
3.2. The ES-MITC3 Formulation
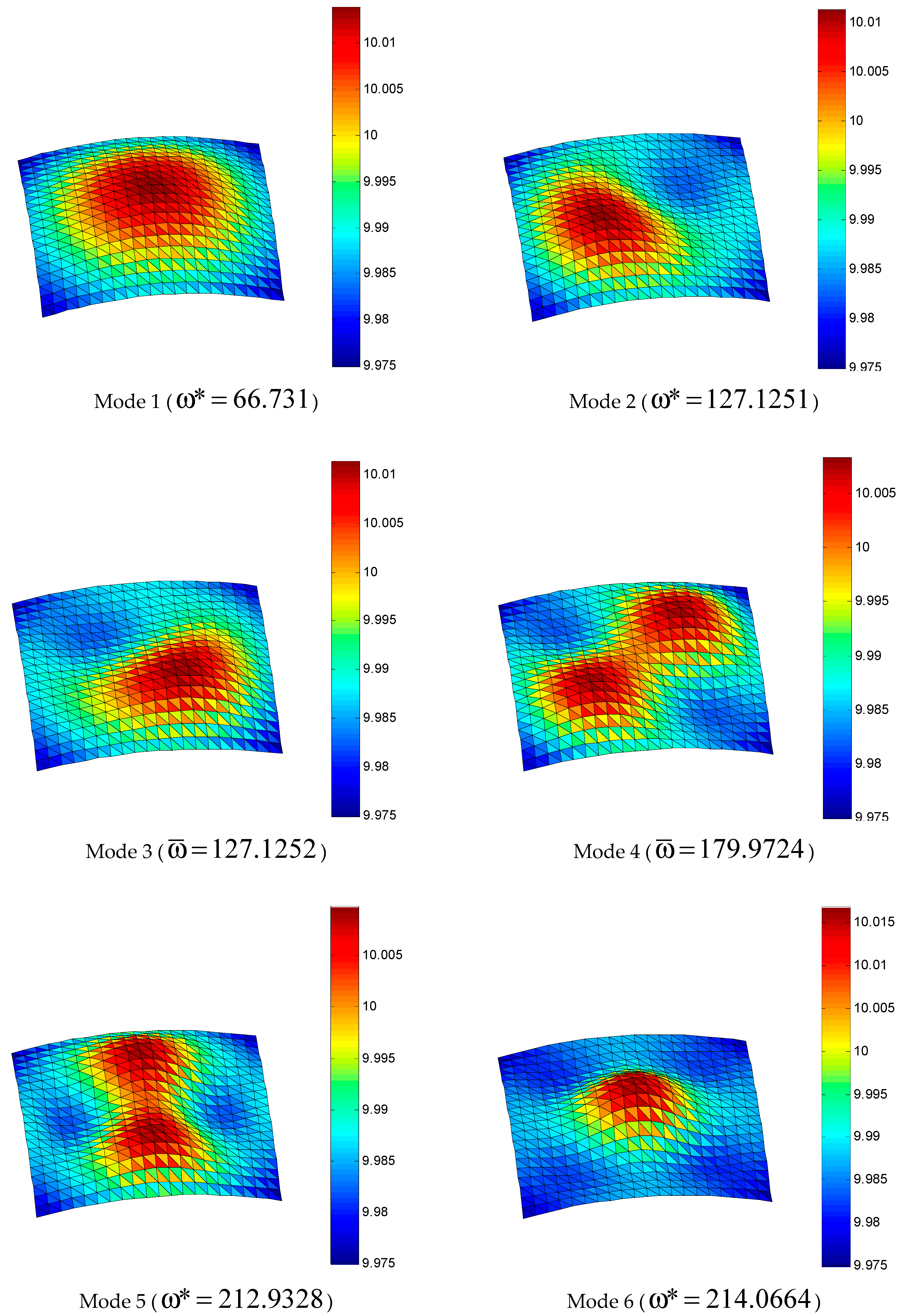
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Woo, J.; Meguid, S. Nonlinear analysis of functionally graded plates and shallow shells. Int. J. Solids Struct. 2001, 38, 7409–7421. [Google Scholar] [CrossRef]
- Matsunaga, H. Free vibration and stability of functionally graded shallow shells according to a 2D higher-order deformation theory. Compos. Struct. 2008, 84, 132–146. [Google Scholar] [CrossRef]
- Duc, N.D.; Quan, T.Q.; Luat, V.D. Nonlinear dynamic analysis and vibration of shear deformable piezoelectric FGM double curved shallow shells under damping-thermo-electro-mechanical loads. Compos. Struct. 2015, 125, 29–40. [Google Scholar] [CrossRef]
- Bich, D.H.; Duc, N.D.; Quan, T.Q. Nonlinear vibration of imperfect eccentrically stiffened functionally graded double curved shallow shells resting on elastic foundation using the first order shear deformation theory. Int. J. Mech. Sci. 2014, 80, 16–28. [Google Scholar] [CrossRef]
- Arciniega, R.A.; Reddy, J.N. Large deformation analysis of functionally graded shells. Int. J. Solids Struct. 2007, 44, 2036–2052. [Google Scholar] [CrossRef]
- Pradyumna, S.; Bandyopadhyay, J.N. Free vibration analysis of functionally graded curved panels using a higher-order finite element formulation. J. Sound Vib. 2008, 318, 176–192. [Google Scholar] [CrossRef]
- Kordkheili, S.A.H.; Naghdabadi, R. Geometrically non-linear thermoelastic analysis of functionally graded shells using finite element method. Int. J. Numer. Methods Eng. 2007, 72, 964–986. [Google Scholar] [CrossRef]
- Chau-Dinh, T.; Nguyen-Duy, Q.; Nguyen-Xuan, H. Improvement on MITC3 plate finite element using edge-based strain smoothing enhancement for plate analysis. Acta Mech. 2017, 228, 2141–2163. [Google Scholar] [CrossRef]
- Nguyen, T.-K.; Nguyen, V.-H.; Chau-Dinh, T.; Vo, T.P.; Nguyen-Xuan, H. Static and vibration analysis of isotropic and functionally graded sandwich plates using an edge-based MITC3 finite elements. Compos. Part B Eng. 2016, 107, 162–173. [Google Scholar] [CrossRef]
- Pham, Q.-H.; Tran, T.-V.; Pham, T.-D.; Phan, D.-H. An Edge-Based Smoothed MITC3 (ES-MITC3) Shell Finite Element in Laminated Composite Shell Structures Analysis. Int. J. Comput. Methods 2017, 15, 1850060. [Google Scholar] [CrossRef]
- Pham, Q.-H.; Pham, T.-D.; Trinh, Q.V.; Phan, D.-H. Geometrically nonlinear analysis of functionally graded shells using an edge-based smoothed MITC3 (ES-MITC3) finite elements. Eng. Comput. 2019, 1–14. [Google Scholar] [CrossRef]
- Pham-Tien, D.; Pham-Quoc, H.; Vu-Khac, T.; Nguyen-Van, N. Transient Analysis of Laminated Composite Shells Using an Edge-Based Smoothed Finite Element Method. In Proceedings of the International Conference on Advances in Computational Mechanics, Phu Quoc Island, Vietnam, 2–4 August 2017; pp. 1075–1094. [Google Scholar]
- Nguyen, H.N.; Canh, T.N.; Thanh, T.T.; Ke, T.V.; Phan, V.D.; Thom, D.V. Finite Element Modelling of a Composite Shell with Shear Connectors. Symmetry 2019, 11, 527. [Google Scholar] [CrossRef]
- Nguyen-Hoang, S.; Phung-Van, P.; Natarajan, S.; Kim, H.-G. A combined scheme of edge-based and node-based smoothed finite element methods for Reissner–Mindlin flat shells. Eng. Comput. 2016, 32, 267–284. [Google Scholar] [CrossRef]
- Nguyen-Thoi, T.; Phung-Van, P.; Thai-Hoang, C.; Nguyen-Xuan, H. A cell-based smoothed discrete shear gap method (CS-DSG3) using triangular elements for static and free vibration analyses of shell structures. Int. J. Mech. Sci. 2013, 74, 32–45. [Google Scholar] [CrossRef]
- Lee, P.-S.; Bathe, K.-J. Development of MITC isotropic triangular shell finite elements. Comput. Struct. 2004, 82, 945–962. [Google Scholar] [CrossRef]
- Neves, A.; Ferreira, A.; Carrera, E.; Cinefra, M.; Roque, C.; Jorge, R.; Soares, C.; Ferreira, A.; Jorge, R.N.; Soares, C.M.M. Free vibration analysis of functionally graded shells by a higher-order shear deformation theory and radial basis functions collocation, accounting for through-the-thickness deformations. Eur. J. Mech. A/Solids 2013, 37, 24–34. [Google Scholar] [CrossRef]
- Yang, J.; Shen, H.-S. Free vibration and parametric resonance of shear deformable functionally graded cylindrical panels. J. Sound Vib. 2003, 261, 871–893. [Google Scholar] [CrossRef]
- Fazzolari, F.A.; Carrera, E. Refined hierarchical kinematics quasi-3D Ritz models for free vibration analysis of doubly curved FGM shells and sandwich shells with FGM core. J. Sound Vib. 2014, 333, 1485–1508. [Google Scholar] [CrossRef]









| Mode | Method | n | ||||
|---|---|---|---|---|---|---|
| 0 | 0.2 | 2 | 10 | |||
| 1 | ES-MITC3 | 75.4587 | 61.3587 | 40.9880 | 35.3951 | 33.0594 |
| % | 0.2776 | 0.0298 | 0.3963 | 0.7275 | 0.5532 | |
| MITC3 [16] | 72.7508 | 59.0689 | 39.4771 | 34.0744 | 31.8220 | |
| % | 3.3209 | 3.7031 | 4.0679 | 4.4317 | 4.2754 | |
| HSDT FEM [6] | 72.9613 | 60.0269 | 39.1457 | 33.3666 | 32.0274 | |
| % | 3.0412 | 2.1413 | 4.8733 | 6.4169 | 3.6576 | |
| HSDT RBFC-1 [17] | 74.2634 | 60.0061 | 40.5259 | 35.1663 | 32.6108 | |
| % | 1.3108 | 2.1752 | 1.5193 | 1.3693 | 1.9026 | |
| HSDT RBFC-2 [17] | 74.5821 | 60.3431 | 40.8262 | 35.4229 | 32.8593 | |
| % | 0.8873 | 1.6258 | 0.7895 | 0.6496 | 1.1551 | |
| HSDT SAG [18] | 74.5180 | 57.4790 | 40.7500 | 35.8520 | 32.7610 | |
| % | 0.9725 | 6.2950 | 0.9747 | 0.5539 | 1.4508 | |
| ED555 [19] | 75.2498 | 61.3404 | 41.1511 | 35.6545 | 33.2433 | |
| 2 | ES-MITC3 | 144.4760 | 117.6462 | 78.5402 | 67.7320 | 63.3473 |
| % | 0.6724 | 0.6147 | 0.5174 | 0.3138 | 0.4088 | |
| MITC3 [16] | 140.8063 | 114.5113 | 76.4785 | 65.9309 | 61.6559 | |
| % | 1.8847 | 2.0664 | 2.1212 | 2.3537 | 2.2722 | |
| HSDT FEM [6] | 138.5552 | 113.8806 | 74.2915 | 63.2869 | 60.5546 | |
| % | 3.4533 | 2.6058 | 4.9201 | 6.2695 | 4.0178 | |
| HSDT RBFC-1 [17] | 141.6779 | 114.3788 | 76.9725 | 66.6482 | 61.9329 | |
| % | 1.2773 | 2.1797 | 1.4889 | 1.2913 | 1.8331 | |
| HSDT RBFC-2 [17] | 142.4281 | 115.2134 | 77.6639 | 67.1883 | 62.4886 | |
| % | 0.7546 | 1.4660 | 0.6041 | 0.4914 | 0.9523 | |
| HSDT SAG [18] | 144.6630 | 111.7170 | 78.8170 | 69.0750 | 63.3140 | |
| % | 0.8027 | 4.4562 | 0.8717 | 2.3029 | 0.3560 | |
| ED555 [19] | 143.5110 | 116.9275 | 78.1359 | 67.5201 | 63.0894 | |
| 3 | ES-MITC3 | 145.1510 | 118.1985 | 78.9069 | 68.0474 | 63.6440 |
| % | 1.0284 | 0.9602 | 0.8727 | 2.2434 | 0.7658 | |
| MITC3 [16] | 141.7861 | 115.3112 | 77.0122 | 66.3906 | 62.0864 | |
| % | 1.3137 | 1.5061 | 1.5494 | 4.6235 | 1.7003 | |
| HSDT FEM [6] | 138.5552 | 114.0266 | 74.3868 | 63.3668 | 60.6302 | |
| % | 3.5625 | 2.6033 | 4.9056 | 8.9675 | 4.0058 | |
| HSDT RBFC-1 [17] | 141.8485 | 114.5495 | 77.0818 | 66.7332 | 62.0082 | |
| % | 1.2702 | 2.1567 | 1.4604 | 4.1314 | 1.8241 | |
| HSDT RBFC-2 [6] | 142.6024 | 115.3665 | 77.7541 | 67.2689 | 62.5668 | |
| % | 0.7455 | 1.4588 | 0.6010 | 3.3618 | 0.9397 | |
| HSDT SAG [18] | 145.7400 | 112.5310 | 79.4070 | 67.5946 | 63.8060 | |
| % | 1.4383 | 3.8808 | 1.5121 | 2.8939 | 1.0223 | |
| ED555 [19] | 143.6735 | 117.0744 | 78.2242 | 69.6090 | 63.1603 | |
| 4 | ES-MITC3 | 204.0647 | 166.3177 | 111.0461 | 95.6539 | 89.5229 |
| % | 1.1780 | 1.2302 | 1.3863 | 1.2447 | 1.2996 | |
| MITC3 [16] | 195.3261 | 158.8135 | 106.1329 | 91.3802 | 85.4901 | |
| % | 3.1547 | 3.3373 | 3.0995 | 3.2788 | 3.2637 | |
| HSDT FEM [6] | 195.5366 | 160.6235 | 104.7687 | 89.1970 | 85.1788 | |
| % | 3.0503 | 2.2357 | 4.3450 | 5.5896 | 3.6160 | |
| HSDT RBFC-1 [17] | 199.1566 | 160.7355 | 107.9484 | 93.3350 | 86.8160 | |
| % | 1.2555 | 2.1675 | 1.4419 | 1.2097 | 1.7634 | |
| HSDT RBFC-2 [17] | 200.3158 | 162.0337 | 108.9677 | 94.0923 | 87.6341 | |
| % | 0.6808 | 1.3773 | 0.5113 | 0.4081 | 0.8377 | |
| HSDT SAG [18] | 206.9920 | 159.8550 | 112.4570 | 98.3860 | 90.3700 | |
| % | 2.6294 | 2.7034 | 2.6745 | 4.1365 | 2.2581 | |
| ED555 [19] | 201.6888 | 164.2966 | 109.5277 | 94.4779 | 88.3744 | |
| Method | n | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0.2 | 0.5 | 1 | 2 | 10 | |||
| 5 | ES-MITC3 | 73.4741 | 67.2928 | 60.6591 | 53.9842 | 48.1650 | 41.4718 | 33.4122 |
| HSDT FEM [6] | 71.8861 | 68.1152 | 63.1896 | 56.5546 | 36.2487 | 33.6611 | 32.4802 | |
| HSDT RBFC-1 [17] | 73.1640 | 66.6620 | 60.2477 | 53.5430 | 47.5205 | 40.8099 | 33.0576 | |
| HSDT RBFC-2 [17] | 73.6436 | 67.1004 | 60.6568 | 53.9340 | 47.9060 | 41.0985 | 33.2743 | |
| 10 | ES-MITC3 | 72.6253 | 65.5578 | 60.0417 | 53.4874 | 47.7863 | 41.1837 | 33.0311 |
| HSDT FEM [6] | 71.0394 | 67.3320 | 62.4687 | 55.8911 | 35.6633 | 31.1474 | 32.0976 | |
| HSDT RBFC-1 [17] | 72.3304 | 65.8808 | 59.5215 | 52.8800 | 46.9447 | 40.4145 | 32.6810 | |
| HSDT RBFC-2 [17] | 72.8141 | 66.3235 | 59.9353 | 53.2759 | 47.3343 | 40.7046 | 32.8995 | |
| 50 | ES-MITC3 | 72.3439 | 66.3519 | 59.9114 | 53.4282 | 47.7802 | 41.1529 | 32.9058 |
| HSDT FEM [6] | 70.7660 | 67.0801 | 62.2380 | 55.6799 | 35.4745 | 32.9812 | 31.9741 | |
| HSDT RBFC-1 [17] | 72.0614 | 65.6371 | 59.3022 | 52.6864 | 46.7820 | 40.3028 | 32.5594 | |
| HSDT RBFC-2 [17] | 72.5465 | 66.0814 | 59.7178 | 53.0841 | 47.1726 | 40.5923 | 32.7786 | |
| Method | n | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0.2 | 0.5 | 1 | 2 | 10 | |||
| 5 | ES-MITC3 | 42.9913 | 39.3028 | 35.4690 | 31.7485 | 28.6106 | 24.7564 | 19.5592 |
| HSDT FEM [6] | 42.2543 | 40.1621 | 37.2870 | 33.2268 | 27.4449 | 19.3892 | 19.0917 | |
| HSDT RBFC-1 [17] | 42.6701 | 38.7168 | 34.8768 | 30.9306 | 27.5362 | 24.2472 | 19.2796 | |
| HSDT RBFC-2 [17] | 42.7172 | 38.7646 | 34.9273 | 30.9865 | 27.5977 | 24.2839 | 19.3008 | |
| ED555 [19] | 42.7160 | 39.0642 | 35.0811 | 31.0414 | 27.5634 | 24.1245 | 19.3003 | |
| 10 | ES-MITC3 | 42.5231 | 38.9004 | 35.1357 | 31.4868 | 28.4168 | 24.6061 | 19.3492 |
| HSDT FEM [6] | 41.9080 | 39.8472 | 36.9995 | 32.9585 | 27.1879 | 19.1562 | 18.9352 | |
| HSDT RBFC-1 [17] | 42.3153 | 38.3840 | 34.5672 | 30.6485 | 27.2979 | 24.1063 | 19.1193 | |
| HSDT RBFC-2 [17] | 42.3684 | 38.4368 | 34.6219 | 30.7077 | 27.3616 | 24.1444 | 19.1433 | |
| ED555 [19] | 42.3677 | 38.7377 | 34.7661 | 30.7621 | 27.3258 | 23.9848 | 19.1429 | |
| 50 | ES-MITC3 | 42.3669 | 38.7889 | 35.0696 | 31.4631 | 28.4233 | 24.5937 | 19.2798 |
| HSDT FEM [6] | 41.7963 | 39.7465 | 36.9088 | 32.8750 | 27.0961 | 19.0809 | 18.8848 | |
| HSDT RBFC-1 [17] | 42.2008 | 38.2842 | 34.4809 | 30.5759 | 27.2423 | 24.0762 | 19.0675 | |
| HSDT RBFC-2 [17] | 42.2560 | 38.3384 | 34.5365 | 30.6355 | 27.3055 | 24.1125 | 19.0924 | |
| ED555 [19] | 42.2553 | 38.6391 | 34.6904 | 30.6890 | 27.2682 | 23.9515 | 19.0922 | |
| Method | n | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0.2 | 0.5 | 1 | 2 | 10 | |||
| 5 | ES-MITC3 | 44.4405 | 40.6238 | 36.6449 | 32.7529 | 29.4124 | 25.2893 | 20.2096 |
| HSDT FEM [6] | 44.0073 | 41.7782 | 38.7731 | 34.6004 | 28.7459 | 20.4691 | 19.8838 | |
| HSDT RBFC-1 [17] | 44.4555 | 40.3936 | 36.4453 | 32.3691 | 28.7833 | 25.0772 | 20.0818 | |
| HSDT RBFC-2 [17] | 44.4697 | 40.4211 | 36.6004 | 32.4101 | 28.8329 | 25.1038 | 20.0927 | |
| ED555 [19] | 44.4671 | 40.7166 | 36.6297 | 32.4645 | 28.7996 | 24.9403 | 20.0915 | |
| 10 | ES-MITC3 | 42.9198 | 39.2373 | 35.4098 | 31.6957 | 28.5633 | 24.7153 | 19.5267 |
| HSDT FEM [6] | 42.3579 | 40.2608 | 37.3785 | 33.3080 | 27.5110 | 19.4357 | 19.1385 | |
| HSDT RBFC-1 [17] | 42.7709 | 38.8074 | 34.9574 | 31.0012 | 27.5984 | 24.3034 | 19.3251 | |
| HSDT RBFC-2 [17] | 42.8180 | 38.8551 | 35.0080 | 31.0572 | 27.6602 | 24.3401 | 19.3464 | |
| ED555 [19] | 42.8169 | 39.1556 | 35.1622 | 31.1122 | 27.6258 | 24.1803 | 19.3459 | |
| 50 | ES-MITC3 | 42.4046 | 38.8147 | 35.0835 | 31.4662 | 28.4197 | 24.5977 | 19.2966 |
| HSDT FEM [6] | 41.8145 | 39.7629 | 36.9234 | 32.8881 | 27.1085 | 19.0922 | 18.8930 | |
| HSDT RBFC-1 [17] | 42.2192 | 38.2988 | 34.4922 | 30.5840 | 27.2474 | 24.0791 | 19.0759 | |
| HSDT RBFC-2 [17] | 42.2741 | 38.3528 | 34.5478 | 30.6437 | 27.3109 | 24.1168 | 19.1006 | |
| ED555 [19] | 42.2735 | 38.6538 | 34.7018 | 30.6975 | 27.2741 | 23.9567 | 19.1004 | |
| Method | n | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0.2 | 0.5 | 1 | 2 | 10 | |||
| 5 | ES-MITC3 | 74.3416 | 68.0034 | 61.2122 | 54.3761 | 48.3922 | 41.5911 | 33.7972 |
| HSDT FEM [6] | 73.5550 | 69.6597 | 64.6114 | 57.8619 | 37.3914 | 34.6658 | 33.2343 | |
| HSDT RBFC-1 [17] | 74.8207 | 68.2142 | 61.6902 | 54.8597 | 48.6656 | 41.6016 | 33.8061 | |
| HSDT RBFC-2 [17] | 75.2810 | 68.6329 | 62.0789 | 55.2302 | 49.0328 | 41.8796 | 34.0141 | |
| 10 | ES-MITC3 | 72.8831 | 66.7331 | 60.1352 | 53.5040 | 47.7428 | 41.1652 | 33.1447 |
| HSDT FEM [6] | 71.4659 | 67.7257 | 62.8299 | 56.2222 | 35.9568 | 33.4057 | 32.2904 | |
| HSDT RBFC-1 [17] | 72.7536 | 66.2686 | 59.8745 | 53.1956 | 47.2135 | 40.5990 | 32.8722 | |
| HSDT RBFC-2 [17] | 73.2322 | 66.7063 | 60.2831 | 53.5864 | 47.5990 | 40.8883 | 33.0884 | |
| 50 | ES-MITC3 | 72.3889 | 66.3780 | 59.9190 | 53.4192 | 47.7612 | 41.1495 | 32.9258 |
| HSDT FEM [6] | 70.7832 | 67.0956 | 62.2519 | 55.6923 | 35.4861 | 32.9916 | 31.9819 | |
| HSDT RBFC-1 [17] | 72.0784 | 65.6498 | 59.3112 | 52.6921 | 46.7849 | 40.3049 | 32.5671 | |
| HSDT RBFC-2 [17] | 72.5633 | 66.0938 | 59.7265 | 53.0895 | 47.1574 | 40.5946 | 32.7862 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, T.D.; Pham, Q.H.; Phan, V.D.; Nguyen, H.N.; Do, V.T. Free Vibration Analysis of Functionally Graded Shells Using an Edge-Based Smoothed Finite Element Method. Symmetry 2019, 11, 684. https://doi.org/10.3390/sym11050684
Pham TD, Pham QH, Phan VD, Nguyen HN, Do VT. Free Vibration Analysis of Functionally Graded Shells Using an Edge-Based Smoothed Finite Element Method. Symmetry. 2019; 11(5):684. https://doi.org/10.3390/sym11050684
Chicago/Turabian StylePham, Tien Dat, Quoc Hoa Pham, Van Duc Phan, Hoang Nam Nguyen, and Van Thom Do. 2019. "Free Vibration Analysis of Functionally Graded Shells Using an Edge-Based Smoothed Finite Element Method" Symmetry 11, no. 5: 684. https://doi.org/10.3390/sym11050684
APA StylePham, T. D., Pham, Q. H., Phan, V. D., Nguyen, H. N., & Do, V. T. (2019). Free Vibration Analysis of Functionally Graded Shells Using an Edge-Based Smoothed Finite Element Method. Symmetry, 11(5), 684. https://doi.org/10.3390/sym11050684





