The Symmetric Difference Distance: A New Way to Evaluate the Evolution of Interfaces along Molecular Dynamics Trajectories; Application to Influenza Hemagglutinin
Abstract
1. Introduction
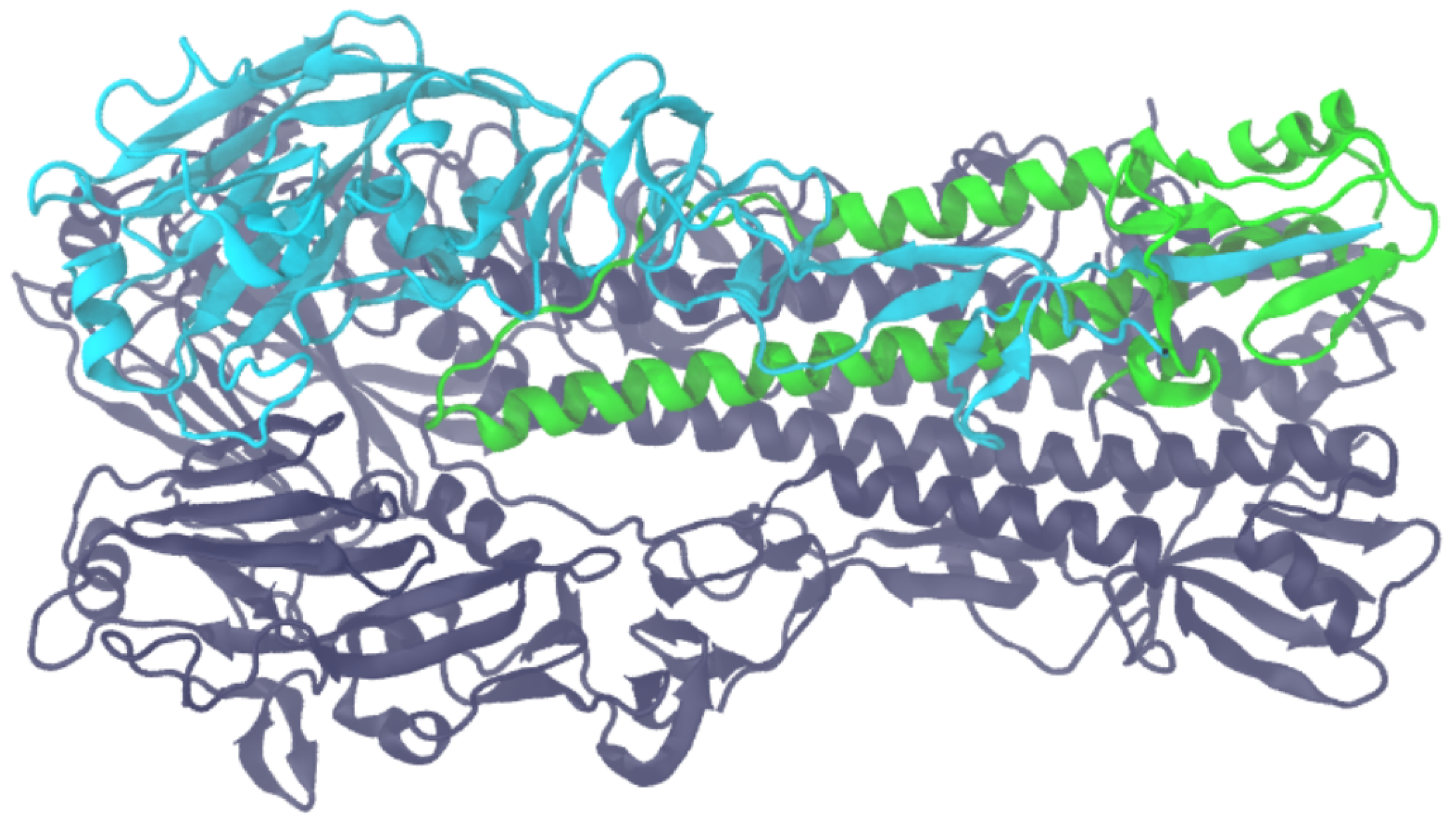
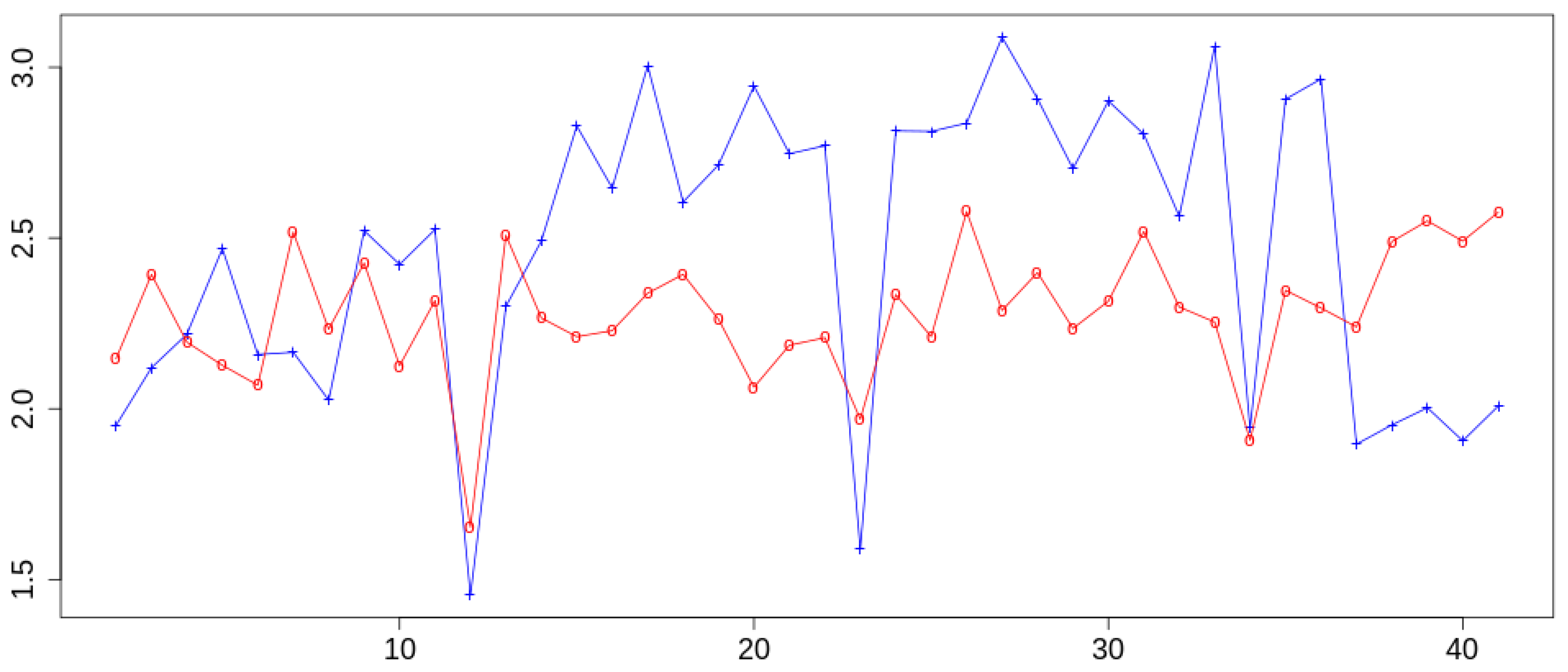
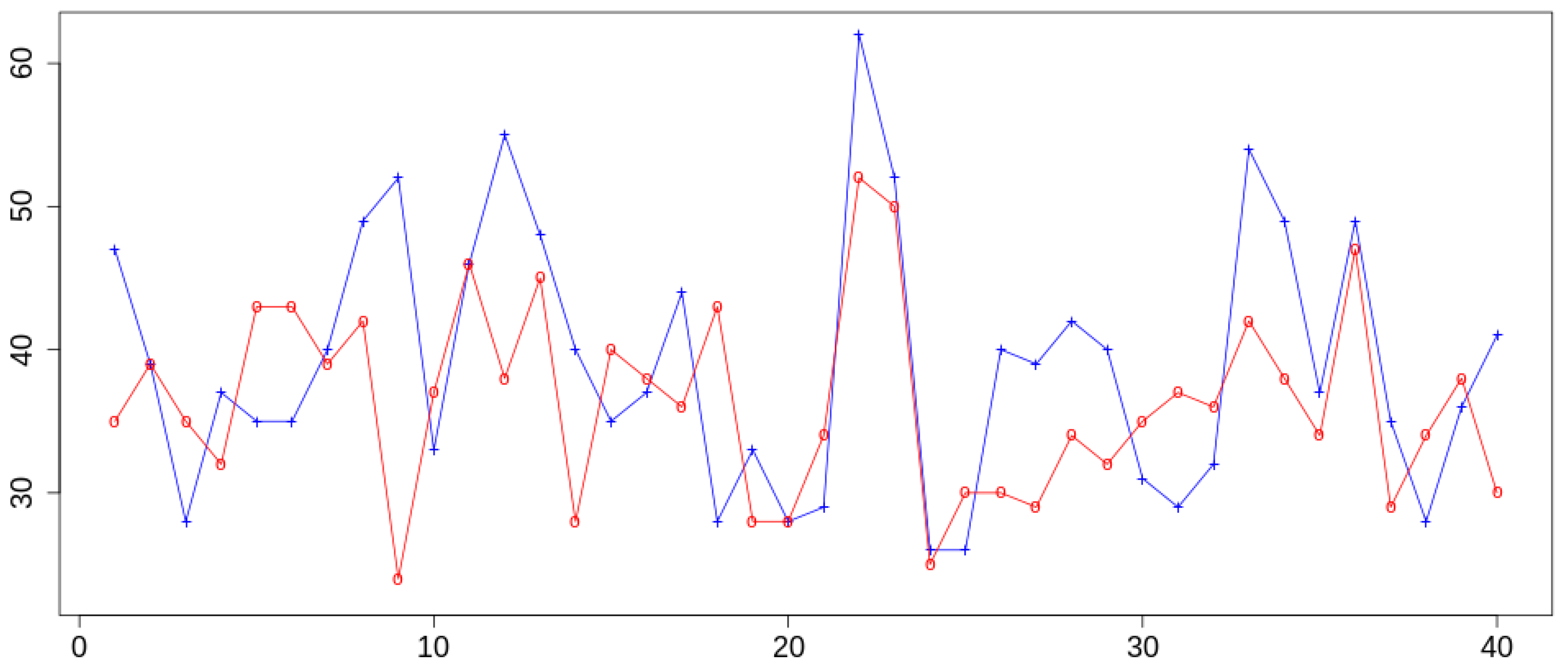
2. Results and Discussion
3. Methods
3.1. Computation of Interfaces within Macromolecular Complexes
- The cutoff method.
- The loss of accessible surface area upon binding.
- The Voronoi tessellation method.
- Generate the first part of the interface, constituted by the non-redundant set of all nearest neighbors of the atoms of A among the atoms of B.
- Generate the second part of the interface, constituted by the non-redundant set of all nearest neighbors of the atoms of B among the atoms of A.
3.2. Computation of Interfaces in Macromolecular Polymers
3.3. Evaluation of the Dissimilarity between Two Interfaces
3.4. Comparison with Other Dissimilarity Measures
3.5. Steps of the Methodology
- Generate the frames of the MD simulation.
- For each frame, generate the global interface with the procedure described in Section 3.2.
- For each couple of successive frames, evaluate the dissimilarity between the interfaces with the SDD, as described in Section 3.3.
- Follow the evolution of the interface along the trajectory using the SDD as a coordinate varying as a function of the time.
4. Conclusions
- It is parameter free.
- No spatial alignment is needed, thus no non-trivial numerical solver is needed.
- The problem of molecular graph symmetries occurring in some contexts for residues Val, Leu, Arg, Phe, Tyr, Glu, and Asp, which is almost always neglected when computing RMSD values, does not exist in our approach.
- All the steps of our algorithm can be coded by a beginner in programming.
- The dissimilarity between interfaces is measured with a distance (see Appendix A).
- Unwanted contributions of meaningless parts of macromolecules can be discarded (e.g., disordered parts in macromolecules, etc.).
- Images of optimal superpositions of full macromolecules are too overloaded compared to those of optimal superpositions of interfaces.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| HA | Hemagglutinin |
| MD | Molecular Dynamics |
| PDB | Protein Data Bank |
| PPI | Protein–Protein Interaction |
| RMSD | Root Mean Squared Deviation |
| RMSF | Root Mean Squared Fluctuation |
| RNN | Reciprocal Nearest Neighbors |
| SASA | Solvent Accessible Surface Area |
| SDD | Symmetric Difference Distance |
Appendix A. Definition and Properties of Distances
- 1.
- (symmetry)
- 2.
- 3.
- 4.
- (triangle inequality)
- Removing the symmetry condition would mean that there exist two elements x and y such that : understanding this result may be difficult.
- Removing the condition would mean that there exists an element x such that : what should one think about such an element?
- Many authors define dissimilarities between objects, although the third condition does not stand: nothing can be deduced when a null distance is observed between two distinct element x and y, a really embarrassing situation.
- The triangle inequality is useful, as well: it would be difficult to understand a situation where three distinct elements x, y, and z would be such that .
Appendix B. Interfaces Residues of the Mean Frames
References
- Thompson, W.W.; Weintraub, E.; Dhankhar, P.; Cheng, P.Y.; Brammer, L.; Meltzer, M.I.; Bresee, J.S.; Shay, D.K. Estimates of US influenza-associated deaths made using four different methods. Influenza Other Respir. Viruses 2009, 3, 37–49. [Google Scholar] [CrossRef] [PubMed]
- Viboud, C.; Grais, R.F.; Lafont, B.A.P.; Miller, M.A.; Simonsen, L. Multinational Impact of the 1968 Hong Kong Influenza pandemic: Evidence for a smoldering pandemic. J. Infect. Dis. 2005, 192, 233–248. [Google Scholar] [CrossRef]
- Gamblin, S.J.; Haire, L.F.; Russell, R.J.; Stevens, D.J.; Xiao, B.; Ha, Y.; Vasisht, N.; Steinhauer, D.A.; Daniels, R.S.; Elliot, A.; et al. The structure and receptor binding properties of the 1918 Influenza hemagglutinin. Science 2004, 303, 1838–1842. [Google Scholar] [CrossRef] [PubMed]
- Simonsen, L.; Spreeuwenberg, P.; Lustig, R.; Taylor, R.J.; Fleming, D.M.; Kroneman, M.; Van Kerkhove, M.D.; Mounts, A.W.; Paget, W.J. GLaMOR Collaborating Teams. Global mortality estimates for the 2009 Influenza pandemic from the GLaMOR project: A modeling study. PLoS Med. 2013, 10, e1001558. [Google Scholar] [CrossRef]
- Gamblin, S.J.; Skehel, J.J. Influenza hemagglutinin and neuraminidase membrane glycoproteins. J. Biol. Chem. 2010, 285, 28403–28409. [Google Scholar] [CrossRef]
- Smrt, S.T.; Lorieau, J.L. Membrane fusion and infection of the Influenza hemagglutinin. In Protein Reviews (Advances in Experimental Medicine and Biology, 966); Atassi, M.Z., Ed.; Springer: Singapore, 2017; Volume 18, pp. 37–54. [Google Scholar] [CrossRef]
- Skehel, J.J.; Wiley, D.C. Receptor binding and membrane fusion in virus entry: The Influenza hemagglutinin. Annu. Rev. Biochem. 2000, 69, 531–569. [Google Scholar] [CrossRef]
- Perrier, A.; Eluard, M.; Petitjean, M.; Vanet, A. Design of new inhibitors against hemagglutinin of Influenza. J. Phys. Chem. B 2019, 123, 582–592. [Google Scholar] [CrossRef]
- The PyMOL Molecular Graphics System, Version 1.8.4.0; Schrödinger, LLC: New York, NY, USA, 2016; Available online: http://www.pymol.org (accessed on 18 April 2019).
- Petitjean, M. On the root mean square quantitative chirality and quantitative symmetry measures. J. Math. Phys. 1999, 40, 4587–4595. [Google Scholar] [CrossRef][Green Version]
- Petitjean, M. Chiral mixtures. J. Math. Phys. 2002, 43, 4147–4157. [Google Scholar] [CrossRef]
- Deza, M.M.; Deza, E. Encyclopedia of Distances; Springer: Berlin, Germany, 2009; p. 46. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: https://www.R-project.org/ (accessed on 18 April 2019).
- Meslamani, J.E.; André, F.; Petitjean, M. Assessing the geometric diversity of cytochrome P450 ligand conformers by hierarchical clustering with a stop criterion. J. Chem. Inf. Model. 2009, 49, 330–337. [Google Scholar] [CrossRef] [PubMed]
- Petitjean, M. Interactive maximal common 3D substructure searching with the combined SDM/RMS algorithm. Comput. Chem. 1998, 22, 463–465. [Google Scholar] [CrossRef]
- Dequeker, C.; Laine, E.; Carbone, A. INTerface Builder: A fast protein–protein interface reconstruction tool. J. Chem. Inf. Model. 2017, 57, 2613–2617. [Google Scholar] [CrossRef]
- Xue, L.C.; Dobbs, D.; Bonvin, A.M.J.J.; Honavar, V. Computational prediction of protein interfaces: A review of data driven methods. FEBS Lett. 2015, 23, 3516–3526. [Google Scholar] [CrossRef]
- Wang, W.; Yang, Y.; Yin, J.; Gong, X. Different protein–protein interface patterns predicted by different machine learning methods. Sci. Rep. 2017, 7, 16023. [Google Scholar] [CrossRef]
- De Vries, S.J.; Bonvin, A.M.J.J. How proteins get in touch: Interface prediction in the study of bio-molecular complexes. Curr. Prot. Peptide Sci. 2008, 9, 394–406. [Google Scholar] [CrossRef]
- Bondi, A. Van der Waals volumes and radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Allinger, N.; Zhou, X.; Bergsma, J. Molecular mechanics parameters. J. Mol. Struct. 1994, 312, 69–83. [Google Scholar] [CrossRef]
- Gavezzotti, A. The calculation of molecular volumes and the use of volume analysis in the investigation of structured media and of solid-state organic reactivity. J. Am. Chem. Soc. 1983, 105, 5220–5225. [Google Scholar] [CrossRef]
- Petitjean, M. On the analytical calculation of van der Waals surfaces and volumes: Some numerical aspects. J. Comput. Chem. 1994, 15, 507–523. [Google Scholar] [CrossRef]
- Petitjean, M. Spheres unions and intersections and some of their applications in molecular modeling. In Distance Geometry: Theory, Methods, and Applications; Mucherino, A., Lavor, C., Liberti, L., Maculan, N., Eds.; Springer: New York, NY, USA, 2013; Chapter 4; pp. 61–83. [Google Scholar] [CrossRef]
- Cazals, F.; Proust, F.; Bahadur, R.P.; Janin, J. Revisiting the Voronoi description of protein–protein interfaces. Prot. Sci. 2006, 15, 2082–2092. [Google Scholar] [CrossRef] [PubMed]
- Bouvier, B.; Grünberg, R.; Nilges, M.; Cazals, F. Shelling the Voronoi interface of protein–protein complexes reveals patterns of residue conservation, dynamics, and composition. Proteins 2009, 76, 677–692. [Google Scholar] [CrossRef]
- Gore, S.P.; Burke, D.F.; Blundell, T.L. PROVAT: A tool for Voronoi tessellation analysis of protein structures and complexes. Bioinformatics 2005, 21, 3316–3317. [Google Scholar] [CrossRef][Green Version]
- Edelsbrunner, H. Voronoi Diagrams. In Algorithms in Combinatorial Geometry; Brauer, W., Rozenberg, G., Salomaa, A., Eds.; Springer: Berlin, Germany, 1987; Chapter 13; pp. 293–334. [Google Scholar]
- Laville, P.; Martin, J.; Launay, G.; Regad, L.; Camproux, A.-C.; de Vries, S.; Petitjean, M. A non-parametric method to compute protein-protein and protein-ligands interfaces. Application to HIV-2 protease-inhibitors complexes. bioRXiv 2018, 498923. [Google Scholar] [CrossRef]
- Cerisier, N.; Regad, L.; Triki, D.; Camproux, A.-C.; Petitjean, M. Cavity versus ligand shape descriptors: Application to urokinase binding pockets. J. Comput. Biol. 2017, 24, 1134–1137. [Google Scholar] [CrossRef]
- Eppstein, D.; Paterson, M.S.; Yao, F.F. On nearest-neighbor graphs. Discrete Comput. Geom. 1997, 17, 263–282. [Google Scholar] [CrossRef]
- Martin, J.; Regad, L.; Etchebest, C.; Camproux, A.-C. Taking advantage of local structure descriptors to analyze interresidue contacts in protein structures and protein complexes. Proteins 2008, 73, 672–689. [Google Scholar] [CrossRef]
- Triki, D.; Cano Contreras, M.E.; Flatters, D.; Visseaux, B.; Descamps, D.; Camproux, A.-C.; Regad, L. Analysis of the HIV-2 protease’s adaptation to various ligands: Characterization of backbone asymmetry using a structural alphabet. Sci. Rep. 2018, 8, 710. [Google Scholar] [CrossRef]
- McDonald, I.K.; Thornton, J.M. Satisfying hydrogen bonding potential in proteins. J. Mol. Biol. 1994, 238, 777–793. [Google Scholar] [CrossRef]
- Gao, M.; Skolnick, J. iAlign: A method for the structural comparison of protein–protein interfaces. Bioinformatics 2010, 26, 2259–2265. [Google Scholar] [CrossRef]
- Esque, J.; Oguey, C.; de Brevern, A.G. Comparative analysis of threshold and tessellation methods for determining protein contacts. J. Chem. Inf. Model 2011, 51, 493–507. [Google Scholar] [CrossRef]
- Mohammadiarani, H.; Shaw, V.S.; Neubig, R.R.; Vashisth, H. Interpreting hydrogen–deuterium exchange events in proteins using atomistic simulations: Case studies on regulators of G-protein signaling proteins. J. Phys. Chem. B 2018, 122, 9314–9323. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, M.; Mohammadiarani, H.; Shaw, V.S.; Richard, R.; Neubig, R.R.; Vashisth, H. Interplay of cysteine exposure and global protein dynamics in small-molecule recognition by a regulator of G-protein signaling protein. Proteins 2019, 87, 146–156. [Google Scholar] [CrossRef] [PubMed]
- Shaw, V.S.; Mohammadiarani, H.; Vashisth, H.; Neubig, R.R. Differential protein dynamics of regulators of G-protein signaling: Role in specificity of small-molecule inhibitors. J. Am. Chem. Soc. 2018, 140, 3454–3460. [Google Scholar] [CrossRef] [PubMed]
- Mohammadiarani, H.; Vashisth, H. Insulin mimetic peptide S371 folds into a helical structure. J. Comput. Chem. 2017, 38, 1158–1166. [Google Scholar] [CrossRef] [PubMed]
- Petitjean, M. Geometric molecular similarity from volume-based distance minimization: Application to saxitoxin and tetrodotoxin. J. Comput. Chem. 1995, 16, 80–90. [Google Scholar] [CrossRef]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozeel, V.; Perrier, A.; Vanet, A.; Petitjean, M. The Symmetric Difference Distance: A New Way to Evaluate the Evolution of Interfaces along Molecular Dynamics Trajectories; Application to Influenza Hemagglutinin. Symmetry 2019, 11, 662. https://doi.org/10.3390/sym11050662
Ozeel V, Perrier A, Vanet A, Petitjean M. The Symmetric Difference Distance: A New Way to Evaluate the Evolution of Interfaces along Molecular Dynamics Trajectories; Application to Influenza Hemagglutinin. Symmetry. 2019; 11(5):662. https://doi.org/10.3390/sym11050662
Chicago/Turabian StyleOzeel, Valentin, Aurélie Perrier, Anne Vanet, and Michel Petitjean. 2019. "The Symmetric Difference Distance: A New Way to Evaluate the Evolution of Interfaces along Molecular Dynamics Trajectories; Application to Influenza Hemagglutinin" Symmetry 11, no. 5: 662. https://doi.org/10.3390/sym11050662
APA StyleOzeel, V., Perrier, A., Vanet, A., & Petitjean, M. (2019). The Symmetric Difference Distance: A New Way to Evaluate the Evolution of Interfaces along Molecular Dynamics Trajectories; Application to Influenza Hemagglutinin. Symmetry, 11(5), 662. https://doi.org/10.3390/sym11050662




