Abstract
The flow and heat transfer analysis in the conventional nanofluid and hybrid nanofluid was carried out in the present study. The present work also focused on the comparative analysis of entropy generation in conventional and hybrid nanofluid flow. The flows of both types of nanofluid were assumed to be over a thin needle in the presence of thermal dissipation. The temperature at the surface of the thin needle and the fluid in the free stream region were supposed to be constant. Modified Maxwell Garnet (MMG) and the Brinkman model were utilized for effective thermal conductivity and dynamic viscosity. The numerical solutions of the self-similar equations were obtained by using the Runge-Kutta Fehlberg scheme (RKFS). The Matlab in-built solver bvp4c was also used to solve the nonlinear dimensionless system of differential equations. The present numerical results were compared to the existing limiting outcomes in the literature and were found to be in excellent agreement. The analysis demonstrated that the rate of entropy generation reduced with the decreasing velocity of the thin needle as compared to the free stream velocity. The hybrid nanofluid flow with less velocity was compared to the regular nanofluid under the same circumstances. Furthermore, the enhancement in the temperature profile of the hybrid nanofluid was high as compared to the regular nanofluid. The influences of relevant physical parameters on flow, temperature distribution, and entropy generation are depicted graphically and discussed herein.
1. Introduction
The first law of thermodynamics deals with conservation and conversion of energy. It stipulates that when a thermodynamic process is carried out, energy is neither gained nor lost. Energy only transforms from one form into another, and the energy balance is maintained. The law presumes that any change of a thermodynamic state can take place in either direction. However, this is not true, particularly in the inter-conversion of heat and work. Processes proceed spontaneously in certain directions—but not in opposite directions—even though the reversal of processes does not violate the first law. The second law of thermodynamics puts a limit on the conversion of a given amount of heat into work. Complete conversion of heat into work is not possible, i.e., a portion of heat supplied to any thermodynamic system must be rejected. This simply implies that the efficiency of any thermodynamic system can never be equal to 100%. Entropy is the measure of unviable energy (the portion of energy that is not utilizable). The amount of unviable energy increases with the increase in entropy generation. Consequently, the efficiency of the thermal system declines. Bejan [1] introduced the innovative idea of minimization of entropy generation (MEG) to enhance the quality of energy. Recently, Afridi et al. [2] utilized the Sparrow-Quack-Boerner local non-similarity approach to study the effects of thermal dissipation on entropy generation in mixed convection flow under the influence of a constant magnetic field. Flow over a bidirectional stretching sheet with entropy generation was reported by Afridi and Qasim [3]. Numerical study of entropy generation in a fluid flow over a curved surface with variable thermal conductivity was studied by Afridi et al. [4]. The comparative analysis of entropy generation in nanofluid and working fluid flow over a curved surface was carried out by Afridi et al. [5]. Butt et al. [6] studied the inclination effects on entropy generation in a flow of nanofluid over a stretching cylinder. Makinde and Eegunjobi [7] studied the entropy production in the presence of magnetic field heat source, thermal radiation, and porous medium. The combined effects of the porous medium and the magnetic field on the rate of entropy production were reported by Butt et al. [8]. The second law analysis of fluid flow between the two-permeable stretched surface with Hall effects was carried out by Khan et al. [9]. Some of the recent and innovative research on entropy generation in fluid flow is mentioned in [10,11,12,13,14].
Cooling by fluid flow has received considerable attention in a variety of fields, such as electronics automobile and metallic plate cooling. In all such cooling processes, different working fluids such as water, propylene glycol, ethylene glycol (C2H6O2) bio fluids, engine oil, polymeric solutions, blends of water and glycol, and other basic fluids are utilized as coolants. To enhance the thermal conductivity of liquid coolants, several researchers played an important role in the past two decades. Choi et al. [15] introduced the idea of boosting the thermal conductivity of working fluids by insertion of nanoparticles. Nanofluids are basically the amalgamation of solid nanoparticles and liquid coolants. This new type of coolant revolutionized the modern industrial world. The nanoparticles have amazing capabilities to increase the heat transfer phenomenon and the thermal conductivity of the working fluid. After the seminal work of Choi et al. [15], several researchers investigated the effects by adding different solid nanoparticles into the various working fluids (base fluids) [16,17,18,19,20,21,22,23,24,25,26]. Recently, an advanced version of nanofluid known as hybrid nanofluid was introduced. Hybrid nanofluid is colloidal suspensions of two distinct nanoparticles in the base fluid. Hybrid nanofluid has numerous applications in medical, lubrication, solar heating, refrigeration, microfluids, electronic cooling, nuclear system cooling, welding, vehicle thermal management, and generator cooling. The hybrid nanofluid works more efficiently as a cooling agent compared to regular nanofluid. Recently, Devi and Devi [27] reported the influences of mass suction on heat transfer in hybrid nanofluid flow over an elastic permeable stretching surface. Afridi et al. [28] compared the flow and heat transfer in two different base fluids and two different hybrid fluid flows by utilizing the three-stage Lobatto IIIA formula. Farooq et al. [29] reported the transpiration effects on entropy generation in hybrid nanofluid flow with energy dissipation. Some recent innovative research on hybrid nanofluid is mentioned in [30,31,32,33,34].
The aim of this study was to report the impacts of energy dissipation on heat transfer and entropy generation in the flow of conventional and hybrid nanofluid. The boundary layer flow was considered to be over a moving thin needle in the presence of parallel stream flow. It is worth mentioning that the probes of measuring devices such as a shielded thermocouple or a hot wire anemometer are often a thin wire or needle-like in shape. Therefore, the analysis of fluid flow over needle-shaped bodies is of considerable practical interest [35].
The parallel stream flow was assumed to be in the direction of the moving needle. The partially coupled governing equations were changed into dimensionless forms by virtue of similarity transformations. The numerical solution of the dimensionless nonlinear equations was obtained by using shooting and the Runge-Kutta Fehlberg scheme. The following sections consist of a mathematical formulation, a numerical solution, and a graphical representation of the numerical solution, qualitative discussions, and concluding remarks.
2. Mathematical Formulation
Consider the flow of hybrid nanofluid over a thin needle with frictional heating (energy dissipation). The coordinate system and the geometry of the physical flow model are shown in Figure 1. The free stream velocity is in the direction of the x-axis, i.e., along the surface of the thin needle. The velocity of the thin needle and the temperature at the surface of the thin needle are supposed to be constant. Furthermore, the temperature in the free stream region is considered to be constant such that . Following the Tiwari and Dass Model (TDM) [36] with boundary layer approximations, the governing equations for the hybrid nanofluid are:
with the following boundary conditions:
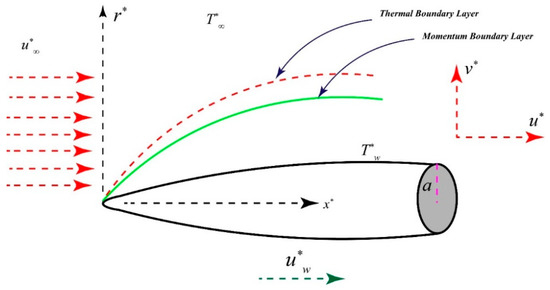
Figure 1.
Geometry of the problem with coordinates axes.
Here, represents the velocity components along the and -axes, respectively, shows the local temperature within the boundary layer, [37] describes the shape of the surface of the thin needle, shows the size of the needle, is the axial coordinate, represents the kinematic viscosity of the base fluid, and shows the composite velocity. On the other hand, the effective thermal conductivity , viscosity , specific heat at constant pressure , density , and thermal diffusivity of the hybrid nanofluid are defined as [33]:
We introduce the dimensionless variables as [37]:
where denotes stream function defined such that and , stands for dimensionless stream function, is the similarity variable, presents the dimensionless temperature distribution, the subscripts and denote the hybrid nanofluid and the base fluid, respectively, and indicates composite velocity.
Equation (1) is identically satisfied by Equation (9), whereas Equations (2)–(4) yield:
Here, stands for velocity ratio parameter, and for the solid volume fraction of copper and aluminum oxide nanoparticles, respectively, for Eckert number, and for Prandtl number. The above-mentioned parameters are defined as follows:
3. Irreversibility Analysis
The entropy generation due to frictional and thermal irreversibilities in the two-dimensional flow of the hybrid nanofluid over a thin needle is given by [38]:
The first term on the right side of Equation (14) indicates the heat transfer irreversibility (H.T.I) (entropy generation due to heat transfer), and the last term represents the frictional irreversibility (entropy generation due to frictional heating). To non-dimentionalized Equation (14), the characteristic entropy generation is defined as given below:
With the utilization of dimensionless variables defined in Equations (9) and (15), Equation (14) takes the following useful form:
Here, is the heat transfer irreversibility and is the fluid friction irreversibility.
4. Numerical Solution
The non-linear self-similar Equations (10) and (11) with the dimensionless boundary conditions were solved by applying the Fehlberg fourth order Runge-Kutta method and the shooting technique. The Fehlberg fourth order Runge-Kutta method works for first order initial value problems. Since our problem was boundary value and higher order, we first reduced our problem to a first order initial value problem. The following are the three basic steps:
- Convert Equations and to a set of first order initial value problems.
- The shooting technique is used to determine the missing initial conditions such that the conditions at are satisfied.
- Finally, the Fehlberg fourth order Runge-Kutta method (initial value problem method) is utilized to get the required numerical solutions.
The fourth order accurate solution is defined as follows:
Each iteration consists of five steps that are given below:
Equations and with the corresponding boundary conditions (12) are transformed to a system of initial value problems by taking:
By substituting Equation (19) in the Equations (10)–(12), we obtain a system of first order differential equations with initial conditions, as given below:
The missing initial conditions and are calculated by the utilization of an iterative scheme known as the shooting technique such that the boundary conditions and are satisfied. The iterative procedure continues until the solution converges to the desired accuracy of . Furthermore, the step size used in the simulation is = 0.001.
5. Results and Discussion
The dimensionless Equations (10) and (11) were highly nonlinear and had variable coefficients. Therefore, it was not possible to obtain the closed form solution of these equations. This fact forced us to solve these equations numerically. The Runge-Kutta Fehlberg schemes (RKFS) and the shooting method (SM) were utilized to get the solution of Equations (10) and (11) numerically. To analyze the impacts of different parameters on , and , the obtained numerical results were plotted against the similarity variable for various values of emerging parameters. The solid volume fractions of aluminum oxide and copper nanoparticles are represented by and , respectively, whereas . The thermophysical properties of nanoparticles and base fluid (water) are tabulated in Table 1. Table 2 shows the comparison of the present numerical values and the existing values in the literature when and . It was found that the numerical values were close enough and validated our numerical simulation.

Table 1.
Thermophysical properties of base fluid (water) and some nanoparticles.

Table 2.
Numerical values of when and .
Figure 2 demonstrates the variation of the velocity profile with the thickness of the thin needle . The plot shows that enhanced with the decreasing of . Physically, the drag force decreased as the size of the needle diminished; consequently, the velocity enhanced. The hybrid nanofluid flowed with less velocity compared to the regular nanofluid. This was because the density rose with the hybridity and consequently slowed down the fluid motion.
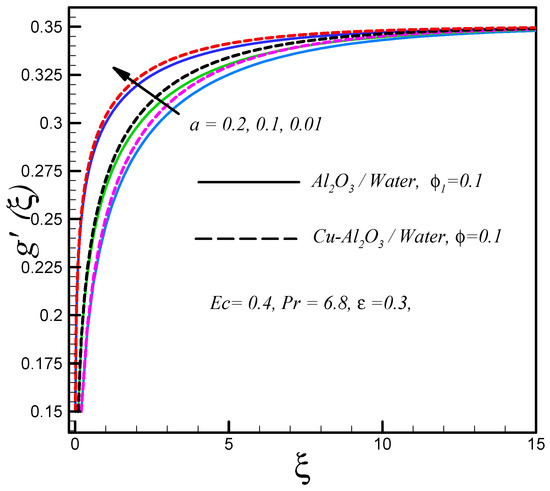
Figure 2.
Effects of on .
Figure 3 shows that temperature dropped with the decreasing values of . Figure 3 also reveals that, under the same circumstances, the temperature of the hybrid nanofluid was higher than the regular nanofluid. High thermal conductivity of the hybrid nanofluid was responsible for these high values of temperature.
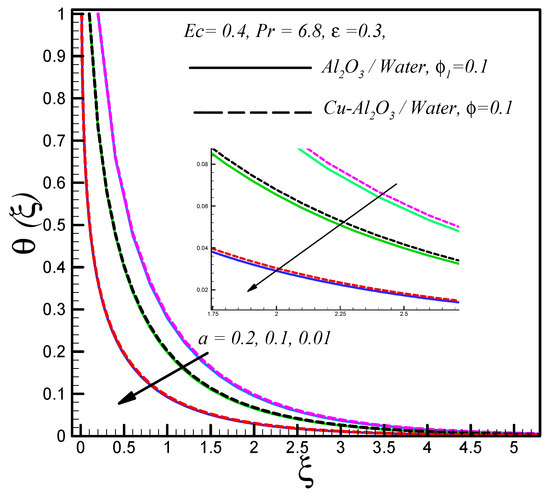
Figure 3.
Effects of on .
The increase in the thermal dissipation parameter (Eckert number ) enhanced the temperature of both types of nanofluids, as demonstrated in Figure 4. This rise in temperature was due to the increment in friction between the nanofluid layers. The kinetic energy of the nanofluid converted into the thermal energy because of the frictional heating, which lead to rise in the temperature.
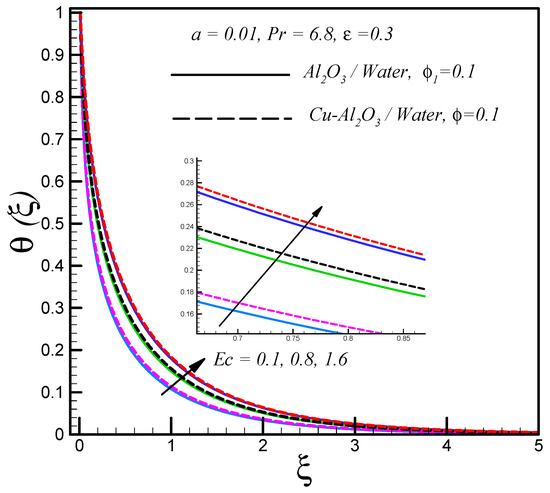
Figure 4.
Effects of on .
The temperature had direct relation with the solid volume fraction of the nanoparticles, as shown in Figure 5. Furthermore, it was also observed that the hybrid nanofluid had a thick thermal boundary layer as compared to the regular nanofluid, and this was because of the high thermal conductivity of the hybrid nanofluid.
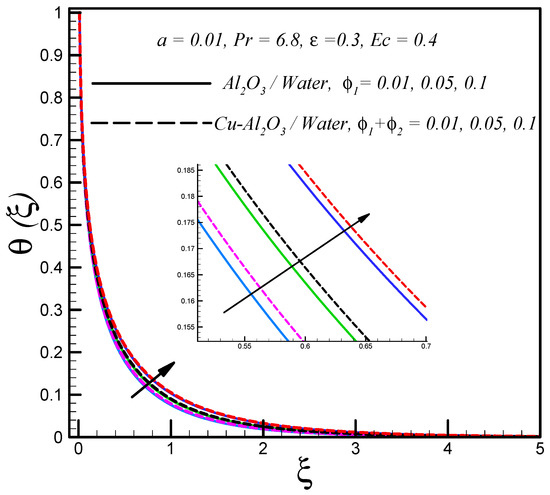
Figure 5.
Effects of solid volume fraction on .
The effect of the thickness of the thin needle on entropy generation is represented in Figure 6. The plot reveals that decreased with increasing for both types of nanofluids, but for the fixed value of , less entropy was generated in the regular nanofluid as compared to the hybrid nanofluid. Furthermore, the surface of the thin needle was the region where maximum entropy was generated.
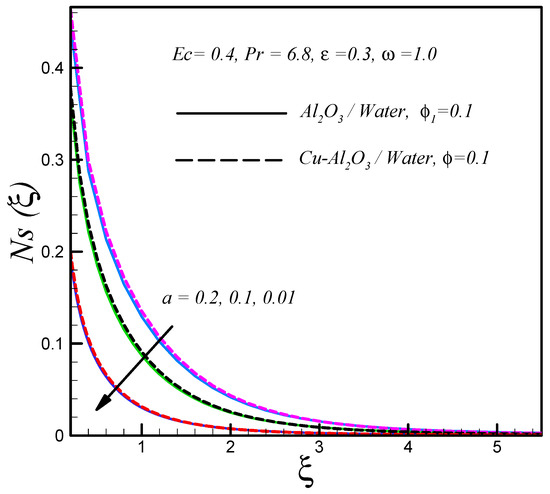
Figure 6.
Effects of on .
The effects of Eckert number and solid volume fraction of both nanoparticles on entropy generation are respectively shown in Figure 7 and Figure 8. These plots show that enhanced with these parameters.
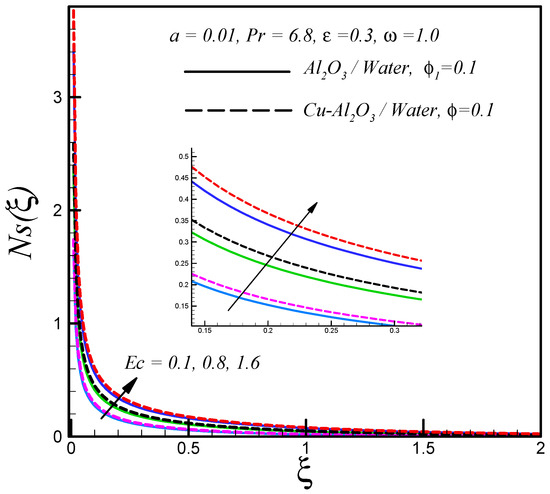
Figure 7.
Effects of on .
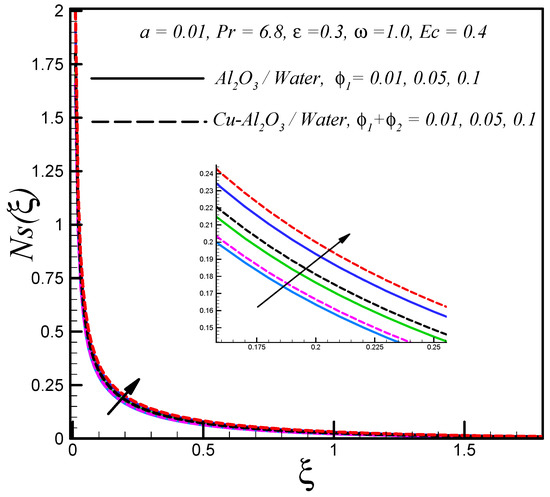
Figure 8.
Effects of solid volume fraction on .
The reduction in entropy generation was observed with the rising of , as shown in Figure 9.
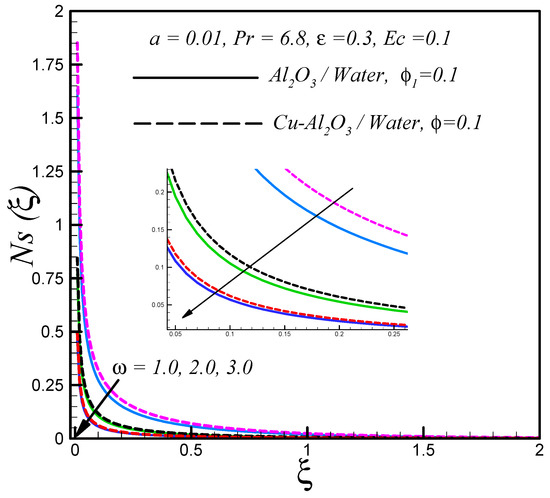
Figure 9.
Effects of on .
The impacts of the velocity ratio parameter on entropy generation are shown in Figure 10 and Figure 11. It was found that entropy generation enhanced with the velocity ratio parameter subjected to the condition that the free stream velocity was less than the velocity of the thin needle. The decrement in was observed with the rising of the velocity ratio parameter subjected to the condition that the velocity of the thin needle was less than that of the free stream velocity.
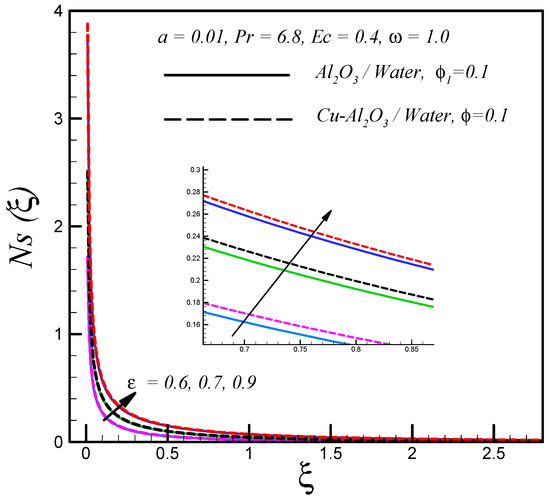
Figure 10.
Effects of on when .
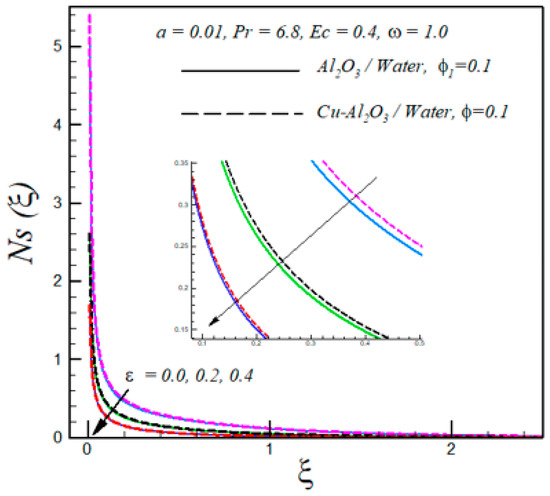
Figure 11.
Effects of on when .
6. Conclusions
A theoretical study of heat transfer and entropy generation in the flow of dissipative hybrid nanofluid over a needle was conducted. The results of this study led to the following prime conclusions:
- The temperature and the entropy generation were found to decrease with needle size decrement.
- The velocity profile was reduced with the increment in the size of the needle.
- The velocity of the hybrid nanofluid was observed to be lower than the regular nanofluid , whereas the rate of heat transfer was greater in the hybrid nanofluid as compared to the regular nanofluid.
- A reduction in entropy generation was found by raising the values of .
- It was perceived that and temperature distribution were directly proportional to Eckert number and .
- High entropy generation was found in the hybrid nanofluid as compared to the regular one.
Author Contributions
Conceptualization, M.I.A., I.T. and M.G.; methodology, M.I.A., N.A.K. and I.T.; software, M.I.A. and I.T.; validation, M.I.A. and I.T.; formal analysis, M.I.A., and M.O. and I.T.; investigation, M.I.A. and I.T.; resources, M.I.A., I.T. and M.O.; data curation, M.I.A., N.A.K. and I.T.; writing—original draft preparation, M.I.A.; writing—review and editing, I.T., N.A.K. and M.G.; visualization, M.I.A., I.T. and M.O.; supervision, I.T. and M.G.; project administration, I.T., M.G. and M.O.; funding acquisition, I.T. and M.O.
Funding
M. Osman would like to thank Deanship of Scientific Research at Majmaah University for supporting this work under the Project Number No. 1440-111.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bejan, A. Fundamentals of exergy analysis, entropy generation minimization, and the generation of flow architecture. Int. J. Energy Res. 2002, 26, 0–43. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Khan, N.A.; Makinde, O.D. Minimization of Entropy Generation in MHD Mixed Convection Flow with Energy Dissipation and Joule Heating: Utilization of Sparrow-Quack-Boerner Local Non-Similarity Method. Defect Diffus. Forum 2018, 387, 63–77. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M. Entropy Generation in Three Dimensional Flow of Dissipative Fluid. Int. J. Appl. Comput. Math. 2017, 4, 16. [Google Scholar] [CrossRef]
- Afridi, M.I.; Wakif, A.; Qasim, M.; Hussanan, A. Irreversibility Analysis of Dissipative Fluid Flow Over A Curved Surface Stimulated by Variable Thermal Conductivity and Uniform Magnetic Field: Utilization of Generalized Differential Quadrature Method. Entropy 2018, 20, 943. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Wakif, A.; Hussanan, A. Second Law Analysis of Dissipative Nanofluid Flow over a Curved Surface in the Presence of Lorentz Force: Utilization of the Chebyshev–Gauss–Lobatto Spectral Method. Nanomaterials 2019, 9, 195. [Google Scholar] [CrossRef]
- Butt, A.S.; Tufail, M.N.; Ali, A.; Dar, A. Theoretical investigation of entropy generation effects in nanofluid flow over an inclined stretching cylinder. Int. J. Exergy 2019, 28, 126–157. [Google Scholar] [CrossRef]
- Makinde, O.D.; Eegunjobi, A.S. Entropy generation in a couple stress fluid flow through a vertical channel filled with saturated porous media. Entropy 2013, 15, 4589–4606. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A.; Mehmood, A. Numerical investigation of magnetic field effects on entropy generation in viscous flow over a stretching cylinder embedded in a porous medium. Energy 2016, 99, 237–249. [Google Scholar] [CrossRef]
- Khan, Z.H.; Makinde, O.D.; Ahmad, R.; Khan, W.A. Numerical Study of Unsteady MHD Flow and Entropy Generation in a Rotating Permeable Channel with Slip and Hall Effects. Commun. Theor. Phys. 2018, 70, 641. [Google Scholar] [CrossRef]
- Adesanya, S.O.; Makinde, O.D. Effects of couple stresses on entropy generation rate in a porous channel with convective heating. Comput. Appl. Math. 2015, 34, 293–307. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Tayebi, T.; Chamkha, A.J.; Hashim, I. Effect of rotating solid cylinder on entropy generation and convective heat transfer in a wavy porous cavity heated from below. Int. Commun. Heat Mass Transf. 2018, 95, 197–209. [Google Scholar] [CrossRef]
- Alsabery, A.; Ishak, M.; Chamkha, A.; Hashim, I. Entropy generation analysis and natural convection in a nanofluid-filled square cavity with a concentric solid insert and different temperature distributions. Entropy 2018, 20, 336. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Nasiri, M.; Shadloo, M.S.; Yang, Z. Entropy Generation in a Circular Tube Heat Exchanger Using Nanofluids: Effects of Different Modeling Approaches. Heat Transf. Eng. 2017, 38, 853–866. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Bagheri, S.; Momoniat, E.; Freidoonimehr, N. Entropy analysis of convective MHD flow of third grade non-Newtonian fluid over a stretching sheet. Ain Shams Eng. J. 2015, 8, 77–85. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab: Lemont, IL, USA, 1995.
- Hsiao, K.L. To promote radiation electrical MHD activation energy thermal extrusion manufacturing system efficiency by using Carreau-Nanofluid with parameters control method. Energy 2017, 130, 486–499. [Google Scholar] [CrossRef]
- Boulahia, Z.; Wakif, A.; Chamkha, A.J.; Amanulla, C.H.; Sehaqui, R. Effects of Wavy Wall Amplitudes on Mixed Convection Heat Transfer in a Ventilated Wavy Cavity Filled by Copper-Water Nanofluid Containing a Central Circular Cold Body. J. Nanofluids 2019, 8, 1170–1178. [Google Scholar] [CrossRef]
- Hsiao, K.L. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Gedik, E.; Chamkha, A.J.; Hashim, I. Effects of two-phase nanofluid model and localized heat source/sink on natural convection in a square cavity with a solid circular cylinder. Comput. Methods Appl. Mech. Eng. 2019, 346, 952–981. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Ali, F.; Eid, M.R.; Sehaqui, R. Numerical Analysis of the Unsteady Natural Convection MHD Couette Nanofluid Flow in the Presence of Thermal Radiation Using Single and Two-Phase Nanofluid Models for Cu–Water Nanofluids. Int. J. Appl. Comput. Math. 2018, 4, 1–27. [Google Scholar] [CrossRef]
- Hashim, I.; Alsabery, A.I.; Sheremet, M.A.; Chamkha, A.J. Numerical investigation of natural convection of Al2O3-water nanofluid in a wavy cavity with conductive inner block using Buongiorno’s two-phase model. Adv. Powder Technol. 2019, 30, 399–414. [Google Scholar] [CrossRef]
- Ranjbarzadeh, R.; Moradikazerouni, A.; Bakhtiari, R.; Asadi, A.; Afrand, M. An experimental study on stability and thermal conductivity of water/silica nanofluid: Eco-friendly production of nanoparticles. J. Clean. Prod. 2019, 206, 1089–1100. [Google Scholar] [CrossRef]
- Moradikazerouni, A.; Hajizadeh, A.; Safaei, M.R.; Afrand, M.; Yarmand, H.; Zulkifli, N.W.B.M. Assessment of thermal conductivity enhancement of nano-antifreeze containing single-walled carbon nanotubes: Optimal artificial neural network and curve-fitting. Phys. A Stat. Mech. Appl. 2019, 521, 138–145. [Google Scholar] [CrossRef]
- Asadi, A.; Pourfattah, F. Heat transfer performance of two oil-based nanofluids containing ZnO and MgO nanoparticles; a comparative experimental investigation. Powder Technol. 2019, 343, 296–308. [Google Scholar] [CrossRef]
- Asadi, A.; Asadi, M.; Rezaniakolaei, A.; Rosendahl, L.A.; Wongwises, S. An experimental and theoretical investigation on heat transfer capability of Mg (OH)2/MWCNT-engine oil hybrid nano-lubricant adopted as a coolant and lubricant fluid. Appl. Therm. Eng. 2018, 129, 577–586. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Goodarzi, M.; Reiszadeh, M.; Afrand, M. Evaluation of MWCNTs-ZnO/5W50 nanolubricant by design of an artificial neural network for predicting viscosity and its optimization. J. Mol. Liq. 2019, 277, 921–931. [Google Scholar] [CrossRef]
- Devi, S.A.; Devi, S.S.U. Numerical Investigation of Hydromagnetic Hybrid Cu—Al2O3/Water Nanofluid Flow over a Permeable Stretching Sheet with Suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Khan, N.A.; Hamdani, M. Heat Transfer Analysis of Cu–Al2O3–Water and Cu–Al2O3–Kerosene Oil Hybrid Nanofluids in the Presence of Frictional Heating: Using 3-Stage Lobatto IIIA Formula. J. Nanofluids 2019, 8, 885–891. [Google Scholar] [CrossRef]
- Farooq, U.; Afridi, M.; Qasim, M.; Lu, D. Transpiration and Viscous Dissipation Effects on Entropy Generation in Hybrid Nanofluid Flow over a Nonlinear Radially Stretching Disk. Entropy 2018, 20, 668. [Google Scholar] [CrossRef]
- DEVI, S.U.M.A.; Devi, S.P.A. Heat Transfer Enhancement of Cu−Al2O3/Water Hybrid Nanofluid Flow over a Stretching Sheet. J. Niger. Math. Soc. 2017, 36, 419–433. [Google Scholar]
- Devi, S.S.U.; Devi, S.P.A. Numerical investigation of three-dimensional hybrid Cu–Al2O3/water nanofluid flow over a stretching sheet with effecting Lorentz force subject to Newtonian heating. Can. J. Phys. 2016, 94, 490–496. [Google Scholar] [CrossRef]
- Gorla, R.S.R.; Siddiqa, S.; Mansour, M.A.; Rashad, A.M.; Salah, T. Heat source/sink effects on a hybrid nanofluid-filled porous cavity. J. Thermophys. Heat Transf. 2017, 31, 847–857. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Miroshnichenko, I.V.; Sheremet, M.A. Numerical analysis of unsteady conjugate natural convection of hybrid water-based nanofluid in a semicircular cavity. J. Therm. Sci. Eng. Appl. 2017, 9, 41004. [Google Scholar] [CrossRef]
- Asadi, A. A guideline towards easing the decision-making process in selecting an effective nanofluid as a heat transfer fluid. Energy Convers. Manag. 2018, 175, 1–10. [Google Scholar] [CrossRef]
- Ahmad, S.; Arifin, N.M.; Nazar, R.; Pop, I. Mixed convection boundary layer flow along vertical thin needles: Assisting and opposing flows. Int. Commun. Heat Mass Transf. 2008, 35, 157–162. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Lee, L.L. Boundary layer over a thin needle. Phys. fluids 1967, 10, 820–822. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Khan, I.; Tlili, I. Entropy generation in MHD mixed convection stagnation-point flow in the presence of joule and frictional heating. Case Stud. Therm. Eng. 2018, 12, 292–300. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Boundary layer flow over a continuously moving thin needle in a parallel free stream. Chin. Phys. Lett. 2007, 24, 2895. [Google Scholar] [CrossRef]
- Chen, J.L.S.; Smith, T.N. Forced convection heat transfer from nonisothermal thin needles. J. Heat Transf. 1978, 100, 358–362. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).