Boundary Layer Flow through Darcy–Brinkman Porous Medium in the Presence of Slip Effects and Porous Dissipation
Abstract
:1. Introduction
2. Mathematical Formulation
| Dimensionless Physical Parameters | Notations | Definitions |
| Brinkmann parameter | ||
| Porosity parameter | ||
| Suction/injection parameter | ||
| Prandtl number | ||
| Eckert number | ||
| Velocity slip parameter | ||
| Thermal slip parameter |
3. Solution Methodologies
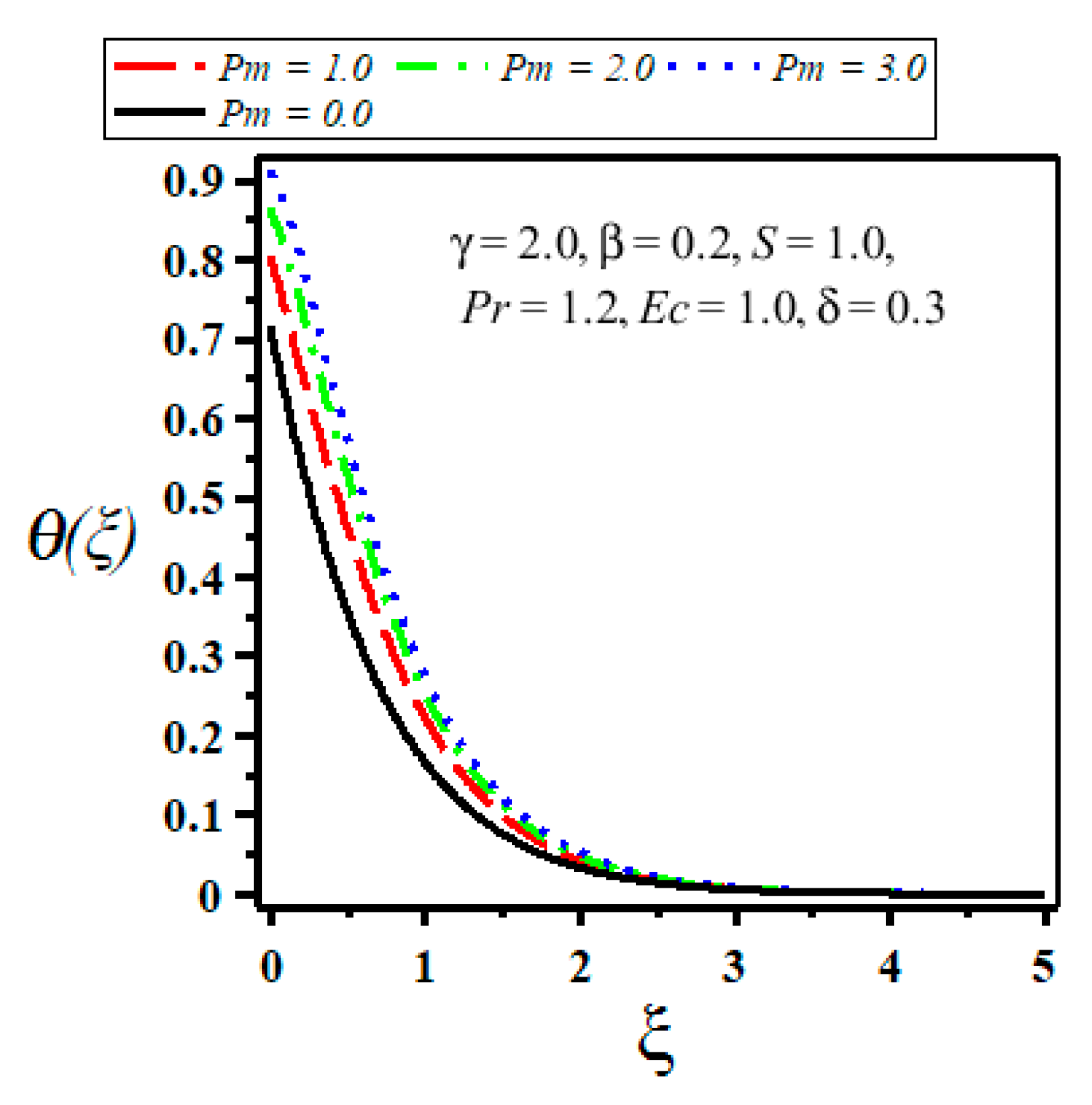
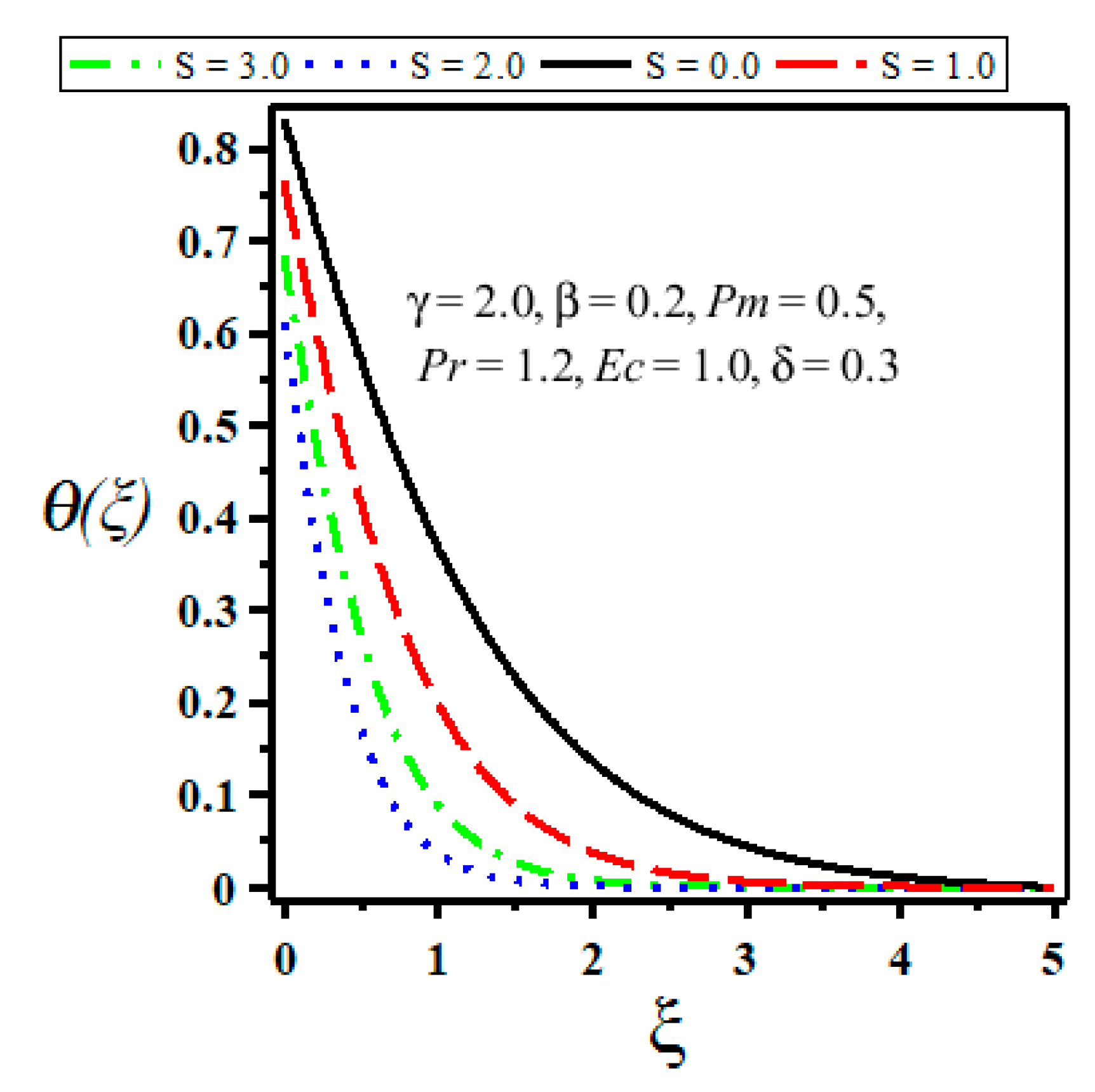
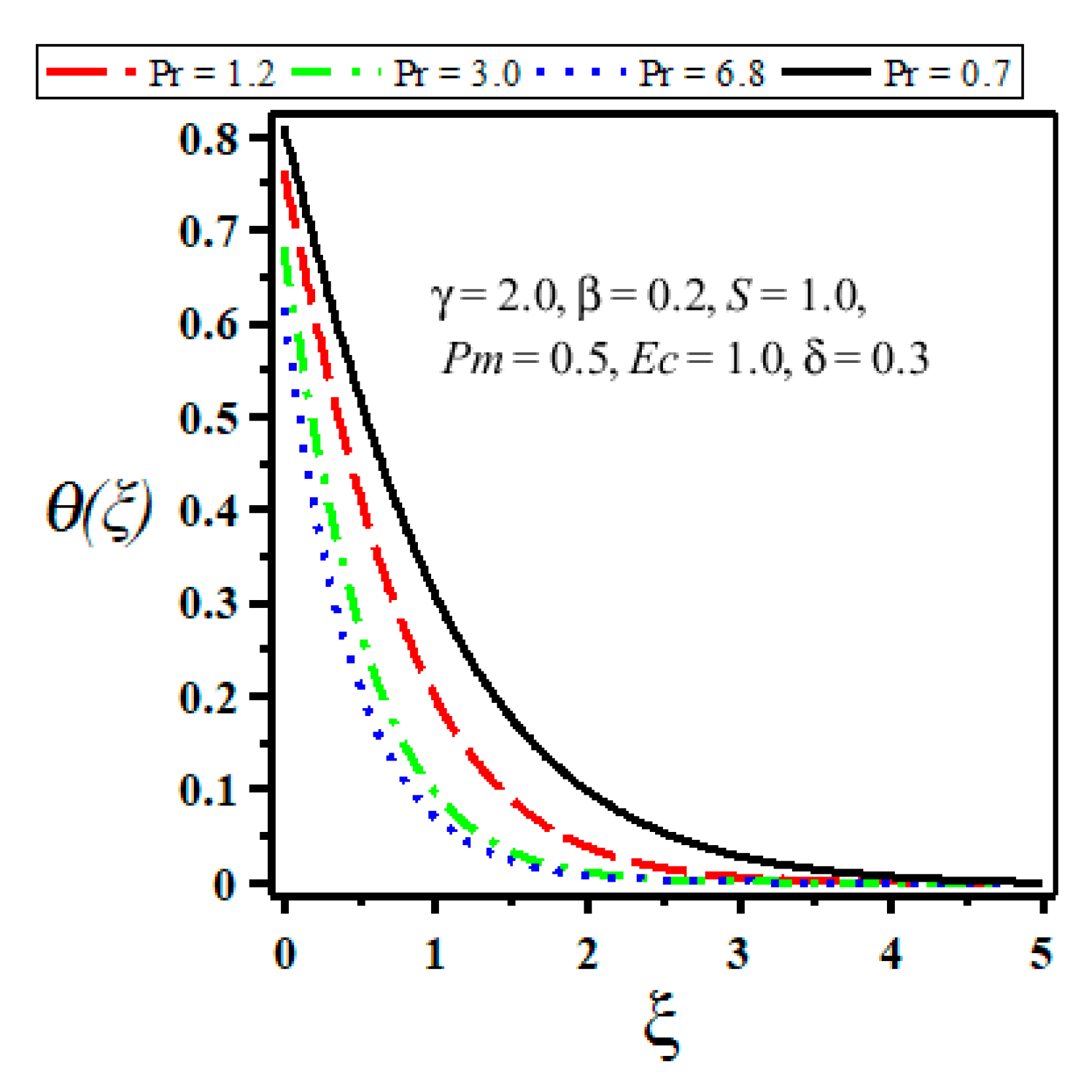
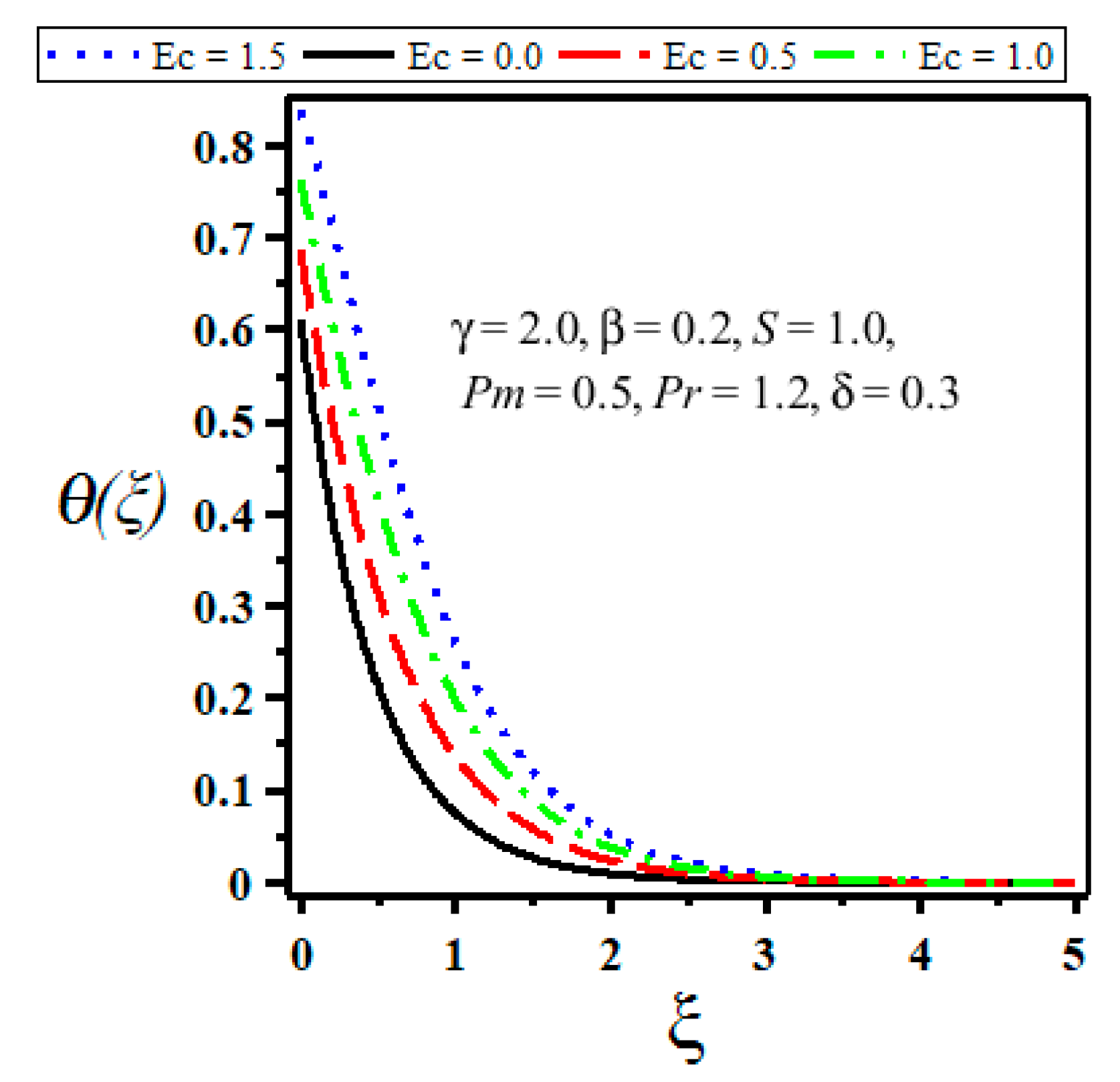
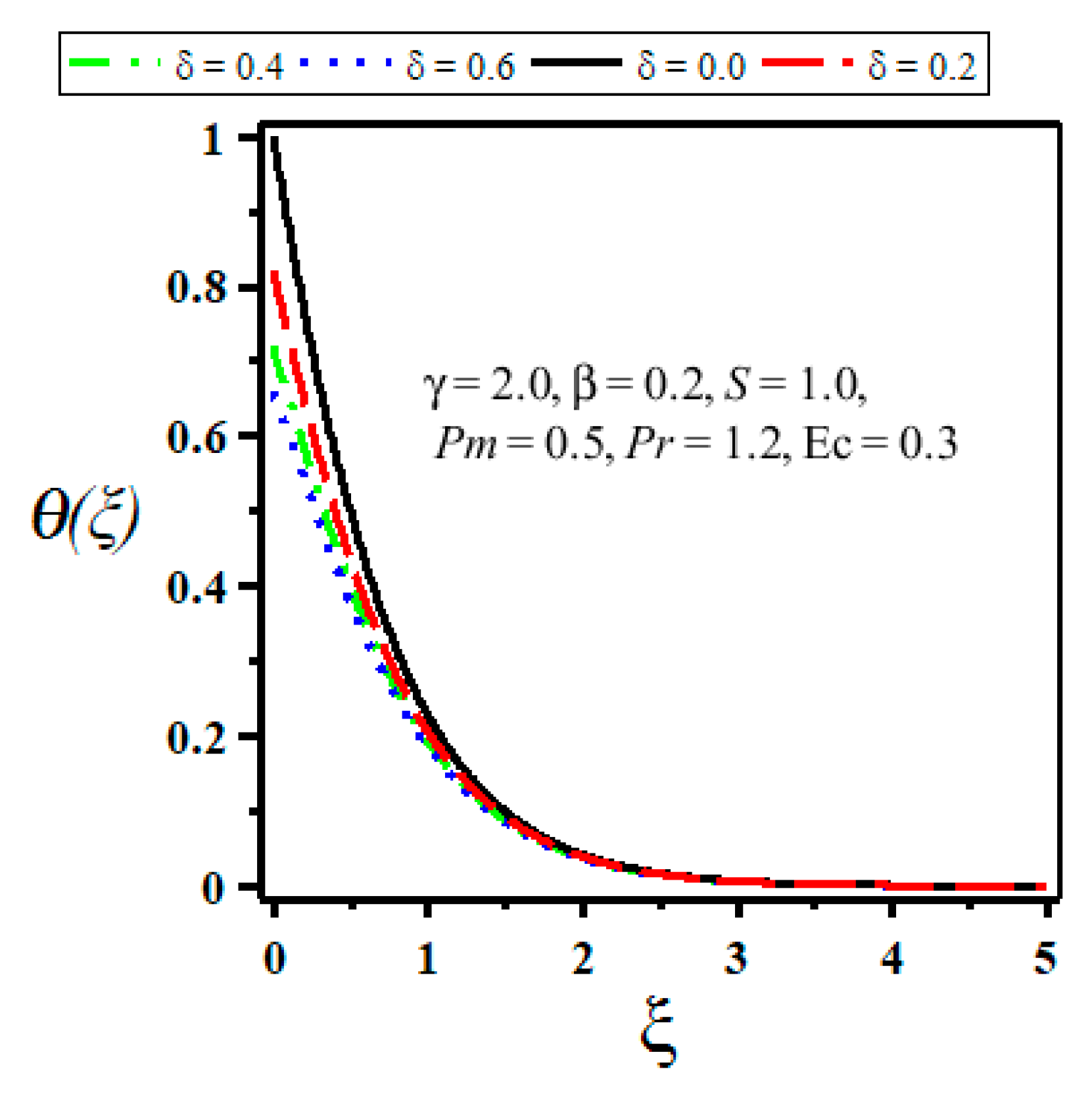
4. Results and Discussion
5. Conclusions
- (i)
- Both velocity and temperature decrease with the increase of suction parameter.
- (ii)
- The slip parameter has high impact on skin friction coefficient as compared with no-slip condition.
- (iii)
- Heat transfer rate is reduced due to increase in Eckert number and thermal slip parameter.
Author Contributions
Funding
Conflicts of Interest
References
- Patil, P.R.; Vaidyanathan, G. Effect of variable viscosity on thermohaline convection in a porous medium. J. Hydrol. 1982, 57, 147–161. [Google Scholar] [CrossRef]
- Ingham, D.B.; Pop, I. Transport Phenomena in Porous Media; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Vafai, K. Handbook of Porous Media; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Makinde, O.D.; Mhone, P.Y. Heat transfer to MHD oscillatory flow in a channel filled with porous medium. Rom. J. Phys. 2005, 50, 931–938. [Google Scholar]
- Yu, L.H.; Wang, C.Y. Darcy-Brinkman flow through a bumpy channel. Transp. Porous Media 2013, 97, 281–294. [Google Scholar] [CrossRef]
- Wang, C.Y. Darcy-Brinkman flow over a grooved surface. Transp. Porous Media 2010, 84, 219–227. [Google Scholar] [CrossRef]
- Liu, H.; Patil, P.R.; Narusawa, U. On Darcy-Brinkman equation: Viscous flow between two parallel plates packed with regular square arrays of cylinders. Entropy 2007, 9, 118–131. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. Zamp 1970, 4, 645–647. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Hydromagnetic flow and heat transfer adjacent to a stretching vertical sheet. Heat Mass Transf. 2008, 44, 921–927. [Google Scholar] [CrossRef]
- Chamkha, A.J. Hydromagnetic three-dimensional free convection on a vertical stretching surface with heat generation or absorption. Int. J. Heat Fluid Flow 1999, 20, 84–92. [Google Scholar] [CrossRef]
- Salleh, M.Z.; Nazar, R.; Pop, I. Boundary layer flow and heat transfer over a stretching sheet with Newtonian heating. J. Taiwan Inst. Chem. Eng. 2010, 41, 651–655. [Google Scholar] [CrossRef]
- Hsiao, K.L. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
- Hussanan, A.; Salleh, M.Z.; Khan, I. Microstructure and inertial characteristics of a magnetite ferrofluid over a stretching/shrinking sheet using effective thermal conductivity model. J. Mol. Liq. 2018, 255, 64–75. [Google Scholar] [CrossRef]
- Jamaludin, A.; Nazar, R.; Pop, I. Mixed convection stagnation-point flow of a nanofluid past a permeable stretching/shrinking sheet in the presence of thermal radiation and heat source/sink. Energies 2019, 12, 788. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Effect of thermal radiation on unsteady mixed convection flow and heat transfer over a porous stretching surface in porous medium. Int. J. Heat Mass Transf. 2009, 52, 3261–3265. [Google Scholar] [CrossRef]
- Chauhan, D.S.; Agrawal, R. MHD flow through a porous medium adjacent to a stretching sheet: Numerical and an approximate solution. Eur. Phys. J. Plus 2011, 126, 47. [Google Scholar] [CrossRef]
- Pal, D.; Mondal, H. Influence of chemical reaction and thermal radiation on mixed convection heat and mass transfer over a stretching sheet in Darcian porous medium with Soret and Dufour effects. Energy Convers. Manag. 2012, 62, 102–108. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, C.; Zhang, X.; Zhang, J. Flow and radiation heat transfer of a nanofluid over a stretching sheet with velocity slip and temperature jump in porous medium. J. Frankl. Inst. 2013, 350, 990–1007. [Google Scholar] [CrossRef]
- Hussanan, A.; Salleh, M.Z.; Khan, I.; Tahar, R.M. Heat transfer in magnetohydrodynamic flow of a casson fluid with porous medium and Newtonian heating. J. Nanofluids 2017, 6, 784–793. [Google Scholar] [CrossRef]
- Yasin, M.H.M.; Ishak, A.; Pop, I. Boundary layer flow and heat transfer past a permeable shrinking surface embedded in a porous medium with a second-order slip: A stability analysis. Appl. Therm. Eng. 2017, 115, 1407–1411. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary layer flow past a stretching surface in a porous medium saturated by a nanofluid: Brinkman-Forchheimer model. PLoS ONE 2012, 7, e47031. [Google Scholar] [CrossRef]
- Khan, Z.H.; Qasim, M.; Haq, R.U.; Al-Mdallal, Q.M. Closed form dual nature solutions of fluid flow and heat transfer over a stretching/shrinking sheet in a porous medium. Chin. J. Phys. 2017, 55, 1284–1293. [Google Scholar] [CrossRef]
- Zhang, T.; Jia, L.; Yang, L.; Jaluria, Y. Effect of viscous heating on heat transfer performance in microchannel slip flow region. Int. J. Heat Mass Transf. 2010, 53, 4927–4934. [Google Scholar] [CrossRef]
- Hooman, K.; Ejlali, A. Effects of viscous heating, fluid property variation, velocity slip, and temperature jump on convection through parallel plate and circular microchannels. Int. Commun. Heat Mass Transf. 2010, 37, 34–38. [Google Scholar] [CrossRef]
- Hussanan, A.; Khan, I.; Salleh, M.Z.; Shafie, S. Slip effects on unsteady free convective heat and mass transfer flow with Newtonian heating. Therm. Sci. 2016, 20, 1939–1952. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, B. Effects of second-order slip on the flow of a fractional Maxwell MHD fluid. J. Assoc. Arab Univ. Basic Appl. Sci. 2017, 24, 232–241. [Google Scholar] [CrossRef]
- Jing, D.; Song, S.; Pan, Y.; Wang, X. Size dependences of hydraulic resistance and heat transfer of fluid flow in elliptical microchannel heat sinks with boundary slip. Int. J. Heat Mass Transf. 2018, 119, 647–653. [Google Scholar] [CrossRef]
- Andersson, H.I. Slip flow past a stretching surface. Acta Mech. 2002, 158, 121–125. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Analytic heat and mass transfer of the mixed hydrodynamic/thermal slip MHD viscous flow over a stretching sheet. Int. J. Mech. Sci. 2011, 53, 886–896. [Google Scholar] [CrossRef]
- Yazdi, M.H.; Abdullah, S.; Hashim, I.; Sopian, K. Effects of viscous dissipation on the slip MHD flow and heat transfer past a permeable surface with convective boundary conditions. Energies 2011, 4, 2273–2294. [Google Scholar] [CrossRef]
- Hsiao, K.L. Stagnation electrical MHD nanofluid mixed convection with slip boundary on a stretching sheet. Appl. Therm. Eng. 2016, 98, 850–861. [Google Scholar] [CrossRef]
- Shampine, L.F.; Kierzenka, J. Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. Tutor. Notes 2000, 2000, 1–27. [Google Scholar]
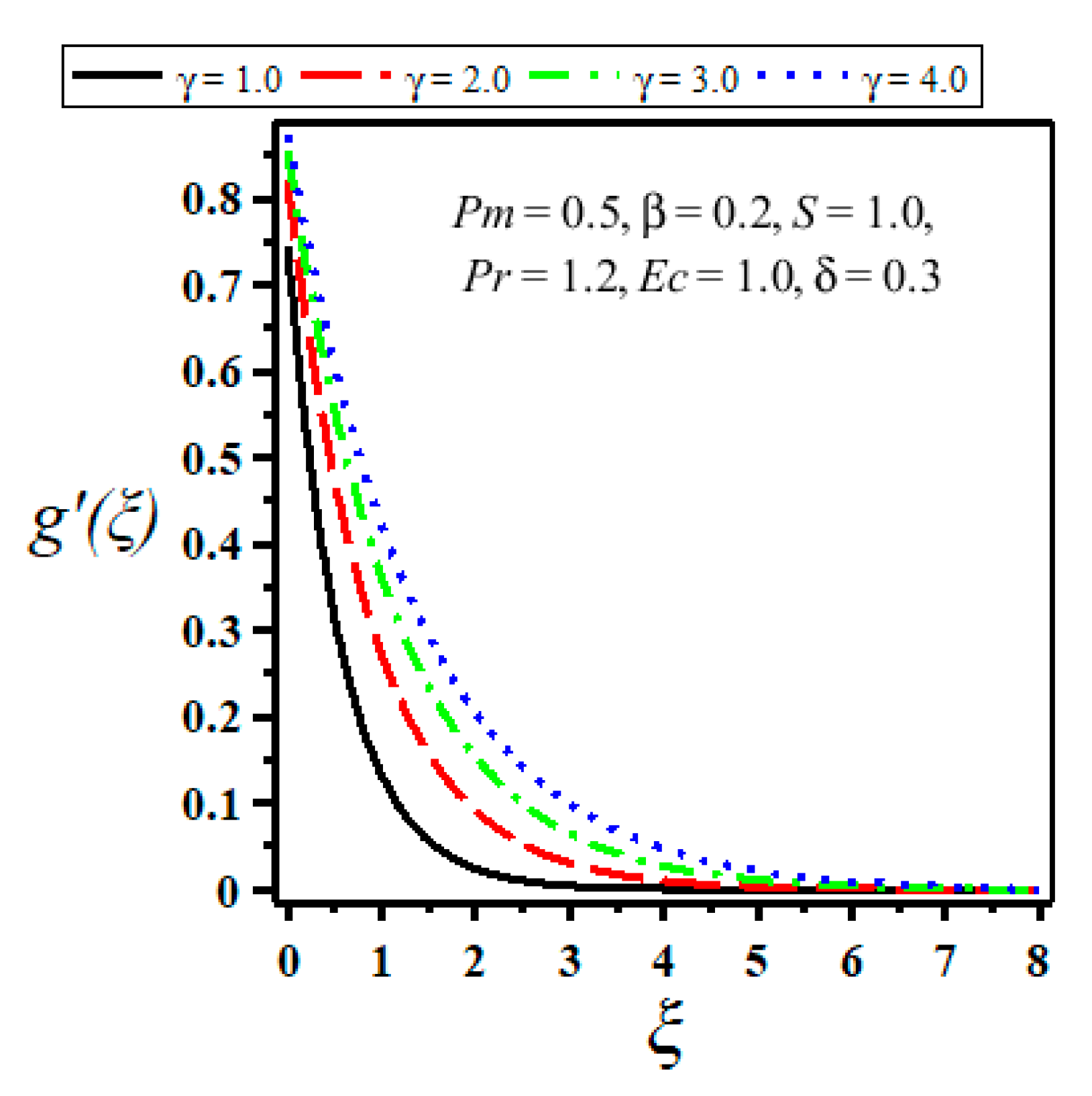
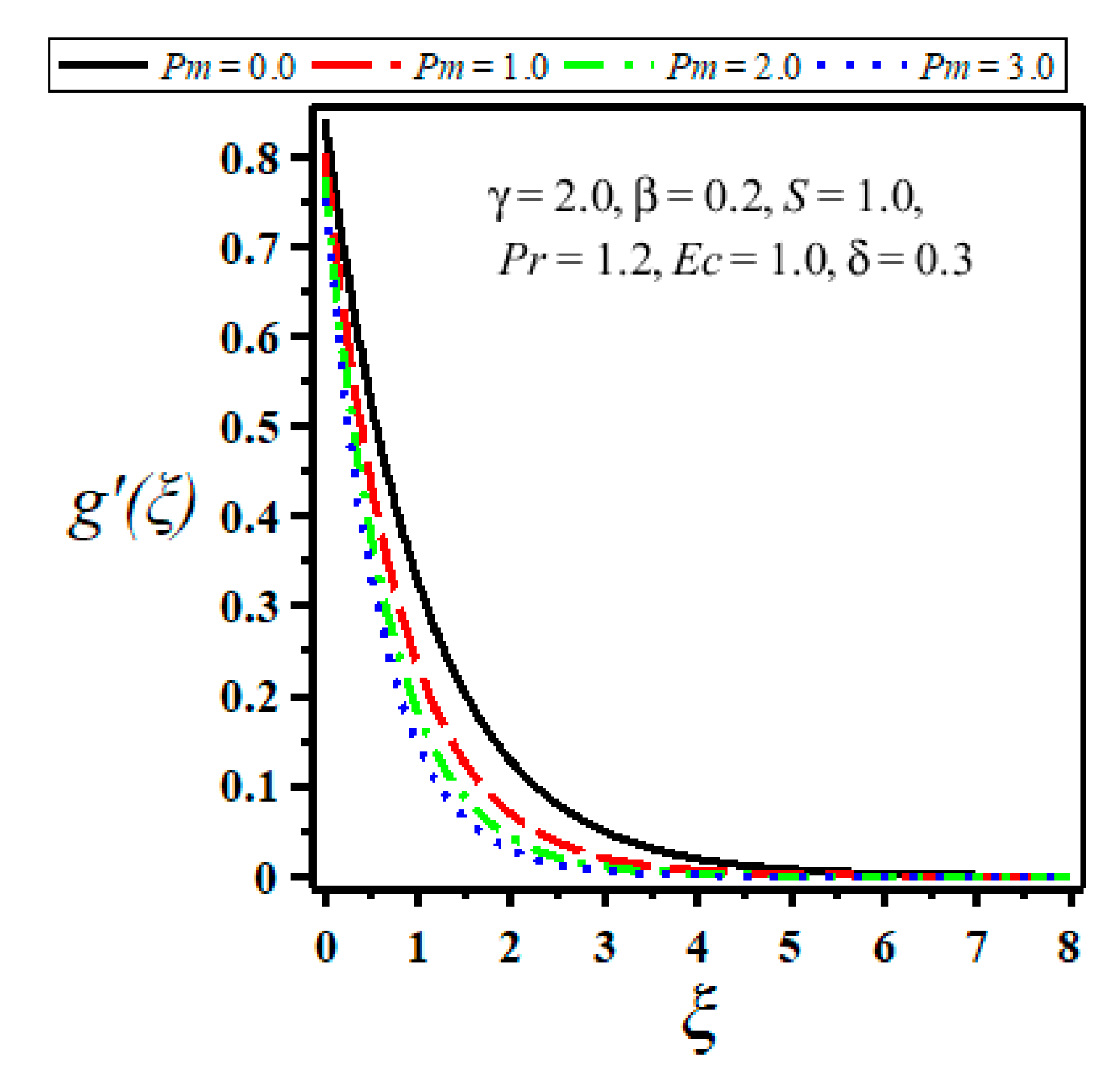
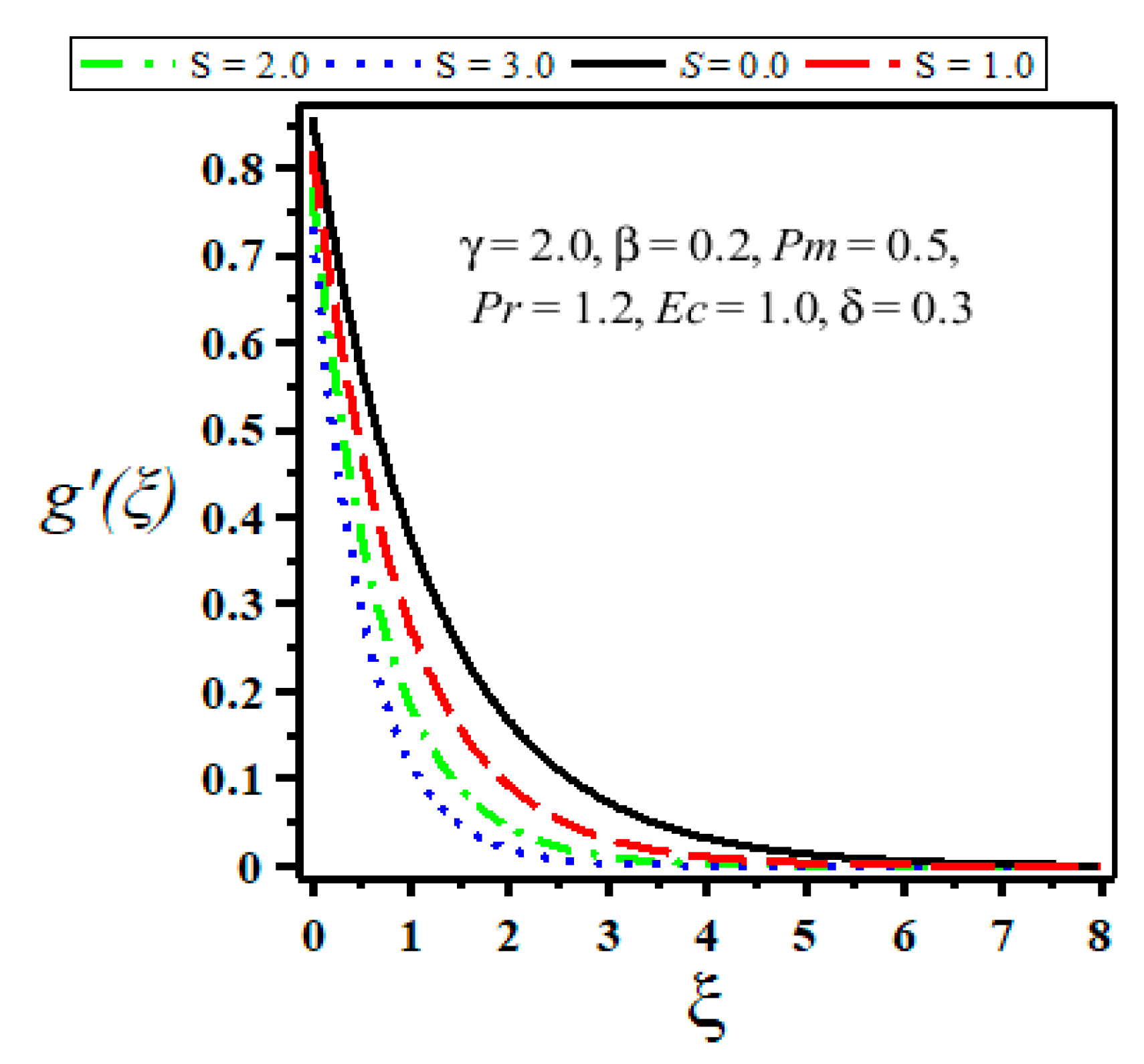
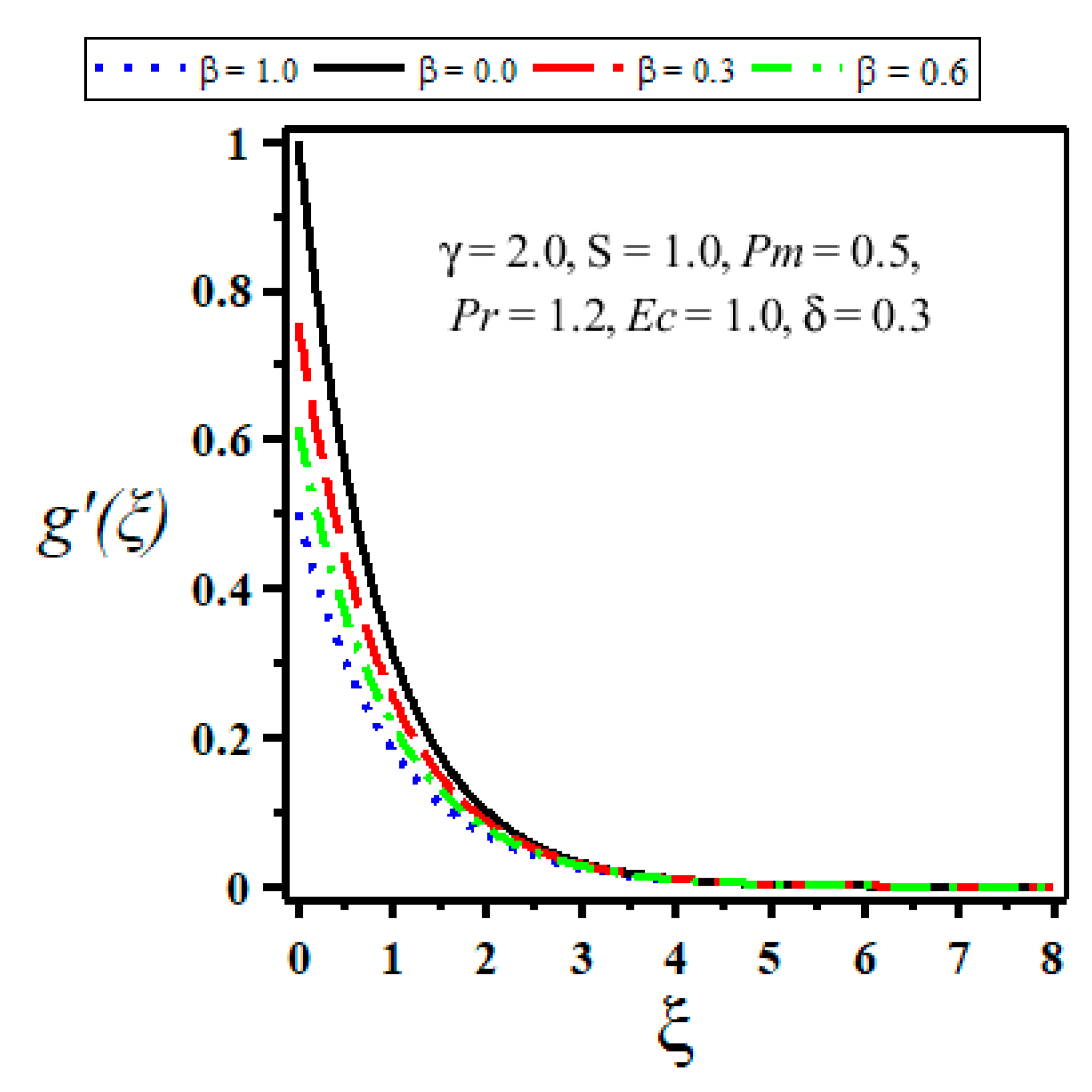

| Velocity Slip Parameter | ||||
|---|---|---|---|---|
| Andersson [22] | Present | Andersson [22] | Present | |
| 0.0 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 0.1 | 0.9128 | 0.91278 | 0.8721 | 0.87215 |
| 0.2 | 0.8447 | 0.84471 | 0.7764 | 0.77645 |
| 0.5 | 0.7044 | 0.70436 | 0.5912 | 0.59127 |
| 1.0 | 0.5698 | 0.56974 | 0.4302 | 0.43025 |
| 2.0 | 0.4320 | 0.43183 | 0.2840 | 0.28408 |
| 5.0 | 0.2758 | 0.27530 | 0.1448 | 0.14493 |
| 10.0 | 0.1876 | 0.18670 | 0.0812 | 0.08132 |
| 20.0 | 0.1242 | 0.12285 | 0.0438 | 0.04385 |
| 50.0 | 0.0702 | 0.06801 | 0.0186 | 0.01863 |
| 100.0 | 0.0450 | 0.04225 | 0.0095 | 0.00957 |
| Physical Parameters | ||||
|---|---|---|---|---|
| Exact (See Equation (11)) | Numerical (Shooting Method) | |||
| 1.0 | 1.0 | 0.5 | 1.82287 | 1.82287 |
| 2.0 | 1.0 | 0.5 | 1.15138 | 1.15140 |
| 3.0 | 1.0 | 0.5 | 0.89314 | 0.89324 |
| 0.5 | 0.0 | 0.3 | 1.61245 | 1.61245 |
| 0.5 | 1.0 | 0.3 | 2.89736 | 2.89736 |
| 0.5 | 2.0 | 0.3 | 4.56904 | 4.56905 |
| 2.0 | 0.5 | 0.0 | 0.84307 | 0.84336 |
| 2.0 | 0.5 | 0.4 | 0.97094 | 0.97098 |
| 2.0 | 0.5 | 0.8 | 1.08188 | 1.08188 |
| Physical Parameters | ||||
|---|---|---|---|---|
| Shooting Method | bvp4c | |||
| 1.0 | 1.0 | 0.5 | 0.610511 | 0.610497 |
| 2.0 | 1.0 | 0.5 | 0.500008 | 0.500006 |
| 3.0 | 1.0 | 0.5 | 0.439566 | 0.439507 |
| 0.5 | 0.0 | 0.3 | 0.550438 | 0.550437 |
| 0.5 | 1.0 | 0.3 | 0.712228 | 0.712227 |
| 0.5 | 2.0 | 0.3 | 0.808872 | 0.808872 |
| 2.0 | 0.5 | 0.0 | 0.406493 | 0.406209 |
| 2.0 | 0.5 | 0.4 | 0.452006 | 0.451987 |
| 2.0 | 0.5 | 0.8 | 0.485908 | 0.485905 |
| Physical Parameters | ||||||
|---|---|---|---|---|---|---|
| Shooting Method | bvp4c | |||||
| 0.7 | 0.5 | 1.0 | 0.4 | 2.0 | 0.456141 | 0.456203 |
| 1.2 | 0.5 | 1.0 | 0.4 | 2.0 | 0.538161 | 0.538197 |
| 6.8 | 0.5 | 1.0 | 0.4 | 2.0 | 0.738928 | 0.738983 |
| 3.0 | 0.0 | 1.0 | 0.4 | 2.0 | 0.738078 | 0.738124 |
| 3.0 | 0.6 | 1.0 | 0.4 | 2.0 | 0.642319 | 0.642382 |
| 3.0 | 1.2 | 1.0 | 0.4 | 2.0 | 0.546560 | 0.546591 |
| 3.0 | 1.0 | 0.0 | 0.4 | 2.0 | 2.208602 | 2.208638 |
| 3.0 | 1.0 | 0.6 | 0.4 | 2.0 | 0.820808 | 0.820821 |
| 3.0 | 1.0 | 1.2 | 0.4 | 2.0 | 0.504071 | 0.504105 |
| 3.0 | 1.0 | 1.0 | 0.0 | 2.0 | 0.640207 | 0.640288 |
| 3.0 | 1.0 | 1.0 | 0.5 | 2.0 | 0.566207 | 0.566224 |
| 3.0 | 1.0 | 1.0 | 1.0 | 2.0 | 0.517044 | 0.517133 |
| 3.0 | 1.0 | 1.0 | 0.4 | 1.0 | 0.619665 | 0.619690 |
| 3.0 | 1.0 | 1.0 | 0.4 | 2.0 | 0.578480 | 0.578501 |
| 3.0 | 1.0 | 1.0 | 0.4 | 3.0 | 0.546450 | 0.546487 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kausar, M.S.; Hussanan, A.; Mamat, M.; Ahmad, B. Boundary Layer Flow through Darcy–Brinkman Porous Medium in the Presence of Slip Effects and Porous Dissipation. Symmetry 2019, 11, 659. https://doi.org/10.3390/sym11050659
Kausar MS, Hussanan A, Mamat M, Ahmad B. Boundary Layer Flow through Darcy–Brinkman Porous Medium in the Presence of Slip Effects and Porous Dissipation. Symmetry. 2019; 11(5):659. https://doi.org/10.3390/sym11050659
Chicago/Turabian StyleKausar, Muhammad Salman, Abid Hussanan, Mustafa Mamat, and Babar Ahmad. 2019. "Boundary Layer Flow through Darcy–Brinkman Porous Medium in the Presence of Slip Effects and Porous Dissipation" Symmetry 11, no. 5: 659. https://doi.org/10.3390/sym11050659
APA StyleKausar, M. S., Hussanan, A., Mamat, M., & Ahmad, B. (2019). Boundary Layer Flow through Darcy–Brinkman Porous Medium in the Presence of Slip Effects and Porous Dissipation. Symmetry, 11(5), 659. https://doi.org/10.3390/sym11050659




