Significance of Velocity Slip in Convective Flow of Carbon Nanotubes

Abstract

The present article inspects velocity slip impacts in three-dimensional flow of water based carbon nanotubes because of a stretchable rotating disk. Nanoparticles like single and multi walled carbon nanotubes (CNTs) are utilized. Graphical outcomes have been acquired for both single-walled carbon nanotubes (SWCNTs) and multi-walled carbon nanotubes (MWCNTs). The heat transport system is examined in the presence of thermal convective condition. Proper variables lead to a strong nonlinear standard differential framework. The associated nonlinear framework has been tackled by an optimal homotopic strategy. Diagrams have been plotted so as to examine how the temperature and velocities are influenced by different physical variables. The coefficients of skin friction and Nusselt number have been exhibited graphically. Our results indicate that the skin friction coefficient and Nusselt number are enhanced for larger values of nanoparticle volume fraction.

1. Introduction

The investigation of liquid flow by a rotating disk has various applications in aviation science, pivot of hardware, synthetic enterprises and designing, creating frameworks of warm power, rotor-stator frameworks, medicinal contraption, electronic and PC putting away apparatuses, gem developing wonders, machines of air cleaning, nourishment preparing advances, turbo apparatus and numerous others. Von Karman [1] analyzed flow of thick fluid by a rotating disk. Turkyilmazoglu and Senel [2] explored effects of heat and mass transport in thick liquid flow over a permeable rotating disk. Rashidi et al. [3] dissected MHD flow of viscous liquid because of a turn of disk. Turkyilmazoglu [4] exhibited nanoliquid flow by a rotating plate. Hatami et al. [5] examined laminar flow of a thick nanofluid because of the revolution and constriction of disks. Nanoliquid flow because of an extending disk is considered by Mustafa et al. [6]. Sheikholeslami et al. [7] examined nanoliquid flow by a slanted rotatory plate. Recently Hayat et al. [8] analyzed MHD nanoliquid flow over a rotatory disk with slip impacts.

Carbon nanotubes (CNTs) were first discovered by Lijima in 1991. CNTs have long cylindrical pofiles such as frames of carbon atoms with diameter ranges from 0.70–50 nm. CNTs have individual importance in nano-technology, hardwater, air purification systems, structural composite materials, conductive plastics, extra strong fibres, sensors, flat-panel displays, gas storage, biosensors and many others. Thus Choi et al. [9] examined anamolous enhancement of thermal conductivity in nanotubes suspension. Ramasubramaniam et al. [10] examined homogeneous polymer composites/carbon nanotubes for electrical utilizations. Xue [11] proposed a relation for CNT-based composites. Heat transfer enhancement using carbon nanotubes-based-non-Newtonian nanofluids is discussed by Kamali et al. [12]. Wang et al. [13] illustrated laminar flows of nanofluids containing single-walled carbon nanotubes (SWCNT) and multi-walled carbon nanotubes (MWCNTs). Hammouch et al. [14] analyzed squeezed flow of CNTs between parallel disks. Thermal transfer upgrade in front aligned contracting channel by taking FMWCNT nanoliquids is analyzed by Safaei et al. [15]. MHD flow of carbon nanotubes is portrayed by Ellahi et ai. [16]. Karimipour et al. [17] dissected MHD laminar flow of carbon nanotubes in a microchannel with a uniform warmth transition. Hayat et al. [18] represented homogeneous-heterogeneous responses in nanofluid flows over a non-direct extending surface of variable thickness. Unsteady squeezed flow of CNTs with convective surface was contemplated by Hayat et al. [19]. Hayat et al. [20] likewise talked about Darcy Forchheimer flow of CNTs over a turning plate. Further relevant investigations on nanofluids can be seen through the studies [21,22,23,24,25].

Motivated by the aforementioned applications of rotating flows, the underlying objective of this article is to develop a mathematical model for three-dimensional flow of water-based carbon nanotubes because of a stretchable rotating disk considering velocity slip effects. Thermal conductivity of carbon nanotubes is estimated through the well-known Xue model. Such research work was not carried out in the past even in the absence of a convective heating surface. Researchers also found that dispersion of carbon nanotubes in water elevates the thermal conductivity of the resulting nanofluid by $100\%$ (see Choi et al. [9]). Both single-walled carbon nanotubes (SWCNTs) and multi-walled carbon nanotubes (MWCNTs) are considered. Optimal homotopic strategy (OHAM) [26,27,28,29,30,31,32,33,34,35] is utilized for solutions of temperature and velocities. Impacts of different flow variables are examined and investigated. Nusselt number and skin friction have been analyzed graphically. Emphasis is given to the role of the main ingredients of the problem, namely volume fraction of carbon nanotubes and a rotating stretchable disk. The benefits of carbon nanotubes towards heat transfer enhancement are also justified via thorough analysis.

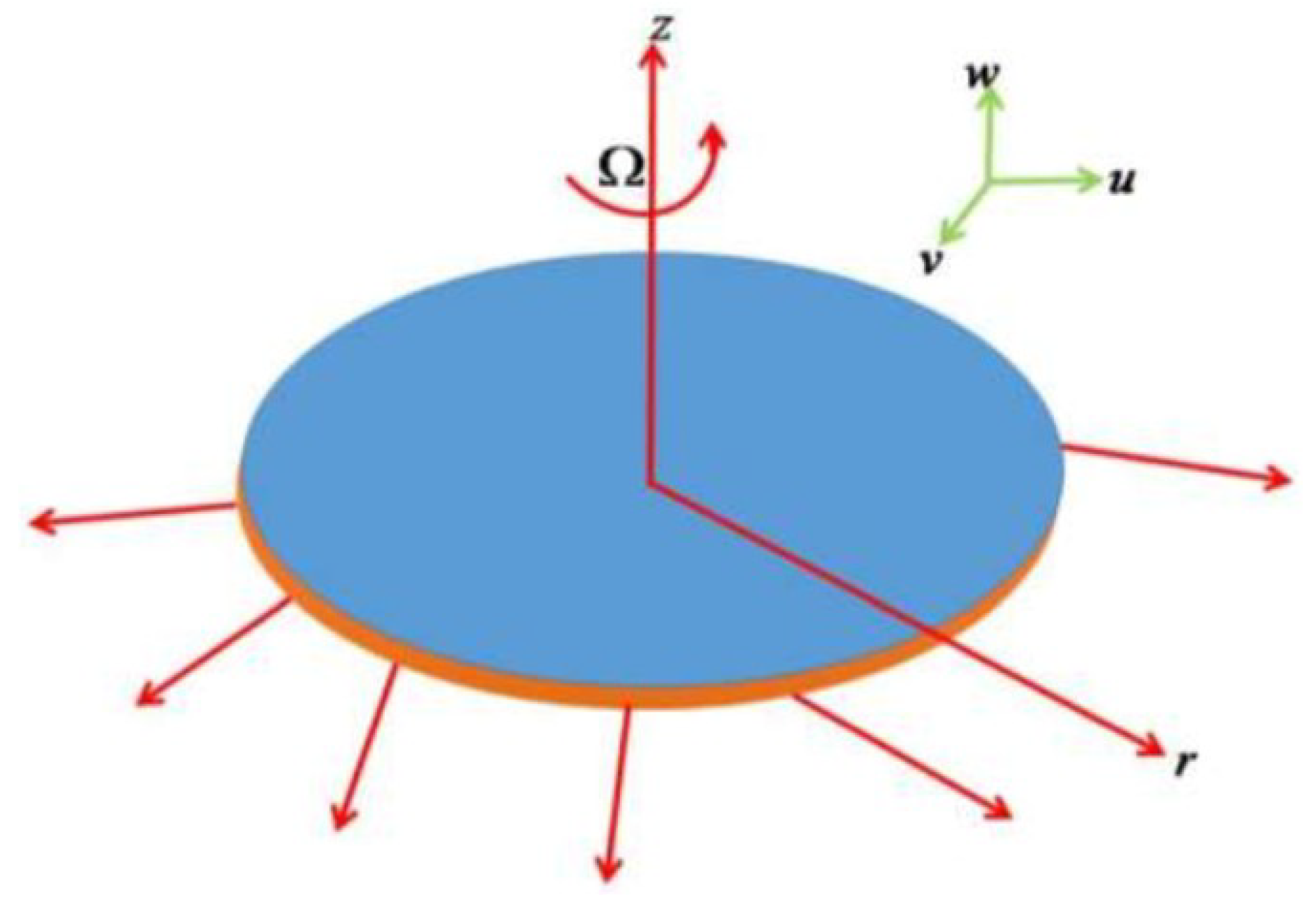
2. Mathematical Formulation

Let us assume three-dimensional flow of water-based carbon nanotubes by a stretchable rotating disk. The disk at $z=0$ rotates subject to constant angular velocity $\mathsf{\Omega }$ (see Figure 1). Let us assume CNT nanoparticles: SWCNTs and MWCNTs within base liquid (water). Due to axial symmetry, derivatives of $\phi$ are neglected. The surface of the disk has temperature $T_f$, while ambient fluid temperature is $T_{\infty }.$ The velocity components are $(u,v,w)$ in cylindrical coordinate $(r,\phi ,z)$ respectively. The resulting boundary-layer expressions are [8,20]:

$$\frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial w}{\partial z}=0,$$

(1)

$$u\frac{\partial u}{\partial r}-\frac{v^2}{r}+w\frac{\partial u}{\partial z}={\nu }_{nf}\left(\frac{{\partial }^{2}u}{\partial r^2}+\frac{{\partial }^{2}u}{\partial z^2}+\frac{1}{r}\frac{\partial u}{\partial r}-\frac{u}{r^2}\right),$$

(2)

$$u\frac{\partial v}{\partial r}+\frac{uv}{r}+w\frac{\partial v}{\partial z}={\nu }_{nf}\left(\frac{{\partial }^{2}v}{\partial r^2}+\frac{{\partial }^{2}v}{\partial z^2}+\frac{1}{r}\frac{\partial v}{\partial r}-\frac{v}{r^2}\right),$$

(3)

$$u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}={\nu }_{nf}\left(\frac{{\partial }^{2}w}{\partial r^2}+\frac{{\partial }^{2}w}{\partial z^2}+\frac{1}{r}\frac{\partial w}{\partial r}\right),$$

(4)

$$u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}={\alpha }_{nf}\left(\frac{{\partial }^{2}T}{\partial r^2}+\frac{{\partial }^{2}T}{\partial z^2}+\frac{1}{r}\frac{\partial T}{\partial r}\right),$$

(5)

with subjected boundary conditions [8]:

$$u=rs+L_1{\mu }_{nf}\frac{\partial u}{\partial z},v=r\mathsf{\Omega }+L_1{\mu }_{nf}\frac{\partial v}{\partial z},w=0,-k_{nf}\frac{\partial T}{\partial z}=h_f\left(T_f-T\right)\mathrm{at}z=0,$$

(6)

$$u\to 0,v\to 0,T\to T_{\infty }\mathrm{as}z\to \infty .$$

(7)

Figure 1. Geometry of the problem.

Here $u,$ v and $w$ depict flow velocities in increasing directions of $r,$ $\phi$ and z respectively, while ${\nu }_{nf}=({\mu }_{nf}/{\rho }_{nf})$ stands for kinematic viscosity, ${\alpha }_{nf}=k_{nf}/{\left(\rho c_p\right)}_{nf}$ for thermal diffusivity, ${\mu }_{nf}$ for dynamic viscosity, $L_1$ for wall-slip coefficient, T for fluid temperature, $k_{nf}$ for thermal conductivity of nanofluids, ${\rho }_{nf}$ for effective density, $k_{CNT}$ for thermal conductivity of CNTs and ${\left(\rho c_p\right)}_{nf}$ for effective heat capacitance of nanoparticle material. Xue [11] proposed a theoratical model which is expressed by

$$\begin{array}{ccc}{\rho }_{nf}\hfill & =\hfill & {\rho }_f\left(1-\varphi \right)+{\rho }_{CNT}\varphi ,{\mu }_{nf}=\frac{{\mu }_f}{{\left(1-\varphi \right)}^{2.5}},\hfill \\ {\left(\rho c_p\right)}_{nf}\hfill & =\hfill & {\left(\rho c_p\right)}_f\left(1-\varphi \right)+{\left(\rho c_p\right)}_{CNT}\varphi ,\hfill \\ \frac{k_{nf}}{k_f}\hfill & =\hfill & \frac{\left(1-\varphi \right)+2\varphi \frac{k_{CNT}}{k_{CNT}-k_f}ln\frac{k_{CNT}+k_f}{2k_f}}{\left(1-\varphi \right)+2\varphi \frac{k_f}{k_{CNT}-k_f}ln\frac{k_{CNT}+k_f}{2k_f}},\hfill \end{array}$$

(8)

where $\varphi$ represents solid volume fraction of nanoparticles and $nf$ represents thermophysical properties of nanofluid. Table 1 describes thermo-physical features of water and CNT.

Table 1. Thermophysical features of water and carbon nanotubes (CNT).

Physical Features	Water	CNT
		SWCNTs	MWCNTs
$\rho$ (kg/m${}^3)$	$997.1$	2600	1600
k (W/mK)	$0.613$	6600	3000
$c_p$ (J/kgK)	4179	425	796

We now introduce the following transformations:

$$\begin{array}{c}u=r\mathsf{\Omega }{f}^{\prime }\left(\zeta \right),v=r\mathsf{\Omega }g\left(\zeta \right),w=-\sqrt{2{\nu }_f\mathsf{\Omega }}f\left(\zeta \right),\\ \zeta =z{\left(\frac{2\mathsf{\Omega }}{{\nu }_f}\right)}^{1/2},\theta \left(\zeta \right)=\frac{T-T_{\infty }}{T_f-T_{\infty }}.\end{array}.$$

(9)

Expression $\left(1\right)$ is automatically satisfied while Equations $\left(2\right)$–$\left(8\right)$ yield

$$\frac{1}{{(1-\varphi )}^{5/2}(1-\varphi +\frac{{\rho }_{CNT}}{{\rho }_f}\varphi )}{f}^{‴}\left(\zeta \right)+f\left(\zeta \right)f^{″}\left(\zeta \right)-\frac{1}{2}{f}^{\prime 2}\left(\zeta \right)+\frac{1}{2}{g}^2\left(\zeta \right)=0,$$

(10)

$$\frac{1}{{(1-\varphi )}^{5/2}(1-\varphi +\frac{{\rho }_{CNT}}{{\rho }_f}\varphi )}{g}^{″}\left(\zeta \right)+f\left(\zeta \right)g^{\prime }\left(\zeta \right)-f^{\prime }\left(\zeta \right)g\left(\zeta \right)=0,$$

(11)

$$\frac{1}{Pr}\frac{k_{nf}}{k_f}{\theta }^{″}\left(\zeta \right)+\left(1-\varphi +\varphi \frac{{\left(\rho c_p\right)}_{CNT}}{{\left(\rho c_p\right)}_f}\right)f\left(\zeta \right){\theta }^{\prime }\left(\zeta \right)=0,$$

(12)

with the boundary conditions

$$f\left(0\right)=0,f^{\prime }\left(0\right)=C+\frac{\alpha }{{(1-\varphi )}^{5/2}}{f}^{″}\left(0\right),g\left(0\right)=1+\frac{\alpha }{{(1-\varphi )}^{5/2}}{g}^{\prime }\left(0\right),{\theta }^{\prime }\left(0\right)=-\frac{k_f}{k_{nf}}Bi\left(1-\theta \left(0\right)\right),$$

(13)

$$f^{\prime }\left(\infty \right)\to 0,g(\infty )\to 0,\theta \left(\infty \right)\to 0.$$

(14)

Here C stands for stretching-strength parameter, $\alpha$ for velocity slip number, Pr for Prandtl number and $Bi$ for the Biot number. These numbers are described by:

$$C=\frac{s}{\mathsf{\Omega }},\alpha =L_1{\mu }_f{\left(\frac{2\mathsf{\Omega }}{{\nu }_f}\right)}^{1/2},Bi=\frac{h_f}{k_f}{\left(\frac{{\nu }_f}{2\mathsf{\Omega }}\right)}^{1/2},Pr=\frac{{\nu }_f{\left(\rho c_p\right)}_f}{k_f}.$$

(15)

Nusselt number and skin friction are defined by

$$\left.\begin{array}{c}{\mathrm{Re}}_r^{-1/2}N{u}_r=-\frac{k_{nf}}{k_f}{\theta }^{\prime }\left(0\right),\\ {\mathrm{Re}}_r^{1/2}{C}_f=\frac{1}{{\left(1-\varphi \right)}^{5/2}}{\left(f^{″}{\left(0\right)}^2+g^{\prime }{\left(0\right)}^2\right)}^{1/2},\end{array}\right\},$$

(16)

where Re${}_r=2\mathsf{\Omega }{r}^2/{\nu }_f$ depicts the local Reynolds number.

3. Solutions by OHAM

The optimal solutions of expressions (10)–(12) through $\left(13\right)$ and $\left(14\right)$ have been established by considering optimal homotopic strategy (OHAM). The proper operators and guesses are

$$f_0\left(\zeta \right)=\frac{C}{\left(1+\frac{\alpha }{{(1-\varphi )}^{5/2}}\right)}(1-e^{-\zeta }),g_0\left(\zeta \right)=\frac{1}{\left(1+\frac{\alpha }{{(1-\varphi )}^{5/2}}\right)}{e}^{-\zeta },{\theta }_0\left(\zeta \right)=\frac{Bi}{\left(\frac{k_{nf}}{k_f}+Bi\right)}{e}^{-\zeta },$$

(17)

$${\mathcal{L}}_g=\frac{d^{2}g}{d{\zeta }^2}-g,{\mathcal{L}}_{\theta }=\frac{d^2\theta }{d{\zeta }^2}-\theta ,{\mathcal{L}}_f=\frac{d^{3}f}{d{\zeta }^3}-\frac{df}{d\zeta }.$$

(18)

The above operators satisfy

$${\mathcal{L}}_f\left[F_1^{****}+F_2^{****}{e}^{\zeta }+F_3^{****}{e}^{-\zeta }\right]=0,{\mathcal{L}}_g\left[F_4^{****}{e}^{\zeta }+F_5^{****}{e}^{-\zeta }\right]=0,{\mathcal{L}}_{\theta }\left[F_6^{****}{e}^{\zeta }+F_7^{****}{e}^{-\zeta }\right]=0,$$

(19)

in which $F_i^{****}$ (i = 1–7) portrays arbitrary constants. The m-th and zero-th order systems are easily established in view of above operators. By using BVPh2.0 of the software Mathematica, the obtained deformation problems have been computed.

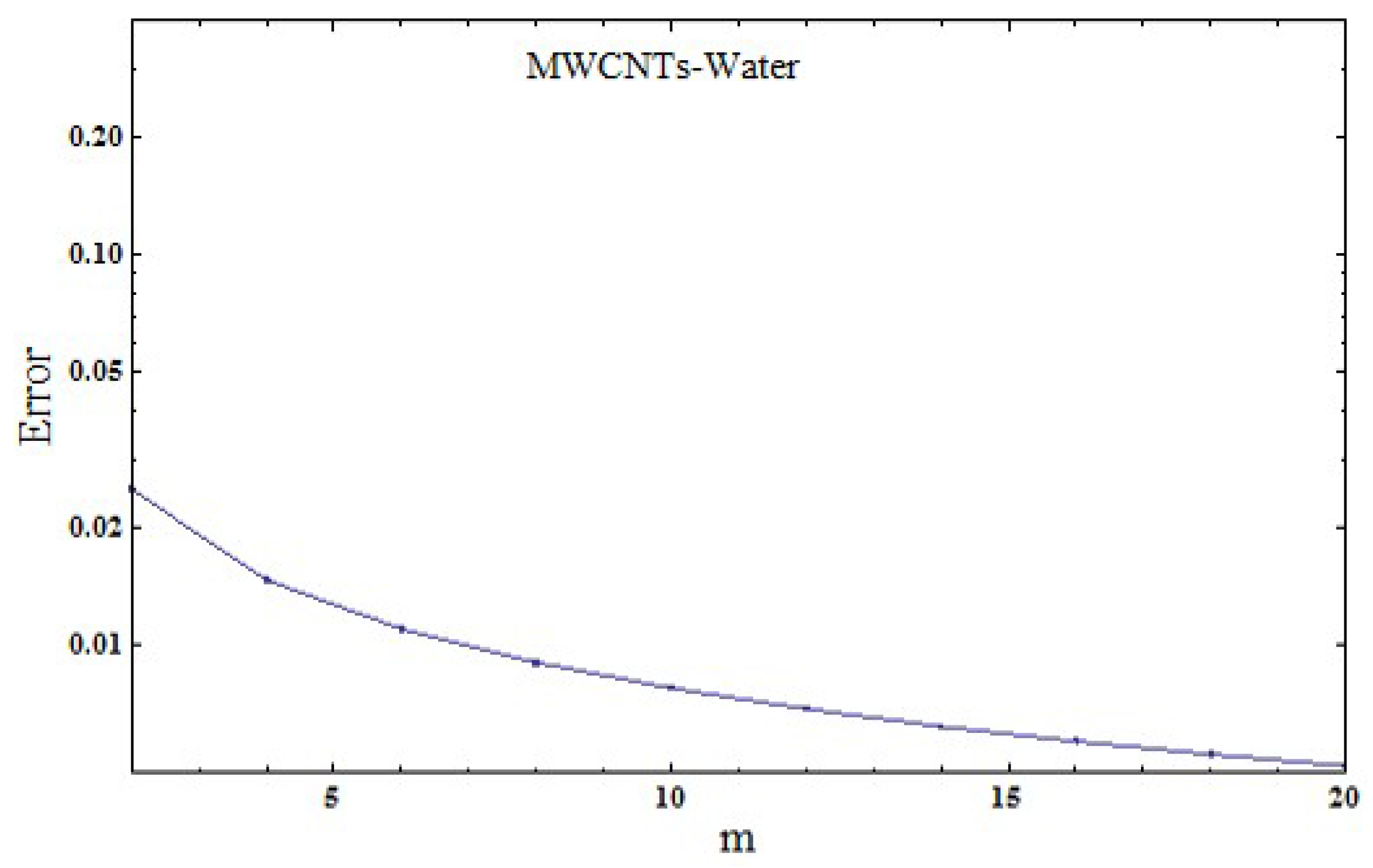
4. Optimal Convergence-Control Parameters

In homotopic solutions, the non zero auxiliary variables ${\hslash }_f,$ $h_g$ and ${\hslash }_{\theta }$ determine the convergence portion and also rate of homotopy solution. The idea of minimization has been applied by defining averaged squared residuals errors as proposed by Liao [26].

$${\epsilon }_m^f={\frac{1}{k+1}}_{j=0}^k{\left[{\mathcal{N}}_f{\left({}_{i=0}^m\widehat{f}\left(\zeta \right),{}_{i=0}^m\widehat{g}\left(\zeta \right)\right)}_{\zeta =j\delta \zeta }\right]}^2,$$

(20)

$${\epsilon }_m^g={\frac{1}{k+1}}_{j=0}^k{\left[{\mathcal{N}}_g{\left({}_{i=0}^m\widehat{f}\left(\zeta \right),{}_{i=0}^m\widehat{g}\left(\zeta \right)\right)}_{\zeta =j\delta \zeta }\right]}^2,$$

(21)

$${\epsilon }_m^{\theta }={\frac{1}{k+1}}_{j=0}^k{\left[{\mathcal{N}}_{\theta }{\left({}_{i=0}^m\widehat{f}\left(\zeta \right),{}_{i=0}^m\widehat{g}\left(\zeta \right),{}_{i=0}^m\widehat{\theta }\left(\zeta \right)\right)}_{\zeta =j\delta \zeta }\right]}^2.$$

(22)

Following Liao [26]:

$${\epsilon }_m^t={\epsilon }_m^f+{\epsilon }_m^g+{\epsilon }_m^{\theta },$$

(23)

where ${\epsilon }_m^t$ represents total squared residual error, $\delta \zeta =0.5$ and $k=20.$ At the second order of deformations, convergence-control parameters for SWCNTs–water have optimal values i.e., $h_f=-0.35923,$ $h_g=-0.736096$ and $h_{\theta }=-0.00105197$ and total averaged squared residuals error is ${\epsilon }_m^t=-0.0255367$ while optimal data of convergence-control parameters for MWCNTs–water is $h_f=-0.385385,$ $h_g=-0.729057$ and $h_{\theta }=-0.00232643$ and total averaged squared residuals error is ${\epsilon }_m^t=-0.025173$. Figure 2 and Figure 3 display error plots for MWCNTs–water and SWCNTs–water. Table 2 and Table 3 show that averaged squared residuals error decreases for higher order deformations.

Figure 2. Error sketch for SWCNTs-Water.

Figure 3. Error sketch for MWCNTs-Water.

Table 2. Individual averaged squared residuals errors for single-walled carbon nanotubes (SWCNTs)–water.

m	${\mathit{\epsilon }}_{\mathit{m}}^{\mathit{f}}$	${\mathit{\epsilon }}_{\mathit{m}}^{\mathit{g}}$	${\mathit{\epsilon }}_{\mathit{m}}^{\mathit{\theta }}$
2	$9.95225\times {10}^{-5}$	$2.35341\times {10}^{-2}$	$7.29447\times {10}^{-7}$
6	$4.17686\times {10}^{-5}$	$1.03083\times {10}^{-2}$	$6.04738\times {10}^{-7}$
10	$2.95796\times {10}^{-5}$	$7.24672\times {10}^{-3}$	$5.69806\times {10}^{-7}$
14	$2.37325\times {10}^{-5}$	$5.77429\times {10}^{-3}$	$5.53122\times {10}^{-7}$
18	$2.01939\times {10}^{-5}$	$4.88653\times {10}^{-3}$	$5.43213\times {10}^{-7}$
20	$1.88867\times {10}^{-5}$	$4.55942\times {10}^{-3}$	$5.39608\times {10}^{-7}$

Table 3. Individual averaged squared residuals errors for single-walled carbon nanotubes (MWCNTs)–water.

m	${\mathit{\epsilon }}_{\mathit{m}}^{\mathit{f}}$	${\mathit{\epsilon }}_{\mathit{m}}^{\mathit{g}}$	${\mathit{\epsilon }}_{\mathit{m}}^{\mathit{\theta }}$
2	$1.0164\times {10}^{-4}$	$2.40503\times {10}^{-2}$	$7.29447\times {10}^{-7}$
6	$4.27165\times {10}^{-5}$	$1.05447\times {10}^{-2}$	$6.04522\times {10}^{-7}$
10	$3.02678\times {10}^{-5}$	$7.41739\times {10}^{-3}$	$5.69547\times {10}^{-7}$
14	$2.42942\times {10}^{-5}$	$5.91293\times {10}^{-3}$	$5.52829\times {10}^{-7}$
18	$2.06785\times {10}^{-5}$	$5.00567\times {10}^{-3}$	$5.42892\times {10}^{-7}$
20	$1.93426\times {10}^{-5}$	$4.67132\times {10}^{-3}$	$5.39275\times {10}^{-7}$

5. Results and Discussion

The present section presents behaviors of various physical parameters like stretching-strength parameter $C,$ volume fraction $\varphi ,$ velocity slip parameter $\alpha$ and Biot number $Bi$ on radial $f^{\prime }\left(\zeta \right)$ and azimuthal $g\left(\zeta \right)$ velocities and temperature $\theta \left(\zeta \right).$ The results are obtained for both SWCNTs and MWCNTs. Figure 4 shows variation in the radial velocity $f^{\prime }\left(\zeta \right)$ for larger values of $\alpha$. Radial velocity $f^{\prime }\left(\zeta \right)$ shows reduction for increasing values of $\alpha$. Figure 5 presents impact of stretching-strength parameter C on radial velocity $f^{\prime }\left(\zeta \right)$. For larger values of $C,$ the radial velocity shows an increasing trend. Figure 6 depicts the effect of nanoparticle volume fraction $\varphi$ on radial velocity $f^{\prime }\left(\zeta \right)$. For higher $\varphi$, the radial velocity $f^{\prime }\left(\zeta \right)$ is increased. Figure 7 presents that how velocity slip parameter $\alpha$ affects the azimuthal velocity $g\left(\zeta \right)$. It is observed that an increment in velocity slip parameter $\alpha$ lead to lower $g\left(\zeta \right)$. Figure 8 depicts impact of C on azimuthal velocity $g\left(\zeta \right)$. Azimuthal velocity reduces for larger values of streching-strength parameter. Figure 9 depicts the impact of nanoparticles volume fraction $\varphi$ on $g\left(\zeta \right)$. The azimuthal velocity $g\left(\zeta \right)$ is increased for higher estimations of $\varphi$. Figure 10 examines that how Biot number $Bi$ affects the temperature profile. For higher values of $Bi,$ the temperature field $\theta \left(\zeta \right)$ is enhanced. Higher estimations of Biot number correspond to stronger convection which produces higher temperature field and more associated layer thickness. Figure 11 highlights the impact of stretching-strength parameter C on temperature field $\theta \left(\zeta \right)$. Temperature field $\theta \left(\zeta \right)$ is reduced for increasing values of C. Figure 12 presents that how volume fraction $\varphi$ affects the temperature field $\theta \left(\zeta \right)$. Higher values of $\varphi$ shows an enhancement in temperature $\theta \left(\zeta \right)$. Figure 13 shows the effects of volume fraction $\varphi$ and velocity slip parameter $\alpha$ on Re${}_r^{1/2}{C}_f.$ Skin friction Re${}_r^{1/2}{C}_f$ is increased for higher estimations of $\varphi$. Figure 14 displays the behavior of the volume fraction $\varphi$ and Biot number $Bi$ on Nusselt number Re${}_r^{-1/2}N{u}_r$. The Nusselt number is enhanced for increasing values of $\varphi$.

Figure 4. Sketch of $f^{\prime }$$\left(\zeta \right)$ for $\alpha .$

Figure 5. Sketch of $f^{\prime }$$\left(\zeta \right)$ for C.

Figure 6. Sketch of $f^{\prime }$$\left(\zeta \right)$ for $\varphi$.

Figure 7. Sketch of g$\left(\zeta \right)$ for $\alpha .$

Figure 8. Sketch of g$\left(\zeta \right)$ for C.

Figure 9. Sketch of g$\left(\zeta \right)$ for $\varphi .$

Figure 10. Sketch of $\theta$$\left(\zeta \right)$ for $Bi.$

Figure 11. Sketch of $\theta$$\left(\zeta \right)$ for C.

Figure 12. Sketch of $\theta$$\left(\zeta \right)$ for $\varphi .$

Figure 13. Sketch of Re${}_r^{1/2}{C}_f$ for $\varphi$ and $\alpha .$

Figure 14. Sketch of Re${}_r^{-1/2}N{u}_r$ for $\varphi$ and $Bi$.

6. Conclusions

Three-dimensional flow of carbon nanotubes by a stretchable rotating disk with velocity slip effects is studied. Heat transport is explained by convective heating surface. The key findings of current research are listed below:

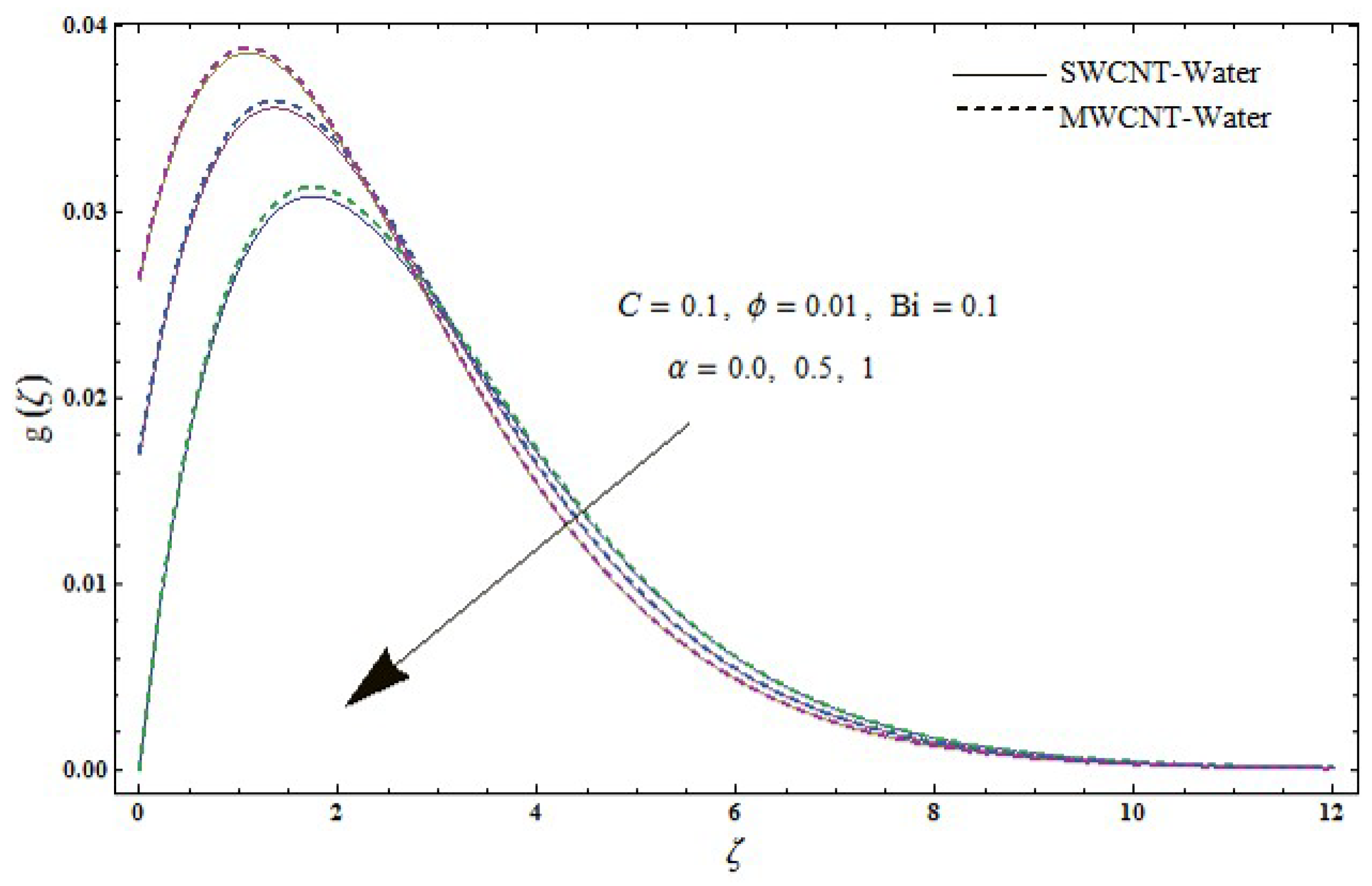
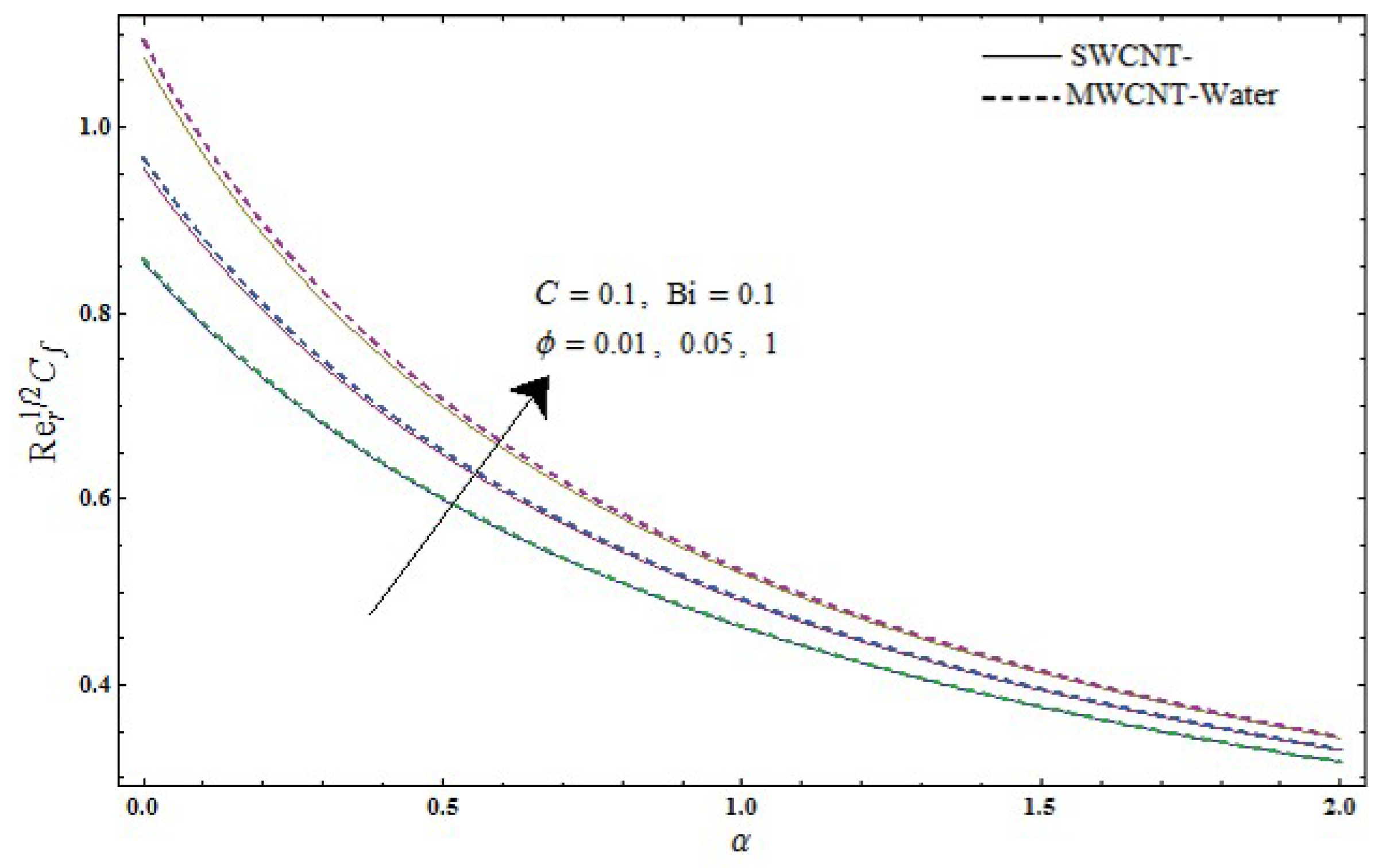
• Both velocities $f^{\prime }\left(\zeta \right)$ and $g\left(\zeta \right)$ show reduction for higher values of velocity slip parameter $\alpha$.
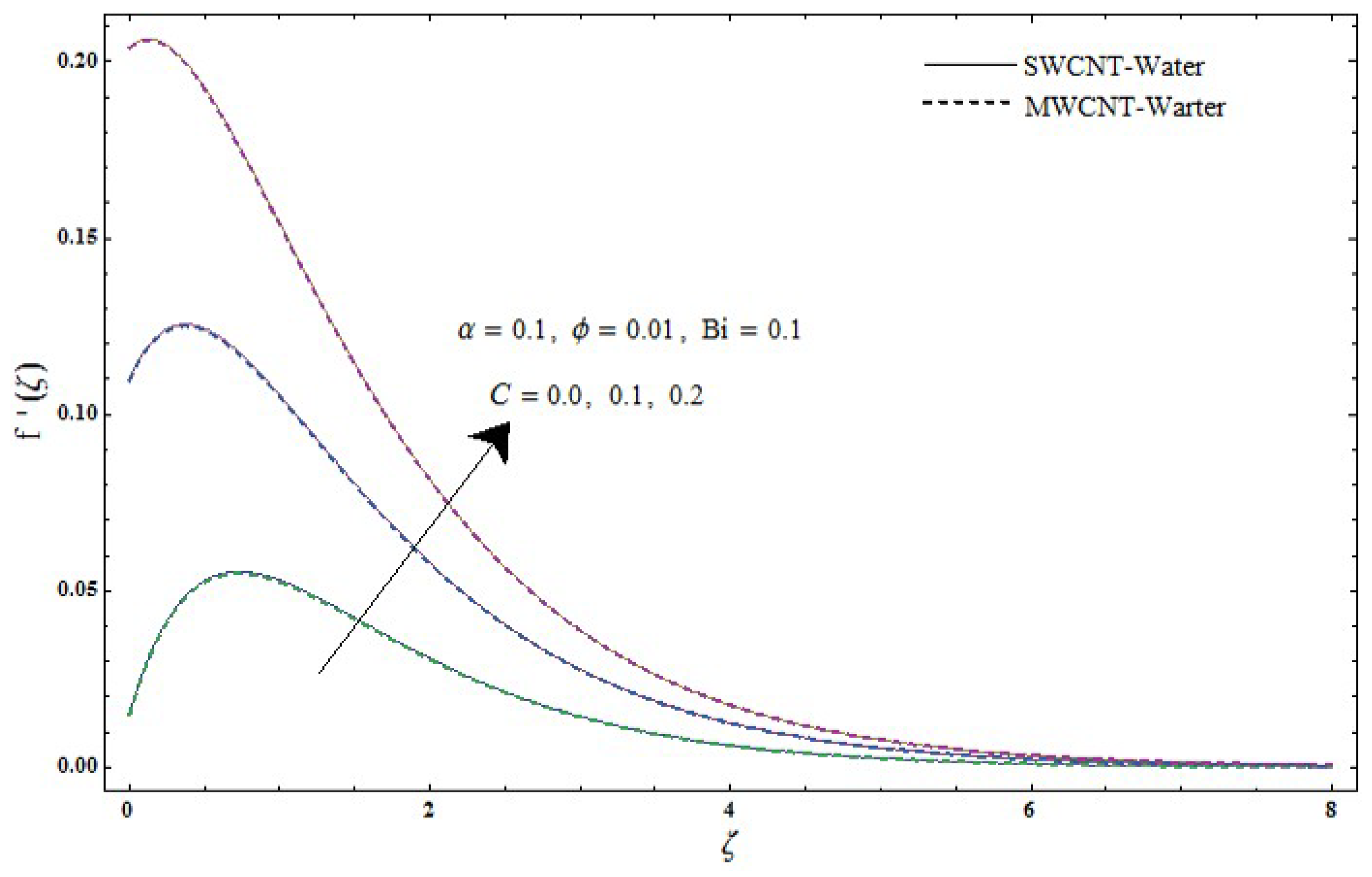
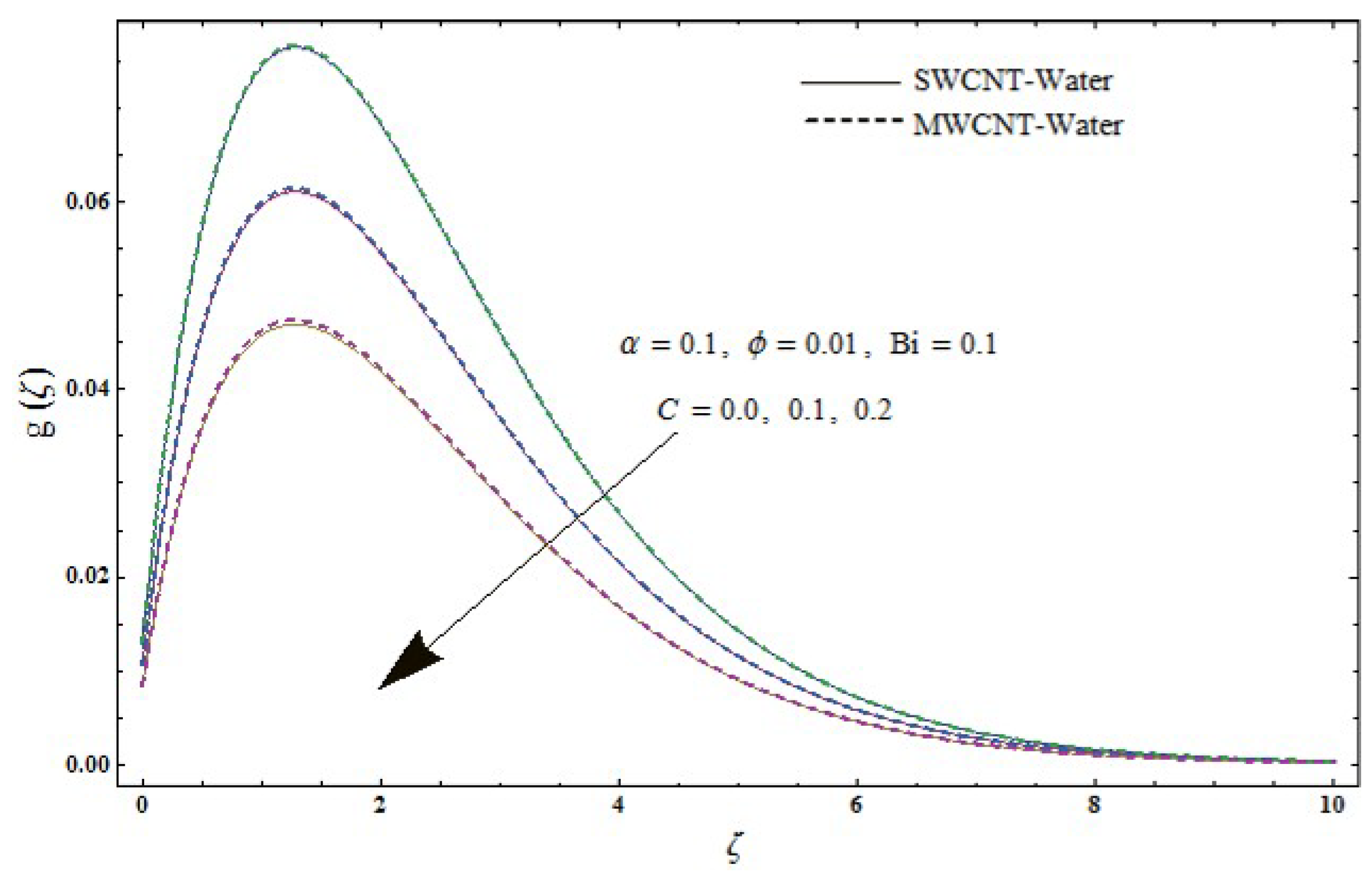
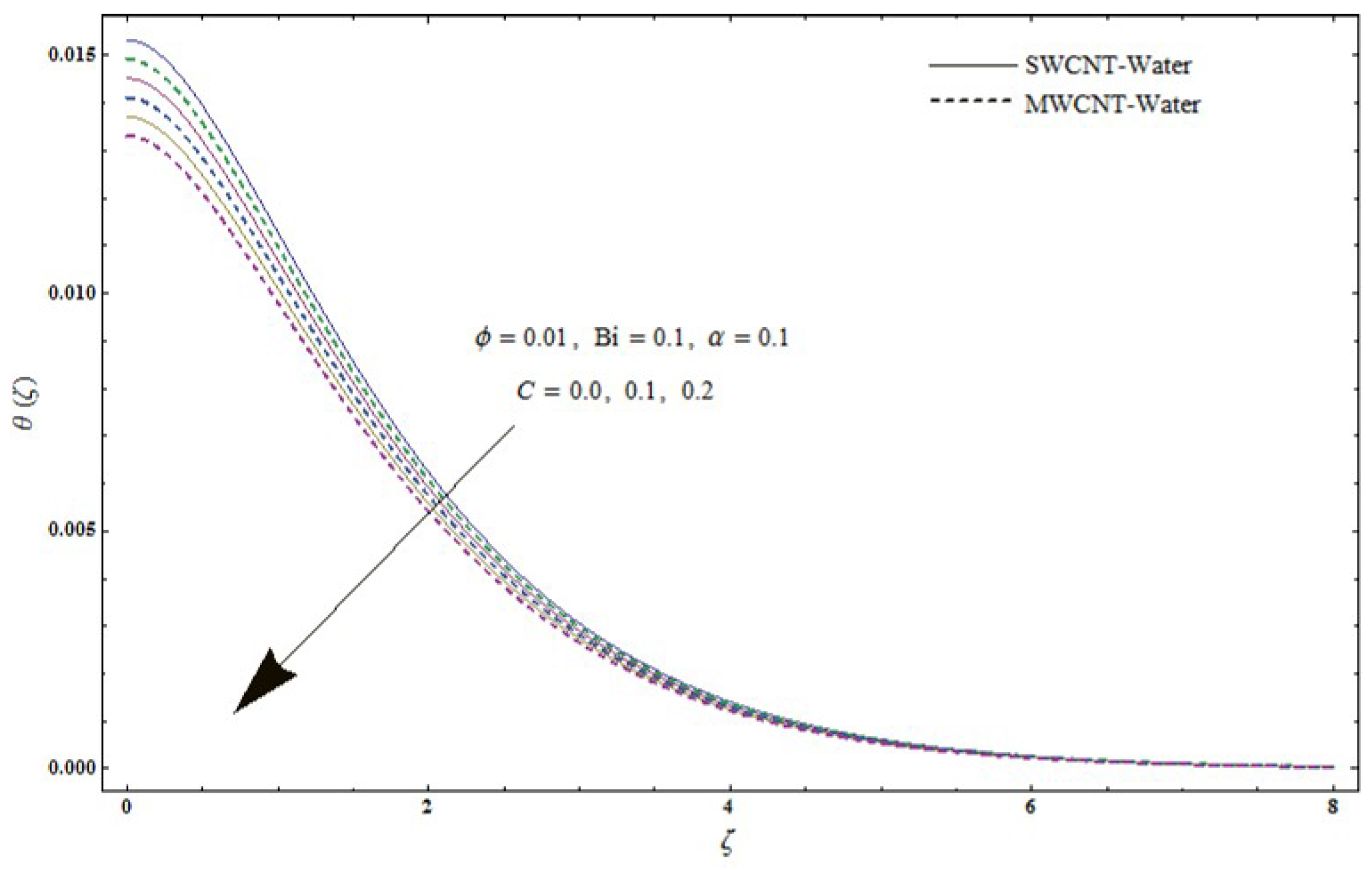
• Larger stretching-strength parameter C presents an increase in radial velocity $f^{\prime }\left(\zeta \right)$ while opposite trend is noticed for azimuthal velocity $g\left(\zeta \right)$ and temperature $\theta \left(\zeta \right)$.
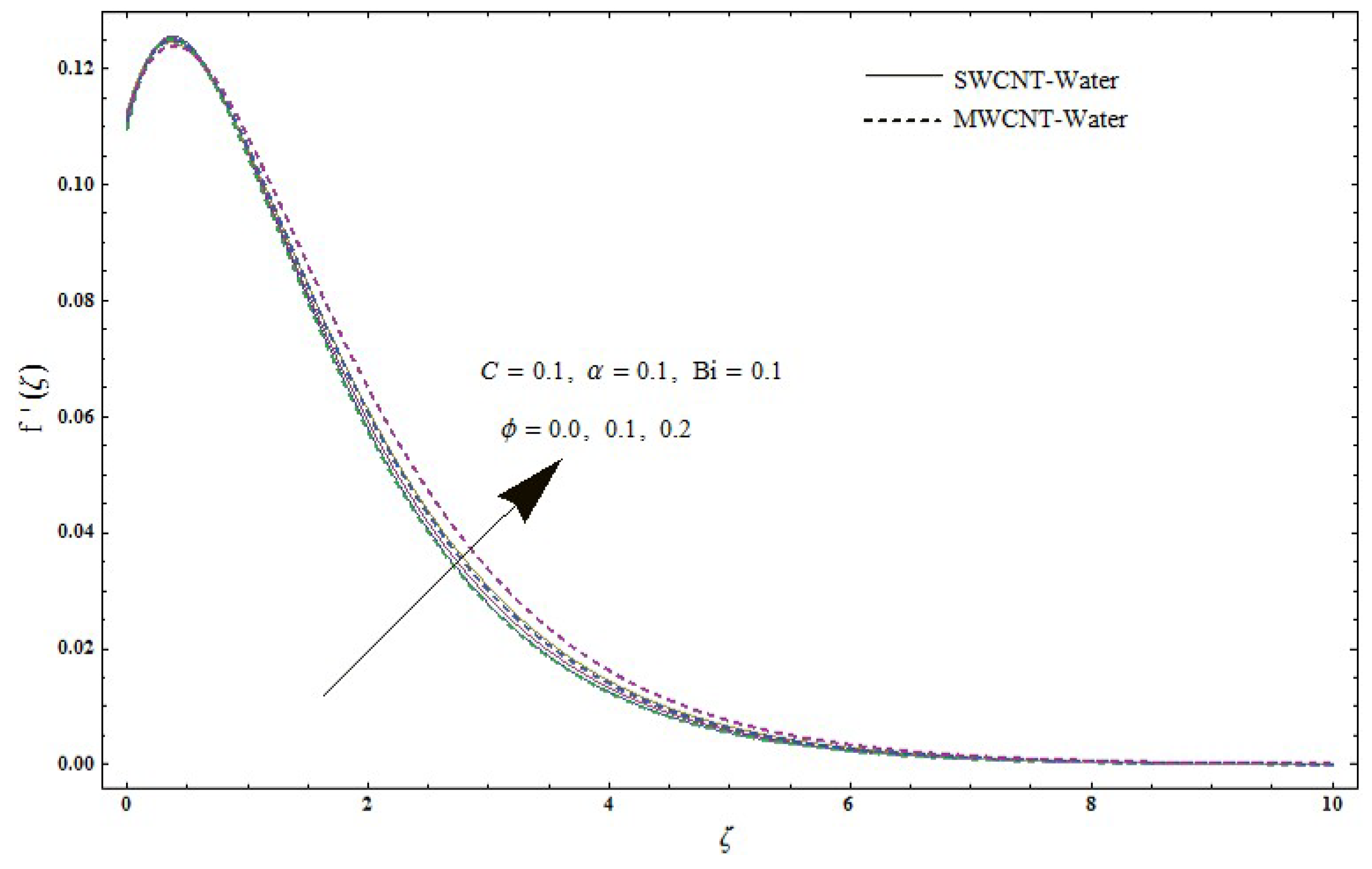
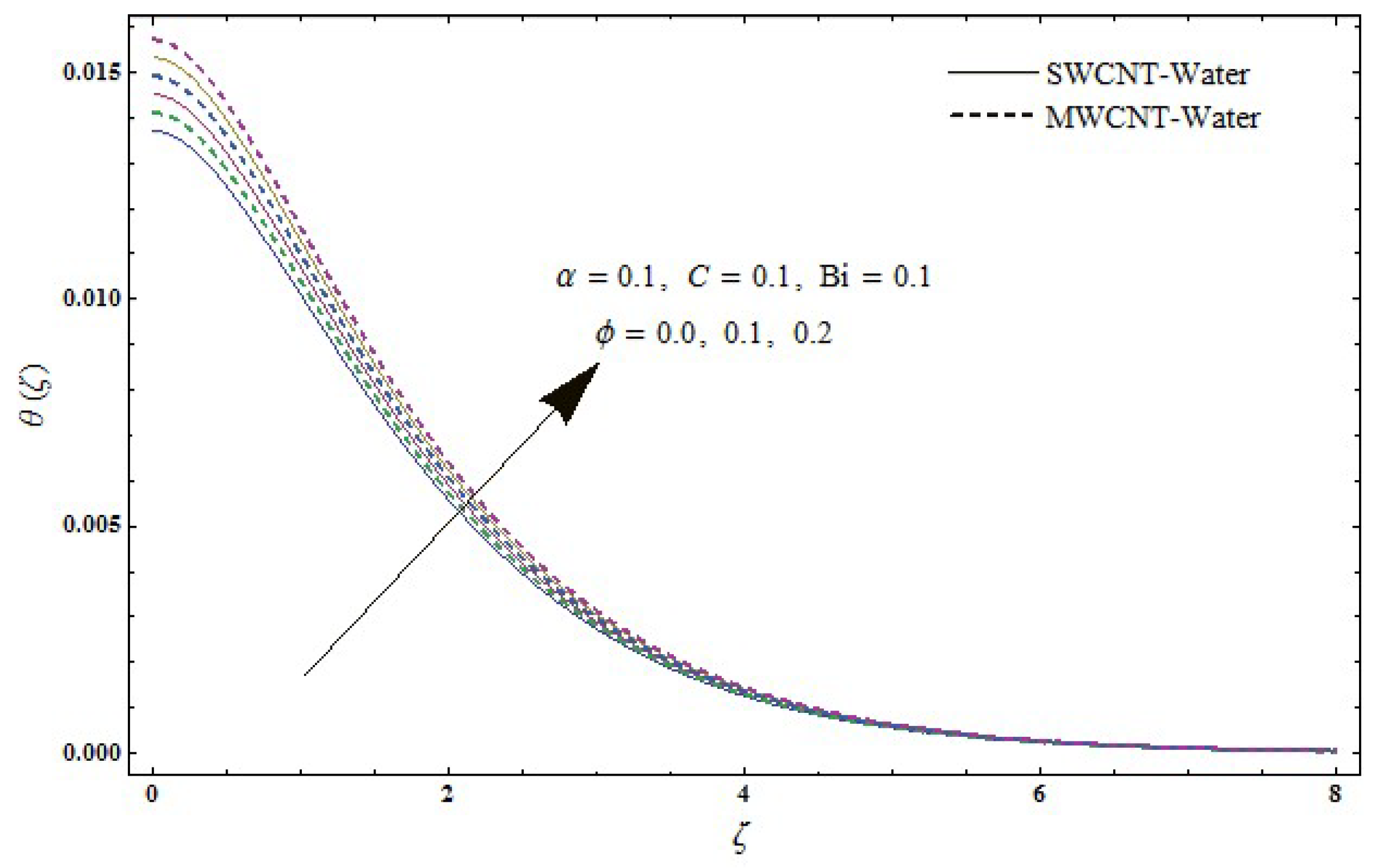
• For higher estimations of the volume fraction $\varphi ,$ both the velocity and temperatue field are enhanced.
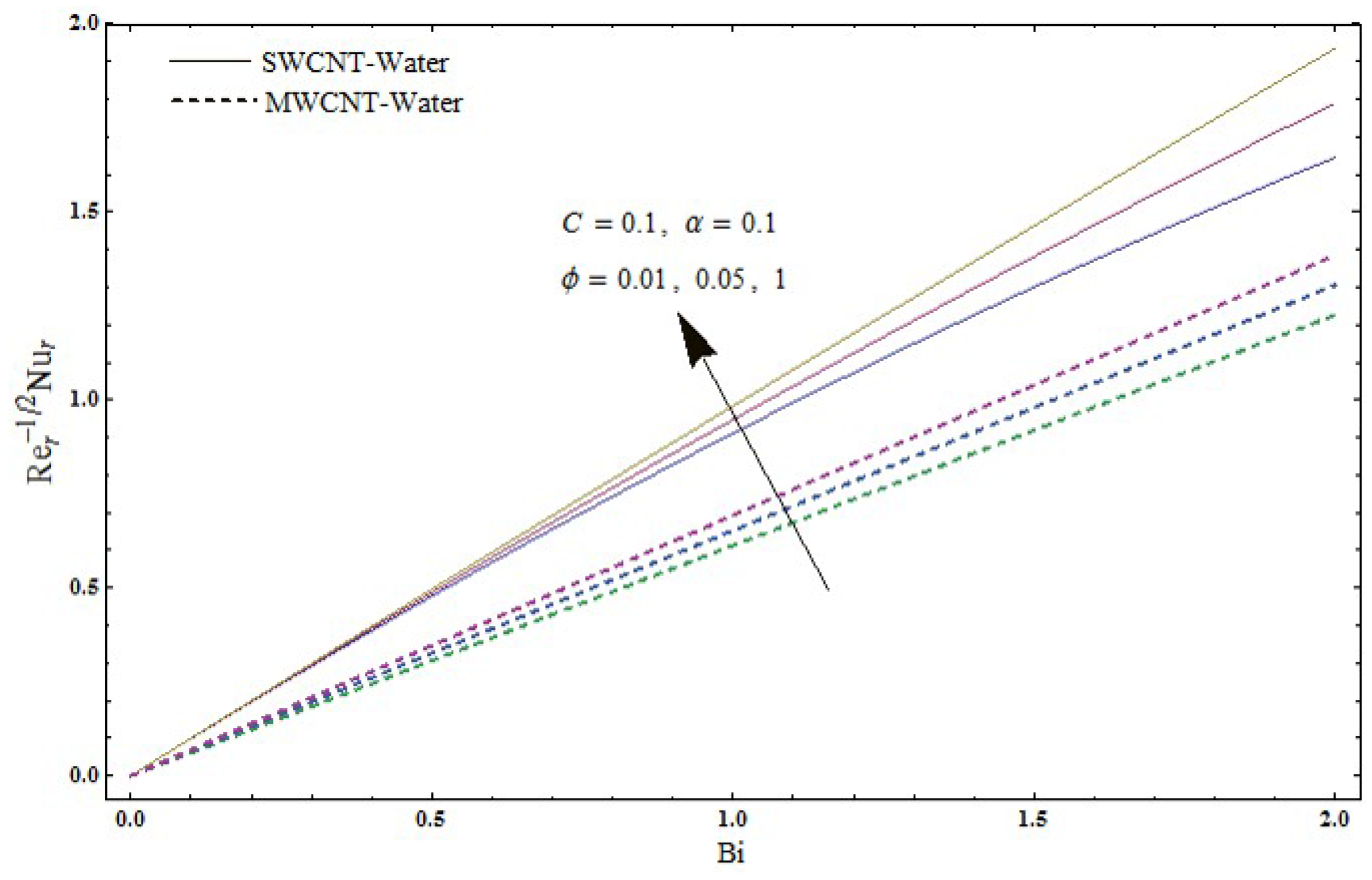
• Temperature field $\theta \left(\zeta \right)$ is enhanced for larger values of the Biot number $Bi$.
• Nusselt number Re${}_r^{-1/2}N{u}_r$ is increased for larger values of volume fraction $\varphi$.
• Coefficient of skin-friction Re${}_r^{1/2}{C}_f$ increases for higher volume fraction $\varphi$ and velocity slip parameter $\alpha .$
• The used technique for the solution’s development has advantages over the other in the sense of the following points:
  • It is independent of small/large physical parameters.
  • It provides a simple way to ensure the convergence of series solutions.
  • It provides a large freedom to choose the base functions and related auxiliary linear operators.