Abstract
Device-free localization (DFL) locates targets without being equipped with the attached devices, which is of great significance for intrusion detection or monitoring in the era of the Internet-of-Things (IoT). Aiming at solving the problems of low accuracy and low robustness in DFL approaches, in this paper, we first treat the RSS signal as an RSS-image matrix and conduct a process of eliminating the background to dig out the variation component with distinguished features. Then, we make use of these feature-rich images by formulating DFL as an image classification problem. Furthermore, a deep convolutional neural network (CNN) is designed to extract features automatically for classification. The localization performance of the proposed background elimination-based CNN (BE-CNN) scheme is validated with a real-world dataset of outdoor DFL. In addition, we also validate the robust performance of the proposal by conducting numerical experiments with different levels of noise. Experimental results demonstrate that the proposed scheme has an obvious advantage in terms of improving localization accuracy and robustness for DFL. Particularly, the BE-CNN can maintain the highest localization accuracy of 100%, even in noisy conditions when the SNR is over −5 dB. The BE-based methods can outperform all the corresponding raw data-based methods in terms of the localization accuracy. In addition, the proposed method can outperform the comparison methods, deep neural network with autoencoder, K-nearest-neighbor (KNN), support vector machines (SVM), etc., in terms of the localization accuracy and robustness.
1. Introduction
Wireless technologies have attracted tremendous attention in intrusion detection in the past few years [1,2,3,4]. The localization technique based on the wireless sensor network (WSN) has spawned a wide set of the Internet-of-Things (IoT) [5] applications, e.g., for intrusion detection and in security, for monitoring the statuses or positions of aging people in elderly health-care in a smart home, for locating the survivors in some emergency scenarios, for location-information-based services in some smart shopping centers, and so on [6].
To support these above-mentioned applications, many wireless localization technologies [7,8] have been developed. For some wireless localization technologies, the target must be equipped with or carry an attached device, e.g., a smart phone or a tag; for example, the techniques of radio-frequency identification (RFID) [9] and GPS [10]. However, in some emergency scenarios, especially for intrusion monitoring or detection, it may be impossible to pre-equip any attached devices on the target.
Fortunately, device-free localization (DFL) [11,12], as an emerging technology, is proposed to tackle this problem. DFL has been developed for target localization that need not equip the target with any extra tags or devices. As shown in Figure 1, DFL systems are deployed to collect data on the target’s locations based on WSNs, and then, the sensed data are sent to an edge server for processing. Through the edge server, some important locations or target-related information can be dug out for the user to access. As with the description of Figure 1, the user can be the security personnel or a property administrator of buildings, a guard for the military, etc. Therefore, the DFL model is applicable to the various IoT applications [13] as described at the beginning of the Introduction, e.g., intrusion detection and monitoring for security.
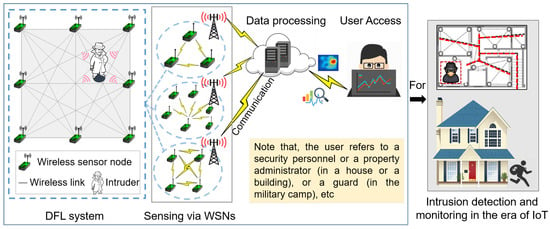
Figure 1.
Internet-of-Things (IoT) fundamental blocks with device-free localization (DFL) technique for the indoor scenario of intrusion detection and monitoring in a smart city.
In the DFL system, a number of wireless sensors are deployed and communicate with each other. Every sensor node is employed to transmit wireless signals turn-by-turn, and the other nodes receive signals according to a time-schedule. Research [14,15] has shown that the received-signal-strength (RSS) or the channel-state-information (CSI) can be used in the DFL problem, as it is affected differently by human movements and easily acquired. This means that if the targets enter the monitoring area of the DFL system or change their locations, they will derive specific wireless signals, i.e., RSS matrices (here, we take the RSS signal as an example). From this point of view, the locations of the targets can be estimated by analyzing the RSS matrices.
However, the corresponding relationship of the location-RSS is not accessible directly. To solve this problem, many previous research works regarded the DFL problem as a classification problem, arranged the collected wireless signals into vectors, and then employed the machine learning methods [16,17] to extract features for classification. The commonly-used algorithms [18,19] include support vector machines (SVM), K-nearest-neighbor (KNN), sparse coding, and deep neural networks. For these existing classification methods, deep learning is especially attractive because of its ability to process a large amount of data, extract complex features, and obtain outstanding performance in various fields. Nonetheless, since the variation of the signal derived by the target is exceedingly weak and easily affected by the environment, such as the surrounding noise, there still exist the problems of low accuracy and low robustness in the DFL approaches. Especially when the environment is complex, such as blockage, scattering, etc., it will make the quality of the RSS signal worse. The low quality of RSS matrices makes it hard to recognize their features, which results in an adverse influence on the feature extraction.
In this paper, aiming at improving the localization accuracy and robustness for DFL, we make full use of features underlying the collected RSS matrices and propose a background elimination (BE)-based convolutional neural network (BE-CNN) scheme. CNN has promoted the significant progress in many applications, e.g., object detection and recognition, intelligent systems for monitoring skin diseases, and so on [20,21,22], because of its excellent performance in feature extraction. Taking advantage of CNN, in this paper, we first convert the RSS signal into an RSS-image matrix and then conduct a process of eliminating the background to dig out the variation components with distinguished features. Furthermore, the image matrices have specific patterns associated with different reference points (RPs) and have similar patterns at the same RP. Therefore, we make use of these feature-rich images by transforming the DFL problem into the image classification problem, where each RP is regarded as one class. Besides, we estimate the target’s location as that of the RP with the most similar features of the collected matrix. Finally, a deep CNN is designed to extract features automatically to perform classification. It is expected that we will achieve an accurate and robust localization process.
To be more specific, we present the framework of the BE-CNN scheme for DFL in Figure 2. From left to right, it first collects the wireless signals, i.e., RSS matrices in this paper, and then pre-process all the raw RSS matrices by BE processing. In addition, all the processed RSS matrices with various classes of labels are input into the CNN for training. After the training procedure, the trained CNN can be employed to estimate the target’s positions in the testing stage.
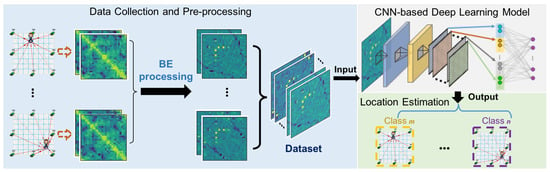
Figure 2.
Illustration of the framework of the proposed background elimination pre-processing based convolutional neural network (BE-CNN).
We summarize the three major contributions of this paper as follows:
- We devise the RSS signal as the image matrix and then transform the DFL problem into the image classification problem.
- We propose a scheme of BE-CNN for the outdoor localization scenario, extracting features from the RSS-image automatically.
- The performance of the proposed BE-CNN scheme is validated on real-world datasets of outdoor DFL and compared with other baseline and state-of-the-art DFL methods.
The rest of this paper is organized as follows. Section 2 presents the previous related works. In Section 3, we formulate the DFL problem as a classification problem and also devise the BE scheme. Section 4 presents the algorithm. Section 5 evaluates the performance of our proposal. Finally, we conclude the whole work in Section 6.
2. Related Work
We summarize the development of DFL and the related works about the methods of solving the DFL problem in this section.
Youssef et al. [23] firstly introduced the concept of device-free passive localization. In their work, the DFL was realized by using the RSS values. Moussa et al. [24] treated the DFL problem as a fingerprint-matching problem and then employed Wi-Fi equipment for intrusion detection and monitoring. Wilson et al. [25] firstly proposed the radio-tomographic-imaging (RTI) technology, which used RSS measurements to get images of the moving targets. Zhang et al. [26] eliminated the effects of noise in DFL by increasing the monitoring area and employed more sensor nodes. Inspired by these pioneering related works, many important research works [27,28] have been conducted, which indeed promoted the development of DFL. For example, Seifeldin et al. [29] designed the large-scale DFL system, which tracked entities in real environments. Wang et al. [15] and Gao et al. [30] proposed to realize the target localization by Wi-Fi equipment based on radio maps, which were constructed by CSI matrices. Liang et al. [31] focused on algorithms to eliminate the influences of outliers.
Based on the above works of DFL, in order to improve the performance, such as localization accuracy and detecting efficiency, many different approaches were proposed. Hong et al.[32] developed a novel localization system and employed the SVMs based on the combination of the spatial and temporal signals to evaluate the localization performance. Zhou et al. [33] compared the localization algorithm based on the principle components analysis with SVM classification and SVM regression. Tran et al. [34] represented fingerprints as a dissimilarity measurement between a pair of locations and employed the KNN algorithm to realize the DFL. Zheng et al. [35] proposed an energy-efficient localization system and made use of adaptive weighted KNN to track targets with high accuracy. The above-mentioned methods belong to the traditional method, which have limits in exploiting the collected data and learning complex features. The current attractive deep neural networks, which perform feature extraction automatically, had achieved good performance in DFL. Wang et al. [36] designed DFL experiments and proposed a deep neural network (DNN) with the sparse autoencoder to locate the target’s position. Zhao et al. [19] designed a four-layer neural network and employed restricted Boltzmann machines as a pre-training method to improve the accuracy and anti-noise capacity for outdoor localization. Zhou et al. [37] designed two neural networks for two DFL experiments and made use of them to analyze the CSI fingerprint patterns. Huang et al. [38] designed data argumentation based on the raw collected data to enlarge the dataset and employed a deep neural network to solve the localization problem.
In contrast with the above works, which extended the original RSS matrices into vectors, we first assumed each matrix as an image matrix as described at the end of Section 1. Then, based on analyzing the RSS matrices derived by the target in different locations, the BE-CNN scheme was proposed for improving the robustness and localization accuracy.
3. Problem Statement
3.1. Description of the Device-Free Localization Problem
Figure 3a illustrates a model of the DFL system. From this figure, the monitoring area is surrounded by a series of wireless sensor nodes, which are normally called anchor points (APs). All these APs can communicate with each other by transmitting or receiving wireless signals. The wireless links shown in Figure 3a are the communication between every pair of APs.
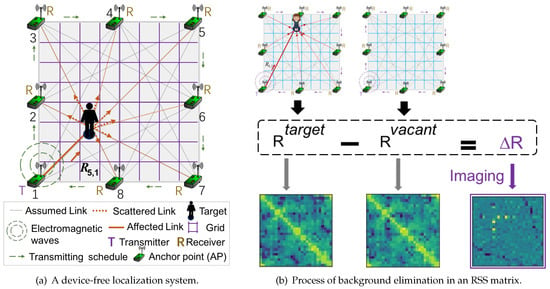
Figure 3.
Process of background elimination in an RSS matrix.
Here, when there is no target in the DFL system, i.e., vacant, let represent the RSS matrix consisting of the measurements collected from all the APs. Note that each AP transmits signals in turns, and other APs receive signals according to a time-schedule. For example, as shown in Figure 3a, AP1 performs as a transmitter, while the rest of the APs, from AP2–AP8, receive signals. That is to say, if there is a total of D sensors deployed in the DFL system, e.g., D = 8 in Figure 3a, there will be a total number of RSS measurements collected. Here, let denote the RSS measurement of the link from the nth node to the mth node. Similar to , when the target enters the detection area, means an RSS matrix of all the wireless links.
There is no doubt that when the target exits the detection area, it will affect a series of the wireless links (or RSS measurements). For example, in Figure 3a, the target will scatter or absorb the signals from AP1, which results in changing the corresponding RSS measurements, e.g., changing from to . Since the RSS signals are easily measured and they are changed differently in association with the target’s positions, the RSS measurements derived by the object could be exploited to estimate the target’s position.
3.2. Transformation of DFL the Problem into the Image-Classification Problem
As shown in Figure 3b, in order to dig out the useful variation components of the signals derived from the target, we performed a BE scheme to eliminate the effect of the background. Therefore, all the collected RSS matrices were pre-processed by subtracting the signal collected in the vacant detection area. Here, denotes the signal variations, which are shown as:
Then, the variation RSS matrix can be established as follows:
As described in Section 3.1, different target’s positions will derive different patterns in the RSS matrices if each RSS matrix is regarded as the image matrix. Figure 3b shows the imaging process of the variation matrix , which converts the RSS matrix into an image matrix. Note that different colors in the image matrices represent the RSS measurements in their associated RSS matrices. It is obvious that after the BE process, the image matrix of had more clear features than the original RSS matrix .
Since each image matrix reflects a specific pattern associated with the target’s position, the image matrices derived from the same arrangement of the target contain similar features, i.e., patterns; whereas, if the target shifts positions from one grid to another, the corresponding image matrices will be obtained with different patterns. Hence, these different matrices include the specific features that are associated with the corresponding locations of the target. Therefore, each RP of the monitoring area can be treated as one class of locations. Therefore, the localization problem can be transformed into the image classification problem that could be effectively addressed with the CNN.
3.3. Dataset Construction
As shown in Figure 3a, the detection area was discretized into many grids, and each grid acted as one reference point (RP), i.e., one class. Suppose that the total number of grids is L. Thus, all the potential locations of this detection area compose L classes in this localization problem. For each class, i.e., RP (for , L), we conducted experiments with P trials. Regarding each trial, an RSS matrix, (, P), can be organized. Therefore, we can get the dataset with location information for all grids and trials shown as . Here, we let S denote the total sample-number of (for ) and let (, S) denote the sth sample of the entire dataset.
4. Proposed Approach
The CNN [39], one kind of deep neural network, has attracted tremendous attraction because of its notable ability to deal with data with two or three dimensions, e.g., the signals of videos or images. As shown in Figure 4, illustrating a schematic diagram of a CNN architecture, the image is input for feature extraction, and then, the final layer outputs probabilities for each class.
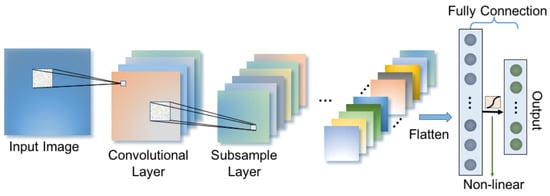
Figure 4.
Schematic architecture of the convolutional neural network (CNN).
In the convolutional layer, a series of two-dimensional kernels was employed to convolve with the receptive field of the feature maps from the former layer to extract data-specific feature maps. Note that the output from the previous layer was employed as the input for the next layer. For a given feature map from the former layer, the output after convolution is shown in:
where * denotes the operation of convolution, and are the parameter terms connecting the convolutional layer, and f(·) denotes the rectified linear unit (ReLU). The ReLU is the non-linear activation function, which is defined as , where z indicates the linear output of each layer.
Furthermore, a filter concatenation technology is exploited in this paper. By employing this technique, features of different resolutions from the data can be captured [40]. Figure 5 illustrates the details of filter concatenation in this paper. The larger filter, i.e., 9 × 9 in this paper, can capture the more general features, and the smaller filter, i.e., 3 × 3 in this paper, finds details. Although filter concatenation increases computational cost, it can improve the performance of classification.
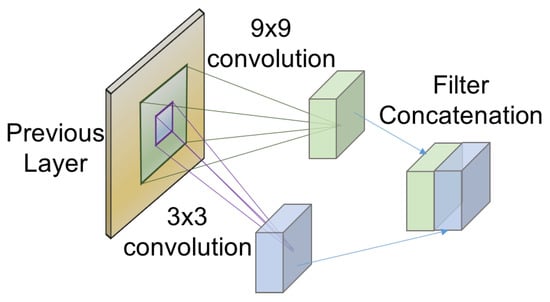
Figure 5.
Schematic diagram of the convolutional filter concatenation.
Generally, the subsampling is performed by pooling, i.e., max pooling in this paper, which reduces the computational complexity of the neural network prone to over-fitting. However, this subsampling operation also loses some information of the data. Springenberg et al. [41] proposed that a convolutional layer with an increased stride can also achieve high accuracy with a shallower architecture, especially on some image recognition tasks. We compare these two subsampling operations in this work.
Additionally, the “dropout” operation in fully-connected layers means randomly making some units inactive in every epoch. This forces the neural network to extract different combinations of features from preceding layers. This operation can also avoiding over-fitting at the same time. Finally, an output layer is followed to predict the probabilities of each class by employing the softmax regression function [42].
In the training stage, the labeled training data () were employed. To update the parameters in the neural network, the cross-entropy error function was employed to compute the error between the real labels and the predictions . This error function is defined as:
In the following experiments, the cost function is optimized by the Adam optimizer via backpropagation.
5. Performance Evaluation
In this section, the performance of the BE-CNN scheme is evaluated on the real-world dataset, named the Outdoor RTIdataset, which is from the SPANLab of University of Utah [25]. All the validation experiments were performed in the TensorFlow 1.2.0 open source software, which was on the operation system with a GeForce GTX 1080 GPU and 32 GB of memory.
5.1. Configurations of the Experiment
In the outdoor DFL experiments, Crossbow TelosB nodes were employed for the wireless sensor network. All the sensor nodes work in the 2.4-GHz frequency band used the IEEE 802.15.4 protocol. A TelosB node was refitted as a base station that collected the signals and then sent them to the computer via USB. The layout of the wireless sensor network is illustrated in Figure 6. The detection area was 21 × 21 feet square surrounded by 28 TelosB nodes. Each node was deployed three feet away from the ground and three feet between two neighbor nodes. In addition, the monitoring area was discretized into 36 grids.
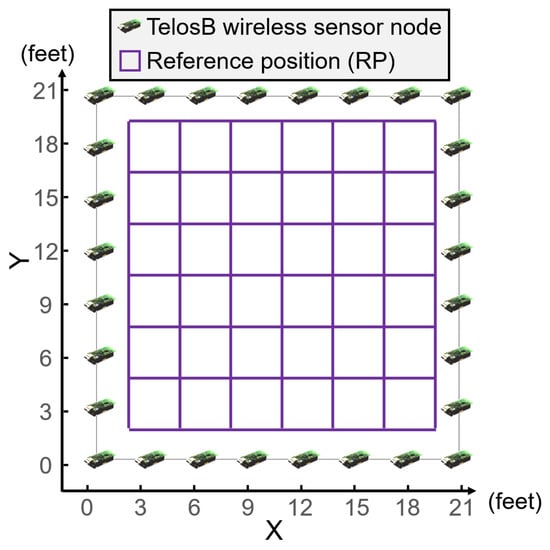
Figure 6.
Experimental layout of the outdoor DFL scenario. The reference-point (RP) IDs of the top row are from RP-31–RP-36; the RPs of the second row are from RP-25–RP-30; RPs of the third row are from RP-19–RP-24; RPs of the forth row are from RP-13–RP-18; RPs of the fifth row are from RP-7–RP-12; RPs of the bottom row are from RP-1–RP-6.
In the DFL experiment, RSSs were measured for 30 trials in a short time interval with a person in the each RP. The total RSS samples were split into two sets for each RP, where 25 samples were used for training, and the remaining five were used as the testing data. We selected all 36 RPs as testing locations for performance evaluation, as shown in Figure 6. Therefore, in all the following experiments, there were 900 samples for training and 180 samples for testing.
In this paper, we employed localization accuracy, defined in Equation (5), as the metric to perform the evaluation of BE-CNN. Suppose that is the total number of all testing samples and is the number of testing samples that were correctly estimated. Thus, the localization accuracy is defined by:
5.2. Data Pre-Processing
To illustrate the features in the samples of RSS image matrices, we took the signal data collected in two RPs, i.e., RP2 and RP4, as examples, as shown in Figure 7. From this figure, the first row presents the image formations of raw signals, which were collected directly by sensors, and the second row shows the variation signals obtained after BE pre-processing. Comparing the images of raw data, the patterns seemed very similar between RP2 and RP4, which can hardly be classified artificially. After the BE pre-processing, not only the patterns of images appeared clear, but also the differences of patterns between RP2 and RP4 became more obvious, which benefited the feature extraction.
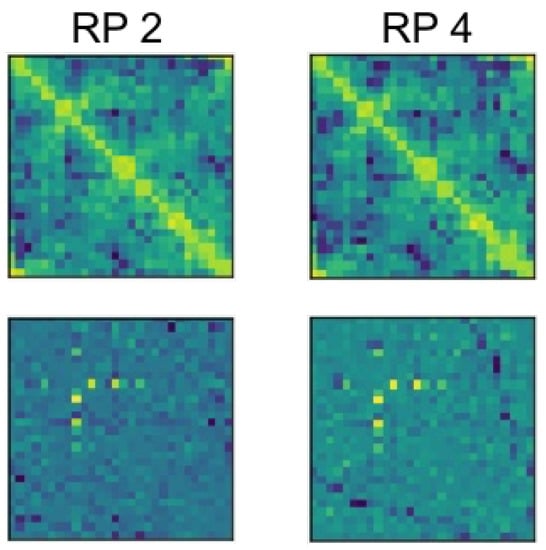
Figure 7.
Comparisons of the raw RSS matrices (top row) and background eliminated RSS matrices (bottom row). Here, the data of Reference Position 2 (RP2) and RP4 are taken as the examples.
In the common DFL experiments, the signal data are generally collected involving a certain level of noise. For example, there may be some adverse dynamic information, for example the electro-magnetic interference from the surrounding electronic devices or equipment, which may lead to various noise with different degrees in the RSS signals in practical applications. Due to the fact that the RSS is easily affected by noise, the robustness and localization accuracy of DFL algorithms will seriously decrease with the increasing degree of noise.
To evaluate the robustness against noise of the proposed scheme, we performed experiments by adding noise at different levels. Figure 8 shows the image formations of pre-processed raw noiseless signal data and the associated noisy signal with the different degrees of the signal-to-noise ratio (SNR). The SNR is defined as: , where and represent the power of the noise and the power of the signal, respectively. Note that the noiseless data denote the raw data without adding Gaussian noise in the entire paper. In Figure 8, except for the left noiseless data, the other three data had noise separately added with SNR levels of 10 dB, 0 dB, and −10 dB. It showed a clear tendency that the noise of the images became more and more serious as the SNR decreased, which made their features more difficult to extract. Note that these levels of noise were added into the entire dataset including the training samples and testing samples. All these noise cases were exploited to evaluate the performance of our proposal with respect to the localization accuracy and robustness.
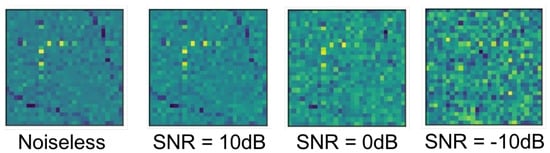
Figure 8.
Featured images of the noiseless signal and noisy signal with different SNR. Here, RP4 is taken as the example.
5.3. Localization Performance of the BE-CNN Scheme for the Outdoor DFL
5.3.1. Optimal Parameters of the BE-CNN
In this part, we optimize the main parameters for BE-CNN used in locating the target. Based on the properties of the CNN, we mainly discuss four factors that may significantly influence its localization performance. They are the number of filters for each layer, the size of convolutional filters (or called kernel size), the number of convolutional layers, and subsampling layers. The above-mentioned parameters are normally decided by trial and error according to the performance of the specifically-designed structure. The procedure of optimizing these parameters is presented as follows:
(1) The number of filters for each convolutional layer: Normally, the more filters that are employed, the richer information we can get from the previous feature maps. Generally, the convolutional filter number differs in different architectures [43]. Referring to the previously-related research of CNN [43] and our preliminary experimental results, we chose 32 as the filter number in this work.
(2) The kernel size: Table 1 shows the localization accuracy performed by BE-CNN with different kernel sizes on the noisy signals. Here, we present three conditions in which the kernel sizes are , , and for BE-CNNs with two convolutional layers, respectively. Note that “−” denotes filter concatenation in this paper. The number of each convolutional filter was set to 32, and there was no pooling layer employed for subsampling. We performed the experiments 30 times with the noisy data. The results showed that the BE-CNN can obtain the highest accuracy by employing the kernel size of .

Table 1.
Training the simulation parameters with different kernel sizes in terms of localization accuracy.
(3) The number of convolutional layers and subsampling operation: Based on the decided kernel size and filter number, we compare the performance of BE-CNN with different numbers of convolutional layers and different subsampling operations. Table 2 shows clearly that when the BE-CNN was designed without pooling operation, it always had better performance in localization accuracy than the BE-CNN with pooling. In addition, when the BE-CNN included two convolutional layers, it could reach the highest localization accuracy of 100% on the noisy data when SNR is −5 dB. Note that all the localization accuracies were average results of experiments run 30 times.

Table 2.
Training simulation parameters with hyper-parameters in terms of localization accuracy.
After performing several experiments by trial and error for the localization performance, the hyperparameters of the BE-CNN for outdoor DFL were as summarized in Table 3. In this architecture, we employed two convolutional layers with 32 filters for each layer. In addition, the convolutional filter size was 9 × 9 for the first layer and 3 × 3 for the second layer. The feature maps learned from the two layers were concatenated before flattening. To avoid the “overfitting” problem, we set a dropout rate of 0.4 for the training of each batch.

Table 3.
Optimal parameters of the BE-CNN for outdoor localization.
5.3.2. Localization Performance Comparison of the BE-CNN Scheme
In this subsection, we exploited the localization performance of the BE-CNN scheme together with other compared approaches. In order to validate the merit of BE pre-processing, we performed experiments on both raw data and the BE processed data by employing CNN, KNN, and SVM. When testing on noiseless data, whether the input data were raw data or data after BE pre-processing, all three methods can reach the highest accuracy of 100%. However, when performing on noisy data, the localization performance was obviously different, as shown in Figure 9.
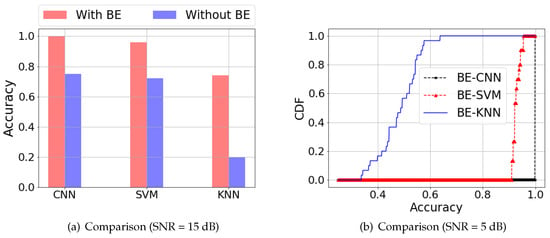
Figure 9.
Comparison (SNR = 5 dB)
Note that Figure 9a shows the impact on localization accuracy by employing BE processing on the noisy dataset with SNR = 15 dB. We performed experiments 30 times for each condition. When employing BE-CNN, the localization accuracy was 100%, while the accuracy obtained without BE was 74.6%. The accuracy obtained by BE-SVM and BE-KNN was 17.7% and 54.2% higher than the corresponding ones without BE. From this figure, it is obvious that no matter which method is employed, the BE-based ones can achieve higher accuracy. Figure 9b shows the cumulative distribution function (CDF) result for the localization accuracy by employing BE-CNN, BE-KNN, and BE-SVM. The input data were added noise with the SNR = −5 dB. Experiments were performed 30 times for each condition. Among the 30 experiments, the BE-CNN could always accurately locate the target with accuracy of 100%, which is obviously higher than 88.9%, which was the average accuracy obtained by the BE-SVM. Compared with BE-CNN, the BE-KNN could hardly locate the target when the level of noise was equal or higher than 5 dB. This demonstrates that our proposed BE-CNN outperformed the other two methods in this outdoor DFL, even when the noise was severe.
Except for the above-mentioned two baseline methods, to demonstrate the priority of the BE-CNN, we compared its performance with a deep neural network, autoencoder [44]. In this paper, we utilized the suggested architecture from [44], which achieved good classification performance. In the corresponding experiments, there were three hidden layers that had respectively 200, 100 and 50 neurons for the encoder part. Furthermore, two more methods using the same open dataset were also evaluated. One is called the sparse representation classification method with a CVXtool (SRC-CVX) [45], where the CVX is a commonly-used convex-optimization toolbox. Another one is the sparse coding method based on the iterative shrinkage-thresholding algorithm (SC-ISTA) [16]. The dataset used in the two works was the raw RSS signals without conducting the process of background elimination.
The comparison results are shown in Table 4, which were based on the noisy dataset with SNR equal to 5 dB. The localization accuracies in this table are all average results based on 30 experiments for each condition. It is obvious that the BE-CNN can achieve stably the highest localization accuracy of 100%, which outperformed all the other methods under the noisy condition.

Table 4.
Localization accuracy compared with other methods. SC-ISTA, sparse coding method based on the iterative shrinkage-thresholding algorithm.
Furthermore, to explore the impact of the different DFL system scenarios, we performed experiments by employing a lesser number of sensors. In other words, the distance between two adjacent sensors became farther. As shown in Figure 10, we compared the localization accuracy by employing 7, 8 and all 28 sensor nodes. The distance between every two adjacent sensors by employing seven and eight sensors was about 12 feet and nine feet, respectively. Note that raw data without noise and different levels of noisy data, with SNR from 5–25 dB, were employed in these experiments. In this figure, there was a tendency that with the increasing of the SNR, the accuracy went up gradually and then become stable. When seven sensor nodes were employed in the DFL system, the localization accuracy obtained by BE-CNN was 92.9%. If we increased the number of sensor to eight, the localization accuracy went up sharply to 98.9%, when the SNR was higher than 10 dB. It can be concluded that the least number of sensors in the DFL system for accurate localization was eight, and each sensor was about nine feet away from each other.
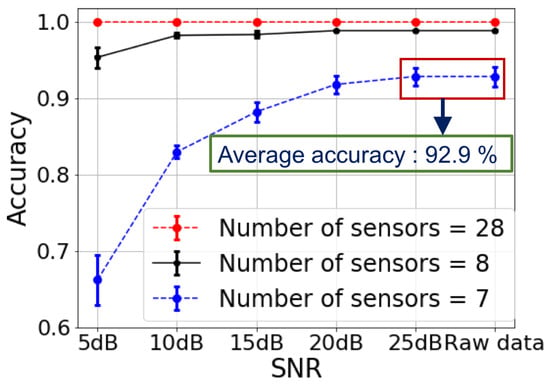
Figure 10.
Comparisons of localization accuracy by employing different numbers of sensors. Here, the distance between the adjacent sensors is 3 feet, 9 feet, and 12 feet for sensor numbers of 28, 8, and 7, respectively.
To summarize, the proposed BE-CNN scheme can maintain the highest localization accuracy of 100% when the data have a noise level of SNR greater than −5 dB, which means the proposed BE-CNN has great robustness to noisy data. The above results verify the dominance of the proposed BE-CNN on both localization accuracy and anti-noise ability.
5.4. Discussion on the Drawbacks and Future Work
(a) Regarding the drawbacks of the proposed scheme, CNN can achieve good performance by convolutional feature extraction with multiple filters of different kernel sizes. However, in some monitoring systems, if the sensor number is few, there will be some limitations in choosing the range of the kernel size. In this case, the performance of BE-CNN may decrease with the sensor number. In addition, CNN has a limited performance in processing the image signal with some outliers. However, in the DFL system, the RSS signal may contain some outliers that will result in the degradation of the localization performance of the BE-CNN scheme. (b) Future work: Therefore, considering the above-mentioned drawbacks, in the future work, we plan to exploit the DFL algorithms with more robust performance in challenging environments. Meanwhile, taking advantage of some outlier-elimination techniques, e.g., robust principal component analysis, we would like to develop a scheme that is robust to data with outliers.
6. Conclusions
Aiming at solving the problems of low accuracy and low robustness in DFL approaches, we first treated the RSS signal as an RSS-image matrix and conducted a process of eliminating the background to dig out the variation components with distinguished features. Then, we made use of these feature-rich images by formulating DFL as an image classification problem. Furthermore, a deep CNN was designed to extract features automatically for classification.
The localization performance of the BE-CNN scheme was validated with a real-world dataset of outdoor DFL. In addition, we also validated the robust performance of the proposal by conducting numerical experiments with different degrees of noise. According to the experiment results, when conducting experiments on the noiseless dataset, the BE-CNN could maintain the highest localization accuracy of 100%. For the noisy dataset, for the range of SNR from 15–−15 dB, the localization accuracies of the BE-based methods were all higher than the corresponding raw data-based methods. This demonstrates the value of BE pre-processing. In addition, the BE-CNN could maintain a high accuracy of 100% on the noisy dataset with an SNR higher than −5 dB.
In summary, the experimental results clearly demonstrated that the BE-CNN could achieve high accuracy localization results in outdoor DFL. In addition, the localization performance and robustness of the proposed approach were better than the comparison methods especially under the conditions with heavy noise. All these results demonstrated the effectiveness and the good performance of the BE-CNN in solving the DFL problem.
Author Contributions
For this article, formal analysis, L.Z. and H.H.; funding acquisition, S.D. and C.S.; methodology, L.Z. and S.D.; project administration, S.D. and C.S.; supervision, S.D. and C.S.; validation, H.H.; visualization, Z.H. and L.Z.; writing–original draft, L.Z.; writing–review & editing, X.L. and S.D.
Funding
This work was supported by the JSPS Kiban(B) (Project Number 18H03240) and the JSPS Kiban(C) (Project Number 18K11298), Japan, and in part by the National Natural Science Foundation of China (Grant Number 61803096).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Meng, W. Intrusion detection in the era of IoT: Building trust via traffic filtering and sampling. Computer 2018, 51, 36–43. [Google Scholar] [CrossRef]
- Kolias, C.; Kambourakis, G.; Stavrou, A.; Gritzalis, S. Intrusion detection in 802.11 networks: Empirical evaluation of threats and a public dataset. IEEE Commun. Surv. Tutor. 2016, 18, 184–208. [Google Scholar] [CrossRef]
- Meng, W.; Tischhauser, E.W.; Wang, Q.; Wang, Y.; Han, J. When intrusion detection meets blockchain technology: A review. IEEE Access 2018, 6, 10179–10188. [Google Scholar] [CrossRef]
- Kolias, C.; Kambourakis, G.; Maragoudakis, M. Swarm intelligence in intrusion detection: A survey. Comput. Secur. 2011, 30, 625–642. [Google Scholar] [CrossRef]
- Li, Z.; Yang, Z.; Xie, S. Computing Resource Trading for Edge-Cloud-assisted Internet of Things. IEEE Trans. Ind. Inform. 2019. [Google Scholar] [CrossRef]
- Zhao, L.; Huang, H.; Li, X.; Ding, S.; Zhao, H.; Han, Z. An Accurate and Robust Approach of Device-Free Localization with Convolutional Autoencoder. IEEE Int. Things J. 2019. [Google Scholar] [CrossRef]
- Kuutti, S.; Fallah, S.; Katsaros, K.; Dianati, M.; Mccullough, F.; Mouzakitis, A. A Survey of the State-of-the-Art Localization Techniques and Their Potentials for Autonomous Vehicle Applications. IEEE Int. Things J. 2018, 5, 829–846. [Google Scholar] [CrossRef]
- Liu, B.; Zhou, W.; Zhu, T.; Gao, L.; Luan, T.H.; Zhou, H. Silence is Golden: Enhancing Privacy of Location-Based Services by Content Broadcasting and Active Caching in Wireless Vehicular Networks. IEEE Trans. Veh. Technol. 2016, 65, 9942–9953. [Google Scholar] [CrossRef]
- Scherhäufl, M.; Pichler, M.; Stelzer, A. UHF RFID localization based on phase evaluation of passive tag arrays. IEEE Trans. Instrum. Meas. 2015, 64, 913–922. [Google Scholar] [CrossRef]
- Aly, H.; Basalamah, A.; Youssef, M. Accurate and energy-efficient GPS-less outdoor localization. ACM Trans. Spat. Algorithms Syst. (TSAS) 2017, 3, 4. [Google Scholar] [CrossRef]
- Kianoush, S.; Savazzi, S.; Vicentini, F.; Rampa, V.; Giussani, M. Device-Free RF Human Body Fall Detection and Localization in Industrial Workplaces. IEEE Int. Things J. 2017, 4, 351–362. [Google Scholar] [CrossRef]
- Huang, H.; Guo, S.; Li, P.; Miyazaki, T. Stochastic Analysis on the Deactivation-Controlled Epidemic Routing in DTNs with Multiple Sinks. Ad Hoc Sens. Wirel. Netw. 2017, 38, 143–167. [Google Scholar]
- Zafari, F.; Gkelias, A.; Leung, K. A survey of indoor localization systems and technologies. arXiv 2017, arXiv:1709.01015. [Google Scholar] [CrossRef]
- Wu, K.; Xiao, J.; Yi, Y.; Gao, M.; Ni, L.M. Fila: Fine-grained indoor localization. In Proceedings of the INFOCOM 2012, Orlando, FL, USA, 25–30 March 2012; pp. 2210–2218. [Google Scholar]
- Wang, X.; Gao, L.; Mao, S.; Pandey, S. CSI-Based Fingerprinting for Indoor Localization: A Deep Learning Approach. IEEE Trans. Veh. Technol. 2017, 66, 763–776. [Google Scholar] [CrossRef]
- Huang, H.; Zhao, H.; Li, X.; Ding, S.; Zhao, L.; Li, Z. An Accurate and Efficient Device-Free Localization Approach Based on Sparse Coding in Subspace. IEEE Access 2018, 6, 61782–61799. [Google Scholar] [CrossRef]
- Ruan, W.; Sheng, Q.Z.; Yao, L.; Li, X.; Falkner, N.J.; Yang, L. Device-free human localization and tracking with UHF passive RFID tags: A data-driven approach. J. Netw. Comput. Appl. 2018, 104, 78–96. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, X.; Wang, X.; Zhang, X. Device-Free Wireless Localization Using Artificial Neural Networks in Wireless Sensor Networks. Wirel. Commun. Mob. Comput. 2018, 2018, 4201367. [Google Scholar] [CrossRef]
- Zhao, L.; Huang, H.; Ding, S.; Li, X. An Accurate and Efficient Device-Free Localization Approach Based on Gaussian Bernoulli Restricted Boltzmann Machine. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 2323–2328. [Google Scholar]
- Woźniak, M.; Połap, D. Object detection and recognition via clustered features. Neurocomputing 2018, 320, 76–84. [Google Scholar] [CrossRef]
- Połap, D.; Winnicka, A.; Serwata, K.; Kęsik, K.; Woźniak, M. An Intelligent System for Monitoring Skin Diseases. Sensors 2018, 18, 2552. [Google Scholar] [CrossRef]
- Połap, D.; Woźniak, M.; Wei, W.; Damaševičius, R. Multi-threaded learning control mechanism for neural networks. Future Gener. Comput. Syst. 2018, 87, 16–34. [Google Scholar] [CrossRef]
- Youssef, M.; Mah, M.; Agrawala, A. Challenges: Device-free passive localization for wireless environments. In Proceedings of the 13th annual ACM International Conference on Mobile Computing and Networking, Montréal, QC, Canada, 9–14 September 2007; pp. 222–229. [Google Scholar]
- Moussa, M.; Youssef, M. Smart cevices for smart environments: Device-free passive detection in real environments. In Proceedings of the 2009 IEEE International Conference on Pervasive Computing and Communications, Galveston, TX, USA, 9–13 March 2009; pp. 1–6. [Google Scholar]
- Wilson, J.; Patwari, N. Radio tomographic imaging with wireless networks. IEEE Trans. Mob. Comput. 2010, 9, 621–632. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, Y.; Guo, X.; Ni, L.M. Rass: A real-time, accurate, and scalable system for tracking transceiver-free objects. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 996–1008. [Google Scholar] [CrossRef]
- Sabek, I.; Youssef, M.; Vasilakos, A.V. ACE: An accurate and efficient multi-entity device-free WLAN localization system. IEEE Trans. Mob. Comput. 2015, 14, 261–273. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, K.; Jiang, N.; Guo, X.; Li, Y.; Wang, G. An exponential-Rayleigh model for RSS-based device-free localization and tracking. IEEE Trans. Mob. Comput. 2015, 14, 484–494. [Google Scholar] [CrossRef]
- Seifeldin, M.; Saeed, A.; Kosba, A.E.; El-Keyi, A.; Youssef, M. Nuzzer: A large-scale device-free passive localization system for wireless environments. IEEE Trans. Mob. Comput. 2013, 12, 1321–1334. [Google Scholar] [CrossRef]
- Gao, Q.; Wang, J.; Ma, X.; Feng, X.; Wang, H. CSI-Based Device-Free Wireless Localization and Activity Recognition Using Radio Image Features. IEEE Trans. Veh. Technol. 2017, 66, 10346–10356. [Google Scholar] [CrossRef]
- Liang, J.; Wang, D.; Su, L.; Chen, B.; Chen, H.; So, H.C. Robust MIMO radar target localization via nonconvex optimization. Signal Process. 2016, 122, 33–38. [Google Scholar] [CrossRef]
- Hong, J.; Ohtsuki, T. Signal eigenvector-based device-free passive localization using array sensor. IEEE Trans. Veh. Technol. 2015, 64, 1354–1363. [Google Scholar] [CrossRef]
- Zhou, R.; Lu, X.; Zhao, P.; Chen, J. Device-Free Presence Detection and Localization With SVM and CSI Fingerprinting. IEEE Sens. J. 2017, 17, 7990–7999. [Google Scholar] [CrossRef]
- Tran, D.A.; Gong, S.; Vo, Q. Geometric-based KNN localization using sensor dissimilarity information. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017; pp. 1–6. [Google Scholar]
- Zheng, K.; Wang, H.; Li, H.; Xiang, W.; Lei, L.; Qiao, J.; Shen, X.S. Energy-efficient localization and tracking of mobile devices in wireless sensor networks. IEEE Trans. Veh. Technol. 2017, 66, 2714–2726. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.; Gao, Q.; Yue, H.; Wang, H. Device-Free Wireless Localization and Activity Recognition: A Deep Learning Approach. IEEE Trans. Veh. Technol. 2017, 66, 6258–6267. [Google Scholar] [CrossRef]
- Zhou, R.; Hao, M.; Lu, X.; Tang, M.; Fu, Y. Device-Free Localization Based on CSI Fingerprints and Deep Neural Networks. In Proceedings of the 2018 15th Annual IEEE International Conference on Sensing, Communication, and Networking (SECON), Hong Kong, China, 11–13 June 2018; pp. 1–9. [Google Scholar]
- Huang, H.; Lin, S. WiDet: Wi-Fi Based Device-Free Passive Person Detection with Deep Convolutional Neural Networks. In Proceedings of the 21st ACM International Conference on Modeling, Analysis and Simulation of Wireless and Mobile Systems, Montreal, QC, Canada, 28 October–2 November 2018; pp. 53–60. [Google Scholar]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Springenberg, J.T.; Dosovitskiy, A.; Brox, T.; Riedmiller, M. Striving for simplicity: The all convolutional net. arXiv 2014, arXiv:1412.6806. [Google Scholar]
- Heckerman, D.; Meek, C. Models and Selection Criteria for Regression and Classification; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1997. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Seyfioğlu, M.S.; Özbayğglu, A.M.; Gurbuz, S.Z. Deep convolutional autoencoder for radar-based classification of similar aided and unaided human activities. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1709–1723. [Google Scholar] [CrossRef]
- Wang, D.; Guo, X.; Zou, Y. Accurate and robust device-free localization approach via sparse representation in presence of noise and outliers. In Proceedings of the 2016 IEEE International Conference on Digital Signal Processing (DSP), Beijing, China, 16–18 October 2016; pp. 199–203. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).