Effect of Quantum Gravity on the Stability of Black Holes
Abstract
1. Introduction
2. 4-Dimension Gauged Super-Gravity Black Holes
3. 5-Dimension Gauged Super-Gravity Black Holes
4. 7-Dimension Black Holes in Theory of Gauged Super-Gravity
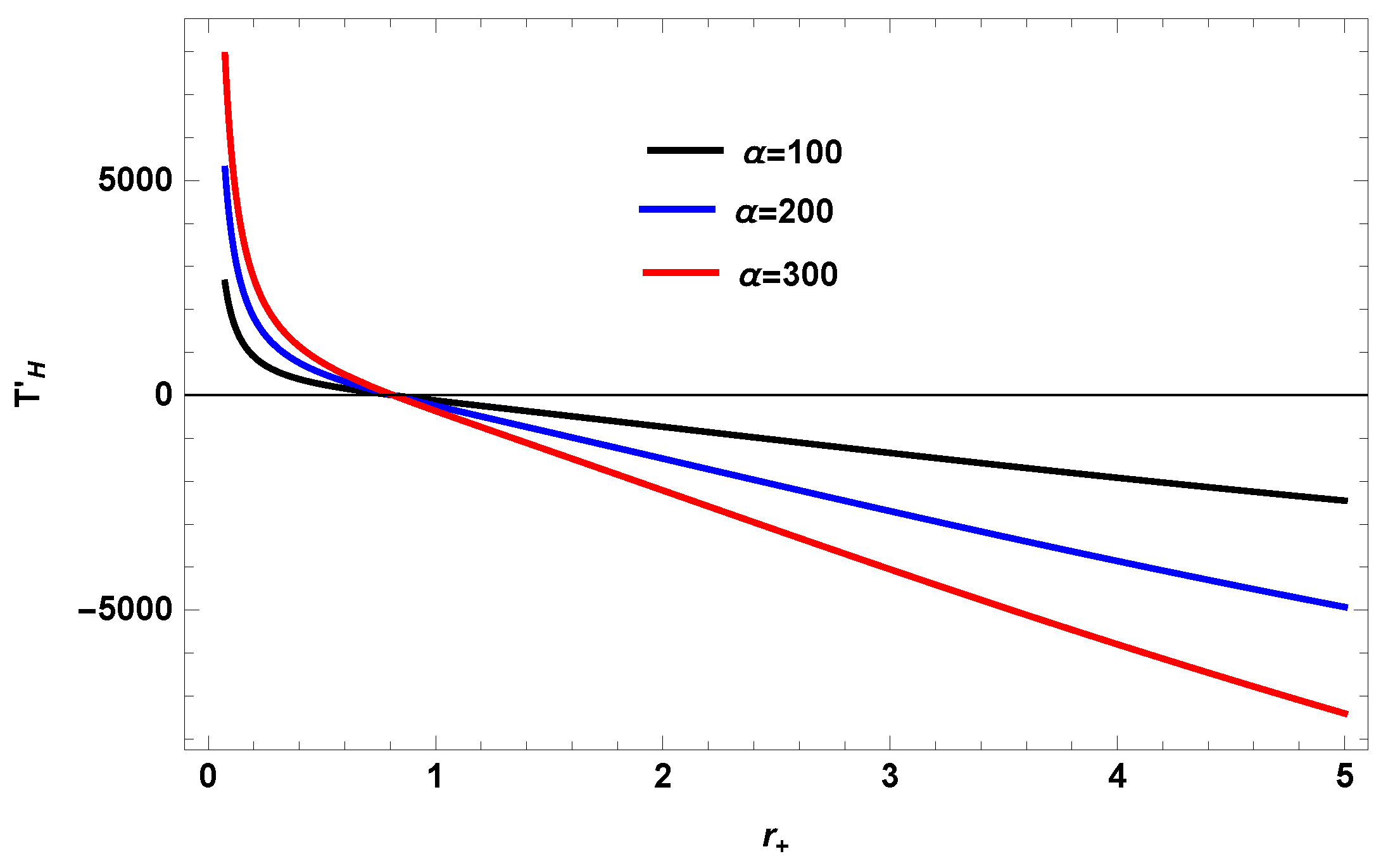
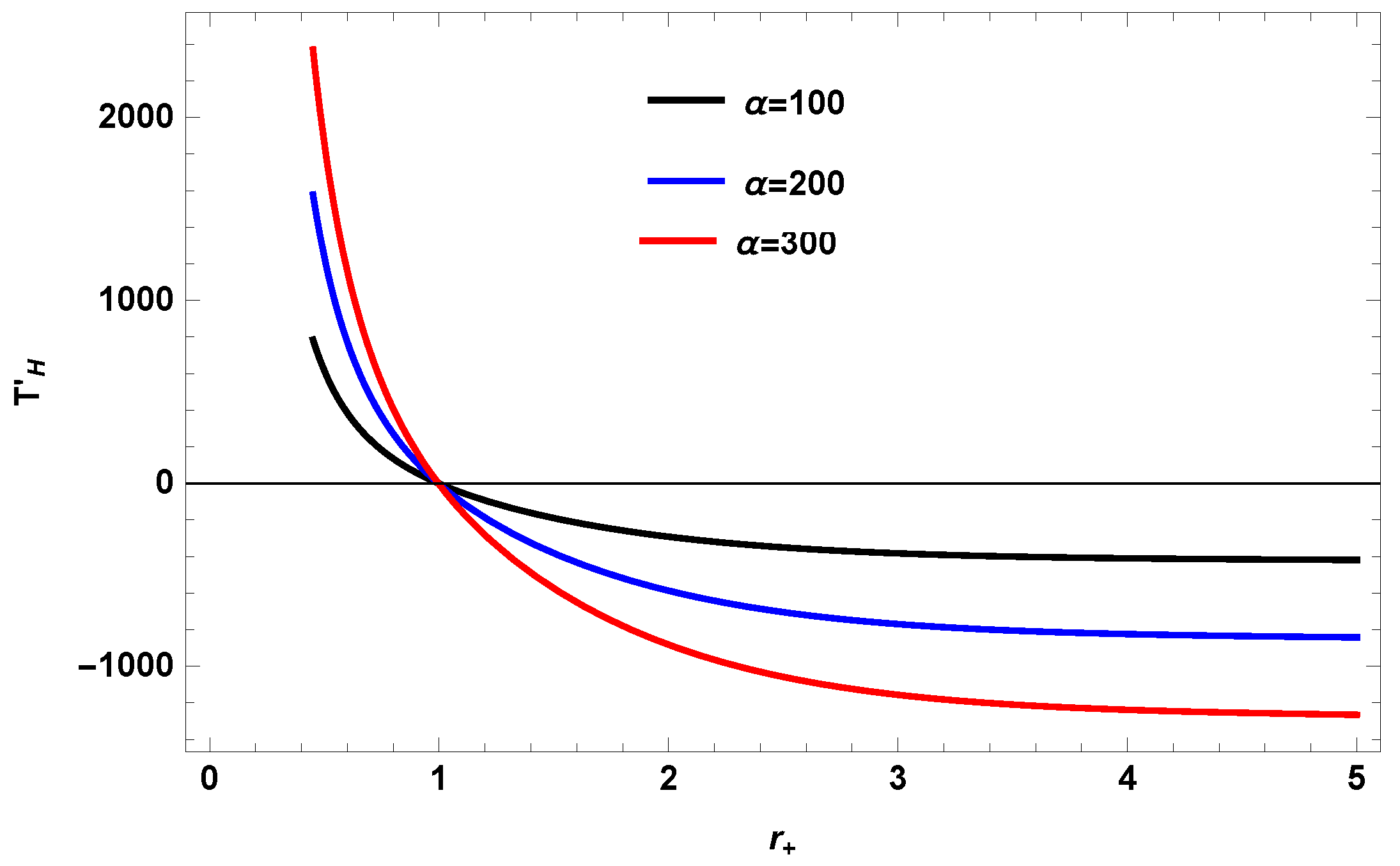
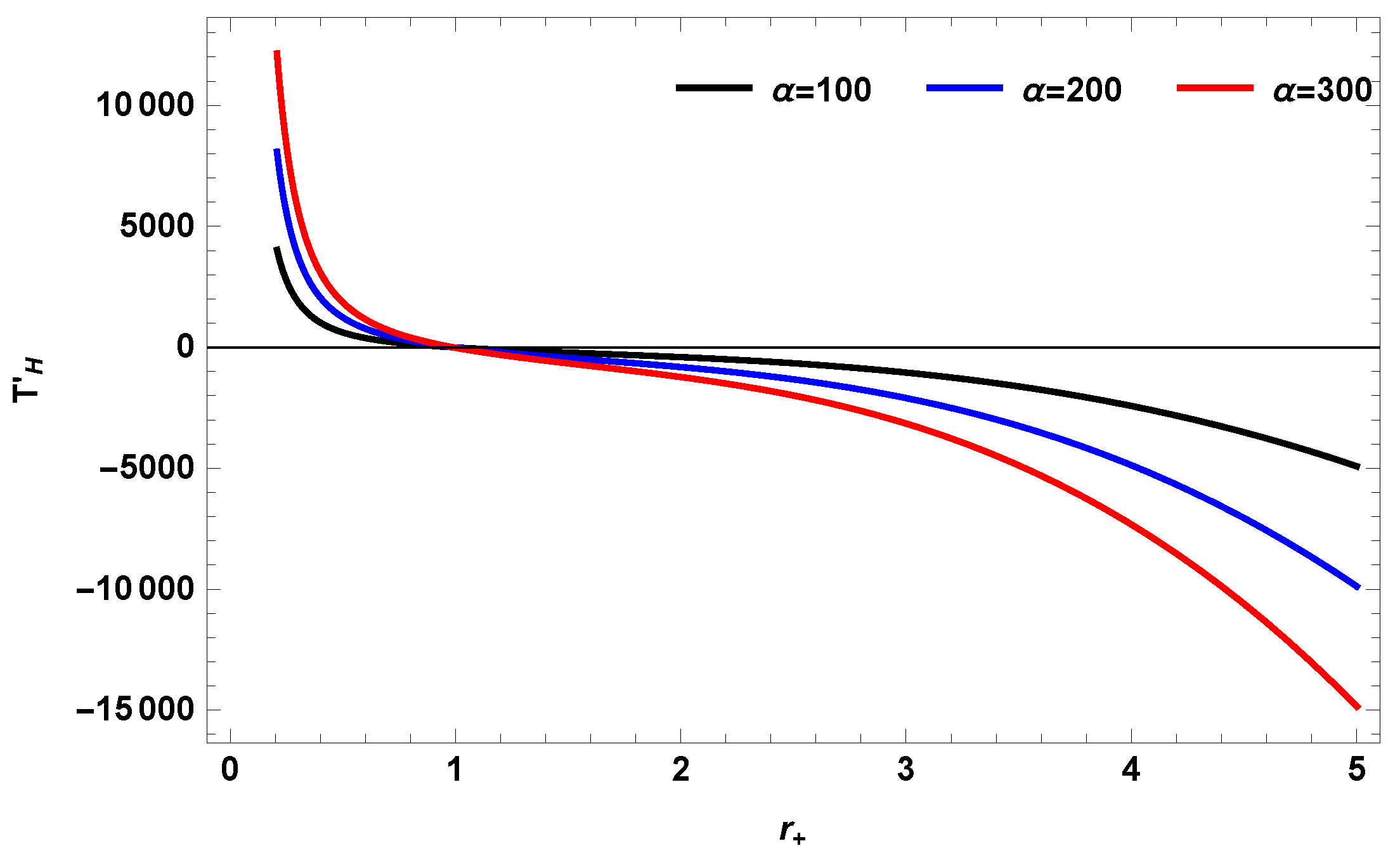
5. Graphical Analysis
Versus
6. Conclusions and Discussion
- In the presence of charges, the BH was initially stable and attained a stability in a small domain and then becomes unstable till .
- The 4D, 5D and 7D BHs remained stable and unstable in quantum gravity minima and maxima respectively.
- The 4D, 5D and 7D BHs in the theory of gauged super-gravity remains unstable in the presence of the charge and correction parameter .
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Akhmedov, E.T.; Akhmedova, V.; Singleton, D.; Pilling, T. Thermal radiation of various gravitational backgrounds. Int. J. Mod. Phys. A 2007, 22, 1705–1715. [Google Scholar] [CrossRef]
- Chowdhury, B.D. Problems with tunneling of thin shells from black holes. Pramana 2008, 70, 3–26. [Google Scholar] [CrossRef]
- Jiang, Q.Q. Dirac particle tunneling from black rings. Phys. Rev. D 2008, 78, 044009. [Google Scholar] [CrossRef]
- Akhmedov, E.T.; Pilling, T.; Singleton, D. Subtleties in the quasiclassical calculation of Hawking radiation. Int. J. Mod. Phys. D 2008, 17, 2453–2458. [Google Scholar] [CrossRef]
- Akhmedova, V.; Pilling, T.; Gill, A.D.; Singleton, D. Temporal contribution to gravitational WKB-like calculations. Phys. Lett. B 2008, 666, 269–271. [Google Scholar] [CrossRef]
- Akhmedova, V.; Pilling, T.; Gill, A.D.; Singleton, D. Comments on anomaly versus WKB/tunneling methods for calculating Unruh radiation. Phys. Lett. B 2009, 673, 227–231. [Google Scholar] [CrossRef]
- Ali, A.F.; Das, S.; Vagenas, E.C. Discreteness of Space from the Generalized Uncertainty Principle. Phys. Lett. B 2009, 678, 497–499. [Google Scholar] [CrossRef]
- Corda, C. Interferometric detection of gravitational waves: The definitive test for General Relativity. Int. J. Mod. Phys. D 2009, 18, 2275–2282. [Google Scholar] [CrossRef]
- Singleton, D.; Vagenas, E.C.; Zhu, T.; Ren, J.R. Insights and possible resolution to the information loss paradox via the tunneling picture. JHEP 2010, 1008, 089. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: from F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Capozziello, S.; Laurentis, M.D. Extended Theories of Gravity. Phys. Rept. 2011, 509, 167. [Google Scholar] [CrossRef]
- Valerio, F.; Salvatore, C. Beyond Einstein Gravity: A survey of Gravitational Theories for Cosmology and Astrophysics; Fundamental Theories of Physics; Spring: New York, NY, USA, 2011. [Google Scholar]
- Yale, A. Exact Hawking Radiation of Scalars, Fermions, and Bosons Using the Tunneling Method without Back-Reaction. Phys. Lett. B 2011, 697, 398–403. [Google Scholar] [CrossRef]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155–228. [Google Scholar] [CrossRef]
- Sharif, M.; Javed, W. Fermion tunneling for traversable wormholes. Can. J. Phys. 2013, 91, 43–47. [Google Scholar] [CrossRef]
- Corda, C.; Hendi, S.H.; Katebi, R.; Schmidt, N.O. Effective state, Hawking radiation and quasi-normal modes for Kerr black holes. JHEP 2013, 6, 8. [Google Scholar] [CrossRef]
- Jan, K.; Gohar, H. Hawking radiation of scalars from accelerating and rotating black hole with NUT parameter. Astrophys. Space Sci. 2014, 350, 279–284. [Google Scholar] [CrossRef]
- Kruglov, S.I. Black hole emission of vector particles in (1+1) dimensions. Int. J. Mod. Phys. A 2014, 29, 1450118. [Google Scholar] [CrossRef]
- Matsumoto, M.; Yoshino, H.; Kodama, H. Time evolution of a thin black ring via Hawking radiation. Phys. Rev. D 2014, 89, 044016. [Google Scholar] [CrossRef]
- Li, X.Q.; Chen, G.R. Massive vector particles tunneling from Kerr and Kerr-Newman black holes. Phys. Lett. B 2015, 751, 34–38. [Google Scholar] [CrossRef]
- Corda, C. Precise model of Hawking radiation from the tunnelling mechanism. Class. Quantum Grav. 2015, 32, 195007. [Google Scholar] [CrossRef]
- Anacleto, M.A.; Brito, F.A.; Luna, G.C.; Passos, E.; Spinelly, J. Quantum-corrected finite entropy of noncommutative acoustic balck holes. Annals Phys. 2015, 362, 436. [Google Scholar] [CrossRef][Green Version]
- Lin, H.; Saifullah, K.; Yau, S.T. Accelerating black hole, spin- fields and C-metric. Mod. Phys. Lett. A 2015, 30, 1550044. [Google Scholar] [CrossRef]
- Chen, G.R.; Huang, Y.C. Hawking radiation of vector particles as tunneling from the apparent horizon of Vaidya black holes. Int. J. Mod. Phys. A 2015, 30, 1550083. [Google Scholar] [CrossRef]
- Anacleto, M.A.; Brito, F.A.; Passos, E. Quantum-corrected self-dual black hole entropy in tunneling formalism with GUP. Phys. Lett. B 2015, 749, 181–186. [Google Scholar] [CrossRef]
- Lin, G.; Zu, X. Scalar Particles Tunneling and Effect of Quantum Gravity. J. Appl. Math. Phys. 2015, 3, 134–139. [Google Scholar]
- Feng, Z.; Chen, Y.; Zu, X. Hawking radiation of vector particles via tunneling from 4-dimensional and 5-dimensional black holes. Astrophys. Space Sci. 2015, 359, 48. [Google Scholar] [CrossRef]
- Saleh, M.; Thomas, B.B.; Kofane, T.C. Hawking radiation from a five-dimensional Lovelock black hole. Front. Phys. 2015, 10, 100401. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D. Inflationary Cosmology in Modified Gravity Theories. Symmetry 2015, 7, 220–240. [Google Scholar] [CrossRef]
- Övgun, A.; Jusufi, K. Massive Vector Particles Tunneling From Noncommutative Charged Black Holes and its GUP-corrected Thermodynamics. Eur. Phys. J. Plus 2016, 131, 177. [Google Scholar] [CrossRef]
- Jusufi, K.; Övgun, A. Hawking Radiation of Scalar and Vector Particles From 5D Myers-Perry Balck Holes. Int. J. Theor. Phys. 2017, 56, 1725. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; Laurentis, M.D.; Saridakis, E.N. f(T) teleparallel gravity and cosmology. Rept. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef] [PubMed]
- Singh, T.I.; Meitei, I.A.; Singh, K.Y. Hawking radiation as tunneling of vector particles from Kerr-Newman black hole. Astrophys. Space Sci. 2016, 361, 103. [Google Scholar] [CrossRef]
- Jusufi, K.; Övgun, A. Tunneling of Massive Vector Particles From Rotating Charged Black Strings. Astrophys. Space Sci. 2016, 361, 207. [Google Scholar] [CrossRef]
- Li, R.; Zhao, J.K. Massive Vector Particles Tunneling from the Neutral Rotating Anti-di Sitter Black Holes in Conformal Gravity. Commun. Theor. Phys. 2016, 65, 469–472. [Google Scholar] [CrossRef]
- Ghrsel, H.; Sakalli, I. Hawking Radiation of Massive Vector Particles From Warped AdS3 Black Hole. Can. J. Phys. 2016, 94, 147–149. [Google Scholar] [CrossRef]
- Li, X.Q. Massive vector particles tunneling from black holes influenced by the generalized uncertainty principle. Phys. Lett. B 2016, 763, 80–86. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2011, 692, 1–104. [Google Scholar] [CrossRef]
- Corda, C. The future of gravitational theories in the era of the gravitational wave astronomy. Int. J. Mod. Phys. D 2018, 27, 1850060. [Google Scholar] [CrossRef]
- Javed, W.; Ali, R.; Abbas, G. Charged Vector Particles Tunneling From Black Ring and 5D Black Hole. Can. J. Phys. 2019, 97, 176–186. [Google Scholar] [CrossRef]
- Cvetič, M.; Gubser, S.S. Phases of R-charged Black Holes, Spinning Branes and Strongly Coupled Gauge Theories. JHEP 1999, 9904, 024. [Google Scholar] [CrossRef]
- Behrndt, K.; Cvetic, M.; Sabra, W.A. Non-Extreme Black Holes of Five Dimensional N=2 AdS Supergravity. Nucl. Phys. B 1999, 553, 317–332. [Google Scholar] [CrossRef]
- Javed, W.; Abbas, G.; Ali, R. Charged vector particle tunneling from a pair of accelerating and rotating and 5D gauged super-gravity black holes. Eur. Phys. J. C 2017, 77, 296. [Google Scholar] [CrossRef]
- Shivalingaswamy, T.; Kagali, B.A. Eigenenergies of a Relativistic Particle in an Infinite Range Linear Potential Using WKB Method. Eur. J. Phys. Educ. 2011, 2, 1309. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, R.; Bamba, K.; Shah, S.A.A. Effect of Quantum Gravity on the Stability of Black Holes. Symmetry 2019, 11, 631. https://doi.org/10.3390/sym11050631
Ali R, Bamba K, Shah SAA. Effect of Quantum Gravity on the Stability of Black Holes. Symmetry. 2019; 11(5):631. https://doi.org/10.3390/sym11050631
Chicago/Turabian StyleAli, Riasat, Kazuharu Bamba, and Syed Asif Ali Shah. 2019. "Effect of Quantum Gravity on the Stability of Black Holes" Symmetry 11, no. 5: 631. https://doi.org/10.3390/sym11050631
APA StyleAli, R., Bamba, K., & Shah, S. A. A. (2019). Effect of Quantum Gravity on the Stability of Black Holes. Symmetry, 11(5), 631. https://doi.org/10.3390/sym11050631






