Quantum-Resistant Identity-Based Signature with Message Recovery and Proxy Delegation

Abstract

Digital signature with proxy delegation, which is a secure ownership enforcement tool, allows an original signer to delegate signature rights to a third party called proxy, so that the proxy can sign messages on behalf of the original signer. Many real-world applications make use of this secure mechanism, e.g., digital property transfer. A traditional digital signature mechanism is required to bind a message and its signature together for verification. This may yield extra cost in bandwidth while the sizes of message and signature are relatively huge. Message recovery signature, enabling to reduce the cost of bandwidth, embeds a message into the corresponding signature; therefore, only the signature will be transmitted to the verifier and the message can further be recovered from the signature. In this paper, we, for the first time, propose a novel digital signature scheme in the identity-based context with proxy delegation and message recovery features and, more importantly, our scheme is quantum resistant, in a particular lattice-based signature. Our scheme achieves delegation information and signature existential unforgeability against adaptive chosen warrant and identity. Compared with the seminal lattice-based message recovery signature, our scheme is independent from public key infrastructure, realizes delegation transfer of signature rights, and compresses signature length ulteriorly. To the best of our knowledge, this paper is the first of its type.

1. Introduction

Digital signature aims at message authenticity, which can be verified by everyone with a message/signature pair. Considering the practical application, a digital signature also needs to have special properties for special functionality requirements, such as signature with delegation functionality—proxy signature. Proxy signature, which was first proposed by Mambo [1], allows an original signer to delegate his signing right to a proxy signer, so that the proxy signer can sign a message on behalf of the original signer. Proxy signature is suitable for the case where the original signer is temporarily absent so that the proxy is delegated to make a signature on behalf of the original signer. It has many real-world applications (e.g., digital property transfer) and practical variants in the literature (e.g., [2]). We note that there have been some research works by far related to proxy delegation, such as [3,4,5,6,7,8,9], in which they focus on decryption delegation. This paper deals with signature delegation.

Message recovery signature is a kind of digital signature with message recovery property, and was first proposed by Nyberg and Rueppel in [10]. Compared with the traditional digital signature, a message can be embedded into the signature. As a result, only the signature itself is required in the verification stage instead of the message and signature pair in the traditional version. It reduces the amount of information to be transmitted, and thus can save the transmission bandwidth dramatically.

Combining a message recovery signature and a proxy signature, a proxy signature with message recovery emerges, which owns a hidden message and the functionality of signing right delegation transfer. Furthermore, in order to simplify key management, Singh [11] combined identity-based signature with proxy signature with message recovery, and introduced the concept of identity-based proxy signature scheme with message recovery. Such scheme can work without the existence of public key infrastructure, and the legitimacy of the user’s public key is not required to be verified.

1.1. Related Work

Many researchers have paid attention to proxy signature with message recovery, and a lot of contributions [12,13,14,15,16] have been proposed in the literature. The schemes introduced in [12,13,15,16] are based on a discrete logarithm problem, the one proposed in [14] is based on a decisional Diffie–Hellman problem and a computational Diffie-Hellman problem. However, all these problems are solvable with a quantum computer [17], so that security of schemes [12,13,14,15,16] will be unreliable in the quantum era, and it is significant to construct a quantum-resistible proxy signature with message recovery.

Lattice-based cryptography is an excellent branch of post-quantum cryptography. For almost two decades, lattice-based cryptography has been on the fast track of development. Some unsolved questions in traditional cryptography, such as construction of a fully homomorphic encryption scheme [18], have found their realization in lattice-based cryptography. Due to a reliable security guarantee and powerful functionality, lattice-based cryptography becomes the preferred tool for our topic—an identity-based proxy signature scheme with message recovery.

Lattice signature is the building foundation of our topic. In 2008, Gentry et al. [19] designed the first provably secure lattice signature scheme. In 2012, Micciancio et al. [20] proposed a new trapdoor generation algorithm and gave a lattice signature scheme with better efficiency and security. In the same year, Lyubashevsky [21] gave a lattice signature scheme with better efficiency following a special lattice with simpler computations. In 2014, Bai et al. [22] proposed an improved compression technique for lattice signature in [21]. Lattice signatures in [19,20] and [21,22] are two main frames for lattice signature schemes, and the latter is with better performance.

Lattice signature schemes [19,20,21,22] are all basic signature schemes. We will consider message recovery and delegation of signing right in identity-based environment. In 2013, Tian et al. [23] proposed lattice-based message recovery signature scheme following [21]. His scheme is based on public key infrastructure without expressing delegation of signing rights. In 2016, Wang Li [24] proposed an identity-based proxy signature scheme in lattice, which follows the idea of [19] and doesn’t hide messages. In 2017, Faguo Wu et al. [25] gave a lattice proxy signature with message recovery based on public key infrastructure.

1.2. Our Contribution

In this paper, we build an efficient and secure identity-based proxy signature scheme with message recovery in lattice-based cryptography. Our scheme is based on the lattice signature without trapdoors [21]. Inspired by the signature compression technique in [22], we introduce the random error matrix $E_{id}$ with enough small entries, let $\left(A\right|I)\left(\begin{array}{c}{S}_{id}\\ E_{id}\end{array}\right)=A{S}_{id}+E_{id}=H_1\left(id\right)$. According to the learning with errors problem, we keep $S_{id}$ instead of $(S_{id},E_{id})$, as the secret key of user $id$. Correspondingly, the signature is $S_{id}c+y$ rather than $(S_{id}c+y,E_{id}c+y)$ in our scheme. These operations add more randomness to user secret key extraction, and reduce signature length with $E_{id}c+y$.

For proxy signature, we change the traditional idea that the original signer generates the delegated secret key and passes it to the proxy signer through the secure channel. Following the idea of two-party signature in [26], our delegated secret key is obtained with the help of proxy signer’s secret key and original signer’s public delegation information. Therefore, delegated secret key extraction is controlled by the proxy signer and original signer, and no secure channel is required between them. Moreover, anyone can verify the validity of delegation information because it is public.

Speaking of message recovery, we adopt the technique in [23]. Compared with the scheme in [23], our scheme takes the following three advantages. Firstly, our scheme is identity-based and does not rely on public key infrastructure maintenance. Secondly, our scheme realizes delegation transfer of signing rights. Thirdly, our scheme condenses signature length. The comparing details of two schemes are described in Section 5.

In addition, we divide the security definition in [11] into two factors: delegation information existential unforgeability against adaptive chosen warrant and identity, signature existential unforgeability against adaptive chosen message and identity. The former guarantees delegation information is credible, and the latter guarantees that proxy signature is credible. Our security definition is more comprehensive.

The rest of the paper is organized as follows. We present an overview of background knowledge in Section 2. Then, we propose our model and security definitions for an identity-based proxy signature scheme with message recovery in Section 3. In Section 4, we provide the identity-based proxy signature scheme with message recovery in lattice-based cryptography. Correctness, security, and performance analysis are discussed in Section 5. Finally, we conclude this paper in Section 6.

2. Preliminaries

2.1. Notations

$\mathbb{Z}$ is the set of integers, and $\mathbb{N}$ is the set of natural numbers. Let q be a polynomial-size prime number, ${\mathbb{Z}}_q$ is the set of integers in $(-q/2,q/2]$. For $a\in \mathbb{Z}$ and $d\in \mathbb{N}$, ${\left[a\right]}_{2^d}\in (-2^{d-1},2^{d-1}]$ is the unique integer satisfying $a\equiv {\left[a\right]}_{2^d}\left(mod{2}^d\right)$, $\lfloor a_d\rceil =\left(a-{\left[a\right]}_{2^d}\right)/2^d$. For $e\in {\mathbb{Z}}^m$, $e_{\left(i\right)}$ is the i-th entry of e, $∥e∥={∥e∥}_2=\sqrt{{\displaystyle \sum _{i=1}^m}{e}_{\left(i\right)}^2}$ is the Euclidean norm of e, and ${‖e‖}_{\infty }={max}_{1\le i\le m}\left|e_{\left(i\right)}\right|$. For matrix $T\in {\mathbb{Z}}^{m\times n}$, $T(i,j)$ is the entry in i-th row and j-th column, $∥T∥$ is the largest Euclidean norm of its column vectors, and $\tilde{T}$ is its Gram–Schmidt orthogonalization. If $s_1$ and $s_2$ are two bit strings, $s_1\Vert s_2$ is their concatenation, $s_1\oplus s_2$ is the result of xor computation. In addition, ${\left|s_1\right|}^{l_1}$ is the prefix of $s_1$ with length $l_1$, ${\left|s_1\right|}_{l_2}$ is the suffix of $s_1$ with length $l_2$.

2.2. Lattice Theory

In this subsection, basic concepts and major algorithms related to our scheme are illustrated. For readers who are interested in details, please see literature [19,27,28].

Definition 1.

Algorithm TrapGen $\left(q,m\right)$, with $m\ge 5nlogq$, outputs a pair $\left(A,T\right)$ which satisfies the following conditions: 1. $A\in {\mathbb{Z}}_q^{n\times m}$ follows uniform distribution with overwhelming probability; 2. $T\in {\mathbb{Z}}^{m\times m}$, $\Vert T\Vert \le O(nlogq)$ and $\Vert \tilde{T}\Vert \le O\left(\sqrt{nlogq}\right)$ 3. $AT=0\left(modq\right)$

Definition 2.

${\mathbb{D}}_{\sigma }$ is a discrete Gaussian distribution on $\mathbb{Z}$, with center 0 and standard deviation σ. ${\mathbb{D}}_{\sigma }^{m\times n}$ is a matrix with m rows and n columns, and every entry in the matrix follows the distribution ${\mathbb{D}}_{\sigma }$.

Definition 3.

For $A\in {\mathbb{Z}}_q^{n\times m}$, a short basis T of ${\mathsf{\Lambda }}_q^{\perp }\left(A\right)$, $u\in {\mathbb{Z}}_q^n$, and Gaussian parameter $\sigma \ge ∥\tilde{T}∥·\omega \left(\sqrt{logm}\right)$, algorithm SamplePre $\left(A,T,u,\sigma \right)$ outputs some $e\in {\mathbb{Z}}^m$ such that $\Vert e\Vert \le \sigma \sqrt{m}$ and $Ae=u\left(modq\right)$.

Definition 4.

Given a uniform random matrix $A\in {\mathbb{Z}}_q^{n\times m}$, the small integer solution (SIS) problem is to find a short vector $v\in {\mathbb{Z}}^m$, such that $Av=0\left(modq\right)$ and $\Vert v\Vert \le \beta$ for some appropriate parameter β.

Definition 5.

Given a pair $\left(A,A^{\top }s+e\right)$, where $A\in {\mathbb{Z}}_q^{n\times m}$ follows uniform distribution with overwhelming probability, $s\leftarrow {\mathbb{D}}_{\sigma }^n$, $e\leftarrow {\mathbb{D}}_{\sigma }^m$ for appropriate parameter σ, the learning with errors (LWE) problem is to find s.

With appropriate parameters, LWE and SIS problems are notably hard average problems in lattice theory, and they are the security basis of most cryptographic systems in lattice.

3. Identity-Based Proxy Signature with Message Recovery

Our model and security definitions for an identity-based proxy signature scheme with message recovery (IDPSWM) come from the literature [11], and two adjustments are made.

• In our model, the delegation information is public, everyone may verify its legality; whereas, in [11], the delegation information is sent to the proxy signer secretly, and only the proxy signer can verify its legality. Therefore, a secure channel is unnecessary to transmit delegation information in our model, and every user can verify delegation information legality.
• To make it easier to understand, we divide scheme security into two factors: delegation information existential unforgeability against adaptive chosen warrant and identity (EUF-ID-CWA), signature existential unforgeability against adaptive chosen message and identity (EUF-ID-CMA). EUF-ID-CWA security assures that delegation information is believable. EUF-ID-CMA security assures that signature is believable.

3.1. Our Model

There are three types of users: the original signer, the proxy signer, and the verifier, as well as a private key generator (PKG) in the system; their roles are as follows:

• $Setup\left(n\right)$: PKG inputs the security parameter n, outputs system public parameters $params$ and the system secret master key $msk$.
• $KeyExtract\left(msk,id\right)$: Given an identity $id$, PKG makes use of the system secret master key $msk$ and provides the secret key $s{k}_{id}$ for the identity $id$.
• $DelGen\left(s{k}_{i{d}_O},i{d}_P,w\right)$: The original signer $i{d}_O$ inputs his secret key $s{k}_{i{d}_O}$, and the warrant w associated with proxy signer $i{d}_P$, computes the delegation $W_{O\to P}$, and publishes delegation information $d_g=(i{d}_O,i{d}_P,w,W_{O\to P})$ to all system users.
• $DelVer\left(d_g=(i{d}_O,i{d}_P,w,W_{O\to P})\right)$: For arbitrary system users, he verifies the legality of delegation information $d_g=(i{d}_O,i{d}_P,w,W_{O\to P})$. If it is legal, the output is 1, the delegation is accepted; otherwise, the output is 0, and the delegation is rejected.
• $PkeyGen\left(s{k}_{i{d}_P},d_g=(i{d}_O,i{d}_P,w,W_{O\to P})\right)$: The proxy signer $i{d}_P$ verifies whether the delegation information $d_g=(i{d}_O,i{d}_P,w,W_{O\to P})$ is valid. If it is invalid, he rejects this delegation. Otherwise, he inputs his secret key $s{k}_{i{d}_P}$ and the delegation information $d_g=(i{d}_O,i{d}_P,w,W_{O\to P})$, outputs the delegated secret key $s{k}_{O,P,w}$.
• $PSign\left(s{k}_{O,P,w},\varpi \right)$: The proxy signer $i{d}_P$ inputs his delegated secret key $s{k}_{O,P,w}$ and the message $\varpi$, outputs the proxy signature $\varsigma$.
• $PVer\left(d_g=(i{d}_O,i{d}_P,w,W_{O\to P}),\varsigma \right)$: For arbitrary system users, he first recovers the message $\varpi$ associated with signature $\varsigma$, and then verifies the legality of the message/ signature pair $\left(\varpi ,\varsigma \right)$ with regard to $d_g=(i{d}_O,i{d}_P,w,W_{O\to P})$. If it is legal, the output is 1, the message is accepted; otherwise, the output is 0, and the message is rejected.

As to scheme correctness, seven algorithms should satisfy the following rules: For every security parameter n, $\left(params,msk\right)\leftarrow Setup\left(n\right)$, $s{k}_{id}\leftarrow KeyExtract\left(msk,id\right)$, $d_g=(i{d}_O,i{d}_P,w,W_{O\to P})\leftarrow DelGen\left(s{k}_{i{d}_O},i{d}_P,w\right)$, $s{k}_{O,P,w}$$\leftarrow PkeyGen$$\left(s{k}_{i{d}_P},d_g=(i{d}_O,i{d}_P,w,W_{O\to P})\right)$, $\varsigma \leftarrow PSign\left(s{k}_{O,P,w},\varpi \right)$, the probability of $1\leftarrow PVer\left(d_g=(i{d}_O,i{d}_P,w,W_{O\to P}),\varsigma \right)$ is overwhelming.

3.2. Security Definitions

Scheme security includes two factors: delegation information existential unforgeability against adaptive chosen warrant and identity (EUF-ID-CWA), signature existential unforgeability against adaptive chosen message and identity (EUF-ID-CMA).

3.2.1. EUF-ID-CWA

EUF-ID-CWA security is described by the next game between a challenger $\mathcal{C}$ and a forger $\mathcal{F}$.

• Initial Phase: The challenger $\mathcal{C}$ runs $Setup$ algorithm to get system public parameters $params$ and the system secret master key $msk$. $\mathcal{C}$ returns $params$ to the forger $\mathcal{F}$ and keeps $msk$ himself.
• Query Phase: The forger $\mathcal{F}$ makes the following queries adaptively with a polynomial bounded number, and the challenger $\mathcal{C}$ has the obligation to make reasonable answers.
  1. $KeyExtract\left(id\right)$: $\mathcal{F}$ selects a user identity $id$, sends it to the challenger $\mathcal{C}$. $\mathcal{C}$ invokes algorithm $KeyExtract\left(msk,id\right)$ to get the associated secret key $s{k}_{id}$. Then, $\mathcal{C}$ returns $s{k}_{id}$ to $\mathcal{F}$.
  2. $DelGen\left(i{d}_O,i{d}_P,w\right)$: $\mathcal{F}$ selects the original signer $i{d}_O$, the proxy signer $i{d}_P$, and the warrant w, and sends all of them to the challenger $\mathcal{C}$. $\mathcal{C}$ executes $KeyExtract\left(i{d}_O\right)$ query to get the associated secret key $s{k}_{i{d}_O}$, and then invokes algorithm $DelGen(s{k}_{i{d}_O},i{d}_p,w)$ to get $W_{O\to P}$ and returns it to $\mathcal{F}$.
• Forge Phase: The forger $\mathcal{F}$ gives his forgery $\left(d_g=(i{d}_O,i{d}_P,w,W_{O\to P})\right)$. If the following conditions are satisfied: $DelVer\left(d_g=(i{d}_O,i{d}_P,w,W_{O\to P})\right)=1$, $i{d}_O$ doesn’t occur in the $KeyExtract$ query, $\left(i{d}_O,i{d}_P,w\right)$ doesn’t occur in the $DelGen$ query, and his attack is successful.

Let ${\epsilon }_1$ be the success probability of $\mathcal{F}$ in this game.

Definition 6.

An identity-based proxy signature scheme with message recovery (IDPSWM) is delegation information existentially unforgeable against adaptive chosen warrant and identity (EUF-ID-CWA), if for every polynomial time forger $\mathcal{F}$, ${\epsilon }_1$ is negligible.

3.2.2. EUF-ID-CMA

EUF-ID-CMA security is demonstrated by the following game between a challenger $\mathcal{C}$ and a forger $\mathcal{F}$.

• Initial Phase: The challenger $\mathcal{C}$ runs the $Setup$ algorithm to get system public parameters $params$ and the system secret master key $msk$. $\mathcal{C}$ returns $params$ to the forger $\mathcal{F}$ and keeps $msk$ secret.
• Query Phase: The forger $\mathcal{F}$ executes the following queries adaptively with a polynomial bounded number, and the challenger $\mathcal{C}$ has to return reasonable answers.
  1. $KeyExtract\left(id\right)$: $\mathcal{F}$ selects a user identity $id$ and sends it to the challenger $\mathcal{C}$. $\mathcal{C}$ invokes algorithm $KeyExtract\left(msk,id\right)$ to get secret key $s{k}_{id}$. Then, $\mathcal{C}$ returns $s{k}_{id}$ to $\mathcal{F}$.
  2.$DelGen(i{d}_O,i{d}_p,w)$: $\mathcal{F}$ selects the original signer $i{d}_O$, the proxy signer $i{d}_P$, and the warrant w, submits them to the challenger $\mathcal{C}$. $\mathcal{C}$ executes $KeyExtract\left(i{d}_0\right)$ query to get the associated secret $s{k}_{i{d}_O}$, and then invokes algorithm $DelGen(s{k}_{i{d}_O},i{d}_p,w)$ to get $W_{O\to P}$ and returns it to $\mathcal{F}$.
  3. $PkeyGen(d_g=(i{d}_O,i{d}_P,w,W_{O\to P}))$: $\mathcal{F}$ sends the delegation information $d_g=(i{d}_O,i{d}_P,w,W_{O\to P})$ to the challenger $\mathcal{C}$. $\mathcal{C}$ verifies its validity firstly. If it isn’t valid, he refuses to respond. Otherwise, $\mathcal{C}$ executes a $KeyExtract\left(i{d}_P\right)$ query to get secret key $s{k}_{i{d}_P}$, invokes algorithm $PkeyGen\left(s{k}_{i{d}_P},d_g=(i{d}_O,i{d}_P,w,W_{O\to P})\right)$ to get delegated secret key $s{k}_{O,P,w}$ and returns it to $\mathcal{F}$.
  4. $PSign\left(d_g=(i{d}_O,i{d}_P,w,W_{O\to P}),\varpi \right)$: $\mathcal{F}$ submits $d_g=(i{d}_O,i{d}_p,w,W_{O\to P})$ and message $\varpi$ to the challenger $\mathcal{C}$. $\mathcal{C}$ verifies the legality of $d_g=(i{d}_O,i{d}_p,w,W_{O\to P})$. If it is illegal, $\mathcal{C}$ rejects answering the query. Otherwise, he executes the $PkeyGen(d_g=(i{d}_O,i{d}_p,w,W_{OP}))$ query to get the delegated secret key $s{k}_{O,P,w}$, invokes algorithm $PSign(s{k}_{O,P,w},\varpi )$ to get signature $\varsigma$, and returns it to $\mathcal{F}$.
• Forge Phase: The forger $\mathcal{F}$ gives his forgery $\left(d_g=(i{d}_O,i{d}_P,w,W_{O\to P}),\varsigma \right)$.
  Recovering the message $\varpi$ from $\varsigma$, if the following conditions hold: $PVer\left(d_g=(i{d}_O,i{d}_P,w,W_{O\to P}),\varsigma \right)=1$, $d_g=(i{d}_O,i{d}_P,w,W_{O\to P})$ doesn’t occur in the $PkeyGen$ query, $\left(d_g=(i{d}_O,i{d}_P,w,W_{O\to P}),\varpi \right)$ doesn’t occur in the $PSign$ query, his attack is successful.

Let ${\epsilon }_2$ be the success probability of $\mathcal{F}$ in the game.

Definition 7.

An identity-based proxy signature scheme with message recovery (IDPSWM) is signature existentially unforgeable against the adaptive chosen message and identity (EUF-ID-CMA), if, for every polynomial time forger $\mathcal{F}$, ${\epsilon }_2$ is negligible.

4. Our Scheme

In this section, we introduce our identity-based proxy signature scheme with message recovery from lattice assumption. Our scheme includes seven algorithms, which also can be seen from Figure 1.

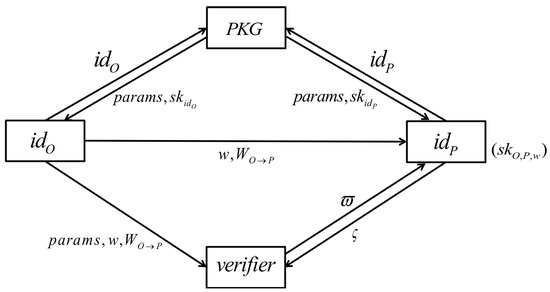
Figure 1. Flow chart of our signature algorithm.

• $Setup\left(n\right)$: Inputting the security parameter n, PKG works as follows:
  1. Invoke $TrapGen\left(q,m\right)$ algorithm to obtain a pair of matrices $(A\in {\mathbb{Z}}_q^{n\times m}$, $T\in {\mathbb{Z}}^{m\times m})$.
  2. Let $H_1:{\left\{0,1\right\}}^{*}\to {\mathbb{Z}}_q^{n\times n}$ be a secure hash function.
  3. Let $H_2,H_5:{\left\{0,1\right\}}^{*}\to {\left\{-1,0,1\right\}}^n$ be secure hash functions, and the image Hamming weight is not larger than ${\lambda }_1$.
  4. Let $H_3:{\left\{0,1\right\}}^{*}\to {\left\{-1,0,1\right\}}^{n\times n}$ be a secure hash function, and every column vector in the image has a small Hamming weight bounded by ${\lambda }_2$.
  5. Let $H_4:{\mathbb{Z}}_q^n\to {\left\{0,1\right\}}^{l_1+l_2}$ be a secure hash function, where $l_2$ is also the length of message $\varpi$.
  6. Let $F_1:{\left\{0,1\right\}}^{l_2}\to {\left\{0,1\right\}}^{l_1}$, $F_2:{\left\{0,1\right\}}^{l_1}\to {\left\{0,1\right\}}^{l_2}$ be encoding functions.
  Finally, PKG outputs public parameters $params$=$(A,H_1,H_2,H_3,$$H_4,H_5,F_1,F_2)$ and the secret master key $msk=T$.
• $KeyExtract\left(msk,id\right)$: Given an identity $id\in {\left\{0,1\right\}}^{*}$, PKG works as follows:
  1. Sample $E_{id}\leftarrow {\mathbb{D}}_{\sigma }^{n\times n}$, such that $\left|E_{id}\left(i,j\right)\right|\le 7\sigma$ for all $i,j=1,\cdots ,n$. If $\left|E_{id}\left(i,j\right)\right|>7\sigma$ for some $i,j$, Resample again. According to [22], the probability of $\left|E_{id}\left(i,j\right)\right|>7\sigma$ for some $i,j$ is less than $1/30$.
  2. Invoke algorithm $SamplePre(A,T,H_1\left(id\right)-E_{id},\sigma )$, provide $S_{id}$ follows the distribution ${\mathbb{D}}_{\sigma }^{m\times n}$, such that $A{S}_{id}=H_1\left(id\right)-E_{id}$.
  3. Return $s{k}_{id}=$$S_{id}$ as secret key for the identity $id$.
• $DelGen\left(s{k}_{i{d}_O},i{d}_P,w\right)$: The original signer $i{d}_O$ inputs his secret key $s{k}_{i{d}_O}=S_{i{d}_O}$, and the warrant $w\in {\left\{0,1\right\}}^{*}$ associated with proxy signer $i{d}_P$ does the following steps:
  1. Sample $y_w$$\leftarrow U\left(D_B^m\right)$, $U\left(D_B^m\right)$ is the uniform distribution on $D_B=\left[-B,B\right]$.
  2. Let $c_w=H_2\left({A{y}_w\left(modq\right)}_d,w\right)$, $z_w=S_{i{d}_O}·c_w+y_w$.
  3. Let $\omega =A{z}_w-H_1\left(i{d}_O\right)·c_w\left(modq\right)$. If $\left|{\left[{\omega }_{\left(i\right)}\right]}_{2^d}\right|>2^{d-1}-7{\lambda }_1\sigma$, go to the first step to resample $y_w$.
  4. Return $W_{O\to P}=\left(z_w,c_w\right)$ with probability $min\left(D_B^m\left(z_w\right)/\left(M·{\mathbb{D}}_{B,S_{i{d}_O}·c_w}^m\left(z_w\right)\right),1\right)$, and publish delegation information $d_g=(i{d}_O,i{d}_P,w,W_{O\to P}=\left(z_w,c_w\right))$ to all users.
• $DelVer\left(d_g=(i{d}_O,i{d}_P,w,W_{O\to P}=\left(z_w,c_w\right))\right)$: For arbitrary users, he verifies the legality of delegation information $d_g=(i{d}_O,i{d}_P,w,W_{O\to P}=\left(z_w,c_w\right))$ as follows:
  1. Compute $\omega =A{z}_w-H_1\left(i{d}_O\right)·c_w\left(modq\right)$.
  2. If $c_w=H_2\left({\lfloor \omega \rceil }_d,w\right)$ and ${∥z_w∥}_{\infty }\le B$, output 1 and accept this delegation. Otherwise, output 0 and reject it.
• $PkeyGen\left(s{k}_{i{d}_P},d_g=(i{d}_O,i{d}_P,w,W_{O\to P}=\left(z_w,c_w\right))\right)$: the proxy signer $i{d}_P$ inputs his secret key $s{k}_{i{d}_P}=S_{i{d}_P}$ and the delegation information $d_g=(i{d}_O,i{d}_P,w,W_{O\to P}=\left(z_w,c_w\right))$, computes $L_w=H_3\left(w,z_w,c_w\right)\in {\left\{-1,0,1\right\}}^{n\times n}$, outputs $s{k}_{O,P,w}=S_{i{d}_P}·L_w\in {\mathbb{D}}_{\sigma ·\sqrt{{\lambda }_2}}^{m\times n}$ as the delegated secret key.
• $PSign(s{k}_{O,P,w},\varpi )$: the proxy signer $i{d}_P$ inputs his delegated secret key $s{k}_{O,P,w}=S_{i{d}_P}·L_w$, the message $\varpi \in {\left\{0,1\right\}}^{l_2}$, does the next steps.
  1. Sample $y\leftarrow U\left(D_B^m\right)$, compute $c^{\prime }=H_4\left({\lfloor Ay(modq)\rceil }_d\right)$.
  2. Let ${\varpi }^{\prime }=F_1\left(\varpi \right)\Vert \left(F_2\left(F_1\left(\varpi \right)\right)\oplus \varpi \right)$, $c=c^{\prime }\oplus {\varpi }^{\prime }$.
  3. Compute $c_0=H_5\left(c\right)$, $z=S_{i{d}_P}·L_w·c_0+y$.
  4. Let $\omega =Az-H_1\left(i{d}_P\right)·L_w·c_0\left(modq\right)$.
  5. If $\left|{\left[{\omega }_{\left(i\right)}\right]}_{2^d}\right|>2^{d-1}-7{\lambda }_1\sqrt{{\lambda }_2}\sigma$, go to the first step to resample y. Otherwise, return proxy signature $\varsigma =\left(z,c\right)$ with probability $min\left(D_B^m\left(z\right)/\left(M·{\mathbb{D}}_{B,S_{i{d}_P}{L}_w{c}_0}^m\left(z\right)\right),1\right)$
• $PVer\left(d_g=(i{d}_O,i{d}_P,w,W_{O\to P}=\left(z_w,c_w\right)),\varsigma =\left(z,c\right)\right)$: For arbitrary user, he verifies the proxy signature with the next steps. Here, we think the legality of delegation information $d_g=(i{d}_O,i{d}_P,w,W_{O\to P}=\left(z_w,c_w\right))$ has already been verified.
  1. Compute $c^{\prime }=H_4\left(\lfloor {Az-H_1\left(i{d}_P\right)·L_w·H_5\left(c\right)\left(modq\right)}_d\rceil \right)$.
  2. Compute ${\varpi }^{\prime }=c\oplus c^{\prime }$, $\varpi ={\left|{\varpi }^{\prime }\right|}_{l_2}\oplus F_2\left({\left|{\varpi }^{\prime }\right|}^{l_1}\right)$.
  3. If $F_1\left(\varpi \right)={\left|{\varpi }^{\prime }\right|}^{l_1}$ and ${∥z∥}_{\infty }<B$, accept the signature and output 1; otherwise, output 0 and reject the signature.

5. Scheme Analysis

5.1. Parameter Setting

n is the system security parameter:

1. For the $TrapGen(q,m)$ algorithm, $q=poly\left(n\right)$, $m=⌈6nlogq⌉$.

2. For the $SamplePre\left(A,T,H_1\left(id\right)-E_{id},\sigma \right)$ algorithm, $\sigma =\omega \left({\left(mlogm\right)}^{1/2}\right).$

3. According to [22], ${\lambda }_1$ satisfies $2^{{\lambda }_1}·\left(\begin{array}{c}n\\ {\lambda }_1\end{array}\right)\ge 2^{128}$.

4. According to [23], $l_1$ and $l_2$ are all about 100.

5. According to [22], $2^d\ge 7{\lambda }_1\sqrt{{\lambda }_2}n\sigma$, $B=14\sigma \left(m-1\right)\sqrt{{\lambda }_1\sqrt{{\lambda }_2}}$.

6. According to [21], M is a small constant of about 8.

5.2. Correctness of the Scheme

1. For $DelVer(d_g=(i{d}_O,i{d}_P,w,W_{O\to P}))$ algorithm, $W_{O\to P}=\left(z_w,c_w\right)$,

$$\begin{array}{cc}\hfill \omega & =A{z}_w-H_1\left(i{d}_O\right)·c_w\left(modq\right)=A\left(S_{i{d}_O}·c_w+y_w\right)-\hfill \\ & \left(A{S}_{i{d}_O}+E_{i{d}_O}\right)·c_w\left(modq\right)\hfill \\ & =A{S}_{i{d}_O}·c_w+A{y}_w-A{S}_{i{d}_O}·c_w-E_{i{d}_O}·c_w\left(modq\right)\hfill \\ & =A{y}_w-E_{i{d}_O}{c}_w\left(modq\right).\hfill \end{array}$$

Because in step 3 of $DelGen\left(s{k}_{i{d}_O},i{d}_P,w\right)$ algorithm, we have:

If $\left|{\left[{\omega }_{\left(i\right)}\right]}_{2^d}\right|>2^{d-1}-7{\lambda }_1\sigma$, go to the first step to resample $y_w$.

Therefore, $\lfloor {\omega }_d\rceil ={\lfloor A{y}_w-E_{i{d}_O}{c}_w\left(modq\right)\rceil }_d$$={A{y}_w\left(modq\right)}_d$, such that $c_w=H_2({\lfloor A{y}_w(modq)\rceil }_d,w)=H_2\left(\lfloor {\omega }_d\rceil ,w\right)$.

In addition, due to $y_w$$\leftarrow D_B^m$, and $z_w=S_{i{d}_O}·c_w+y_w$, $z_w$ follows uniform distribution on ${\left[-B+\gamma ,B-\gamma \right]}^m$ for $\gamma =14\sqrt{{\lambda }_1}\sigma$, so that ${∥z_w∥}_{\infty }\le B$. So far, verification of delegation information is correct.

2. For $PVer(d_g=(i{d}_O,i{d}_p,w,W_{O\to P}).\varsigma =(z,c))$ algorithm,

$$\begin{array}{cc}\hfill \omega & =Az-H_1\left(i{d}_P\right)·L_w·H_5\left(c\right)\left(modq\right),\hfill \\ & =A\left(S_{i{d}_P}·L_w·H_5\left(c\right)+y\right)-\left(A{S}_{i{d}_P}+E_{i{d}_P}\right)·L_w·H_5\left(c\right)\left(modq\right),\hfill \\ & =Ay-E_{i{d}_P}·L_w·H_5\left(c\right)\left(modq\right).\hfill \end{array}$$

Because in step 5 of $PSign(s{k}_{O,P,w},\varpi )$ algorithm, we have:

If $\left|{\left[{\omega }_{\left(i\right)}\right]}_{2^d}\right|>2^{d-1}-7{\lambda }_1\sqrt{{\lambda }_2}\sigma$, go to the first step to resample y.

Therefore, ${\lfloor \omega \rceil }_d={\lfloor Ay-E_{i{d}_P}·L_w·H_5\left(c\right)(modq)\rceil }_d={\lfloor Ay(modq)\rceil }_d$, such that $c^{\prime }=H_4\left({\lfloor Az-H_1\left(i{d}_P\right)·L_w·H_5\left(c\right)(modq)\rceil }_d\right)=H_4\left({\lfloor Ay(modq)\rceil }_d\right)$

Due to $c=c^{\prime }\oplus {\varpi }^{\prime }$, we have ${\varpi }^{\prime }=c\oplus c^{\prime }$. Since ${\varpi }^{\prime }=F_1\left(\varpi \right)\Vert \left(F_2\left(F_1\left(\varpi \right)\right)\oplus \varpi \right)$, the message $\varpi ={\left|{\varpi }^{\prime }\right|}_{l_2}\oplus F_2\left({\left|{\varpi }^{\prime }\right|}^{l_1}\right)$, and $F_1\left(\varpi \right)={\left|{\varpi }^{\prime }\right|}^{l_1}$.

In addition, since $y\leftarrow D_B^m$, and $z=S_{i{d}_P}·L_w·H_5\left(c\right)+y$, z follows uniform distribution on ${[-B+\gamma ,B-\gamma ]}^m$ for $\gamma =14\sqrt{{\lambda }_1{\lambda }_2}\sigma$, so that ${∥z∥}_{\infty }\le B$.

Up to now, proxy signature verification is successful. Combining two points, we draw a conclusion that our scheme is correct.

5.3. Security Analysis

Our scheme security consists of two parts: EUF-ID-CWA security aims at delegation information reliability, EUF-ID-CMA security aims at proxy signature reliability.

5.3.1. EUF-ID-CWA Security

Theorem 1.

Provided that the SIS problem is hard to solve, our identity-based proxy signature scheme with message recovery (IDPSWM) is delegation information existentially unforgeable against adaptive chosen warrant and identity (EUF-ID-CWA).

Proof. 

We prove this theorem by contradiction. Assuming that a polynomial time forger $\mathcal{F}$ has the ability to provide valid and fresh delegation information with some non-negligible probability ${\epsilon }_1$, we can design an algorithm to solve an SIS instance with probability

$$\left({}^1/{}_2-{}^1/{}_{2^{128}}\right)\left({\epsilon }_1-{}^1/{}_{2^{128}}\right)\left(\left({\epsilon }_1-{}^1/{}_{2^{128}}\right)/\left(Q_1+Q_2\right)-{}^1/{}_{2^{128}}\right),$$

where $Q_1$ and $Q_2$ are the times of $H_2\left(w_{ij}\right)$ queries and $DelGen\left(i{d}_i,i{d}_j,w_{ij}\right)$ queries.

That is to say, with an SIS problem instance $\left(A|I_n\right)\in {\mathbb{Z}}_q^{n\times \left(m+n\right)}$, $\mathcal{C}$ interacts with forger $\mathcal{F}$ to find small non-zero vector $e=\left(\begin{array}{c}{e}_1\\ e_2\end{array}\right)$, $e_1\in {\mathbb{Z}}^m$ and $e_2\in {\mathbb{Z}}^n$, such that $\left(A|I_n\right)e=\left(A|I_n\right)\left(\begin{array}{c}{e}_1\\ e_2\end{array}\right)=A{e}_1+e_2=0\left(modq\right)$. The details are as follows:

• Initial Phase: $\mathcal{C}$ selects $F_1:{\{0,1\}}^{l_2}\to {\{0,1\}}^{l_1}$, $F_2:{\{0,1\}}^{l_1}\to {\{0,1\}}^{l_2}$, submits A, $F_1$, and $F_2$ as system parameters to the forger $\mathcal{F}$.
• Query Phase: The forger $\mathcal{F}$ makes the following queries, $\mathcal{C}$ gives reasonable answers:
  1. $H_1\left(i{d}_i\right)$ query: $\mathcal{F}$ selects a user identity $i{d}_i\in {\left\{0,1\right\}}^{*}$, sends it to $\mathcal{C}$. $\mathcal{C}$ samples $S_{i{d}_i}\leftarrow {\mathbb{D}}_{\sigma }^{m\times n}$, $E_{i{d}_i}\leftarrow {\mathbb{D}}_{\sigma }^{n\times n}$, let $H_1\left(i{d}_i\right)=A{S}_{i{d}_i}+E_{i{d}_i}$. He saves $\left(i{d}_i,S_{i{d}_i},A{S}_{i{d}_i}+E_{i{d}_i}\right)$ in the list ${\mathcal{H}}_1$ and returns $H_1\left(i{d}_i\right)=A{S}_{i{d}_i}+E_{i{d}_i}$ to $\mathcal{F}$.
  2. $H_2\left(w_{ij}\right)$ query: $\mathcal{F}$ selects warrant $w_{ij}\in {\left\{0,1\right\}}^{*}$ associated with the original signer $i{d}_i\in {\left\{0,1\right\}}^{*}$, the proxy signer $i{d}_j\in {\left\{0,1\right\}}^{*}$, sends all of them to $\mathcal{C}$. $\mathcal{C}$ randomly samples $c_{ij}\leftarrow {\left\{-1,0,1\right\}}^n$ with Hamming weight less than or equal to ${\lambda }_1$, selects $z_{ij}\leftarrow D_B^m$ uniformly, let $\omega =A{z}_{ij}-H_1\left(i{d}_i\right)·c_{ij}\left(modq\right)$. If some entry in $\omega$ is larger than $2^{d-1}-7{\lambda }_1\sigma$, $\mathcal{C}$ resamples $c_{ij}$ and $z_{ij}$ again. Because $2^d\ge 7{\lambda }_1\sqrt{{\lambda }_2}n\sigma$, the probability that every entry in $\omega$ is smaller than $2^{d-1}-7{\lambda }_1\sigma$ is larger than $1/3$. At last, $\mathcal{C}$ saves $\left(i{d}_i,i{d}_j,w_{ij},c_{ij},z_{ij}\right)$ in list ${\mathcal{H}}_2$ and returns $c_{ij}$ to $\mathcal{F}$.
  3. $KeyExtract\left(i{d}_i\right)$ query: $\mathcal{F}$ selects a user identity $i{d}_i\in {\{0,1\}}^{*}$ and sends it to the challenger $\mathcal{C}$. $\mathcal{C}$ searches list ${\mathcal{H}}_1$ to get $(i{d}_i,D_{i{d}_i},A{S}_{i{d}_i}+E_{i{d}_i})$, and returns $s{k}_{i{d}_i}=S_{i{d}_i}$. If it doesn’t exist, $\mathcal{C}$ queries $H_1\left(i{d}_i\right)$ firstly.
  4. $DelGen\left(i{d}_i,i{d}_j,w_{ij}\right)$ query: $\mathcal{F}$ selects the original signer $i{d}_i\in {\{0,1\}}^{*}$, the proxy signer $i{d}_j\in {\{0,1\}}^{*}$, and the warrant $w_{ij}\in {\{0,1\}}^{*}$, sends all of them to $\mathcal{C}$. $\mathcal{C}$ looks list $H_2$ for $(i{d}_i,i{d}_j,w_{ij},c_{ij},z_{ij})$ and returns $\left(z_{ij},c_{ij}\right)$. If $(i{d}_i,i{d}_j,w_{ij},c_{ij},z_{ij})$ doesn’t exist, $\mathcal{C}$ queries $H_2\left(w_{ij}\right)$ firstly.
• Forge Phase: The forger $\mathcal{F}$ gives his forgery $(i{d}_{i^{*}},i{d}_{j^{*}},w_{i{j}^{*}},W_{i^{*}\to j^{*}}=\left(z^{*},c^{*}\right))$.
  Because $\mathcal{F}$ queries $H_2\left(w_{ij}\right)$ at most $Q_1$ times, queries $DelGen\left(i{d}_i,i{d}_j,w_{ij}\right)$ at most $Q_2$ times, so that the number of $c_{ij}$ is at most $Q_1+Q_2$. Suppose there are $c_1$, $c_2$, ⋯, $c_{Q_1+Q_2}$. For $A{z}^{*}-H_1\left(i{d}_{i^{*}}\right)c^{*}\left(modq\right)$, the probability of $\mathcal{F}$ generates $c^{*}$ such that $c^{*}=H_2\left({\lfloor A{z}^{*}-H_1\left(i{d}_{i^{*}}\right)·c^{*}\left(modq\right)\rceil }_d,w_{i{j}^{*}}\right)$ is $1/\left(2^{128}\right)$, which is negligible, so that $c^{*}$∈$\left\{c_1,c_2,\cdots ,c_{Q_1+Q_2}\right\}$ with overwhelming probability $1-1/\left(2^{128}\right)$.

Because $\mathcal{F}$ gives a successful forgery with probability ${\epsilon }_1$, $(i{d}_{i^{*}},i{d}_{j^{*}},w_{i{j}^{*}},W_{i^{*}\to j^{*}}=\left(z^{*},c^{*}\right))$ is a valid forgery and $c^{*}$∈$\left\{c_1,c_2,\cdots ,c_{Q_1+Q_2}\right\}$ with probability ${\epsilon }_1-1/2^{128}$. Supposing $c^{*}=c_t$, we further conclude that it comes from a $H_2$ query rather than a $DelGen$ query.

If $c^{*}=c_t$ comes from $DelGen\left(i{d}_{i_t},i{d}_{j_t},w_{i{j}_t}\right)$ query, then

$$c^{*}=H_2\left(\lfloor A{z}^{*}-H_1\left(i{d}_{i^{*}}\right)·c^{*}\left(modq\right){\rceil }_d,w_{i{j}^{*}}\right)=H_2\left(\lfloor A{z}_t-H_1\left(i{d}_{i_t}\right)·c^{*}\left(modq\right){\rceil }_d,w_{i{j}_t}\right).$$

If $w_{i{j}^{*}}$≠$w_{i{j}_t}$ or $\lfloor A{z}^{*}-H_1\left(i{d}_{i^{*}}\right)·c^{*}\left(modq\right){\rceil }_d$≠$\lfloor A{z}_t-H_1\left(i{d}_{i_t}\right)·c^{*}\left(modq\right){\rceil }_d$, then a collision in $H_2$ is obtained.

Therefore, $w_{i{j}^{*}}$=$w_{i{j}_t}$, which leads to $\left(i{d}_{i^{*}},i{d}_{j^{*}},w_{i{j}^{*}}\right)=\left(i{d}_{i_t},i{d}_{j_t},w_{i{j}_t}\right)$(because the warrant includes the identity information), and the entries of $A\left(z^{*}-z_t\right)$$\left(modq\right)$ are in $\left[-2^d,2^d\right]$.

If $z^{*}=z_t$, $(i{d}_{i^{*}},i{d}_{j^{*}},w_{i{j}^{*}},W_{i^{*}\to j^{*}}=\left(z^{*},c^{*}\right))$= $(i{d}_{i_t},i{d}_{j_t},w_{i{j}_t},W_{i_t\to j_t}=\left(z_t,c_t\right))$, it isn’t a successful forgery.

If $z^{*}\ne z_t$, let $e_1=z^{*}-z_t$, $e_2=-A\left(z^{*}-z_t\right)\left(modq\right)$, then $A{e}_1+e_2=0\left(modq\right)$, and ${∥e_1∥}_{\infty }\le 2B$, ${∥e_2∥}_{\infty }\le 2^d$. The SIS instance is solved.

Now, we know $c^{*}=c_t$ comes from $H_2\left(w_{ij}\right)$ query, and invoke $\mathcal{F}$ again. Due to General Forking Lemma [29], with a probability not less than

$$\left({\epsilon }_1-{}^1/{}_{2^{128}}\right)\left(\left({\epsilon }_1-{}^1/{}_{2^{128}}\right)/\left(Q_1+Q_2\right)-{}^1/{}_{2^{128}}\right),$$

we obtain a different valid delegation information $\left(\overline{z},\overline{c}\right)$ on $\left(i{d}_{i^{*}},i{d}_{j^{*}},w_{i{j}^{*}}\right)$, and $\overline{c}\ne c^{*}$.

Then, $\lfloor A{z}^{*}-H_1\left(i{d}_{i^{*}}\right)·c^{*}\left(modq\right){\rceil }_d={\lfloor A\overline{z}-H_1\left(i{d}_{i^{*}}\right)·\overline{c}\left(modq\right)\rceil }_d,$ which means $A{z}^{*}-H_1\left(i{d}_{i^{*}}\right)·c^{*}+e=$$A\overline{z}-H_1\left(i{d}_{i^{*}}\right)·\overline{c}\left(modq\right)$ for ${∥e∥}_{\infty }\le 2^{d-1}$. Replacing $H_1\left(i{d}_{i^{*}}\right)$ with $A{S}_{i{d}_{i^{*}}}+E_{i{d}_{i^{*}}}$, we have $A\left(z^{*}-\overline{z}+S_{i{d}_{i^{*}}}\left(\overline{c}-c^{*}\right)\right)+e+E_{i{d}_{i^{*}}}\left(\overline{c}-c^{*}\right)=0\left(modq\right)$. Let $e_1=z^{*}-\overline{z}+S_{i{d}_{i^{*}}}\left(\overline{c}-c^{*}\right)$, $e_2=e+E_{i{d}_{i^{*}}}\left(\overline{c}-c^{*}\right)$, then ${∥e_1∥}_{\infty }\le 2B+2{\lambda }_1\sigma$, ${∥e_2∥}_{\infty }\le 2^{d-1}+2{\lambda }_1\sigma$. In addition, $S_{i{d}_{i^{*}}}$ and $E_{i{d}_{i^{*}}}$ have a variety of options, $\mathcal{F}$ doesn’t know which pair $\left(S_{i{d}_{i^{*}}},E_{i{d}_{i^{*}}}\right)$ is used to build $e_1$ and $e_2$. Therefore, the probability of $\left(e_1,e_2\right)\ne \left(0,0\right)$ is at least $1/2$. □

5.3.2. EUF-ID-CMA Security

Theorem 2.

Provided that the SIS problem is hard to solve, our identity-based proxy signature scheme with message recovery (IDPSWM) is signature existentially unforgeable against adaptive chosen message and identity (EUF-ID-CMA).

Proof. 

We prove this theorem by contradiction. Assuming that a polynomial time forger $\mathcal{F}$ has the ability to provide a valid and fresh proxy signature with some non-negligible probability ${\epsilon }_2$, we can design an algorithm $\mathcal{C}$ to solve an SIS problem instance with probability

$$\left({}^1/{}_2-{}^1/{}_{2^{128}}\right)\left({\epsilon }_2-{}^1/{}_{2^{128}}\right)\left(\left({\epsilon }_2-{}^1/{}_{2^{128}}\right)/\left(Q_3+Q_4\right)-{}^1/{}_{2^{128}}\right),$$

where $Q_3$ and $Q_4$ are the times of $H_5\left(c\right)$ queries and $PSign\left((i{d}_i,i{d}_j,w_{ij},c_{ij},z_{ij}),{\varpi }_k\right)$ queries.

That is to say, with an SIS problem instance $\left(A|I_n\right)\in {\mathbb{Z}}_q^{n\times \left(m+n\right)}$, $\mathcal{C}$ interacts with forger $\mathcal{F}$ to find a small non-zero vector $e=\left(\begin{array}{c}{e}_1\\ e_2\end{array}\right)$, $e_1\in {\mathbb{Z}}^m$ and $e_2\in {\mathbb{Z}}^n$, such that $\left(A|I_n\right)e=\left(A|I_n\right)\left(\begin{array}{c}{e}_1\\ e_2\end{array}\right)=A{e}_1+e_2=0\left(modq\right)$. The details are as follows:

• Initial Phase: $\mathcal{C}$ selects $F_1:{\{0,1\}}^{l_2}\to {\{0,1\}}^{l_1}$, $F_2:{\{0,1\}}^{l_1}\to {\{0,1\}}^{l_2}$, submits A, $F_1$, and $F_2$ as system parameters to the forger $\mathcal{F}$.
• Query Phase: The forger $\mathcal{F}$ makes the following queries, $\mathcal{C}$ gives reasonable answers:
  1. $H_1\left(i{d}_i\right)$ query: $\mathcal{F}$ selects a user identity $i{d}_i\in {\left\{0,1\right\}}^{*}$, and sends it to $\mathcal{C}$. $\mathcal{C}$ samples $S_{i{d}_i}\leftarrow {\mathbb{D}}_{\sigma }^{m\times n}$, $E_{i{d}_i}\leftarrow {\mathbb{D}}_{\sigma }^{n\times n}$, let $H_1\left(i{d}_i\right)=A{S}_{i{d}_i}+E_{i{d}_i}$. He saves $\left(i{d}_i,S_{i{d}_i},A{S}_{i{d}_i}+E_{i{d}_i}\right)$ in the list ${\mathcal{H}}_1$ and returns $H_1\left(i{d}_i\right)=A{S}_{i{d}_i}+E_{i{d}_i}$ to $\mathcal{F}$.
  2. $H_2\left(w_{ij}\right)$ query: $\mathcal{F}$ selects warrant $w_{ij}\in {\left\{0,1\right\}}^{*}$ associated with the original signer $i{d}_i\in {\left\{0,1\right\}}^{*}$, the proxy signer $i{d}_j\in {\left\{0,1\right\}}^{*}$, sends all of them to $\mathcal{C}$. $\mathcal{C}$ randomly samples $c_{ij}\leftarrow {\left\{-1,0,1\right\}}^n$ with Hamming weight less than or equal to ${\lambda }_1$, selects $z_{ij}\leftarrow D_B^m$ uniformly, let $\omega =A{z}_{ij}-H_1\left(i{d}_i\right)·c_{ij}\left(modq\right)$. If some entry in $\omega$ is larger than $2^{d-1}-7{\lambda }_1\sigma$, $\mathcal{C}$ resamples $c_{ij}$ and $z_{ij}$ again. Because $2^d\ge 7{\lambda }_1\sqrt{{\lambda }_2}n\delta$, the probability that every entry in $\omega$ is smaller than $2^{d-1}-7{\lambda }_1\sigma$ is larger than $1/3$. At last, $\mathcal{C}$ saves $\left(i{d}_i,i{d}_j,w_{ij},c_{ij},z_{ij}\right)$ in list ${\mathcal{H}}_2$ and returns $c_{ij}$ to $\mathcal{F}$.
  3. $H_4\left(y\right)$ query: $\mathcal{F}$ selects $y\leftarrow U\left(D_B^m\right)$ randomly, sends it to $\mathcal{C}$. $\mathcal{C}$ selects $c^{\prime }$$\in {\left\{0,1\right\}}^{l_1+l_2}$ uniformly and randomly. Then, $\mathcal{C}$ saves $\left(y,\lfloor Ay\left(modq\right){\rceil }_d,c^{\prime }\right)$ in list ${\mathcal{H}}_4$ and returns $c^{\prime }$ to $\mathcal{F}$.
  4.$H_5\left(c\right)$ query: $\mathcal{F}$ sends $c\in {\left\{0,1\right\}}^{l_1+l_2}$ and submits it to $\mathcal{C}$. $\mathcal{C}$ chooses $c_0\leftarrow {\left\{-1,0,1\right\}}^n$ with Hamming weight less than or equal to ${\lambda }_1$. Then, $\mathcal{C}$ saves $\left(c,c_0\right)$ in list ${\mathcal{H}}_5$ and returns $c_0$ to $\mathcal{F}$.
  5. $KeyExtract\left(i{d}_i\right)$ query: $\mathcal{F}$ selects a user identity $i{d}_i\in {\{0,1\}}^{*}$, sends it to the challenger $\mathcal{C}$. $\mathcal{C}$ searches list ${\mathcal{H}}_1$ to get $(i{d}_i,S_{i{d}_i},A{S}_{i{d}_i}+E_{i{d}_i})$, returns $s{k}_{i{d}_i}=S_{i{d}_i}$. If it doesn’t exist, $\mathcal{C}$ queries $H_1\left(i{d}_i\right)$ firstly.
  6. $DelGen\left(i{d}_i,i{d}_j,w_{ij}\right)$ query: $\mathcal{F}$ selects the original signer $i{d}_i\in {\{0,1\}}^{*}$, the proxy signer $i{d}_j\in {\{0,1\}}^{*}$, and the warrant $w_{ij}\in {\{0,1\}}^{*}$ sends all of them to $\mathcal{C}$. $\mathcal{C}$ looks list $H_2$ for $(i{d}_i,i{d}_j,w_{ij},c_{ij},z_{ij})$ and returns $\left(z_{ij},c_{ij}\right)$. If $(i{d}_i,i{d}_j,w_{ij},c_{ij},z_{ij})$ doesn’t exist, $\mathcal{C}$ queries $H_2\left(w_{ij}\right)$ firstly.
  7. $PkeyGen\left(i{d}_i,i{d}_j,w_{ij},z_{ij},c_{ij}\right)$ query: $\mathcal{F}$ sends the delegation information $\left(i{d}_i,i{d}_j,w_{ij},z_{ij},c_{ij}\right)$ to the challenger $\mathcal{C}$. $\mathcal{C}$ verifies its validity firstly. If it isn’t valid, he refuses to respond. Otherwise, $\mathcal{C}$ executes $KeyExtract\left(i{d}_j\right)$ query to get secret key $s{k}_{i{d}_j}=S_{i{d}_j}$, computes $L_{w_{ij}}=H_3\left(w_{ij},z_{ij},c_{ij}\right)$ and $s{k}_{i,j,w_{ij}}=S_{i{d}_j}·L_{w_{ij}}$, returns $s{k}_{i,j,w_{ij}}$ to $\mathcal{F}$.
  8. $PSign\left((i{d}_i,i{d}_j,w_{ij},z_{ij},c_{ij}),{\varpi }_k\right)$ query: $\mathcal{F}$ submits $(i{d}_i,i{d}_j,w_{ij},z_{ij},c_{ij})$ and message ${\varpi }_k$ to the challenger $\mathcal{C}$. $\mathcal{C}$ verifies the legality of $(i{d}_i,i{d}_j,w_{ij},z_{ij},c_{ij})$. If it is illegal, $\mathcal{C}$ rejects answering the query. Otherwise, he executes $PkeyGen\left(i{d}_i,i{d}_j,w_{ij},z_{ij},c_{ij}\right)$ query to get the delegated secret key $s{k}_{i,j,w_{ij}}$, invokes algorithm $PSign\left(s{k}_{i,j,w_{ij}},{\varpi }_k\right)$ to get signature ${\varsigma }_{ijk}=\left(z_{ijk},c_{ijk}\right)$, and returns it to $\mathcal{F}$.
• Forge Phase: The forger $\mathcal{F}$ gives his forgery signature $(i{d}_{i^{*}},i{d}_{j^{*}},w_{i{j}^{*}},z^{*},c^{*},z_{{\varpi }^{*}},c_{{\varpi }^{*}})$ for message ${\varpi }^{*}$.
  $\mathcal{C}$ invokes $\mathcal{F}$ again. Due to General Forking Lemma [29], with probability $\left({\epsilon }_2-{}^1/{}_{2^{128}}\right)\left(\left({\epsilon }_2-{}^1/{}_{2^{128}}\right)/\left(Q_3+Q_4\right)-{}^1/{}_{2^{128}}\right)$, we obtain a new signature $(i{d}_{i^{*}},i{d}_{j^{*}},w_{i{j}^{*}},z^{*},c^{*},{z^{\prime }}_{{\varpi }^{*}},{c^{\prime }}_{{\varpi }^{*}})$ for message ${\varpi }^{*}$, such that

  $$\lfloor A{z}_{{\varpi }^{*}}-H_1\left(i{d}_{j^{*}}\right)·L_{w_{i{j}^{*}}}·H_5\left(c_{{\varpi }^{*}}\right)\left(modq\right){\rceil }_d$$

  is equivalent to

  $$\lfloor A{z^{\prime }}_{{\varpi }^{*}}-H_1\left(i{d}_{j^{*}}\right)·L_{w_{i{j}^{*}}}·H_5\left({c^{\prime }}_{{\varpi }^{*}}\right)\left(modq\right){\rceil }_d$$

  and $H_5\left({c^{\prime }}_{{\varpi }^{*}}\right)\ne H_5\left(c_{{\varpi }^{*}}\right)$.
  Then, $A{z}_{{\varpi }^{*}}-H_1\left(i{d}_{j^{*}}\right)·L_{w_{i{j}^{*}}}·H_5\left(c_{{\varpi }^{*}}\right)+\widehat{e}$ = $A{z^{\prime }}_{{\varpi }^{*}}-H_1\left(i{d}_{j^{*}}\right)·L_{w_{i{j}^{*}}}·H_5\left({c^{\prime }}_{{\varpi }^{*}}\right)\left(modq\right)$ for ${∥\widehat{e}∥}_{\infty }\le 2^{d-1}$. Replacing $H_1\left(i{d}_{j^{*}}\right)$ with $A{S}_{i{d}_{j^{*}}}+E_{i{d}_{j^{*}}}$, we have $A\left(z_{{\varpi }^{*}}-{z^{\prime }}_{{\varpi }^{*}}+S_{i{d}_{j^{*}}}·L_{w_{i{j}^{*}}}\left(H_5\left({c^{\prime }}_{{\varpi }^{*}}\right)-H_5\left(c_{{\varpi }^{*}}\right)\right)\right)+\widehat{e}+E_{i{d}_{j^{*}}}\left(H_5\left({c^{\prime }}_{{\varpi }^{*}}\right)-H_5\left(c_{{\varpi }^{*}}\right)\right)=0\left(modq\right)$. Let $e_1=z_{{\varpi }^{*}}-{z^{\prime }}_{{\varpi }^{*}}+S_{i{d}_{j^{*}}}·L_{w_{i{j}^{*}}}\left(H_5\left({c^{\prime }}_{{\varpi }^{*}}\right)-H_5\left(c_{{\varpi }^{*}}\right)\right)$, $e_2=\widehat{e}+E_{i{d}_{j^{*}}}\left(H_5\left({c^{\prime }}_{{\varpi }^{*}}\right)-H_5\left(c_{{\varpi }^{*}}\right)\right)$, then ${∥e_1∥}_{\infty }\le 2B+2{\lambda }_1\sqrt{{\lambda }_2}\sigma$, ${∥e_2∥}_{\infty }\le 2^{d-1}+2{\lambda }_1\sigma$. In addition, $S_{i{d}_{i^{*}}}$ and $E_{i{d}_{i^{*}}}$ have a variety of options, $\mathcal{F}$ doesn’t know which pair $\left(S_{i{d}_{j^{*}}},E_{i{d}_{j^{*}}}\right)$ is used to build $e_1$ and $e_2$. Therefore, the probability of $\left(e_1,e_2\right)\ne \left(0,0\right)$ is at least $1/2$.

□

5.4. Performance Analysis

Regarding the performance analysis, we will focus on the following three aspects: signature compression, signing right delegation and message recovery.

Firstly, we take the signature compression technique from [22]. For hash value $H_1\left(id\right)$ for user $id$, we first sample $E_{id}\leftarrow {\mathbb{D}}_{\sigma }^{n\times n}$ such that $\left|E_{id}\left(i,j\right)\right|\le 7\sigma$ for all $i,j=1,\cdots ,n$. Then, we invoke algorithm $S_{id}\leftarrow SamplePre\left(A,T,H_1\left(id\right)-E_{id},\sigma \right)$ such that $A{S}_{id}+E_{id}=H_1\left(id\right)$. We set $S_{id}$ rather than $(S_{id},E_{id})$, as the private key of user $id$. The abandoned $E_{id}$ leads to the signature length reducing from $(S_{id}c+y,E_{id}c+y)$ to $S_{id}c+y$, which is about $nlog\left(14\sigma \left(m-1\right)\sqrt{{\lambda }_1\sqrt{{\lambda }_2}}\right)$ bits. Combining the operation ${\lfloor a\rceil }_d=\left(a-{\left[a\right]}_{2^d}\right)/2^d$, the discarded $E_{id}c+y$ does not affect signature verification algorithm.

For signing right delegation, we make the original signer’s signature $(z_w,c_w)$ for the warrant w public for everyone. Any verifier can take $(w,z_w,c_w)$ to verify the original signer’s signing right transfer to the proxy signer. Besides doing the same operations with the verifier, the proxy signer must embed $(w,z_w,c_w)$ into the generation of proxy signature private key—the delegated secret key. Therefore, the delegated secret key is decided by the original signer and the proxy signer. The original signer can’t deny his authorization to the proxy signer, can’t generate the delegated secret key alone, so that proxy signer’s interests are protected. On the other hand, the proxy signer can’t generate the delegated secret key without the permission of the original signer, thus the interests of the original signer are protected. In addition, no secure channel is necessary between the original signer and proxy signer—because no secret information is transmitted between them.

Thirdly, we use the idea of message recovery signature in [23], hide the message $\varpi$ in the signature, and the message $\varpi$ can be recovered without any secret information, hence only the signature should be transmitted and everyone can verify its legality.

In Table 1, we give the performance comparison between [23] and our scheme. Two schemes are both with message recovery and quantum resistance, and the number of signature verification operations is the same. The differences between two schemes are shown in the following aspects: firstly, the scheme in [23] needs the support of public key infrastructure while our scheme does not need it. Public key infrastructure provides security assurance of the relationship between public key and private key, which is achieved by authoritative authority signing certificates for users. Therefore, public key infrastructure needs to complete certificate allocation, verification, storage and revocation operations, which requires a large amount of bandwidth resources and computing resources. In our scheme, the public key is the user’s identity, and the relationship between the public key and the private key is natural. Therefore, we no longer need the support of the complex public key infrastructure, and the system becomes concise. Secondly, the scheme in [23] does not have the function of proxy authorization, and our scheme has this function. Therefore, our scheme is more powerful. In addition, the scheme in [23] does not introduce signature compression technology, and our scheme introduces signature compression technology to make the signature length shorter. It is clear that our scheme has better functionality compared to the scheme in [23]. However, because we take the signature compression technique from [22] to condense signature length, it is necessary to ensure $\left|{\left[{\omega }_{\left(i\right)}\right]}_{2^d}\right|\le 2^{d-1}-7{\lambda }_1\sqrt{{\lambda }_2}\sigma$. To this end, we repeat operations of signing message with probability not larger than $2/3$—this is our scheme’s extra computation cost. For every operation of signing message and verification, our scheme’s computation cost is comparable with that of the scheme in [23].

Table 1. Performance comparison among Refs. [23] and [25] and our scheme.

	[23]	[25]	Ours
Public key infrastructure	Need	Need	Not need
Delegation of signature right	No	Yes	Yes
Signature compression	No	No	Yes
Message recovery	Yes	Yes	Yes
Quantum resistance	Yes	Yes	Yes
Signature operation	1 time	1 time	5/3 time
Verification operation	1 time	1 time	1 time

The lattice-based proxy signature scheme with message recovery in [25] follows the same frame with the scheme in [23] and ours; we also include it in Table 1. Compared with our scheme, the scheme in [25] bases on public key infrastructure, delegation of signature right depends on secure channel and can’t be verified publicly. In addition, the scheme in [25] doesn’t take signature compression technique, its signature is longer and the number of signature operations is small. According to [30], reduction in message length will reduce energy consumption to a greater extent than reduction in computation. Overall, our scheme is more efficient.

6. Conclusions

In this paper, we first proposed the identity-based proxy signature scheme with message recovery based on the lattice assumptions. In particular, we used the signature compression technique for lattice signature without trapdoors to decrease signature length. We abandoned the secure channel between original signer and proxy signer and made the model possess better environmental adaptability. We also divided the security definition into two factors, making the security analysis much easier to be understood. We introduced the idea of message recovery signature, embedding messages into signatures and shortening the amount of information to be transmitted. For security analysis, our scheme is based on the learning with errors and the small integer solution problems. Finally, we demonstrated our performance via comparison with some related works.