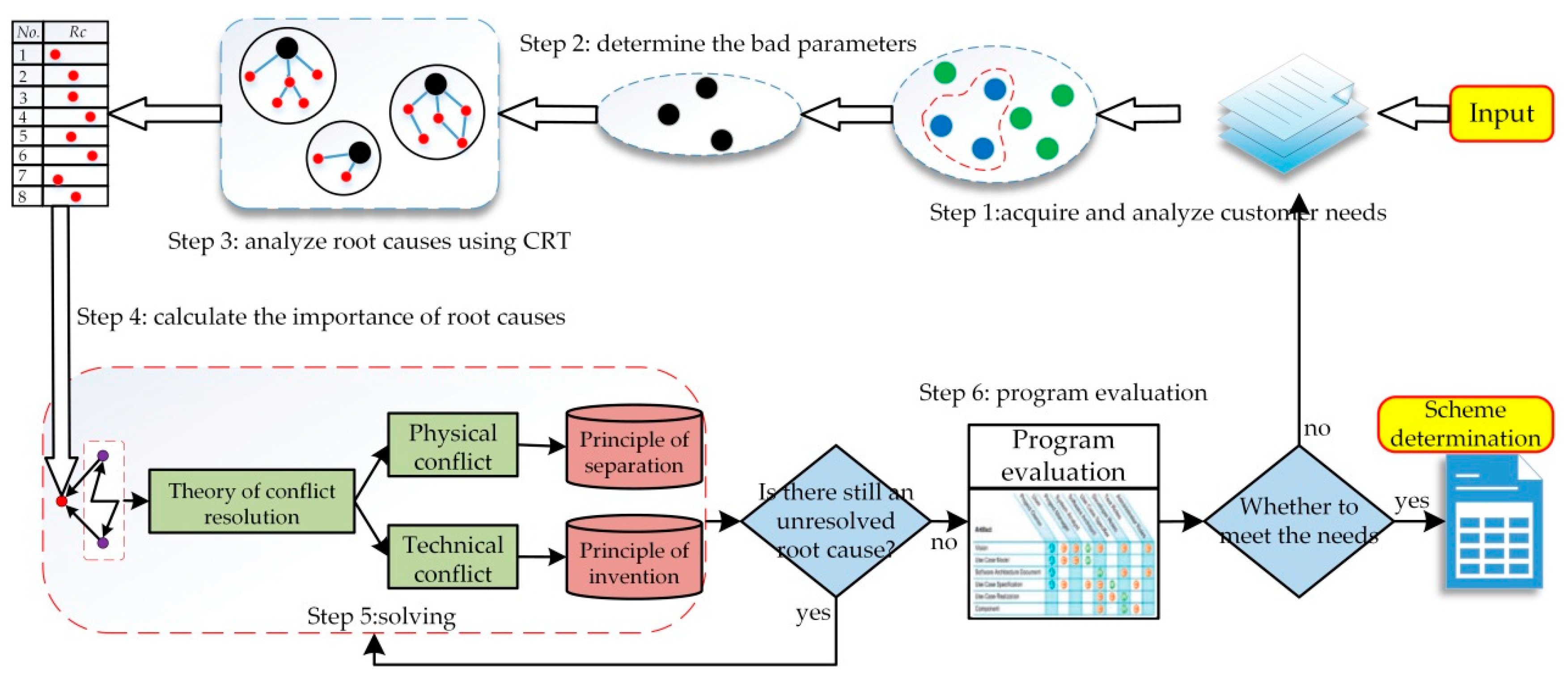
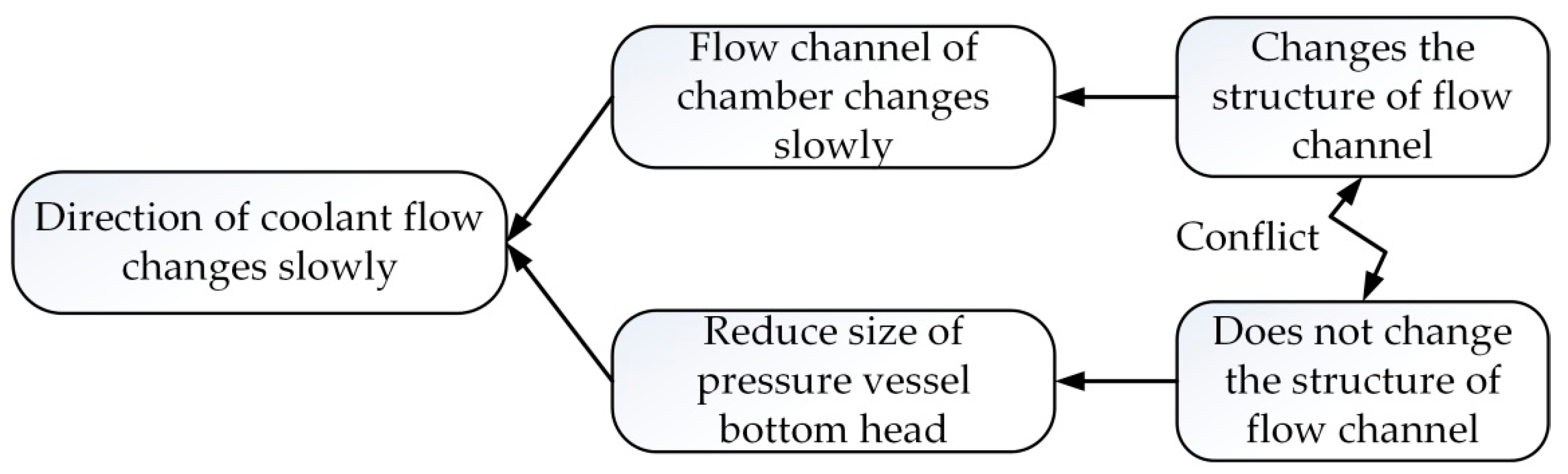
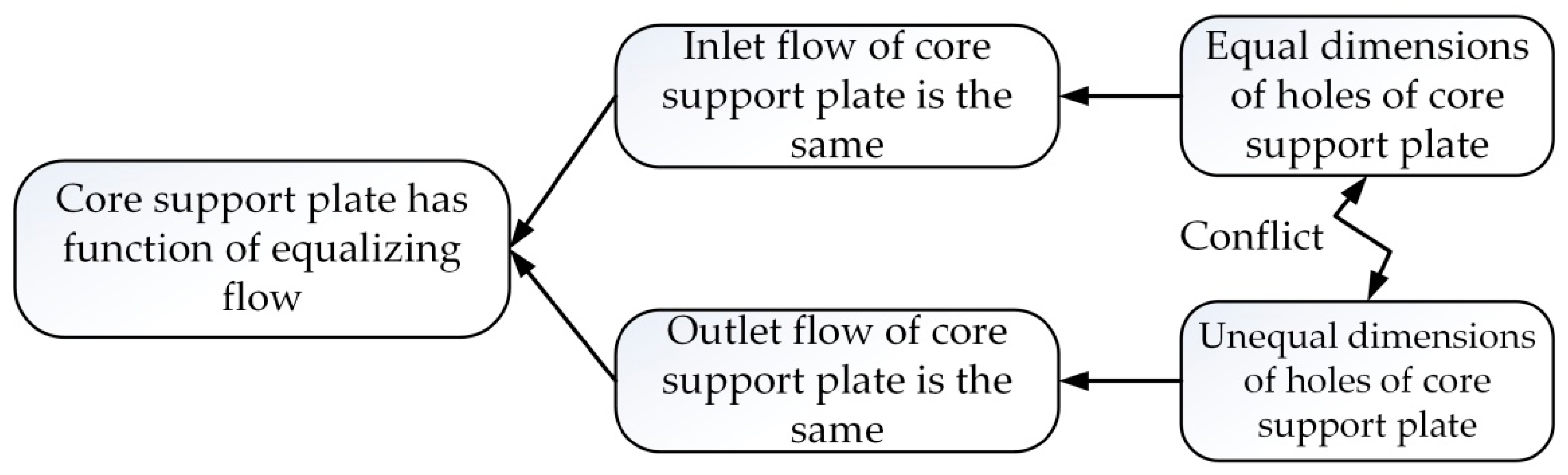
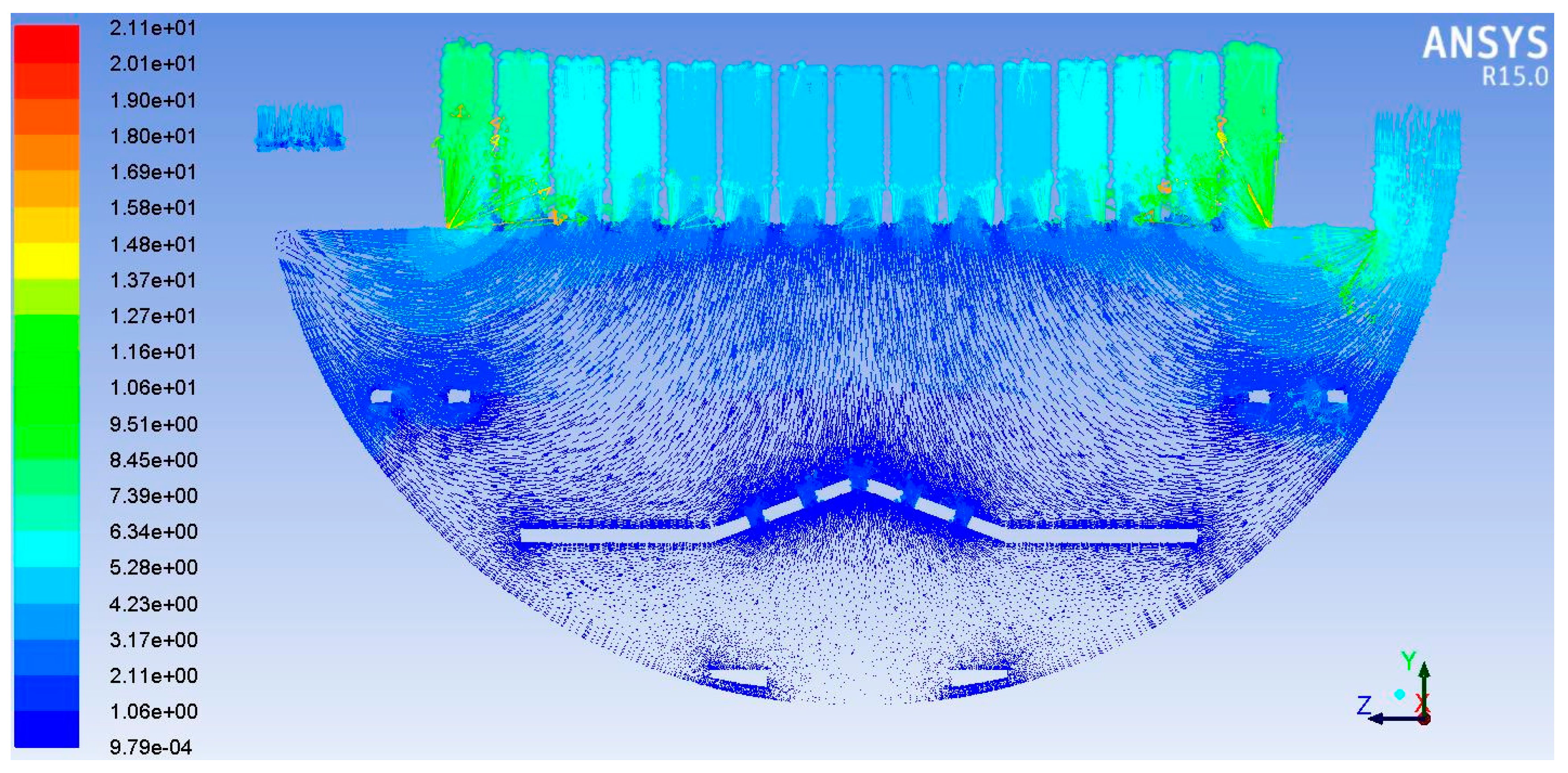
In order to assist designers with obtaining the importance order of core problems from a large number of problems that affect the product system performance, a determination method of core problems based on ANP is proposed in this paper.
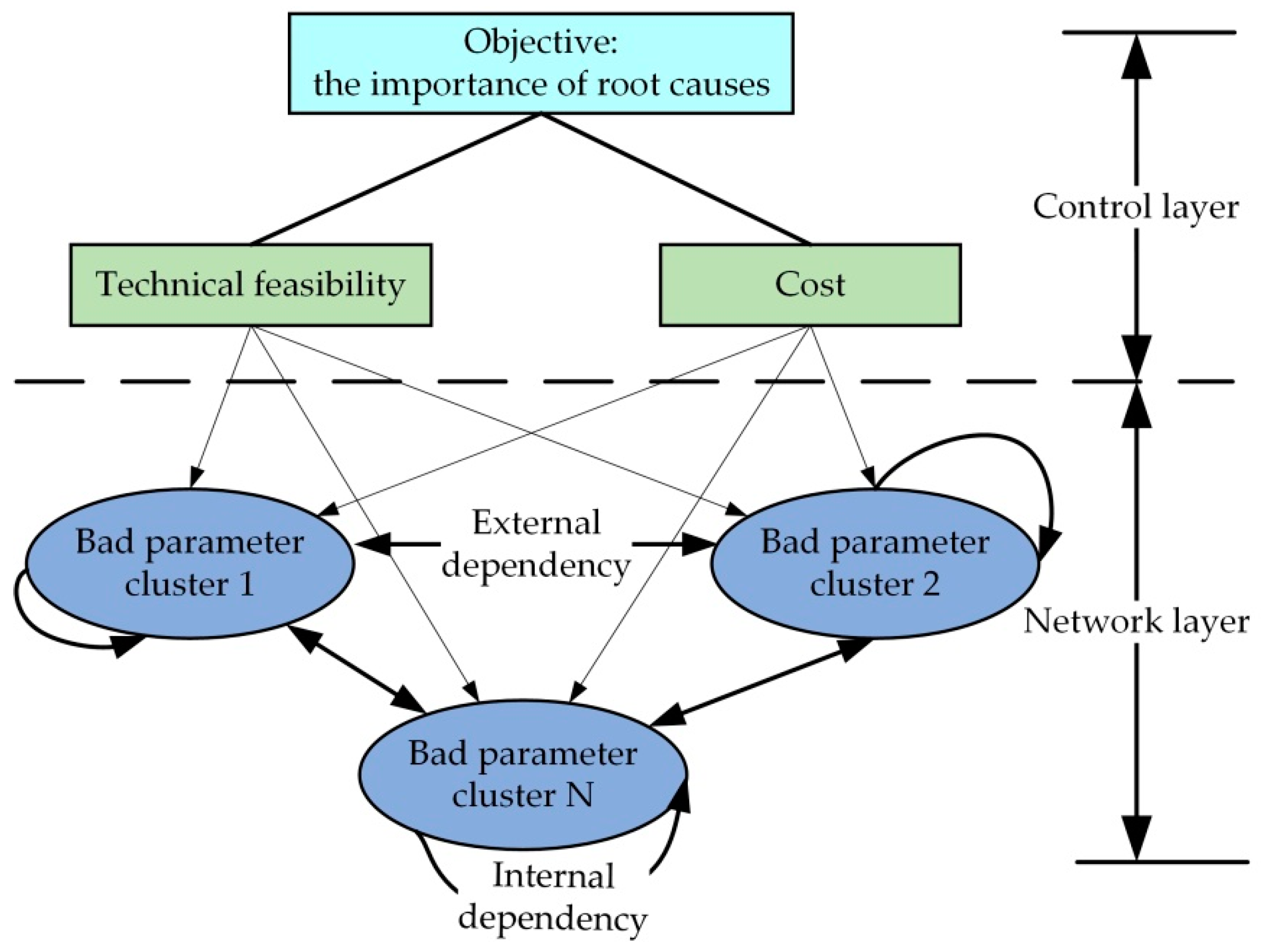
3.1. Construction of Network Layer and Control Layer for Design Problem
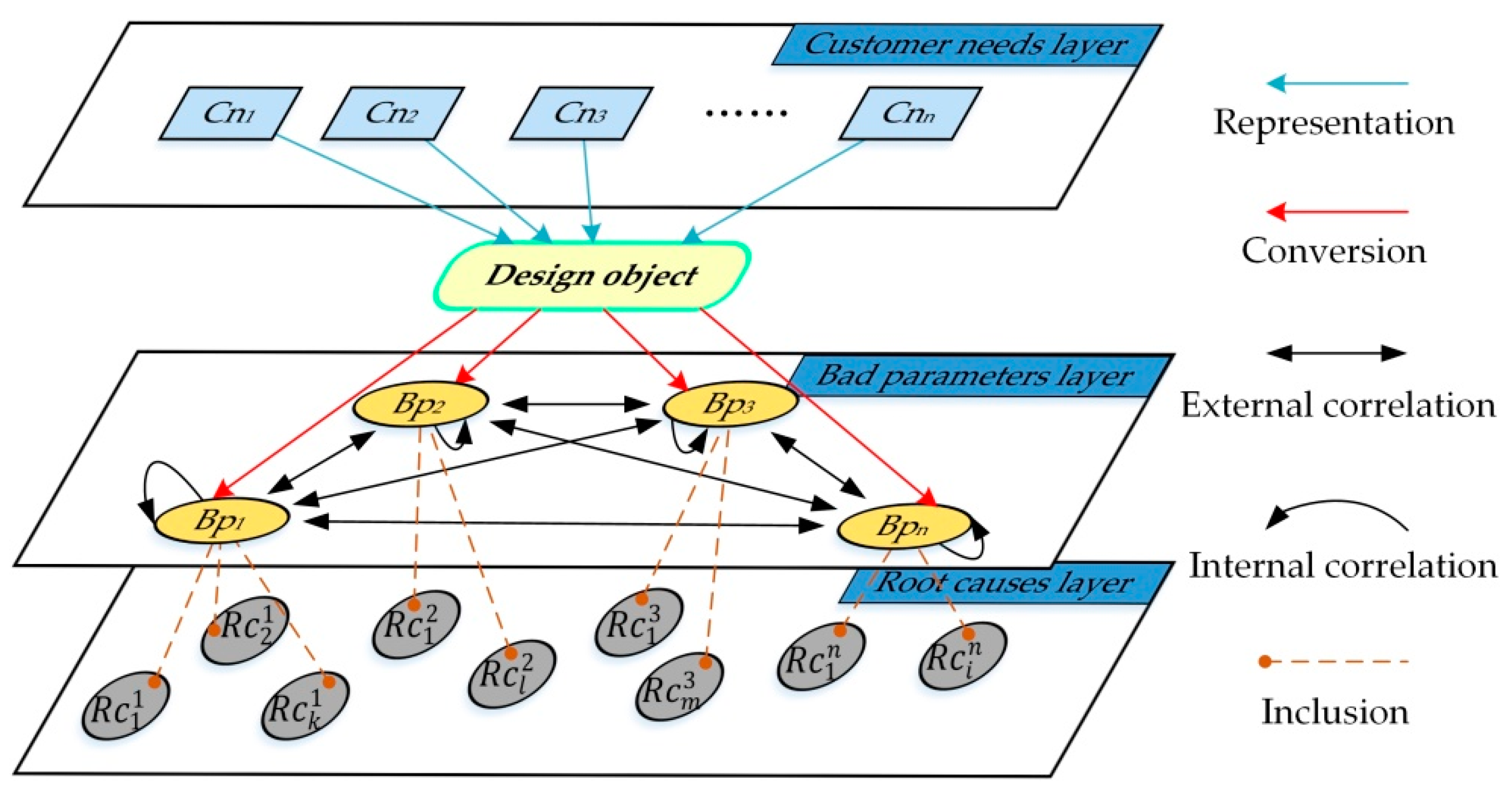
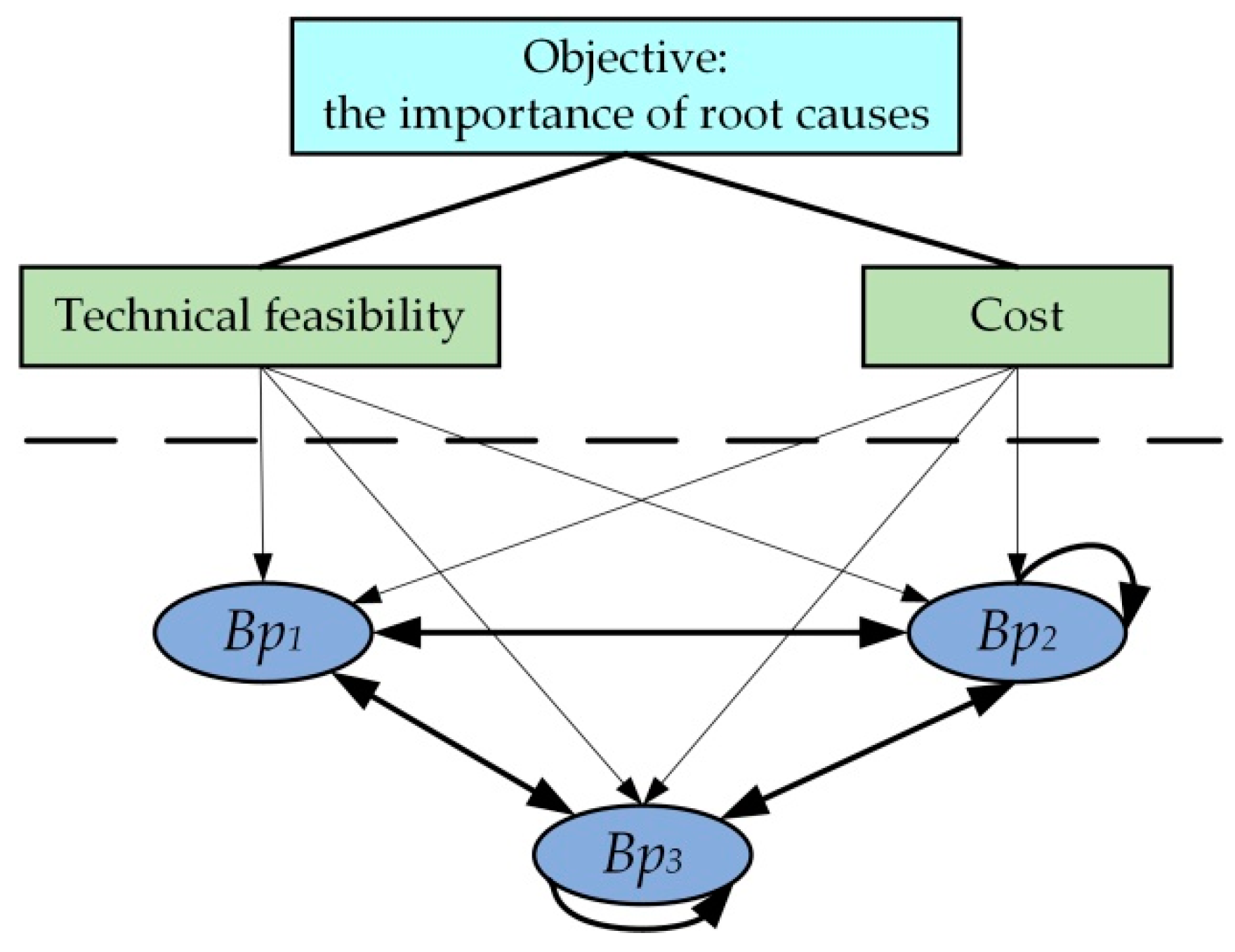
In the hierarchical representation model of the design problem, there is not only an inclusion relationship between the elements in the bad parameters layer and the elements in the root causes layer, but also correlations between bad parameters and root causes. These correlations are characterized by vertical clustering and horizontal correlation. In this paper, a network structure of cluster elements [
33] is adopted to construct the network layer of bad parameters. In order to analyze the correlations among the clusters of different design problems and obtain the core problems that affect the bad parameters, a control layer, including technical feasibility and cost, is constructed to constrain and evaluate the prospect of solving different design problems.
Analytic network process (ANP) is a multicriteria theoretical measuring method. It obtains the relative priority of an indicator by comparing the relative influence of two elements on a third element under a certain potential criterion [
33]. On the one hand, ANP method can be used to consider the correlation of same-level elements with their network structure. On the other hand, it also can be used to constrain and evaluate the ranking of the importance by adopting the control criteria [
34,
35]. According to the characteristics of ANP method and considering network layer and control layer, the ANP method is adopted in this paper to determine the importance order of root causes.
In this paper, every bad parameter (
) in the bad parameters layer is called a cluster, and the root cause (
) is regarded as an element in the bad parameter cluster (
). If an element in a cluster affects or is affected by at least one element in another cluster, it is called an externally dependent correlation between two clusters. If an element in a cluster affects or is affected by at least one element in the same cluster, it is called an internally dependent correlation. On this basis, a product hierarchy model is built, as shown in
Figure 2.
3.2. Calculation of Importance of Root Causes and Determination of Core Problems
The steps to calculate the importance of root causes and determine the core problems with ANP method are as follows:
Step 1: Construct the judgment matrix (
) and calculate the weight vector (
). If an element (
) in a cluster (
i) has an external dependency on an element in another cluster (
m), or has an internal dependency on an element inside its cluster, this element (
) is taken as a subcriterion. The influence degree of the elements in another cluster (
m) to this element (
) is compared in pairs. In this way, the judgment matrix (
) is constructed to calculate the corresponding weight vector (
). When comparing elements in pairs, an industry expert must determine which element has the greater influence on the third party element (
) and by how much. The comparison value E of the two elements is assigned on a scale of 0–9, and the ratio scale as shown in
Table 1. The constructed judgment matrix (
) is a positive reciprocal matrix. Taking the above demonstration as an example, the judgment matrix (
) and weight vector (
) are obtained by pairwise comparison, as shown in
Table 2.
Step 2: Construct supermatrix (
). The obtained weight vector (
) in Step 1 is sequentially written into every column of the matrix in Equation (6). In this way, the submatrix (
) of the supermatrix is constructed. As shown in Equation (7), all clusters are arranged in numerical order. Then the elements in every cluster are placed vertically and horizontally on the left and top of the supermatrix, respectively. Finally, the submatrix (
) calculated by Equation (6) is filled into the corresponding position of the supermatrix (
). (
) is constructed with
p as a control criterion.
Step 3: Construct a weighted supermatrix and limit weighted supermatrix. A certain cluster is taken as a subcriterion; the relative importance of the two clusters connected with it is compared to obtain the judgment matrix and weight vector. For example, with cluster (
) as a subcriterion, the judgment matrix is obtained by comparing the connected clusters in pairs, as shown in
Table 3.
The obtained weight vectors are sequentially written into the respective columns of the matrix in Equation (8) to obtain the weighted matrix
:
Every element (
) of the weighted supermatrix (
) is equal to the corresponding weight (
) in the weighted matrix
multiplied by the submatrix (
) in the supermatrix, as shown in Equation (9). Thus, the weighted supermatrix (
) is obtained:
In order to make the weighted supermatrix (
) accurate, it is necessary to perform a stability treatment on (
) by calculating its
nth power, and letting
n tend to infinity. As shown in Equation (11), the limit weighted supermatrix (
) is obtained when the value of the columns of the weighted supermatrix (
) does not change. The value of each row of the limit weighted supermatrix (
) is the importance (
) of the corresponding element:
Step 4: Calculate the importance of root causes. Technical feasibility (
) and cost (
) are taken as control criteria. So importance (
) and (
) are obtained by calculating the corresponding limit weighted supermatrix according to Steps 1–4. In order to improve the product system performance, two control criteria, technical feasibility (
) and cost (
), are weighted to obtain the corresponding weights (
) and (
). These weights of the control criteria are weighted for importance (
) and (
), respectively, as shown in Equation (12), so as to obtain the importance (
) of root causes:
Step 5: Determine the solving order of root causes and core problems based on the importance. (1) The solution of root causes is carried out in the importance order (). In other words, the higher the importance, the higher the priority of the root causes processing. (2) According to the importance order (), the first root cause () is determined as the core problem () of the bad parameter ().
Based on above contents, the quality and effectiveness of design can be effectively guaranteed. On the one hand, product design activities based on the importance order of core problems will improve the direction of the product system and determine the quality of the design. On the other hand, the solution to the core problem that ranks ahead will be beneficial to solve the non-core problems. This will improve the efficiency of the whole design process.