1. Introduction
Nowadays, the theories of groups and semigroups [
1,
2,
3,
4,
5] are attracting increasing attention, which can be used to express various symmetries and generalized symmetries in the real world. Every group or semigroup has a binary operation that satisfies the associative law. On the other hand, non-associative algebraic structures have great research value. Euclidean space
R3 with multiplication given by the vector cross product is an example of an algebra that is not associative, at the same time; Jordan algebra and Lie algebra are non-associative.
For the generalization of commutative semigroup, the notion of an AG-groupoid (Abel–Grassmann’s groupoid) is introduced in [
6], which is also said to be a left almost semigroup (LA-semigroup). Moreover, a class of non-associative ring with condition
x(
yz) =
z(
yx) is investigated in [
7]; in fact, the condition
x(
yz) =
z(
yx) is a dual distortion of the operation law in AG-groupoids.
An AG-groupoid is a non-associative algebraic structure, but it is a groupoid (
N, *) satisfying the left invertive law:
Now, many characterizations of AG-groupoids and various special subclasses are investigated in [
8,
9,
10,
11,
12,
13]. As a generalization of commutative group (Abelian group) and a special case of quasigroup, Kamran extended the concept of AG-groupoid to AG-group in [
14]. An AG-groupoid is called AG-group if there exists left identity and inverse, and its many properties (similar to the properties of groups) have been revealed successively in [
15,
16].
In this paper, we further analyze and study the structural characteristics of AG-groups, reveal the relationship between AG-groups and commutative groups, and establish filter and quotient algebra theories of AG-groups. The paper is organized as follows.
Section 2 presents several basic concepts and results. Some new properties of AG-groups are investigated in
Section 3, especially some examples of infinite AG-groups, and the authors prove that every weak commutative or alternative AG-group is a commutative group (Abelian group) and every AG-group is quasi-cancellative. In
Section 4, two special classes of AG-groups are studied and the structure theorems are proved. In
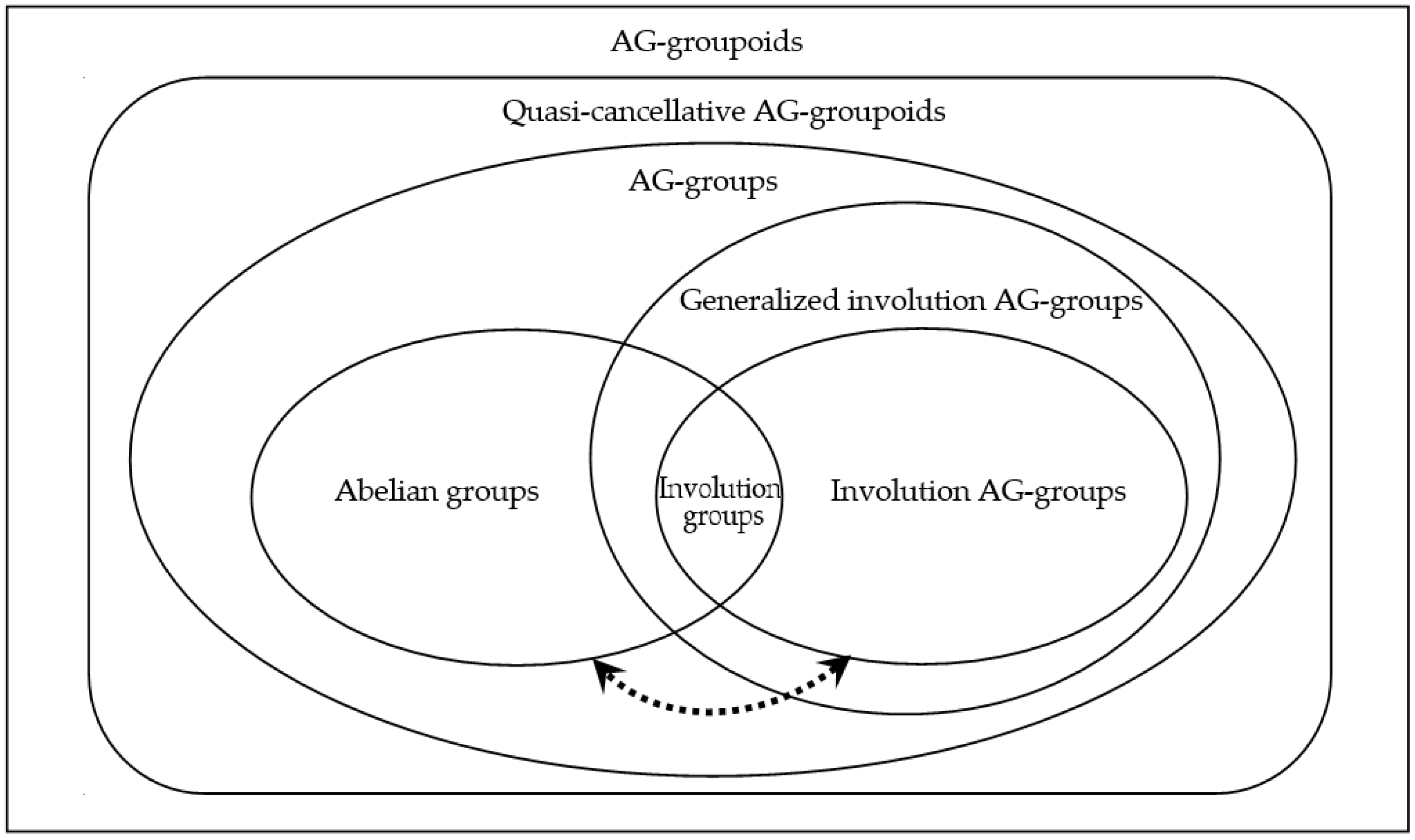
Section 5, the filter theory of AG-groups is established, the quotient structures induced by filters are constructed, and some homomorphism theorems are proved. Finally, the main results of this paper are systematically summarized via a schematic figure.
2. Preliminaries
First, we present some basic notions and properties.
A groupoid (
N, *) is called an AG-groupoid (Abel–Grassmann’s groupoid), if for any
a, b, cN, (
a*b)
*c = (
c*b)
*a. It is easy to verify that in an AG-groupoid (
N, *), the medial law holds:
Let (
N, *) be an AG-groupoid with left identity
e, we have
An AG-groupoid (N, *) is called a locally associative AG-groupoid, if it satisfies a*(a*a) = (a*a)*a, ∀aN.
An AG-groupoid (N, *) is called an AG-band, if it satisfies a*a = a (∀aN).
Definition 1. ([9,10]) Let (N, *) be an AG-groupoid. Then, N is called to be quasi-cancellative if for any a, bN, Proposition 1. ([9,10]) Every AG-band is quasi-cancellative. Definition 2. ([14,15]) An AG-groupoid (N, *) is called an AG-group or a left almost group (LA-group), if there exists left identity eN (that is e*a = a, for all aN), and there exists a−1N such that a−1*a = a* a−1= e (∀
aN).
Proposition 2. ([15]) Assume that (N, *) is an AG-group. We get that (N, *) is a commutative Abel–Grassmann’s Group if and only if it is an associative AG-Group. Proposition 3. ([15]) Let (N, *) be an AG-group with right identity e. Then, (N, *) is an Abelian group. Proposition 4. ([15]) Let (N, *) be an AG-group. Then, (N, *) has exactly one idempotent element, which is the left identity. Proposition 5. ([11]) Let (N, *) be an AG-groupoid with a left identity e. Then, the following conditions are equivalent, - (1)
N is an AG-group.
- (2)
Every element of N has a right inverse.
- (3)
Every element a of N has a unique inverse a−1.
- (4)
The equation x*a = b has a unique solution for all a, bN.
Proposition 6. ([16]) Let (N, *) be an AG-group. Define a binary operationas follows: Then, (N, ) is an Abelian group, denote it by ret(N, *) = (N, ).
3. Some Examples and New Results of AG-Groups
In this section, we give some examples of AG-groups (including some infinite examples), and investigate the characterizations of weak commutative AG-groups, alternative AG-groups and quasi-cancellative AG-groups. Moreover, we obtain two subalgebras from arbitrary AG-group.
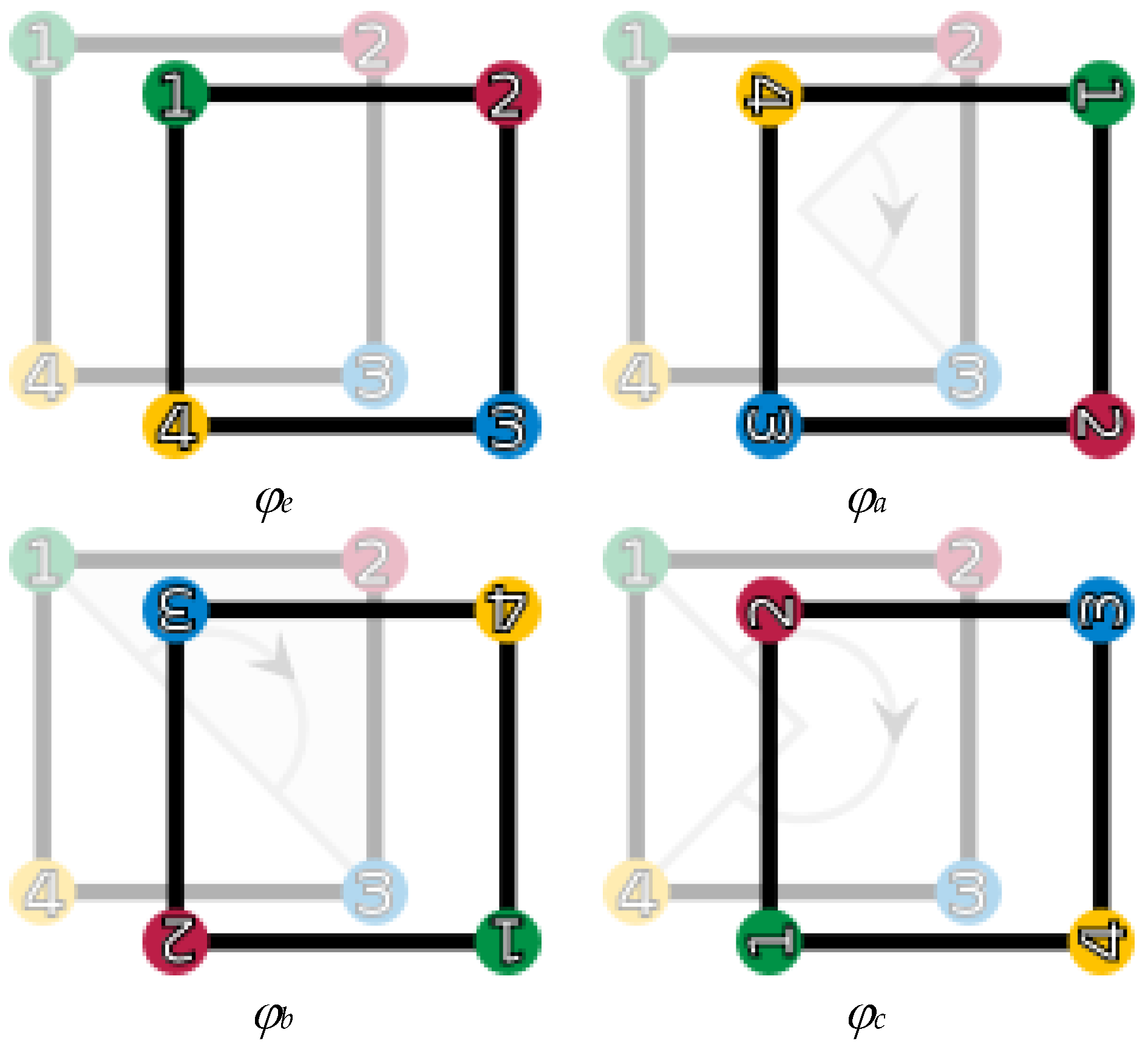
Example 1. Let us consider the rotation transformations of a square. A square is rotated 90°, 180° and 270° to the right (clockwise) and they are denoted by φa,
φb and φc,
respectively (see Figure 1). There is of course the movement that does nothing, which is denoted by φe. The following figure gives an intuitive description of these transformations. Denote N = {φe,
φa,
φb,
φc}. Obviously, two consecutive rotations have the following results: φeφe =
φe, φaφc =
φcφa =
φe, φbφb =
φe. That is, φe−1 =
φe, φa−1 =
φc, φb−1 =
φb,φc−1 =
φa. Now, we define operations * on N as follows: Then, (N, *) satisfies the left invertive law, and the operation * is as follows in Table 1. We can verify that (N, *) is an AG-Group. Example 2. Let X = {(a, b)|a, b∈R−{0}}, where R represents the set of all real numbers. Define binary operation * as follows: Then,Therefore, [(a, b) * (c, d)] * (e, f) = [(e, f) * (c, d)] * (a, b), that is, the operation * satisfies left invertive law. For any (a, b)X, (1, 1) is the left identity of (a, b) and (1/a, b) is the left inverse of (a, b): Therefore, (X, *) is an AG-Group.
Example 3. Let Y = {(a, b)|a∈R, b = 1 or −1}, where R represents the set of all real numbers. Define binary operation * as follows:Then, Because b, f∈ {1, −1},=, and b/f = f/b. We can get b/df = f/bd. Therefore, [(a, b) * (c, d)] * (e, f) = [(e, f) * (c, d)] * (a, b), that is, the operation * satisfies left invertive law. Moreover, we can verify that (1, 1) is the left identity and (1/a,1) is the left inverse of (a,1), since Therefore, (Y, *) is an AG-group.
Example 4. Let Z = {(a, b)|a∈R, b = 1, −1, i, or −i}, where R represents the set of all real numbers and I represents the imaginary unit. Define binary operation * as follows:Then, Because b, f∈{1, −1, i, −i}, hence=, and b/f = f/b. We can get b/df = f/bd. Therefore, [(a, b) * (c, d)] * (e, f) = [(e, f) * (c, d)] * (a, b), that is, the operation * satisfies left invertive law. Therefore, (Z, *) is an AG-groupoid. However, it is not an AG-group, since That is, (1, 1) and (1, −1) are locally identity, not an identity.
Definition 3. Assume that (N, *) is an AG-group. (N, *) is said to be a weak commutative Abel– Grassmann’s group (AG-group), if one of the following conditions holds:
- (1)
e*x−1 = x−1*e, for all x in N;
- (2)
e*x = x*e, for all x in N; or
- (3)
x−1*y−1 = y−1*x−1, for all x, y in N.
Theorem 1. Let (N, *) be an AG-group. We can get that N is a weak commutative AG-group if and only if it is an Abelian group.
Proof. First, we prove that the Conditions (1)–(3) in Definition 3 are equivalent for an AG-group (N, *).
(1)(2): Suppose thatCondition (1) holds in the AG-group (N, *). For all x in N, by = x, we have e* = *e, that is, e*x = x*e.
(2)(3): Suppose that Condition (2) holds in the AG-group (N, *). For all x, y in N, by Proposition 3, we know that N is an Abelian group, that is, x*y = y*x, it follows that * = *.
(3)(1): Suppose that Condition (3) holds in the AG-group (N, *). Then, for all x in N, we have * = * , that is, e*x−1 = x−1*e.
Now, we prove that an AG-group (N, *) satisfying Condition (2) in Definition 3 is an Abelian group. Through Condition (2), e*a = a*e for any a∈N. Then, a*e = e*a = a, which means that e is right identity. Applying Proposition 3, we get that (N, ∗) is an Abelian group. Moreover, obviously, every Abelian group is a weak commutative AG-group. Therefore, the proof is completed. □
Theorem 2. Assume that (N, *) is an AG-group, we have that (N, *) is quasi-cancellative AG-groupoid, that is, if it satisfies the following conditions, for any x, yN,
- (1)
x = x * y and= y*x imply that x = y; and
- (2)
x = y * x and= x * y imply that x = y.
Proof. (1) Suppose that
x =
x*
y and
=
y*
x, where
x,
yN. Then,
That is,
x =
; it follows that
x*
y =
y*
x. Moreover, we have
Combining Equations (b) and (c), we can get
(2) Suppose that
x=
y*
x and
=
x*
y, where
x,
yN. Then,
That is,
x =
; it follows that
x*
y =
y*
x. Then, we have
Combining Equations (e) and (f), we can get
Hence, (N, *) is quasi-cancellative AG-groupoid. □
Definition 4. Let (N, *) be an AG-group. Then, (N, *) is called to be alternative, if it satisfies one of the following conditions,
- (1)
a*(a*b) = (a*a)*b, ∀a, bN; or
- (2)
a*(b*b) = (a*b)*b, ∀a, bN.
Theorem 3. Let (N, *) be an AG-group. Then, (N, *) is alternative if and only if it is an Abelian group.
Proof. (1) Suppose that (N, *) is an alternative AG-group, then Condition (2) in Definition 4 holds. Then, for any a, bN, a*(b*b) = (a*b)*b. Putting b = e and applying left invertive law, we get that a*e = a*(e*e) = (a*e)*e = (e*e)*a = e*a = a; by Proposition 3, we know that (N, *) is an Abelian group.
(2) Suppose that (
N, *) is an alternative AG-group, then Condition (1) in Definition 4 holds. For any
a,
bN, it satisfies
a*(
a*
b) = (
a*
a)*
b. Putting
b =
e, we have (
a*
a)*
e =
a*(
a*
e). According to the arbitrariness of a, we can get that
Let b*a = e, using Condition (1) in Definition 4, (a*a)*b = a*(a*b). It follows that (a*a)*b = ((a*e)*a)*b.
Applying Proposition (3), we know that (N, *) is an Abelian group.
Conversely, it is obvious that every Abelian group is an alternative AG-group. Therefore, the proof is completed. □
Theorem 4. Let (N, *) be an AG-group. DenoteThen, - (1)
U(N) is sub-algebra of N.
- (2)
U(N) is maximal subgroup of N with identity e.
Proof. (1) Obviously, eU(N), that is, U(N) is not empty. Suppose x, yU(N), then x*e = x and y*e = y. Thus, x*y = (x*e)*(y*e) = (x*y)*eU(N). This means that U(N) is a subalgebra of N.
(2) For any
xU(
N), that is,
x*
e =
x. Assume that y is the left inverse of
x in
N, then
y*
x =
e. Thus,
It follows that yU(N). Therefore, U(N) is a group, and it is a subgroup of N with identity e. If M is a subgroup of N with identity e, and U(N)M, then M is an Abelian group (by Proposition (3)) and satisfies x*e = e*x = x, for any xM. Thus, MU(N), it follows that M = U(N). Therefore, U(N) is maximal subgroup of N with identity e. □
Theorem 5. Let (N, *) be an AG-group. Denote P(N) = {xN|aN, s.t x = a*a}. Then
- (1)
P(N) is the subalgebra of N;
- (2)
f is a homomorphism mapping from N to P(N), where f: N→P(N), f(x)=x*x∈P(N).
Proof. (1) Obviously, eP(N), that is, P(N) is not empty. Suppose x, yP(N) and a, bN. Then, a*a = x and b*b = y. Thus, x*y = (a*a)*(b*b) = (a*b)*(a*b)P(N). This means that P(N) is a subalgebra of N.
(2) For any
xN, we have
Therefore, f is a homomorphism mapping from N to P(N). □
4. Involution AG-Groups and Generalized Involution AG-Groups
In this section, we discuss two special classes of AG-groups, that is, involution AG-groups and generalized involution AG-groups. Some research into the involutivity in AG-groupoids is presented in [
16,
17] as the foundation, and further results are given in this section, especially the close relationship between these algebraic structures and commutative groups (Abelian groups), and their structural characteristics.
Definition 5. Let (N, *) be an AG-group. If (N, *) satisfies a*a = e, for any aN, then (N, *) is called an involution AG-Group.
We can verify that (N, *) in Example 1 is an involution AG-Group.
Example 5. Denote N = {a, b, c, d}, define operations * on N as shown in Table 1. We can verify that (N, *) is an involution AG-group (Table 2). Example 6. Let (G, +) be an Abelian group. Define operations * on G as follows:where (−x) is the inverse of x in G. Then, (G, *) is an involution AG-group. Denote (G, *) by der (G, +) (see [15]), and call it derived AG-group by Abelian group (G, +). Theorem 6. Let (N, *) be an AG-group. Then, (N, *) is an involution AG-Group if and only if it satisfies one of the following conditions:
- (1)
P(N) = {e}, where P(N) is defined as Theorem 5.
- (2)
(x*x)*x = x for any x∈N.
Proof. Obviously, (N, *) is an involution AG-group if and only if P(N) = {e}.
If (
N, *) is an involution AG-group, then apply Definition 5, for any
xN,
Conversely, if (
N, *) satisfies the Condition (2), then for any
xN,
This means that (x*x) is an idempotent element. Using Proposition 4, we have x*x = e. Thus, (N, *) is an involution AG-group. □
Theorem 7. Let (N, *) be an involution AG-group. Then, (N,) = ret (N, *) defined in Proposition 6 is an Abelian group, and the derived AG-group der (N, ) by ret (N, *) (see Example 5) is equal to (N, *), that is, Proof. (1) By Proposition 6 and Definition 5, ∀
x,
y,
zN, we can get that
This means that (
N,
) = ret(
N, *) is an Abelian group.
(2) For any
x,
y∈der(ret(
N, *)) = der(
N,
) = (
N, •),
That is, der(ret(N, *)) = (N, •)= (N, *). □
Definition 6. Let (N, *) be an AG-group. Then, (N, *) is called a generalized involution AG-group if it satisfies: for any xN, (x*x)*(x*x) = e.
Obviously, every involution AG-group is a generalized involution AG-group. The inverse is not true, see the following example.
Example 7. Denote N = {e, a, b, c}, and define the operations * on N as shown in Table 3. We can verify that (N, *) is a generalized involution AG-group, but it is not an involution AG-group. Theorem 8. Let (N, *) be a generalized involution AG-group. Define binary relationon N as follows:Then, - (1)
is an equvalent relation on N, and we denote the equivalent class contained x by.
- (2)
The equivalent class contained e byis an involution sub-AG-group.
- (3)
For any x, y, zN, xy implies x*zy*z and z*xz*y.
- (4)
The quotient (N/, *) is an involution AG-group.
Proof. (1) For any aN, we have a*a = a*a, thus aa.
If ab, then a*a = b*b; it is obvious that ba.
If ab and bc, then a*a = b*b and b*b = c*c; it is obvious that a*a = c*c, that is, ac.
Therefore, is an equivalent relation on N.
(2) ∀
x,
y, we have
x*
x =
y*
y =
e*
e =
e, thus
This means that is a subalgebra of N. Thus, is an involution sub-AG-group of N.
(3) Assume that
xy, then
x*
x =
y*
y. Thus,
It follows that x*zy*z and z*xz*y.
(4) By (3), we know that (
N/
, *) is an AG-group. Moreover, for any
Then,
From this, we have
x∈
,
*
. Hence,
*
. That is,
*
. Therefore, (
N/
, *) is an involution AG-group. □
Theorem 9. Let (N, *) be an AG-group, denoteThen, I(N) and GI(N) are sub-algebra of N. I(N) is an involution AG-group and GI(N) is a generalized involution AG-group. Proof. (1) It is obvious that eI(N). For any x, yI(X), we have x*x = e and y*y = e. By medial law, (x*y)*(x*y) = (x*x)*(y*y) = e*e = e. Hence, I(N) is a sub-algebra of N and I(N) is an involution AG-group.
(2) Obviously,
eGI(
N). Assume that
x,
yGI(
X), then
It follows that
x*
yGI(
N), and
GI(
N) is a subalgebra of
N. Moreover, from ((
x*
x)*
x)*
x = (
x*
x)*(
x*
x) =
e, we get that
a = (
x*
x)*
x is the left inverse of
x, and
That is, a = (x*x)*xGI(N). It follows that GI(N) is an AG-group. By the definition of GI(N), we get that GI(N) is a generalized involution AG-group. □
5. Filter of AG-Groups and Homomorphism Theorems
Definition 7. Let (N, *) be an AG-group. A non-empty subset F of N is called a filter of N if, for all x, yN, F satisfies the following properties,
- (1)
eF;
- (2)
x*xF; and
- (3)
xF and x*yF imply that yF.
If F is a filter and subalgebra of N, then F will be called a closed filter of N.
Theorem 10. Let (N, *) be a generalized involution AG-group, I(N) = {xN| e=x*x} be the involution part of N (see Theorem 9). Then, I(N) is a closed filter of N.
Proof. It is obvious that
eI(
N). ∀
xN, since
then
x*
xI(
N). Moreover, assuming that
xI(
N) and
x*
yI(
N), then
Hence, yI(N), and I(N) is a filter of N. By Theorem 9, I(N) is a subalgebra of N. Therefore, I(N) is a closed filter of N. □
Theorem 11. Let (N, *) be an AG-group and F be a closed filter of N. Define binary relationon N as follows: Then,
- (1)
is an equivalent relation on N.
- (2)
xy and ab imply x*ay*b.
- (3)
f: NN/F is a homomorphism mapping, where N/F = {: xN},denote the equivalent class contained x.
Proof. (1) ∀xN, by Definition 7(2), x*xF. Thus, xx.
Assume xy, then x*yF, y*xF. It follows that yx.
Suppose that
xy and
yz. We have
x*
yF,
y*
xF,
y*
zF and
z*
yF. By medial law and Definition 7,
It follows that xz.
Therefore, is an equivalent relation on N.
(2) Suppose that
xy and
ab. We have
x*
yF,
y*
xF,
a*
bF and
b*
aF. By medial law and Definition 7,
It follows that x*ay*b.
(3) Combining (1) and (2), we can obtain (3).
The proof complete. □
Theorem 12. Let (N, *) be a generalized involution AG-group, I(N) the involution part of N (defined as Theorem 9). Then, f: NN/I(N) is a homomorphism mapping, and N/I(N) is involutive, where N/I(N) = {[x]| xN}, [x] is the equivalent class contained x by closed filter I(N).
Proof. It follows from Theorem 10 and Theorem 11. □
Theorem 13. Let (N, *) be an AG-group, P(N) = {xN|aN, s.t x =a*a} be the power part of N (see Theorem 5). Then, P(N) is a closed filter of N.
Proof. It is obvious that eP(N). For any xN, x*xP(N).
Moreover, assume that
xP(
N) and
x*yP(
N), then there exists
a, bN such that
Denote
c =
a−1*b, where
a−1 is the left inverse of
a in
N. Then,
Thus, yP(N). It follows that P(N) is a filter of N. By Theorem 5, P(N) is a subalgebra of N, therefore, P(N) is a closed filter of N. □
Theorem 14. Let (N, *) be an AG-group, P(N) the power part of N (defined as Theorem 13). Then, f: NN/P(N) is a homomorphism mapping, where N/P(N) = {[x]| xN}, [x] is the equivalent class contained x by closed filter P(N).
Proof. It follows from Theorems 11 and 13. □