Abstract
A steady laminar flow over a vertical stretching sheet with the existence of viscous dissipation, heat source/sink, and magnetic fields has been numerically inspected through a shooting scheme based Runge—Kutta–Fehlberg-integration algorithm. The governing equation and boundary layer balance are expressed and then converted into a nonlinear normal system of differential equations using suitable transformations. The impact of the physical parameters on the dimensionless velocity, temperature, the local Nusselt, and skin friction coefficient are described. Results show good agreement with recent researches. Findings reveal that the Nusselt number at the sheet surface augments, since the Hartmann number, stretching velocity ratio A, and Hartmann number Ha increase. Nevertheless, it reduces with respect to the heat generation/absorption coefficient δ.
1. Introduction
The steady laminar flow and heat transfer of a viscous fluid over a vertical stretching sheet with the existence of heat source/sink and magnetic fields has gained significant interest because of its various usages in engineering procedures like geothermal energy extraction, glass fiber, and plasma studies, etc. Several researchers investigated numerically MHD mixed convective stagnation point flow lengthways a perpendicular widening piece in the presence of a heat source/sink in order to evaluate the impacts of relevant physical parameters especially Hartmann number, Stretching velocity ratio and Biot number on velocity and temperature profiles besides to skin friction and heat transfer properties. Using the Runge-Kutta-Fehlberg methods joined with shooting technique [1,2,3,4]. P.R. Sharma et al. [3] analyzed numerically the impacts of an external magnetic field. Tarek M. A. El-Mistikawy [5] focused on the flow resulting from a linearly stretching sheet with a transverse magnetic field. A. Mohammadeina et al. [1] investigated the impacts of thermal radiation and magnetic field on flow of CuO-water nanofluid past a stretching sheet characterized by forced-convection with a stagnation point with suction/injection. S.S. Ghadikolaei et al. [4] investigated the impact of thermal radiation and Joule heating. Wubshet Ibrahim [2] studied numerically the melting heat transfer and magneto hydrodynamic stagnation point flow of a nanofluid pasta extending piece.
Homotopy technique and shooting method have been widely used in many studies to obtain exact and wide-ranging analytic solution [6,7,8,9]. Arif Hussain et al. [6] focused on the thermal and physical properties of features of MHD hyperbolic refraction of fluid flow over a non-linear widening sheet taking into account convective boundary conditions and viscous dissipation. Tasawar Hayat et al. [9] studied convective stream of ferrofluid owing to nonlinear widening curved slip while M. N. Tufail et al. [7] analyzed numerically the heat transmission ended an unsteady widening sheet for an MHD Casson fluid through viscous dissipation impacts using the homotopy method. M. Y. Malik et al. [10] examined numerically an MHD flow of the Carreau fluid over a stretching sheet with inconstant thickness with the Keller box method. T.M. Agbaje et al. [11] proposed the spectral perturbation technique, which is a sequence development method which spreads the usage of the typical trepidation methods. When joined with the Chebyshev pseudo-spectral process, the SPM can provide higher order approximate mathematical resolutions for intricate increases faced in perturbation patterns. Siti Khuzaimah Soida et al. [12] analyzed numerically a stable MHD flow through a centrifugally widening or lessening floppy using the boundary value problem solver in Matlab software.
The temperature profile behavior was investigated by several researchers. U.S. Mahabaleshwar et al. [13] studied an MHD couple stress liquid caused by a perforated sheet experiencing lined widening with radiation. It was found that the temperature rises as the heat source/sink NI parameter and Chandrasekhar number Q augment [13]. M. Ferdows et al. [14] studied a steady two-dimensional free convective flow of a viscous incompressible fluid lengthways a perpendicular stretching sheet. The temperature profiles increase as the combined effect of porous diffusivity and magnetic field R, perturbation parameter increase. The temperature profile augments with the Eckert number Ec [15] and Biot number [6,13] and the magnetic field parameter, radiation and viscous dissipation [7,8,14,15,16,17]. In fact, when variable thickness exists, the radiative heat transfer and viscous dissipation enhance the nanofluid temperature [18]. When the unsteadiness of the stretching sheet extends, temperature rises [19]. The fluid temperature increases with increasing of Brownian motion, thermophoresis [20,21], temperature ratio [1] and heat source/sink parameter [3]. In the other hand, temperature drops when the Casson fluid parameter augments [7] and when the Prandtl number increases [13,20] and as the power law increases [6]. G.S. Seth et al. [19] reported that temperature is reduced when the stretching sheet is nonlinear. The fluid temperature declines with higher values of velocity ratio parameter, suction/injection parameter [1,16], Hartmann number Ha, Prandtl number Pr, thermal stratification parameter [18] or mixed convection parameter k [3]. Whereas, Kai-Long Hsiao [15] found that the temperature impact is improved in parallel with the rise of Prandtl number.
The impacts of significant factors on the solitary velocity for stretching sheet circumstance were discussed in many studies. Decrease in the velocity profile has been reported verses the increase of the Casson fluid parameter [7], non-linearity restriction, flow comportment index, the magnetic field, power law index and Weissenberg number [1,6,7,8]. However, the impacts of power law index and magnetic field parameter are more significant than nonlinearity parameter and Weissenberg number [6]. The dimensionless velocity is reduced when values of volume fraction and dimensionless velocity slip parameters augment [22]. It declines also when mass concentration parameter and permeability parameter augment [4]. Velocity profile is reduced by the combined effect of porous diffusivity [14], with the increase of Hartmann number and suction/injection parameter [23]. Greater values of suction and stretching parameter m and wall thickness parameter reduce velocity profile while lead to the rise of the volume fraction and porosity parameter [17]. The fluid velocity is improved in parallel with increase of velocity ratio, curvature parameter, electric field parameter and material parameter [4]. M. Ferdows et al. [14] reported that velocity profile is enhanced with the increase of the proportion of the flow velocity constraint to stretching sheet indicator and viscosity ratio. G.S. Seth et al. [24] reported that nanofluid velocity is reduced when the stretching sheet is nonlinear whereas when the unsteadiness of the stretching sheet augments velocity is decreased. M. N. Tufail et al. [7] found that as the unsteadiness parameter growths, the velocity decreases close the sheet and increases distant to the sheet. The higher of the slight order derivative causes the quicker velocity of viscoelastic fluids close the platter [25,26,27,28,29,30,31,32]. The temperature and velocity profile behavior was investigated by several researchers with the effect of heat generation/absorption on MHD flow though rare of them trait the effect of an external magnetic field and heat generation/absorption on mixed convictive flow lengthways a perpendicular extending piece [33,34,35,36,37].
An inclusive analysis of the works about nanofluids is presented by Wang et al. [19,20]. The inactivity point flow of a nanofluid near a stretching sheet has been explored by Khan and Pop [21], Mustafa et al. [22], Nazar et al. [23], and Ibrahim et al. [24]. Nadeem and Haq [29] inspected MHD three-dimensional flow of nanofluids past a shrinking sheet with thermal radiation. They employed Boungiorno model and considered the influences of thermophoresis and Brownian motion on the local Nusselt ad Sherwood numbers.
This study includes a numerically solution of MHD boundary layer flow over a vertical stretching sheet with company of heat sink/ source and magnetic fields effect. The governing equations for the problematic have been clearly described with some appropriate changes and then explained numerically via shooting arrangement based RKFI procedure. In this work the effects of relevant physical indicators essentially Hartmann number, Stretching velocity ratio and Biot number on velocity and temperature distributions in addition to the skin friction and heat transfer properties have been investigated. Comparison of the results with research results [3,26,27,28,29,30] shows a good agreement as shown in Table 1.

Table 1.
Numerical results of Nusselt number—θ(0) for diverse Prandtl number when A = 1, A = 0, Ha = 0, and δ = 0.
2. Problem Description
The present study deals with a viscous incompressible fluid that was analyzed through steady laminar flow two-dimensional condition lengthways on an upright stretching sheet that was positioned in the x track and the y axis is perpendicular to the plan of this sheet.
u is the velocity component in x direction.
is the velocity component in y direction.
Taking into consideration that mutually c then a are positive constants; represents the unrestricted stream velocity, while represents the velocity when there is stretching on the sheet.
When a heat source/sink is present, is an outside magnetic field that is practically perpendicular to the sheet.
The principal equations of continuity, momentum, and energy are written as
where
- is the electrical conductivity,
- is the magnetic permeability,
- is the temperature of free stream,
- g is acceleration due to gravity,
- is the volumetric coefficient of thermal expansion,
- k is the thermal conductivity,
- is the kinematic viscosity, and
- is the temperature of the sheet.
When the superficial is heated b > 0 so that cfr4 whereas for cooled superficial b < 0 and .
The boundary conditions are
The forces will be in equilibrium because of the presence of the hydrostatic and magnetic pressure gradient, as mentioned below
Therefore, the momentum equation turns into
3. Scheme Analysis
The subsequent change and dimensionless quantities are used into equations, while taking into account the mentioned boundary condition (4) within the solution of Equations (1) to (3), Equation (7), obtained as:
Therefore, the equation of continuity is approved.
The momentum and energy equation becomes
where major represents the derivative according to ,
is the Hartmann number,
is mixed convection parameter,
is the local Grashof number,
and , and
represent the factor of heat generation/absorption.
The related boundary circumstances are limited to
where represent the rate of velocity
Also, .
Therefore, the Nusselt number and Skin friction are expressed by
Additionally, respectively, the wall shear stress and the heat flux are illustrated, as below:
It is intricate to get the locked procedure explanations because calculations (8) and (9) are significantly nonlinear. Consequently, schemes are obtained by replacing
Thus, the scheme of calculations becomes
Depending on the next conditions
In order to obtain stage-by-stage integration and scheming, which are determined by relying on MATLAB software; the Runge–Kutta fourth order method with the shooting technique is actually used.
4. Stability Analysis
When there exists more than one solution in any fluid flow problem, the stability of solution is necessary to perform in that problem. In order to perform stability analysis, we adopt the algorithm of Merkin [33], Weidman et al. [36], and Rosca and Pop [37].
Step 1: To convert the governing Equations (2) and (3) of fluid flow in unsteady form, we have
Step 2: To introduce a new non-dimensional time variable , and all other similarity variables are also a function of , can be written as,
Step 3: By applying Equation (14) on Equations (12) and (13), we have
and the related boundary conditions are
Step 4: To check the stability of steady flow solutions will satisfy the basic model by introducing the following functions
Here, , and are small relative to . The unknown eigenvalue is γ, which is to be found out.
Step 5: By putting Equation (18) into Equations (15) and (16) and keeping , we have
Along with boundary conditions
Step 6: To relax one boundary condition into an initial condition, as suggested by Weidman et al. [36] and Harris et al. [34]. In this problem, we relaxed into We have to solve Equation (19) and (20) with boundary and relaxed initial condition in order to find the values of smallest eigenvalue γ.
It is worth mentioning that the negative values of γ indicate the growth of disturbance and the flow becomes unstable. On the other hand, if the values of γ are positive, which means that the flow is stable and shows an initial decay. The values of smallest eigenvalue are given in Table 2, which indicate that only first (second) solution is stable (unstable).

Table 2.
Smallest eigenvalue γ when λ = −0.2, Pr = 1, (for Shrinking surface) and (for Stretching surface).
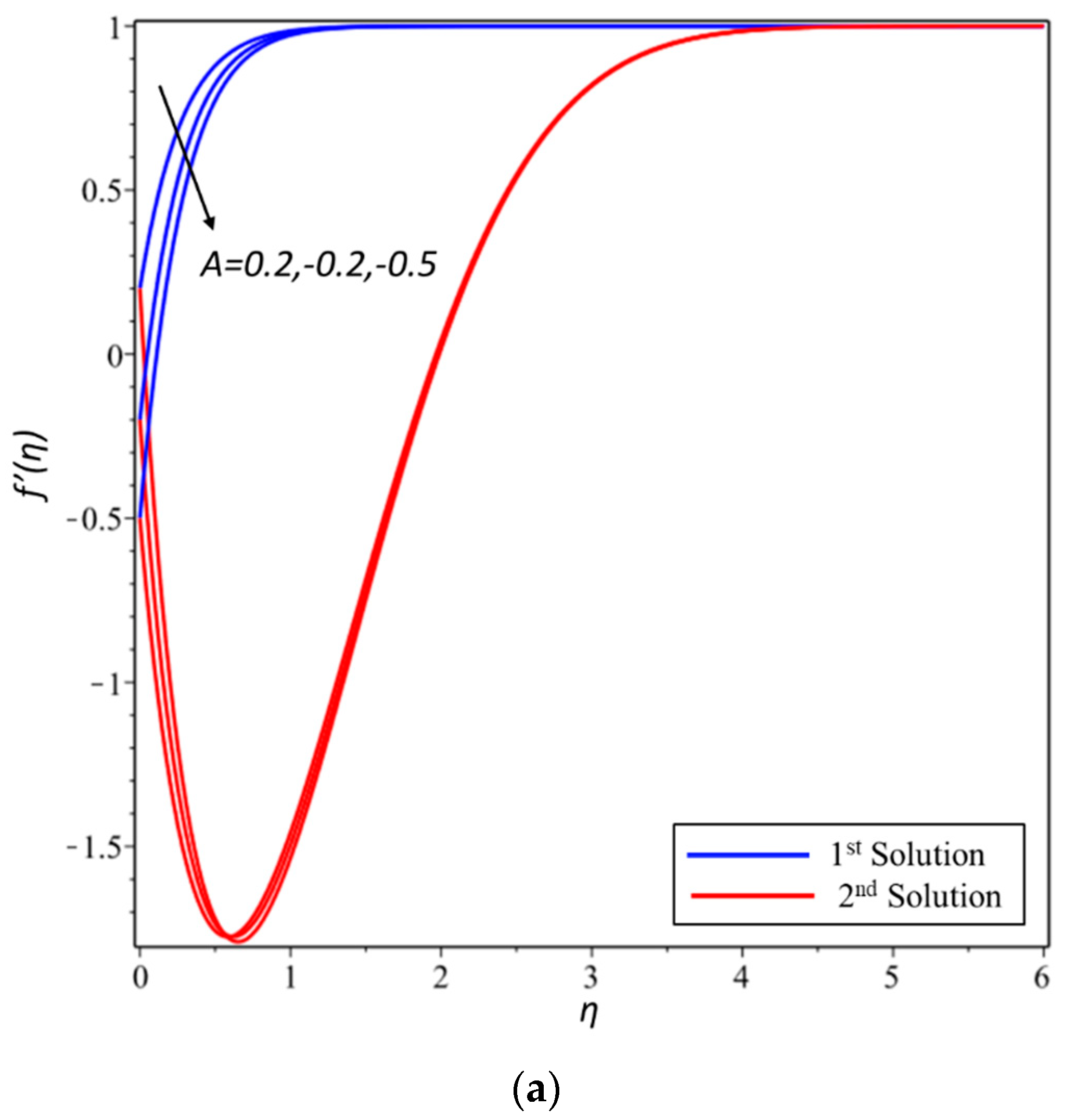
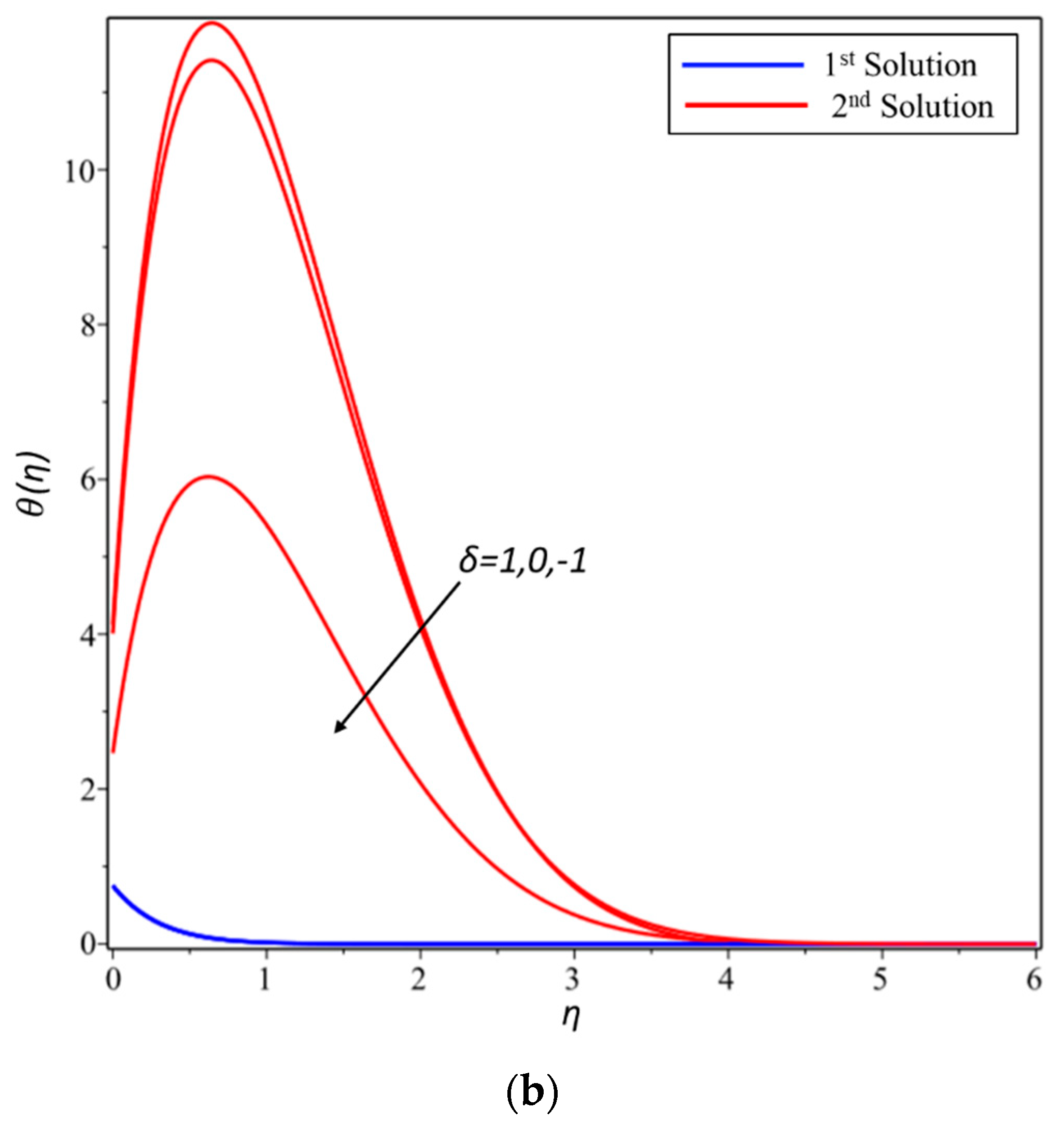
The bvp4c solver function has performed stability analysis. According to Rahman et al. [35], “this collocation formula and the collocation polynomial provides a C1 continuous solution that is fourth order accurate uniformly in [a,b]. Mesh selection and error control are based on the residual of the continuous solution”. As we know, only the first solution is the stable and only the stable solution has physical meaning. In these regards, the various effect of different physical parameters on velocity and temperature profiles have been demonstrated for the first solution only. Finally, from Figure 1a,b, we draw some graphs in order to show the existence of multiple solutions for the opposing flow case.
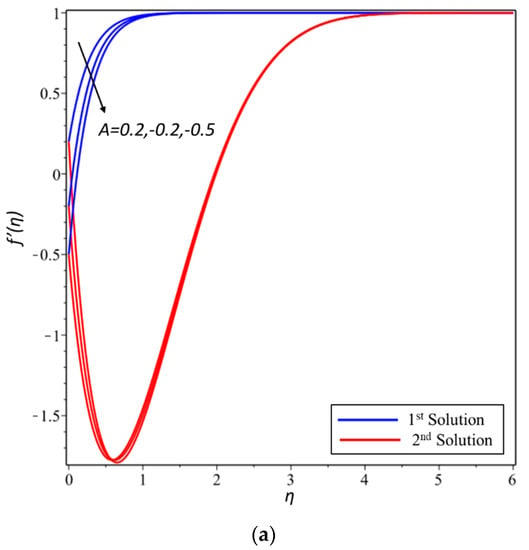
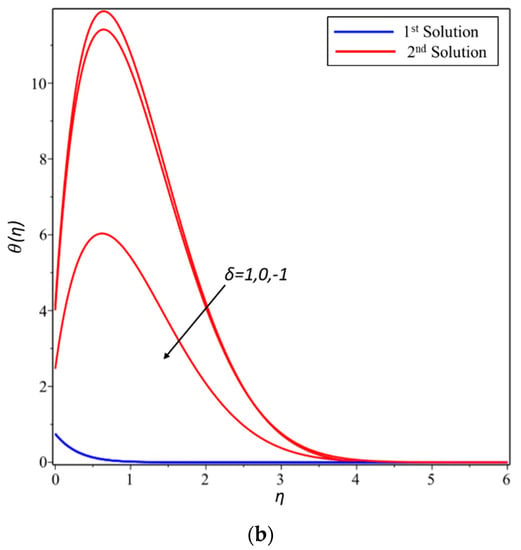
Figure 1.
(a) The existence of multiple solutions for the opposing flow case different parameter A; and, (b) the existence of multiple solutions for the opposing flow case different parameter δ.
5. Results and Discussion
A steady laminar flow above a vertical stretching sheet with the existence of viscous dissipation, heat sink/source, and magnetic fields has been numerically explored by using of RKFI process through shooting scheme. In this work, the effects of pertinent physical parameters are essentially Hartmann number, Stretching velocity ratio, and Biot number on temperature and velocity distributions; also, the skin friction and heat transfer properties have been examined.
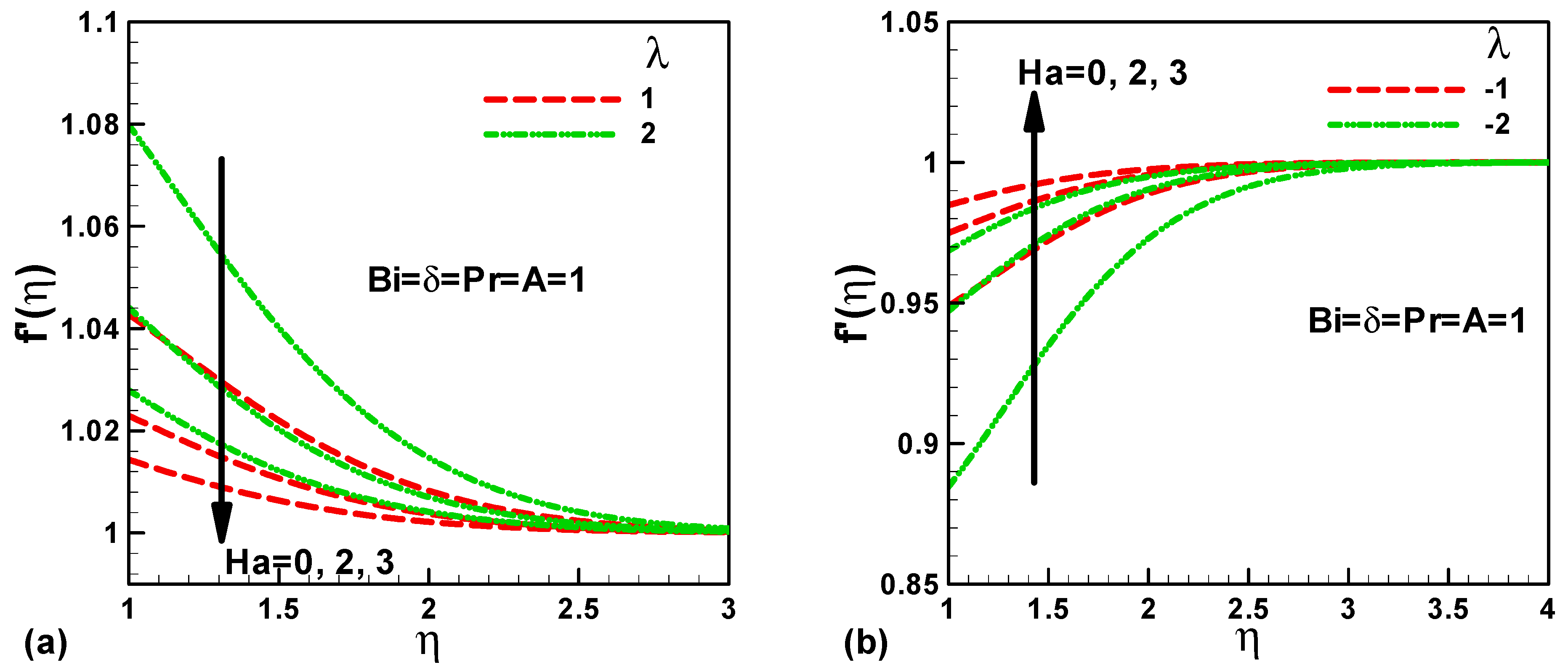
The effect of Hartmann number on dimensionless velocity for mutually opposing and assisting flow are shown in Figure 2a,b respectively, with supplementary parameters are usually the regularly of velocity ratio parameter A = 1, Heat generation/absorption coefficient δ = 1, Prandtl number Pr = 1, and Biot number Bi = 1. It is perceived that, for assisting flow (λ > 0), the dimensionless velocity is the maximum at the superficial of the vertical stretching sheet and it increasingly reduces to the minimum value as it changes to gone after the superficial, while for opposing flow (λ < 0), the dimensionless velocity is the lowest at the surface of the vertical stretching sheet and gradually increases to the maximum value , as it changes away from the superficial, this effect is mathematically obvious in Equation (10). It is additional observed that the velocity profile decreases with the Hartmann number for the assisting flow, whereas, it increases with the Hartmann number for the opposing flow. Consequently, the hydrodynamic boundary layer thickness also depends upon Ha. It is well known that the Hartmann number represents the proportion of electromagnetic force to the viscous force, thus, in the case of assisting flow, increasing the Hartmann number means that electromagnetic force was enhanced when compared to viscous force, which in turn Lorentz force augments, then opposes the flow, and then reduces the velocity profile. Nonetheless, in the situation of opposing flow, there is a reverse effect of the Hartmann number on dimensionless velocity. It should be pointed out that, in the case of assisting flow, (λ > 0) means the heating of the fluid, therefore the thermal buoyancy forces were enhanced. It can be interpreted on this fact that the highest value of dimensionless velocity is near the stretched surface; however, for opposing flow (λ > 0), which means that the fluid is consequently cooled; the thermal buoyancy forces decreases and then we realize the lowest value of dimensionless velocity near the stretched surface. It is worthwhile to note that the velocity profile increases with the mixed convection parameter λ for mutually case opposing and assisting flow due to an increasing of the thermal buoyancy forces. It can be seen that, for buoyancy opposed (λ < 0, opposing), the velocity profile will be significantly affected.
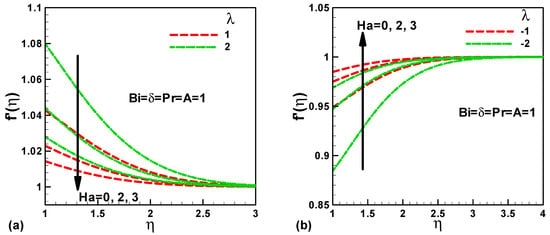
Figure 2.
Variation of dimensionless velocity with Hartmann number for (a) assisting flow and (b) opposing flow.
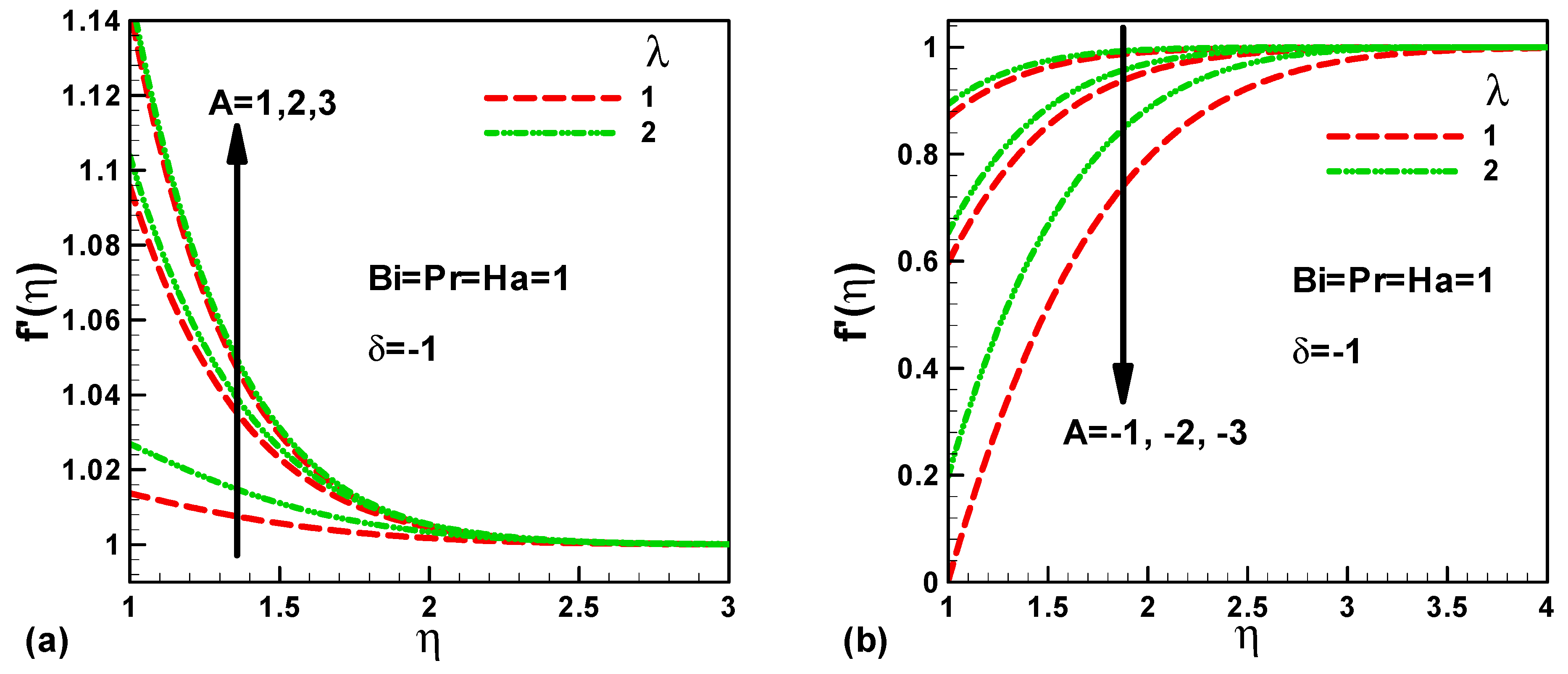
Figure 3a,b, respectively, show the effects of stretching velocity ratio A when stretching in the flow and in the opposite direction, with further parameters sustaining the constant Heat generation/absorption coefficient δ = −1, Prandtl number Pr = 1, Biot number Bi = 1, and Hartmann number Ha = 1. It can be seen that the velocity profile increases with stretching velocity ratio when stretching in the flow direction. Whereas, the velocity profile decreases with stretching velocity ratio when stretching in the opposite direction, this can be attributed to the significant enhancement in pressure on the sheet. Furthermore, it is remarked that the velocity profile augment with mixed convection parameter λ for both stretching in the flow direction and stretching in the opposite direction, as proven in Figure 1. The physical reason behind this is that, by augmenting the mixed convection parameter, the thermal buoyancy forces rise and help to push the flow in y direction, which in turn increases the velocity profile.
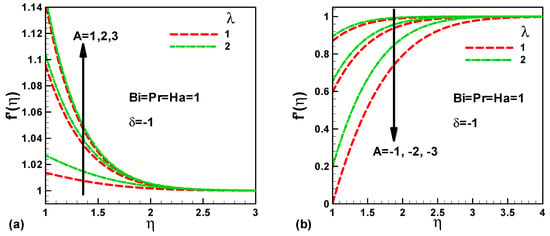
Figure 3.
Variation of dimensionless velocity with stretching velocity ratio when (a) stretching in the flow direction and (b) stretching in the opposite direction.
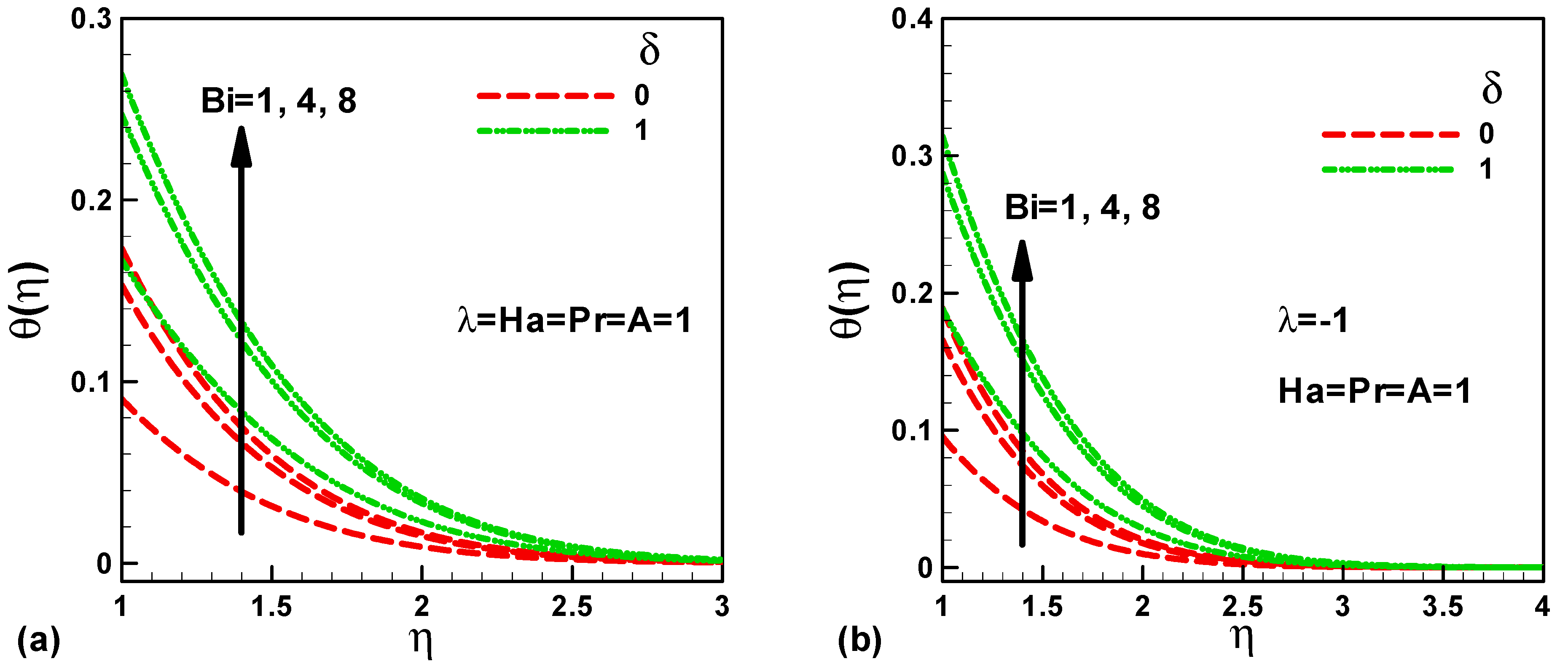
The effects of Biot number in the presence of heat source on the dimensionless temperature for assisting and opposing flow are shown in Figure 4a,b, respectively at Pr = Ha = A = 1. It is clear that the temperature profile is greater at the stretching sheet surface and then exponentially lessens along the streamwise path up to the zero value for both assisting and opposing flow; this effect is proved and designated by the choice of boundary conditions and it is mathematically noticeable in Equation (10). It is worthwhile to note that the dimensionless temperature augment with both Biot number Bi and Heat generation/absorption coefficient δ for both case assisting and opposing flow; therefore, the thermal boundary layer thickness increases. It is well known that the Biot number signifies the proportion of heat convection to heat conduction; therefore increasing the Biot number leads to more heat will be released to the fluid flow, which in turn augments the temperature profile. Similarly, augmenting heat source leads to applying more heat to the fluid flow and it results in enhancing the dimensionless temperature.
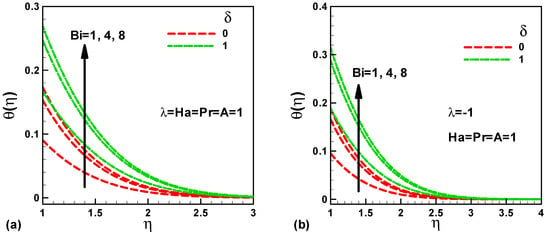
Figure 4.
Variation of dimensionless temperature with Biot number in the presence of heat source for (a) assisting flow and (b) opposing flow.
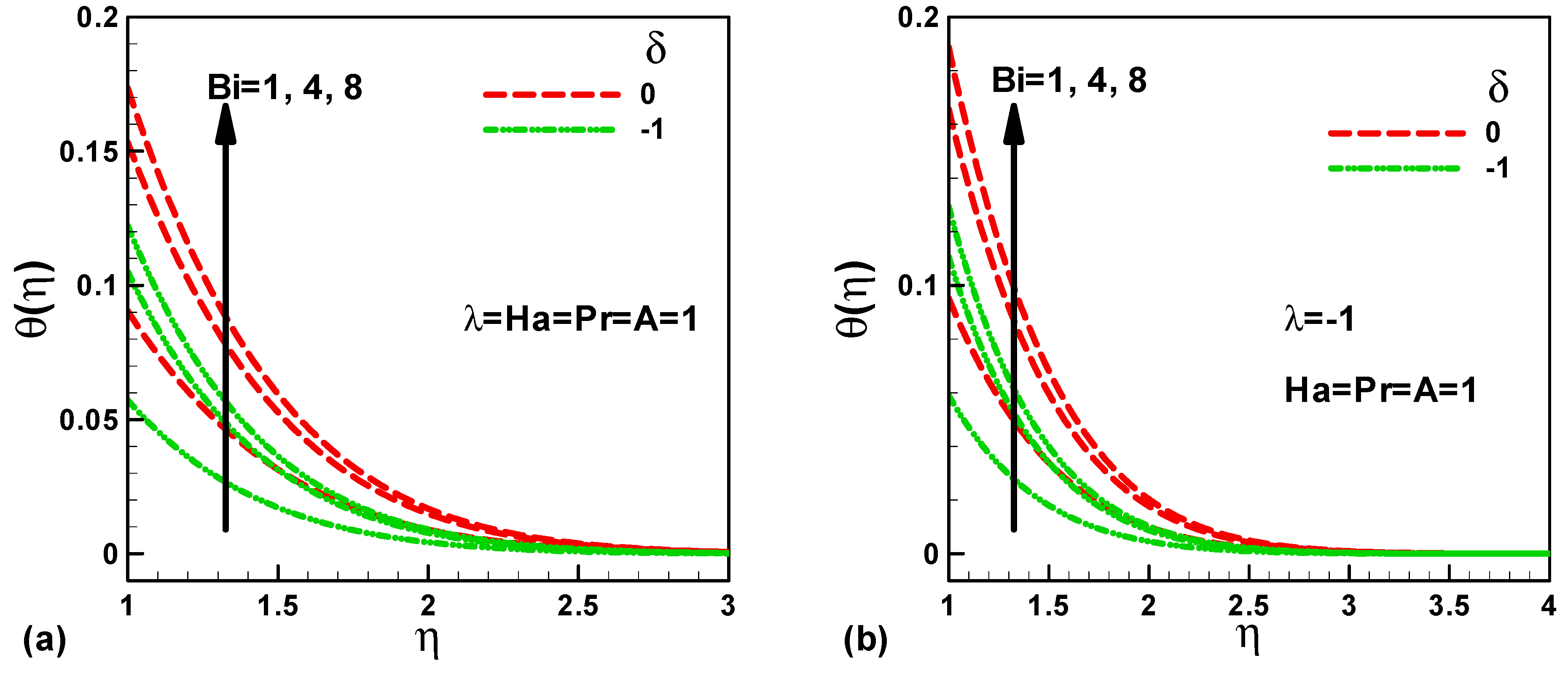
Figure 5a,b, respectively, illustrate the result of Biot number in the company of heat sink on the dimensionless temperature for assisting and opposing flow at Pr = Ha = A = 1. As expected, the temperature profile satisfies the boundary conditions, starting with a higher value at the surface of the sheet and then meaningfully declining to zero value when η increases. Furthermore, it is remarked that dimensionless temperature increases with Biot number, even in the company of heat sink, as shown in Figure 3 in the circumstance of heat basis, so it can be concluded that the temperature profile increase with biot number independent of Heat generation/absorption coefficient δ. It should be pointed out that, for positive values of Heat generation/absorption coefficient, δ acts as a heat source, but for a negative value of Heat generation/absorption coefficient, δ acts as sink source, this signifies that the dimensionless temperature reduced in case of a negative value of δ (heat sink) when compared to a positive value of δ (heat source), as presented in Figure 3. Similarly, the thermal boundary layer thickness decreases.
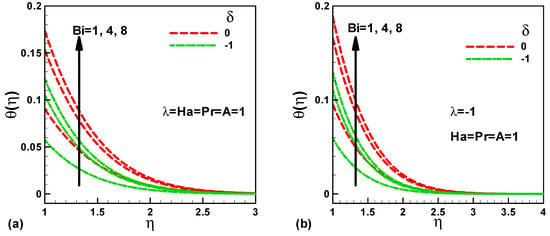
Figure 5.
Variation of dimensionless temperature with Biot number in the presence of heat sink for (a) assisting flow and (b) opposing flow.
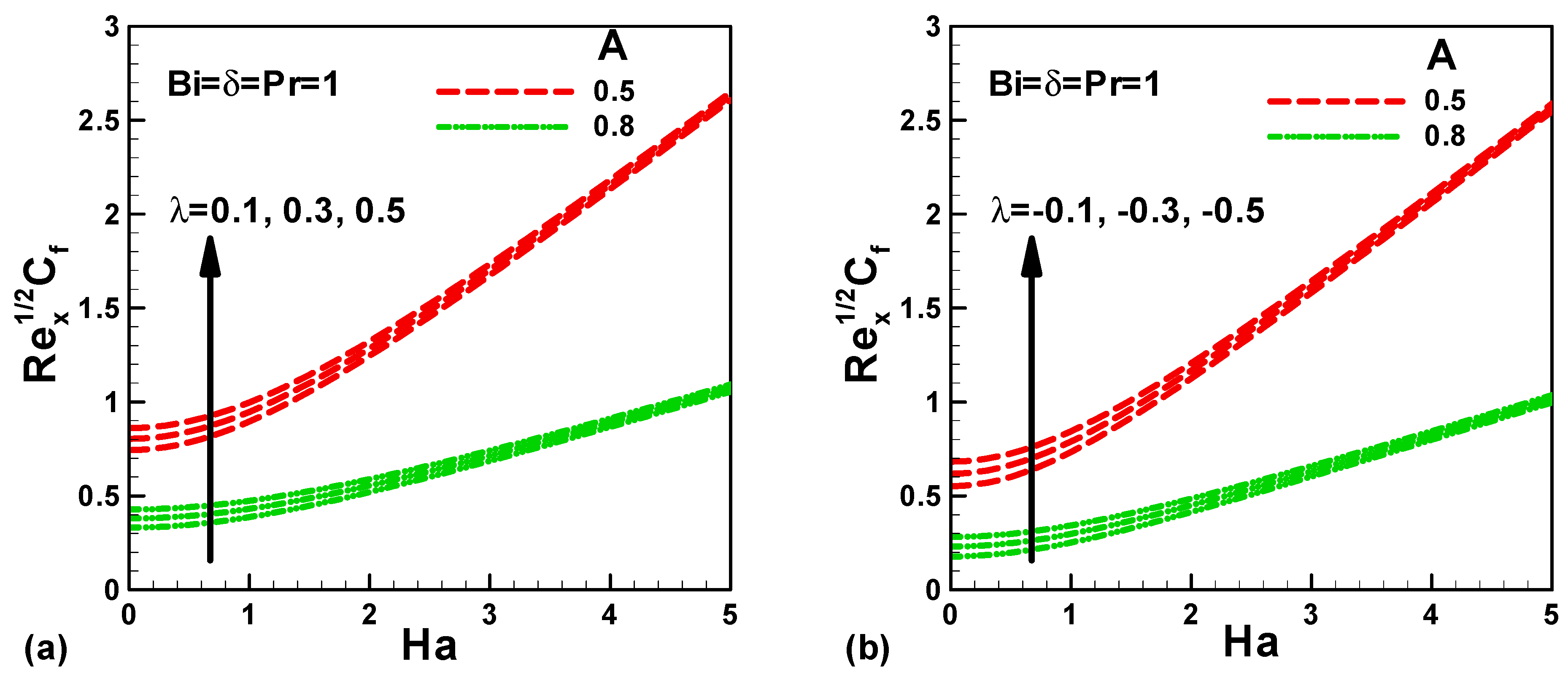
Figure 6a,b, respectively, display the effects of stretching velocity ratio and mixed convection parameter on dimensionless skin friction for both assisting and opposing flow. It is found that the skin friction increases with the mixed convection parameter and Hartmann number Ha, although it drops with the stretching velocity ratio for mutually opposing and assisting flow. This can be attributed to the result of velocity profile in the boundary layer and consequently disturbs the boundary layer thickness, as shown by Figure 1 and Figure 2. On the other hand, the decreasing of skin friction with stretching velocity ratio can be associated to the augmentation of the velocity; therefore, the velocity boundary layer increases. It is well recognized that augmenting velocity means growing the Reynold number which in turn leads to lessening viscous force regarding inertial force, consequently the dropping in viscous force will reduce skin friction. It is valuable to mention that the effect of assisting flows on dimensionless skin friction is slightly more pronounced than that of opposing flow, because the pressure near to the surface is greater than not near to the surface. As observed, the skin friction continually and significantly increases with the Hartmann number, since it represents the ratio of electromagnetic force to the viscous force, therefore the magnetic field will increase and accordingly the Lorentz force will oppose and push the flow to the surface, which in turn augments the skin friction.
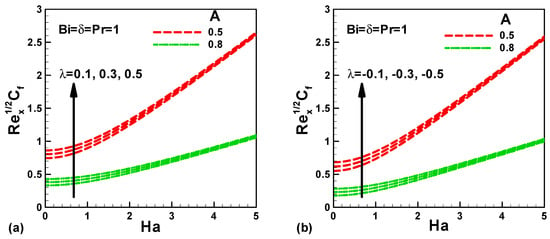
Figure 6.
Variation of dimensionless skin friction with several parameters in the presence of heat source for (a) assisting flow and (b) opposing flow.
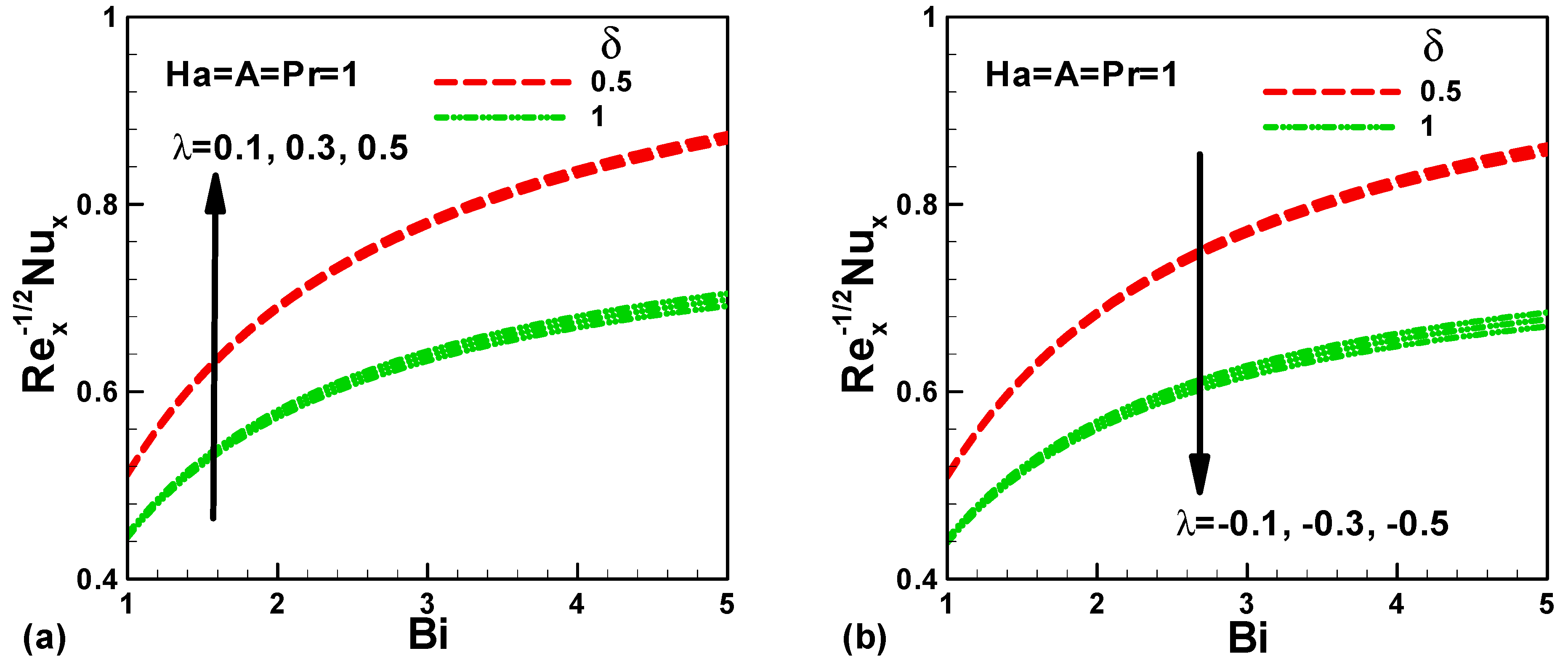
The effects of Biot number Bi, Heat generation/absorption coefficient δ, and mixed convection parameter λ on the dimensionless heat transfer rate for both assisting and opposing flow are illustrated, respectively, in Figure 7a,b. It is indicates that the dimensionless heat transfer rate increase with the Biot number and mixed convection parameter; whereas, it decreases with heat generation/absorption coefficient for both assisting and opposing flow. Physically, this can be attributed to the increase of temperature gradient with respect to the Biot number and mixed convection parameter, as presented by Figure 3 and Figure 4. However, in an unexpected and perplexing result, it can be seen that the dimensionless heat transfer rate decrease with heat generation/absorption coefficient δ, it is well known that Nusselt numbers represent the proportion of convection to conduction heat transfer and in both situation assisting and opposing flow the effect of heat generation/absorption coefficient is more pronounced in conduction more than the convection heat transfer. It is clear that the effect of the mixed convection parameter on the heat transfer rate is slightly perceptible. Finally, the Nusselt number at the sheet surface augments, because the Hartmann number, stretching velocity ratio A, Hartmann number Ha, and mixed convection parameter λ increase. Though, it declines with respect to heat generation/absorption coefficient δ.
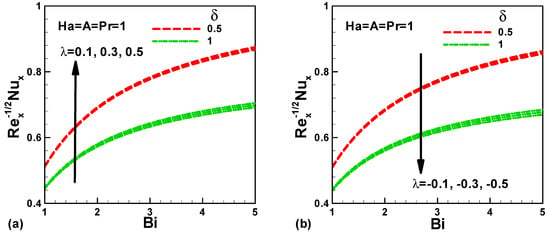
Figure 7.
Variation of dimensionless heat transfer rate with several parameters in the presence of heat source for (a) assisting flow and (b) opposing flow.
6. Conclusions
A steady laminar flow over a vertical stretching sheet with the existence of viscous dissipation, heat source/sink, and magnetic fields has been mathematically explored through shooting arrangement based RKFI procedure. A comparison of the results with research results [3,26,27,28,29] demonstrates good agreement. The influence of relevant involved indicators on temperature and velocity, as well as the Nusselt number and skin friction coefficient are perceived. The main results that are enclosed in this work are concluded, as follows:
- It is perceived that, for assisting flow (λ > 0), the dimensionless velocity is the maximum at the superficial of the vertical stretching sheet and it gradually lessens to the minimum value , as it transfers to gone after the superficial, while for opposing flow (λ < 0), the dimensionless velocity is the lowest at the superficial of the vertical stretching sheet and gradually increases to the maximum value .
- The velocity profile augments with mixed convection parameter λ for both stretching in the flow direction and stretching in the opposite direction.
- The temperature profile is greater at the stretching sheet superficial then exponentially lessens along the streamwise path up to the zero value for both assisting and opposing flow.
- Skin friction increase with a mixed convection parameter and Hartmann number Ha, though it declines by stretching speed ratio for together opposing and assisting flow.
- The effect of mixed convection parameter on the heat transfer rate is slightly perceptible. The Nusselt number at the sheet surface augments, because the Hartmann number, Hartmann number Ha, stretching velocity ratio A, and mixed convection parameter λ increase. Though, it declines according to heat generation/absorption coefficient δ.
Author Contributions
All authors contribute equally in this work in all parts and in all steps.
Acknowledgments
Ibrahim M. Alarifi would like to thank Deanship of Scientific Research at Majmaah University for supporting this work under the Project Number No. 1440-50.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mohammadein, S.A.; Raslan, K.; Abdel-Wahed, M.S.; Abedel-Aal, E.M. KKL-model of MHD CuO-nanofluid flow over a stagnation point stretching sheet with nonlinear thermal radiation and suction/injection. Results Phys. 2018, 10, 194–199. [Google Scholar] [CrossRef]
- Ibrahim, W. Magnetohydrodynamic (MHD) boundary layer stagnation point flow and heat transfer of a nanofluid past a stretching sheet with melting. Propuls. Power Res. 2017, 6, 214–222. [Google Scholar] [CrossRef]
- Sharma, P.R.; Sinha, S.; Yadav, R.S.; Filippov, A.N. MHD mixed convective stagnation point flow along a vertical stretching sheet with heat source/sink. Int. J. Heat Mass Transf. 2018, 117, 780–786. [Google Scholar] [CrossRef]
- SGhadikolaei, S.; Hosseinzadeh, K.H.; Ganji, D.D. MHD raviative boundary layer analysis of micropolar dusty fluid with graphene oxide (Go)-engine oil nanoparticles in a porous medium over a stretching sheet with joule heating effect. Powder Technol. 2018. [Google Scholar] [CrossRef]
- El-Mistikawy, T.M.A. MHD flow due to a linearly stretching sheet with induced magnetic field. Acta Mech. 2016, 227, 3049–3053. [Google Scholar] [CrossRef]
- Hussain, A.; Malik, M.Y.; Salahuddin, T.; Rubab, A.; Khan, M. Effects of viscous dissipation on MHD tangent hyperbolic fluid over a nonlinear stretching sheet with convective boundary conditions. Results Phys. 2017, 7, 3502–3509. [Google Scholar] [CrossRef]
- Tufail, M.N.; Butt, A.S.; Ali, A. Computational modeling of an MHD flow of a non-newtonian fluid over an unsteady stretching sheet with viscous dissipation effects. J. Appl. Mech. Tech. Phys. 2016, 57, 900–907. [Google Scholar] [CrossRef]
- Mabood, F.; Khan, W.A.; Ismail, A.I.M. MHD flow over exponential radiating stretching sheet using homotopy analysis method. J. King Saud Univ. Eng. Sci. 2017, 29, 68–74. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Alsaedi, A.; Ahmad, B. Magnetohydrodynamic (MHD) nonlinear convective flow of Walters-B nanofluid over a nonlinear stretching sheet with variable thickness. Int. J. Heat Mass Transf. 2017, 110, 506–514. [Google Scholar] [CrossRef]
- Malik, M.Y.; Khan, M.; Salahuddin, T. Study of an MHD flow of the carreau fluid flow over a stretching sheet with a variable thickness by using an implicit finite difference scheme. J. Appl. Mech. Tech. Phys. 2017, 58, 1033–1039. [Google Scholar] [CrossRef]
- Agbaje, T.M.; Mondal, S.; Makukula, Z.G.; Motsa, S.S.; Sibanda, P. A new numerical approach to MHD stagnation point flow and heat transfer towards a stretching sheet. Ain Shams Eng. J. 2018, 9, 233–243. [Google Scholar] [CrossRef]
- Soid, S.K.; Ishak, A.; Pop, I. MHD flow and heat transfer over a radially stretching/shrinking disk. Chin. J. Phys. 2018, 56, 58–66. [Google Scholar] [CrossRef]
- Mahabaleshwar, U.S.; Sarris, I.E.; Hill, A.A.; Lorenzini, G.; Pop, I. An MHD couple stress fluid due to a perforated sheet undergoing linear stretching with heat transfer. Int. J. Heat Mass Transf. 2017, 105, 157–167. [Google Scholar] [CrossRef]
- Ferdows, M.; Khalequ, T.S.; Tzirtzilakis, E.E.; Sun, S. Effects of Radiation and Thermal Conductivity on MHD Boundary Layer Flow with Heat Transfer along a Vertical Stretching Sheet in a Porous Medium. J. Eng. Thermophys. 2017, 26, 96–106. [Google Scholar] [CrossRef]
- Hsiao, K.-L. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Thermal stratification effects on MHD radiative flow of nanofluid over nonlinear stretching sheet with variable thickness. J. Comput. Des. Eng. 2018, 5, 232–242. [Google Scholar] [CrossRef]
- Hayat, T.; Rashid, M.; Alsaedi, A. MHD convective flow of magnetite-Fe3O4 nanoparticles by curved stretching sheet. Results Phys. 2017, 7, 3107–3115. [Google Scholar] [CrossRef]
- Daniel, Y.S.; Aziz, Z.A.; Ismail, Z.; Salah, F. Thermal radiation on unsteady electrical MHD flow of nanofluid over stretching sheet with chemical reaction. J. King Saud Univ. Sci. 2017, in press. [Google Scholar] [CrossRef]
- Seth, G.S.; Singha, A.K.; Mandal, M.S.; Banerjee, A.; Bhattacharyya, K. MHD stagnation-point flow and heat transfer past a non-isothermal shrinking/stretching sheet in porous medium with heat sink or source effect. Int. J. Mech. Sci. 2017, 134, 98–111. [Google Scholar] [CrossRef]
- Khan, M.; Hussain, A.; Malik, M.Y.; Salahuddin, T.; Khan, F. Boundary layer flow of MHD tangent hyperbolic nanofluid over a stretching sheet: A numerical investigation. Results Phys. 2017, 7, 2837–2844. [Google Scholar] [CrossRef]
- Madhu, M.; Kishan, N. MHD boundary-layer flow of a non-newtonian nanofluid past a stretching sheet with a heat source/sink. J. Appl. Mech. Tech. Phys. 2016, 57, 908–915. [Google Scholar] [CrossRef]
- Babu, M.J.; Sandeep, N. Three-dimensional MHD slip flow of nanofluids over a slendering stretching sheet with thermophoresis and Brownian motion effects. Adv. Powder Technol. 2016, 27, 2039–2050. [Google Scholar] [CrossRef]
- Khan, I.; Malik, M.Y.; Hussain, A.; Salahuddin, T. Effect of homogenous-heterogeneous reactions on MHD Prandtl fluid flow over a stretching sheet. Results Phys. 2017, 7, 4226–4231. [Google Scholar] [CrossRef]
- Seth, G.S.; Mishra, M.K. Analysis of transient flow of MHD nanofluid past a non-linear stretching sheet considering Navier’s slip boundary condition. Adv. Powder Technol. 2017, 28, 375–384. [Google Scholar] [CrossRef]
- Chen, X.; Ye, Y.; Zhang, X.; Zheng, L. Lie-group similarity solution and analysis for fractional viscoelastic MHD fluid over a stretching sheet. Comput. Math. Appl. 2018, 75, 3002–3011. [Google Scholar] [CrossRef]
- Ramchandran, N.; Chen, T.S.; Armaly, B.F. Mixed convection in stagnation flows adjacent to vertical surfaces. J. Heat Transf. 1988, 110, 373–377. [Google Scholar] [CrossRef]
- Lok, Y.Y.; Amin, N.; Pop, I. Unsteady mixed convection flow of a micropolar fluid near the stagnation point on a vertical surface. Int. J. Therm. Sci. 2006, 45, 1149–1152. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Dual solutions in mixed convection flow near a stagnation point on a vertical porous plate. Int. J. Therm. Sci. 2008, 47, 417–422. [Google Scholar] [CrossRef]
- Ali, F.M.; Nazar, R.; Arifin, N.M.; Pop, I. Mixed convection stagnation point flow on vertical stretching sheet with external magnetic field. Appl. Math. Mech. Engl. Ed. 2014, 35, 155–166. [Google Scholar] [CrossRef]
- Hassanien, I.A.; Gorla, R. Nonsimilar Solutions for Natural Convection in Micropolar Fluids on a Vertical Plate. Int. J. Fluid Mech. Res. 2003, 30, 4–14. [Google Scholar] [CrossRef]
- Li, J.; Zheng, L.; Liu, L. MHD viscoelastic flow and heat transfer over a vertical stretching sheet with Cattaneo-Christov heat flux effects. J. Mol. Liq. 2016, 221, 19–25. [Google Scholar] [CrossRef]
- Freidoonimehr, N.; Rahimi, A.B. Exact-solution of entropy generation for MHD nanofluid flow induced by a stretching/shrinking sheet with transpiration: Dual solution. Adv. Powder Technol. 2017, 28, 671–685. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Rahman, M.M.; Roşca, A.V.; Pop, I. Boundary layer flow of a nanofluid past a permeable exponentially shrinking/stretching surface with second order slip using Buongiorno’s model. Int. J. Heat Mass Transf. 2014, 77, 1133–1143. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Roşca, A.V.; Pop, I. Flow and heat transfer over a vertical permeable stretching/shrinking sheet with a second order slip. Int. J. Heat Mass Transf. 2013, 60, 355–364. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).